Renormalization

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Renormalization 

Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian.

For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in this example, mathematically replaces the initially postulated mass and charge of an electron with the experimentally observed mass and charge. Mathematics and experiments prove that positrons and more massive particles like protons exhibit precisely the same observed charge as the electron – even in the presence of much stronger interactions and more intense clouds of virtual particles.

Renormalization specifies relationships between parameters in the theory when parameters describing large distance scales differ from parameters describing small distance scales. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in further infinities. When describing spacetime as a continuum, certain statistical and quantum mechanical constructions are not well-defined. To define them, or make them unambiguous, a continuum limit must carefully remove "construction scaffolding" of lattices at various scales. Renormalization procedures are based on the requirement that certain physical quantities (such as the mass and charge of an electron) equal observed (experimental) values. That is, the experimental value of the physical quantity yields practical applications, but due to their empirical nature the observed measurement represents areas of quantum field theory that require deeper derivation from theoretical bases.

Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics.

Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Nikolay Bogolyubov and Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through "effective" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each. Wilson clarified which variables of a system are crucial and which are redundant.

Renormalization is distinct from regularization, another technique to control infinities by assuming the existence of new unknown physics at new scales.

Self-interactions in classical physics

Figure 1. Renormalization in quantum electrodynamics: The simple electron/photon interaction that determines the electron's charge at one renormalization point is revealed to consist of more complicated interactions at another.

The problem of infinities first arose in the classical electrodynamics of point particles in the 19th and early 20th century.

The mass of a charged particle should include the mass–energy in its electrostatic field (electromagnetic mass). Assume that the particle is a charged spherical shell of radius r_e. The mass–energy in the field is

${\displaystyle m_{\text{em}}=\int {\frac {1}{2}}E^{2}\,dV=\int _{r_{\text{e}}}^{\infty }{\frac {1}{2}}\left({\frac {q}{4\pi r^{2}}}\right)^{2}4\pi r^{2}\,dr={\frac {q^{2}}{8\pi r_{\text{e}}}},}$

which becomes infinite as r_e → 0. This implies that the point particle would have infinite inertia and thus cannot be accelerated. Incidentally, the value of r_e that makes ${\displaystyle m_{\text{em}}}$ equal to the electron mass is called the classical electron radius, which (setting ${\displaystyle q=e}$ and restoring factors of c and ${\displaystyle \varepsilon _{0}}$) turns out to be

${\displaystyle r_{\text{e}}={\frac {e^{2}}{4\pi \varepsilon _{0}m_{\text{e}}c^{2}}}=\alpha {\frac {\hbar }{m_{\text{e}}c}}\approx 2.8\times 10^{-15}~{\text{m}},}$

where ${\displaystyle \alpha \approx 1/137}$ is the fine-structure constant, and ${\displaystyle \hbar /(m_{\text{e}}c)}$ is the reduced Compton wavelength of the electron.

Renormalization: The total effective mass of a spherical charged particle includes the actual bare mass of the spherical shell (in addition to the mass mentioned above associated with its electric field). If the shell's bare mass is allowed to be negative, it might be possible to take a consistent point limit. This was called renormalization, and Lorentz and Abraham attempted to develop a classical theory of the electron this way. This early work was the inspiration for later attempts at regularization and renormalization in quantum field theory.

(See also regularization (physics) for an alternative way to remove infinities from this classical problem, assuming new physics exists at small scales.)

When calculating the electromagnetic interactions of charged particles, it is tempting to ignore the back-reaction of a particle's own field on itself. (Analogous to the back-EMF of circuit analysis.) But this back-reaction is necessary to explain the friction on charged particles when they emit radiation. If the electron is assumed to be a point, the value of the back-reaction diverges, for the same reason that the mass diverges, because the field is inverse-square.

The Abraham–Lorentz theory had a noncausal "pre-acceleration". Sometimes an electron would start moving before the force is applied. This is a sign that the point limit is inconsistent.

The trouble was worse in classical field theory than in quantum field theory, because in quantum field theory a charged particle experiences Zitterbewegung due to interference with virtual particle–antiparticle pairs, thus effectively smearing out the charge over a region comparable to the Compton wavelength. In quantum electrodynamics at small coupling, the electromagnetic mass only diverges as the logarithm of the radius of the particle.

Divergences in quantum electrodynamics

(a) Vacuum polarization, a.k.a. charge screening. This loop has a logarithmic ultraviolet divergence.

 

(b) Self-energy diagram in QED

 

(c) Example of a “penguin” diagram

When developing quantum electrodynamics in the 1930s, Max Born, Werner Heisenberg, Pascual Jordan, and Paul Dirac discovered that in perturbative corrections many integrals were divergent (see The problem of infinities).

One way of describing the perturbation theory corrections' divergences was discovered in 1947–49 by Hans Kramers, Hans Bethe, Julian Schwinger, Richard Feynman, and Shin'ichiro Tomonaga, and systematized by Freeman Dyson in 1949. The divergences appear in radiative corrections involving Feynman diagrams with closed loops of virtual particles in them.

While virtual particles obey conservation of energy and momentum, they can have any energy and momentum, even one that is not allowed by the relativistic energy–momentum relation for the observed mass of that particle (that is, ${\displaystyle E^{2}-p^{2}}$ is not necessarily the squared mass of the particle in that process, e.g. for a photon it could be nonzero). Such a particle is called off-shell. When there is a loop, the momentum of the particles involved in the loop is not uniquely determined by the energies and momenta of incoming and outgoing particles. A variation in the energy of one particle in the loop can be balanced by an equal and opposite change in the energy of another particle in the loop, without affecting the incoming and outgoing particles. Thus many variations are possible. So to find the amplitude for the loop process, one must integrate over all possible combinations of energy and momentum that could travel around the loop.

These integrals are often divergent, that is, they give infinite answers. The divergences that are significant are the "ultraviolet" (UV) ones. An ultraviolet divergence can be described as one that comes from

• the region in the integral where all particles in the loop have large energies and momenta,
• very short wavelengths and high-frequencies fluctuations of the fields, in the path integral for the field,
• very short proper-time between particle emission and absorption, if the loop is thought of as a sum over particle paths.

So these divergences are short-distance, short-time phenomena.

Shown in the pictures at the right margin, there are exactly three one-loop divergent loop diagrams in quantum electrodynamics:

(a) A photon creates a virtual electron–positron pair, which then annihilates. This is a vacuum polarization diagram.

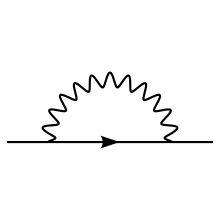
(b) An electron quickly emits and reabsorbs a virtual photon, called a self-energy.

(c) An electron emits a photon, emits a second photon, and reabsorbs the first. This process is shown in the section below in figure 2, and it is called a vertex renormalization. The Feynman diagram for this is also called a “penguin diagram” due to its shape remotely resembling a penguin.

The three divergences correspond to the three parameters in the theory under consideration:

1. The field normalization Z.
2. The mass of the electron.
3. The charge of the electron.

The second class of divergence called an infrared divergence, is due to massless particles, like the photon. Every process involving charged particles emits infinitely many coherent photons of infinite wavelength, and the amplitude for emitting any finite number of photons is zero. For photons, these divergences are well understood. For example, at the 1-loop order, the vertex function has both ultraviolet and infrared divergences. In contrast to the ultraviolet divergence, the infrared divergence does not require the renormalization of a parameter in the theory involved. The infrared divergence of the vertex diagram is removed by including a diagram similar to the vertex diagram with the following important difference: the photon connecting the two legs of the electron is cut and replaced by two on-shell (i.e. real) photons whose wavelengths tend to infinity; this diagram is equivalent to the bremsstrahlung process. This additional diagram must be included because there is no physical way to distinguish a zero-energy photon flowing through a loop as in the vertex diagram and zero-energy photons emitted through bremsstrahlung. From a mathematical point of view, the IR divergences can be regularized by assuming fractional differentiation w.r.t. a parameter, for example:

${\displaystyle \left(p^{2}-a^{2}\right)^{\frac {1}{2}}}$

is well defined at p = a but is UV divergent; if we take the 3⁄2-th fractional derivative with respect to −a², we obtain the IR divergence

${\displaystyle {\frac {1}{p^{2}-a^{2}}},}$

so we can cure IR divergences by turning them into UV divergences.

A loop divergence

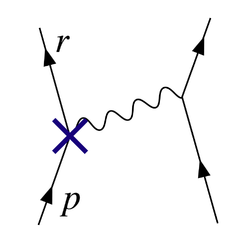
Figure 2. A diagram contributing to electron–electron scattering in QED. The loop has an ultraviolet divergence.

The diagram in Figure 2 shows one of the several one-loop contributions to electron–electron scattering in QED. The electron on the left side of the diagram, represented by the solid line, starts out with 4-momentum p^μ and ends up with 4-momentum r^μ. It emits a virtual photon carrying r^μ − p^μ to transfer energy and momentum to the other electron. But in this diagram, before that happens, it emits another virtual photon carrying 4-momentum q^μ, and it reabsorbs this one after emitting the other virtual photon. Energy and momentum conservation do not determine the 4-momentum q^μ uniquely, so all possibilities contribute equally and we must integrate.

This diagram's amplitude ends up with, among other things, a factor from the loop of

${\displaystyle -ie^{3}\int {\frac {d^{4}q}{(2\pi )^{4}}}\gamma ^{\mu }{\frac {i(\gamma ^{\alpha }(r-q)_{\alpha }+m)}{(r-q)^{2}-m^{2}+i\epsilon }}\gamma ^{\rho }{\frac {i(\gamma ^{\beta }(p-q)_{\beta }+m)}{(p-q)^{2}-m^{2}+i\epsilon }}\gamma ^{\nu }{\frac {-ig_{\mu \nu }}{q^{2}+i\epsilon }}.}$

The various γ^μ factors in this expression are gamma matrices as in the covariant formulation of the Dirac equation; they have to do with the spin of the electron. The factors of e are the electric coupling constant, while the ${\displaystyle i\epsilon }$ provide a heuristic definition of the contour of integration around the poles in the space of momenta. The important part for our purposes is the dependency on q^μ of the three big factors in the integrand, which are from the propagators of the two electron lines and the photon line in the loop.

This has a piece with two powers of q^μ on top that dominates at large values of q^μ (Pokorski 1987, p. 122):

${\displaystyle e^{3}\gamma ^{\mu }\gamma ^{\alpha }\gamma ^{\rho }\gamma ^{\beta }\gamma _{\mu }\int {\frac {d^{4}q}{(2\pi )^{4}}}{\frac {q_{\alpha }q_{\beta }}{(r-q)^{2}(p-q)^{2}q^{2}}}.}$

This integral is divergent and infinite, unless we cut it off at finite energy and momentum in some way.

Similar loop divergences occur in other quantum field theories.

Renormalized and bare quantities

The solution was to realize that the quantities initially appearing in the theory's formulae (such as the formula for the Lagrangian), representing such things as the electron's electric charge and mass, as well as the normalizations of the quantum fields themselves, did not actually correspond to the physical constants measured in the laboratory. As written, they were bare quantities that did not take into account the contribution of virtual-particle loop effects to the physical constants themselves. Among other things, these effects would include the quantum counterpart of the electromagnetic back-reaction that so vexed classical theorists of electromagnetism. In general, these effects would be just as divergent as the amplitudes under consideration in the first place; so finite measured quantities would, in general, imply divergent bare quantities.

To make contact with reality, then, the formulae would have to be rewritten in terms of measurable, renormalized quantities. The charge of the electron, say, would be defined in terms of a quantity measured at a specific kinematic renormalization point or subtraction point (which will generally have a characteristic energy, called the renormalization scale or simply the energy scale). The parts of the Lagrangian left over, involving the remaining portions of the bare quantities, could then be reinterpreted as counterterms, involved in divergent diagrams exactly canceling out the troublesome divergences for other diagrams.

Renormalization in QED

Figure 3. The vertex corresponding to the Z₁ counterterm cancels the divergence in Figure 2.

For example, in the Lagrangian of QED

${\displaystyle {\mathcal {L}}={\bar {\psi }}_{B}\left[i\gamma _{\mu }\left(\partial ^{\mu }+ie_{B}A_{B}^{\mu }\right)-m_{B}\right]\psi _{B}-{\frac {1}{4}}F_{B\mu \nu }F_{B}^{\mu \nu }}$

the fields and coupling constant are really bare quantities, hence the subscript B above. Conventionally the bare quantities are written so that the corresponding Lagrangian terms are multiples of the renormalized ones:

${\displaystyle \left({\bar {\psi }}m\psi \right)_{B}=Z_{0}{\bar {\psi }}m\psi }$

${\displaystyle \left({\bar {\psi }}\left(\partial ^{\mu }+ieA^{\mu }\right)\psi \right)_{B}=Z_{1}{\bar {\psi }}\left(\partial ^{\mu }+ieA^{\mu }\right)\psi }$

${\displaystyle \left(F_{\mu \nu }F^{\mu \nu }\right)_{B}=Z_{3}\,F_{\mu \nu }F^{\mu \nu }.}$

Gauge invariance, via a Ward–Takahashi identity, turns out to imply that we can renormalize the two terms of the covariant derivative piece

${\displaystyle {\bar {\psi }}(\partial +ieA)\psi }$

together (Pokorski 1987, p. 115), which is what happened to Z₂; it is the same as Z₁.

A term in this Lagrangian, for example, the electron–photon interaction pictured in Figure 1, can then be written

${\displaystyle {\mathcal {L}}_{I}=-e{\bar {\psi }}\gamma _{\mu }A^{\mu }\psi -(Z_{1}-1)e{\bar {\psi }}\gamma _{\mu }A^{\mu }\psi }$

The physical constant e, the electron's charge, can then be defined in terms of some specific experiment: we set the renormalization scale equal to the energy characteristic of this experiment, and the first term gives the interaction we see in the laboratory (up to small, finite corrections from loop diagrams, providing such exotica as the high-order corrections to the magnetic moment). The rest is the counterterm. If the theory is renormalizable (see below for more on this), as it is in QED, the divergent parts of loop diagrams can all be decomposed into pieces with three or fewer legs, with an algebraic form that can be canceled out by the second term (or by the similar counterterms that come from Z₀ and Z₃).

The diagram with the Z₁ counterterm's interaction vertex placed as in Figure 3 cancels out the divergence from the loop in Figure 2.

Historically, the splitting of the "bare terms" into the original terms and counterterms came before the renormalization group insight due to Kenneth Wilson.^[20] According to such renormalization group insights, detailed in the next section, this splitting is unnatural and actually unphysical, as all scales of the problem enter in continuous systematic ways.

Running couplings

To minimize the contribution of loop diagrams to a given calculation (and therefore make it easier to extract results), one chooses a renormalization point close to the energies and momenta exchanged in the interaction. However, the renormalization point is not itself a physical quantity: the physical predictions of the theory, calculated to all orders, should in principle be independent of the choice of renormalization point, as long as it is within the domain of application of the theory. Changes in renormalization scale will simply affect how much of a result comes from Feynman diagrams without loops, and how much comes from the remaining finite parts of loop diagrams. One can exploit this fact to calculate the effective variation of physical constants with changes in scale. This variation is encoded by beta-functions, and the general theory of this kind of scale-dependence is known as the renormalization group.

Colloquially, particle physicists often speak of certain physical "constants" as varying with the energy of interaction, though in fact, it is the renormalization scale that is the independent quantity. This running does, however, provide a convenient means of describing changes in the behavior of a field theory under changes in the energies involved in an interaction. For example, since the coupling in quantum chromodynamics becomes small at large energy scales, the theory behaves more like a free theory as the energy exchanged in an interaction becomes large – a phenomenon known as asymptotic freedom. Choosing an increasing energy scale and using the renormalization group makes this clear from simple Feynman diagrams; were this not done, the prediction would be the same, but would arise from complicated high-order cancellations.

For example,

${\displaystyle I=\int _{0}^{a}{\frac {1}{z}}\,dz-\int _{0}^{b}{\frac {1}{z}}\,dz=\ln a-\ln b-\ln 0+\ln 0}$

is ill-defined.

To eliminate the divergence, simply change lower limit of integral into ε_a and ε_b:

${\displaystyle I=\ln a-\ln b-\ln {\varepsilon _{a}}+\ln {\varepsilon _{b}}=\ln {\tfrac {a}{b}}-\ln {\tfrac {\varepsilon _{a}}{\varepsilon _{b}}}}$

Making sure ε_b/ε_a → 1, then I = ln a/b.

Regularization

Since the quantity ∞ − ∞ is ill-defined, in order to make this notion of canceling divergences precise, the divergences first have to be tamed mathematically using the theory of limits, in a process known as regularization (Weinberg, 1995).

An essentially arbitrary modification to the loop integrands, or regulator, can make them drop off faster at high energies and momenta, in such a manner that the integrals converge. A regulator has a characteristic energy scale known as the cutoff; taking this cutoff to infinity (or, equivalently, the corresponding length/time scale to zero) recovers the original integrals.

With the regulator in place, and a finite value for the cutoff, divergent terms in the integrals then turn into finite but cutoff-dependent terms. After canceling out these terms with the contributions from cutoff-dependent counterterms, the cutoff is taken to infinity and finite physical results recovered. If physics on scales we can measure is independent of what happens at the very shortest distance and time scales, then it should be possible to get cutoff-independent results for calculations.

Many different types of regulator are used in quantum field theory calculations, each with its advantages and disadvantages. One of the most popular in modern use is dimensional regularization, invented by Gerardus 't Hooft and Martinus J. G. Veltman, which tames the integrals by carrying them into a space with a fictitious fractional number of dimensions. Another is Pauli–Villars regularization, which adds fictitious particles to the theory with very large masses, such that loop integrands involving the massive particles cancel out the existing loops at large momenta.

Yet another regularization scheme is the lattice regularization, introduced by Kenneth Wilson, which pretends that hyper-cubical lattice constructs our spacetime with fixed grid size. This size is a natural cutoff for the maximal momentum that a particle could possess when propagating on the lattice. And after doing a calculation on several lattices with different grid size, the physical result is extrapolated to grid size 0, or our natural universe. This presupposes the existence of a scaling limit.

A rigorous mathematical approach to renormalization theory is the so-called causal perturbation theory, where ultraviolet divergences are avoided from the start in calculations by performing well-defined mathematical operations only within the framework of distribution theory. In this approach, divergences are replaced by ambiguity: corresponding to a divergent diagram is a term which now has a finite, but undetermined, coefficient. Other principles, such as gauge symmetry, must then be used to reduce or eliminate the ambiguity.

Zeta function regularization

Julian Schwinger discovered a relationship between zeta function regularization and renormalization, using the asymptotic relation:

${\displaystyle I(n,\Lambda )=\int _{0}^{\Lambda }dp\,p^{n}\sim 1+2^{n}+3^{n}+\cdots +\Lambda ^{n}\to \zeta (-n)}$

as the regulator Λ → ∞. Based on this, he considered using the values of ζ(−n) to get finite results. Although he reached inconsistent results, an improved formula studied by Hartle, J. Garcia, and based on the works by E. Elizalde includes the technique of the zeta regularization algorithm

${\displaystyle I(n,\Lambda )={\frac {n}{2}}I(n-1,\Lambda )+\zeta (-n)-\sum _{r=1}^{\infty }{\frac {B_{2r}}{(2r)!}}a_{n,r}(n-2r+1)I(n-2r,\Lambda ),}$

where the B's are the Bernoulli numbers and

${\displaystyle a_{n,r}={\frac {\Gamma (n+1)}{\Gamma (n-2r+2)}}.}$

So every I(m, Λ) can be written as a linear combination of ζ(−1), ζ(−3), ζ(−5), ..., ζ(−m).

Or simply using Abel–Plana formula we have for every divergent integral:

${\displaystyle \zeta (-m,\beta )-{\frac {\beta ^{m}}{2}}-i\int _{0}^{\infty }dt{\frac {(it+\beta )^{m}-(-it+\beta )^{m}}{e^{2\pi t}-1}}=\int _{0}^{\infty }dp\,(p+\beta )^{m}}$

valid when m > 0, Here the zeta function is Hurwitz zeta function and Beta is a positive real number.

The "geometric" analogy is given by, (if we use rectangle method) to evaluate the integral so:

${\displaystyle \int _{0}^{\infty }dx\,(\beta +x)^{m}\approx \sum _{n=0}^{\infty }h^{m+1}\zeta \left(\beta h^{-1},-m\right)}$

Using Hurwitz zeta regularization plus the rectangle method with step h (not to be confused with the Planck constant).

The logarithmic divergent integral has the regularization

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{n+a}}=-\psi (a)+\log(a)}$

since for the Harmonic series ${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+1}}}$ in the limit ${\displaystyle a\to 0}$ we must recover the series ${\displaystyle \sum _{n=0}^{\infty }1=1/2}$

For multi-loop integrals that will depend on several variables ${\displaystyle k_{1},\cdots ,k_{n}}$ we can make a change of variables to polar coordinates and then replace the integral over the angles ${\displaystyle \int d\Omega }$ by a sum so we have only a divergent integral, that will depend on the modulus ${\displaystyle r^{2}=k_{1}^{2}+\cdots +k_{n}^{2}}$ and then we can apply the zeta regularization algorithm, the main idea for multi-loop integrals is to replace the factor ${\displaystyle F(q_{1},\cdots ,q_{n})}$ after a change to hyperspherical coordinates F(r, Ω) so the UV overlapping divergences are encoded in variable r. In order to regularize these integrals one needs a regulator, for the case of multi-loop integrals, these regulator can be taken as

${\displaystyle \left(1+{\sqrt {q}}_{i}q^{i}\right)^{-s}}$

so the multi-loop integral will converge for big enough s using the Zeta regularization we can analytic continue the variable s to the physical limit where s = 0 and then regularize any UV integral, by replacing a divergent integral by a linear combination of divergent series, which can be regularized in terms of the negative values of the Riemann zeta function ζ(−m).

Attitudes and interpretation

The early formulators of QED and other quantum field theories were, as a rule, dissatisfied with this state of affairs. It seemed illegitimate to do something tantamount to subtracting infinities from infinities to get finite answers.

Freeman Dyson argued that these infinities are of a basic nature and cannot be eliminated by any formal mathematical procedures, such as the renormalization method.

Dirac's criticism was the most persistent. As late as 1975, he was saying:

Most physicists are very satisfied with the situation. They say: 'Quantum electrodynamics is a good theory and we do not have to worry about it any more.' I must say that I am very dissatisfied with the situation because this so-called 'good theory' does involve neglecting infinities which appear in its equations, ignoring them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves disregarding a quantity when it is small – not neglecting it just because it is infinitely great and you do not want it!

Another important critic was Feynman. Despite his crucial role in the development of quantum electrodynamics, he wrote the following in 1985:

The shell game that we play is technically called 'renormalization'. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It's surprising that the theory still hasn't been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.

Feynman was concerned that all field theories known in the 1960s had the property that the interactions become infinitely strong at short enough distance scales. This property called a Landau pole, made it plausible that quantum field theories were all inconsistent. In 1974, Gross, Politzer and Wilczek showed that another quantum field theory, quantum chromodynamics, does not have a Landau pole. Feynman, along with most others, accepted that QCD was a fully consistent theory.

The general unease was almost universal in texts up to the 1970s and 1980s. Beginning in the 1970s, however, inspired by work on the renormalization group and effective field theory, and despite the fact that Dirac and various others—all of whom belonged to the older generation—never withdrew their criticisms, attitudes began to change, especially among younger theorists. Kenneth G. Wilson and others demonstrated that the renormalization group is useful in statistical field theory applied to condensed matter physics, where it provides important insights into the behavior of phase transitions. In condensed matter physics, a physical short-distance regulator exists: matter ceases to be continuous on the scale of atoms. Short-distance divergences in condensed matter physics do not present a philosophical problem since the field theory is only an effective, smoothed-out representation of the behavior of matter anyway; there are no infinities since the cutoff is always finite, and it makes perfect sense that the bare quantities are cutoff-dependent.

If QFT holds all the way down past the Planck length (where it might yield to string theory, causal set theory or something different), then there may be no real problem with short-distance divergences in particle physics either; all field theories could simply be effective field theories. In a sense, this approach echoes the older attitude that the divergences in QFT speak of human ignorance about the workings of nature, but also acknowledges that this ignorance can be quantified and that the resulting effective theories remain useful.

Be that as it may, Salam's remark in 1972 seems still relevant

Field-theoretic infinities – first encountered in Lorentz's computation of electron self-mass – have persisted in classical electrodynamics for seventy and in quantum electrodynamics for some thirty-five years. These long years of frustration have left in the subject a curious affection for the infinities and a passionate belief that they are an inevitable part of nature; so much so that even the suggestion of a hope that they may, after all, be circumvented — and finite values for the renormalization constants computed – is considered irrational. Compare Russell's postscript to the third volume of his autobiography The Final Years, 1944–1969 (George Allen and Unwin, Ltd., London 1969), p. 221:

In the modern world, if communities are unhappy, it is often because they have ignorances, habits, beliefs, and passions, which are dearer to them than happiness or even life. I find many men in our dangerous age who seem to be in love with misery and death, and who grow angry when hopes are suggested to them. They think hope is irrational and that, in sitting down to lazy despair, they are merely facing facts.

In QFT, the value of a physical constant, in general, depends on the scale that one chooses as the renormalization point, and it becomes very interesting to examine the renormalization group running of physical constants under changes in the energy scale. The coupling constants in the Standard Model of particle physics vary in different ways with increasing energy scale: the coupling of quantum chromodynamics and the weak isospin coupling of the electroweak force tend to decrease, and the weak hypercharge coupling of the electroweak force tends to increase. At the colossal energy scale of 10¹⁵ GeV (far beyond the reach of our current particle accelerators), they all become approximately the same size (Grotz and Klapdor 1990, p. 254), a major motivation for speculations about grand unified theory. Instead of being only a worrisome problem, renormalization has become an important theoretical tool for studying the behavior of field theories in different regimes.

If a theory featuring renormalization (e.g. QED) can only be sensibly interpreted as an effective field theory, i.e. as an approximation reflecting human ignorance about the workings of nature, then the problem remains of discovering a more accurate theory that does not have these renormalization problems. As Lewis Ryder has put it, "In the Quantum Theory, these [classical] divergences do not disappear; on the contrary, they appear to get worse. And despite the comparative success of renormalisation theory, the feeling remains that there ought to be a more satisfactory way of doing things."

Renormalizability

From this philosophical reassessment, a new concept follows naturally: the notion of renormalizability. Not all theories lend themselves to renormalization in the manner described above, with a finite supply of counterterms and all quantities becoming cutoff-independent at the end of the calculation. If the Lagrangian contains combinations of field operators of high enough dimension in energy units, the counterterms required to cancel all divergences proliferate to infinite number, and, at first glance, the theory would seem to gain an infinite number of free parameters and therefore lose all predictive power, becoming scientifically worthless. Such theories are called nonrenormalizable.

The Standard Model of particle physics contains only renormalizable operators, but the interactions of general relativity become nonrenormalizable operators if one attempts to construct a field theory of quantum gravity in the most straightforward manner (treating the metric in the Einstein–Hilbert Lagrangian as a perturbation about the Minkowski metric), suggesting that perturbation theory is not satisfactory in application to quantum gravity.

However, in an effective field theory, "renormalizability" is, strictly speaking, a misnomer. In nonrenormalizable effective field theory, terms in the Lagrangian do multiply to infinity, but have coefficients suppressed by ever-more-extreme inverse powers of the energy cutoff. If the cutoff is a real, physical quantity—that is, if the theory is only an effective description of physics up to some maximum energy or minimum distance scale—then these additional terms could represent real physical interactions. Assuming that the dimensionless constants in the theory do not get too large, one can group calculations by inverse powers of the cutoff, and extract approximate predictions to finite order in the cutoff that still have a finite number of free parameters. It can even be useful to renormalize these "nonrenormalizable" interactions.

Nonrenormalizable interactions in effective field theories rapidly become weaker as the energy scale becomes much smaller than the cutoff. The classic example is the Fermi theory of the weak nuclear force, a nonrenormalizable effective theory whose cutoff is comparable to the mass of the W particle. This fact may also provide a possible explanation for why almost all of the particle interactions we see are describable by renormalizable theories. It may be that any others that may exist at the GUT or Planck scale simply become too weak to detect in the realm we can observe, with one exception: gravity, whose exceedingly weak interaction is magnified by the presence of the enormous masses of stars and planets.

Renormalization schemes

In actual calculations, the counterterms introduced to cancel the divergences in Feynman diagram calculations beyond tree level must be fixed using a set of renormalisation conditions. The common renormalization schemes in use include:

• Minimal subtraction (MS) scheme and the related modified minimal subtraction (MS-bar) scheme
• On-shell scheme

Besides, there exists a "natural" definition of the renormalized coupling (combined with the photon propagator) as a propagator of dual free bosons, which does not explicitly require introducing the counterterms. 

Renormalization in statistical physics

History

A deeper understanding of the physical meaning and generalization of the renormalization process, which goes beyond the dilatation group of conventional renormalizable theories, came from condensed matter physics. Leo P. Kadanoff's paper in 1966 proposed the "block-spin" renormalization group. The blocking idea is a way to define the components of the theory at large distances as aggregates of components at shorter distances.

This approach covered the conceptual point and was given full computational substance in the extensive important contributions of Kenneth Wilson. The power of Wilson's ideas was demonstrated by a constructive iterative renormalization solution of a long-standing problem, the Kondo problem, in 1974, as well as the preceding seminal developments of his new method in the theory of second-order phase transitions and critical phenomena in 1971. He was awarded the Nobel prize for these decisive contributions in 1982.

Principles

In more technical terms, let us assume that we have a theory described by a certain function ${\displaystyle Z}$ of the state variables ${\displaystyle \{s_{i}\}}$ and a certain set of coupling constants ${\displaystyle \{J_{k}\}}$. This function may be a partition function, an action, a Hamiltonian, etc. It must contain the whole description of the physics of the system.

Now we consider a certain blocking transformation of the state variables ${\displaystyle \{s_{i}\}\to \{{\tilde {s}}_{i}\}}$, the number of ${\displaystyle {\tilde {s}}_{i}}$ must be lower than the number of ${\displaystyle s_{i}}$. Now let us try to rewrite the ${\displaystyle Z}$ function only in terms of the ${\displaystyle {\tilde {s}}_{i}}$. If this is achievable by a certain change in the parameters, ${\displaystyle \{J_{k}\}\to \{{\tilde {J}}_{k}\}}$, then the theory is said to be renormalizable.

The possible macroscopic states of the system, at a large scale, are given by this set of fixed points.

Renormalization group fixed points

The most important information in the RG flow is its fixed points. A fixed point is defined by the vanishing of the beta function associated to the flow. Then, fixed points of the renormalization group are by definition scale invariant. In many cases of physical interest scale invariance enlarges to conformal invariance. One then has a conformal field theory at the fixed point.

The ability of several theories to flow to the same fixed point leads to universality.

If these fixed points correspond to free field theory, the theory is said to exhibit quantum triviality. Numerous fixed points appear in the study of lattice Higgs theories, but the nature of the quantum field theories associated with these remains an open question.

Happiness at work

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Happiness_at_work 

Despite a large body of positive psychological research into the relationship between happiness and productivity, happiness at work has traditionally been seen as a potential by-product of positive outcomes at work, rather than a pathway to business success. Happiness in the workplace is usually dependent on the work environment. During the past two decades, maintaining a level of happiness at work has become more significant and relevant due to the intensification of work caused by economic uncertainty and increase in competition. Nowadays, happiness is viewed by a growing number of scholars and senior executives as one of the major sources of positive outcomes in the workplace. In fact, companies with higher than average employee happiness exhibit better financial performance and customer satisfaction. It is thus beneficial for companies to create and maintain positive work environments and leadership that will contribute to the happiness of their employees.

Happiness is not fundamentally rooted in obtaining sensual pleasures and money, but those factors can influence the well-being of an individual at the workplace. However, extensive research has revealed that freedom and autonomy at a workplace have the most effect on the employee's level of happiness, and other important factors are gaining knowledge and the ability to influence the self's working hours.

Definition

Ryan and Deci offer a definition for happiness in two views: happiness as being hedonic, accompanied with enjoyable feelings and desirable judgements, and happiness as being eudemonic, which involves doing virtuous, moral and meaningful things. Watson et al. claims that the most important approach to explain an individual's experience is in a hedonic tone, which is concerned with the subject's pleasant feelings, satisfying judgments, self-validation and self-actualization. However, some psychologists argue that hedonic happiness is unstable over a long period of time, especially in the absence of eudaimonic well-being. Thus, in order for one to live a happy life one must be concerned with doing virtuous, moral and meaningful things while utilising personal talents and skills.

Antecedents

Organisational culture

Main article: Organisational culture

Organisational culture represents the internal work environment created for operating an organisation. It can also represent how employees are treated by their bosses and peers. An effective organisation should have a culture that takes into account employee's happiness and encourages employee satisfaction. Although each individual has unique talents and personal preferences, the behaviors and beliefs of the people in the same organizations show common properties. This, to some extent, helps organisations to create their own cultural properties.

Jarow concludes that an employee feels satisfied not through comparisons with other peers, but through his/her own happiness and awareness of being in harmony with their colleagues. He uses a term called "carrier" to represent lack of happiness, life in constant tension and never-ending struggle for status.

Employee salary

See also: Well-being contributing factors § Personal finances

There are many reasons that can contribute to happiness at work. However, when individuals are asked with regards to why they work, money is one of the most common answers as it provides people with sustenance, security and privilege. To a large extent, people work to live, and the pecuniary aspect of the work is what sustains the living. Locke, Feren, McCaleb Shaw and Denny argued that no other incentive or motivational technique comes even close to money with respect to its instrumental value.

The income-happiness relationship in life can also be applied in organisational psychology. Some studies have found positively significant relationships between salary level and job satisfaction. Some have suggested that income and happiness at work are positively correlated, and the relationship is stronger for individuals with extrinsic value orientations.

However, others don't believe that salary, in itself, is a very strong factor in job satisfaction. Hundreds of studies and scores of systematic reviews of incentive studies consistently document the ineffectiveness of external rewards. The question regarding this subject has been recently studied by a group of people, including Judge and his colleagues. Their research shows that the intrinsic relationship between job and salary is complex. In their research, they analysed the combined impact of many existing studies to produce a much larger and statistically powerful analysis. By looking at 86 previous studies, they concluded that while it is true to say that money is a driver of employee's happiness, the produced effect is transitory. Judge and his colleagues have reminded us that money may not necessarily make employees happy.

Job security

Main article: Job security

Job security is an important factor to determine whether employees feel happiness at work. Different types of jobs have different levels of job security: in some situations, a position is expected to be offered for a long time, whereas in other jobs an employee may be forced to resign his/ her job. The expectation of the job availability has been related with the job-related well-being and a higher level of job security corresponds to a higher level of job satisfaction alongside a higher level of well-being.

Career development

The option for moving or shifting to alternative roles motivates the employee's participation in the workplace meaning if an employee can see the future potential for a promotion, motivation levels will increase. By contrast, if an organisation does not provide any potential for higher status position in the future, the employee's effectiveness in work will decrease. In addition, the employee may consider whether or not the position would be offered to them in the future. On the other hand, not all of the opportunities for transferring into another activity are aimed to obtain the upward movement. In some cases, they are aimed to prevent the skills obsolescence, provides more future career possibility, as well as directly increasing the skill development.

Job autonomy

Main article: Job control (workplace)

Job autonomy may be defined as the condition of being self-governing or free from excessive external control in the workplace environment. The German philosopher Immanuel Kant believed that autonomy is important to human beings because it is the foundation of human dignity and the source of all morality. Among the models of human growth and development that are centred on autonomy, the most theoretically sophisticated approach has been developed around the concepts of self-regulation and intrinsic motivation. Self-determination theory proposes that 'higher behavioural effectiveness, greater volitional persistence, enhanced subjective well-being, and better assimilation of the individual within his or her social group' result when individuals act from motivations that emanate from the inner self (intrinsic motivation) rather than from sources of external regulation. For self-determination theorists, it is the experience of an external locus of causation (or the belief that one's actions are controlled by external forces) that undermines the most powerful source of natural motivation and that (when chronic) also can lead to stultification, weak self-esteem, anxiety and depression, and alienation. Thus, health and well-being as well as effective performance in social settings are closely related to the experience of autonomy. Hackman and Oldham developed the Job Characteristics Model, a framework that focused attention on autonomy and four other key factors involved in designing enriched work. Work designed to be complex and challenging (characterized by high levels of autonomy, skill variety, identity, significance, and feedback) was theorized to promote high intrinsic motivation, job satisfaction, and overall work performance. Two decades of research in this tradition have shown that job scope or complexity, an additive combination of autonomy and the four other job characteristics: (a) is correlated significantly with more objective ratings of job characteristics; (b) may be reduced to a primary factor consisting of autonomy and skill variety; and (c) has substantial effects on affective and behavioural reactions to work, mostly indirectly through critical psychological states such as experienced responsibility for the outcomes of the work. It is possible to infer from this line of research that the experience of autonomy at work has positive consequences ranging from higher job performance to job satisfaction and enhanced general well-being, which are both related to the concept of happiness at work.

Work–life balance

Main article: Work–life balance

Work–life balance is a state of equilibrium, characterised by a high level of satisfaction, functionality, and effectiveness while successfully performing several tasks simultaneously. The non-work activity is not limited to family life only but also to various occupations and activities of which one's life is composed. Scholars and popular press articles have started promoting the importance of maintaining a work–life balance beginning in the early 1970s and have been increasing ever since. Studies suggest that there is a clear connection between the increase in work related stress to the constant advancements in digital and telecommunications technology. The existence of cell phones and other internet based devices enables access to work related issues in non- working periods, thus, adding more hours and work load. A decrease in the time allocated to non- work related activities and working nonstandard shifts has been proven to have significant negative effects on family and personal life. The immediate effect is a decrease in general well- being as the individual is unable to properly allocate the appropriate amount of time necessary to maintain a balance between the two spheres. Therefore, extensive research has been done on properly managing time as a main strategy of managing stress. It is estimated by the American Psychological Association that the national cost of stress for the US economy is approximately US$500 billion annually.

Some of the physiological effects of stress include cognitive problems (forgetfulness, lack of creativity, inefficient decision making), emotional reactions (mood swings, irritability, depression, lack of motivation), behavioural issues (withdrawal from relationships and social situations, neglecting responsibilities, abuse of drugs and alcohol) and physical symptoms (tiredness, aches and pain, loss of libido).

The condition in which work performance is negatively affected by a high level of stress is termed 'burnout', in which the employee experiences a significant reduction in motivation. According to Vroom's Expectancy Theory, when the outcomes of work performance are offset by the negative impacts on the individual's general well-being, or, are not valued enough by the employee, levels of motivation are low. Time management, prioritising certain tasks and actions according to one's values and beliefs are amongst the suggested course of action for managing stress and maintaining a healthy work–life balance. Psychologists have suggested that when workers have control over their work schedule, they are more capable of balancing work and non- work related activities. The difficulty of distinguishing and balancing between those spheres was defined by sociologist Arlie Russell Hochschild as Time Bind. The reality of constant increase in competition and economic uncertainty frequently forces the employee to compromise the balance for the sake of financial and job security. Therefore, work–life balance policies are created by many businesses and are largely implemented and dealt by line managers and supervisors, rather than at the organizational level as the employee's well-being can be more carefully observed and monitored.

Working relationship

According to Maslow's hierarchy of needs, feeling a sense of belonging to groups is a significant motivation for human beings. Co-workers are an important social group and relationships with them can be a source of pleasure. Three Need theory also suggests that people have a Need for affiliation. Also, person-job fit, the matching between personal abilities and job demand, has important effects on job satisfaction.

Group relationship

Herzberg's Two-Factor theory indicates that co-workers relationship belongs to hygiene needs, which are related to environmental elements. When environmental elements are met, satisfaction will be achieved. Employees tend to be happier and more hardworking when they are in good working environment, for instance, being happy to work in a good working relationship.

Group relationship is important and has effects on employees' absenteeism and turnover rate. Cohesive groups increase job satisfactions. Mann and Baumgartel state that the sense of group belongingness, group pride, group solidarity or group spirit relates inversely to the absenteeism rate. Among the target groups, group with high cohesiveness tend to have low absenteeism rate while group with low cohesiveness tend to have higher absenteeism rate.

Seashore investigated 228 work groups in a heavy-machinery-manufacturing company. His findings suggest that Group cohesiveness helps employees solve their work-related pressure. Seashore define cohesiveness as '1) members perceive themselves to be a part of a group 2) members prefer to remain in the group rather than to leave, and 3) perceive their group to be better than other groups with respect to the way the men get along together, the way they help each other out, and the way they stick together'. Among the target group, the less cohesive the group, the more likely its employees are to feel nervous and jumpy.

Different communication ways in groups contribute to different employees satisfaction. For example, the chain structure results in low satisfaction while the circle structure results in high satisfaction.

Leadership

In relations to the work place, successful leadership will structure and develop relationships amongst employees and consequently, employees will empower each other.

Kurt Lewin argued that there are 3 main styles of leaderships:

1. Autocratic leaders: control the decision-making power and do not consult team members.
2. Democratic leaders: include team members in the decision-making process but make the final decisions.
3. Laissez-faire leaders: team members have huge freedom in how they do their work, and how they set their deadlines.

Management plays an important role in an employee's job satisfaction and happiness. Good leadership can empower employees to work better towards reaching the organisation's goals. For example, if a leader is considerate, the employees will tend to develop a positive attitude towards management and thus, work more effectively.

Feelings, including happiness, are often hidden by employees and should be identified for effective communication in the workplace. Ineffective communication at work is not uncommon, as leaders tend to focus on their own matters and give less attention to employees at a lower rank. Employees, on the other hand, tend to be reluctant to talk about their own problem and assume leaders can figure out the problem. As a result, both leaders and employees can cause repetitive misunderstandings.

Consequences

Job performance

Main article: Job performance

Research shows that employees who are happiest at work are considered to be the most efficient and display the highest levels of performance. For instance, the iOpener Institute found that a happy worker is a high-performing one. The happiest employees only take one-tenth the sick leave of their least happy colleagues as they are in better physical and psychological health than their colleagues. Furthermore, happier employees display a higher level of loyalty, as they tend to stay for far longer periods in their organizations. Happiness at work is the feeling that employee really enjoy what they do and they are proud of themselves, they enjoy people being around, thus they have better performance.

Absence from work

Main article: Absenteeism

Employees' behaviour can be influenced by happiness or unhappiness. People would like to participate in work when they feel happiness, or in the converse, absenteeism might occur. Absenteeism can be defined as the lack of physical presence at a given place and time determined by an individual's work schedule.

Although employee absenteeism is usually associated with the job-related well-being or simply whether the employee feels happiness during the work, other factors are also important. Firstly, the health constraints such as being ill would force the employee absence from the work. Secondly, social and families pressure can also influence the employee's decision to participate in the work.

Employee turnover

Main article: Employee turnover

Employee turnover can be considered as another result derived from employee happiness. In particular, it is more likely that individual employees are able to deal with stress and passive feelings when they are in good mood. As people spend a considerable amount of time in the workplace, factors such as employee relationship, organizational culture and job performance can have a significant impact on work happiness. What is more, Avey and his colleagues use a concept called psychological capital to link employee satisfaction with work related outcomes, especially turnover intention and actual turnover. However, their findings were limited due to some reasons. For example, they omitted an important factor, which was emotional stability. Additionally, other researchers have pointed out that the relationship between work happiness and turnover intention is generally low, even if a dissatisfied employee is more likely to quit his/her job than the satisfied one. Therefore, whether or not employee happiness can be linked with employee's turnover intention is still a moot point.

Measurement

Although there are a few surveys used to measure the happiness or well-being level of people in different countries such as the World Happiness Report, the Happy Planet Index and the OECD Better Life Index, there are no surveys that measure happiness in the specific context of the workplace. There are, however, surveys created to assess the job satisfaction level of employees. Even though job satisfaction is a different concept, it is positively correlated to happiness and subjective well-being. The main job satisfaction scales are: The Job Satisfaction Survey (JSS), The Job Descriptive Index (JDI) and The Minnesota Satisfaction Questionnaire (MSQ). The Job Satisfaction Survey (JSS) assesses nine facets of job satisfaction, as well as overall satisfaction. The facets include pay and pay raises, promotion opportunities, relationship with the immediate supervisor, fringe benefits, rewards given for good performance, rules and procedures, relationship with coworkers, type of work performed and communication within the organization. The scale contains thirty-six items and uses a summated rating scale format. The JSS can provide ten scores. Each of the nine subscales produce a separate score and the total of all items produces a total score. The Job Descriptive Index (JDI) scale assesses five facets which are work, pay, promotion, supervision and coworkers. The entire scale contains seventy-two items with either nine or eighteen items per subscale. Each item is an evaluative adjective or short phrase that is descriptive of the job. The individual has to respond "yes", "uncertain" or "no" for each item. The Minnesota Satisfaction Questionnaire (MSQ) has two versions, a one hundred item long version and a twenty item short form. It covers twenty facets including activity, independence, variety, social status, supervision (human relations), supervision (technical), moral values, security, social service, authority, ability utilization, company policies and practices, compensation, advancement, responsibility, creativity, working conditions, coworkers, recognition and achievement. The long form contains five items per facet, while the short one contains only one.

Statistics

University of Kent research show that career satisfaction stems from living near work, access to the outdoors, mindfulness, flow, non open plan offices, absence of many tight deadlines or long hours, small organisations or self-employment, variety, friends at work, working on a product or service from start to finish, focus, financial freedom, autonomy, positive feedback, helping others, purpose/goals, learning new skill and challenges.

The University of Warwick, UK, mentioned in one of their studies that happy workers are up to 12% more productive than unhappy professionals.

Doctor, dentist, armed forces, teacher, leisure/tourism and journalist are the 6 happiest graduate jobs while social worker, civil servant, estate agent, secretary and administrator are the 5 least happy. According to one study Clergy, CEO's, Agriculturist, Company Secretaries, Regulatory professional, Health managers, Medical Professionals, Farmers and Accommodation managers are the happiest jobs in that order in another study.

On the other hand, social workers, nurses, social workers, medical doctors, and psychiatrists abuse substances and incur mental ill-health at among the highest rates of any occupation. For instance, the psychiatrist burnout rate is 40%.