Wavelet

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Wavelet 

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.

Seismic wavelet

For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly one tenth of a second. If this wavelet were to be convolved with a signal created from the recording of a melody, then the resulting signal would be useful for determining when the Middle C note appeared in the song. Mathematically, a wavelet correlates with a signal if a portion of the signal is similar. Correlation is at the core of many practical wavelet applications.

As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including – but not limited to – audio signals and images. Sets of wavelets are needed to analyze data fully. "Complementary" wavelets decompose a signal without gaps or overlaps so that the decomposition process is mathematically reversible. Thus, sets of complementary wavelets are useful in wavelet-based compression/decompression algorithms, where it is desirable to recover the original information with minimal loss.

In formal terms, this representation is a wavelet series representation of a square-integrable function with respect to either a complete, orthonormal set of basis functions, or an overcomplete set or frame of a vector space, for the Hilbert space of square integrable functions. This is accomplished through coherent states.

In classical physics, the diffraction phenomenon is described by the Huygens–Fresnel principle that treats each point in a propagating wavefront as a collection of individual spherical wavelets. The characteristic bending pattern is most pronounced when a wave from a coherent source (such as a laser) encounters a slit/aperture that is comparable in size to its wavelength. This is due to the addition, or interference, of different points on the wavefront (or, equivalently, each wavelet) that travel by paths of different lengths to the registering surface. Multiple, closely spaced openings (e.g., a diffraction grating), can result in a complex pattern of varying intensity.

Etymology

The word wavelet has been used for decades in digital signal processing and exploration geophysics. The equivalent French word ondelette meaning "small wave" was used by Morlet and Grossmann in the early 1980s.

Wavelet theory

Wavelet theory is applicable to several subjects. All wavelet transforms may be considered forms of time-frequency representation for continuous-time (analog) signals and so are related to harmonic analysis. Discrete wavelet transform (continuous in time) of a discrete-time (sampled) signal by using discrete-time filterbanks of dyadic (octave band) configuration is a wavelet approximation to that signal. The coefficients of such a filter bank are called the shift and scaling coefficients in wavelets nomenclature. These filterbanks may contain either finite impulse response (FIR) or infinite impulse response (IIR) filters. The wavelets forming a continuous wavelet transform (CWT) are subject to the uncertainty principle of Fourier analysis respective sampling theory: Given a signal with some event in it, one cannot assign simultaneously an exact time and frequency response scale to that event. The product of the uncertainties of time and frequency response scale has a lower bound. Thus, in the scaleogram of a continuous wavelet transform of this signal, such an event marks an entire region in the time-scale plane, instead of just one point. Also, discrete wavelet bases may be considered in the context of other forms of the uncertainty principle.

Wavelet transforms are broadly divided into three classes: continuous, discrete and multiresolution-based.

Continuous wavelet transforms (continuous shift and scale parameters)

In continuous wavelet transforms, a given signal of finite energy is projected on a continuous family of frequency bands (or similar subspaces of the L^p function space L²(R) ). For instance the signal may be represented on every frequency band of the form [f, 2f] for all positive frequencies f > 0. Then, the original signal can be reconstructed by a suitable integration over all the resulting frequency components.

The frequency bands or subspaces (sub-bands) are scaled versions of a subspace at scale 1. This subspace in turn is in most situations generated by the shifts of one generating function ψ in L²(R), the mother wavelet. For the example of the scale one frequency band [1, 2] this function is

$${\displaystyle \psi (t)=2\,\operatorname {sinc} (2t)-\,\operatorname {sinc} (t)={\frac {\sin(2\pi t)-\sin(\pi t)}{\pi t}}}$$

with the (normalized) sinc function. That, Meyer's, and two other examples of mother wavelets are:

Meyer

Morlet

Mexican hat

The subspace of scale a or frequency band [1/a, 2/a] is generated by the functions (sometimes called child wavelets)

$${\displaystyle \psi _{a,b}(t)={\frac {1}{\sqrt {a}}}\psi \left({\frac {t-b}{a}}\right),}$$

where a is positive and defines the scale and b is any real number and defines the shift. The pair (a, b) defines a point in the right halfplane R₊ × R.

The projection of a function x onto the subspace of scale a then has the form

$${\displaystyle x_{a}(t)=\int _{\mathbb {R} }WT_{\psi }\{x\}(a,b)\cdot \psi _{a,b}(t)\,db}$$

with wavelet coefficients

$${\displaystyle WT_{\psi }\{x\}(a,b)=\langle x,\psi _{a,b}\rangle =\int _{\mathbb {R} }x(t){\psi _{a,b}(t)}\,dt.}$$

For the analysis of the signal x, one can assemble the wavelet coefficients into a scaleogram of the signal.

See a list of some Continuous wavelets.

Discrete wavelet transforms (discrete shift and scale parameters, continuous in time)

It is computationally impossible to analyze a signal using all wavelet coefficients, so one may wonder if it is sufficient to pick a discrete subset of the upper halfplane to be able to reconstruct a signal from the corresponding wavelet coefficients. One such system is the affine system for some real parameters a > 1, b > 0. The corresponding discrete subset of the halfplane consists of all the points (a^m, nb a^m) with m, n in Z. The corresponding child wavelets are now given as

$${\displaystyle \psi _{m,n}(t)={\frac {1}{\sqrt {a^{m}}}}\psi \left({\frac {t-nba^{m}}{a^{m}}}\right).}$$

A sufficient condition for the reconstruction of any signal x of finite energy by the formula

$${\displaystyle x(t)=\sum _{m\in \mathbb {Z} }\sum _{n\in \mathbb {Z} }\langle x,\,\psi _{m,n}\rangle \cdot \psi _{m,n}(t)}$$

is that the functions ${\displaystyle \{\psi _{m,n}:m,n\in \mathbb {Z} \}}$ form an orthonormal basis of L²(R).

Multiresolution based discrete wavelet transforms (continuous in time)

D4 wavelet

In any discretised wavelet transform, there are only a finite number of wavelet coefficients for each bounded rectangular region in the upper halfplane. Still, each coefficient requires the evaluation of an integral. In special situations this numerical complexity can be avoided if the scaled and shifted wavelets form a multiresolution analysis. This means that there has to exist an auxiliary function, the father wavelet φ in L²(R), and that a is an integer. A typical choice is a = 2 and b = 1. The most famous pair of father and mother wavelets is the Daubechies 4-tap wavelet. Note that not every orthonormal discrete wavelet basis can be associated to a multiresolution analysis; for example, the Journe wavelet admits no multiresolution analysis.

From the mother and father wavelets one constructs the subspaces

$${\displaystyle V_{m}=\operatorname {span} (\phi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\phi _{m,n}(t)=2^{-m/2}\phi (2^{-m}t-n)}$$

$${\displaystyle W_{m}=\operatorname {span} (\psi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\psi _{m,n}(t)=2^{-m/2}\psi (2^{-m}t-n).}$$

The father wavelet ${\displaystyle V_{i}}$ keeps the time domain properties, while the mother wavelets ${\displaystyle W_{i}}$ keeps the frequency domain properties.

From these it is required that the sequence

$${\displaystyle \{0\}\subset \dots \subset V_{1}\subset V_{0}\subset V_{-1}\subset V_{-2}\subset \dots \subset L^{2}(\mathbb {R} )}$$

forms a multiresolution analysis of L² and that the subspaces ${\displaystyle \dots ,W_{1},W_{0},W_{-1},\dots }$ are the orthogonal "differences" of the above sequence, that is, W_m is the orthogonal complement of V_m inside the subspace V_m−1,

$${\displaystyle V_{m}\oplus W_{m}=V_{m-1}.}$$

In analogy to the sampling theorem one may conclude that the space V_m with sampling distance 2^m more or less covers the frequency baseband from 0 to 1/2^m-1. As orthogonal complement, W_m roughly covers the band [1/2^m−1, 1/2^m].

From those inclusions and orthogonality relations, especially ${\displaystyle V_{0}\oplus W_{0}=V_{-1}}$, follows the existence of sequences ${\displaystyle h=\{h_{n}\}_{n\in \mathbb {Z} }}$ and ${\displaystyle g=\{g_{n}\}_{n\in \mathbb {Z} }}$ that satisfy the identities

$${\displaystyle g_{n}=\langle \phi _{0,0},\,\phi _{-1,n}\rangle }$$

so that ${\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}$ and

$${\displaystyle h_{n}=\langle \psi _{0,0},\,\phi _{-1,n}\rangle }$$

so that ${\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}$ The second identity of the first pair is a refinement equation for the father wavelet φ. Both pairs of identities form the basis for the algorithm of the fast wavelet transform.

From the multiresolution analysis derives the orthogonal decomposition of the space L² as

$${\displaystyle L^{2}=V_{j_{0}}\oplus W_{j_{0}}\oplus W_{j_{0}-1}\oplus W_{j_{0}-2}\oplus W_{j_{0}-3}\oplus \cdots }$$

For any signal or function ${\displaystyle S\in L^{2}}$ this gives a representation in basis functions of the corresponding subspaces as

$${\displaystyle S=\sum _{k}c_{j_{0},k}\phi _{j_{0},k}+\sum _{j\leq j_{0}}\sum _{k}d_{j,k}\psi _{j,k}}$$

where the coefficients are

$${\displaystyle c_{j_{0},k}=\langle S,\phi _{j_{0},k}\rangle }$$

and

$${\displaystyle d_{j,k}=\langle S,\psi _{j,k}\rangle .}$$

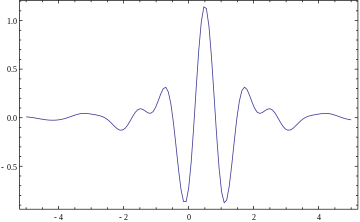
Mother wavelet

For practical applications, and for efficiency reasons, one prefers continuously differentiable functions with compact support as mother (prototype) wavelet (functions). However, to satisfy analytical requirements (in the continuous WT) and in general for theoretical reasons, one chooses the wavelet functions from a subspace of the space ${\displaystyle L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).}$ This is the space of Lebesgue measurable functions that are both absolutely integrable and square integrable in the sense that

$${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|\,dt<\infty }$$

and

$${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt<\infty .}$$

Being in this space ensures that one can formulate the conditions of zero mean and square norm one:

$${\displaystyle \int _{-\infty }^{\infty }\psi (t)\,dt=0}$$

is the condition for zero mean, and

$${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt=1}$$

is the condition for square norm one.

For ψ to be a wavelet for the continuous wavelet transform (see there for exact statement), the mother wavelet must satisfy an admissibility criterion (loosely speaking, a kind of half-differentiability) in order to get a stably invertible transform.

For the discrete wavelet transform, one needs at least the condition that the wavelet series is a representation of the identity in the space L²(R). Most constructions of discrete WT make use of the multiresolution analysis, which defines the wavelet by a scaling function. This scaling function itself is a solution to a functional equation.

In most situations it is useful to restrict ψ to be a continuous function with a higher number M of vanishing moments, i.e. for all integer m < M

$${\displaystyle \int _{-\infty }^{\infty }t^{m}\,\psi (t)\,dt=0.}$$

The mother wavelet is scaled (or dilated) by a factor of a and translated (or shifted) by a factor of b to give (under Morlet's original formulation):

$${\displaystyle \psi _{a,b}(t)={1 \over {\sqrt {a}}}\psi \left({t-b \over a}\right).}$$

For the continuous WT, the pair (a,b) varies over the full half-plane R₊ × R; for the discrete WT this pair varies over a discrete subset of it, which is also called affine group.

These functions are often incorrectly referred to as the basis functions of the (continuous) transform. In fact, as in the continuous Fourier transform, there is no basis in the continuous wavelet transform. Time-frequency interpretation uses a subtly different formulation (after Delprat).

Restriction：

1. ${\displaystyle {\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt}$ when a₁ = a and b₁ = b,
2. ${\displaystyle \Psi (t)}$ has a finite time interval

Comparisons with Fourier transform (continuous-time)

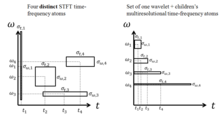
The wavelet transform is often compared with the Fourier transform, in which signals are represented as a sum of sinusoids. In fact, the Fourier transform can be viewed as a special case of the continuous wavelet transform with the choice of the mother wavelet ${\displaystyle \psi (t)=e^{-2\pi it}}$. The main difference in general is that wavelets are localized in both time and frequency whereas the standard Fourier transform is only localized in frequency. The Short-time Fourier transform (STFT) is similar to the wavelet transform, in that it is also time and frequency localized, but there are issues with the frequency/time resolution trade-off.

In particular, assuming a rectangular window region, one may think of the STFT as a transform with a slightly different kernel

$${\displaystyle \psi (t)=g(t-u)e^{-2\pi it}}$$

where ${\displaystyle g(t-u)}$ can often be written as ${\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}$, where ${\displaystyle \Delta _{t}}$ and u respectively denote the length and temporal offset of the windowing function. Using Parseval's theorem, one may define the wavelet's energy as

$${\displaystyle E=\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt={\frac {1}{2\pi }}\int _{-\infty }^{\infty }|{\hat {\psi }}(\omega )|^{2}\,d\omega }$$

From this, the square of the temporal support of the window offset by time u is given by

$${\displaystyle \sigma _{t}^{2}={\frac {1}{E}}\int |t-u|^{2}|\psi (t)|^{2}\,dt}$$

and the square of the spectral support of the window acting on a frequency ${\displaystyle \xi }$

$${\displaystyle \sigma _{\omega }^{2}={\frac {1}{2\pi E}}\int |\omega -\xi |^{2}|{\hat {\psi }}(\omega )|^{2}\,d\omega }$$

Multiplication with a rectangular window in the time domain corresponds to convolution with a ${\displaystyle \operatorname {sinc} (\Delta _{t}\omega )}$ function in the frequency domain, resulting in spurious ringing artifacts for short/localized temporal windows. With the continuous-time Fourier Transform, ${\displaystyle \Delta _{t}\to \infty }$ and this convolution is with a delta function in Fourier space, resulting in the true Fourier transform of the signal ${\displaystyle x(t)}$. The window function may be some other apodizing filter, such as a Gaussian. The choice of windowing function will affect the approximation error relative to the true Fourier transform.

A given resolution cell's time-bandwidth product may not be exceeded with the STFT. All STFT basis elements maintain a uniform spectral and temporal support for all temporal shifts or offsets, thereby attaining an equal resolution in time for lower and higher frequencies. The resolution is purely determined by the sampling width.

In contrast, the wavelet transform's multiresolutional properties enables large temporal supports for lower frequencies while maintaining short temporal widths for higher frequencies by the scaling properties of the wavelet transform. This property extends conventional time-frequency analysis into time-scale analysis.

STFT time-frequency atoms (left) and DWT time-scale atoms (right). The time-frequency atoms are four different basis functions used for the STFT (i.e. four separate Fourier transforms required). The time-scale atoms of the DWT achieve small temporal widths for high frequencies and good temporal widths for low frequencies with a single transform basis set.

The discrete wavelet transform is less computationally complex, taking O(N) time as compared to O(N log N) for the fast Fourier transform. This computational advantage is not inherent to the transform, but reflects the choice of a logarithmic division of frequency, in contrast to the equally spaced frequency divisions of the FFT (fast Fourier transform) which uses the same basis functions as DFT (Discrete Fourier Transform). It is also important to note that this complexity only applies when the filter size has no relation to the signal size. A wavelet without compact support such as the Shannon wavelet would require O(N²). (For instance, a logarithmic Fourier Transform also exists with O(N) complexity, but the original signal must be sampled logarithmically in time, which is only useful for certain types of signals.)

Definition of a wavelet

A wavelet (or a wavelet family) can be defined in various ways:

Scaling filter

An orthogonal wavelet is entirely defined by the scaling filter – a low-pass finite impulse response (FIR) filter of length 2N and sum 1. In biorthogonal wavelets, separate decomposition and reconstruction filters are defined.

For analysis with orthogonal wavelets the high pass filter is calculated as the quadrature mirror filter of the low pass, and reconstruction filters are the time reverse of the decomposition filters.

Daubechies and Symlet wavelets can be defined by the scaling filter.

Scaling function

Wavelets are defined by the wavelet function ψ(t) (i.e. the mother wavelet) and scaling function φ(t) (also called father wavelet) in the time domain.

The wavelet function is in effect a band-pass filter and scaling that for each level halves its bandwidth. This creates the problem that in order to cover the entire spectrum, an infinite number of levels would be required. The scaling function filters the lowest level of the transform and ensures all the spectrum is covered.

For a wavelet with compact support, φ(t) can be considered finite in length and is equivalent to the scaling filter g.

Meyer wavelets can be defined by scaling functions

Wavelet function

The wavelet only has a time domain representation as the wavelet function ψ(t).

For instance, Mexican hat wavelets can be defined by a wavelet function. See a list of a few Continuous wavelets.

History

The development of wavelets can be linked to several separate trains of thought, starting with Haar's work in the early 20th century. Later work by Dennis Gabor yielded Gabor atoms (1946), which are constructed similarly to wavelets, and applied to similar purposes.

Notable contributions to wavelet theory since then can be attributed to Zweig’s discovery of the continuous wavelet transform (CWT) in 1975 (originally called the cochlear transform and discovered while studying the reaction of the ear to sound), Pierre Goupillaud, Grossmann and Morlet's formulation of what is now known as the CWT (1982), Jan-Olov Strömberg's early work on discrete wavelets (1983), the Le Gall–Tabatabai (LGT) 5/3-taps non-orthogonal filter bank with linear phase (1988), Ingrid Daubechies' orthogonal wavelets with compact support (1988), Mallat's non-orthogonal multiresolution framework (1989), Ali Akansu's Binomial QMF (1990), Nathalie Delprat's time-frequency interpretation of the CWT (1991), Newland's harmonic wavelet transform (1993), and set partitioning in hierarchical trees (SPIHT) developed by Amir Said with William A. Pearlman in 1996.

The JPEG 2000 standard was developed from 1997 to 2000 by a Joint Photographic Experts Group (JPEG) committee chaired by Touradj Ebrahimi (later the JPEG president). In contrast to the DCT algorithm used by the original JPEG format, JPEG 2000 instead uses discrete wavelet transform (DWT) algorithms. It uses the CDF 9/7 wavelet transform (developed by Ingrid Daubechies in 1992) for its lossy compression algorithm, and the Le Gall–Tabatabai (LGT) 5/3 wavelet transform (developed by Didier Le Gall and Ali J. Tabatabai in 1988) for its lossless compression algorithm. JPEG 2000 technology, which includes the Motion JPEG 2000 extension, was selected as the video coding standard for digital cinema in 2004.

Timeline

• First wavelet (Haar Wavelet) by Alfréd Haar (1909)
• Since the 1970s: George Zweig, Jean Morlet, Alex Grossmann
• Since the 1980s: Yves Meyer, Didier Le Gall, Ali J. Tabatabai, Stéphane Mallat, Ingrid Daubechies, Ronald Coifman, Ali Akansu, Victor Wickerhauser
• Since the 1990s: Nathalie Delprat, Newland, Amir Said, William A. Pearlman, Touradj Ebrahimi, JPEG 2000

Wavelet transforms

Main article: Wavelet transform

A wavelet is a mathematical function used to divide a given function or continuous-time signal into different scale components. Usually one can assign a frequency range to each scale component. Each scale component can then be studied with a resolution that matches its scale. A wavelet transform is the representation of a function by wavelets. The wavelets are scaled and translated copies (known as "daughter wavelets") of a finite-length or fast-decaying oscillating waveform (known as the "mother wavelet"). Wavelet transforms have advantages over traditional Fourier transforms for representing functions that have discontinuities and sharp peaks, and for accurately deconstructing and reconstructing finite, non-periodic and/or non-stationary signals.

Wavelet transforms are classified into discrete wavelet transforms (DWTs) and continuous wavelet transforms (CWTs). Note that both DWT and CWT are continuous-time (analog) transforms. They can be used to represent continuous-time (analog) signals. CWTs operate over every possible scale and translation whereas DWTs use a specific subset of scale and translation values or representation grid.

There are a large number of wavelet transforms each suitable for different applications. For a full list see list of wavelet-related transforms but the common ones are listed below:

• Continuous wavelet transform (CWT)
• Discrete wavelet transform (DWT)
• Fast wavelet transform (FWT)
• Lifting scheme and generalized lifting scheme
• Wavelet packet decomposition (WPD)
• Stationary wavelet transform (SWT)
• Fractional Fourier transform (FRFT)
• Fractional wavelet transform (FRWT)

Generalized transforms

There are a number of generalized transforms of which the wavelet transform is a special case. For example, Yosef Joseph Segman introduced scale into the Heisenberg group, giving rise to a continuous transform space that is a function of time, scale, and frequency. The CWT is a two-dimensional slice through the resulting 3d time-scale-frequency volume.

Another example of a generalized transform is the chirplet transform in which the CWT is also a two dimensional slice through the chirplet transform.

An important application area for generalized transforms involves systems in which high frequency resolution is crucial. For example, darkfield electron optical transforms intermediate between direct and reciprocal space have been widely used in the harmonic analysis of atom clustering, i.e. in the study of crystals and crystal defects. Now that transmission electron microscopes are capable of providing digital images with picometer-scale information on atomic periodicity in nanostructure of all sorts, the range of pattern recognition and strain/metrology applications for intermediate transforms with high frequency resolution (like brushlets and ridgelets) is growing rapidly.

Fractional wavelet transform (FRWT) is a generalization of the classical wavelet transform in the fractional Fourier transform domains. This transform is capable of providing the time- and fractional-domain information simultaneously and representing signals in the time-fractional-frequency plane.

Applications

Generally, an approximation to DWT is used for data compression if a signal is already sampled, and the CWT for signal analysis. Thus, DWT approximation is commonly used in engineering and computer science, and the CWT in scientific research.

Like some other transforms, wavelet transforms can be used to transform data, then encode the transformed data, resulting in effective compression. For example, JPEG 2000 is an image compression standard that uses biorthogonal wavelets. This means that although the frame is overcomplete, it is a tight frame (see types of frames of a vector space), and the same frame functions (except for conjugation in the case of complex wavelets) are used for both analysis and synthesis, i.e., in both the forward and inverse transform. For details see wavelet compression.

A related use is for smoothing/denoising data based on wavelet coefficient thresholding, also called wavelet shrinkage. By adaptively thresholding the wavelet coefficients that correspond to undesired frequency components smoothing and/or denoising operations can be performed.

Wavelet transforms are also starting to be used for communication applications. Wavelet OFDM is the basic modulation scheme used in HD-PLC (a power line communications technology developed by Panasonic), and in one of the optional modes included in the IEEE 1901 standard. Wavelet OFDM can achieve deeper notches than traditional FFT OFDM, and wavelet OFDM does not require a guard interval (which usually represents significant overhead in FFT OFDM systems).

As a representation of a signal

Often, signals can be represented well as a sum of sinusoids. However, consider a non-continuous signal with an abrupt discontinuity; this signal can still be represented as a sum of sinusoids, but requires an infinite number, which is an observation known as Gibbs phenomenon. This, then, requires an infinite number of Fourier coefficients, which is not practical for many applications, such as compression. Wavelets are more useful for describing these signals with discontinuities because of their time-localized behavior (both Fourier and wavelet transforms are frequency-localized, but wavelets have an additional time-localization property). Because of this, many types of signals in practice may be non-sparse in the Fourier domain, but very sparse in the wavelet domain. This is particularly useful in signal reconstruction, especially in the recently popular field of compressed sensing. (Note that the short-time Fourier transform (STFT) is also localized in time and frequency, but there are often problems with the frequency-time resolution trade-off. Wavelets are better signal representations because of multiresolution analysis.)

This motivates why wavelet transforms are now being adopted for a vast number of applications, often replacing the conventional Fourier transform. Many areas of physics have seen this paradigm shift, including molecular dynamics, chaos theory, ab initio calculations, astrophysics, gravitational wave transient data analysis, density-matrix localisation, seismology, optics, turbulence and quantum mechanics. This change has also occurred in image processing, EEG, EMG, ECG analyses, brain rhythms, DNA analysis, protein analysis, climatology, human sexual response analysis, general signal processing, speech recognition, acoustics, vibration signals, computer graphics, multifractal analysis, and sparse coding. In computer vision and image processing, the notion of scale space representation and Gaussian derivative operators is regarded as a canonical multi-scale representation.

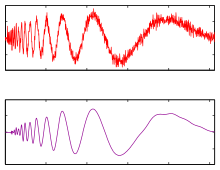
Wavelet denoising

Signal denoising by wavelet transform thresholding

Suppose we measure a noisy signal ${\displaystyle x=s+v}$, where s represents the signal and v represents the noise. Assume s has a sparse representation in a certain wavelet basis, and ${\displaystyle v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)}$

Let the wavelet transform of ${\displaystyle x}$ be ${\displaystyle y=W^{T}x=W^{T}s+W^{T}v=p+z}$. ${\displaystyle p=W^{T}s}$, the wavelet transform of the signal component. ${\displaystyle z=W^{T}v}$, the wavelet transform of the noise component.

Most elements in p are 0 or close to 0, and ${\displaystyle z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)}$

Since W is orthogonal, the estimation problem amounts to recovery of a signal in iid Gaussian noise. As p is sparse, one method is to apply a Gaussian mixture model for p.

Assume a prior ${\displaystyle p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})}$, ${\displaystyle \sigma _{1}^{2}}$ is the variance of "significant" coefficients, and ${\displaystyle \sigma _{2}^{2}}$ is the variance of "insignificant" coefficients.

Then ${\displaystyle {\tilde {p}}=E(p/y)=\tau (y)y}$, ${\displaystyle \tau (y)}$ is called the shrinkage factor, which depends on the prior variances ${\displaystyle \sigma _{1}^{2}}$ and ${\displaystyle \sigma _{2}^{2}}$. By setting coefficients that fall below a shrinkage threshold to zero, once the inverse transform is applied, an expectedly small amount of signal is lost due to the sparsity assumption. The larger coefficients are expected to primarily represent signal due to sparsity, and statistically very little of the signal, albeit the majority of the noise, is expected to be represented in such lower magnitude coefficients... therefore the zeroing-out operation is expected to remove most of the noise and not much signal. Typically, the above-threshold coefficients are not modified during this process. Some algorithms for wavelet-based denoising may attenuate larger coefficients as well, based on a statistical estimate of the amount of noise expected to be removed by such an attenuation.

At last, apply the inverse wavelet transform to obtain ${\displaystyle {\tilde {s}}=W{\tilde {p}}}$

Multiscale climate network

Agarwal et al. proposed wavelet based advanced linear and nonlinear methods to construct and investigate Climate as complex networks at different timescales. Climate networks constructed using SST datasets at different timescale averred that wavelet based multi-scale analysis of climatic processes holds the promise of better understanding the system dynamics that may be missed when processes are analyzed at one timescale only. 

Refusal of work

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Refusal_of_work 

Refusal of work is behavior in which a person refuses regular employment.

As actual behavior, with or without a political or philosophical program, it has been practiced by various subcultures and individuals. It is frequently engaged in by those who critique the concept of work, and it has a long history. Radical political positions have openly advocated refusal of work. From within Marxism it has been advocated by Paul Lafargue and the Italian workerist/autonomists (e.g. Antonio Negri, Mario Tronti), the French ultra-left (e.g. Échanges et Mouvement); and within anarchism (especially Bob Black and the post-left anarchy tendency).

Abolition of unfree labour

International human rights law does not recognize the refusal of work or right not to work by itself except the right to strike. However the Abolition of Forced Labour Convention adopted by International Labour Organization in 1957 prohibits all forms of forced labour.

Concerns over wage slavery

Main article: Wage slavery

Wage slavery refers to a situation where a person's livelihood depends on wages, especially when the dependence is total and immediate. It is a negatively connoted term used to draw an analogy between slavery and wage labor, and to highlight similarities between owning and employing a person. The term 'wage slavery' has been used to criticize economic exploitation and social stratification, with the former seen primarily as unequal bargaining power between labor and capital (particularly when workers are paid comparatively low wages, e.g. in sweatshops), and the latter as a lack of workers' self-management. The criticism of social stratification covers a wider range of employment choices bound by the pressures of a hierarchical social environment (i.e. working for a wage not only under threat of starvation or poverty, but also of social stigma or status diminution).

Similarities between wage labor and slavery were noted at least as early as Cicero. Before the American Civil War, Southern defenders of African American slavery invoked the concept to favorably compare the condition of their slaves to workers in the North. With the advent of the industrial revolution, thinkers such as Proudhon and Marx elaborated the comparison between wage labor and slavery in the context of a critique of property not intended for active personal use.

The introduction of wage labor in 18th century Britain was met with resistance—giving rise to the principles of syndicalism. Historically, some labor organizations and individual social activists, have espoused workers' self-management or worker cooperatives as possible alternatives to wage labor.

Political views

Marxism

Paul Lafargue and The Right to be Lazy

Main article: The Right to Be Lazy

 

Paul Lafargue, author of book critical of work titled:The Right to Be Lazy

The Right to be Lazy is an essay by Cuban-born French revolutionary Marxist Paul Lafargue, written from his London exile in 1880. The essay polemicizes heavily against then-contemporary liberal, conservative, Christian and even socialist ideas of work. Lafargue criticizes these ideas from a Marxist perspective as dogmatic and ultimately false by portraying the degeneration and enslavement of human existence when being subsumed under the primacy of the "right to work", and argues that "laziness", combined with human creativity, is an important source of human progress.

He manifests that "When, in our civilized Europe, we would find a trace of the native beauty of man, we must go seek it in the nations where economic prejudices have not yet uprooted the hatred of work ... The Greeks in their era of greatness had only contempt for work: their slaves alone were permitted to labor: the free man knew only exercises for the body and mind ... The philosophers of antiquity taught contempt for work, that degradation of the free man, the poets sang of idleness, that gift from the Gods." And so he says "Proletarians, brutalized by the dogma of work, listen to the voice of these philosophers, which has been concealed from you with jealous care: A citizen who gives his labor for money degrades himself to the rank of slaves." (The last sentence paraphrasing Cicero.)

Situationist International

Raoul Vaneigem, important theorist of the post-surrealist Situationist International which was influential in the May 68 events in France, wrote The Book of Pleasures. In it he says that "You reverse the perspective of power by returning to pleasure the energies stolen by work and constraint ... As sure as work kills pleasure, pleasure kills work. If you are not resigned to dying of disgust, then you will be happy enough to rid your life of the odious need to work, to give orders (and obey them), to lose and to win, to keep up appearances, and to judge and be judged."

Autonomism

Main article: Autonomism

Autonomist philosopher Bifo defines refusal of work as not "so much the obvious fact that workers do not like to be exploited, but something more. It means that the capitalist restructuring, the technological change, and the general transformation of social institutions are produced by the daily action of withdrawal from exploitation, of rejection of the obligation to produce surplus value, and to increase the value of capital, reducing the value of life." More simply he states "Refusal of work means ... I don't want to go to work because I prefer to sleep. But this laziness is the source of intelligence, of technology, of progress. Autonomy is the self-regulation of the social body in its independence and in its interaction with the disciplinary norm."

As a social development Bifo remembers,

that one of the strong ideas of the movement of autonomy proletarians during the 70s was the idea "precariousness is good". Job precariousness is a form of autonomy from steady regular work, lasting an entire life. In the 1970s many people used to work for a few months, then to go away for a journey, then back to work for a while. This was possible in times of almost full employment and in times of egalitarian culture. This situation allowed people to work in their own interest and not in the interest of capitalists, but quite obviously this could not last forever, and the neoliberal offensive of the 1980s was aimed to reverse the rapport de force."

As a response to these developments his view is that "the dissemination of self-organized knowledge can create a social framework containing infinite autonomous and self-reliant worlds."

From this possibility of self-determination even the notion of workers' self-management is seen as problematic since "Far from the emergence of proletarian power, ... this self-management as a moment of the self-harnessing of the workers to capitalist production in the period of real subsumption ... Mistaking the individual capitalist (who, in real subsumption disappears into the collective body of share ownership on one side, and hired management on the other) rather than the enterprise as the problem, ... the workers themselves became a collective capitalist, taking on responsibility for the exploitation of their own labor. Thus, far from breaking with 'work', ... the workers maintained the practice of clocking-in, continued to organize themselves and the community around the needs of the factory, paid themselves from profits arising from the sale of watches, maintained determined relations between individual work done and wage, and continued to wear their work shirts throughout the process."

André Gorz

André Gorz was an Austrian and French social philosopher. Also a journalist, he co-founded Le Nouvel Observateur weekly in 1964. A supporter of Jean-Paul Sartre's existentialist version of Marxism after World War Two, in the aftermath of the May '68 student riots, he became more concerned with political ecology. His central theme was wage labour issues such as liberation from work, the just distribution of work, social alienation, and a guaranteed basic income. Among his works critical of work and the work ethic include Critique de la division du travail (Seuil, 1973. Collective work), Farewell to the Working Class (1980 – Galilée and Le Seuil, 1983, Adieux au Prolétariat), Critique of Economic Reason (Verso, 1989 first published 1988) and Reclaiming Work: Beyond the Wage-Based Society (1999).

Anarchism

The Abolition of Work

Bob Black, contemporary American anarchist associated with the post-left anarchy tendency

The Abolition of Work, Bob Black's most widely read essay, draws upon the ideas of Charles Fourier, William Morris, Herbert Marcuse, Paul Goodman, and Marshall Sahlins. In it he argues for the abolition of the producer- and consumer-based society, where, Black contends, all of life is devoted to the production and consumption of commodities. Attacking Marxist state socialism as much as market capitalism, Black argues that the only way for humans to be free is to reclaim their time from jobs and employment, instead turning necessary subsistence tasks into free play done voluntarily—an approach referred to as "ludic". The essay argues that "no-one should ever work", because work—defined as compulsory productive activity enforced by economic or political means—is the source of most of the misery in the world. Black denounces work for its compulsion, and for the forms it takes—as subordination to a boss, as a "job" which turns a potentially enjoyable task into a meaningless chore, for the degradation imposed by systems of work-discipline, and for the large number of work-related deaths and injuries—which Black typifies as "homicide". He views the subordination enacted in workplaces as "a mockery of freedom", and denounces as hypocrites the various theorists who support freedom while supporting work. Subordination in work, Black alleges, makes people stupid and creates fear of freedom. Because of work, people become accustomed to rigidity and regularity, and do not have the time for friendship or meaningful activity. Most workers, he states, are dissatisfied with work (as evidenced by petty deviance on the job), so that what he says should be uncontroversial; however, it is controversial only because people are too close to the work-system to see its flaws.

Play, in contrast, is not necessarily rule-governed, and is performed voluntarily, in complete freedom, as a gift economy. He points out that hunter-gatherer societies are typified by play, a view he backs up with the work of Marshall Sahlins; he recounts the rise of hierarchal societies, through which work is cumulatively imposed, so that the compulsive work of today would seem incomprehensibly oppressive even to ancients and medieval peasants. He responds to the view that "work", if not simply effort or energy, is necessary to get important but unpleasant tasks done, by claiming that first of all, most important tasks can be rendered ludic, or "salvaged" by being turned into game-like and craft-like activities, and secondly that the vast majority of work does not need doing at all. The latter tasks are unnecessary because they only serve functions of commerce and social control that exist only to maintain the work-system as a whole. As for what is left, he advocates Charles Fourier's approach of arranging activities so that people will want to do them. He is also skeptical but open-minded about the possibility of eliminating work through labor-saving technologies. He feels the left cannot go far enough in its critiques because of its attachment to building its power on the category of workers, which requires a valorization of work.

Total Liberation

In 2022, Green Theory & Praxis Journal published a Total Liberation Pathway which involved "an abolition of compulsory work for all beings." Described as a source code to be adapted based on local and changing conditions, the proposal involved reducing humans' workweek to 10 hours and transforming it into voluntary and self-managed hobbies, while freeing animals, ecosystems, plants, minerals, and the planet Earth from exploitation. Referring to climate models, the proposal suggested that it would be possible to provide a comfortable life for all human beings while rewilding at least 75% of the Earth and achieving the ambitious 300 parts per million and 1 degree Celsius climate targets of 2010's People’s Agreement of Cochabamba.

Stigmatization of people who don't work

Those who engage in refusal of work break one of the most powerful social norms of contemporary society. Hence they frequently receive harassment from people, sometimes irrespective of whether they made the choice to leave work behind or not. In Nazi Germany the so-called, "work-shy" individuals were rounded up and imprisoned in Nazi concentration camps as black triangle prisoners in the so-called "Aktion Arbeitsscheu Reich".

Other derogatory terms and their history

Cynic philosophical school

Cynicism (Greek: κυνισμός), in its original form, refers to the beliefs of an ancient school of Greek philosophers known as the Cynics (Greek: Κυνικοί, Latin: Cynici). Their philosophy was that the purpose of life was to live a life of Virtue in agreement with Nature. This meant rejecting all conventional desires for wealth, power, health, and fame, and by living a simple life free from all possessions. They believed that the world belonged equally to everyone, and that suffering was caused by false judgments of what was valuable and by the worthless customs and conventions which surrounded society.

Diogenes of Sinope – depicted by Jean-Léon Gérôme

The first philosopher to outline these themes was Antisthenes, who had been a pupil of Socrates in the late 5th century BCE. He was followed by Diogenes of Sinope, who lived in a tub on the streets of Athens. Diogenes took Cynicism to its logical extremes, and came to be seen as the archetypal Cynic philosopher. He was followed by Crates of Thebes who gave away a large fortune so he could live a life of Cynic poverty in Athens. Cynicism spread with the rise of Imperial Rome in the 1st century, and Cynics could be found begging and preaching throughout the cities of the Empire. It finally disappeared in the late 5th century, although many of its ascetic and rhetorical ideas were adopted by early Christianity. The name Cynic derives from the Greek word κυνικός, kynikos, "dog-like" and that from κύων, kyôn, "dog" (genitive: kynos).

It seems certain that the word dog was also thrown at the first Cynics as an insult for their shameless rejection of conventional manners, and their decision to live on the streets. Diogenes, in particular, was referred to as the Dog.

"Slackers"

The term slacker is commonly used to refer to a person who avoids work (especially British English), or (primarily in North American English) an educated person who is viewed as an underachiever.

While use of the term slacker dates back to about 1790 or 1898 depending on the source, it gained some recognition during the British Gezira Scheme, when Sudanese labourers protested their relative powerlessness by working lethargically, a form of protest known as 'slacking'. The term achieved a boost in popularity after its use in the films Back to the Future and Slacker.

NEET

NEET is an acronym for the government classification for people currently "Not in Employment, Education or Training". It was first used in the United Kingdom but its use has spread to other countries, including the United States, Japan, China, and South Korea.

In the United Kingdom, the classification comprises people aged between 16 and 24 (some 16-year-olds are still of compulsory education age). In Japan, the classification comprises people aged between 15 and 34 who are unemployed, unmarried, not enrolled in school or engaged in housework, and not seeking work or the technical training needed for work. The "NEET group" is not a uniform set of individuals but consists of those who will be NEET for a short time while essentially testing out a variety of opportunities and those who have major and often multiple issues and are at long term risk of remaining disengaged.

In Brazil, "nem-nem" (short of nem estudam nem trabalham (neither study nor work) is a term with similar meaning.

In Spanish-speaking countries, "ni-ni" (short of ni estudia ni trabaja) is also applied.

"Freeters" and parasite singles

Freeter (フリーター, furītā) (other spellings below) is a Japanese expression for people between the age of 15 and 34 who lack full-time employment or are unemployed, excluding homemakers and students. They may also be described as underemployed or freelance workers. These people do not start a career after high school or university but instead usually live as so-called parasite singles with their parents and earn some money with low skilled and low paid jobs.

The word freeter or freeta was first used around 1987 or 1988 and is thought to be an amalgamation of the English word free (or perhaps freelance) and the German word Arbeiter ("worker").

Parasite single (パラサイトシングル, parasaito shinguru) is a Japanese term for a single person who lives with their parents until their late twenties or early thirties in order to enjoy a carefree and comfortable life. In English, the expression "sponge" or "basement dweller" may sometimes be used.

The expression is mainly used in reference to Japanese society, but similar phenomena can also be found in other countries worldwide. In Italy, 30-something singles still relying on their mothers are joked about, being called Bamboccioni (literally: grown-up babies) and in Germany they are known as Nesthocker (German for an altricial bird), who are still living at Hotel Mama ^[de].

Such behaviour is considered normal in Greece, both because of the traditional strong family ties and because of the low wages.

Welfare queens

A Welfare queen is a derogatory term for a person, almost exclusively female and usually a single mother, who lives primarily from welfare and other public assistance funds. The term implies that the person collects welfare, charity, or other handouts either fraudulently or excessively and that the person intentionally chooses to live "on the dole" as opposed to seeking gainful employment, ostensibly due to laziness.

Vagrancy

A vagrant is derogatory term for a person in a situation of poverty, who wanders from place to place without a home or regular employment or income. Many towns in the developed world have shelters for vagrants. Common terminology is a tramp or a 'gentleman of the road'.

Laws against vagrancy in the United States have partly been invalidated as violative of the due process clauses of the U.S. Constitution. However, the FBI report on crime in the United States for 2005 lists 24,359 vagrancy violations.

"Hobos", "tramps", and "bums"

Two hobos walking along railroad tracks, after being put off a train. One is carrying a bindle.

A hobo is a migratory worker or homeless vagabond, often penniless. The term originated in the western—probably northwestern—United States during the last decade of the 19th century. Unlike tramps, who worked only when they were forced to, and bums, who did not work at all, hobos were workers who wandered.

In British English and traditional American English usage, a tramp is a long term homeless person who travels from place to place as an itinerant vagrant, traditionally walking or hiking all year round.

While some tramps may do odd jobs from time to time, unlike other temporarily homeless people they do not seek out regular work and support themselves by other means such as begging or scavenging. This is in contrast to:

• bum, a stationary homeless person who does not work, and who begs or steals for a living in one place.
• hobo, a homeless person who travels from place to place looking for work, often by "freighthopping", illegally catching rides on freight trains
• Schnorrer, a Yiddish term for a person who travels from city to city begging.

Both terms, "tramp" and "hobo" (and the distinction between them), were in common use between the 1880s and the 1940s. Their populations and the usage of the terms increased during the Great Depression.

Like "hobo" and "bum", the word "tramp" is considered vulgar in American English usage, having been subsumed in more polite contexts by words such as "homeless person." In colloquial American English, the word "tramp" can also mean a sexually promiscuous female or even prostitute. Tramps used to be known euphemistically in England and Wales as "gentlemen of the road".

Tramp is derived from the Middle English as a verb meaning to "walk with heavy footsteps", and to go hiking. Bart Kennedy, a self-described tramp of 1900 US, once said "I listen to the tramp, tramp of my feet, and wonder where I was going, and why I was going."

"Gutter punks"

A gutter punk is a homeless or transient individual, often through means of freighthopping or hitchhiking. Gutter punks are often juveniles who are in some way associated with the anarcho-punk subculture. In certain regions, gutter punks are notorious for panhandling and often display cardboard signs that make statements about their lifestyles. Gutter punks are generally characterized as being voluntarily unemployed.