A Medley of Potpourri

Monday, October 3, 2022

Animal navigation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Animal_navigation

Manx shearwaters can fly straight home when released, navigating thousands of miles over land or sea.

Animal navigation is the ability of many animals to find their way accurately without maps or instruments. Birds such as the Arctic tern, insects such as the monarch butterfly and fish such as the salmon regularly migrate thousands of miles to and from their breeding grounds, and many other species navigate effectively over shorter distances.

Dead reckoning, navigating from a known position using only information about one's own speed and direction, was suggested by Charles Darwin in 1873 as a possible mechanism. In the 20th century, Karl von Frisch showed that honey bees can navigate by the sun, by the polarization pattern of the blue sky, and by the earth's magnetic field; of these, they rely on the sun when possible. William Tinsley Keeton showed that homing pigeons could similarly make use of a range of navigational cues, including the sun, earth's magnetic field, olfaction and vision. Ronald Lockley demonstrated that a small seabird, the Manx shearwater, could orient itself and fly home at full speed, when released far from home, provided either the sun or the stars were visible.

Several species of animal can integrate cues of different types to orient themselves and navigate effectively. Insects and birds are able to combine learned landmarks with sensed direction (from the earth's magnetic field or from the sky) to identify where they are and so to navigate. Internal 'maps' are often formed using vision, but other senses including olfaction and echolocation may also be used.

The ability of wild animals to navigate may be adversely affected by products of human activity. For example, there is evidence that pesticides may interfere with bee navigation, and that lights may harm turtle navigation.

Early research

Karl von Frisch (1953) discovered that honey bee workers can navigate, and indicate the range and direction to food to other workers with a waggle dance.

In 1873, Charles Darwin wrote a letter to Nature magazine, arguing that animals including man have the ability to navigate by dead reckoning, even if a magnetic 'compass' sense and the ability to navigate by the stars is present:

With regard to the question of the means by which animals find their way home from a long distance, a striking account, in relation to man, will be found in the English translation of the Expedition to North Siberia, by Von Wrangell. He there describes the wonderful manner in which the natives kept a true course towards a particular spot, whilst passing for a long distance through hummocky ice, with incessant changes of direction, and with no guide in the heavens or on the frozen sea. He states (but I quote only from memory of many years standing) that he, an experienced surveyor, and using a compass, failed to do that which these savages easily effected. Yet no one will suppose that they possessed any special sense which is quite absent in us. We must bear in mind that neither a compass, nor the north star, nor any other such sign, suffices to guide a man to a particular spot through an intricate country, or through hummocky ice, when many deviations from a straight course are inevitable, unless the deviations are allowed for, or a sort of "dead reckoning" is kept. All men are able to do this in a greater or less degree, and the natives of Siberia apparently to a wonderful extent, though probably in an unconscious manner. This is effected chiefly, no doubt, by eyesight, but partly, perhaps, by the sense of muscular movement, in the same manner as a man with his eyes blinded can proceed (and some men much better than others) for a short distance in a nearly straight line, or turn at right angles, or back again. The manner in which the sense of direction is sometimes suddenly disarranged in very old and feeble persons, and the feeling of strong distress which, as I know, has been experienced by persons when they have suddenly found out that they have been proceeding in a wholly unexpected and wrong direction, leads to the suspicion that some part of the brain is specialised for the function of direction.

Later in 1873, Joseph John Murphy replied to Darwin, writing back to Nature with a description of how he, Murphy, believed animals carried out dead reckoning, by what is now called inertial navigation:

If a ball is freely suspended from the roof of a railway carriage it will receive a shock sufficient to move it, when the carriage is set in motion: and the magnitude and direction of the shock … will depend on the magnitude and direction of the force with which the carriage begins to move … [and so] … every change in … the motion of the carriage … will give a shock of corresponding magnitude and direction to the ball. Now, it is conceivably quite possible, though such delicacy of mechanism is not to be hoped for, that a machine should be constructed … for registering the magnitude and direction of all these shocks, with the time at which each occurred … from these data the position of the carriage … might be calculated at any moment.

Karl von Frisch (1886–1982) studied the European honey bee, demonstrating that bees can recognize a desired compass direction in three different ways: by the sun, by the polarization pattern of the blue sky, and by the earth's magnetic field. He showed that the sun is the preferred or main compass; the other mechanisms are used under cloudy skies or inside a dark beehive.

William Tinsley Keeton (1933–1980) studied homing pigeons, showing that they were able to navigate using the earth's magnetic field, the sun, as well as both olfactory and visual cues.

Donald Griffin (1915–2003) studied echolocation in bats, demonstrating that it was possible and that bats used this mechanism to detect and track prey, and to "see" and thus navigate through the world around them.

Ronald Lockley (1903–2000), among many studies of birds in over fifty books, pioneered the science of bird migration. He made a twelve-year study of shearwaters such as the Manx shearwater, living on the remote island of Skokholm. These small seabirds make one of the longest migrations of any bird—10,000 kilometres—but return to the exact nesting burrow on Skokholm year after year. This behaviour led to the question of how they navigated.

Mechanisms

Lockley began his book Animal Navigation with the words:

How do animals find their way over apparently trackless country, through pathless forests, across empty deserts, over and under featureless seas? ... They do so, of course, without any visible compass, sextant, chronometer or chart...

Many mechanisms of spatial cognition have been proposed for animal navigation: there is evidence for a number of them. Investigators have often been forced to discard the simplest hypotheses - for example, some animals can navigate on a dark and cloudy night, when neither landmarks nor celestial cues like sun, moon, or stars are visible. The major mechanisms known or hypothesized are described in turn below.

Remembered landmarks

Animals including mammals, birds and insects such as bees and wasps (Ammophila and Sphex), are capable of learning landmarks in their environment, and of using these in navigation.

Orientation by the sun

The sandhopper, Talitrus saltator, uses the sun and its internal clock to determine direction.

Some animals can navigate using celestial cues such as the position of the sun. Since the sun moves in the sky, navigation by this means also requires an internal clock. Many animals depend on such a clock to maintain their circadian rhythm. Animals that use sun compass orientation are fish, birds, sea-turtles, butterflies, bees, sandhoppers, reptiles, and ants.

When sandhoppers (such as Talitrus saltator) are taken up a beach, they easily find their way back down to the sea. It has been shown that this is not simply by moving downhill or towards the sight or sound of the sea. A group of sandhoppers were acclimatised to a day/night cycle under artificial lighting, whose timing was gradually changed until it was 12 hours out of phase with the natural cycle. Then, the sandhoppers were placed on the beach in natural sunlight. They moved away from the sea, up the beach. The experiment implied that the sandhoppers use the sun and their internal clock to determine their heading, and that they had learnt the actual direction down to the sea on their particular beach.

Experiments with Manx shearwaters showed that when released "under a clear sky" far from their nests, the seabirds first oriented themselves and then flew off in the correct direction. But if the sky was overcast at the time of release, the shearwaters flew around in circles.

Monarch butterflies use the sun as a compass to guide their southwesterly autumn migration from Canada to Mexico.

Orientation by the night sky

In a pioneering experiment, Lockley showed that warblers placed in a planetarium showing the night sky oriented themselves towards the south; when the planetarium sky was then very slowly rotated, the birds maintained their orientation with respect to the displayed stars. Lockley observes that to navigate by the stars, birds would need both a "sextant and chronometer": a built-in ability to read patterns of stars and to navigate by them, which also requires an accurate time-of-day clock.

In 2003, the African dung beetle Scarabaeus zambesianus was shown to navigate using polarization patterns in moonlight, making it the first animal known to use polarized moonlight for orientation. In 2013, it was shown that dung beetles can navigate when only the Milky Way or clusters of bright stars are visible, making dung beetles the only insects known to orient themselves by the galaxy.

Orientation by polarised light

Rayleigh sky model shows how polarization of light can indicate direction to bees.

Some animals, notably insects such as the honey bee, are sensitive to the polarisation of light. Honey bees can use polarized light on overcast days to estimate the position of the sun in the sky, relative to the compass direction they intend to travel. Karl von Frisch's work established that bees can accurately identify the direction and range from the hive to a food source (typically a patch of nectar-bearing flowers). A worker bee returns to the hive and signals to other workers the range and direction relative to the sun of the food source by means of a waggle dance. The observing bees are then able to locate the food by flying the implied distance in the given direction, though other biologists have questioned whether they necessarily do so, or are simply stimulated to go and search for food. However, bees are certainly able to remember the location of food, and to navigate back to it accurately, whether the weather is sunny (in which case navigation may be by the sun or remembered visual landmarks) or largely overcast (when polarised light may be used).

Magnetoreception

The homing pigeon can quickly return to its home, using cues such as the earth's magnetic field to orient itself.

Some animals, including mammals such as blind mole rats (Spalax) and birds such as pigeons, are sensitive to the earth's magnetic field.

Homing pigeons use magnetic field information with other navigational cues. Pioneering researcher William Keeton showed that time-shifted homing pigeons could not orient themselves correctly on a clear sunny day, but could do so on an overcast day, suggesting that the birds prefer to rely on the direction of the sun, but switch to using a magnetic field cue when the sun is not visible. This was confirmed by experiments with magnets: the pigeons could not orient correctly on an overcast day when the magnetic field was disrupted.

Olfaction

Returning salmon may use olfaction to identify the river in which they developed.

Olfactory navigation has been suggested as a possible mechanism in pigeons. Papi's 'mosaic' model argues that pigeons build and remember a mental map of the odours in their area, recognizing where they are by the local odour. Wallraff's 'gradient' model argues that there is a steady, large-scale gradient of odour which remains stable for long periods. If there were two or more such gradients in different directions, pigeons could locate themselves in two dimensions by the intensities of the odours. However it is not clear that such stable gradients exist. Papi did find evidence that anosmic pigeons (unable to detect odours) were much less able to orient and navigate than normal pigeons, so olfaction does seem to be important in pigeon navigation. However, it is not clear how olfactory cues are used.

Olfactory cues may be important in salmon, which are known to return to the exact river where they hatched. Lockley reports experimental evidence that fish such as minnows can accurately tell the difference between the waters of different rivers. Salmon may use their magnetic sense to navigate to within reach of their river, and then use olfaction to identify the river at close range.

Gravity receptors

GPS tracing studies indicate that gravity anomalies could play a role in homing pigeon navigation.

Other senses

Biologists have considered other senses that may contribute to animal navigation. Many marine animals such as seals are capable of hydrodynamic reception, enabling them to track and catch prey such as fish by sensing the disturbances their passage leaves behind in the water. Marine mammals such as dolphins, and many species of bat, are capable of echolocation, which they use both for detecting prey and for orientation by sensing their environment.

Way-marking

The wood mouse is the first non-human animal to be observed, both in the wild and under laboratory conditions, using movable landmarks to navigate. While foraging, they pick up and distribute visually conspicuous objects, such as leaves and twigs, which they then use as landmarks during exploration, moving the markers when the area has been explored.

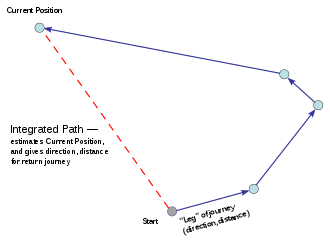
Path integration

Path integration sums the vectors of distance and direction travelled from a start point to estimate current position, and so the path back to the start.

Dead reckoning, in animals usually known as path integration, means the putting together of cues from different sensory sources within the body, without reference to visual or other external landmarks, to estimate position relative to a known starting point continuously while travelling on a path that is not necessarily straight. Seen as a problem in geometry, the task is to compute the vector to a starting point by adding the vectors for each leg of the journey from that point.

Since Darwin's On the Origins of Certain Instincts (quoted above) in 1873, path integration has been shown to be important to navigation in animals including ants, rodents and birds. When vision (and hence the use of remembered landmarks) is not available, such as when animals are navigating on a cloudy night, in the open ocean, or in relatively featureless areas such as sandy deserts, path integration must rely on idiothetic cues from within the body.

Studies by Wehner in the Sahara desert ant (Cataglyphis bicolor) demonstrate effective path integration to determine directional heading (by polarized light or sun position) and to compute distance (by monitoring leg movement or optical flow).

Path integration in mammals makes use of the vestibular organs, which detect accelerations in the three dimensions, together with motor efference, where the motor system tells the rest of the brain which movements were commanded, and optic flow, where the visual system signals how fast the visual world moves past the eyes. Information from other senses such as echolocation and magnetoreception may also be integrated in certain animals. The hippocampus is the part of the brain that integrates linear and angular motion to encode a mammal's relative position in space.

David Redish states that "The carefully controlled experiments of Mittelstaedt and Mittelstaedt (1980) and Etienne (1987) have demonstrated conclusively that [path integration in mammals] is a consequence of integrating internal cues from vestibular signals and motor efferent copy".

Effects of human activity

Neonicotinoid pesticides may impair the ability of bees to navigate. Bees exposed to low levels of thiamethoxam were less likely to return to their colony, to an extent sufficient to compromise a colony's survival.

Light pollution attracts and disorients photophilic animals, those that follow light. For example, hatchling sea turtles follow bright light, particularly bluish light, altering their navigation. Disrupted navigation in moths can easily be observed around bright lamps on summer nights. Insects gather around these lamps at high densities instead of navigating naturally.

Penrose tiling

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Penrose_tiling

A Penrose tiling with rhombi exhibiting fivefold symmetry

A Penrose tiling is an example of an aperiodic tiling. Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and aperiodic means that shifting any tiling with these shapes by any finite distance, without rotation, cannot produce the same tiling. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s.

There are several different variations of Penrose tilings with different tile shapes. The original form of Penrose tiling used tiles of four different shapes, but this was later reduced to only two shapes: either two different rhombi, or two different quadrilaterals called kites and darts. The Penrose tilings are obtained by constraining the ways in which these shapes are allowed to fit together. This may be done in several different ways, including matching rules, substitution tiling or finite subdivision rules, cut and project schemes, and coverings. Even constrained in this manner, each variation yields infinitely many different Penrose tilings.

Roger Penrose in the foyer of the Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, standing on a floor with a Penrose tiling

Penrose tilings are self-similar: they may be converted to equivalent Penrose tilings with different sizes of tiles, using processes called inflation and deflation. The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling. They are quasicrystals: implemented as a physical structure a Penrose tiling will produce diffraction patterns with Bragg peaks and five-fold symmetry, revealing the repeated patterns and fixed orientations of its tiles. The study of these tilings has been important in the understanding of physical materials that also form quasicrystals. Penrose tilings have also been applied in architecture and decoration, as in the floor tiling shown.

Background and history

Periodic and aperiodic tilings

Figure 1. Part of a periodic tiling with two prototiles

Covering a flat surface ("the plane") with some pattern of geometric shapes ("tiles"), with no overlaps or gaps, is called a tiling. The most familiar tilings, such as covering a floor with squares meeting edge-to-edge, are examples of periodic tilings. If a square tiling is shifted by the width of a tile, parallel to the sides of the tile, the result is the same pattern of tiles as before the shift. A shift (formally, a translation) that preserves the tiling in this way is called a period of the tiling. A tiling is called periodic when it has periods that shift the tiling in two different directions.

The tiles in the square tiling have only one shape, and it is common for other tilings to have only a finite number of shapes. These shapes are called prototiles, and a set of prototiles is said to admit a tiling or tile the plane if there is a tiling of the plane using only these shapes. That is, each tile in the tiling must be congruent to one of these prototiles.

A tiling that has no periods is non-periodic. A set of prototiles is said to be aperiodic if all of its tilings are non-periodic, and in this case its tilings are also called aperiodic tilings. Penrose tilings are among the simplest known examples of aperiodic tilings of the plane by finite sets of prototiles.

Earliest aperiodic tilings

An aperiodic set of Wang dominoes.

The subject of aperiodic tilings received new interest in the 1960s when logician Hao Wang noted connections between decision problems and tilings. In particular, he introduced tilings by square plates with colored edges, now known as Wang dominoes or tiles, and posed the "Domino Problem": to determine whether a given set of Wang dominoes could tile the plane with matching colors on adjacent domino edges. He observed that if this problem were undecidable, then there would have to exist an aperiodic set of Wang dominoes. At the time, this seemed implausible, so Wang conjectured no such set could exist.

Robinson's six prototiles

Wang's student Robert Berger proved that the Domino Problem was undecidable (so Wang's conjecture was incorrect) in his 1964 thesis, and obtained an aperiodic set of 20,426 Wang dominoes. He also described a reduction to 104 such prototiles; the latter did not appear in his published monograph, but in 1968, Donald Knuth detailed a modification of Berger's set requiring only 92 dominoes.

The color matching required in a tiling by Wang dominoes can easily be achieved by modifying the edges of the tiles like jigsaw puzzle pieces so that they can fit together only as prescribed by the edge colorings. Raphael Robinson, in a 1971 paper which simplified Berger's techniques and undecidability proof, used this technique to obtain an aperiodic set of just six prototiles.

Development of the Penrose tilings

The first Penrose tiling (tiling P1 below) is an aperiodic set of six prototiles, introduced by Roger Penrose in a 1974 paper, based on pentagons rather than squares. Any attempt to tile the plane with regular pentagons necessarily leaves gaps, but Johannes Kepler showed, in his 1619 work Harmonices Mundi, that these gaps can be filled using pentagrams (star polygons), decagons and related shapes. Kepler extended this tiling by five polygons and found no periodic patterns, and already conjectured that every extension would introduce a new feature hence creating an aperiodic tiling. Traces of these ideas can also be found in the work of Albrecht Dürer. Acknowledging inspiration from Kepler, Penrose found matching rules for these shapes, obtaining an aperiodic set. These matching rules can be imposed by decorations of the edges, as with the Wang tiles. Penrose's tiling can be viewed as a completion of Kepler's finite Aa pattern.

A non-Penrose tiling by pentagons and thin rhombs in the early 18th-century Pilgrimage Church of Saint John of Nepomuk at Zelená hora, Czech Republic

Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by Martin Gardner in his January 1977 "Mathematical Games" column in Scientific American.

In 1981, N. G. de Bruijn provided two different methods to construct Penrose tilings. De Bruijn's "multigrid method" obtains the Penrose tilings as the dual graphs of arrangements of five families of parallel lines. In his "cut and project method", Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In these approaches, the Penrose tiling is viewed as a set of points, its vertices, while the tiles are geometrical shapes obtained by connecting vertices with edges.

Penrose tilings

A P1 tiling using Penrose's original set of six prototiles

The three types of Penrose tiling, P1–P3, are described individually below. They have many common features: in each case, the tiles are constructed from shapes related to the pentagon (and hence to the golden ratio), but the basic tile shapes need to be supplemented by matching rules in order to tile aperiodically. These rules may be described using labeled vertices or edges, or patterns on the tile faces; alternatively, the edge profile can be modified (e.g. by indentations and protrusions) to obtain an aperiodic set of prototiles.

Original pentagonal Penrose tiling (P1)

Penrose's first tiling uses pentagons and three other shapes: a five-pointed "star" (a pentagram), a "boat" (roughly 3/5 of a star) and a "diamond" (a thin rhombus). To ensure that all tilings are non-periodic, there are matching rules that specify how tiles may meet each other, and there are three different types of matching rule for the pentagonal tiles. Treating these three types as different prototiles gives a set of six prototiles overall. It is common to indicate the three different types of pentagonal tiles using three different colors, as in the figure above right.

Kite and dart tiling (P2)

Part of the plane covered by Penrose tiling of type P2 (kite and dart). Created by applying several deflations, see section below.

Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called Robinson triangles, after 1975 notes by Robinson.

Kite and dart tiles (top) and the seven possible vertex figures in a P2 tiling.

The kite is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
The dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.

The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices. Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.

These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). Apart from the ace and the sun, all of these vertex figures force the placement of additional tiles.

Rhombus tiling (P3)

Matching rule for Penrose rhombs using circular arcs or edge modifications to enforce the tiling rules

Matching rule for Penrose rhombs using parabolic edges to enforce the tiling rules

A Penrose Tiling using Penrose Rhombuses with parabolic edges

The third tiling uses a pair of rhombuses (often referred to as "rhombs" in this context) with equal sides but different angles. Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled: no two tiles may form a parallelogram, as this would allow a periodic tiling, but this constraint is not sufficient to force aperiodicity, as figure 1 above shows.

There are two kinds of tile, both of which can be decomposed into Robinson triangles.

The thin rhomb t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhomb may be bisected along its short diagonal to form a pair of acute Robinson triangles.
The thick rhomb T has angles of 72, 108, 72, and 108 degrees. The T rhomb may be bisected along its long diagonal to form a pair of obtuse Robinson triangles; in contrast to the P2 tiling, these are larger than the acute triangles.

The matching rules distinguish sides of the tiles, and entail that tiles may be juxtaposed in certain particular ways but not in others. Two ways to describe these matching rules are shown in the image on the right. In one form, tiles must be assembled such that the curves on the faces match in color and position across an edge. In the other, tiles must be assembled such that the bumps on their edges fit together.

There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only seven of these combinations to appear (although one of these arises in two ways).

The various combinations of angles and facial curvature allow construction of arbitrarily complex tiles, such as the Penrose chickens.

Features and constructions

Golden ratio and local pentagonal symmetry

Several properties and common features of the Penrose tilings involve the golden ratio $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ (approximately 1.618). This is the ratio of chord lengths to side lengths in a regular pentagon, and satisfies $φ$ = 1 + 1/ $φ$ .

Pentagon with an inscribed thick rhomb (light), acute Robinson triangles (lightly shaded) and a small obtuse Robinson triangle (darker). Dotted lines give additional edges for inscribed kites and darts.

Consequently, the ratio of the lengths of long sides to short sides in the (isosceles) Robinson triangles is $φ$ :1. It follows that the ratio of long side lengths to short in both kite and dart tiles is also $φ$ :1, as are the length ratios of sides to the short diagonal in the thin rhomb t, and of long diagonal to sides in the thick rhomb T. In both the P2 and P3 tilings, the ratio of the area of the larger Robinson triangle to the smaller one is $φ$ :1, hence so are the ratios of the areas of the kite to the dart, and of the thick rhomb to the thin rhomb. (Both larger and smaller obtuse Robinson triangles can be found in the pentagon on the left: the larger triangles at the top – the halves of the thick rhomb – have linear dimensions scaled up by $φ$ compared to the small shaded triangle at the base, and so the ratio of areas is $φ$ ²:1.)

Any Penrose tiling has local pentagonal symmetry, in the sense that there are points in the tiling surrounded by a symmetric configuration of tiles: such configurations have fivefold rotational symmetry about the center point, as well as five mirror lines of reflection symmetry passing through the point, a dihedral symmetry group. This symmetry will generally preserve only a patch of tiles around the center point, but the patch can be very large: Conway and Penrose proved that whenever the colored curves on the P2 or P3 tilings close in a loop, the region within the loop has pentagonal symmetry, and furthermore, in any tiling, there are at most two such curves of each color that do not close up.

There can be at most one center point of global fivefold symmetry: if there were more than one, then rotating each about the other would yield two closer centers of fivefold symmetry, which leads to a mathematical contradiction. There are only two Penrose tilings (of each type) with global pentagonal symmetry: for the P2 tiling by kites and darts, the center point is either a "sun" or "star" vertex.

Inflation and deflation

A pentagon decomposed into six smaller pentagons (half a dodecahedral net) with gaps

Many of the common features of Penrose tilings follow from a hierarchical pentagonal structure given by substitution rules: this is often referred to as inflation and deflation, or composition and decomposition, of tilings or (collections of) tiles. The substitution rules decompose each tile into smaller tiles of the same shape as those used in the tiling (and thus allow larger tiles to be "composed" from smaller ones). This shows that the Penrose tiling has a scaling self-similarity, and so can be thought of as a fractal, using the same process as the pentaflake.

Penrose originally discovered the P1 tiling in this way, by decomposing a pentagon into six smaller pentagons (one half of a net of a dodecahedron) and five half-diamonds; he then observed that when he repeated this process the gaps between pentagons could all be filled by stars, diamonds, boats and other pentagons. By iterating this process indefinitely he obtained one of the two P1 tilings with pentagonal symmetry.

Robinson triangle decompositions

Robinson triangles and their decompositions

The substitution method for both P2 and P3 tilings can be described using Robinson triangles of different sizes. The Robinson triangles arising in P2 tilings (by bisecting kites and darts) are called A-tiles, while those arising in the P3 tilings (by bisecting rhombs) are called B-tiles. The smaller A-tile, denoted A_S, is an obtuse Robinson triangle, while the larger A-tile, A_L, is acute; in contrast, a smaller B-tile, denoted B_S, is an acute Robinson triangle, while the larger B-tile, B_L, is obtuse.

Concretely, if A_S has side lengths (1, 1, $φ$ ), then A_L has side lengths ( $φ$ , $φ$ , 1). B-tiles can be related to such A-tiles in two ways:

If B_S has the same size as A_L then B_L is an enlarged version $φ$ A_S of A_S, with side lengths ( $φ$ , $φ$ , $φ$ ² = 1 + $φ$ ) – this decomposes into an A_L tile and A_S tile joined along a common side of length 1.
If instead B_L is identified with A_S, then B_S is a reduced version (1/ $φ$ )A_L of A_L with side lengths (1/ $φ$ ,1/ $φ$ ,1) – joining a B_S tile and a B_L tile along a common side of length 1 then yields (a decomposition of) an A_L tile.

In these decompositions, there appears to be an ambiguity: Robinson triangles may be decomposed in two ways, which are mirror images of each other in the (isosceles) axis of symmetry of the triangle. In a Penrose tiling, this choice is fixed by the matching rules. Furthermore, the matching rules also determine how the smaller triangles in the tiling compose to give larger ones.

Partial inflation of star to yield rhombs, and of a collection of rhombs to yield an ace.

It follows that the P2 and P3 tilings are mutually locally derivable: a tiling by one set of tiles can be used to generate a tiling by another. For example, a tiling by kites and darts may be subdivided into A-tiles, and these can be composed in a canonical way to form B-tiles and hence rhombs. The P2 and P3 tilings are also both mutually locally derivable with the P1 tiling (see figure 2 above).

The decomposition of B-tiles into A-tiles may be written

B_S = A_L, B_L = A_L + A_S

(assuming the larger size convention for the B-tiles), which can be summarized in a substitution matrix equation:

{\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.

Combining this with the decomposition of enlarged $φ$ A-tiles into B-tiles yields the substitution

{\displaystyle {\begin{pmatrix}\varphi A_{L}\\\varphi A_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,,}

so that the enlarged tile $φ$ A_L decomposes into two A_L tiles and one A_S tiles. The matching rules force a particular substitution: the two A_L tiles in a $φ$ A_L tile must form a kite, and thus a kite decomposes into two kites and a two half-darts, and a dart decomposes into a kite and two half-darts. Enlarged $φ$ B-tiles decompose into B-tiles in a similar way (via $φ$ A-tiles).

Composition and decomposition can be iterated, so that, for example

{\displaystyle \varphi ^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}

The number of kites and darts in the nth iteration of the construction is determined by the nth power of the substitution matrix:

{\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{pmatrix}}\,,

where F_n is the nth Fibonacci number. The ratio of numbers of kites to darts in any sufficiently large P2 Penrose tiling pattern therefore approximates to the golden ratio $φ$ . A similar result holds for the ratio of the number of thick rhombs to thin rhombs in the P3 Penrose tiling.

Deflation for P2 and P3 tilings

Consecutive deflations of the 'sun' vertex in a Penrose tiling of type P2

Consecutive deflations of a tile-set in a Penrose tiling of type P3

8th deflation of the 'sun' vertex in a Penrose tiling of type P2

Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.

This rule for dividing the tiles is a subdivision rule.

Name	Initial tiles	Generation 1	Generation 2	Generation 3
Half-kite
Half-dart
Sun
Star

The above table should be used with caution. The half kite and half dart deflation are useful only in the context of deflating a larger pattern as shown in the sun and star deflations. They give incorrect results if applied to single kites and darts.

In addition, the simple subdivision rule generates holes near the edges of the tiling which are just visible in the top and bottom illustrations on the right. Additional forcing rules are useful.

Consequences and applications

Inflation and deflation yield a method for constructing kite and dart (P2) tilings, or rhombus (P3) tilings, known as up-down generation.

The Penrose tilings, being non-periodic, have no translational symmetry – the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore, no finite patch can uniquely determine a full Penrose tiling, nor even determine which position within the tiling is being shown.

This shows in particular that the number of distinct Penrose tilings (of any type) is uncountably infinite. Up-down generation yields one method to parameterize the tilings, but other methods use Ammann bars, pentagrids, or cut and project schemes.

Art and architecture

Pentagonal and decagonal Girih-tile pattern on a spandrel from the Darb-i Imam shrine, Isfahan, Iran (1453 C.E.)
Salesforce Transit Center in San Francisco. The outer "skin", made of white aluminum, is perforated in the pattern of a Penrose tiling.
Penrose tiling on the floor in Computer Center 3 (CC-3), IIIT Allahabad

The aesthetic value of tilings has long been appreciated, and remains a source of interest in them; hence the visual appearance (rather than the formal defining properties) of Penrose tilings has attracted attention. The similarity with certain decorative patterns used in North Africa and the Middle East has been noted; the physicists Peter J. Lu and Paul Steinhardt have presented evidence that a Penrose tiling underlies examples of medieval Islamic geometric patterns, such as the girih (strapwork) tilings at the Darb-e Imam shrine in Isfahan.

Drop City artist Clark Richert used Penrose rhombs in artwork in 1970, derived by projecting the rhombic triacontahedron shadow onto a plane observing the embedded "fat" rhombi and "skinny" rhombi which tile together to produce the non-periodic tessellation. Art historian Martin Kemp has observed that Albrecht Dürer sketched similar motifs of a rhombus tiling.

San Francisco's new $2.2 billion Transbay Transit Center features perforations in its exterior's undulating white metal skin in the Penrose pattern.

The floor of the atrium of the Bayliss Building at The University of Western Australia is tiled with Penrose tiles.

In 1979, Miami University used a Penrose tiling executed in terrazzo to decorate the Bachelor Hall courtyard in their Department of Mathematics and Statistics.

In Indian Institute of Information Technology, Allahabad, since the first phase of construction in 2001, academic buildings were designed on the basis of "Penrose Geometry", styled on tessellations developed by Roger Penrose. In many places in those buildings, the floor has geometric patterns composed of Penrose tiling.

The Andrew Wiles Building, the location of the Mathematics Department at the University of Oxford as of October 2013, includes a section of Penrose tiling as the paving of its entrance.

The pedestrian part of the street Keskuskatu in central Helsinki is paved using a form of Penrose tiling. The work was finished in 2014.