Diffusion MRI

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Diffusion_MRI 

 

DTI Color Map
MeSH	D038524

Diffusion-weighted magnetic resonance imaging (DWI or DW-MRI) is the use of specific MRI sequences as well as software that generates images from the resulting data that uses the diffusion of water molecules to generate contrast in MR images. It allows the mapping of the diffusion process of molecules, mainly water, in biological tissues, in vivo and non-invasively. Molecular diffusion in tissues is not random, but reflects interactions with many obstacles, such as macromolecules, fibers, and membranes. Water molecule diffusion patterns can therefore reveal microscopic details about tissue architecture, either normal or in a diseased state. A special kind of DWI, diffusion tensor imaging (DTI), has been used extensively to map white matter tractography in the brain.

Introduction

In diffusion weighted imaging (DWI), the intensity of each image element (voxel) reflects the best estimate of the rate of water diffusion at that location. Because the mobility of water is driven by thermal agitation and highly dependent on its cellular environment, the hypothesis behind DWI is that findings may indicate (early) pathologic change. For instance, DWI is more sensitive to early changes after a stroke than more traditional MRI measurements such as T1 or T2 relaxation rates. A variant of diffusion weighted imaging, diffusion spectrum imaging (DSI), was used in deriving the Connectome data sets; DSI is a variant of diffusion-weighted imaging that is sensitive to intra-voxel heterogeneities in diffusion directions caused by crossing fiber tracts and thus allows more accurate mapping of axonal trajectories than other diffusion imaging approaches.

Diffusion-weighted images are very useful to diagnose vascular strokes in the brain. It is also used more and more in the staging of non-small-cell lung cancer, where it is a serious candidate to replace positron emission tomography as the 'gold standard' for this type of disease. Diffusion tensor imaging is being developed for studying the diseases of the white matter of the brain as well as for studies of other body tissues (see below). DWI is most applicable when the tissue of interest is dominated by isotropic water movement e.g. grey matter in the cerebral cortex and major brain nuclei, or in the body—where the diffusion rate appears to be the same when measured along any axis. However, DWI also remains sensitive to T1 and T2 relaxation. To entangle diffusion and relaxation effects on image contrast, one may obtain quantitative images of the diffusion coefficient, or more exactly the apparent diffusion coefficient (ADC). The ADC concept was introduced to take into account the fact that the diffusion process is complex in biological tissues and reflects several different mechanisms.

Diffusion tensor imaging (DTI) is important when a tissue—such as the neural axons of white matter in the brain or muscle fibers in the heart—has an internal fibrous structure analogous to the anisotropy of some crystals. Water will then diffuse more rapidly in the direction aligned with the internal structure (axial diffusion), and more slowly as it moves perpendicular to the preferred direction (radial diffusion). This also means that the measured rate of diffusion will differ depending on the direction from which an observer is looking.

Diffusion Basis Spectrum Imaging (DBSI) further separates DTI signals into discrete anisotropic diffusion tensors and a spectrum of isotropic diffusion tensors to better differentiate sub-voxel cellular structures. For example, anisotropic diffusion tensors correlate to axonal fibers, while low isotropic diffusion tensors correlate to cells and high isotropic diffusion tensors correlate to larger structures (such as the lumen or brain ventricles).

Traditionally, in diffusion-weighted imaging (DWI), three gradient-directions are applied, sufficient to estimate the trace of the diffusion tensor or 'average diffusivity', a putative measure of edema. Clinically, trace-weighted images have proven to be very useful to diagnose vascular strokes in the brain, by early detection (within a couple of minutes) of the hypoxic edema.

More extended DTI scans derive neural tract directional information from the data using 3D or multidimensional vector algorithms based on six or more gradient directions, sufficient to compute the diffusion tensor. The diffusion tensor model is a rather simple model of the diffusion process, assuming homogeneity and linearity of the diffusion within each image voxel. From the diffusion tensor, diffusion anisotropy measures such as the fractional anisotropy (FA), can be computed. Moreover, the principal direction of the diffusion tensor can be used to infer the white-matter connectivity of the brain (i.e. tractography; trying to see which part of the brain is connected to which other part).

Recently, more advanced models of the diffusion process have been proposed that aim to overcome the weaknesses of the diffusion tensor model. Amongst others, these include q-space imaging and generalized diffusion tensor imaging.

Mechanism

Diffusion imaging is an MRI method that produces in vivo magnetic resonance images of biological tissues sensitized with the local characteristics of molecular diffusion, generally water (but other moieties can also be investigated using MR spectroscopic approaches). MRI can be made sensitive to the motion of molecules. Regular MRI acquisition utilizes the behavior of protons in water to generate contrast between clinically relevant features of a particular subject. The versatile nature of MRI is due to this capability of producing contrast related to the structure of tissues at the microscopic level. In a typical ${\displaystyle T_{1}}$-weighted image, water molecules in a sample are excited with the imposition of a strong magnetic field. This causes many of the protons in water molecules to precess simultaneously, producing signals in MRI. In ${\displaystyle T_{2}}$-weighted images, contrast is produced by measuring the loss of coherence or synchrony between the water protons. When water is in an environment where it can freely tumble, relaxation tends to take longer. In certain clinical situations, this can generate contrast between an area of pathology and the surrounding healthy tissue.

To sensitize MRI images to diffusion, the magnetic field strength (B1) is varied linearly by a pulsed field gradient. Since precession is proportional to the magnet strength, the protons begin to precess at different rates, resulting in dispersion of the phase and signal loss. Another gradient pulse is applied in the same magnitude but with opposite direction to refocus or rephase the spins. The refocusing will not be perfect for protons that have moved during the time interval between the pulses, and the signal measured by the MRI machine is reduced. This "field gradient pulse" method was initially devised for NMR by Stejskal and Tanner  who derived the reduction in signal due to the application of the pulse gradient related to the amount of diffusion that is occurring through the following equation:

${\displaystyle {\frac {S(TE)}{S_{0}}}=\exp \left[-\gamma ^{2}G^{2}\delta ^{2}\left(\Delta -{\frac {\delta }{3}}\right)D\right]}$

where ${\displaystyle S_{0}}$ is the signal intensity without the diffusion weighting, ${\displaystyle S}$ is the signal with the gradient, ${\displaystyle \gamma }$ is the gyromagnetic ratio, ${\displaystyle G}$ is the strength of the gradient pulse, ${\displaystyle \delta }$ is the duration of the pulse, ${\displaystyle \Delta }$ is the time between the two pulses, and finally, ${\displaystyle D}$ is the diffusion-coefficient.

In order to localize this signal attenuation to get images of diffusion one has to combine the pulsed magnetic field gradient pulses used for MRI (aimed at localization of the signal, but those gradient pulses are too weak to produce a diffusion related attenuation) with additional "motion-probing" gradient pulses, according to the Stejskal and Tanner method. This combination is not trivial, as cross-terms arise between all gradient pulses. The equation set by Stejskal and Tanner then becomes inaccurate and the signal attenuation must be calculated, either analytically or numerically, integrating all gradient pulses present in the MRI sequence and their interactions. The result quickly becomes very complex given the many pulses present in the MRI sequence, and as a simplification, Le Bihan suggested gathering all the gradient terms in a "b factor" (which depends only on the acquisition parameters) so that the signal attenuation simply becomes:

${\displaystyle {\frac {S(TE)}{S_{0}}}=\exp(-b\cdot ADC)}$

Also, the diffusion coefficient, ${\displaystyle D}$, is replaced by an apparent diffusion coefficient, ${\displaystyle ADC}$, to indicate that the diffusion process is not free in tissues, but hindered and modulated by many mechanisms (restriction in closed spaces, tortuosity around obstacles, etc.) and that other sources of IntraVoxel Incoherent Motion (IVIM) such as blood flow in small vessels or cerebrospinal fluid in ventricles also contribute to the signal attenuation. At the end, images are "weighted" by the diffusion process: In those diffusion-weighted images (DWI) the signal is more attenuated the faster the diffusion and the larger the b factor is. However, those diffusion-weighted images are still also sensitive to T1 and T2 relaxivity contrast, which can sometimes be confusing. It is possible to calculate "pure" diffusion maps (or more exactly ADC maps where the ADC is the sole source of contrast) by collecting images with at least 2 different values, ${\displaystyle b_{1}}$ and ${\displaystyle b_{2}}$, of the b factor according to:

${\displaystyle \mathrm {ADC} (x,y,z)=\ln[S_{2}(x,y,z)/S_{1}(x,y,z)]/(b_{1}-b_{2})}$

Although this ADC concept has been extremely successful, especially for clinical applications, it has been challenged recently, as new, more comprehensive models of diffusion in biological tissues have been introduced. Those models have been made necessary, as diffusion in tissues is not free. In this condition, the ADC seems to depend on the choice of b values (the ADC seems to decrease when using larger b values), as the plot of ln(S/So) is not linear with the b factor, as expected from the above equations. This deviation from a free diffusion behavior is what makes diffusion MRI so successful, as the ADC is very sensitive to changes in tissue microstructure. On the other hand, modeling diffusion in tissues is becoming very complex. Among most popular models are the biexponential model, which assumes the presence of 2 water pools in slow or intermediate exchange and the cumulant-expansion (also called Kurtosis) model, which does not necessarily require the presence of 2 pools.

Diffusion model

Given the concentration ${\displaystyle \rho }$ and flux ${\displaystyle J}$, Fick's first law gives a relationship between the flux and the concentration gradient:

${\displaystyle J(x,t)=-D\nabla \rho (x,t)}$

where D is the diffusion coefficient. Then, given conservation of mass, the continuity equation relates the time derivative of the concentration with the divergence of the flux:

${\displaystyle {\frac {\partial \rho (x,t)}{\partial t}}=-\nabla \cdot J(x,t)}$

Putting the two together, we get the diffusion equation:

${\displaystyle {\frac {\partial \rho (x,t)}{\partial t}}=D\nabla ^{2}\rho (x,t).}$

Magnetization dynamics

With no diffusion present, the change in nuclear magnetization over time is given by the classical Bloch equation

${\displaystyle {\frac {d{\vec {M}}}{dt}}=\gamma {\vec {M}}\times {\vec {B}}-{\frac {M_{x}{\vec {i}}+M_{y}{\vec {j}}}{T_{2}}}-{\frac {(M_{z}-M_{0}){\vec {k}}}{T_{1}}}}$

which has terms for precession, T2 relaxation, and T1 relaxation.

In 1956, H.C. Torrey mathematically showed how the Bloch equations for magnetization would change with the addition of diffusion. Torrey modified Bloch's original description of transverse magnetization to include diffusion terms and the application of a spatially varying gradient. Since the magnetization ${\displaystyle M}$ is a vector, there are 3 diffusion equations, one for each dimension. The Bloch-Torrey equation is:

${\displaystyle {\frac {d{\vec {M}}}{dt}}=\gamma {\vec {M}}\times {\vec {B}}-{\frac {M_{x}{\vec {i}}+M_{y}{\vec {j}}}{T_{2}}}-{\frac {(M_{z}-M_{0}){\vec {k}}}{T_{1}}}+\nabla \cdot {\vec {D}}\nabla {\vec {M}}}$

where ${\displaystyle {\vec {D}}}$ is now the diffusion tensor.

For the simplest case where the diffusion is isotropic the diffusion tensor is a multiple of the identity:

${\displaystyle {\vec {D}}=D\cdot {\vec {I}}=D\cdot {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},}$

then the Bloch-Torrey equation will have the solution

${\displaystyle {M}={M}_{\text{bloch}}e^{-{\frac {1}{3}}\gamma ^{2}G^{2}t^{3}D}\sim e^{-bD_{0}}}$

The exponential term will be referred to as the attenuation ${\displaystyle A}$. Anisotropic diffusion will have a similar solution for the diffusion tensor, except that what will be measured is the apparent diffusion coefficient (ADC). In general, the attenuation is:

${\displaystyle A=e^{-\sum _{i,j}b_{ij}D_{ij}}}$

where the ${\displaystyle b_{ij}}$ terms incorporate the gradient fields ${\displaystyle G_{x}}$, ${\displaystyle G_{y}}$, and ${\displaystyle G_{z}}$.

Grayscale

The standard grayscale of DWI images is to represent increased diffusion restriction as brighter.^[18]

ADC image

ADC image of the same case of cerebral infarction as seen on DWI in section above

An apparent diffusion coefficient (ADC) image, or an ADC map, is an MRI image that more specifically shows diffusion than conventional DWI, by eliminating the T2 weighting that is otherwise inherent to conventional DWI. ADC imaging does so by acquiring multiple conventional DWI images with different amounts of DWI weighting, and the change in signal is proportional to the rate of diffusion. Contrary to DWI images, the standard grayscale of ADC images is to represent a smaller magnitude of diffusion as darker.

Cerebral infarction leads to diffusion restriction, and the difference between images with various DWI weighting will therefore be minor, leading to an ADC image with low signal in the infarcted area. A decreased ADC may be detected minutes after a cerebral infarction. The high signal of infarcted tissue on conventional DWI is a result of its partial T2 weighting.

Diffusion tensor imaging

Diffusion tensor imaging (DTI) is a magnetic resonance imaging technique that enables the measurement of the restricted diffusion of water in tissue in order to produce neural tract images instead of using this data solely for the purpose of assigning contrast or colors to pixels in a cross-sectional image. It also provides useful structural information about muscle—including heart muscle—as well as other tissues such as the prostate.

In DTI, each voxel has one or more pairs of parameters: a rate of diffusion and a preferred direction of diffusion—described in terms of three-dimensional space—for which that parameter is valid. The properties of each voxel of a single DTI image are usually calculated by vector or tensor math from six or more different diffusion weighted acquisitions, each obtained with a different orientation of the diffusion sensitizing gradients. In some methods, hundreds of measurements—each making up a complete image—are made to generate a single resulting calculated image data set. The higher information content of a DTI voxel makes it extremely sensitive to subtle pathology in the brain. In addition the directional information can be exploited at a higher level of structure to select and follow neural tracts through the brain—a process called tractography.

A more precise statement of the image acquisition process is that the image-intensities at each position are attenuated, depending on the strength (b-value) and direction of the so-called magnetic diffusion gradient, as well as on the local microstructure in which the water molecules diffuse. The more attenuated the image is at a given position, the greater diffusion there is in the direction of the diffusion gradient. In order to measure the tissue's complete diffusion profile, one needs to repeat the MR scans, applying different directions (and possibly strengths) of the diffusion gradient for each scan.

Mathematical foundation—tensors

See also: Principal axis theorem

Diffusion MRI relies on the mathematics and physical interpretations of the geometric quantities known as tensors. Only a special case of the general mathematical notion is relevant to imaging, which is based on the concept of a symmetric matrix. Diffusion itself is tensorial, but in many cases the objective is not really about trying to study brain diffusion per se, but rather just trying to take advantage of diffusion anisotropy in white matter for the purpose of finding the orientation of the axons and the magnitude or degree of anisotropy. Tensors have a real, physical existence in a material or tissue so that they do not move when the coordinate system used to describe them is rotated. There are numerous different possible representations of a tensor (of rank 2), but among these, this discussion focuses on the ellipsoid because of its physical relevance to diffusion and because of its historical significance in the development of diffusion anisotropy imaging in MRI.

The following matrix displays the components of the diffusion tensor:

${\displaystyle {\bar {D}}={\begin{vmatrix}D_{\color {red}xx}&D_{xy}&D_{xz}\\D_{xy}&D_{\color {red}yy}&D_{yz}\\D_{xz}&D_{yz}&D_{\color {red}zz}\end{vmatrix}}}$

The same matrix of numbers can have a simultaneous second use to describe the shape and orientation of an ellipse and the same matrix of numbers can be used simultaneously in a third way for matrix mathematics to sort out eigenvectors and eigenvalues as explained below.

Physical tensors

The idea of a tensor in physical science evolved from attempts to describe the quantity of physical properties. The first properties they were applied to were those that can be described by a single number, such as temperature. Properties that can be described this way are called scalars; these can be considered tensors of rank 0, or 0th-order tensors. Tensors can also be used to describe quantities that have directionality, such as mechanical force. These quantities require specification of both magnitude and direction, and are often represented with a vector. A three-dimensional vector can be described with three components: its projection on the x, y, and z axes. Vectors of this sort can be considered tensors of rank 1, or 1st-order tensors.

A tensor is often a physical or biophysical property that determines the relationship between two vectors. When a force is applied to an object, movement can result. If the movement is in a single direction, the transformation can be described using a vector—a tensor of rank 1. However, in a tissue, diffusion leads to movement of water molecules along trajectories that proceed along multiple directions over time, leading to a complex projection onto the Cartesian axes. This pattern is reproducible if the same conditions and forces are applied to the same tissue in the same way. If there is an internal anisotropic organization of the tissue that constrains diffusion, then this fact will be reflected in the pattern of diffusion. The relationship between the properties of driving force that generate diffusion of the water molecules and the resulting pattern of their movement in the tissue can be described by a tensor. The collection of molecular displacements of this physical property can be described with nine components—each one associated with a pair of axes xx, yy, zz, xy, yx, xz, zx, yz, zy. These can be written as a matrix similar to the one at the start of this section.

Diffusion from a point source in the anisotropic medium of white matter behaves in a similar fashion. The first pulse of the Stejskal Tanner diffusion gradient effectively labels some water molecules and the second pulse effectively shows their displacement due to diffusion. Each gradient direction applied measures the movement along the direction of that gradient. Six or more gradients are summed to get all the measurements needed to fill in the matrix, assuming it is symmetric above and below the diagonal (red subscripts).

In 1848, Henri Hureau de Sénarmont applied a heated point to a polished crystal surface that had been coated with wax. In some materials that had "isotropic" structure, a ring of melt would spread across the surface in a circle. In anisotropic crystals the spread took the form of an ellipse. In three dimensions this spread is an ellipsoid. As Adolf Fick showed in the 1850s, diffusion exhibits many of the same patterns as those seen in the transfer of heat.

Mathematics of ellipsoids

At this point, it is helpful to consider the mathematics of ellipsoids. An ellipsoid can be described by the formula: ax² + by² + cz² = 1. This equation describes a quadric surface. The relative values of a, b, and c determine if the quadric describes an ellipsoid or a hyperboloid.

As it turns out, three more components can be added as follows: ax² + by² + cz² + dyz + ezx + fxy = 1. Many combinations of a, b, c, d, e, and f still describe ellipsoids, but the additional components (d, e, f) describe the rotation of the ellipsoid relative to the orthogonal axes of the Cartesian coordinate system. These six variables can be represented by a matrix similar to the tensor matrix defined at the start of this section (since diffusion is symmetric, then we only need six instead of nine components—the components below the diagonal elements of the matrix are the same as the components above the diagonal). This is what is meant when it is stated that the components of a matrix of a second order tensor can be represented by an ellipsoid—if the diffusion values of the six terms of the quadric ellipsoid are placed into the matrix, this generates an ellipsoid angled off the orthogonal grid. Its shape will be more elongated if the relative anisotropy is high.

When the ellipsoid/tensor is represented by a matrix, we can apply a useful technique from standard matrix mathematics and linear algebra—that is to "diagonalize" the matrix. This has two important meanings in imaging. The idea is that there are two equivalent ellipsoids—of identical shape but with different size and orientation. The first one is the measured diffusion ellipsoid sitting at an angle determined by the axons, and the second one is perfectly aligned with the three Cartesian axes. The term "diagonalize" refers to the three components of the matrix along a diagonal from upper left to lower right (the components with red subscripts in the matrix at the start of this section). The variables ax², by², and cz² are along the diagonal (red subscripts), but the variables d, e and f are "off diagonal". It then becomes possible to do a vector processing step in which we rewrite our matrix and replace it with a new matrix multiplied by three different vectors of unit length (length=1.0). The matrix is diagonalized because the off-diagonal components are all now zero. The rotation angles required to get to this equivalent position now appear in the three vectors and can be read out as the x, y, and z components of each of them. Those three vectors are called "eigenvectors" or characteristic vectors. They contain the orientation information of the original ellipsoid. The three axes of the ellipsoid are now directly along the main orthogonal axes of the coordinate system so we can easily infer their lengths. These lengths are the eigenvalues or characteristic values.

Diagonalization of a matrix is done by finding a second matrix that it can be multiplied with followed by multiplication by the inverse of the second matrix—wherein the result is a new matrix in which three diagonal (xx, yy, zz) components have numbers in them but the off-diagonal components (xy, yz, zx) are 0. The second matrix provides eigenvector information.

Measures of anisotropy and diffusivity

Visualization of DTI data with ellipsoids.

In present-day clinical neurology, various brain pathologies may be best detected by looking at particular measures of anisotropy and diffusivity. The underlying physical process of diffusion causes a group of water molecules to move out from a central point, and gradually reach the surface of an ellipsoid if the medium is anisotropic (it would be the surface of a sphere for an isotropic medium). The ellipsoid formalism functions also as a mathematical method of organizing tensor data. Measurement of an ellipsoid tensor further permits a retrospective analysis, to gather information about the process of diffusion in each voxel of the tissue.

In an isotropic medium such as cerebrospinal fluid, water molecules are moving due to diffusion and they move at equal rates in all directions. By knowing the detailed effects of diffusion gradients we can generate a formula that allows us to convert the signal attenuation of an MRI voxel into a numerical measure of diffusion—the diffusion coefficient D. When various barriers and restricting factors such as cell membranes and microtubules interfere with the free diffusion, we are measuring an "apparent diffusion coefficient", or ADC, because the measurement misses all the local effects and treats the attenuation as if all the movement rates were solely due to Brownian motion. The ADC in anisotropic tissue varies depending on the direction in which it is measured. Diffusion is fast along the length of (parallel to) an axon, and slower perpendicularly across it.

Once we have measured the voxel from six or more directions and corrected for attenuations due to T2 and T1 effects, we can use information from our calculated ellipsoid tensor to describe what is happening in the voxel. If you consider an ellipsoid sitting at an angle in a Cartesian grid then you can consider the projection of that ellipse onto the three axes. The three projections can give you the ADC along each of the three axes ADC_x, ADC_y, ADC_z. This leads to the idea of describing the average diffusivity in the voxel which will simply be

${\displaystyle (ADC_{x}+ADC_{y}+ADC_{z})/3=ADC_{i}}$

We use the i subscript to signify that this is what the isotropic diffusion coefficient would be with the effects of anisotropy averaged out.

The ellipsoid itself has a principal long axis and then two more small axes that describe its width and depth. All three of these are perpendicular to each other and cross at the center point of the ellipsoid. We call the axes in this setting eigenvectors and the measures of their lengths eigenvalues. The lengths are symbolized by the Greek letter λ. The long one pointing along the axon direction will be λ₁ and the two small axes will have lengths λ₂ and λ₃. In the setting of the DTI tensor ellipsoid, we can consider each of these as a measure of the diffusivity along each of the three primary axes of the ellipsoid. This is a little different from the ADC since that was a projection on the axis, while λ is an actual measurement of the ellipsoid we have calculated.

The diffusivity along the principal axis, λ₁ is also called the longitudinal diffusivity or the axial diffusivity or even the parallel diffusivity λ_∥. Historically, this is closest to what Richards originally measured with the vector length in 1991. The diffusivities in the two minor axes are often averaged to produce a measure of radial diffusivity

${\displaystyle \lambda _{\perp }=(\lambda _{2}+\lambda _{3})/2.}$

This quantity is an assessment of the degree of restriction due to membranes and other effects and proves to be a sensitive measure of degenerative pathology in some neurological conditions. It can also be called the perpendicular diffusivity (${\displaystyle \lambda _{\perp }}$).

Another commonly used measure that summarizes the total diffusivity is the Trace—which is the sum of the three eigenvalues,

${\displaystyle \mathrm {tr} (\Lambda )=\lambda _{1}+\lambda _{2}+\lambda _{3}}$

where ${\displaystyle \Lambda }$ is a diagonal matrix with eigenvalues ${\displaystyle \lambda _{1}}$, ${\displaystyle \lambda _{2}}$ and ${\displaystyle \lambda _{3}}$ on its diagonal.

If we divide this sum by three we have the mean diffusivity,

${\displaystyle \mathrm {MD} =(\lambda _{1}+\lambda _{2}+\lambda _{3})/3}$

which equals ADC_i since

${\displaystyle {\begin{aligned}\mathrm {tr} (\Lambda )/3&=\mathrm {tr} (V^{-1}V\Lambda )/3\\&=\mathrm {tr} (V\Lambda V^{-1})/3\\&=\mathrm {tr} (D)/3\\&=ADC_{i}\end{aligned}}}$

where ${\displaystyle V}$ is the matrix of eigenvectors and ${\displaystyle D}$ is the diffusion tensor. Aside from describing the amount of diffusion, it is often important to describe the relative degree of anisotropy in a voxel. At one extreme would be the sphere of isotropic diffusion and at the other extreme would be a cigar or pencil shaped very thin prolate spheroid. The simplest measure is obtained by dividing the longest axis of the ellipsoid by the shortest = (λ₁/λ₃). However, this proves to be very susceptible to measurement noise, so increasingly complex measures were developed to capture the measure while minimizing the noise. An important element of these calculations is the sum of squares of the diffusivity differences = (λ₁ − λ₂)² + (λ₁ − λ₃)² + (λ₂ − λ₃)². We use the square root of the sum of squares to obtain a sort of weighted average—dominated by the largest component. One objective is to keep the number near 0 if the voxel is spherical but near 1 if it is elongate. This leads to the fractional anisotropy or FA which is the square root of the sum of squares (SRSS) of the diffusivity differences, divided by the SRSS of the diffusivities. When the second and third axes are small relative to the principal axis, the number in the numerator is almost equal the number in the denominator. We also multiply by ${\displaystyle 1/{\sqrt {2}}}$ so that FA has a maximum value of 1. The whole formula for FA looks like this:

${\displaystyle \mathrm {FA} ={\frac {\sqrt {3((\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2})}}{\sqrt {2(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2})}}}}$

The fractional anisotropy can also be separated into linear, planar, and spherical measures depending on the "shape" of the diffusion ellipsoid. For example, a "cigar" shaped prolate ellipsoid indicates a strongly linear anisotropy, a "flying saucer" or oblate spheroid represents diffusion in a plane, and a sphere is indicative of isotropic diffusion, equal in all directions If the eigenvalues of the diffusion vector are sorted such that ${\displaystyle \lambda _{1}\geq \lambda _{2}\geq \lambda _{3}\geq 0}$, then the measures can be calculated as follows:

For the linear case, where ${\displaystyle \lambda _{1}\gg \lambda _{2}\simeq \lambda _{3}}$,

${\displaystyle C_{l}={\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

For the planar case, where ${\displaystyle \lambda _{1}\simeq \lambda _{2}\gg \lambda _{3}}$,

${\displaystyle C_{p}={\frac {2(\lambda _{2}-\lambda _{3})}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

For the spherical case, where ${\displaystyle \lambda _{1}\simeq \lambda _{2}\simeq \lambda _{3}}$,

${\displaystyle C_{s}={\frac {3\lambda _{3}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

Each measure lies between 0 and 1 and they sum to unity. An additional anisotropy measure can used to describe the deviation from the spherical case:

${\displaystyle C_{a}=C_{l}+C_{p}=1-C_{s}={\frac {\lambda _{1}+\lambda _{2}-2\lambda _{3}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

There are other metrics of anisotropy used, including the relative anisotropy (RA):

${\displaystyle \mathrm {RA} ={\frac {\sqrt {(\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2}}}{{\sqrt {3}}\operatorname {E} [\lambda ]}}}$

and the volume ratio (VR):

${\displaystyle \mathrm {VR} ={\frac {\lambda _{1}\lambda _{2}\lambda _{3}}{\operatorname {E} [\lambda ]^{3}}}}$

Applications

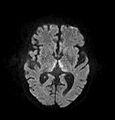
The most common application of conventional DWI (without DTI) is in acute brain ischemia. DWI directly visualizes the ischemic necrosis in cerebral infarction in the form of a cytotoxic edema, appearing as a high DWI signal within minutes of arterial occlusion. With perfusion MRI detecting both the infarcted core and the salvageable penumbra, the latter can be quantified by DWI and perfusion MRI.

• 

  DWI showing necrosis (shown as brighter) in a cerebral infarction

• 

  DWI showing restricted diffusion in the medial dorsal thalami consistent with Wernicke encephalopathy

• 

  DWI showing cortical ribbon-like high signal consistent with diffusion restriction in a patient with known MELAS syndrome

Another application area of DWI is in oncology. Tumors are in many instances highly cellular, giving restricted diffusion of water, and therefore appear with a relatively high signal intensity in DWI. DWI is commonly used to detect and stage tumors, and also to monitor tumor response to treatment over time. DWI can also be collected to visualize the whole body using a technique called 'diffusion-weighted whole-body imaging with background body signal suppression' (DWIBS). Some more specialized diffusion MRI techniques such as diffusion kurtosis imaging (DKI) have also been shown to predict the response of cancer patients to chemotherapy treatment.

The principal application is in the imaging of white matter where the location, orientation, and anisotropy of the tracts can be measured. The architecture of the axons in parallel bundles, and their myelin sheaths, facilitate the diffusion of the water molecules preferentially along their main direction. Such preferentially oriented diffusion is called anisotropic diffusion.

Tractographic reconstruction of neural connections via DTI

 

See https://doi.org/10.3389/fsurg.2020.00019 for more information

The imaging of this property is an extension of diffusion MRI. If a series of diffusion gradients (i.e. magnetic field variations in the MRI magnet) are applied that can determine at least 3 directional vectors (use of 6 different gradients is the minimum and additional gradients improve the accuracy for "off-diagonal" information), it is possible to calculate, for each voxel, a tensor (i.e. a symmetric positive definite 3×3 matrix) that describes the 3-dimensional shape of diffusion. The fiber direction is indicated by the tensor's main eigenvector. This vector can be color-coded, yielding a cartography of the tracts' position and direction (red for left-right, blue for superior-inferior, and green for anterior-posterior). The brightness is weighted by the fractional anisotropy which is a scalar measure of the degree of anisotropy in a given voxel. Mean diffusivity (MD) or trace is a scalar measure of the total diffusion within a voxel. These measures are commonly used clinically to localize white matter lesions that do not show up on other forms of clinical MRI.

Applications in the brain:

• Tract-specific localization of white matter lesions such as trauma and in defining the severity of diffuse traumatic brain injury. The localization of tumors in relation to the white matter tracts (infiltration, deflection), has been one of the most important initial applications. In surgical planning for some types of brain tumors, surgery is aided by knowing the proximity and relative position of the corticospinal tract and a tumor.
• Diffusion tensor imaging data can be used to perform tractography within white matter. Fiber tracking algorithms can be used to track a fiber along its whole length (e.g. the corticospinal tract, through which the motor information transit from the motor cortex to the spinal cord and the peripheral nerves). Tractography is a useful tool for measuring deficits in white matter, such as in aging. Its estimation of fiber orientation and strength is increasingly accurate, and it has widespread potential implications in the fields of cognitive neuroscience and neurobiology.
• The use of DTI for the assessment of white matter in development, pathology and degeneration has been the focus of over 2,500 research publications since 2005. It promises to be very helpful in distinguishing Alzheimer's disease from other types of dementia. Applications in brain research include the investigation of neural networks in vivo, as well as in connectomics.

Applications for peripheral nerves:

• Brachial plexus: DTI can differentiate normal nerves (as shown in the tractogram of the spinal cord and brachial plexus and 3D 4k reconstruction here) from traumatically injured nerve roots.
• Cubital Tunnel Syndrome: metrics derived from DTI (FA and RD) can differentiate asymptomatic adults from those with compression of the ulnar nerve at the elbow
• Carpal Tunnel Syndrome: Metrics derived from DTI (lower FA and MD) differentiate healthy adults from those with carpal tunnel syndrome

Research

Early in the development of DTI based tractography, a number of researchers pointed out a flaw in the diffusion tensor model. The tensor analysis assumes that there is a single ellipsoid in each imaging voxel— as if all of the axons traveling through a voxel traveled in exactly the same direction. This is often true, but it can be estimated that in more than 30% of the voxels in a standard resolution brain image, there are at least two different neural tracts traveling in different directions that pass through each other. In the classic diffusion ellipsoid tensor model, the information from the crossing tract just appears as noise or unexplained decreased anisotropy in a given voxel. David Tuch was among the first to describe a solution to this problem. The idea is best understood by conceptually placing a kind of geodesic dome around each image voxel. This icosahedron provides a mathematical basis for passing a large number of evenly spaced gradient trajectories through the voxel—each coinciding with one of the apices of the icosahedron. Basically, we are now going to look into the voxel from a large number of different directions (typically 40 or more). We use "n-tuple" tessellations to add more evenly spaced apices to the original icosahedron (20 faces)—an idea that also had its precedents in paleomagnetism research several decades earlier. We just want to know which direction lines turn up the maximum anisotropic diffusion measures. If there is a single tract, there will be just two maxima pointing in opposite directions. If two tracts cross in the voxel, there will be two pairs of maxima, and so on. We can still use tensor math to use the maxima to select groups of gradients to package into several different tensor ellipsoids in the same voxel, or use more complex higher rank tensors analyses, or we can do a true "model free" analysis that just picks the maxima and go on about doing the tractography.

The Q-Ball method of tractography is an implementation in which David Tuch provides a mathematical alternative to the tensor model. Instead of forcing the diffusion anisotropy data into a group of tensors, the mathematics used deploys both probability distributions and a classic bit of geometric tomography and vector math developed nearly 100 years ago—the Funk Radon Transform.

Summary

For DTI, it is generally possible to use linear algebra, matrix mathematics and vector mathematics to process the analysis of the tensor data.

In some cases, the full set of tensor properties is of interest, but for tractography it is usually necessary to know only the magnitude and orientation of the primary axis or vector. This primary axis—the one with the greatest length—is the largest eigenvalue and its orientation is encoded in its matched eigenvector. Only one axis is needed as it is assumed the largest eigenvalue is aligned with the main axon direction to accomplish tractography.

Sustainable development

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Intuition

Sustainable development requires six central capacities.

Sustainable development is an organizing principle for meeting human development goals while also sustaining the ability of natural systems to provide the natural resources and ecosystem services on which the economy and society depend. The desired result is a state of society where living conditions and resources are used to continue to meet human needs without undermining the integrity and stability of the natural system. Sustainable development was defined in the 1987 Brundtland Report as "development that meets the needs of the present generation without compromising the ability of future generations to meet their own needs". As the concept of sustainable development developed, it has shifted its focus more towards the economic development, social development and environmental protection for future generations.

Sustainable development was first institutionalized with the Rio Process initiated at the 1992 Earth Summit in Rio de Janeiro. In 2015 the United Nations General Assembly adopted the Sustainable Development Goals (SDGs) (2015 to 2030) and explained how the goals are integrated and indivisible to achieve sustainable development at the global level. The 17 goals address the global challenges, including poverty, inequality, climate change, environmental degradation, peace, and justice.

Sustainable development is interlinked with the normative concept of sustainability. UNESCO formulated a distinction between the two concepts as follows: "Sustainability is often thought of as a long-term goal (i.e. a more sustainable world), while sustainable development refers to the many processes and pathways to achieve it." The concept of sustainable development has been criticized in various ways. While some see it as paradoxical (or an oxymoron) and regard development as inherently unsustainable, others are disappointed in the lack of progress that has been achieved so far. Part of the problem is that "development" itself is not consistently defined.

Definition

In 1987, the United Nations World Commission on Environment and Development released the report Our Common Future, commonly called the Brundtland Report. The report included a definition of "sustainable development" which is now widely used:

Sustainable development is development that meets the needs of the present without compromising the ability of future generations to meet their own needs. It contains two key concepts within it:

• The concept of 'needs', in particular, the essential needs of the world's poor, to which overriding priority should be given; and
• The idea of limitations imposed by the state of technology and social organization on the environment's ability to meet present and future needs.
  — World Commission on Environment and Development, Our Common Future (1987)

Related concepts

Sustainability

Visual representations of sustainability and its three dimensions: Left, sustainability as three intersecting circles. Right top, a nested approach. Right bottom, literal 'pillars'. The schematic with the nested ellipses emphasizes a hierarchy of the dimensions, putting "environment" as the foundation for the other two.

 

Sustainability is a societal goal that broadly aims for humans to safely co-exist on planet Earth over a long time. Specific definitions of sustainability are difficult to agree on and therefore vary in the literature and over time. The concept of sustainability can be used to guide decisions at the global, national and individual level (e.g. sustainable living). Sustainability is commonly described along the lines of three dimensions (also called pillars): environmental, economic and social. Many publications state that the environmental dimension (also referred to as "planetary integrity" or "ecological integrity") should be regarded as the most important one. Accordingly, in everyday usage of the term, sustainability is often focused on the environmental aspects. The most dominant environmental issues since around 2000 have been climate change, loss of biodiversity, loss of ecosystem services, land degradation, and air and water pollution. Humanity is now exceeding several "planetary boundaries".

Development of the concept

See also: Sustainability

Sustainable development has its roots in ideas about sustainable forest management, which were developed in Europe during the 17th and 18th centuries. In response to a growing awareness of the depletion of timber resources in England, John Evelyn argued, in his 1662 essay Sylva, that "sowing and planting of trees had to be regarded as a national duty of every landowner, in order to stop the destructive over-exploitation of natural resources." In 1713, Hans Carl von Carlowitz, a senior mining administrator in the service of Elector Frederick Augustus I of Saxony published Sylvicultura economics, a 400-page work on forestry. Building upon the ideas of Evelyn and French minister Jean-Baptiste Colbert, von Carlowitz developed the concept of managing forests for sustained yield. His work influenced others, including Alexander von Humboldt and Georg Ludwig Hartig, eventually leading to the development of the science of forestry. This, in turn, influenced people like Gifford Pinchot, the first head of the US Forest Service, whose approach to forest management was driven by the idea of wise use of resources, and Aldo Leopold whose land ethic was influential in the development of the environmental movement in the 1960s.

Following the publication of Rachel Carson's Silent Spring in 1962, the developing environmental movement drew attention to the relationship between economic growth and environmental degradation. Kenneth E. Boulding, in his influential 1966 essay The Economics of the Coming Spaceship Earth, identified the need for the economic system to fit itself to the ecological system with its limited pools of resources. Another milestone was the 1968 article by Garrett Hardin that popularized the term "tragedy of the commons". One of the first uses of the term sustainable in the contemporary sense was by the Club of Rome in 1972 in its classic report on the Limits to Growth, written by a group of scientists led by Dennis and Donella Meadows of the Massachusetts Institute of Technology. Describing the desirable "state of global equilibrium", the authors wrote: "We are searching for a model output that represents a world system that is sustainable without sudden and uncontrolled collapse and capable of satisfying the basic material requirements of all of its people." That year also saw the publication of the influential A Blueprint for Survival book.

In 1975, an MIT research group prepared ten days of hearings on "Growth and Its Implication for the Future" for the US Congress, the first hearings ever held on sustainable development.

In 1980, the International Union for Conservation of Nature published a world conservation strategy that included one of the first references to sustainable development as a global priority and introduced the term "sustainable development". Two years later, the United Nations World Charter for Nature raised five principles of conservation by which human conduct affecting nature is to be guided and judged.

Since the Brundtland Report, the concept of sustainable development has developed beyond the initial intergenerational framework to focus more on the goal of "socially inclusive and environmentally sustainable economic growth". In 1992, the UN Conference on Environment and Development published the Earth Charter, which outlines the building of a just, sustainable, and peaceful global society in the 21st century. The action plan Agenda 21 for sustainable development identified information, integration, and participation as key building blocks to help countries achieve development that recognizes these interdependent pillars. Furthermore, Agenda 21 emphasizes that broad public participation in decision-making is a fundamental prerequisite for achieving sustainable development.

The Rio Protocol was a huge leap forward: for the first time, the world agreed on a sustainability agenda. In fact, a global consensus was facilitated by neglecting concrete goals and operational details. The Sustainable Development Goals (SDGs) now have concrete targets (unlike the results from the Rio Process) but no methods for sanctions.

Dimensions

Main article: Sustainability § Dimensions of sustainability

Sustainable development, like sustainability, is regarded to have three dimensions (also called pillars, domains, aspects, spheres and globalized etc.): the environment, economy and society.

"Wedding cake" model for the sustainable development goals, which is similar to the nested circle diagram, whereby the environmental dimension or system is the basis for the other two dimensions.

 

Three different areas of sustainability are normally distinguished: the environmental, the social, and the economic. Several terms are in use for this concept in the literature: authors speak of three pillars, dimensions, components, aspects, perspectives, factors or goals, and all mean the same thing in this context. The emergence of the three dimensions paradigm has little theoretical foundation but gradually emerged without a single point of origin. Nevertheless, the distinction itself is rarely questioned, and the "three dimension" conception of sustainability is a dominant interpretation within the literature.

Critique

Main article: Sustainability § Critique

Further information: Weak and strong sustainability, Degrowth, and Eco-economic decoupling

The concept of sustainable development has been and still is, subject to criticism, including the question of what is to be sustained in sustainable development. It has been argued that there is no such thing as sustainable use of a non-renewable resource, since any positive rate of exploitation will eventually lead to the exhaustion of earth's finite stock; this perspective renders the Industrial Revolution as a whole unsustainable.

The sustainable development debate is based on the assumption that societies need to manage three types of capital (economic, social, and natural), which may be non-substitutable and whose consumption might be irreversible. Natural capital can not necessarily be substituted by economic capital. While it is possible that we can find ways to replace some natural resources, it is much less likely that they will ever be able to replace ecosystem services, such as the protection provided by the ozone layer, or the climate stabilizing function of the Amazonian forest.

The concept of sustainable development has been criticized from different angles. While some see it as paradoxical (or an oxymoron) and regard development as inherently unsustainable, others are disappointed in the lack of progress that has been achieved so far. Part of the problem is that "development" itself is not consistently defined.

The vagueness of the Brundtland definition of sustainable development has been criticized as follows: The definition has "opened up the possibility of downplaying sustainability. Hence, governments spread the message that we can have it all at the same time, i.e. economic growth, prospering societies and a healthy environment. No new ethic is required. This so-called weak version of sustainability is popular among governments, and businesses, but profoundly wrong and not even weak, as there is no alternative to preserving the earth’s ecological integrity."

Pathways

Further information: Sustainability § Sustainability transitions

Requirements

Six interdependent capacities are deemed to be necessary for the successful pursuit of sustainable development. These are the capacities to measure progress towards sustainable development; promote equity within and between generations; adapt to shocks and surprises; transform the system onto more sustainable development pathways; link knowledge with action for sustainability; and to devise governance arrangements that allow people to work together

Improving on environmental aspects

Further information: Human impact on the environment and Ecological footprint

 

Deforestation of the Amazon rainforest. Deforestation and increased road-building in the Amazon rainforest are a concern because of increased human encroachment upon wilderness areas, increased resource extraction and further threats to biodiversity.

Environmental sustainability concerns the natural environment and how it endures and remains diverse and productive. Since natural resources are derived from the environment, the state of air, water, and climate is of particular concern. Environmental sustainability requires society to design activities to meet human needs while preserving the life support systems of the planet. This, for example, entails using water sustainably, using renewable energy and sustainable material supplies (e.g. harvesting wood from forests at a rate that maintains the biomass and biodiversity).

An unsustainable situation occurs when natural capital (the total of nature's resources) is used up faster than it can be replenished. Sustainability requires that human activity only uses nature's resources at a rate at which they can be replenished naturally. The concept of sustainable development is intertwined with the concept of carrying capacity. Theoretically, the long-term result of environmental degradation is the inability to sustain human life.

Important operational principles of sustainable development were published by Herman Daly in 1990: renewable resources should provide a sustainable yield (the rate of harvest should not exceed the rate of regeneration); for non-renewable resources there should be equivalent development of renewable substitutes; waste generation should not exceed the assimilative capacity of the environment.

Summary of different levels of consumption of natural resources.

Consumption of natural resources	State of the environment	State of sustainability
More than nature's ability to replenish	Environmental degradation	Not sustainable
Equal to nature's ability to replenish	Environmental equilibrium	Steady state economy
Less than nature's ability to replenish	Environmental renewal	Environmentally sustainable

Land use changes, agriculture and food

Further information: Environmental impact of agriculture

Environmental problems associated with industrial agriculture and agribusiness are now being addressed through approaches such as sustainable agriculture, organic farming and more sustainable business practices. The most cost-effective climate change mitigation options include afforestation, sustainable forest management, and reducing deforestation. At the local level there are various movements working towards sustainable food systems which may include less meat consumption, local food production, slow food, sustainable gardening, and organic gardening. The environmental effects of different dietary patterns depend on many factors, including the proportion of animal and plant foods consumed and the method of food production.

Materials and waste

Further information: Cradle-to-cradle

 

Relationship between ecological footprint and Human Development Index (HDI)

 

Before flue-gas desulfurization was installed, the air-polluting emissions from this power plant in New Mexico contained excessive amounts of sulfur dioxide.

As global population and affluence have increased, so has the use of various materials increased in volume, diversity, and distance transported. Included here are raw materials, minerals, synthetic chemicals (including hazardous substances), manufactured products, food, living organisms, and waste. By 2050, humanity could consume an estimated 140 billion tons of minerals, ores, fossil fuels and biomass per year (three times its current amount) unless the economic growth rate is decoupled from the rate of natural resource consumption. Developed countries' citizens consume an average of 16 tons of those four key resources per capita per year, ranging up to 40 or more tons per person in some developed countries with resource consumption levels far beyond what is likely sustainable. By comparison, the average person in India today consumes four tons per year.

Sustainable use of materials has targeted the idea of dematerialization, converting the linear path of materials (extraction, use, disposal in landfill) to a circular material flow that reuses materials as much as possible, much like the cycling and reuse of waste in nature. Dematerialization is being encouraged through the ideas of industrial ecology, eco design and ecolabelling.

This way of thinking is expressed in the concept of circular economy, which employs reuse, sharing, repair, refurbishment, remanufacturing and recycling to create a closed-loop system, minimizing the use of resource inputs and the creation of waste, pollution and carbon emissions. Building electric vehicles has been one of the most popular ways in the field of sustainable development, the potential of using reusable energy and reducing waste offered a perspective in sustainable development. The European Commission has adopted an ambitious Circular Economy Action Plan in 2020, which aims at making sustainable products the norm in the EU.

Biodiversity and ecosystem services

In 2019, a summary for policymakers of the largest, most comprehensive study to date of biodiversity and ecosystem services was published by the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. It recommended that human civilization will need a transformative change, including sustainable agriculture, reductions in consumption and waste, fishing quotas and collaborative water management.

The 2022 IPCC report emphasizes how there have been many studies done on the loss of biodiversity, and provides additional strategies to decrease the rate of our declining biodiversity. The report suggests how preserving natural ecosystems, fire and soil management, and reducing the competition for land can create positive impacts on our environment, and contribute to sustainable development.

A sewage treatment plant that uses solar energy, located at Santuari de Lluc monastery, Majorca.

Management of human consumption and impacts

Further information: Consumption (economics), Overconsumption, and Micro-sustainability

 

Waste generation, measured in kilograms per person per day

The environmental impact of a community or humankind as a whole depends both on population and impact per person, which in turn depends in complex ways on what resources are being used, whether or not those resources are renewable, and the scale of the human activity relative to the carrying capacity of the ecosystems involved. Careful resource management can be applied at many scales, from economic sectors like agriculture, manufacturing and industry, to work organizations, the consumption patterns of households and individuals, and the resource demands of individual goods and services.

The underlying driver of direct human impacts on the environment is human consumption. This impact is reduced by not only consuming less but also making the full cycle of production, use, and disposal more sustainable. Consumption of goods and services can be analyzed and managed at all scales through the chain of consumption, starting with the effects of individual lifestyle choices and spending patterns, through to the resource demands of specific goods and services, the impacts of economic sectors, through national economies to the global economy. Key resource categories relating to human needs are food, energy, raw materials and water.

Improving on economic and social aspects

Further information: Corporate sustainability and Sustainable business

It has been suggested that because of rural poverty and overexploitation, environmental resources should be treated as important economic assets, called natural capital. Economic development has traditionally required a growth in the gross domestic product. This model of unlimited personal and GDP growth may be over. Sustainable development may involve improvements in the quality of life for many but may necessitate a decrease in resource consumption. "Growth" generally ignores the direct effect that the environment may have on social welfare, whereas "development" takes it into account.

As early as the 1970s, the concept of sustainability was used to describe an economy "in equilibrium with basic ecological support systems". Scientists in many fields have highlighted The Limits to Growth, and economists have presented alternatives, for example a 'steady-state economy', to address concerns over the impacts of expanding human development on the planet. In 1987, the economist Edward Barbier published the study The Concept of Sustainable Economic Development, where he recognized that goals of environmental conservation and economic development are not conflicting and can be reinforcing each other.

A World Bank study from 1999 concluded that based on the theory of genuine savings (defined as "traditional net savings less the value of resource depletion and environmental degradation plus the value of investment in human capital"), policymakers have many possible interventions to increase sustainability, in macroeconomics or purely environmental. Several studies have noted that efficient policies for renewable energy and pollution are compatible with increasing human welfare, eventually reaching a golden-rule steady state.

A meta review in 2002 looked at environmental and economic valuations and found a "lack of concrete understanding of what “sustainability policies” might entail in practice". A study concluded in 2007 that knowledge, manufactured and human capital (health and education) has not compensated for the degradation of natural capital in many parts of the world. It has been suggested that intergenerational equity can be incorporated into a sustainable development and decision making, as has become common in economic valuations of climate economics.

The 2022 IPCC Sixth Assessment Report discussed how ambitious climate change mitigation policies have created negative social and economical impacts when they are not aligned with sustainable development goals. As a result, the transition towards sustainable development mitigation policies has slowed down which is why the inclusivity and considerations of justice of these policies may weaken or support improvements on certain regions as there are other limiting factors such as poverty, food insecurity, and water scarcity that may impede the governments application of policies that aim to build a low carbon future.

The World Business Council for Sustainable Development published a Vision 2050 document in 2021 to show "How business can lead the transformations the world needs". The vision states that "we envision a world in which 9+billion people can live well, within planetary boundaries, by 2050." This report was highlighted by The Guardian as "the largest concerted corporate sustainability action plan to date – include reversing the damage done to ecosystems, addressing rising greenhouse gas emissions and ensuring societies move to sustainable agriculture."

Gender and leadership in sustainable development

Gender and sustainable development have been examined, focusing on women's leadership potential and barriers to it. While leadership roles in sustainable development have become more androgynous over time, patriarchal structures and perceptions continue to constrain women from becoming leaders. Some hidden issues are women's lack of self-confidence, impeding access to leadership roles, but men can potentially play a role as allies for women's leadership.

Barriers

There are barriers that small and medium enterprises face when implementing sustainable development such as lack of expertise, lack of resources, and high initial capital cost of implementing sustainability measures.

Globally, the lack of political will is a barrier to achieving sustainable development. To overcome this impediment, governments must jointly form an agreement of social and political strength. Efforts to enact reforms or design and implement programs to decrease the harmful effects of human behaviors allow for progress toward present and future environmental sustainability goals. The Paris Agreement exemplifies efforts of political will on a global level, a multinational agreement between 193 parties  intended to strengthen the global response to climate change by reducing emissions and working together to adjust to the consequent effects of climate change. Experts continue to firmly suggest that governments should do more outside of The Paris Agreement, there persist a greater need for political will.

Sustainable Development Goals

The United Nations Sustainable Development Goals

 

The Sustainable Development Goals (SDGs) or Global Goals are a collection of 17 interlinked global goals designed to be a "shared blueprint for peace and prosperity for people and the planet, now and into the future". The SDGs were set up in 2015 by the United Nations General Assembly (UN-GA) and are intended to be achieved by 2030. They are included in a UN-GA Resolution called the 2030 Agenda or what is colloquially known as Agenda 2030. The SDGs were developed in the Post-2015 Development Agenda as the future global development framework to succeed the Millennium Development Goals which were ended in 2015. The SDGs emphasize the interconnected environmental, social and economic aspects of sustainable development, by putting sustainability at their center.

The 17 SDGs are: No poverty, zero hunger, good health and well-being, quality education, gender equality, clean water and sanitation, affordable and clean energy, decent work and economic growth, industry, innovation and infrastructure, Reduced Inequality, Sustainable Cities and Communities, Responsible Consumption and Production, Climate Action, Life Below Water, Life On Land, Peace, Justice, and Strong Institutions, Partnerships for the Goals. Though the goals are broad and interdependent, two years later (6 July 2017), the SDGs were made more "actionable" by a UN Resolution adopted by the General Assembly. The resolution identifies specific targets for each goal, along with indicators that are being used to measure progress toward each target. The year by which the target is meant to be achieved is usually between 2020 and 2030. For some of the targets, no end date is given.

There are cross-cutting issues and synergies between the different goals. Cross-cutting issues include gender equality, education, culture and health. With regards to SDG 13 on climate action, the IPCC sees robust synergies, particularly for the SDGs 3 (health), 7 (clean energy), 11 (cities and communities), 12 (responsible consumption and production) and 14 (oceans). Synergies amongst the SDGs are "the good antagonists of trade-offs". Some of the known and much discussed conceptual problem areas of the SDGs include: The fact that there are competing and too many goals (resulting in problems of trade-offs), that they are weak on environmental sustainability and that there are difficulties with tracking qualitative indicators. For example, these are two difficult trade-offs to consider: "How can ending hunger be reconciled with environmental sustainability? (SDG targets 2.3 and 15.2) How can economic growth be reconciled with environmental sustainability? (SDG targets 9.2 and 9.4) "

Education for sustainable development

Education for sustainable development (ESD) is a term used by the United Nations and is defined as education that encourages changes in knowledge, skills, values and attitudes to enable a more sustainable and just society for all. ESD aims to empower and equip current and future generations to meet their needs using a balanced and integrated approach to the economic, social and environmental dimensions of sustainable development.

Agenda 21 was the first international document that identified education as an essential tool for achieving sustainable development and highlighted areas of action for education. ESD is a component of measurement in an indicator for Sustainable Development Goal 12 (SDG) for "responsible consumption and production". SDG 12 has 11 targets and target 12.8 is "By 2030, ensure that people everywhere have the relevant information and awareness for sustainable development and lifestyles in harmony with nature." 20 years after the Agenda 21 document was declared, the ‘Future we want’ document was declared in the Rio+20 UN Conference on Sustainable Development, stating that "We resolve to promote education for sustainable development and to integrate sustainable development more actively into education beyond the Decade of Education for Sustainable Development."

One version of education for Sustainable Development recognizes modern-day environmental challenges and seeks to define new ways to adjust to a changing biosphere, as well as engage individuals to address societal issues that come with them  In the International Encyclopedia of Education, this approach to education is seen as an attempt to "shift consciousness toward an ethics of life-giving relationships that respects the interconnectedness of man to his natural world" in order to equip future members of society with environmental awareness and a sense of responsibility to sustainability.

For UNESCO, education for sustainable development involves:

integrating key sustainable development issues into teaching and learning. This may include, for example, instruction about climate change, disaster risk reduction, biodiversity, and poverty reduction and sustainable consumption. It also requires participatory teaching and learning methods that motivate and empower learners to change their behaviours and take action for sustainable development. ESD consequently promotes competencies like critical thinking, imagining future scenarios and making decisions in a collaborative way.

The Thessaloniki Declaration, presented at the "International Conference on Environment and Society: Education and Public Awareness for Sustainability" by UNESCO and the Government of Greece (December 1997), highlights the importance of sustainability not only with regards to the natural environment, but also with "poverty, health, food security, democracy, human rights, and peace".

Serendipity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Serendipity

Serendipity is an unplanned fortunate discovery. Serendipity is a common occurrence throughout the history of product invention and scientific discovery. Serendipity is also seen as a potential design principle for online activities that would present a wide array of information and viewpoints, rather than just re-enforcing a user's opinion.

Etymology

The first noted use of "serendipity" was by Horace Walpole on 28 January 1754. In a letter he wrote to his friend Horace Mann, Walpole explained an unexpected discovery he had made about a lost painting of Bianca Cappello by Giorgio Vasari by reference to a Persian fairy tale, The Three Princes of Serendip. The princes, he told his correspondent, were "always making discoveries, by accidents and sagacity, of things which they were not in quest of." The name comes from Serendip, an old Persian name for Sri Lanka (Ceylon), hence Sarandib by Arab traders. It is derived from the Sanskrit Siṃhaladvīpaḥ (Siṃhalaḥ, Sri Lanka + dvīpaḥ, island).

The word has been exported into many other languages, with the general meaning of “unexpected discovery” or “fortunate chance”.

Applications

Inventions

Serendipitous inventions

Post-It Note

 

 

Velcro

 

 

Silly Putty

 

 

Popsicle

 

 

Penicillin

The term "serendipity" is often applied to inventions made by chance rather than intent. Andrew Smith, editor of The Oxford Companion to American Food and Drink, has speculated that most everyday products had serendipitous roots, with many early ones related to animals. The origin of cheese, for example, possibly originated in the nomad practice of storing milk in the stomach of a dead camel that was attached to the saddle of a live one, thereby mixing rennet from the stomach with the milk stored within.

Other examples of serendipity in inventions include:

• The Post-It Note, which emerged after 3M scientist Spencer Silver produced a weak adhesive, and a colleague used it to keep bookmarks in place on a church hymnal.
• Silly Putty, which came from a failed attempt at synthetic rubber.
• The use of sensors to prevent automobile air bags from killing children, which came from a chair developed by the MIT Media Lab for a Penn and Teller magic show.
• The microwave oven. Raytheon scientist Percy Spencer first patented the idea behind it after noticing that emissions from radar equipment had melted the candy in his pocket.
• The Velcro hook-and-loop fastener. George de Mestral came up with the idea after a bird hunting trip when he viewed cockleburs stuck to his pants under a microscope and saw that each burr was covered with tiny hooks.
• The Popsicle, whose origins go back to San Francisco where Frank Epperson, age 11, accidentally left a mix of water and soda powder outside to freeze overnight.
• Polymer teflon, which Roy J. Plunkett observed forming a white mass inside a pressure bottle during an effort to make a new CFCs refrigerant.
• The antibiotic penicillin, which was discovered by Sir Alexander Fleming after returning from a vacation to find that a Petri dish containing staphylococcus culture had been infected by a Penicillium mold, and no bacteria grew near it.

Discoveries

The serendipitous discovery of a new species of lacewing, Semachrysa jade, was made on Flickr

Serendipity contributed to entomologist Shaun Winterton discovering Semachrysa jade, a new species of lacewing, which he found not in its native Malaysia, but on the photo-sharing site Flickr. Winterton's discovery was aided by Flickr's ability to present images that are personalized to a user's interests, thereby increasing the odds he would chance upon the photo. Computer scientist Jaime Teevan has argued that serendipitous discovery is promoted by such personalization, writing that "people don’t know what to do with random new information. Instead, we want information that is at the fringe of what we already know, because that is when we have the cognitive structures to make sense of the new ideas."

Online activity

Serendipity is a design principle for online activity that would present viewpoints that diverge from those participants already hold. Harvard Law professor Cass Sunstein argues that such an "architecture of serendipity" would promote a healthier democracy. Like a great city or university, "a well-functioning information market" provides exposure to new ideas, people, and ways of life, "Serendipity is crucial because it expands your horizons. You need that if you want to be free." The idea has potential application in the design of social media, information searches, and web browsing.

Related terms

Several uncommonly used terms have been derived from the concept and name of serendipity.

William Boyd coined the term zemblanity in the late twentieth century to mean somewhat the opposite of serendipity: "making unhappy, unlucky and expected discoveries occurring by design". The derivation is speculative, but believed to be from Nova Zembla, a barren archipelago once the site of Russian nuclear testing.

Bahramdipity is derived directly from Bahram Gur as characterized in The Three Princes of Serendip. It describes the suppression of serendipitous discoveries or research results by powerful individuals.

In addition, Solomon & Bronstein (2018) further distinguish between perceptual and realised pseudo-serendipity and nemorinity.