From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Gravitational_potential
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.
Potential energy
The gravitational potential (V) at a location is the gravitational potential energy (U) at that location per unit mass:
where m is the mass of the object. Potential energy is equal (in magnitude, but negative) to the work done by the gravitational field moving a body to its given position in space from infinity. If the body has a mass of 1 kilogram, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity.
In some situations, the equations can be simplified by assuming a field that is nearly independent of position. For instance, in a region close to the surface of the Earth, the gravitational acceleration, g, can be considered constant. In that case, the difference in potential energy from one height to another is, to a good approximation, linearly related to the difference in height:
Mathematical form
The gravitational potential V at a distance x from a point mass of mass M can be defined as the work W that needs to be done by an external agent to bring a unit mass in from infinity to that point:
The gravitational field, and thus the acceleration of a small body in the space around the massive object, is the negative gradient of the gravitational potential. Thus the negative of a negative gradient yields positive acceleration toward a massive object. Because the potential has no angular components, its gradient is
The potential associated with a mass distribution is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x1, ..., xn and have masses m1, ..., mn, then the potential of the distribution at the point x is
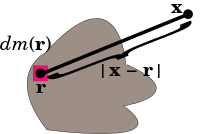
If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space R3, then the potential is the convolution of −G/|r| with dm. In good cases this equals the integral
If V is a potential function coming from a continuous mass distribution ρ(r), then ρ can be recovered using the Laplace operator, Δ:
The integral may be expressed in terms of known transcendental functions for all ellipsoidal shapes, including the symmetrical and degenerate ones. These include the sphere, where the three semi axes are equal; the oblate (see reference ellipsoid) and prolate spheroids, where two semi axes are equal; the degenerate ones where one semi axes is infinite (the elliptical and circular cylinder) and the unbounded sheet where two semi axes are infinite. All these shapes are widely used in the applications of the gravitational potential integral (apart from the constant G, with 𝜌 being a constant charge density) to electromagnetism.
Spherical symmetry
A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass was concentrated at the center, and thus effectively as a point mass, by the shell theorem. On the surface of the earth, the acceleration is given by so-called standard gravity g, approximately 9.8 m/s2, although this value varies slightly with latitude and altitude. The magnitude of the acceleration is a little larger at the poles than at the equator because Earth is an oblate spheroid.
Within a spherically symmetric mass distribution, it is possible to solve Poisson's equation in spherical coordinates. Within a uniform spherical body of radius R, density ρ, and mass m, the gravitational force g inside the sphere varies linearly with distance r from the center, giving the gravitational potential inside the sphere, which is
General relativity
In general relativity, the gravitational potential is replaced by the metric tensor. When the gravitational field is weak and the sources are moving very slowly compared to light-speed, general relativity reduces to Newtonian gravity, and the metric tensor can be expanded in terms of the gravitational potential.
Multipole expansion
The potential at a point x is given by
The potential can be expanded in a series of Legendre polynomials. Represent the points x and r as position vectors relative to the center of mass. The denominator in the integral is expressed as the square root of the square to give
(See "mathematical form".) The integrand can be expanded as a Taylor series in Z = r/|x|, by explicit calculation of the coefficients. A less laborious way of achieving the same result is by using the generalized binomial theorem. The resulting series is the generating function for the Legendre polynomials:
This shows that elongation of the body causes a lower potential in the direction of elongation, and a higher potential in perpendicular directions, compared to the potential due to a spherical mass, if we compare cases with the same distance to the center of mass. (If we compare cases with the same distance to the surface, the opposite is true.)
Numerical values
The absolute value of gravitational potential at a number of locations with regards to the gravitation from the Earth, the Sun, and the Milky Way is given in the following table; i.e. an object at Earth's surface would need 60 MJ/kg to "leave" Earth's gravity field, another 900 MJ/kg to also leave the Sun's gravity field and more than 130 GJ/kg to leave the gravity field of the Milky Way. The potential is half the square of the escape velocity.
| Location | with respect to | ||
|---|---|---|---|
| Earth | Sun | Milky Way | |
| Earth's surface | 60 MJ/kg | 900 MJ/kg | ≥ 130 GJ/kg |
| LEO | 57 MJ/kg | 900 MJ/kg | ≥ 130 GJ/kg |
| Voyager 1 (17,000 million km from Earth) | 23 J/kg | 8 MJ/kg | ≥ 130 GJ/kg |
| 0.1 light-year from Earth | 0.4 J/kg | 140 kJ/kg | ≥ 130 GJ/kg |
Compare the gravity at these locations.










![{\displaystyle V(r)={\frac {2}{3}}\pi G\rho \left[r^{2}-3R^{2}\right]={\frac {Gm}{2R^{3}}}\left[r^{2}-3R^{2}\right],\qquad r\leq R,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9edacd57f6ef05612224090a38b674c9e164ccab)