Generalized linear model

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Generalized_linear_model 

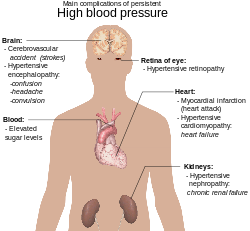
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.

Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed.

Intuition

Ordinary linear regression predicts the expected value of a given unknown quantity (the response variable, a random variable) as a linear combination of a set of observed values (predictors). This implies that a constant change in a predictor leads to a constant change in the response variable (i.e. a linear-response model). This is appropriate when the response variable can vary, to a good approximation, indefinitely in either direction, or more generally for any quantity that only varies by a relatively small amount compared to the variation in the predictive variables, e.g. human heights.

However, these assumptions are inappropriate for some types of response variables. For example, in cases where the response variable is expected to be always positive and varying over a wide range, constant input changes lead to geometrically (i.e. exponentially) varying, rather than constantly varying, output changes. As an example, suppose a linear prediction model learns from some data (perhaps primarily drawn from large beaches) that a 10 degree temperature decrease would lead to 1,000 fewer people visiting the beach. This model is unlikely to generalize well over different sized beaches. More specifically, the problem is that if you use the model to predict the new attendance with a temperature drop of 10 for a beach that regularly receives 50 beachgoers, you would predict an impossible attendance value of −950. Logically, a more realistic model would instead predict a constant rate of increased beach attendance (e.g. an increase of 10 degrees leads to a doubling in beach attendance, and a drop of 10 degrees leads to a halving in attendance). Such a model is termed an exponential-response model (or log-linear model, since the logarithm of the response is predicted to vary linearly).

Similarly, a model that predicts a probability of making a yes/no choice (a Bernoulli variable) is even less suitable as a linear-response model, since probabilities are bounded on both ends (they must be between 0 and 1). Imagine, for example, a model that predicts the likelihood of a given person going to the beach as a function of temperature. A reasonable model might predict, for example, that a change in 10 degrees makes a person two times more or less likely to go to the beach. But what does "twice as likely" mean in terms of a probability? It cannot literally mean to double the probability value (e.g. 50% becomes 100%, 75% becomes 150%, etc.). Rather, it is the odds that are doubling: from 2:1 odds, to 4:1 odds, to 8:1 odds, etc. Such a model is a log-odds or logistic model.

Generalized linear models cover all these situations by allowing for response variables that have arbitrary distributions (rather than simply normal distributions), and for an arbitrary function of the response variable (the link function) to vary linearly with the predictors (rather than assuming that the response itself must vary linearly). For example, the case above of predicted number of beach attendees would typically be modeled with a Poisson distribution and a log link, while the case of predicted probability of beach attendance would typically be modelled with a Bernoulli distribution (or binomial distribution, depending on exactly how the problem is phrased) and a log-odds (or logit) link function.

Overview

In a generalized linear model (GLM), each outcome Y of the dependent variables is assumed to be generated from a particular distribution in an exponential family, a large class of probability distributions that includes the normal, binomial, Poisson and gamma distributions, among others. The mean, μ, of the distribution depends on the independent variables, X, through:

${\displaystyle \mathrm{E}(\mathbf{Y}|\mathbf{X})=\mathit{\mu }=g^{-1}(\mathbf{X}\mathit{\beta })}$

where E(Y|X) is the expected value of Y conditional on X; Xβ is the linear predictor, a linear combination of unknown parameters β; g is the link function.

In this framework, the variance is typically a function, V, of the mean:

${\displaystyle \mathrm{Var}(\mathbf{Y}|\mathbf{X})=\mathrm{V}(g^{-1}(\mathbf{X}\mathit{\beta })).}$

It is convenient if V follows from an exponential family of distributions, but it may simply be that the variance is a function of the predicted value.

The unknown parameters, β, are typically estimated with maximum likelihood, maximum quasi-likelihood, or Bayesian techniques.

Model components

The GLM consists of three elements:

1. A particular distribution for modeling ${\displaystyle Y}$ from among those which are considered exponential families of probability distributions,

2. A linear predictor ${\displaystyle \eta =X\beta }$, and

3. A link function ${\displaystyle g}$ such that ${\displaystyle \mathrm{E}(Y\mid X)=\mu =g^{-1}(\eta )}$.

Probability distribution

An overdispersed exponential family of distributions is a generalization of an exponential family and the exponential dispersion model of distributions and includes those families of probability distributions, parameterized by ${\displaystyle \mathit{\theta }}$ and ${\displaystyle \tau }$, whose density functions f (or probability mass function, for the case of a discrete distribution) can be expressed in the form

${\displaystyle f_Y(\mathbf{y}\mid \mathit{\theta },\tau )=h(\mathbf{y},\tau )\exp \left(\frac{\mathbf{b}(\mathit{\theta }{)}^{\mathrm{T}}\mathbf{T}(\mathbf{y})-A(\mathit{\theta })}{d(\tau )}\right).}$

The dispersion parameter, ${\displaystyle \tau }$, typically is known and is usually related to the variance of the distribution. The functions ${\displaystyle h(\mathbf{y},\tau )}$, ${\displaystyle \mathbf{b}(\mathit{\theta })}$, ${\displaystyle \mathbf{T}(\mathbf{y})}$, ${\displaystyle A(\mathit{\theta })}$, and ${\displaystyle d(\tau )}$ are known. Many common distributions are in this family, including the normal, exponential, gamma, Poisson, Bernoulli, and (for fixed number of trials) binomial, multinomial, and negative binomial.

For scalar ${\displaystyle \mathbf{y}}$ and ${\displaystyle \mathit{\theta }}$ (denoted ${\displaystyle y}$ and ${\displaystyle \theta }$ in this case), this reduces to

${\displaystyle f_Y(y\mid \theta ,\tau )=h(y,\tau )\exp \left(\frac{b(\theta )T(y)-A(\theta )}{d(\tau )}\right).}$

${\displaystyle \mathit{\theta }}$ is related to the mean of the distribution. If ${\displaystyle \mathbf{b}(\mathit{\theta })}$ is the identity function, then the distribution is said to be in canonical form (or natural form). Note that any distribution can be converted to canonical form by rewriting ${\displaystyle \mathit{\theta }}$ as ${\displaystyle {\mathit{\theta }}^{\prime }}$ and then applying the transformation ${\displaystyle \mathit{\theta }=\mathbf{b}({\mathit{\theta }}^{\prime })}$. It is always possible to convert ${\displaystyle A(\mathit{\theta })}$ in terms of the new parametrization, even if ${\displaystyle \mathbf{b}({\mathit{\theta }}^{\prime })}$ is not a one-to-one function; see comments in the page on exponential families. If, in addition, ${\displaystyle \mathbf{T}(\mathbf{y})}$ is the identity and ${\displaystyle \tau }$ is known, then ${\displaystyle \mathit{\theta }}$ is called the canonical parameter (or natural parameter) and is related to the mean through

${\displaystyle \mathit{\mu }=\mathrm{E}(\mathbf{y})=\mathrm{\nabla }A(\mathit{\theta }).}$

For scalar ${\displaystyle \mathbf{y}}$ and ${\displaystyle \mathit{\theta }}$, this reduces to

${\displaystyle \mu =\mathrm{E}(y)=A^{\prime }(\theta ).}$

Under this scenario, the variance of the distribution can be shown to be

${\displaystyle \mathrm{Var}(\mathbf{y})={\mathrm{\nabla }}^{2}A(\mathit{\theta })d(\tau ).}$

For scalar ${\displaystyle \mathbf{y}}$ and ${\displaystyle \mathit{\theta }}$, this reduces to

${\displaystyle \mathrm{Var}(y)=A^{″}(\theta )d(\tau ).}$

Linear predictor

The linear predictor is the quantity which incorporates the information about the independent variables into the model. The symbol η (Greek "eta") denotes a linear predictor. It is related to the expected value of the data through the link function.

η is expressed as linear combinations (thus, "linear") of unknown parameters β. The coefficients of the linear combination are represented as the matrix of independent variables X. η can thus be expressed as

${\displaystyle \eta =\mathbf{X}\mathit{\beta }.}$

Link function

The link function provides the relationship between the linear predictor and the mean of the distribution function. There are many commonly used link functions, and their choice is informed by several considerations. There is always a well-defined canonical link function which is derived from the exponential of the response's density function. However, in some cases it makes sense to try to match the domain of the link function to the range of the distribution function's mean, or use a non-canonical link function for algorithmic purposes, for example Bayesian probit regression.

When using a distribution function with a canonical parameter ${\displaystyle \theta }$, the canonical link function is the function that expresses ${\displaystyle \theta }$ in terms of ${\displaystyle \mu }$, i.e. ${\displaystyle \theta =b(\mu )}$. For the most common distributions, the mean ${\displaystyle \mu }$ is one of the parameters in the standard form of the distribution's density function, and then ${\displaystyle b(\mu )}$ is the function as defined above that maps the density function into its canonical form. When using the canonical link function, ${\displaystyle b(\mu )=\theta =\mathbf{X}\mathit{\beta }}$, which allows ${\displaystyle {\mathbf{X}}^{\mathrm{T}}\mathbf{Y}}$ to be a sufficient statistic for ${\displaystyle \mathit{\beta }}$.

Following is a table of several exponential-family distributions in common use and the data they are typically used for, along with the canonical link functions and their inverses (sometimes referred to as the mean function, as done here).

Common distributions with typical uses and canonical link functions

Distribution	Support of distribution	Typical uses	Link name	Link function, ${\displaystyle \mathbf{X}\mathit{\beta }=g(\mu )}$	Mean function
Normal	real: ${\displaystyle (-\mathrm{\infty },+\mathrm{\infty })}$	Linear-response data	Identity	${\displaystyle \mathbf{X}\mathit{\beta }=\mu }$	${\displaystyle \mu =\mathbf{X}\mathit{\beta }}$
Exponential	real: ${\displaystyle (0,+\mathrm{\infty })}$	Exponential-response data, scale parameters	Negative inverse	${\displaystyle \mathbf{X}\mathit{\beta }=-{\mu }^{-1}}$	${\displaystyle \mu =-(\mathbf{X}\mathit{\beta }{)}^{-1}}$
Gamma
Inverse Gaussian	real: ${\displaystyle (0,+\mathrm{\infty })}$		Inverse squared	${\displaystyle \mathbf{X}\mathit{\beta }={\mu }^{-2}}$	${\displaystyle \mu =(\mathbf{X}\mathit{\beta }{)}^{-1/2}}$
Poisson	integer: ${\displaystyle 0,1,2,\dots }$	count of occurrences in fixed amount of time/space	Log	${\displaystyle \mathbf{X}\mathit{\beta }=\ln (\mu )}$	${\displaystyle \mu =\exp (\mathbf{X}\mathit{\beta })}$
Bernoulli	integer: ${\displaystyle \{0,1\}}$	outcome of single yes/no occurrence	Logit	${\displaystyle \mathbf{X}\mathit{\beta }=\ln \left(\frac{\mu }{1-\mu }\right)}$	${\displaystyle \mu =\frac{\exp (\mathbf{X}\mathit{\beta })}{1+\exp (\mathbf{X}\mathit{\beta })}=\frac{1}{1+\exp (-\mathbf{X}\mathit{\beta })}}$
Binomial	integer: ${\displaystyle 0,1,\dots ,N}$	count of # of "yes" occurrences out of N yes/no occurrences		${\displaystyle \mathbf{X}\mathit{\beta }=\ln \left(\frac{\mu }{n-\mu }\right)}$
Categorical	integer: ${\displaystyle [0,K)}$	outcome of single K-way occurrence		${\displaystyle \mathbf{X}\mathit{\beta }=\ln \left(\frac{\mu }{1-\mu }\right)}$
	K-vector of integer: ${\displaystyle [0,1]}$, where exactly one element in the vector has the value 1
Multinomial	K-vector of integer: ${\displaystyle [0,N]}$	count of occurrences of different types (1 .. K) out of N total K-way occurrences

In the cases of the exponential and gamma distributions, the domain of the canonical link function is not the same as the permitted range of the mean. In particular, the linear predictor may be positive, which would give an impossible negative mean. When maximizing the likelihood, precautions must be taken to avoid this. An alternative is to use a noncanonical link function.

In the case of the Bernoulli, binomial, categorical and multinomial distributions, the support of the distributions is not the same type of data as the parameter being predicted. In all of these cases, the predicted parameter is one or more probabilities, i.e. real numbers in the range ${\displaystyle [0,1]}$. The resulting model is known as logistic regression (or multinomial logistic regression in the case that K-way rather than binary values are being predicted).

For the Bernoulli and binomial distributions, the parameter is a single probability, indicating the likelihood of occurrence of a single event. The Bernoulli still satisfies the basic condition of the generalized linear model in that, even though a single outcome will always be either 0 or 1, the expected value will nonetheless be a real-valued probability, i.e. the probability of occurrence of a "yes" (or 1) outcome. Similarly, in a binomial distribution, the expected value is Np, i.e. the expected proportion of "yes" outcomes will be the probability to be predicted.

For categorical and multinomial distributions, the parameter to be predicted is a K-vector of probabilities, with the further restriction that all probabilities must add up to 1. Each probability indicates the likelihood of occurrence of one of the K possible values. For the multinomial distribution, and for the vector form of the categorical distribution, the expected values of the elements of the vector can be related to the predicted probabilities similarly to the binomial and Bernoulli distributions.

Fitting

Maximum likelihood

The maximum likelihood estimates can be found using an iteratively reweighted least squares algorithm or a Newton's method with updates of the form:

${\displaystyle {\mathit{\beta }}^{(t+1)}={\mathit{\beta }}^{(t)}+{\mathcal{J}}^{-1}({\mathit{\beta }}^{(t)})u({\mathit{\beta }}^{(t)}),}$

where ${\displaystyle \mathcal{J}({\mathit{\beta }}^{(t)})}$ is the observed information matrix (the negative of the Hessian matrix) and ${\displaystyle u({\mathit{\beta }}^{(t)})}$ is the score function; or a Fisher's scoring method:

${\displaystyle {\mathit{\beta }}^{(t+1)}={\mathit{\beta }}^{(t)}+{\mathcal{I}}^{-1}({\mathit{\beta }}^{(t)})u({\mathit{\beta }}^{(t)}),}$

where ${\displaystyle \mathcal{I}({\mathit{\beta }}^{(t)})}$ is the Fisher information matrix. Note that if the canonical link function is used, then they are the same.

Bayesian methods

In general, the posterior distribution cannot be found in closed form and so must be approximated, usually using Laplace approximations or some type of Markov chain Monte Carlo method such as Gibbs sampling.

Examples

General linear models

Further information: General linear model

A possible point of confusion has to do with the distinction between generalized linear models and general linear models, two broad statistical models. Co-originator John Nelder has expressed regret over this terminology.

The general linear model may be viewed as a special case of the generalized linear model with identity link and responses normally distributed. As most exact results of interest are obtained only for the general linear model, the general linear model has undergone a somewhat longer historical development. Results for the generalized linear model with non-identity link are asymptotic (tending to work well with large samples).

Linear regression

A simple, very important example of a generalized linear model (also an example of a general linear model) is linear regression. In linear regression, the use of the least-squares estimator is justified by the Gauss–Markov theorem, which does not assume that the distribution is normal.

From the perspective of generalized linear models, however, it is useful to suppose that the distribution function is the normal distribution with constant variance and the link function is the identity, which is the canonical link if the variance is known. Under these assumptions, the least-squares estimator is obtained as the maximum-likelihood parameter estimate.

For the normal distribution, the generalized linear model has a closed form expression for the maximum-likelihood estimates, which is convenient. Most other GLMs lack closed form estimates.

Binary data

See also: Binary regression

When the response data, Y, are binary (taking on only values 0 and 1), the distribution function is generally chosen to be the Bernoulli distribution and the interpretation of μ_i is then the probability, p, of Y_i taking on the value one.

There are several popular link functions for binomial functions.

Logit link function

The most typical link function is the canonical logit link:

${\displaystyle g(p)=\ln \left(\frac{p}{1-p}\right).}$

GLMs with this setup are logistic regression models (or logit models).

Probit link function as popular choice of inverse cumulative distribution function

Alternatively, the inverse of any continuous cumulative distribution function (CDF) can be used for the link since the CDF's range is ${\displaystyle [0,1]}$, the range of the binomial mean. The normal CDF ${\displaystyle \mathrm{\Phi }}$ is a popular choice and yields the probit model. Its link is

${\displaystyle g(p)={\mathrm{\Phi }}^{-1}(p).}$

The reason for the use of the probit model is that a constant scaling of the input variable to a normal CDF (which can be absorbed through equivalent scaling of all of the parameters) yields a function that is practically identical to the logit function, but probit models are more tractable in some situations than logit models. (In a Bayesian setting in which normally distributed prior distributions are placed on the parameters, the relationship between the normal priors and the normal CDF link function means that a probit model can be computed using Gibbs sampling, while a logit model generally cannot.)

Complementary log-log (cloglog)

The complementary log-log function may also be used:

${\displaystyle g(p)=\log (-\log (1-p)).}$

This link function is asymmetric and will often produce different results from the logit and probit link functions. The cloglog model corresponds to applications where we observe either zero events (e.g., defects) or one or more, where the number of events is assumed to follow the Poisson distribution. The Poisson assumption means that

${\displaystyle Pr(0)=\exp (-\mu ),}$

where μ is a positive number denoting the expected number of events. If p represents the proportion of observations with at least one event, its complement

${\displaystyle (1-p)=Pr(0)=\exp (-\mu ),}$

and then

${\displaystyle (-\log (1-p))=\mu .}$

A linear model requires the response variable to take values over the entire real line. Since μ must be positive, we can enforce that by taking the logarithm, and letting log(μ) be a linear model. This produces the "cloglog" transformation

${\displaystyle \log (-\log (1-p))=\log (\mu ).}$

Identity link

The identity link g(p) = p is also sometimes used for binomial data to yield a linear probability model. However, the identity link can predict nonsense "probabilities" less than zero or greater than one. This can be avoided by using a transformation like cloglog, probit or logit (or any inverse cumulative distribution function). A primary merit of the identity link is that it can be estimated using linear math—and other standard link functions are approximately linear matching the identity link near p = 0.5.

Variance function

The variance function for "quasibinomial" data is:

${\displaystyle \mathrm{Var}(Y_i)=\tau {\mu }_i(1-{\mu }_i)}$

where the dispersion parameter τ is exactly 1 for the binomial distribution. Indeed, the standard binomial likelihood omits τ. When it is present, the model is called "quasibinomial", and the modified likelihood is called a quasi-likelihood, since it is not generally the likelihood corresponding to any real family of probability distributions. If τ exceeds 1, the model is said to exhibit overdispersion.

Multinomial regression

The binomial case may be easily extended to allow for a multinomial distribution as the response (also, a Generalized Linear Model for counts, with a constrained total). There are two ways in which this is usually done:

Ordered response

If the response variable is ordinal, then one may fit a model function of the form:

${\displaystyle g({\mu }_m)={\eta }_m={\beta }_0+X_1{\beta }_1+\cdots +X_p{\beta }_p+{\gamma }_2+\cdots +{\gamma }_m={\eta }_1+{\gamma }_2+\cdots +{\gamma }_m\text{ where }{\mu }_m=\mathrm{P}(Y\le m).}$

for m > 2. Different links g lead to ordinal regression models like proportional odds models or ordered probit models.

Unordered response

If the response variable is a nominal measurement, or the data do not satisfy the assumptions of an ordered model, one may fit a model of the following form:

${\displaystyle g({\mu }_m)={\eta }_m={\beta }_{m,0}+X_1{\beta }_{m,1}+\cdots +X_p{\beta }_{m,p}\text{ where }{\mu }_m=\mathrm{P}(Y=m\mid Y\in \{1,m\}).}$

for m > 2. Different links g lead to multinomial logit or multinomial probit models. These are more general than the ordered response models, and more parameters are estimated.

Count data

Another example of generalized linear models includes Poisson regression which models count data using the Poisson distribution. The link is typically the logarithm, the canonical link.

The variance function is proportional to the mean

${\displaystyle \mathrm{var}(Y_i)=\tau {\mu }_i,}$

where the dispersion parameter τ is typically fixed at exactly one. When it is not, the resulting quasi-likelihood model is often described as Poisson with overdispersion or quasi-Poisson.

Extensions

Correlated or clustered data

The standard GLM assumes that the observations are uncorrelated. Extensions have been developed to allow for correlation between observations, as occurs for example in longitudinal studies and clustered designs:

• Generalized estimating equations (GEEs) allow for the correlation between observations without the use of an explicit probability model for the origin of the correlations, so there is no explicit likelihood. They are suitable when the random effects and their variances are not of inherent interest, as they allow for the correlation without explaining its origin. The focus is on estimating the average response over the population ("population-averaged" effects) rather than the regression parameters that would enable prediction of the effect of changing one or more components of X on a given individual. GEEs are usually used in conjunction with Huber–White standard errors.
• Generalized linear mixed models (GLMMs) are an extension to GLMs that includes random effects in the linear predictor, giving an explicit probability model that explains the origin of the correlations. The resulting "subject-specific" parameter estimates are suitable when the focus is on estimating the effect of changing one or more components of X on a given individual. GLMMs are also referred to as multilevel models and as mixed model. In general, fitting GLMMs is more computationally complex and intensive than fitting GEEs.

Generalized additive models

Generalized additive models (GAMs) are another extension to GLMs in which the linear predictor η is not restricted to be linear in the covariates X but is the sum of smoothing functions applied to the x_is:

${\displaystyle \eta ={\beta }_0+f_1(x_1)+f_2(x_2)+\cdots }$

The smoothing functions f_i are estimated from the data. In general this requires a large number of data points and is computationally intensive.

Cardiology

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Cardiology

 

Blood flow diagram of the human heart. Blue components indicate de-oxygenated blood pathways and red components indicate oxygenated blood pathways.
System	Cardiovascular
Subdivisions	Interventional Cardiology, Clinical Cardiac Electrophysiology, Heart Failure and Transplant Cardiology, Nuclear Cardiology, Adult Congenital Heart Disease, Pediatric Cardiology, Echocardiography, Cardiovascular Imaging
Significant diseases	Heart disease, Cardiovascular disease, Atherosclerosis, Cardiomyopathy, Hypertension (High Blood Pressure)
Significant tests	Blood tests, electrophysiology study, cardiac imaging, ECG, echocardiograms, stress test
Specialist	Cardiologist
Glossary	Glossary of medicine

Cardiologist

Occupation
Names	Physician Surgeon
Occupation type	Specialty
Activity sectors	Medicine, Surgery
Description
Education required	Doctor of Medicine (M.D.) Doctor of Osteopathic Medicine (D.O.) Bachelor of Medicine, Bachelor of Surgery (M.B.B.S.) Bachelor of Medicine, Bachelor of Surgery (MBChB)
Fields of employment	Hospitals, Clinics

Cardiology (from Ancient Greek καρδίᾱ (kardiā) 'heart', and -λογία (-logia) 'study') is the study of the heart. Cardiology is a branch of medicine that deals with disorders of the heart and the cardiovascular system. The field includes medical diagnosis and treatment of congenital heart defects, coronary artery disease, heart failure, valvular heart disease, and electrophysiology. Physicians who specialize in this field of medicine are called cardiologists, a specialty of internal medicine. Pediatric cardiologists are pediatricians who specialize in cardiology. Physicians who specialize in cardiac surgery are called cardiothoracic surgeons or cardiac surgeons, a specialty of general surgery.

Specializations

All cardiologists in the branch of medicine study the disorders of the heart, but the study of adult and child heart disorders each require different training pathways. Therefore, an adult cardiologist (often simply called "cardiologist") is inadequately trained to take care of children, and pediatric cardiologists are not trained to treat adult heart disease. Surgical aspects are not included in cardiology and are in the domain of cardiothoracic surgery. For example, coronary artery bypass surgery (CABG), cardiopulmonary bypass and valve replacement are surgical procedures performed by surgeons, not cardiologists. However, some minimally invasive procedures such as cardiac catheterization and pacemaker implantation are performed by cardiologists who have additional training in non-surgical interventions (interventional cardiology and electrophysiology respectively).

Adult cardiology

Cardiology is a specialty of internal medicine. To be a cardiologist in the United States, a three-year residency in internal medicine is followed by a three-year fellowship in cardiology. It is possible to specialize further in a sub-specialty. Recognized sub-specialties in the U.S. by the Accreditation Council for Graduate Medical Education are cardiac electrophysiology, echocardiography, interventional cardiology, and nuclear cardiology. Recognized subspecialties in the U.S. by the American Osteopathic Association Bureau of Osteopathic Specialists include clinical cardiac electrophysiology and interventional cardiology. In India, a three-year residency in General Medicine or Pediatrics after M.B.B.S. and then three years of residency in cardiology are needed to be a D.M./Diplomate of National Board (DNB) in Cardiology.

Per Doximity, adult cardiologists earn an average of $436,849 per year in the U.S.

Cardiac electrophysiology

Main article: Cardiac electrophysiology

Cardiac electrophysiology is the science of elucidating, diagnosing, and treating the electrical activities of the heart. The term is usually used to describe studies of such phenomena by invasive (intracardiac) catheter recording of spontaneous activity as well as of cardiac responses to programmed electrical stimulation (PES). These studies are performed to assess complex arrhythmias, elucidate symptoms, evaluate abnormal electrocardiograms, assess risk of developing arrhythmias in the future, and design treatment. These procedures increasingly include therapeutic methods (typically radiofrequency ablation, or cryoablation) in addition to diagnostic and prognostic procedures. Other therapeutic modalities employed in this field include antiarrhythmic drug therapy and implantation of pacemakers and automatic implantable cardioverter-defibrillators (AICD).

The cardiac electrophysiology study typically measures the response of the injured or cardiomyopathic myocardium to PES on specific pharmacological regimens in order to assess the likelihood that the regimen will successfully prevent potentially fatal sustained ventricular tachycardia (VT) or ventricular fibrillation (VF) in the future. Sometimes a series of electrophysiology-study drug trials must be conducted to enable the cardiologist to select the one regimen for long-term treatment that best prevents or slows the development of VT or VF following PES. Such studies may also be conducted in the presence of a newly implanted or newly replaced cardiac pacemaker or AICD.

Clinical cardiac electrophysiology

Main article: Clinical cardiac electrophysiology

Clinical cardiac electrophysiology is a branch of the medical specialty of cardiology and is concerned with the study and treatment of rhythm disorders of the heart. Cardiologists with expertise in this area are usually referred to as electrophysiologists. Electrophysiologists are trained in the mechanism, function, and performance of the electrical activities of the heart. Electrophysiologists work closely with other cardiologists and cardiac surgeons to assist or guide therapy for heart rhythm disturbances (arrhythmias). They are trained to perform interventional and surgical procedures to treat cardiac arrhythmia.

The training required to become an electrophysiologist is long and requires 8 years after medical school (within the U.S.). Three years of internal medicine residency, three years of cardiology fellowship, and two years of clinical cardiac electrophysiology.

Cardiogeriatrics

Main article: Cardiogeriatrics

Cardiogeriatrics, or geriatric cardiology, is the branch of cardiology and geriatric medicine that deals with the cardiovascular disorders in elderly people.

Cardiac disorders such as coronary heart disease, including myocardial infarction, heart failure, cardiomyopathy, and arrhythmias such as atrial fibrillation, are common and are a major cause of mortality in elderly people. Vascular disorders such as atherosclerosis and peripheral arterial disease cause significant morbidity and mortality in aged people.

Imaging

Further information: Echocardiography, Cardiac magnetic resonance imaging, and Computed tomography of the heart

Cardiac imaging includes echocardiography (echo), cardiac magnetic resonance imaging (CMR), and computed tomography of the heart. Those who specialize in cardiac imaging may undergo more training in all imaging modes or focus on a single imaging modality.

Echocardiography (or "echo") uses standard two-dimensional, three-dimensional, and Doppler ultrasound to create images of the heart. Those who specialize in echo may spend a significant amount of their clinical time reading echos and performing transesophageal echo, in particular using the latter during procedures such as insertion of a left atrial appendage occlusion device.

Cardiac MRI utilizes special protocols to image heart structure and function with specific sequences for certain diseases such as hemochromatosis and amyloidosis.

Cardiac CT utilizes special protocols to image heart structure and function with particular emphasis on coronary arteries.

Interventional cardiology

Main article: Interventional cardiology

Interventional cardiology is a branch of cardiology that deals specifically with the catheter based treatment of structural heart diseases. A large number of procedures can be performed on the heart by catheterization, including angiogram, angioplasty, atherectomy, and stent implantation. These procedures all involve insertion of a sheath into the femoral artery or radial artery (but, in practice, any large peripheral artery or vein) and cannulating the heart under X-ray visualization (most commonly fluoroscopy). This cannulation allows indirect access to the heart, bypassing the trauma caused by surgical opening of the chest.

The main advantages of using the interventional cardiology or radiology approach are the avoidance of the scars and pain, and long post-operative recovery. Additionally, interventional cardiology procedure of primary angioplasty is now the gold standard of care for an acute myocardial infarction. This procedure can also be done proactively, when areas of the vascular system become occluded from atherosclerosis. The Cardiologist will thread this sheath through the vascular system to access the heart. This sheath has a balloon and a tiny wire mesh tube wrapped around it, and if the cardiologist finds a blockage or stenosis, they can inflate the balloon at the occlusion site in the vascular system to flatten or compress the plaque against the vascular wall. Once that is complete a stent is placed as a type of scaffold to hold the vasculature open permanently.

Cardiomyopathy/heart failure

Specialization of general cardiology to just that of the cardiomyopathies leads to also specializing in heart transplant and pulmonary hypertension. Cardiomyopathy is a heart disease of the heart muscle, where the heart muscle becomes inflamed and thick.

Cardiooncology

Main article: Cardiooncology

A recent specialization of cardiology is that of cardiooncology. This area specializes in the cardiac management in those with cancer and, in particular, those with plans for chemotherapy or whom have experienced cardiac complications of chemotherapy.

Preventive cardiology and cardiac rehabilitation

Further information: Cardiac rehabilitation

In recent times, the focus is gradually shifting to preventive cardiology due to increased cardiovascular disease burden at an early age. According to the WHO, 37% of all premature deaths are due to cardiovascular diseases and out of this, 82% are in low and middle income countries. Clinical cardiology is the sub specialty of cardiology which looks after preventive cardiology and cardiac rehabilitation. Preventive cardiology also deals with routine preventive checkup though noninvasive tests, specifically electrocardiography, fasegraphy, stress tests, lipid profile and general physical examination to detect any cardiovascular diseases at an early age, while cardiac rehabilitation is the upcoming branch of cardiology which helps a person regain their overall strength and live a normal life after a cardiovascular event. A subspecialty of preventive cardiology is sports cardiology. Because heart disease is the leading cause of death in the world including United States (cdc.gov), national health campaigns and randomized control research has developed to improve heart health.

Pediatric cardiology

Tetralogy of Fallot

Helen B. Taussig is known as the founder of pediatric cardiology. She became famous through her work with Tetralogy congenital heart defect in which oxygenated and deoxygenated blood enters the circulatory system resulting from a ventricular septal defect (VSD) right beneath the aorta. This condition causes newborns to have a bluish-tint, cyanosis, and have a deficiency of oxygen to their tissues, hypoxemia. She worked with Alfred Blalock and Vivien Thomas at the Johns Hopkins Hospital where they experimented with dogs to look at how they would attempt to surgically cure these "blue babies". They eventually figured out how to do just that by the anastomosis of the systemic artery to the pulmonary artery and called this the Blalock-Taussig Shunt.

Tetralogy of Fallot, pulmonary atresia, double outlet right ventricle, transposition of the great arteries, persistent truncus arteriosus, and Ebstein's anomaly are various congenital cyanotic heart diseases, in which the blood of the newborn is not oxygenated efficiently, due to the heart defect.

Adult congenital heart disease

As more children with congenital heart disease are surviving into adulthood, a hybrid of adult & pediatric cardiology has emerged called adult congenital heart disease (ACHD). This field can be entered as either adult or pediatric cardiology. ACHD specializes in congenital diseases in the setting of adult diseases (e.g., coronary artery disease, COPD, diabetes) that is, otherwise, atypical for adult or pediatric cardiology.

The heart

Blood flow through the valves

 

Main article: Heart

As the center focus of cardiology, the heart has numerous anatomical features (e.g., atria, ventricles, heart valves) and numerous physiological features (e.g., systole, heart sounds, afterload) that have been encyclopedically documented for many centuries.

Disorders of the heart lead to heart disease and cardiovascular disease and can lead to a significant number of deaths: cardiovascular disease is the leading cause of death in the U.S. and caused 24.95% of total deaths in 2008.

The primary responsibility of the heart is to pump blood throughout the body. It pumps blood from the body — called the systemic circulation — through the lungs — called the pulmonary circulation — and then back out to the body. This means that the heart is connected to and affects the entirety of the body. Simplified, the heart is a circuit of the circulation. While plenty is known about the healthy heart, the bulk of study in cardiology is in disorders of the heart and restoration, and where possible, of function.

The heart is a muscle that squeezes blood and functions like a pump. The heart's systems can be classified as either electrical or mechanical, and both of these systems are susceptible to failure or dysfunction.

The electrical system of the heart is centered on the periodic contraction (squeezing) of the muscle cells that is caused by the cardiac pacemaker located in the sinoatrial node. The study of the electrical aspects is a sub-field of electrophysiology called cardiac electrophysiology and is epitomized with the electrocardiogram (ECG/EKG). The action potentials generated in the pacemaker propagate throughout the heart in a specific pattern. The system that carries this potential is called the electrical conduction system. Dysfunction of the electrical system manifests in many ways and may include Wolff–Parkinson–White syndrome, ventricular fibrillation, and heart block.

The mechanical system of the heart is centered on the fluidic movement of blood and the functionality of the heart as a pump. The mechanical part is ultimately the purpose of the heart and many of the disorders of the heart disrupt the ability to move blood. Heart failure is one condition in which the mechanical properties of the heart have failed or are failing, which means insufficient blood is being circulated. Failure to move a sufficient amount of blood through the body can cause damage or failure of other organs and may result in death if severe.

Coronary circulation

Main article: Coronary circulation

Coronary circulation is the circulation of blood in the blood vessels of the heart muscle (the myocardium). The vessels that deliver oxygen-rich blood to the myocardium are known as coronary arteries. The vessels that remove the deoxygenated blood from the heart muscle are known as cardiac veins. These include the great cardiac vein, the middle cardiac vein, the small cardiac vein and the anterior cardiac veins.

As the left and right coronary arteries run on the surface of the heart, they can be called epicardial coronary arteries. These arteries, when healthy, are capable of autoregulation to maintain coronary blood flow at levels appropriate to the needs of the heart muscle. These relatively narrow vessels are commonly affected by atherosclerosis and can become blocked, causing angina or myocardial infarction (a.k.a a heart attack). The coronary arteries that run deep within the myocardium are referred to as subendocardial.

The coronary arteries are classified as "end circulation", since they represent the only source of blood supply to the myocardium; there is very little redundant blood supply, which is why blockage of these vessels can be so critical.

Cardiac examination

Main article: Cardiac examination

The cardiac examination (also called the "precordial exam"), is performed as part of a physical examination, or when a patient presents with chest pain suggestive of a cardiovascular pathology. It would typically be modified depending on the indication and integrated with other examinations especially the respiratory examination.

Like all medical examinations, the cardiac examination follows the standard structure of inspection, palpation and auscultation.

Heart disorders

Main article: List of heart disorders

Cardiology is concerned with the normal functionality of the heart and the deviation from a healthy heart. Many disorders involve the heart itself, but some are outside of the heart and in the vascular system. Collectively, the two are jointly termed the cardiovascular system, and diseases of one part tend to affect the other.

Coronary artery disease

Main article: Coronary artery disease

Coronary artery disease, also known as "ischemic heart disease", is a group of diseases that includes: stable angina, unstable angina, myocardial infarction, and is one of the causes of sudden cardiac death. It is within the group of cardiovascular diseases of which it is the most common type. A common symptom is chest pain or discomfort which may travel into the shoulder, arm, back, neck, or jaw. Occasionally it may feel like heartburn. Usually symptoms occur with exercise or emotional stress, last less than a few minutes, and get better with rest. Shortness of breath may also occur and sometimes no symptoms are present. The first sign is occasionally a heart attack. Other complications include heart failure or an irregular heartbeat.

Risk factors include: high blood pressure, smoking, diabetes, lack of exercise, obesity, high blood cholesterol, poor diet, and excessive alcohol, among others. Other risks include depression. The underlying mechanism involves atherosclerosis of the arteries of the heart. A number of tests may help with diagnoses including: electrocardiogram, cardiac stress testing, coronary computed tomographic angiography, and coronary angiogram, among others.

Prevention is by eating a healthy diet, regular exercise, maintaining a healthy weight and not smoking. Sometimes medication for diabetes, high cholesterol, or high blood pressure are also used. There is limited evidence for screening people who are at low risk and do not have symptoms. Treatment involves the same measures as prevention. Additional medications such as antiplatelets including aspirin, beta blockers, or nitroglycerin may be recommended. Procedures such as percutaneous coronary intervention (PCI) or coronary artery bypass surgery (CABG) may be used in severe disease. In those with stable CAD it is unclear if PCI or CABG in addition to the other treatments improve life expectancy or decreases heart attack risk.

In 2013 CAD was the most common cause of death globally, resulting in 8.14 million deaths (16.8%) up from 5.74 million deaths (12%) in 1990. The risk of death from CAD for a given age has decreased between 1980 and 2010 especially in developed countries. The number of cases of CAD for a given age has also decreased between 1990 and 2010. In the U.S. in 2010 about 20% of those over 65 had CAD, while it was present in 7% of those 45 to 64, and 1.3% of those 18 to 45. Rates are higher among men than women of a given age.

Cardiomyopathy

Main article: Cardiomyopathy

Heart failure or formally cardiomyopathy, is the impaired function of the heart and there are numerous causes and forms of heart failure.

Cardiac arrhythmia

Main article: Arrhythmia

Cardiac arrhythmia, also known as "cardiac dysrhythmia" or "irregular heartbeat", is a group of conditions in which the heartbeat is too fast, too slow, or irregular in its rhythm. A heart rate that is too fast – above 100 beats per minute in adults – is called tachycardia. A heart rate that is too slow – below 60 beats per minute – is called bradycardia. Many types of arrhythmia present no symptoms. When symptoms are present, they may include palpitations, or feeling a pause between heartbeats. More serious symptoms may include lightheadedness, passing out, shortness of breath, or chest pain. While most types of arrhythmia are not serious, some predispose a person to complications such as stroke or heart failure. Others may result in cardiac arrest.

There are four main types of arrhythmia: extra beats, supraventricular tachycardias, ventricular arrhythmias, and bradyarrhythmias. Extra beats include premature atrial contractions, premature ventricular contractions, and premature junctional contractions. Supraventricular tachycardias include atrial fibrillation, atrial flutter, and paroxysmal supraventricular tachycardia. Ventricular arrhythmias include ventricular fibrillation and ventricular tachycardia. Arrhythmias are due to problems with the electrical conduction system of the heart. Arrhythmias may occur in children; however, the normal range for the heart rate is different and depends on age. A number of tests can help diagnose arrhythmia, including an electrocardiogram and Holter monitor.

Most arrhythmias can be effectively treated. Treatments may include medications, medical procedures such as a pacemaker, and surgery. Medications for a fast heart rate may include beta blockers or agents that attempt to restore a normal heart rhythm such as procainamide. This later group may have more significant side effects especially if taken for a long period of time. Pacemakers are often used for slow heart rates. Those with an irregular heartbeat are often treated with blood thinners to reduce the risk of complications. Those who have severe symptoms from an arrhythmia may receive urgent treatment with a jolt of electricity in the form of cardioversion or defibrillation.

Arrhythmia affects millions of people. In Europe and North America, as of 2014, atrial fibrillation affects about 2% to 3% of the population. Atrial fibrillation and atrial flutter resulted in 112,000 deaths in 2013, up from 29,000 in 1990. Sudden cardiac death is the cause of about half of deaths due to cardiovascular disease or about 15% of all deaths globally. About 80% of sudden cardiac death is the result of ventricular arrhythmias. Arrhythmias may occur at any age but are more common among older people.

Cardiac arrest

Main article: Cardiac arrest

Cardiac arrest is a sudden stop in effective blood flow due to the failure of the heart to contract effectively. Symptoms include loss of consciousness and abnormal or absent breathing. Some people may have chest pain, shortness of breath, or nausea before this occurs. If not treated within minutes, death usually occurs.

The most common cause of cardiac arrest is coronary artery disease. Less common causes include major blood loss, lack of oxygen, very low potassium, heart failure, and intense physical exercise. A number of inherited disorders may also increase the risk including long QT syndrome. The initial heart rhythm is most often ventricular fibrillation. The diagnosis is confirmed by finding no pulse. While a cardiac arrest may be caused by heart attack or heart failure these are not the same.

Prevention includes not smoking, physical activity, and maintaining a healthy weight. Treatment for cardiac arrest is immediate cardiopulmonary resuscitation (CPR) and, if a shockable rhythm is present, defibrillation. Among those who survive targeted temperature management may improve outcomes. An implantable cardiac defibrillator may be placed to reduce the chance of death from recurrence.

In the United States, cardiac arrest outside of hospital occurs in about 13 per 10,000 people per year (326,000 cases). In hospital cardiac arrest occurs in an additional 209,000 Cardiac arrest becomes more common with age. It affects males more often than females. The percentage of people who survive with treatment is about 8%. Many who survive have significant disability. Many U.S. television shows, however, have portrayed unrealistically high survival rates of 67%.

Hypertension

Main article: Hypertension

Hypertension, also known as "high blood pressure", is a long term medical condition in which the blood pressure in the arteries is persistently elevated. High blood pressure usually does not cause symptoms. Long term high blood pressure, however, is a major risk factor for coronary artery disease, stroke, heart failure, peripheral vascular disease, vision loss, and chronic kidney disease.

Lifestyle factors can increase the risk of hypertension. These include excess salt in the diet, excess body weight, smoking, and alcohol consumption. Hypertension can also be caused by other diseases, or occur as a side-effect of drugs.

Blood pressure is expressed by two measurements, the systolic and diastolic pressures, which are the maximum and minimum pressures, respectively. Normal blood pressure when at rest is within the range of 100–140 millimeters mercury (mmHg) systolic and 60–90 mmHg diastolic. High blood pressure is present if the resting blood pressure is persistently at or above 140/90 mmHg for most adults. Different numbers apply to children. When diagnosing high blood pressure, ambulatory blood pressure monitoring over a 24-hour period appears to be more accurate than "in-office" blood pressure measurement at a physician's office or other blood pressure screening location.

Lifestyle changes and medications can lower blood pressure and decrease the risk of health complications. Lifestyle changes include weight loss, decreased salt intake, physical exercise, and a healthy diet. If changes in lifestyle are insufficient, blood pressure medications may be used. A regimen of up to three medications effectively controls blood pressure in 90% of people. The treatment of moderate to severe high arterial blood pressure (defined as >160/100 mmHg) with medication is associated with an improved life expectancy and reduced morbidity. The effect of treatment for blood pressure between 140/90 mmHg and 160/100 mmHg is less clear, with some studies finding benefits while others do not. High blood pressure affects between 16% and 37% of the population globally. In 2010, hypertension was believed to have been a factor in 18% (9.4 million) deaths.

Essential vs Secondary hypertension

Main articles: Essential hypertension and Secondary hypertension

Essential hypertension is the form of hypertension that by definition has no identifiable cause. It is the most common type of hypertension, affecting 95% of hypertensive patients, it tends to be familial and is likely to be the consequence of an interaction between environmental and genetic factors. Prevalence of essential hypertension increases with age, and individuals with relatively high blood pressure at younger ages are at increased risk for the subsequent development of hypertension. Hypertension can increase the risk of cerebral, cardiac, and renal events.

Secondary hypertension is a type of hypertension which is caused by an identifiable underlying secondary cause. It is much less common than essential hypertension, affecting only 5% of hypertensive patients. It has many different causes including endocrine diseases, kidney diseases, and tumors. It also can be a side effect of many medications.

Complications of hypertension

Main complications of persistent high blood pressure

 

Main article: Complications of hypertension

Complications of hypertension are clinical outcomes that result from persistent elevation of blood pressure. Hypertension is a risk factor for all clinical manifestations of atherosclerosis since it is a risk factor for atherosclerosis itself. It is an independent predisposing factor for heart failure, coronary artery disease, stroke, renal disease, and peripheral arterial disease. It is the most important risk factor for cardiovascular morbidity and mortality, in industrialized countries.

Congenital heart defects

Main article: Congenital heart defect

A congenital heart defect, also known as a "congenital heart anomaly" or "congenital heart disease", is a problem in the structure of the heart that is present at birth. Signs and symptoms depend on the specific type of problem. Symptoms can vary from none to life-threatening. When present they may include rapid breathing, bluish skin, poor weight gain, and feeling tired. It does not cause chest pain. Most congenital heart problems do not occur with other diseases. Complications that can result from heart defects include heart failure.

The cause of a congenital heart defect is often unknown. Certain cases may be due to infections during pregnancy such as rubella, use of certain medications or drugs such as alcohol or tobacco, parents being closely related, or poor nutritional status or obesity in the mother. Having a parent with a congenital heart defect is also a risk factor. A number of genetic conditions are associated with heart defects including Down syndrome, Turner syndrome, and Marfan syndrome. Congenital heart defects are divided into two main groups: cyanotic heart defects and non-cyanotic heart defects, depending on whether the child has the potential to turn bluish in color. The problems may involve the interior walls of the heart, the heart valves, or the large blood vessels that lead to and from the heart.

Congenital heart defects are partly preventable through rubella vaccination, the adding of iodine to salt, and the adding of folic acid to certain food products. Some defects do not need treatment. Other may be effectively treated with catheter based procedures or heart surgery. Occasionally a number of operations may be needed. Occasionally heart transplantation is required. With appropriate treatment outcomes, even with complex problems, are generally good.

Heart defects are the most common birth defect. In 2013 they were present in 34.3 million people globally. They affect between 4 and 75 per 1,000 live births depending upon how they are diagnosed. About 6 to 19 per 1,000 cause a moderate to severe degree of problems. Congenital heart defects are the leading cause of birth defect-related deaths. In 2013 they resulted in 323,000 deaths down from 366,000 deaths in 1990.

Tetralogy of Fallot

Tetralogy of Fallot is the most common congenital heart disease arising in 1–3 cases per 1,000 births. The cause of this defect is a ventricular septal defect (VSD) and an overriding aorta. These two defects combined causes deoxygenated blood to bypass the lungs and going right back into the circulatory system. The modified Blalock-Taussig shunt is usually used to fix the circulation. This procedure is done by placing a graft between the subclavian artery and the ipsilateral pulmonary artery to restore the correct blood flow.

Pulmonary atresia

Pulmonary atresia happens in 7–8 per 100,000 births and is characterized by the aorta branching out of the right ventricle. This causes the deoxygenated blood to bypass the lungs and enter the circulatory system. Surgeries can fix this by redirecting the aorta and fixing the right ventricle and pulmonary artery connection.

There are two types of pulmonary atresia, classified by whether or not the baby also has a ventricular septal defect.

• Pulmonary atresia with an intact ventricular septum: This type of pulmonary atresia is associated with complete and intact septum between the ventricles.
• Pulmonary atresia with a ventricular septal defect: This type of pulmonary atresia happens when a ventricular septal defect allows blood to flow into and out of the right ventricle.

Double outlet right ventricle

Double outlet right ventricle (DORV) is when both great arteries, the pulmonary artery and the aorta, are connected to the right ventricle. There is usually a VSD in different particular places depending on the variations of DORV, typically 50% are subaortic and 30%. The surgeries that can be done to fix this defect can vary due to the different physiology and blood flow in the defected heart. One way it can be cured is by a VSD closure and placing conduits to restart the blood flow between the left ventricle and the aorta and between the right ventricle and the pulmonary artery. Another way is systemic-to-pulmonary artery shunt in cases associated with pulmonary stenosis. Also, a balloon atrial septostomy can be done to relieve hypoxemia caused by DORV with the Taussig-Bing anomaly while surgical correction is awaited.

Transposition of great arteries

Dextro-transposition of the Great Arteries

There are two different types of transposition of the great arteries, Dextro-transposition of the great arteries and Levo-transposition of the great arteries, depending on where the chambers and vessels connect. Dextro-transposition happens in about 1 in 4,000 newborns and is when the right ventricle pumps blood into the aorta and deoxygenated blood enters the bloodstream. The temporary procedure is to create an atrial septal defect. A permanent fix is more complicated and involves redirecting the pulmonary return to the right atrium and the systemic return to the left atrium, which is known as the Senning procedure. The Rastelli procedure can also be done by rerouting the left ventricular outflow, dividing the pulmonary trunk, and placing a conduit in between the right ventricle and pulmonary trunk. Levo-transposition happens in about 1 in 13,000 newborns and is characterized by the left ventricle pumping blood into the lungs and the right ventricle pumping the blood into the aorta. This may not produce problems at the beginning, but will eventually due to the different pressures each ventricle uses to pump blood. Switching the left ventricle to be the systemic ventricle and the right ventricle to pump blood into the pulmonary artery can repair levo-transposition.

Persistent truncus arteriosus

Persistent truncus arteriosus is when the truncus arteriosus fails to split into the aorta and pulmonary trunk. This occurs in about 1 in 11,000 live births and allows both oxygenated and deoxygenated blood into the body. The repair consists of a VSD closure and the Rastelli procedure.

Ebstein anomaly

Ebstein's anomaly is characterized by a right atrium that is significantly enlarged and a heart that is shaped like a box. This is very rare and happens in less than 1% of congenital heart disease cases. The surgical repair varies depending on the severity of the disease.

Pediatric cardiology is a sub-specialty of pediatrics. To become a pediatric cardiologist in the U.S., one must complete a three-year residency in pediatrics, followed by a three-year fellowship in pediatric cardiology. Per doximity, pediatric cardiologists make an average of $303,917 in the U.S.

Diagnostic tests in cardiology

Main article: Diagnostic tests in cardiology

Diagnostic tests in cardiology are the methods of identifying heart conditions associated with healthy vs. unhealthy, pathologic heart function. The starting point is obtaining a medical history, followed by Auscultation. Then blood tests, electrophysiological procedures, and cardiac imaging can be ordered for further analysis. Electrophysiological procedures include electrocardiogram, cardiac monitoring, cardiac stress testing, and the electrophysiology study.

Trials

Cardiology is known for randomized controlled trials that guide clinical treatment of cardiac diseases. While dozens are published every year, there are landmark trials that shift treatment significantly. Trials often have an acronym of the trial name, and this acronym is used to reference the trial and its results. Some of these landmark trials include:

• V-HeFT (1986) — use of vasodilators (hydralazine & isosorbide dinitrate) in heart failure
• ISIS-2 (1988) — use of aspirin in myocardial infarction
• CASE I (1991) — use of antiarrhythmic agents after a heart attack increases mortality
• SOLVD (1991) — use of ACE inhibitors in heart failure
• 4S (1994) — statins reduce risk of heart disease
• CURE (1991) — use of dual antiplatelet therapy in NSTEMI
• MIRACLE (2002) — use of cardiac resynchronization therapy in heart failure
• SCD-HeFT (2005) — the use of implantable cardioverter-defibrillator in heart failure
• RELY (2009), ROCKET-AF (2011), ARISTOTLE (2011) — use of DOACs in atrial fibrillation instead of warfarin
• ISCHEMIA (2020) — medical therapy is as good as coronary stents in stable heart disease

Cardiology community

Associations

• American College of Cardiology
• American Heart Association
• European Society of Cardiology
• Heart Rhythm Society
• Canadian Cardiovascular Society
• Indian Heart Association
• National Heart Foundation of Australia
• Cardiology Society of India

Journals

Main category: Cardiology journals

• Acta Cardiologica
• American Journal of Cardiology
• Annals of Cardiac Anaesthesia
• Current Research: Cardiology
• Cardiology in Review
• Circulation
• Circulation Research
• Clinical and Experimental Hypertension
• Clinical Cardiology
• EP – Europace
• European Heart Journal
• Heart
• Heart Rhythm
• International Journal of Cardiology
• Journal of the American College of Cardiology
• Pacing and Clinical Electrophysiology
• Indian Heart Journal

Cardiologists

Cardiologist

Occupation
Names	Doctor, Medical Specialist
Occupation type	Specialty
Activity sectors	Medicine
Description
Education required	Doctor of Medicine (M.D.) Doctor of Osteopathic Medicine (D.O.) Bachelor of Medicine, Bachelor of Surgery (M.B.B.S.)
Fields of employment	Hospitals, Clinics

Main article: List of cardiologists

• Robert Atkins (1930–2003), known for the Atkins diet
• Eugene Braunwald (born 1929), editor of Braunwald's Heart Disease and 1000+ publications
• Wallace Brigden (1916–2008), identified cardiomyopathy
• Manoj Durairaj (1971– ), cardiologist from Pune, India who received Pro Ecclesia et Pontifice
• Willem Einthoven (1860–1927), a physiologist who built the first practical ECG and won the 1924 Nobel Prize in Physiology or Medicine ("for the discovery of the mechanism of the electrocardiogram")
• Werner Forssmann (1904–1979), who infamously performed the first human catheterization on himself that led to him being let go from Berliner Charité Hospital, quitting cardiology as a speciality, and then winning the 1956 Nobel Prize in Physiology or Medicine ("for their discoveries concerning heart catheterization and pathological changes in the circulatory system")
• Andreas Gruentzig (1939–1985), first developed balloon angioplasty
• William Harvey (1578–1657), wrote Exercitatio Anatomica de Motu Cordis et Sanguinis in Animalibus that first described the closed circulatory system and whom Forssmann described as founding cardiology in his Nobel lecture
• Murray S. Hoffman (born 1924) As president of the Colorado Heart Association, he initiated one of the first jogging programs promoting cardiac health
• Max Holzmann (1899–1994), co-founder of the Swiss Society of Cardiology, president from 1952 to 1955
• Samuel A. Levine (1891–1966), recognized the sign known as Levine's sign as well as the current grading of the intensity of heart murmurs, known as the Levine scale
• Henry Joseph Llewellyn "Barney" Marriott (1917–2007), ECG interpretation and Practical Electrocardiography
• Bernard Lown (born 1921), original developer of the defibrillator
• Woldemar Mobitz (1889–1951), described and classified the two types of second-degree atrioventricular block often called "Mobitz Type I" and "Mobitz Type II"
• Jacqueline Noonan (born 1928), discoverer of Noonan syndrome that is the top syndromic cause of congenital heart disease
• John Parkinson (1885–1976), known for Wolff–Parkinson–White syndrome
• Helen B. Taussig (1898–1986), founder of pediatric cardiology and extensively worked on blue baby syndrome
• Paul Dudley White (1886–1973), known for Wolff–Parkinson–White syndrome
• Fredrick Arthur Willius (1888-1872), founder of the cardiology department at the Mayo Clinic and an early pioneer of electrocardiography
• Louis Wolff (1898–1972), known for Wolff–Parkinson–White syndrome
• Karel Frederik Wenckebach (1864–1940), first described what is now called type I second-degree atrioventricular block in 1898