| Neuromuscular junction | |
|---|---|
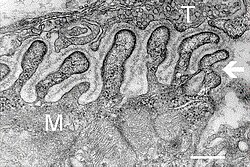 Electron micrograph
showing a cross section through the neuromuscular junction. T is the
axon terminal, M is the muscle fiber. The arrow shows junctional folds
with basal lamina. Active zones are visible on the tips between the folds. Scale is 0.3 μm. Source: NIMH | |
 Detailed view of a neuromuscular junction: | |
| Details | |
| Identifiers | |
| Latin | synapssis neuromuscularis; junctio neuromuscularis |
| MeSH | D009469 |
| TH | H2.00.06.1.02001 |
| FMA | 61803 |
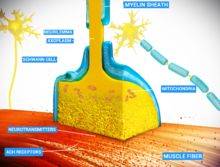
A neuromuscular junction (or myoneural junction) is a chemical synapse between a motor neuron and a muscle fiber. It allows the motor neuron to transmit a signal to the muscle fiber, causing muscle contraction.
Muscles require innervation to function—and even just to maintain muscle tone, avoiding atrophy. In the neuromuscular system nerves from the central nervous system and the peripheral nervous system are linked and work together with muscles. Synaptic transmission at the neuromuscular junction begins when an action potential reaches the presynaptic terminal of a motor neuron, which activates voltage-gated calcium channels to allow calcium ions to enter the neuron. Calcium ions bind to sensor proteins (synaptotagmins) on synaptic vesicles, triggering vesicle fusion with the cell membrane and subsequent neurotransmitter release from the motor neuron into the synaptic cleft. In vertebrates, motor neurons release acetylcholine (ACh), a small molecule neurotransmitter, which diffuses across the synaptic cleft and binds to nicotinic acetylcholine receptors (nAChRs) on the cell membrane of the muscle fiber, also known as the sarcolemma. nAChRs are ionotropic receptors, meaning they serve as ligand-gated ion channels. The binding of ACh to the receptor can depolarize the muscle fiber, causing a cascade that eventually results in muscle contraction.
Neuromuscular junction diseases can be of genetic and autoimmune origin. Genetic disorders, such as Congenital myasthenic syndrome, can arise from mutated structural proteins that comprise the neuromuscular junction, whereas autoimmune diseases, such as myasthenia gravis, occur when antibodies are produced against nicotinic acetylcholine receptors on the sarcolemma.
Structure and function
Quantal transmission
At the neuromuscular junction presynaptic motor axons terminate 30 nanometers from the cell membrane or sarcolemma of a muscle fiber. The sarcolemma at the junction has invaginations called postjunctional folds, which increase its surface area facing the synaptic cleft. These postjunctional folds form the motor endplate, which is studded with nicotinic acetylcholine receptors (nAChRs) at a density of 10,000 receptors/micrometer2. The presynaptic axons terminate in bulges called terminal boutons (or presynaptic terminals) that project toward the postjunctional folds of the sarcolemma. In the frog each motor nerve terminal contains about 300,000 vesicles, with an average diameter of 0.05 micrometers. The vesicles contain acetylcholine. Some of these vesicles are gathered into groups of fifty, positioned at active zones close to the nerve membrane. Active zones are about 1 micrometer apart. The 30 nanometer cleft between nerve ending and endplate contains a meshwork of acetylcholinesterase (AChE) at a density of 2,600 enzyme molecules/micrometer2, held in place by the structural proteins dystrophin and rapsyn. Also present is the receptor tyrosine kinase protein MuSK, a signaling protein involved in the development of the neuromuscular junction, which is also held in place by rapsyn.
About once every second in a resting junction randomly one of the synaptic vesicles fuses with the presynaptic neuron's cell membrane in a process mediated by SNARE proteins. Fusion results in the emptying of the vesicle's contents of 7000–10,000 acetylcholine molecules into the synaptic cleft, a process known as exocytosis. Consequently, exocytosis releases acetylcholine in packets that are called quanta. The acetylcholine quantum diffuses through the acetylcholinesterase meshwork, where the high local transmitter concentration occupies all of the binding sites on the enzyme in its path. The acetylcholine that reaches the endplate activates ~2,000 acetylcholine receptors, opening their ion channels which permits sodium ions to move into the endplate producing a depolarization of ~0.5 mV known as a miniature endplate potential (MEPP). By the time the acetylcholine is released from the receptors the acetylcholinesterase has destroyed its bound ACh, which takes about ~0.16 ms, and hence is available to destroy the ACh released from the receptors.
When the motor nerve is stimulated there is a delay of only 0.5 to 0.8 msec between the arrival of the nerve impulse in the motor nerve terminals and the first response of the endplate The arrival of the motor nerve action potential at the presynaptic neuron terminal opens voltage-dependent calcium channels and Ca2+ ions flow from the extracellular fluid into the presynaptic neuron's cytosol. This influx of Ca2+ causes several hundred neurotransmitter-containing vesicles to fuse with the presynaptic neuron's cell membrane through SNARE proteins to release their acetylcholine quanta by exocytosis. The endplate depolarization by the released acetylcholine is called an endplate potential (EPP). The EPP is accomplished when ACh binds the nicotinic acetylcholine receptors (nAChR) at the motor end plate, and causes an influx of sodium ions. This influx of sodium ions generates the EPP (depolarization), and triggers an action potential that travels along the sarcolemma and into the muscle fiber via the T-tubules (transverse tubules) by means of voltage-gated sodium channels. The conduction of action potentials along the T-tubules stimulates the opening of voltage-gated Ca2+ channels which are mechanically coupled to Ca2+ release channels in the sarcoplasmic reticulum. The Ca2+ then diffuses out of the sarcoplasmic reticulum to the myofibrils so it can stimulate contraction. The endplate potential is thus responsible for setting up an action potential in the muscle fiber which triggers muscle contraction. The transmission from nerve to muscle is so rapid because each quantum of acetylcholine reaches the endplate in millimolar concentrations, high enough to combine with a receptor with a low affinity, which then swiftly releases the bound transmitter.
Acetylcholine receptors
- Ion channel linked receptor
- Ions
- Ligand (such as acetylcholine)
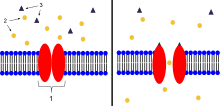
Acetylcholine is a neurotransmitter synthesized from dietary choline and acetyl-CoA (ACoA), and is involved in the stimulation of muscle tissue in vertebrates as well as in some invertebrate animals. In vertebrates, the acetylcholine receptor subtype that is found at the neuromuscular junction of skeletal muscles is the nicotinic acetylcholine receptor (nAChR), which is a ligand-gated ion channel. Each subunit of this receptor has a characteristic "cys-loop", which is composed of a cysteine residue followed by 13 amino acid residues and another cysteine residue. The two cysteine residues form a disulfide linkage which results in the "cys-loop" receptor that is capable of binding acetylcholine and other ligands. These cys-loop receptors are found only in eukaryotes, but prokaryotes possess ACh receptors with similar properties. Not all species use a cholinergic neuromuscular junction; e.g. crayfish and fruit flies have a glutamatergic neuromuscular junction.
AChRs at the skeletal neuromuscular junction form heteropentamers composed of two α, one β, one ɛ, and one δ subunits. When a single ACh ligand binds to one of the α subunits of the ACh receptor it induces a conformational change at the interface with the second AChR α subunit. This conformational change results in the increased affinity of the second α subunit for a second ACh ligand. AChRs, therefore, exhibit a sigmoidal dissociation curve due to this cooperative binding. The presence of the inactive, intermediate receptor structure with a single-bound ligand keeps ACh in the synapse that might otherwise be lost by cholinesterase hydrolysis or diffusion. The persistence of these ACh ligands in the synapse can cause a prolonged post-synaptic response.
Development
The development of the neuromuscular junction requires signaling from both the motor neuron's terminal and the muscle cell's central region. During development, muscle cells produce acetylcholine receptors (AChRs) and express them in the central regions in a process called prepatterning. Agrin, a heparin proteoglycan, and MuSK kinase are thought to help stabilize the accumulation of AChR in the central regions of the myocyte. MuSK is a receptor tyrosine kinase—meaning that it induces cellular signaling by binding phosphate molecules to self regions like tyrosines, and to other targets in the cytoplasm. Upon activation by its ligand agrin, MuSK signals via two proteins called "Dok-7" and "rapsyn", to induce "clustering" of acetylcholine receptors. ACh release by developing motor neurons produces postsynaptic potentials in the muscle cell that positively reinforces the localization and stabilization of the developing neuromuscular junction.
These findings were demonstrated in part by mouse "knockout" studies. In mice which are deficient for either agrin or MuSK, the neuromuscular junction does not form. Further, mice deficient in Dok-7 did not form either acetylcholine receptor clusters or neuromuscular synapses.
The development of neuromuscular junctions is mostly studied in model organisms, such as rodents. In addition, in 2015 an all-human neuromuscular junction has been created in vitro using human embryonic stem cells and somatic muscle stem cells. In this model presynaptic motor neurons are activated by optogenetics and in response synaptically connected muscle fibers twitch upon light stimulation.
Research methods
José del Castillo and Bernard Katz used ionophoresis to determine the location and density of nicotinic acetylcholine receptors (nAChRs) at the neuromuscular junction. With this technique, a microelectrode was placed inside the motor endplate of the muscle fiber, and a micropipette filled with acetylcholine (ACh) is placed directly in front of the endplate in the synaptic cleft. A positive voltage was applied to the tip of the micropipette, which caused a burst of positively charged ACh molecules to be released from the pipette. These ligands flowed into the space representing the synaptic cleft and bound to AChRs. The intracellular microelectrode monitored the amplitude of the depolarization of the motor endplate in response to ACh binding to nicotinic (ionotropic) receptors. Katz and del Castillo showed that the amplitude of the depolarization (excitatory postsynaptic potential) depended on the proximity of the micropipette releasing the ACh ions to the endplate. The farther the micropipette was from the motor endplate, the smaller the depolarization was in the muscle fiber. This allowed the researchers to determine that the nicotinic receptors were localized to the motor endplate in high density.
Toxins are also used to determine the location of acetylcholine receptors at the neuromuscular junction. α-Bungarotoxin is a toxin found in the snake species Bungarus multicinctus that acts as an ACh antagonist and binds to AChRs irreversibly. By coupling assayable enzymes such as horseradish peroxidase (HRP) or fluorescent proteins such as green fluorescent protein (GFP) to the α-bungarotoxin, AChRs can be visualized and quantified.
Toxins that affect the neuromuscular junction
Nerve gases
Nerve gases bind to and phosphorylate AChE, effectively deactivating them. The accumulation of ACh within the synaptic cleft causes muscle cells to be perpetually contracted, leading to severe complications such as paralysis and death within minutes of exposure.
Botulinum toxin
Botulinum toxin (also known as botulinum neurotoxin, and commercially sold under the trade name Botox) inhibits the release of acetylcholine at the neuromuscular junction by interfering with SNARE proteins. This toxin crosses into the nerve terminal through the process of endocytosis and subsequently cleaves SNARE proteins, preventing the ACh vesicles from fusing with the intracellular membrane. This induces a transient flaccid paralysis and chemical denervation localized to the striated muscle that it has affected. The inhibition of ACh release does not set in until approximately two weeks after the injection is made. Three months after the inhibition occurs, neuronal activity begins to regain partial function, and six months after, complete neuronal function is regained.
Tetanus toxin
Tetanus toxin, also known as tetanospasmin is a potent neurotoxin produced by Clostridium tetani and causes the disease state, tetanus. The LD50 of this toxin has been measured to be approximately 1 ng/kg, making it second only to botulinum toxin D as the deadliest toxin in the world. It functions very similarly to botulinum neurotoxin by attaching and endocytosing into the presynaptic nerve terminal and interfering with SNARE proteins. It differs from botulinum neurotoxin in a few ways, most apparently in its end state, wherein tetanospasmin causes spastic paralysis as opposed to the flaccid paralysis demonstrated with botulinum neurotoxin.
Latrotoxin
Latrotoxin (α-Latrotoxin) found in venom of widow spiders also affects the neuromuscular junction by causing the release of acetylcholine from the presynaptic cell. Mechanisms of action include binding to receptors on the presynaptic cell activating the IP3/DAG pathway and release of calcium from intracellular stores and pore formation resulting in influx of calcium ions directly. Either mechanism causes increased calcium in presynaptic cell, which then leads to release of synaptic vesicles of acetylcholine. Latrotoxin causes pain, muscle contraction and if untreated potentially paralysis and death.
Snake venom
Snake venoms act as toxins at the neuromuscular junction and can induce weakness and paralysis. Venoms can act as both presynaptic and postsynaptic neurotoxins.
Presynaptic neurotoxins, commonly known as β-neurotoxins, affect the presynaptic regions of the neuromuscular junction. The majority of these neurotoxins act by inhibiting the release of neurotransmitters, such as acetylcholine, into the synapse between neurons. However, some of these toxins have also been known to enhance neurotransmitter release. Those that inhibit neurotransmitter release create a neuromuscular blockade that prevents signaling molecules from reaching their postsynaptic target receptors. In doing so, the victim of these snake bite suffer from profound weakness. Such neurotoxins do not respond well to anti-venoms. After one hour of inoculation of these toxins, including notexin and taipoxin, many of the affected nerve terminals show signs of irreversible physical damage, leaving them devoid of any synaptic vesicles.
Postsynaptic neurotoxins, otherwise known as α-neurotoxins, act oppositely to the presynaptic neurotoxins by binding to the postsynaptic acetylcholine receptors. This prevents interaction between the acetylcholine released by the presynaptic terminal and the receptors on the postsynaptic cell. In effect, the opening of sodium channels associated with these acetylcholine receptors is prohibited, resulting in a neuromuscular blockade, similar to the effects seen due to presynaptic neurotoxins. This causes paralysis in the muscles involved in the affected junctions. Unlike presynaptic neurotoxins, postsynaptic toxins are more easily affected by anti-venoms, which accelerate the dissociation of the toxin from the receptors, ultimately causing a reversal of paralysis. These neurotoxins experimentally and qualitatively aid in the study of acetylcholine receptor density and turnover, as well as in studies observing the direction of antibodies toward the affected acetylcholine receptors in patients diagnosed with myasthenia gravis.
Diseases
Any disorder that compromises the synaptic transmission between a motor neuron and a muscle cell is categorized under the umbrella term of neuromuscular diseases. These disorders can be inherited or acquired and can vary in their severity and mortality. In general, most of these disorders tend to be caused by mutations or autoimmune disorders. Autoimmune disorders, in the case of neuromuscular diseases, tend to be humoral mediated, B cell mediated, and result in an antibody improperly created against a motor neuron or muscle fiber protein that interferes with synaptic transmission or signaling.
Autoimmune
Myasthenia gravis
Myasthenia gravis is an autoimmune disorder where the body makes antibodies against either the acetylcholine receptor (AchR) (in 80% of cases), or against postsynaptic muscle-specific kinase (MuSK) (0–10% of cases). In seronegative myasthenia gravis low density lipoprotein receptor-related protein 4 is targeted by IgG1, which acts as a competitive inhibitor of its ligand, preventing the ligand from binding its receptor. It is not known if seronegative myasthenia gravis will respond to standard therapies.
Neonatal MG
Neonatal MG is an autoimmune disorder that affects 1 in 8 children born to mothers who have been diagnosed with myasthenia gravis (MG). MG can be transferred from the mother to the fetus by the movement of AChR antibodies through the placenta. Signs of this disease at birth include weakness, which responds to anticholinesterase medications, as well as fetal akinesia, or the lack of fetal movement. This form of the disease is transient, lasting for about three months. However, in some cases, neonatal MG can lead to other health effects, such as arthrogryposis and even fetal death. These conditions are thought to be initiated when maternal AChR antibodies are directed to the fetal AChR and can last until the 33rd week of gestation, when the γ subunit of AChR is replaced by the ε subunit.
Lambert-Eaton myasthenic syndrome
Lambert–Eaton myasthenic syndrome (LEMS) is an autoimmune disorder that affects the presynaptic portion of the neuromuscular junction. This rare disease can be marked by a unique triad of symptoms: proximal muscle weakness, autonomic dysfunction, and areflexia. Proximal muscle weakness is a product of pathogenic autoantibodies directed against P/Q-type voltage-gated calcium channels, which in turn leads to a reduction of acetylcholine release from motor nerve terminals on the presynaptic cell. Examples of autonomic dysfunction caused by LEMS include erectile dysfunction in men, constipation, and, most commonly, dry mouth. Less common dysfunctions include dry eyes and altered perspiration. Areflexia is a condition in which tendon reflexes are reduced and it may subside temporarily after a period of exercise.
50–60% of the patients that are diagnosed with LEMS also have present an associated tumor, which is typically small-cell lung carcinoma (SCLC). This type of tumor also expresses voltage-gated calcium channels. Oftentimes, LEMS also occurs alongside myasthenia gravis.
Treatment for LEMS consists of using 3,4-diaminopyridine as a first measure, which serves to increase the compound muscle action potential as well as muscle strength by lengthening the time that voltage-gated calcium channels remain open after blocking voltage-gated potassium channels. In the US, treatment with 3,4-diaminopyridine for eligible LEMS patients is available at no cost under an expanded access program. Further treatment includes the use of prednisone and azathioprine in the event that 3,4-diaminopyridine does not aid in treatment.
Neuromyotonia
Neuromyotonia (NMT), otherwise known as Isaac's syndrome, is unlike many other diseases present at the neuromuscular junction. Rather than causing muscle weakness, NMT leads to the hyperexcitation of motor nerves. NMT causes this hyperexcitation by producing longer depolarizations by down-regulating voltage-gated potassium channels, which causes greater neurotransmitter release and repetitive firing. This increase in rate of firing leads to more active transmission and as a result, greater muscular activity in the affected individual. NMT is also believed to be of autoimmune origin due to its associations with autoimmune symptoms in the individual affected.
Genetic
Congenital myasthenic syndromes
Congenital myasthenic syndromes (CMS) are very similar to both MG and LEMS in their functions, but the primary difference between CMS and those diseases is that CMS is of genetic origins. Specifically, these syndromes are diseases incurred due to mutations, typically recessive, in 1 of at least 10 genes that affect presynaptic, synaptic, and postsynaptic proteins in the neuromuscular junction. Such mutations usually arise in the ε-subunit of AChR, thereby affecting the kinetics and expression of the receptor itself. Single nucleotide substitutions or deletions may cause loss of function in the subunit. Other mutations, such as those affecting acetylcholinesterase and acetyltransferase, can also cause the expression of CMS, with the latter being associated specifically with episodic apnea. These syndromes can present themselves at different times within the life of an individual. They may arise during the fetal phase, causing fetal akinesia, or the perinatal period, during which certain conditions, such as arthrogryposis, ptosis, hypotonia, ophthalmoplegia, and feeding or breathing difficulties, may be observed. They could also activate during adolescence or adult years, causing the individual to develop slow-channel syndrome.
Treatment for particular subtypes of CMS (postsynaptic fast-channel CMS) is similar to treatment for other neuromuscular disorders. 3,4-Diaminopyridine, the first-line treatment for LEMS, is under development as an orphan drug for CMS in the US, and available to eligible patients under an expanded access program at no cost.