Dirac large numbers hypothesis

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Dirac_large_numbers_hypothesis

Paul Dirac

The Dirac large numbers hypothesis (LNH) is an observation made by Paul Dirac in 1937 relating ratios of size scales in the Universe to that of force scales. The ratios constitute very large, dimensionless numbers: some 40 orders of magnitude in the present cosmological epoch. According to Dirac's hypothesis, the apparent similarity of these ratios might not be a mere coincidence but instead could imply a cosmology with these unusual features:

• The strength of gravity, as represented by the gravitational constant, is inversely proportional to the age of the universe: ${\displaystyle G\propto 1/t}$
• The mass of the universe is proportional to the square of the universe's age: ${\displaystyle M\propto t^2}$.
• Physical constants are actually not constant. Their values depend on the age of the Universe.

Background

LNH was Dirac's personal response to a set of large number "coincidences" that had intrigued other theorists of his time. The "coincidences" began with Hermann Weyl (1919), who speculated that the observed radius of the universe, R_U, might also be the hypothetical radius of a particle whose rest energy is equal to the gravitational self-energy of the electron:

${\displaystyle \frac{R_{\text{U}}}{r_{\text{e}}}\approx \frac{r_{\text{H}}}{r_{\text{e}}}\approx 4.1666763\cdot {10}^{42}\approx {10}^{42.62\dots },}$

where,

${\displaystyle r_{\text{e}}=\frac{e^2}{4\pi {ϵ}_0{m}_{\text{e}}{c}^2}\approx 3.7612682\cdot {10}^{-16}\mathrm{m}}$

${\displaystyle r_{\text{H}}=\frac{e^2}{4\pi {ϵ}_0{m}_{\text{H}}{c}^2}\approx 1.5671987\cdot {10}^{27}\mathrm{m}}$ with ${\displaystyle m_{\text{H}}{c}^2=\frac{G{m}_{\text{e}}^2}{r_{\text{e}}}}$

and r_e is the classical electron radius, m_e is the mass of the electron, m_H denotes the mass of the hypothetical particle, and r_H is its electrostatic radius.

The coincidence was further developed by Arthur Eddington (1931) who related the above ratios to N, the estimated number of charged particles in the universe:

${\displaystyle \frac{e^2}{4\pi {ϵ}_{0}G{m}_{\text{e}}^2}\approx 4.1666763\cdot {10}^{42}\approx \sqrt{N}}$.

In addition to the examples of Weyl and Eddington, Dirac was also influenced by the primeval-atom hypothesis of Georges Lemaître, who lectured on the topic in Cambridge in 1933. The notion of a varying-G cosmology first appears in the work of Edward Arthur Milne a few years before Dirac formulated LNH. Milne was inspired not by large number coincidences but by a dislike of Einstein's general theory of relativity. For Milne, space was not a structured object but simply a system of reference in which relations such as this could accommodate Einstein's conclusions:

${\displaystyle G=\left(\frac{c^3}{M_{\text{U}}}\right)t,}$

where M_U is the mass of the universe and t is the age of the universe. According to this relation, G increases over time.

Dirac's interpretation of the large number coincidences

The Weyl and Eddington ratios above can be rephrased in a variety of ways, as for instance in the context of time:

${\displaystyle \frac{ct}{r_{\text{e}}}\approx 3.47\cdot {10}^{41}\approx {10}^{42},}$

where t is the age of the universe, ${\displaystyle c}$ is the speed of light and r_e is the classical electron radius. Hence, in units where c = 1 and r_e = 1, the age of the universe is about 10⁴⁰ units of time. This is the same order of magnitude as the ratio of the electrical to the gravitational forces between a proton and an electron:

${\displaystyle \frac{e^2}{4\pi {ϵ}_{0}G{m}_{\text{p}}{m}_{\text{e}}}\approx {10}^{40}.}$

Hence, interpreting the charge ${\displaystyle e}$ of the electron, the masses ${\displaystyle m_{\text{p}}}$ and ${\displaystyle m_{\text{e}}}$ of the proton and electron, and the permittivity factor ${\displaystyle 4\pi {ϵ}_0}$ in atomic units (equal to 1), the value of the gravitational constant is approximately 10⁻⁴⁰. Dirac interpreted this to mean that ${\displaystyle G}$ varies with time as ${\displaystyle G\approx 1/t}$. Although George Gamow noted that such a temporal variation does not necessarily follow from Dirac's assumptions, a corresponding change of G has not been found. According to general relativity, however, G is constant, otherwise the law of conserved energy is violated. Dirac met this difficulty by introducing into the Einstein field equations a gauge function β that describes the structure of spacetime in terms of a ratio of gravitational and electromagnetic units. He also provided alternative scenarios for the continuous creation of matter, one of the other significant issues in LNH:

• 'additive' creation (new matter is created uniformly throughout space) and
• 'multiplicative' creation (new matter is created where there are already concentrations of mass).

Later developments and interpretations

Dirac's theory has inspired and continues to inspire a significant body of scientific literature in a variety of disciplines. In the context of geophysics, for instance, Edward Teller seemed to raise a serious objection to LNH in 1948^[8] when he argued that variations in the strength of gravity are not consistent with paleontological data. However, George Gamow demonstrated in 1962 how a simple revision of the parameters (in this case, the age of the Solar System) can invalidate Teller's conclusions. The debate is further complicated by the choice of LNH cosmologies: In 1978, G. Blake argued that paleontological data is consistent with the "multiplicative" scenario but not the "additive" scenario. Arguments both for and against LNH are also made from astrophysical considerations. For example, D. Falik argued that LNH is inconsistent with experimental results for microwave background radiation whereas Canuto and Hsieh argued that it is consistent. One argument that has created significant controversy was put forward by Robert Dicke in 1961. Known as the anthropic coincidence or fine-tuned universe, it simply states that the large numbers in LNH are a necessary coincidence for intelligent beings since they parametrize fusion of hydrogen in stars and hence carbon-based life would not arise otherwise.

Various authors have introduced new sets of numbers into the original "coincidence" considered by Dirac and his contemporaries, thus broadening or even departing from Dirac's own conclusions. Jordan (1947) noted that the mass ratio for a typical star (specifically, a star of the Chandrasekhar mass, itself a constant of nature, approx. 1.44 solar masses) and an electron approximates to 10⁶⁰, an interesting variation on the 10⁴⁰ and 10⁸⁰ that are typically associated with Dirac and Eddington respectively. (The physics defining the Chandrasekhar mass produces a ratio that is the −3/2 power of the gravitational fine-structure constant, 10⁻⁴⁰.)

Modern studies

Several authors have recently identified and pondered the significance of yet another large number, approximately 120 orders of magnitude. This is for example the ratio of the theoretical and observational estimates of the energy density of the vacuum, which Nottale (1993) and Matthews (1997) associated in an LNH context with a scaling law for the cosmological constant. Carl Friedrich von Weizsäcker identified 10¹²⁰ with the ratio of the universe's volume to the volume of a typical nucleon bounded by its Compton wavelength, and he identified this ratio with the sum of elementary events or bits of information in the universe. Valev (2019)  found equation connecting cosmological parameters (for example density of the universe) and Planck units (for example Planck density). This ratio of densities, and other ratios (using four fundamental constants: speed of light in vacuum c, Newtonian constant of gravity G, reduced Planck constant ℏ, and Hubble constant H) computes to an exact number, 32.8·10¹²⁰. This provides evidence of the Dirac large numbers hypothesis by connecting the macro-world and the micro-world.

Time-variation of fundamental constants

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Time-variation_of_fundamental_constants 

The term physical constant expresses the notion of a physical quantity subject to experimental measurement which is independent of the time or location of the experiment. The constancy (immutability) of any "physical constant" is thus subject to experimental verification.

Paul Dirac in 1937 speculated that physical constants such as the gravitational constant or the fine-structure constant might be subject to change over time in proportion of the age of the universe. Experiments conducted since then have put upper bounds on their time-dependence. This concerns the fine-structure constant, the gravitational constant and the proton-to-electron mass ratio specifically, for all of which there are ongoing efforts to improve tests on their time-dependence.

The immutability of these fundamental constants is an important cornerstone of the laws of physics as currently known; the postulate of the time-independence of physical laws is tied to that of the conservation of energy (Noether theorem), so that the discovery of any variation would imply the discovery of a previously unknown law of force.

In a more philosophical context, the conclusion that these quantities are constant raises the question of why they have the specific value they do in what appears to be a "fine-tuned universe", while their being variable would mean that their known values are merely an accident of the current time at which we happen to measure them.

Dimensionality

Further information: System of measurement and Natural units

It is problematic to discuss the proposed rate of change (or lack thereof) of a single dimensional physical constant in isolation. The reason for this is that the choice of a system of units may arbitrarily select any physical constant as its basis, making the question of which constant is undergoing change an artefact of the choice of units.

For example, in SI units, the speed of light has been given a defined value in 1983. Thus, it was meaningful to experimentally measure the speed of light in SI units prior to 1983, but it is not so now. Tests on the immutability of physical constants look at dimensionless quantities, i.e. ratios between quantities of like dimensions, in order to escape this problem. Changes in physical constants are not meaningful if they result in an observationally indistinguishable universe. For example, a "change" in the speed of light c would be meaningless if accompanied by a corresponding "change" in the elementary charge e so that the ratio e²:c (the fine-structure constant) remained unchanged.

Natural units are systems of units entirely based in fundamental constants. In such systems, it is meaningful to measure any specific quantity which is not used in the definition of units. For example, in Stoney units, the elementary charge is set to e = 1 while the reduced Planck constant is subject to measurement, ħ ≈ 137.03, and in Planck units, the reduced Planck constant is set to ħ = 1, while the elementary charge is subject to measurement, e ≈ (137.03)^1/2. The 2019 redefinition of SI base units expresses all SI base units in terms of fundamental physical constants, effectively transforming the SI system into a system of natural units.

Fine-structure constant

In 1999, evidence for time variability of the fine-structure constant based on observation of quasars was announced but a much more precise study based on CH molecules did not find any variation. An upper bound of 10⁻¹⁷ per year for the time variation, based on laboratory measurements, was published in 2008. Observations of a quasar of the universe at only 0.8 billion years old with AI analysis method employed on the Very Large Telescope (VLT) found a spatial variation preferred over a no-variation model at the ${\displaystyle 3.9\sigma }$ level.

The time-variation of fine-structure constant is equivalent to the time-variation of one or more of: speed of light, Planck constant, vacuum permittivity, and elementary charge, since ${\displaystyle \alpha =\frac{e^2}{2{ϵ}_{0}ch}}$.

Speed of light

Main article: Variable speed of light

Gravitational constant

The gravitational constant G is difficult to measure with precision, and conflicting measurements in the 2000s have inspired the controversial suggestions of a periodic variation of its value in a 2015 paper. However, while its value is not known to great precision, the possibility of observing type Ia supernovae which happened in the universe's remote past, paired with the assumption that the physics involved in these events is universal, allows for an upper bound of less than 10⁻¹⁰ per year for ${\displaystyle |\dot{G}/G|}$ over the last nine billion years. The quantity ${\displaystyle |\dot{G}/G|}$ is simply the change in time of the gravitational constant, denoted by ${\displaystyle \dot{G}}$, divided by G.

As a dimensional quantity, the value of the gravitational constant and its possible variation will depend on the choice of units; in Planck units, for example, its value is fixed at G = 1 by definition. A meaningful test on the time-variation of G would require comparison with a non-gravitational force to obtain a dimensionless quantity, e.g. through the ratio of the gravitational force to the electrostatic force between two electrons, which in turn is related to the dimensionless fine-structure constant.

Proton-to-electron mass ratio

An upper bound of the change in the proton-to-electron mass ratio has been placed at 10⁻⁷ over a period of 7 billion years (or 10⁻¹⁶ per year) in a 2012 study based on the observation of methanol in a distant galaxy.

Cosmological constant

Further information: Cosmological constant, Vacuum energy, and Dark energy

The cosmological constant is a measure of the energy density of the vacuum. It was first measured, and found to have a positive value, in the 1990s. It is currently (as of 2015) estimated at 10⁻¹²² in Planck units. Possible variations of the cosmological constant over time or space are not amenable to observation, but it has been noted that, in Planck units, its measured value is suggestively close to the reciprocal of the age of the universe squared, Λ ≈ T⁻². Barrow and Shaw proposed a modified theory in which Λ is a field evolving in such a way that its value remains Λ ~ T⁻² throughout the history of the universe.

Informatics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Informatics

Informatics is the study of computational systems. According to the ACM Europe Council and Informatics Europe, informatics is synonymous with computer science and computing as a profession, in which the central notion is transformation of information. In other countries, the term "informatics" is used with a different meaning in the context of library science, in which case it is synonymous with data storage and retrieval.

Different meanings

Informatics Forum, completed in 2008. It houses researchers of the University of Edinburgh's School of Informatics.

In some countries, depending on local interpretations, the term "informatics" is used synonymously to mean information systems, information science, information theory, information engineering, information technology, information processing, or other theoretical or practical fields. In Germany, the term informatics almost exactly corresponds to modern computer science. Accordingly, universities in continental Europe usually translate "informatics" as computer science, or sometimes information and computer science, although technical universities may translate it as computer science & engineering.

In the United States, however, the term informatics is mostly used in context of data science, library science or its applications in healthcare (health informatics), where it first appeared in the US.

The University of Washington uses this term to refer to social computing. In some countries, this term is associated with natural computation and neural computation.

The Government of Canada uses the term to refer to operational units offering network and computer services to the various departments.

Etymology

See also: Computer science § Etymology, and History of computer science

In 1956, the German informatician Karl Steinbuch and engineer Helmut Gröttrup coined the word Informatik when they developed the Informatik-Anlage for the Quelle mail-order management, one of the earliest commercial applications of data processing. In April 1957, Steinbuch published a paper called Informatik: Automatische Informationsverarbeitung ("Informatics: Automatic Information Processing"). The morphology—informat-ion + -ics—uses "the accepted form for names of sciences, as conics, mathematics, linguistics, optics, or matters of practice, as economics, politics, tactics", and so, linguistically, the meaning extends easily to encompass both the science of information and the practice of information processing. The German word Informatik is usually translated to English as computer science by universities or computer science & engineering by technical universities (German equivalents for institutes of technology). Depending on the context, informatics is also translated into computing, scientific computing or information and computer technology. The French term informatique was coined in 1962 by Philippe Dreyfus. In the same month was also proposed independently by Walter F. Bauer (1924–2015) and associates who co-founded software company Informatics Inc. The term for the new discipline quickly spread throughout Europe, but it did not catch on in the United States. Over the years, many different definitions of informatics have been developed, most of them claim that the essence of informatics is one of these concepts: information processing, algorithms, computation, information, algorithmic processes, computational processes or computational systems.

See also: Computational informatics

The earliest uses of the term informatics in the United States was during the 1950s with the beginning of computer use in healthcare. Early practitioners interested in the field soon learned that there were no formal education programs, and none emerged until the late 1960s. They introduced the term informatics only in the context of archival science, which is only a small part of informatics. Professional development, therefore, played a significant role in the development of health informatics. According to Imhoff et al., 2001, healthcare informatics is not only the application of computer technology to problems in healthcare, but covers all aspects of generation, handling, communication, storage, retrieval, management, analysis, discovery, and synthesis of data information and knowledge in the entire scope of healthcare. Furthermore, they stated that the primary goal of health informatics can be distinguished as follows: To provide solutions for problems related to data, information, and knowledge processing. To study general principles of processing data information and knowledge in medicine and healthcare. The term health informatics quickly spread throughout the United States in various forms such as nursing informatics, public health informatics or medical informatics. Analogous terms were later introduced for use of computers in various fields, such as business informatics, forest informatics, legal informatics etc. These fields still mainly use term informatics in context of library science.

Informatics as library science

See also: Library science

In the fields of geoinformatics or irrigation informatics, the term -informatics usually mean information science, in context related to library science. This was the first meaning of informatics introduced in Russia in 1966 by A.I. Mikhailov, R.S. Gilyarevskii, and A.I. Chernyi, which referred to a scientific discipline that studies the structure and properties of scientific information. In this context, the term was also used by the International Neuroinformatics Coordinating Facility. Some scientists use this term, however, to refer to the science of information processing, not data management.

In the English-speaking world, the term informatics was first widely used in the compound medical informatics, taken to include "the cognitive, information processing, and communication tasks of medical practice, education, and research, including information science and the technology to support these tasks". Many such compounds are now in use; they can be viewed as different areas of "applied informatics".

Informatics as information processing science

See also: Cognitive Science § Namings

In the early 1990s, K.K. Kolin proposed an interpretation of informatics as a fundamental science that studies information processes in nature, society, and technical systems.

A broad interpretation of informatics, as "the study of the structure, algorithms, behaviour, and interactions of natural and artificial computational systems," was introduced by the University of Edinburgh in 1994. This has led to the merger of the institutes of computer science, artificial intelligence and cognitive science into a single School of Informatics in 2002.

More than a dozen nearby universities joined Scottish Informatics and Computer Science Alliance. Some non-European universities have also adopted this definition (e.g. Kyoto University School of Informatics).

In 2003, Yingxu Wang popularized term cognitive informatics, described as follows:

Supplementary to matter and energy, information is the third essence for modeling the world. Cognitive informatics focuses on internal information processing mechanisms and the natural intelligence of the brain.

Informatics as a fundamental science of information in natural and artificial systems was proposed again in Russia in 2006.

In 2007, the influential book Decoding the Universe was published.

Former president of Association for Computing Machinery, Peter Denning wrote in 2007:

The old definition of computer science - the study of phenomena surrounding computers - is now obsolete. Computing is the study of natural and artificial information processes.

The 2008 Research Assessment Exercise, of the UK Funding Councils, includes a new, Computer Science and Informatics, unit of assessment (UoA), whose scope is described as follows:

The UoA includes the study of methods for acquiring, storing, processing, communicating and reasoning about information, and the role of interactivity in natural and artificial systems, through the implementation, organisation and use of computer hardware, software and other resources. The subjects are characterised by the rigorous application of analysis, experimentation and design.

In 2008, the construction of the Informatics Forum was completed. In 2018, the MIT Schwarzman College of Computing was established. Its construction is planned to be completed in 2021.

Controversial fields

• evolutionary informatics - a new field that comes from the concept of an intelligent design. According to Evolutionary Informatics Lab, evolutionary informatics studies how evolving systems incorporate, transform, and export information. In 2017, the influential book "Introduction To Evolutionary Informatics" was published.

Electrolyte

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Electrolyte

An electrolyte is a medium containing ions that is electrically conducting through the movement of those ions, but not conducting electrons. This includes most soluble salts, acids, and bases dissolved in a polar solvent, such as water. Upon dissolving, the substance separates into cations and anions, which disperse uniformly throughout the solvent. Solid-state electrolytes also exist. In medicine and sometimes in chemistry, the term electrolyte refers to the substance that is dissolved.

Electrically, such a solution is neutral. If an electric potential is applied to such a solution, the cations of the solution are drawn to the electrode that has an abundance of electrons, while the anions are drawn to the electrode that has a deficit of electrons. The movement of anions and cations in opposite directions within the solution amounts to a current. Some gases, such as hydrogen chloride (HCl), under conditions of high temperature or low pressure can also function as electrolytes. Electrolyte solutions can also result from the dissolution of some biological (e.g., DNA, polypeptides) or synthetic polymers (e.g., polystyrene sulfonate), termed "polyelectrolytes", which contain charged functional groups. A substance that dissociates into ions in solution or in the melt acquires the capacity to conduct electricity. Sodium, potassium, chloride, calcium, magnesium, and phosphate in a liquid phase are examples of electrolytes.

In medicine, electrolyte replacement is needed when a person has prolonged vomiting or diarrhea, and as a response to sweating due to strenuous athletic activity. Commercial electrolyte solutions are available, particularly for sick children (such as oral rehydration solution, Suero Oral, or Pedialyte) and athletes (sports drinks). Electrolyte monitoring is important in the treatment of anorexia and bulimia.

In science, electrolytes are one of the main components of electrochemical cells.

In clinical medicine, mentions of electrolytes usually refer metonymically to the ions, and (especially) to their concentrations (in blood, serum, urine, or other fluids). Thus, mentions of electrolyte levels usually refer to the various ion concentrations, not to the fluid volumes.

Etymology

The word electrolyte derives from Ancient Greek ήλεκτρο- (ēlectro-), prefix related to electricity, and λυτός (lytos), meaning "able to be untied or loosened".

History

Svante Arrhenius, father of the concept of electrolyte dissociation in aqueous solution for which he received the Nobel Prize in Chemistry in 1903.

In his 1884 dissertation, Svante Arrhenius put forth his explanation of solid crystalline salts disassociating into paired charged particles when dissolved, for which he won the 1903 Nobel Prize in Chemistry. Arrhenius's explanation was that in forming a solution, the salt dissociates into charged particles, to which Michael Faraday (1791-1867) had given the name "ions" many years earlier. Faraday's belief had been that ions were produced in the process of electrolysis. Arrhenius proposed that, even in the absence of an electric current, solutions of salts contained ions. He thus proposed that chemical reactions in solution were reactions between ions.

Shortly after Arrhenius's hypothesis of ions, Franz Hofmeister and Siegmund Lewith found that different ion types displayed different effects on such things as the solubility of proteins. A consistent ordering of these different ions on the magnitude of their effect arises consistently in many other systems as well. This has since become known as the Hofmeister series. While the origins of these effects are not abundantly clear and have been debated throughout the past century, it has been suggested that the charge density of these ions is important and might actually have explanations originating from the work of Charles-Augustin de Coulomb over 200 years ago.

Formation

Electrolyte solutions are normally formed when salt is placed into a solvent such as water and the individual components dissociate due to the thermodynamic interactions between solvent and solute molecules, in a process called "solvation". For example, when table salt (sodium chloride), NaCl, is placed in water, the salt (a solid) dissolves into its component ions, according to the dissociation reaction

NaCl_(s) → Na⁺_(aq) + Cl⁻_(aq)

It is also possible for substances to react with water, producing ions. For example, carbon dioxide gas dissolves in water to produce a solution that contains hydronium, carbonate, and hydrogen carbonate ions.

Molten salts can also be electrolytes as, for example, when sodium chloride is molten, the liquid conducts electricity. In particular, ionic liquids, which are molten salts with melting points below 100 °C, are a type of highly conductive non-aqueous electrolytes and thus have found more and more applications in fuel cells and batteries.

An electrolyte in a solution may be described as "concentrated" if it has a high concentration of ions, or "dilute" if it has a low concentration. If a high proportion of the solute dissociates to form free ions, the electrolyte is strong; if most of the solute does not dissociate, the electrolyte is weak. The properties of electrolytes may be exploited using electrolysis to extract constituent elements and compounds contained within the solution.

Alkaline earth metals form hydroxides that are strong electrolytes with limited solubility in water, due to the strong attraction between their constituent ions. This limits their application to situations where high solubility is required.

In 2021 researchers have found that electrolyte can "substantially facilitate electrochemical corrosion studies in less conductive media".

Physiological importance

See also: Electrochemical gradient, Acid-base homeostasis, and Water–electrolyte imbalance

In physiology, the primary ions of electrolytes are sodium (Na⁺), potassium (K⁺), calcium (Ca²⁺), magnesium (Mg²⁺), chloride (Cl⁻), hydrogen phosphate (HPO₄²⁻), and hydrogen carbonate (HCO₃⁻). The electric charge symbols of plus (+) and minus (−) indicate that the substance is ionic in nature and has an imbalanced distribution of electrons, the result of chemical dissociation. Sodium is the main electrolyte found in extracellular fluid and potassium is the main intracellular electrolyte; both are involved in fluid balance and blood pressure control.

All known multicellular lifeforms require a subtle and complex electrolyte balance between the intracellular and extracellular environments. In particular, the maintenance of precise osmotic gradients of electrolytes is important. Such gradients affect and regulate the hydration of the body as well as blood pH, and are critical for nerve and muscle function. Various mechanisms exist in living species that keep the concentrations of different electrolytes under tight control.

Both muscle tissue and neurons are considered electric tissues of the body. Muscles and neurons are activated by electrolyte activity between the extracellular fluid or interstitial fluid, and intracellular fluid. Electrolytes may enter or leave the cell membrane through specialized protein structures embedded in the plasma membrane called "ion channels". For example, muscle contraction is dependent upon the presence of calcium (Ca²⁺), sodium (Na⁺), and potassium (K⁺). Without sufficient levels of these key electrolytes, muscle weakness or severe muscle contractions may occur.

Electrolyte balance is maintained by oral, or in emergencies, intravenous (IV) intake of electrolyte-containing substances, and is regulated by hormones, in general with the kidneys flushing out excess levels. In humans, electrolyte homeostasis is regulated by hormones such as antidiuretic hormones, aldosterone and parathyroid hormones. Serious electrolyte disturbances, such as dehydration and overhydration, may lead to cardiac and neurological complications and, unless they are rapidly resolved, will result in a medical emergency.

Measurement

Measurement of electrolytes is a commonly performed diagnostic procedure, performed via blood testing with ion-selective electrodes or urinalysis by medical technologists. The interpretation of these values is somewhat meaningless without analysis of the clinical history and is often impossible without parallel measurements of renal function. The electrolytes measured most often are sodium and potassium. Chloride levels are rarely measured except for arterial blood gas interpretations since they are inherently linked to sodium levels. One important test conducted on urine is the specific gravity test to determine the occurrence of an electrolyte imbalance.

Rehydration

In oral rehydration therapy, electrolyte drinks containing sodium and potassium salts replenish the body's water and electrolyte concentrations after dehydration caused by exercise, excessive alcohol consumption, diaphoresis (heavy sweating), diarrhea, vomiting, intoxication or starvation. Athletes exercising in extreme conditions (for three or more hours continuously, e.g. a marathon or triathlon) who do not consume electrolytes risk dehydration (or hyponatremia).

A home-made electrolyte drink can be made by using water, sugar and salt in precise proportions. It is important to include glucose (sugar) to utilise the co-transport mechanism of sodium and glucose. Commercial preparations are also available for both human and veterinary use.

Electrolytes are commonly found in fruit juices, sports drinks, milk, nuts, and many fruits and vegetables (whole or in juice form) (e.g., potatoes, avocados).

Electrochemistry

Main article: Electrolysis

When electrodes are placed in an electrolyte and a voltage is applied, the electrolyte will conduct electricity. Lone electrons normally cannot pass through the electrolyte; instead, a chemical reaction occurs at the cathode, providing electrons to the electrolyte. Another reaction occurs at the anode, consuming electrons from the electrolyte. As a result, a negative charge cloud develops in the electrolyte around the cathode, and a positive charge develops around the anode. The ions in the electrolyte neutralize these charges, enabling the electrons to keep flowing and the reactions to continue.

Electrolytic cell producing chlorine (Cl₂) and sodium hydroxide (NaOH) from a solution of common salt.

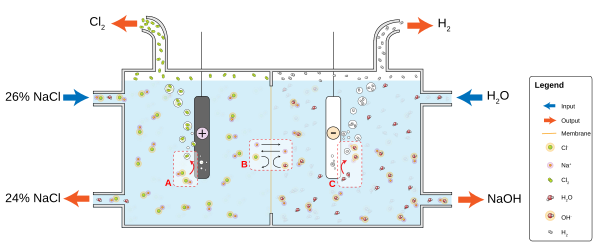
For example, in a solution of ordinary table salt (sodium chloride, NaCl) in water, the cathode reaction will be

2 H₂O + 2e⁻ → 2 OH⁻ + H₂

and hydrogen gas will bubble up; the anode reaction is

2 NaCl → 2 Na⁺ + Cl₂ + 2e⁻

and chlorine gas will be liberated into solution where it reacts with the sodium and hydroxyl ions to produce sodium hypochlorite - household bleach. The positively charged sodium ions Na⁺ will react toward the cathode, neutralizing the negative charge of OH⁻ there, and the negatively charged hydroxide ions OH⁻ will react toward the anode, neutralizing the positive charge of Na⁺ there. Without the ions from the electrolyte, the charges around the electrode would slow down continued electron flow; diffusion of H⁺ and OH⁻ through water to the other electrode takes longer than movement of the much more prevalent salt ions. Electrolytes dissociate in water because water molecules are dipoles and the dipoles orient in an energetically favorable manner to solvate the ions.

In other systems, the electrode reactions can involve the metals of the electrodes as well as the ions of the electrolyte.

Electrolytic conductors are used in electronic devices where the chemical reaction at a metal-electrolyte interface yields useful effects.

• In batteries, two materials with different electron affinities are used as electrodes; electrons flow from one electrode to the other outside of the battery, while inside the battery the circuit is closed by the electrolyte's ions. Here, the electrode reactions convert chemical energy to electrical energy.
• In some fuel cells, a solid electrolyte or proton conductor connects the plates electrically while keeping the hydrogen and oxygen fuel gases separated.
• In electroplating tanks, the electrolyte simultaneously deposits metal onto the object to be plated, and electrically connects that object in the circuit.
• In operation-hours gauges, two thin columns of mercury are separated by a small electrolyte-filled gap, and, as charge is passed through the device, the metal dissolves on one side and plates out on the other, causing the visible gap to slowly move along.
• In electrolytic capacitors the chemical effect is used to produce an extremely thin dielectric or insulating coating, while the electrolyte layer behaves as one capacitor plate.
• In some hygrometers the humidity of air is sensed by measuring the conductivity of a nearly dry electrolyte.
• Hot, softened glass is an electrolytic conductor, and some glass manufacturers keep the glass molten by passing a large current through it.

Solid electrolytes

Main articles: Fast ion conductor and Solid-state electrolyte

Solid electrolytes can be mostly divided into four groups described below.

Gel electrolytes

Gel electrolytes – closely resemble liquid electrolytes. In essence, they are liquids in a flexible lattice framework. Various additives are often applied to increase the conductivity of such systems.

Polymer electrolytes

Main article: Polymer electrolytes

Dry polymer electrolytes – differ from liquid and gel electrolytes in the sense that salt is dissolved directly into the solid medium. Usually it is a relatively high dielectric constant polymer (PEO, PMMA, PAN, polyphosphazenes, siloxanes, etc.) and a salt with low lattice energy. In order to increase the mechanical strength and conductivity of such electrolytes, very often composites are used, and inert ceramic phase is introduced. There are two major classes of such electrolytes: polymer-in-ceramic, and ceramic-in-polymer.

Ceramic electrolytes

Solid ceramic electrolytes – ions migrate through the ceramic phase by means of vacancies or interstitials within the lattice. There are also glassy-ceramic electrolytes.

Organic plastic electrolytes

Organic ionic plastic crystals – are a type organic salts exhibiting mesophases (i.e. a state of matter intermediate between liquid and solid), in which mobile ions are orientationally or rotationally disordered while their centers are located at the ordered sites in the crystal structure. They have various forms of disorder due to one or more solid–solid phase transitions below the melting point and have therefore plastic properties and good mechanical flexibility as well as improved electrode|electrolyte interfacial contact. In particular, protic organic ionic plastic crystals (POIPCs), which are solid protic organic salts formed by proton transfer from a Brønsted acid to a Brønsted base and in essence are protic ionic liquids in the molten state, have found to be promising solid-state proton conductors for fuel cells. Examples include 1,2,4-triazolium perfluorobutanesulfonate and imidazolium methanesulfonate.

In culture

Electrolytes were an important part of the movie Idiocracy, where stupid people in the future used a drink called Brawndo for everything "because it has electrolytes", without understanding what electrolytes are.