Electrical conductor

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Electrical_conductor

Overhead conductors carry electric power from generating stations to customers.

In physics and electrical engineering, a conductor is an object or type of material that allows the flow of charge (electric current) in one or more directions. Materials made of metal are common electrical conductors. Electric current is generated by the flow of negatively charged electrons, positively charged holes, and positive or negative ions in some cases.

In order for current to flow within a closed electrical circuit, it is not necessary for one charged particle to travel from the component producing the current (the current source) to those consuming it (the loads). Instead, the charged particle simply needs to nudge its neighbor a finite amount, who will nudge its neighbor, and on and on until a particle is nudged into the consumer, thus powering it. Essentially what is occurring is a long chain of momentum transfer between mobile charge carriers; the Drude model of conduction describes this process more rigorously. This momentum transfer model makes metal an ideal choice for a conductor; metals, characteristically, possess a delocalized sea of electrons which gives the electrons enough mobility to collide and thus affect a momentum transfer.

As discussed above, electrons are the primary mover in metals; however, other devices such as the cationic electrolyte(s) of a battery, or the mobile protons of the proton conductor of a fuel cell rely on positive charge carriers. Insulators are non-conducting materials with few mobile charges that support only insignificant electric currents.

Resistance and conductance

A piece of resistive material with electrical contacts on both ends.

 

Main article: Electrical resistance and conductance

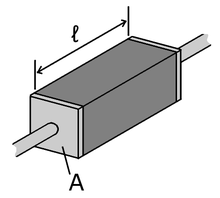
The resistance of a given conductor depends on the material it is made of, and on its dimensions. For a given material, the resistance is inversely proportional to the cross-sectional area. For example, a thick copper wire has lower resistance than an otherwise-identical thin copper wire. Also, for a given material, the resistance is proportional to the length; for example, a long copper wire has higher resistance than an otherwise-identical short copper wire. The resistance R and conductance G of a conductor of uniform cross section, therefore, can be computed as

${\displaystyle \begin{array}{rl}R& =\rho \frac{\ell }{A},\\ G& =\sigma \frac{A}{\ell }.\end{array}}$

where ${\displaystyle \ell }$ is the length of the conductor, measured in metres [m], A is the cross-section area of the conductor measured in square metres [m²], σ (sigma) is the electrical conductivity measured in siemens per meter (S·m⁻¹), and ρ (rho) is the electrical resistivity (also called specific electrical resistance) of the material, measured in ohm-metres (Ω·m). The resistivity and conductivity are proportionality constants, and therefore depend only on the material the wire is made of, not the geometry of the wire. Resistivity and conductivity are reciprocals: ${\displaystyle \rho =1/\sigma }$. Resistivity is a measure of the material's ability to oppose electric current.

This formula is not exact: It assumes the current density is totally uniform in the conductor, which is not always true in practical situation. However, this formula still provides a good approximation for long thin conductors such as wires.

Another situation this formula is not exact for is with alternating current (AC), because the skin effect inhibits current flow near the center of the conductor. Then, the geometrical cross-section is different from the effective cross-section in which current actually flows, so the resistance is higher than expected. Similarly, if two conductors are near each other carrying AC current, their resistances increase due to the proximity effect. At commercial power frequency, these effects are significant for large conductors carrying large currents, such as busbars in an electrical substation, or large power cables carrying more than a few hundred amperes.

Aside from the geometry of the wire, temperature also has a significant effect on the efficacy of conductors. Temperature affects conductors in two main ways, the first is that materials may expand under the application of heat. The amount that the material will expand is governed by the thermal expansion coefficient specific to the material. Such an expansion (or contraction) will change the geometry of the conductor and therefore its characteristic resistance. However, this effect is generally small, on the order of 10⁻⁶. An increase in temperature will also increase the number of phonons generated within the material. A phonon is essentially a lattice vibration, or rather a small, harmonic kinetic movement of the atoms of the material. Much like the shaking of a pinball machine, phonons serve to disrupt the path of electrons, causing them to scatter. This electron scattering will decrease the number of electron collisions and therefore will decrease the total amount of current transferred.

Conductor materials

Main article: Electrical resistivity and conductivity

Further information: Copper conductor and Aluminum building wiring

 

Material	ρ [Ω·m] at 20°C	σ [S/m] at 20°C
Silver, Ag	1.59 × 10−8	6.30 × 107
Copper, Cu	1.68 × 10−8	5.96 × 107
Aluminum, Al	2.82 × 10−8	3.50 × 107

Conduction materials include metals, electrolytes, superconductors, semiconductors, plasmas and some nonmetallic conductors such as graphite and conductive polymers.

Copper has a high conductivity. Annealed copper is the international standard to which all other electrical conductors are compared; the International Annealed Copper Standard conductivity is 58 MS/m, although ultra-pure copper can slightly exceed 101% IACS. The main grade of copper used for electrical applications, such as building wire, motor windings, cables and busbars, is electrolytic-tough pitch (ETP) copper (CW004A or ASTM designation C100140). If high conductivity copper must be welded or brazed or used in a reducing atmosphere, then oxygen-free high conductivity copper (CW008A or ASTM designation C10100) may be used. Because of its ease of connection by soldering or clamping, copper is still the most common choice for most light-gauge wires.

Silver is 6% more conductive than copper, but due to cost it is not practical in most cases. However, it is used in specialized equipment, such as satellites, and as a thin plating to mitigate skin effect losses at high frequencies. Famously, 14,700 short tons (13,300 t) of silver on loan from the United States Treasury were used in the making of the calutron magnets during World War II due to wartime shortages of copper. 

Aluminum wire is the most common metal in electric power transmission and distribution. Although only 61% of the conductivity of copper by cross-sectional area, its lower density makes it twice as conductive by mass. As aluminum is roughly one-third the cost of copper by weight, the economic advantages are considerable when large conductors are required.

The disadvantages of aluminum wiring lie in its mechanical and chemical properties. It readily forms an insulating oxide, making connections heat up. Its larger coefficient of thermal expansion than the brass materials used for connectors causes connections to loosen. Aluminum can also "creep", slowly deforming under load, which also loosens connections. These effects can be mitigated with suitably designed connectors and extra care in installation, but they have made aluminum building wiring unpopular past the service drop.

Organic compounds such as octane, which has 8 carbon atoms and 18 hydrogen atoms, cannot conduct electricity. Oils are hydrocarbons, since carbon has the property of tetracovalency and forms covalent bonds with other elements such as hydrogen, since it does not lose or gain electrons, thus does not form ions. Covalent bonds are simply the sharing of electrons. Hence, there is no separation of ions when electricity is passed through it. Liquids made of compounds with only covalent bonds cannot conduct electricity. Certain organic ionic liquids, by contrast, can conduct an electric current.

While pure water is not an electrical conductor, even a small portion of ionic impurities, such as salt, can rapidly transform it into a conductor.

Wire size

Wires are measured by their cross sectional area. In many countries, the size is expressed in square millimetres. In North America, conductors are measured by American wire gauge for smaller ones, and circular mils for larger ones.

Conductor ampacity

The ampacity of a conductor, that is, the amount of current it can carry, is related to its electrical resistance: a lower-resistance conductor can carry a larger value of current. The resistance, in turn, is determined by the material the conductor is made from (as described above) and the conductor's size. For a given material, conductors with a larger cross-sectional area have less resistance than conductors with a smaller cross-sectional area.

For bare conductors, the ultimate limit is the point at which power lost to resistance causes the conductor to melt. Aside from fuses, most conductors in the real world are operated far below this limit, however. For example, household wiring is usually insulated with PVC insulation that is only rated to operate to about 60 °C, therefore, the current in such wires must be limited so that it never heats the copper conductor above 60 °C, causing a risk of fire. Other, more expensive insulation such as Teflon or fiberglass may allow operation at much higher temperatures.

Isotropy

If an electric field is applied to a material, and the resulting induced electric current is in the same direction, the material is said to be an isotropic electrical conductor. If the resulting electric current is in a different direction from the applied electric field, the material is said to be an anisotropic electrical conductor.

Scalar–tensor theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Scalar%E2%80%93tensor_theory 

In theoretical physics, a scalar–tensor theory is a field theory that includes both a scalar field and a tensor field to represent a certain interaction. For example, the Brans–Dicke theory of gravitation uses both a scalar field and a tensor field to mediate the gravitational interaction.

Tensor fields and field theory

Modern physics tries to derive all physical theories from as few principles as possible. In this way, Newtonian mechanics as well as quantum mechanics are derived from Hamilton's principle of least action. In this approach, the behavior of a system is not described via forces, but by functions which describe the energy of the system. Most important are the energetic quantities known as the Hamiltonian function and the Lagrangian function. Their derivatives in space are known as Hamiltonian density and the Lagrangian density. Going to these quantities leads to the field theories.

Modern physics uses field theories to explain reality. These fields can be scalar, vectorial or tensorial. An example of a scalar field is the temperature field. An example of a vector field is the wind velocity field. An example of a tensor field is the stress tensor field in a stressed body, used in continuum mechanics.

Gravity as field theory

In physics, forces (as vectorial quantities) are given as the derivative (gradient) of scalar quantities named potentials. In classical physics before Einstein, gravitation was given in the same way, as consequence of a gravitational force (vectorial), given through a scalar potential field, dependent of the mass of the particles. Thus, Newtonian gravity is called a scalar theory. The gravitational force is dependent of the distance r of the massive objects to each other (more exactly, their centre of mass). Mass is a parameter and space and time are unchangeable.

Einstein's theory of gravity, the General Relativity (GR) is of another nature. It unifies space and time in a 4-dimensional manifold called space-time. In GR there is no gravitational force, instead, the actions we ascribed to being a force are the consequence of the local curvature of space-time. That curvature is defined mathematically by the so-called metric, which is a function of the total energy, including mass, in the area. The derivative of the metric is a function that approximates the classical Newtonian force in most cases. The metric is a tensorial quantity of degree 2 (it can be given as a 4x4 matrix, an object carrying 2 indices).

Another possibility to explain gravitation in this context is by using both tensor (of degree n>1) and scalar fields, i.e. so that gravitation is given neither solely through a scalar field nor solely through a metric. These are scalar–tensor theories of gravitation.

The field theoretical start of General Relativity is given through the Lagrange density. It is a scalar and gauge invariant (look at gauge theories) quantity dependent on the curvature scalar R. This Lagrangian, following Hamilton's principle, leads to the field equations of Hilbert and Einstein. If in the Lagrangian the curvature (or a quantity related to it) is multiplied with a square scalar field, field theories of scalar–tensor theories of gravitation are obtained. In them, the gravitational constant of Newton is no longer a real constant but a quantity dependent of the scalar field.

Mathematical formulation

An action of such a gravitational scalar–tensor theory can be written as follows:

${\displaystyle S=\frac{1}{c}\int d^{4}x\sqrt{-g}\frac{1}{2\mu }\times \left[\mathrm{\Phi }R-\frac{\omega (\mathrm{\Phi })}{\mathrm{\Phi }}({\mathrm{\partial }}_{\sigma }\mathrm{\Phi }{)}^2-V(\mathrm{\Phi })+2\mu {\mathcal{L}}_m(g_{\mu \nu },\mathrm{\Psi })\right],}$

where ${\displaystyle g}$ is the metric determinant, ${\displaystyle R}$ is the Ricci scalar constructed from the metric ${\displaystyle g_{\mu \nu }}$, ${\displaystyle \mu }$ is a coupling constant with the dimensions ${\displaystyle L^{-1}{M}^{-1}{T}^2}$, ${\displaystyle V(\mathrm{\Phi })}$ is the scalar-field potential, ${\displaystyle {\mathcal{L}}_m}$ is the material Lagrangian and ${\displaystyle \mathrm{\Psi }}$ represents the non-gravitational fields. Here, the Brans–Dicke parameter ${\displaystyle \omega }$ has been generalized to a function. Although ${\displaystyle \mu }$ is often written as being ${\displaystyle 8\pi G/c^4}$, one has to keep in mind that the fundamental constant ${\displaystyle G}$ there, is not the constant of gravitation that can be measured with, for instance, Cavendish type experiments. Indeed, the empirical gravitational constant is generally no longer a constant in scalar–tensor theories, but a function of the scalar field ${\displaystyle \mathrm{\Phi }}$. The metric and scalar-field equations respectively write:

${\displaystyle R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R=\frac{\mu }{\mathrm{\Phi }}{T}_{\mu \nu }+\frac{1}{\mathrm{\Phi }}[{\mathrm{\nabla }}_{\mu }{\mathrm{\nabla }}_{\nu }-g_{\mu \nu }◻]\mathrm{\Phi }+\frac{\omega (\mathrm{\Phi })}{{\mathrm{\Phi }}^2}({\mathrm{\partial }}_{\mu }\mathrm{\Phi }{\mathrm{\partial }}_{\nu }\mathrm{\Phi }-\frac{1}{2}{g}_{\mu \nu }({\mathrm{\partial }}_{\alpha }\mathrm{\Phi }{)}^2)-g_{\mu \nu }\frac{V(\mathrm{\Phi })}{2\mathrm{\Phi }},}$

and

${\displaystyle \frac{2\omega (\mathrm{\Phi })+3}{\mathrm{\Phi }}◻\mathrm{\Phi }=\frac{\mu }{\mathrm{\Phi }}T-\frac{{\omega }^{\prime }(\mathrm{\Phi })}{\mathrm{\Phi }}({\mathrm{\partial }}_{\sigma }\mathrm{\Phi }{)}^2+V^{\prime }(\mathrm{\Phi })-2\frac{V(\mathrm{\Phi })}{\mathrm{\Phi }}.}$

Also, the theory satisfies the following conservation equation, implying that test-particles follow space-time geodesics such as in general relativity:

${\displaystyle {\mathrm{\nabla }}_{\sigma }{T}^{\mu \sigma }=0,}$

where ${\displaystyle T^{\mu \sigma }}$ is the stress-energy tensor defined as

${\displaystyle T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}{\mathcal{L}}_m)}{\delta g^{\mu \nu }}.}$

The Newtonian approximation of the theory

Developing perturbatively the theory defined by the previous action around a Minkowskian background, and assuming non-relativistic gravitational sources, the first order gives the Newtonian approximation of the theory. In this approximation, and for a theory without potential, the metric writes

${\displaystyle g_{00}=-1+2\frac{U}{c^2}+\mathcal{O}(c^{-3}),g_{0i}=\mathcal{O}(c^{-2}),g_{ij}={\delta }_{ij}+\mathcal{O}(c^{-1}),}$

with ${\displaystyle U}$ satisfying the following usual Poisson equation at the lowest order of the approximation:

${\displaystyle \mathrm{△}U=8\pi G_{\mathrm{e}\mathrm{f}\mathrm{f}}\rho +\mathcal{O}(c^{-1}),}$

where ${\displaystyle \rho }$ is the density of the gravitational source and ${\displaystyle G_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{2{\omega }_0+4}{2{\omega }_0+3}\frac{G}{{\mathrm{\Phi }}_0}}$ (the subscript ${\displaystyle {}_0}$ indicates that the corresponding value is taken at present cosmological time and location). Therefore, the empirical gravitational constant is a function of the present value of the scalar-field background ${\displaystyle {\mathrm{\Phi }}_0}$ and therefore theoretically depends on time and location. However, no deviation from the constancy of the Newtonian gravitational constant has been measured, implying that the scalar-field background ${\displaystyle {\mathrm{\Phi }}_0}$ is pretty stable over time. Such a stability is not theoretically generally expected but can be theoretically explained by several mechanisms.

The first post-Newtonian approximation of the theory

Developing the theory at the next level leads to the so-called first post-Newtonian order. For a theory without potential and in a system of coordinates respecting the weak isotropy condition (i.e., ${\displaystyle g_{ij}\propto {\delta }_{ij}+\mathcal{O}(c^{-3})}$), the metric takes the following form:

${\displaystyle g_{00}=-1+\frac{2W}{c^2}-\beta \frac{2W^2}{c^4}+\mathcal{O}(c^{-5})}$

${\displaystyle g_{0i}=-(\gamma +1)\frac{2W_i}{c^3}+\mathcal{O}(c^{-4})}$

${\displaystyle g_{ij}={\delta }_{ij}\left(1+\gamma \frac{2W}{c^2}\right)+\mathcal{O}(c^{-3})}$

with

${\displaystyle ◻W+\frac{1+2\beta -3\gamma }{c^2}W\mathrm{△}W+\frac{2}{c^2}(1+\gamma ){\mathrm{\partial }}_{t}J=-4\pi G_{\mathrm{e}\mathrm{f}\mathrm{f}}\mathrm{\Sigma }+\mathcal{O}(c^{-3}),}$

${\displaystyle \mathrm{△}{W}_i-\mathrm{\partial }{x}_{i}J=-4\pi G_{\mathrm{e}\mathrm{f}\mathrm{f}}{\mathrm{\Sigma }}^i+\mathcal{O}(c^{-1}),}$

where ${\displaystyle J}$ is a function depending on the coordinate gauge

${\displaystyle J={\mathrm{\partial }}_{t}W+{\mathrm{\partial }}_k{W}_k+\mathcal{O}(c^{-1}).}$

It corresponds to the remaining diffeomorphism degree of freedom that is not fixed by the weak isotropy condition. The sources are defined as

${\displaystyle \mathrm{\Sigma }=\frac{1}{c^2}(T^{00}+\gamma T^{kk}),{\mathrm{\Sigma }}^i=\frac{1}{c}{T}^{0i},}$

the so-called post-Newtonian parameters are

${\displaystyle \gamma =\frac{{\omega }_0+1}{{\omega }_0+2},}$

${\displaystyle \beta =1+\frac{{\omega }_0^{\mathrm{\prime }}}{(2{\omega }_0+3)(2{\omega }_0+4{)}^2},}$

and finally the empirical gravitational constant ${\displaystyle G_{\mathrm{e}\mathrm{f}\mathrm{f}}}$ is given by

${\displaystyle G_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{2{\omega }_0+4}{2{\omega }_0+3}G,}$

where ${\displaystyle G}$ is the (true) constant that appears in the coupling constant ${\displaystyle \mu }$ defined previously.

Observational constraints on the theory

Current observations indicate that ${\displaystyle \gamma -1=(2.1\pm 2.3)\times {10}^{-5}}$, which means that ${\displaystyle {\omega }_0>40000}$. Although explaining such a value in the context of the original Brans–Dicke theory is impossible, Damour and Nordtvedt found that the field equations of the general theory often lead to an evolution of the function ${\displaystyle \omega }$ toward infinity during the evolution of the universe. Hence, according to them, the current high value of the function ${\displaystyle \omega }$ could be a simple consequence of the evolution of the universe.

The best current constraint on the post-Newtonian parameter ${\displaystyle \beta }$ comes from Mercury's perihelion shift and is ${\displaystyle |\beta -1|<3\times {10}^{-3}}$.

Both constraints show that while the theory is still a potential candidate to replace general relativity, the scalar field must be very weakly coupled in order to explain current observations.

Generalized scalar-tensor theories have also been proposed as explanation for the accelerated expansion of the universe but the measurement of the speed of gravity with the gravitational wave event GW170817 has ruled this out.

Higher-dimensional relativity and scalar–tensor theories

After the postulation of the General Relativity of Einstein and Hilbert, Theodor Kaluza and Oskar Klein proposed in 1917 a generalization in a 5-dimensional manifold: Kaluza–Klein theory. This theory possesses a 5-dimensional metric (with a compactified and constant 5th metric component, dependent on the gauge potential) and unifies gravitation and electromagnetism, i.e. there is a geometrization of electrodynamics.

This theory was modified in 1955 by P. Jordan in his Projective Relativity theory, in which, following group-theoretical reasonings, Jordan took a functional 5th metric component that led to a variable gravitational constant G. In his original work, he introduced coupling parameters of the scalar field, to change energy conservation as well, according to the ideas of Dirac.

Following the Conform Equivalence theory, multidimensional theories of gravity are conform equivalent to theories of usual General Relativity in 4 dimensions with an additional scalar field. One case of this is given by Jordan's theory, which, without breaking energy conservation (as it should be valid, following from microwave background radiation being of a black body), is equivalent to the theory of C. Brans and Robert H. Dicke of 1961, so that it is usually spoken about the Brans–Dicke theory. The Brans–Dicke theory follows the idea of modifying Hilbert-Einstein theory to be compatible with Mach's principle. For this, Newton's gravitational constant had to be variable, dependent of the mass distribution in the universe, as a function of a scalar variable, coupled as a field in the Lagrangian. It uses a scalar field of infinite length scale (i.e. long-ranged), so, in the language of Yukawa's theory of nuclear physics, this scalar field is a massless field. This theory becomes Einsteinian for high values for the parameter of the scalar field.

In 1979, R. Wagoner proposed a generalization of scalar–tensor theories using more than one scalar field coupled to the scalar curvature.

JBD theories although not changing the geodesic equation for test particles, change the motion of composite bodies to a more complex one. The coupling of a universal scalar field directly to the gravitational field gives rise to potentially observable effects for the motion of matter configurations to which gravitational energy contributes significantly. This is known as the "Dicke–Nordtvedt" effect, which leads to possible violations of the Strong as well as the Weak Equivalence Principle for extended masses.

JBD-type theories with short-ranged scalar fields use, according to Yukawa's theory, massive scalar fields. The first of this theories was proposed by A. Zee in 1979. He proposed a Broken-Symmetric Theory of Gravitation, combining the idea of Brans and Dicke with the one of Symmetry Breakdown, which is essential within the Standard Model SM of elementary particles, where the so-called Symmetry Breakdown leads to mass generation (as a consequence of particles interacting with the Higgs field). Zee proposed the Higgs field of SM as scalar field and so the Higgs field to generate the gravitational constant.

The interaction of the Higgs field with the particles that achieve mass through it is short-ranged (i.e. of Yukawa-type) and gravitational-like (one can get a Poisson equation from it), even within SM, so that Zee's idea was taken 1992 for a scalar–tensor theory with Higgs field as scalar field with Higgs mechanism. There, the massive scalar field couples to the masses, which are at the same time the source of the scalar Higgs field, which generates the mass of the elementary particles through Symmetry Breakdown. For vanishing scalar field, this theories usually go through to standard General Relativity and because of the nature of the massive field, it is possible for such theories that the parameter of the scalar field (the coupling constant) does not have to be as high as in standard JBD theories. Though, it is not clear yet which of these models explains better the phenomenology found in nature nor if such scalar fields are really given or necessary in nature. Nevertheless, JBD theories are used to explain inflation (for massless scalar fields then it is spoken of the inflation field) after the Big Bang as well as the quintessence. Further, they are an option to explain dynamics usually given through the standard cold dark matter models, as well as MOND, Axions (from Breaking of a Symmetry, too), MACHOS,...

Connection to string theory

A generic prediction of all string theory models is that the spin-2 graviton has a spin-0 partner called the dilaton. Hence, string theory predicts that the actual theory of gravity is a scalar–tensor theory rather than general relativity. However, the precise form of such a theory is not currently known because one does not have the mathematical tools in order to address the corresponding non-perturbative calculations. Besides, the precise effective 4-dimensional form of the theory is also confronted to the so-called landscape issue.

Other possible scalar–tensor theories

• Degenerate Higher-Order Scalar-Tensor theories

Theories with non-minimal scalar-matter coupling

• Dilaton gravity
• Chameleon theory
• Pressuron theory