Fractal dimension

From Wikipedia, the free encyclopedia

11.5 x 200 = 2300 km

 

28 x 100 = 2800 km

 

70 x 50 = 3500 km

Figure 1. As the length of the measuring stick is scaled smaller and smaller, the total length of the coastline measured increases (See Coastline paradox).

In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.

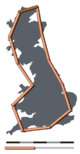
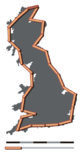
The main idea of "fractured" dimensions has a long history in mathematics, but the term itself was brought to the fore by Benoit Mandelbrot based on his 1967 paper on self-similarity in which he discussed fractional dimensions. In that paper, Mandelbrot cited previous work by Lewis Fry Richardson describing the counter-intuitive notion that a coastline's measured length changes with the length of the measuring stick used (see Fig. 1). In terms of that notion, the fractal dimension of a coastline quantifies how the number of scaled measuring sticks required to measure the coastline changes with the scale applied to the stick. There are several formal mathematical definitions of fractal dimension that build on this basic concept of change in detail with change in scale: see the section Examples.

Ultimately, the term fractal dimension became the phrase with which Mandelbrot himself became most comfortable with respect to encapsulating the meaning of the word fractal, a term he created. After several iterations over years, Mandelbrot settled on this use of the language: "...to use fractal without a pedantic definition, to use fractal dimension as a generic term applicable to all the variants."

One non-trivial example is the fractal dimension of a Koch snowflake. It has a topological dimension of 1, but it is by no means rectifiable: the length of the curve between any two points on the Koch snowflake is infinite. No small piece of it is line-like, but rather it is composed of an infinite number of segments joined at different angles. The fractal dimension of a curve can be explained intuitively by thinking of a fractal line as an object too detailed to be one-dimensional, but too simple to be two-dimensional. Therefore its dimension might best be described not by its usual topological dimension of 1 but by its fractal dimension, which is often a number between one and two; in the case of the Koch snowflake, it is approximately 1.2619.

Introduction

Figure 2. A 32-segment quadric fractal scaled and viewed through boxes of different sizes. The pattern illustrates self similarity. The theoretical fractal dimension for this fractal is 5/3 ≈ 1.67; its empirical fractal dimension from box counting analysis is ±1% using fractal analysis software.

A fractal dimension is an index for characterizing fractal patterns or sets by quantifying their complexity as a ratio of the change in detail to the change in scale. Several types of fractal dimension can be measured theoretically and empirically (see Fig. 2). Fractal dimensions are used to characterize a broad spectrum of objects ranging from the abstract to practical phenomena, including turbulence, river networks, urban growth, human physiology, medicine, and market trends. The essential idea of fractional or fractal dimensions has a long history in mathematics that can be traced back to the 1600s, but the terms fractal and fractal dimension were coined by mathematician Benoit Mandelbrot in 1975.

Fractal dimensions were first applied as an index characterizing complicated geometric forms for which the details seemed more important than the gross picture. For sets describing ordinary geometric shapes, the theoretical fractal dimension equals the set's familiar Euclidean or topological dimension. Thus, it is 0 for sets describing points (0-dimensional sets); 1 for sets describing lines (1-dimensional sets having length only); 2 for sets describing surfaces (2-dimensional sets having length and width); and 3 for sets describing volumes (3-dimensional sets having length, width, and height). But this changes for fractal sets. If the theoretical fractal dimension of a set exceeds its topological dimension, the set is considered to have fractal geometry.

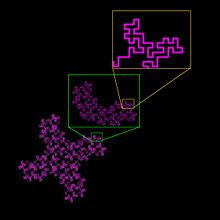
Unlike topological dimensions, the fractal index can take non-integer values, indicating that a set fills its space qualitatively and quantitatively differently from how an ordinary geometrical set does. For instance, a curve with a fractal dimension very near to 1, say 1.10, behaves quite like an ordinary line, but a curve with fractal dimension 1.9 winds convolutedly through space very nearly like a surface. Similarly, a surface with fractal dimension of 2.1 fills space very much like an ordinary surface, but one with a fractal dimension of 2.9 folds and flows to fill space rather nearly like a volume. This general relationship can be seen in the two images of fractal curves in Fig.2 and Fig. 3 – the 32-segment contour in Fig. 2, convoluted and space filling, has a fractal dimension of 1.67, compared to the perceptibly less complex Koch curve in Fig. 3, which has a fractal dimension of approximately 1.2619.

Figure 3. The Koch curve is a classic iterated fractal curve. It is a theoretical construct that is made by iteratively scaling a starting segment. As shown, each new segment is scaled by 1/3 into 4 new pieces laid end to end with 2 middle pieces leaning toward each other between the other two pieces, so that if they were a triangle its base would be the length of the middle piece, so that the whole new segment fits across the traditionally measured length between the endpoints of the previous segment. Whereas the animation only shows a few iterations, the theoretical curve is scaled in this way infinitely. Beyond about 6 iterations on an image this small, the detail is lost.

The relationship of an increasing fractal dimension with space-filling might be taken to mean fractal dimensions measure density, but that is not so; the two are not strictly correlated. Instead, a fractal dimension measures complexity, a concept related to certain key features of fractals: self-similarity and detail or irregularity. These features are evident in the two examples of fractal curves. Both are curves with topological dimension of 1, so one might hope to be able to measure their length and derivative in the same way as with ordinary curves. But we cannot do either of these things, because fractal curves have complexity in the form of self-similarity and detail that ordinary curves lack. The self-similarity lies in the infinite scaling, and the detail in the defining elements of each set. The length between any two points on these curves is infinite, no matter how close together the two points are, which means that it is impossible to approximate the length of such a curve by partitioning the curve into many small segments. Every smaller piece is composed of an infinite number of scaled segments that look exactly like the first iteration. These are not rectifiable curves, meaning they cannot be measured by being broken down into many segments approximating their respective lengths. They cannot be meaningfully characterized by finding their lengths and derivatives. However, their fractal dimensions can be determined, which shows that both fill space more than ordinary lines but less than surfaces, and allows them to be compared in this regard.

The two fractal curves described above show a type of self-similarity that is exact with a repeating unit of detail that is readily visualized. This sort of structure can be extended to other spaces (e.g., a fractal that extends the Koch curve into 3-d space has a theoretical D=2.5849). However, such neatly countable complexity is only one example of the self-similarity and detail that are present in fractals. The example of the coast line of Britain, for instance, exhibits self-similarity of an approximate pattern with approximate scaling. Overall, fractals show several types and degrees of self-similarity and detail that may not be easily visualized. These include, as examples, strange attractors for which the detail has been described as in essence, smooth portions piling up, the Julia set, which can be seen to be complex swirls upon swirls, and heart rates, which are patterns of rough spikes repeated and scaled in time. Fractal complexity may not always be resolvable into easily grasped units of detail and scale without complex analytic methods but it is still quantifiable through fractal dimensions.

History

The terms fractal dimension and fractal were coined by Mandelbrot in 1975, about a decade after he published his paper on self-similarity in the coastline of Britain. Various historical authorities credit him with also synthesizing centuries of complicated theoretical mathematics and engineering work and applying them in a new way to study complex geometries that defied description in usual linear terms. The earliest roots of what Mandelbrot synthesized as the fractal dimension have been traced clearly back to writings about nondifferentiable, infinitely self-similar functions, which are important in the mathematical definition of fractals, around the time that calculus was discovered in the mid-1600s. There was a lull in the published work on such functions for a time after that, then a renewal starting in the late 1800s with the publishing of mathematical functions and sets that are today called canonical fractals (such as the eponymous works of von Koch, Sierpiński, and Julia), but at the time of their formulation were often considered antithetical mathematical "monsters". These works were accompanied by perhaps the most pivotal point in the development of the concept of a fractal dimension through the work of Hausdorff in the early 1900s who defined a "fractional" dimension that has come to be named after him and is frequently invoked in defining modern fractals.

See Fractal history for more information

Role of scaling

Figure 4. Traditional notions of geometry for defining scaling and dimension.
${\displaystyle 1}$, ${\displaystyle 1^2=1}$, ${\displaystyle 1^3=1}$
${\displaystyle 2}$, ${\displaystyle 2^2=4}$, ${\displaystyle 2^3=8}$
${\displaystyle 3}$, ${\displaystyle 3^2=9}$, ${\displaystyle 3^3=27}$ 

The concept of a fractal dimension rests in unconventional views of scaling and dimension. As Fig. 4 illustrates, traditional notions of geometry dictate that shapes scale predictably according to intuitive and familiar ideas about the space they are contained within, such that, for instance, measuring a line using first one measuring stick then another 1/3 its size, will give for the second stick a total length 3 times as many sticks long as with the first. This holds in 2 dimensions, as well. If one measures the area of a square then measures again with a box of side length 1/3 the size of the original, one will find 9 times as many squares as with the first measure. Such familiar scaling relationships can be defined mathematically by the general scaling rule in Equation 1, where the variable ${\displaystyle N}$ stands for the number of measurement units (sticks, squares, etc.), ${\displaystyle \epsilon }$ for the scaling factor, and ${\displaystyle D}$ for the fractal dimension:

${\displaystyle N={\epsilon }^{-D}.}$

(1)

This scaling rule typifies conventional rules about geometry and dimension – referring to the examples above, it quantifies that ${\displaystyle D=1}$ for lines because ${\displaystyle N=3}$ when ${\displaystyle \epsilon =\frac{1}{3}}$, and that ${\displaystyle D=2}$ for squares because ${\displaystyle N=9}$ when ${\displaystyle \epsilon =\frac{1}{3}.}$

Figure 5. The first four iterations of the Koch snowflake, which has a Hausdorff dimension of approximately 1.2619.

The same rule applies to fractal geometry but less intuitively. To elaborate, a fractal line measured at first to be one length, when remeasured using a new stick scaled by 1/3 of the old may be 4 times as many scaled sticks long rather than the expected 3 (see Fig. 5). In this case, ${\displaystyle N=4}$ when ${\displaystyle \epsilon =\frac{1}{3},}$ and the value of ${\displaystyle D}$ can be found by rearranging Equation 1:

${\displaystyle {\log }_{\epsilon }N=-D=\frac{\log N}{\log \epsilon }.}$

(2)

That is, for a fractal described by ${\displaystyle N=4}$ when ${\displaystyle \epsilon =\frac{1}{3}}$, such as the Koch snowflake, ${\displaystyle D=1.26185\dots }$, a non-integer value that suggests the fractal has a dimension not equal to the space it resides in.

Of note, images shown in this page are not true fractals because the scaling described by ${\displaystyle D}$ cannot continue past the point of their smallest component, a pixel. However, the theoretical patterns that the images represent have no discrete pixel-like pieces, but rather are composed of an infinite number of infinitely scaled segments and do indeed have the claimed fractal dimensions.

D is not a unique descriptor

Figure 6. Two L-systems branching fractals that are made by producing 4 new parts for every 1/3 scaling so have the same theoretical ${\displaystyle D}$ as the Koch curve and for which the empirical box counting ${\displaystyle D}$ has been demonstrated with 2% accuracy.

As is the case with dimensions determined for lines, squares, and cubes, fractal dimensions are general descriptors that do not uniquely define patterns. The value of D for the Koch fractal discussed above, for instance, quantifies the pattern's inherent scaling, but does not uniquely describe nor provide enough information to reconstruct it. Many fractal structures or patterns could be constructed that have the same scaling relationship but are dramatically different from the Koch curve, as is illustrated in Figure 6.

For examples of how fractal patterns can be constructed, see Fractal, Sierpinski triangle, Mandelbrot set, Diffusion limited aggregation, L-System.

Fractal surface structures

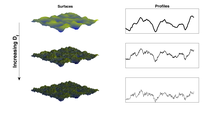
The concept of fractality is applied increasingly in the field of surface science, providing a bridge between surface characteristics and functional properties. Numerous surface descriptors are used to interpret the structure of nominally flat surfaces, which often exhibit self-affine features across multiple length-scales. Mean surface roughness, usually denoted R_A, is the most commonly applied surface descriptor, however numerous other descriptors including mean slope, root mean square roughness (R_RMS) and others are regularly applied. It is found however that many physical surface phenomena cannot readily be interpreted with reference to such descriptors, thus fractal dimension is increasingly applied to establish correlations between surface structure in terms of scaling behavior and performance. The fractal dimensions of surfaces have been employed to explain and better understand phenomena in areas of contact mechanics, frictional behavior, electrical contact resistance and transparent conducting oxides.

Figure 7: Illustration of increasing surface fractality. Self-affine surfaces (left) and corresponding surface profiles (right) showing increasing fractal dimension D_f

Examples

The concept of fractal dimension described in this article is a basic view of a complicated construct. The examples discussed here were chosen for clarity, and the scaling unit and ratios were known ahead of time. In practice, however, fractal dimensions can be determined using techniques that approximate scaling and detail from limits estimated from regression lines over log vs log plots of size vs scale. Several formal mathematical definitions of different types of fractal dimension are listed below. Although for compact sets with exact affine self-similarity all these dimensions coincide, in general they are not equivalent:

• Box counting dimension: D is estimated as the exponent of a power law.

${\displaystyle D_0=\underset{\epsilon \to 0}{lim}\frac{\log N(\epsilon )}{\log \frac{1}{\epsilon }}.}$

• Information dimension: D considers how the average information needed to identify an occupied box scales with box size; ${\displaystyle p}$ is a probability.

${\displaystyle D_1=\underset{\epsilon \to 0}{lim}\frac{-⟨\log p_{\epsilon }⟩}{\log \frac{1}{\epsilon }}}$

• Correlation dimension: D is based on ${\displaystyle M}$ as the number of points used to generate a representation of a fractal and g_ε, the number of pairs of points closer than ε to each other.

${\displaystyle D_2=\underset{M\to \mathrm{\infty }}{lim}\underset{\epsilon \to 0}{lim}\frac{\log (g_{\epsilon }/M^2)}{\log \epsilon }}$^{[citation needed]}

• Generalized or Rényi dimensions: The box-counting, information, and correlation dimensions can be seen as special cases of a continuous spectrum of generalized dimensions of order α, defined by:

${\displaystyle D_{\alpha }=\underset{\epsilon \to 0}{lim}\frac{\frac{1}{\alpha -1}\log (\sum _i{p}_i^{\alpha })}{\log \epsilon }}$

• Higuchi dimension

${\displaystyle D=\frac{d\log (L(k))}{d\log (k)}}$

• Lyapunov dimension
• Multifractal dimensions: a special case of Rényi dimensions where scaling behaviour varies in different parts of the pattern.
• Uncertainty exponent
• Hausdorff dimension: For any subset ${\displaystyle S}$ of a metric space ${\displaystyle X}$ and ${\displaystyle d\ge 0}$, the d-dimensional Hausdorff content of S is defined by

${\displaystyle C_H^d(S):=inf\{\sum _i{r}_i^d:\text{ there is a cover of }S\text{ by balls with radii }{r}_i>0\}.}$

The Hausdorff dimension of S is defined by

${\displaystyle {\dim }_{\mathrm{H}}(X):=inf\{d\ge 0:C_H^d(X)=0\}.}$

• Packing dimension
• Assouad dimension
• Local connected dimension

Estimating from real-world data

Many real-world phenomena exhibit limited or statistical fractal properties and fractal dimensions that have been estimated from sampled data using computer based fractal analysis techniques. Practically, measurements of fractal dimension are affected by various methodological issues, and are sensitive to numerical or experimental noise and limitations in the amount of data. Nonetheless, the field is rapidly growing as estimated fractal dimensions for statistically self-similar phenomena may have many practical applications in various fields including astronomy, acoustics, geology and earth sciences, diagnostic imaging, ecology, electrochemical processes, image analysis, biology and medicine, neuroscience, network analysis, physiology, physics, and Riemann zeta zeros. Fractal dimension estimates have also been shown to correlate with Lempel-Ziv complexity in real-world data sets from psychoacoustics and neuroscience.

An alternative to a direct measurement, is considering a mathematical model that resembles formation of a real-world fractal object. In this case, a validation can also be done by comparing other than fractal properties implied by the model, with measured data. In colloidal physics, systems composed of particles with various fractal dimensions arise. To describe these systems, it is convenient to speak about a distribution of fractal dimensions, and eventually, a time evolution of the latter: a process that is driven by a complex interplay between aggregation and coalescence.

One Big Union (concept)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/One_Big_Union_(concept) 

IWW sticker, 1910s

The One Big Union is an idea originating in the late 19th and early 20th centuries amongst trade unionists to unite the interests of workers and offer solutions to all labour problems.

Unions initially organized as craft unions. Workers were organized by their skill: carpenters, plumbers, bricklayers, each into their respective unions. Capitalists could often divide craft unionists along these lines in demarcation disputes. As capitalist enterprises and state bureaucracies became more centralized and larger, some workers felt that their institutions needed to become similarly large. A simultaneous disenchantment with the perceived weakness of craft unions caused many unions to organize along industrial lines. The idea of the "one big union" is championed by anarchist syndicalists to organize effectively.

As envisioned by the Industrial Workers of the World (IWW), which for many years prior to 1919 had been associated with the concept, One Big Union was not just the idea that all workers should be organized into one big union. In the 1911 pamphlet One Big Union, IWW supporters Thomas J. Hagerty and William Trautmann enumerated two goals: One Big Union needed to "combine the wage-workers in such a way that it can most successfully fight the battles and protect the interests of the workers of today in their struggles for fewer hours of toil, more wages and better conditions," and it also "must offer a final solution of the labor problem – an emancipation from strikes, injunctions, bull-pens, and scabbing of one against the other."

One Big Union was the notional organizational concept, while the IWW's revolutionary industrial unionism was the organizing method by which that concept could be realized. "Organizing the One Big Union of all workers the world over" was meant to achieve "working class control". But the One Big Union organizations were resisted by government and industry, and subverted by existing trade unions. By 1925, only the slogan of One Big Union remained.

One Big Union in practice

The Industrial Workers of the World (IWW) adopted and promoted the concept of the One Big Union after the publication of the One Big Union pamphlet in 1911; the IWW continues to use the phrase. Members of the IWW historically, and currently, signed and sign letters (and other communications) with the closing, "Yours for the O.B.U." Many commentators regard One Big Union as synonymous with the Industrial Workers of the World. One of the popular IWW publications was called One Big Union Monthly.

The IWW promoted the One Big Union concept in various ways, including as an invitation to racial equality. One IWW leaflet proclaimed:

To Colored Workingmen and Women: If you are a wage worker you are welcome in the I.W.W. halls, no matter what your color. By this you may see that the I.W.W. is not a white man's union, not a black man's union, not a red or yellow man's union, but a working man's union. All of the working class in one big union.

The IWW used the same sort of arguments to welcome women into the workforce. The appeal subsequently proclaimed the intent to organize "all wage workers ... into One Big Union, regardless of creed, color, or nationality ... An injury to one is an injury to all." The One Big Union idea had the immediate goals of better pay, shorter hours, and better surroundings. The IWW propagandized, "Organize in one big union and fight for a chance to live as human beings should live. All together now and victory will be ours."

History

North America

Founding organizations

In North America, the most significant early impetus for the One Big Union concept came from the Western Federation of Miners (WFM) which was headquartered in Denver, Colorado. The WFM and its allies first launched the Western Labor Union (WLU). The Western Labor Union was initially intended to displace the conservative American Federation of Labor (AFL) in the West. The WLU's rebranding in 1902 as the American Labor Union (ALU)^[12] was a direct response to actions by (AFL) President Samuel Gompers.

The WFM and the ALU then cooperated to found the IWW. The IWW was conceived as a global union with the goal of organizing the entire world. The concept of One Big Union, growing out of the IWW's revolutionary program, evolved over a period of time:

[I]n moving toward revolutionary industrial unionism, Denver's labor radicals were not building from scratch; rather, they drew upon and elaborated ideas and strategies generated by the previous twenty years of Denver's labor history ... [A]lthough the labor wars of 1903–4 may have triggered the formation of the IWW, the ideological synthesis it would uphold had been worked out in the American Labor Union's leadership by the summer of 1903 ...

The WFM had been founded as a conservative trade union after a bitter and violent strike in Coeur d'Alene in 1892. The WFM conducted a successful strike in Cripple Creek in 1894, notable for the exceedingly rare intervention of the state on the side of the striking miners. But the strike which some historians believe shaped the philosophy and tactics of the WFM, and which ultimately resulted in the WFM embracing revolutionary industrial unionism and the eventual promulgation of the One Big Union concept, occurred against mine owners in Leadville. Out of that struggle came the November 1897 proclamation of the State Trades and Labor Council of Montana, a document which broke with the past – declaring that "the old form of organization is unable to cope with the recent aggressions of plutocracy" – and called for a new type of labour organization.

The WFM wasn't that organization. It had poured resources into the Leadville strike, and yet was defeated. Additional resources which had been promised by the AFL were not provided. The solution was organizing western labourers and western unions into a new umbrella-like federation (i.e., the WLU, the ALU, and eventually, the IWW). These conclusions represented "an absolute rejection" of the AFL, of its conservative philosophy and its complacent demeanour.

But the WFM did undergo substantial changes. In contrast to the AFL, the WFM,

... opened itself to all potential members and also to ideas and values in conflict with Capitalism. It accepted any member of a bona fide union without initiation fee upon presentation of a valid union card. It demanded neither a closed shop nor an exclusive employment contract. It sought jobs for all, not merely the organized and highly skilled few.

Members of the WFM "... saw no advantage to huddling within their traditional crafts; they sought to mobilize all workers across a given industry to confront employers – and governments – with their aggregate clout. With little stake in the status quo, they invested their faith in sweeping political programs to remedy the grim conditions in which they worked and lived."

In 1905, WFM leaders initiated a meeting of thirty prominent socialists and labour radicals in Chicago. This group analysed industrial and social relations from the revolutionary viewpoint and drafted a manifesto. Enumerating labour's grievances, it criticized craft unions for creating a skilled aristocracy, and suggested "one big industrial union" embracing all industries and "founded on the class struggle". Printed in great quantities, this invitation to the first convention of the IWW was sent around the country.

The One Big Union concept grows

The IWW organized in the United States, Canada, Australia, and other countries, employed creative tactics, and advocated the general strike as a favourite method for workers to gain control of industries. But One Big Union spread far beyond the IWW. The revolutionary character of the OBU can be appreciated from a statement by the Brotherhood of Metal Workers' Industrial Union, a 1909 offshoot of the International Association of Machinists. In 1919, this organization published the following,

The workers, not only of America, but of all countries, are determined to get the full value of the price they paid and will yet pay. There can be no peace until the workers not only control, but also own, the means of life, liberty, and happiness. To accomplish this, it necessitates the ownership of all industries by a government of workers, for the workers, which can and will be accomplished by the One Big Union.

Also in 1919, the International Federation of Workers in the Hotel, Restaurant, Lunchroom, Club and Catering Industry (IFWHRLC) called upon its members to terminate any AFL memberships and was judged by investigators, on the basis of an explanation of industrial unionism in the Hotel Worker, one of its publications, to be a "revolutionary organization based upon the One Big Union principle, having for its objective the establishment of a new social order and the seizure of industry." The Hotel Worker stated, in part:

Under industrial unionism, all the Workers in one industry form One Big Union of that industry.

Instead of being split up into a lot of separate units, with divided and often conflicting interests, they strengthen and unite their forces in one mighty and irresistible combination.

The Journeymen Bakers' and Confectioners' International Union of America (JBCIUA) came under suspicion for hosting a delegation of the IWW, and for forming a committee to explore a merger with the IFWHRLC. Investigators concluded that such events confirmed "the organization of One Big Union along I. W. W. lines to control all the workers in the food industry in this state, as well as in the greater part of the country." Cognizant of repression of the period that came to be called the Red Scare, the JBCIUA passed a resolution which stated, in part, "... that our best friends and advisors are being martyrized by the capitalistic system, in the present period of worst reaction, and have been thrown into jail for long terms."

In 1919 in the United States the newly formed Communist Labor Party (CLP) sought to attach itself to the One Big Union movement, and to industrial unionism. The CLP urged all its members to join industrial unions. The IWW concluded that the Russian revolution and local communist activities had a divisive effect on the general anti-capitalist movement, but this effect was not immediately apparent.

Canada

Main article: One Big Union (Canada)

In 1919 in Canada, unionists who were discontent with policies of the Trades and Labour Congress of the Dominion formed a union called "One Big Union" (OBU). The Canadian OBU movement had been inspired by the IWW, and like the IWW, it favoured the general strike. The concept of One Big Union in western Canada did not gain widespread acceptance until the Western Labor News reported that the idea had been adopted by the Australian Workers International Industrial Union in South Melbourne, Australia. That Australian workers' organization went beyond industrial unionism to advocate the abolition of private ownership of the means of production. Because of recent history in Western Canada, an increasing acceptance of industrial unionism accompanied a growing appreciation of the general strike, and the need for an OBU to call it. A mood of militancy had been growing in Western Canada for some time.

The OBU spread rapidly in Canada. Lodges, trades councils, and provincial federations withdrew from their international organizations, and joined the OBU, culminating in a membership of nearly fifty thousand the first year. The OBU also generated considerable support for dual affiliation. This incarnation of the OBU movement was also attacked by mainstream labour, in the person of John L. Lewis and other AFL officials.

The One Big Union organization in Canada differed structurally from the IWW. While the IWW organized on industrial lines, the OBU of Canada focused more on organizing workers geographically. The absence of an existing industrial union structure within the Canadian OBU resulted in the defection of 20,000 members of the Lumber Workers Industrial Union (LWIU). According to the 1922 publication Industrial Unionism in America, "Their withdrawal was a staggering blow from which the O. B. U. [never] recovered."

When the IWW in the United States was suppressed during the Red Scare and the Palmer Raids, there was pressure to similarly attack Canada's One Big Union movement:

The movement was got well under way with a basis of I.W.W. and Socialist support; Calgary was a centre of the movement as it had been in the Alberta mining unrest of these years. So obvious was the current of thought that the Calgary Herald of Sept. 6th struck a warning note: "There is an element in Western Canada that is somewhat akin to the I.W.W. if not actually affiliated with and controlled by it. Let the I.W.W. of Canada or their imitators, beware lest the strong hand of the law does not stretch out and grasp them as it has their friends on the other side of the 49th parallel. There is a feeling throughout the country that it would be better for all concerned if a few of them were behind the bars."

The Canadian government imprisoned the most prominent members of the Canadian OBU.

Australia

The One Big Union movement was organized in Australia. The concept was initially considered in 1908, when the idea of adopting the preamble of the Industrial Workers of the World was voted upon by the New South Wales Trade Union Congress, and the first concrete step toward one big union was adopted in 1912. In 1917, George Beeby, the labour minister for the New South Wales government, said in a speech,

... an important conference of Trade Unionists was held in Sydney to further the idea of one big union. The men responsible for that gathering openly said that their object was to get the Unionists formed into a one big union organisation which, at any time, by the proclamation of a general strike, could stop all production and transport, and force from any government in office whatever concessions were demanded. ... The men at the head of this movement are in favour of direct action as against political action ... With consummate skill the men who initiated this idea have got possession of the whole Labour movement.

An organization called the One Big Union Propaganda League (OBUPL) was formed in Brisbane on 10 September 1918, growing out of former IWW strongholds in the north.^[43] With help from IWW members, the OBUPL gained considerable support from the rank and file of craft unions, emphasizing job control and bottom-up organizing.

Australian trade union officials, succeeded in changing the character of the OBU from that envisioned by the IWW, and also by the Workers' International Industrial Union (WIIU), a group that had split off from the IWW, and was active in Australia. The One Big Union movement ceased to challenge capitalism in Australia, but rather sought to function within capitalism; it evolved from an industrial to a craft basis; it developed into a top-down bureaucracy. By 1924 the Australian OBU ceased to be viable.

In 1927, the Australian Council of Trade Unions was established as an attempt to establish a One Big Union.

Relationship with mainstream unions

The goal of the IWW – as interpreted by government investigators in 1920 – was "to break up the system of craft or trade unions, and to organize workers into One Big Union having subdivisions along the lines of industry, rather than those of trade." That interpretation appears to have been accepted by American Federation of Labor Gompers who in 1922 expressed his belief that the One Big Union idea was designed primarily to put the American Federation of Labor out of business. Gompers undermined any labour actions that he perceived might be related to the One Big Union movement; for example, the Winnipeg General Strike and the Seattle General Strike. A 1919 editorial in Revolutionary Age, the official organ of the Left Wing Section of the Socialist Party, proclaimed:

The union bureaucrats are particularly against industrial unionism, since industrial unionism ends craft divisions and craft disputes, which constitute the power of the union bureaucracy. In Canada, the One Big Union – Industrial Unionism – has captured the imagination of the organized workers. The One Big Union directed the great general strike in Canada; but, says an observer, "the International Brotherhoods have come out against the strikers, shrewdly foreseeing in the One Big Union the destruction of their organization." This is a damning indictment of the old unionism.

In June 1919, the American Federation of Labor (AFL), in session in Atlantic City, New Jersey, passed resolutions in general opposition to the general strike. The official report of these proceedings described the convention as the "largest and in all probability the most important Convention ever held" by the organization, in part for having engineered the "overwhelming defeat of the so-called Radical element" via crushing a 'One Big Union' proposition and a proposal for a nationwide general strike, both by a vote of more than 20 to 1." The AFL amended its constitution to disallow any central labour union (i.e., regional labour councils) from "taking a strike vote without prior authorization of the national officers of the union concerned." The change was intended to "check the spread of general strike sentiment and prevent recurrences of what happened at Seattle and is now going on at Winnipeg." The penalty for any unauthorized strike vote was revocation of that body's charter.

In 1919 the Lusk Committee, charged with exposing and stamping out radicalism of all types, issued a report that found the AFL to be "free from the taint of revolutionary radicalism." It found one AFL affiliate, the International Ladies' Garment Workers' Union (ILGWU), to have "marked radical tendencies ... it is founded upon the principles of class struggle ... it adopts the One Big Union idea and seeks to bring about the overthrow of society."

One Big Union Canada also came under considerable pressure from the Canadian Trades and Labour Congress and the AFL. The United Mine Workers (UMW), in particular, came to an agreement with employers to freeze out the Canadian One Big Union.

In June 1919, the UMW revoked the charter of District 18, which included Alberta and British Columbia, for joining the OBU. The UMW International persuaded a number of locals to return to the parent organization. The UMW then came to an agreement with employers which would effectively lock out the OBU. With One Big Union seen as the greater threat, employers agreed to require UMW membership on the part of all employees in and around the mines. The companies implemented the dues checkoff to seal the new agreement.

OBU members refused to work under circumstances where they were assessed dues for an organization to which they no longer belonged, and a number of mines organized by the OBU were therefore closed down. The OBU sought relief from the courts, but the courts sided with the United Mine Workers and the employers. The employers and the UMW then together secured injunctions against any OBU members to prevent any interference with UMW miners. The O.B.U. Bulletin for 23 October 1920 reported that the UMW had thirteen such injunctions issued, and had set aside a million dollars to fight the OBU. The Canadian OBU concluded that "Officials of the U.M.W. of A. are the same bunch of crooks who have so often betrayed the miners of the U.S. in their struggles and strikes at the instance of their government and the owners." The OBU felt particularly angry that the UMW invoked the aid of both the employers and a "ruthless capitalist government" in order to crush a rival union organization.

Criticism

The One Big Union organizations adopted some principles of One Big Union as initially promoted by the IWW. The OBU idea became popular in Australia at a time when some syndicalist-leaning labour leaders had started moving toward communism.

Although the One Big Union organizations frequently formed with the help of IWW members or members of IWW offshoot-organizations such as the WIIU, the OBU organizations frequently incurred criticism from the original industrial union organizations. The IWW advocated organizing bottom-up, the OBU in Australia operated increasingly top-down. The IWW advocated job control, the Australian OBU did not. Shop committees and rank and file participation which had been so important to IWW members were de-emphasized. The OBU in Australia was described as "the plum extracted from the IWW cake to keep down discontent among the dupes".

The Industrial Union News of the WIIU criticized the structure of the Canadian One Big Union organization, declaring "the O.B.U. seeks to masquerade under the guise of industrial unionism while organized on a territorial plane, without sound foundations and building from the top down". The Industrial Union News also criticized the Canadian OBU for not providing for elections of officials by the entire membership. The OBU was described as "not red but pale pink", and in league with the "reactionary Socialist Party of Canada".

The IWW publication Solidarity of 10 July 1920 stated that labour fakirs had seized control of the OBU, and had organized new branches of the OBU in the United States in opposition to the IWW.

Marian Dutton Savage, who published a book on industrial unionism in 1922, saw problems with the organizational structure of the Canadian OBU:

In neglecting to give adequate recognition to the ties binding workers of the same industry together and in seeking to rely instead on the general feeling of solidarity in the working class, the O. B. U., like the Knights of Labor, has failed to understand the psychology of those it has sought to win and hold. If it is difficult to make skilled and unskilled workers in the same industry realize their community of interest, it is doubly difficult to make those in different industries feel a strong bond of union. The I. W. W. has faced this fact and, unlike the O. B. U., seeks to unite all who work in an industry in one international union having a large measure of control over its own affairs. Although it preaches the brotherhood of all workers as ardently as does the O. B. U., it recognizes that each industry has its own particular problems which can best be solved by workers in that industry, and considers that loyalty to one industry need in no way impair loyalty to the I. W. W. or to the working class as a whole. If the O. B. U. had adopted the same course it would not have lost the strongest group which had affiliated with it.