Earth radius

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Earth_radius

 

Earth radius
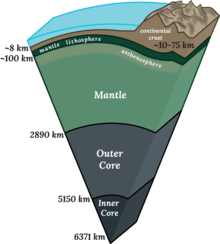Cross section of Earth's Interior
General information
Unit system	astronomy, geophysics
Unit of	distance
Symbol	R🜨, ${\displaystyle R_E}$, ${\displaystyle {\mathcal{R}}_{\mathrm{e}\mathrm{E}}^{\mathrm{N}}}$
Conversions
1 R🜨 in ...	... is equal to ...
SI base unit	6.3781×106 m
Metric system	6,357 to 6,378 km
English units	3,950 to 3,963 mi

Geodesy

Earth radius (denoted as R_🜨 or ${\displaystyle R_E}$) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) (equatorial radius, denoted a) to a minimum of nearly 6,357 km (3,950 mi) (polar radius, denoted b).

A nominal Earth radius is sometimes used as a unit of measurement in astronomy and geophysics, which is recommended by the International Astronomical Union to be the equatorial value.

A globally-average value is usually considered to be 6,371 kilometres (3,959 mi) with a 0.3% variability (±10 km) for the following reasons. The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the mean radius (R₁) of three radii measured at two equator points and a pole; the authalic radius, which is the radius of a sphere with the same surface area (R₂); and the volumetric radius, which is the radius of a sphere having the same volume as the ellipsoid (R₃). All three values are about 6,371 kilometres (3,959 mi).

Other ways to define and measure the Earth's radius involve the radius of curvature. A few definitions yield values outside the range between the polar radius and equatorial radius because they include local or geoidal topography or because they depend on abstract geometrical considerations.

Introduction

A scale diagram of the oblateness of the 2003 IERS reference ellipsoid, with north at the top. The light blue region is a circle. The outer edge of the dark blue line is an ellipse with the same minor axis as the circle and the same eccentricity as the Earth. The red line represents the Karman line 100 km (62 mi) above sea level, while the yellow area denotes the altitude range of the ISS in low Earth orbit.

Main articles: Figure of the Earth, Earth ellipsoid, and Reference ellipsoid

Earth's rotation, internal density variations, and external tidal forces cause its shape to deviate systematically from a perfect sphere. Local topography increases the variance, resulting in a surface of profound complexity. Our descriptions of Earth's surface must be simpler than reality in order to be tractable. Hence, we create models to approximate characteristics of Earth's surface, generally relying on the simplest model that suits the need.

Each of the models in common use involve some notion of the geometric radius. Strictly speaking, spheres are the only solids to have radii, but broader uses of the term radius are common in many fields, including those dealing with models of Earth. The following is a partial list of models of Earth's surface, ordered from exact to more approximate:

• The actual surface of Earth
• The geoid, defined by mean sea level at each point on the real surface
• A spheroid, also called an ellipsoid of revolution, geocentric to model the entire Earth, or else geodetic for regional work
• A sphere

In the case of the geoid and ellipsoids, the fixed distance from any point on the model to the specified center is called "a radius of the Earth" or "the radius of the Earth at that point". It is also common to refer to any mean radius of a spherical model as "the radius of the earth". When considering the Earth's real surface, on the other hand, it is uncommon to refer to a "radius", since there is generally no practical need. Rather, elevation above or below sea level is useful.

Regardless of the model, any radius falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (3,950 to 3,963 mi). Hence, the Earth deviates from a perfect sphere by only a third of a percent, which supports the spherical model in most contexts and justifies the term "radius of the Earth". While specific values differ, the concepts in this article generalize to any major planet.

Physics of Earth's deformation

Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by

${\displaystyle q=\frac{a^3{\omega }^2}{GM},}$

where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet. For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.

The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).

Not all deformations originate within the Earth. Gravitational attraction from the Moon or Sun can cause the Earth's surface at a given point to vary by tenths of a meter over a nearly 12-hour period (see Earth tide).

Radius and local conditions

Al-Biruni's (973 – c. 1050) method for calculation of the Earth's radius simplified measuring the circumference compared to taking measurements from two locations distant from each other.

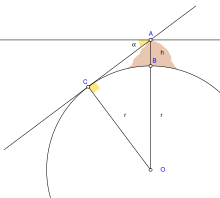
Given local and transient influences on surface height, the values defined below are based on a "general purpose" model, refined as globally precisely as possible within 5 m (16 ft) of reference ellipsoid height, and to within 100 m (330 ft) of mean sea level (neglecting geoid height).

Additionally, the radius can be estimated from the curvature of the Earth at a point. Like a torus, the curvature at a point will be greatest (tightest) in one direction (north–south on Earth) and smallest (flattest) perpendicularly (east–west). The corresponding radius of curvature depends on the location and direction of measurement from that point. A consequence is that a distance to the true horizon at the equator is slightly shorter in the north–south direction than in the east–west direction.

In summary, local variations in terrain prevent defining a single "precise" radius. One can only adopt an idealized model. Since the estimate by Eratosthenes, many models have been created. Historically, these models were based on regional topography, giving the best reference ellipsoid for the area under survey. As satellite remote sensing and especially the Global Positioning System gained importance, true global models were developed which, while not as accurate for regional work, best approximate the Earth as a whole.

Extrema: equatorial and polar radii

The following radii are derived from the World Geodetic System 1984 (WGS-84) reference ellipsoid. It is an idealized surface, and the Earth measurements used to calculate it have an uncertainty of ±2 m in both the equatorial and polar dimensions. Additional discrepancies caused by topographical variation at specific locations can be significant. When identifying the position of an observable location, the use of more precise values for WGS-84 radii may not yield a corresponding improvement in accuracy.

The value for the equatorial radius is defined to the nearest 0.1 m in WGS-84. The value for the polar radius in this section has been rounded to the nearest 0.1 m, which is expected to be adequate for most uses. Refer to the WGS-84 ellipsoid if a more precise value for its polar radius is needed.

• The Earth's equatorial radius a, or semi-major axis, is the distance from its center to the equator and equals 6,378.1370 km (3,963.1906 mi). The equatorial radius is often used to compare Earth with other planets.

• The Earth's polar radius b, or semi-minor axis, is the distance from its center to the North and South Poles, and equals 6,356.7523 km (3,949.9028 mi).

Location-dependent radii

Three different radii as a function of Earth's latitude. R is the geocentric radius; M is the meridional radius of curvature; and N is the prime vertical radius of curvature.

Geocentric radius

Not to be confused with Geocentric distance.

The geocentric radius is the distance from the Earth's center to a point on the spheroid surface at geodetic latitude φ:

${\displaystyle R(\phi )=\sqrt{\frac{(a^2\cos \phi {)}^2+(b^2\sin \phi {)}^2}{(a\cos \phi {)}^2+(b\sin \phi {)}^2}}}$

where a and b are, respectively, the equatorial radius and the polar radius.

The extrema geocentric radii on the ellipsoid coincide with the equatorial and polar radii. They are vertices of the ellipse and also coincide with minimum and maximum radius of curvature.

Radii of curvature

See also: Spheroid § Curvature

Principal radii of curvature

There are two principal radii of curvature: along the meridional and prime-vertical normal sections.

Meridional

In particular, the Earth's meridional radius of curvature (in the north–south direction) at φ is:

${\displaystyle M(\phi )=\frac{(ab{)}^2}{((a\cos \phi {)}^2+(b\sin \phi {)}^2{)}^{\frac{3}{2}}}=\frac{a(1-e^2)}{(1-e^2{\sin }^2\phi {)}^{\frac{3}{2}}}=\frac{1-e^2}{a^2}N(\phi {)}^3.}$

where ${\displaystyle e}$ is the eccentricity of the earth. This is the radius that Eratosthenes measured in his arc measurement.

Prime vertical

The length PQ, called the prime vertical radius, is ${\displaystyle N(\varphi )}$. The length IQ is equal to ${\displaystyle e^{2}N(\varphi )}$. ${\displaystyle R=(X,Y,Z)}$.

If one point had appeared due east of the other, one finds the approximate curvature in the east–west direction.

This Earth's prime-vertical radius of curvature, also called the Earth's transverse radius of curvature, is defined perpendicular (orthogonal) to M at geodetic latitude φ and is:

${\displaystyle N(\phi )=\frac{a^2}{\sqrt{(a\cos \phi {)}^2+(b\sin \phi {)}^2}}=\frac{a}{\sqrt{1-e^2{\sin }^2\phi }}.}$

N can also be interpreted geometrically as the normal distance from the ellipsoid surface to the polar axis. The radius of a parallel of latitude is given by ${\displaystyle p=N\cos (\phi )}$.

Polar and equatorial radius of curvature

The Earth's meridional radius of curvature at the equator equals the meridian's semi-latus rectum:

b²/a = 6,335.439 km

The Earth's prime-vertical radius of curvature at the equator equals the equatorial radius, N = a.

The Earth's polar radius of curvature (either meridional or prime-vertical) is:

a²/b = 6,399.594 km

Extended content

Combined radii of curvature

Azimuthal

The Earth's azimuthal radius of curvature, along an Earth normal section at an azimuth (measured clockwise from north) α and at latitude φ, is derived from Euler's curvature formula as follows:

${\displaystyle R_{\mathrm{c}}=\frac{1}{{\displaystyle \frac{{\cos }^2\alpha }{M}}+{\displaystyle \frac{{\sin }^2\alpha }{N}}}.}$

Non-directional

It is possible to combine the principal radii of curvature above in a non-directional manner.

The Earth's Gaussian radius of curvature at latitude φ is:

${\displaystyle R_{\mathrm{a}}(\phi )=\frac{1}{\sqrt{K}}=\frac{1}{2\pi }{\int }_0^{2\pi }{R}_{\mathrm{c}}(\alpha )d\alpha =\sqrt{MN}=\frac{a^{2}b}{(a\cos \phi {)}^2+(b\sin \phi {)}^2}=\frac{a\sqrt{1-e^2}}{1-e^2{\sin }^2\phi }.}$

Where K is the Gaussian curvature, ${\displaystyle K={\kappa }_1{\kappa }_2=\frac{detB}{detA}}$.

The Earth's mean radius of curvature at latitude φ is:

${\displaystyle R_{\mathrm{m}}=\frac{2}{{\displaystyle \frac{1}{M}}+{\displaystyle \frac{1}{N}}}}$

Global radii

The Earth can be modeled as a sphere in many ways. This section describes the common ways. The various radii derived here use the notation and dimensions noted above for the Earth as derived from the WGS-84 ellipsoid; namely,

Equatorial radius: a = (6378.1370 km)

Polar radius: b = (6356.7523 km)

A sphere being a gross approximation of the spheroid, which itself is an approximation of the geoid, units are given here in kilometers rather than the millimeter resolution appropriate for geodesy.

Nominal radius

In astronomy, the International Astronomical Union denotes the nominal equatorial Earth radius as ${\displaystyle {\mathcal{R}}_{\mathrm{e}\mathrm{E}}^{\mathrm{N}}}$, which is defined to be 6,378.1 km (3,963.2 mi). The nominal polar Earth radius is defined as ${\displaystyle {\mathcal{R}}_{\mathrm{p}\mathrm{E}}^{\mathrm{N}}}$ = 6,356.8 km (3,949.9 mi). These values correspond to the zero Earth tide convention. Equatorial radius is conventionally used as the nominal value unless the polar radius is explicitly required. The nominal radius serves as a unit of length for astronomy. (The notation is defined such that it can be easily generalized for other planets; e.g., ${\displaystyle {\mathcal{R}}_{\mathrm{p}\mathrm{J}}^{\mathrm{N}}}$ for the nominal polar Jupiter radius.)

Arithmetic mean radius

Equatorial (a), polar (b) and arithmetic mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale)

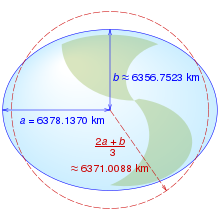
In geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the Earth's arithmetic mean radius (denoted R₁) to be

${\displaystyle R_1=\frac{2a+b}{3}}$

The factor of two accounts for the biaxial symmetry in Earth's spheroid, a specialization of triaxial ellipsoid. For Earth, the arithmetic mean radius is 6,371.0088 km (3,958.7613 mi).

Authalic radius

See also: Authalic latitude

Earth's authalic radius (meaning "equal area") is the radius of a hypothetical perfect sphere that has the same surface area as the reference ellipsoid. The IUGG denotes the authalic radius as R₂. A closed-form solution exists for a spheroid:

${\displaystyle R_2=\sqrt{\frac{a^2+\frac{b^2}{e}\ln \left(\frac{1+e}{b/a}\right)}{2}}=\sqrt{\frac{a^2}{2}+\frac{b^2}{2}\frac{{\tanh }^{-1}e}{e}}=\sqrt{\frac{A}{4\pi }},}$

where e² = a² − b²/a² and A is the surface area of the spheroid.

For the Earth, the authalic radius is 6,371.0072 km (3,958.7603 mi).

The authalic radius ${\displaystyle R_2}$ also corresponds to the radius of (global) mean curvature, obtained by averaging the Gaussian curvature, ${\displaystyle K}$, over the surface of the ellipsoid. Using the Gauss–Bonnet theorem, this gives

${\displaystyle \frac{\int KdA}{A}=\frac{4\pi }{A}=\frac{1}{R_2^2}.}$

Volumetric radius

Another spherical model is defined by the Earth's volumetric radius, which is the radius of a sphere of volume equal to the ellipsoid. The IUGG denotes the volumetric radius as R₃.

${\displaystyle R_3=\sqrt[3]{a^{2}b}.}$

For Earth, the volumetric radius equals 6,371.0008 km (3,958.7564 mi).

Rectifying radius

See also: Quarter meridian and Rectifying latitude

Another global radius is the Earth's rectifying radius, giving a sphere with circumference equal to the perimeter of the ellipse described by any polar cross section of the ellipsoid. This requires an elliptic integral to find, given the polar and equatorial radii:

${\displaystyle M_{\mathrm{r}}=\frac{2}{\pi }{\int }_0^{\frac{\pi }{2}}\sqrt{a^2{\cos }^2\phi +b^2{\sin }^2\phi }d\phi .}$

The rectifying radius is equivalent to the meridional mean, which is defined as the average value of M:

${\displaystyle M_{\mathrm{r}}=\frac{2}{\pi }{\int }_0^{\frac{\pi }{2}}M(\phi )d\phi .}$

For integration limits of [0,π/2], the integrals for rectifying radius and mean radius evaluate to the same result, which, for Earth, amounts to 6,367.4491 km (3,956.5494 mi).

The meridional mean is well approximated by the semicubic mean of the two axes,

${\displaystyle M_{\mathrm{r}}\approx {\left(\frac{a^{\frac{3}{2}}+b^{\frac{3}{2}}}{2}\right)}^{\frac{2}{3}},}$

which differs from the exact result by less than 1 μm (4×10⁻⁵ in); the mean of the two axes,

${\displaystyle M_{\mathrm{r}}\approx \frac{a+b}{2},}$

about 6,367.445 km (3,956.547 mi), can also be used.

Topographical radii

See also: Earth § Size and shape

The mathematical expressions above apply over the surface of the ellipsoid. The cases below considers Earth's topography, above or below a reference ellipsoid. As such, they are topographical geocentric distances, R_t, which depends not only on latitude.

Topographical extremes

• Maximum R_t: the summit of Chimborazo is 6,384.4 km (3,967.1 mi) from the Earth's center.
• Minimum R_t: the floor of the Arctic Ocean is 6,352.8 km (3,947.4 mi) from the Earth's center.

Topographical global mean

The topographical mean geocentric distance averages elevations everywhere, resulting in a value 230 m larger than the IUGG mean radius, the authalic radius, or the volumetric radius. This topographical average is 6,371.230 km (3,958.899 mi) with uncertainty of 10 m (33 ft).

Derived quantities: diameter, circumference, arc-length, area, volume

Earth's diameter is simply twice Earth's radius; for example, equatorial diameter (2a) and polar diameter (2b). For the WGS84 ellipsoid, that's respectively:

• 2a = 12,756.2740 km (7,926.3812 mi),
• 2b = 12,713.5046 km (7,899.8055 mi).

Earth's circumference equals the perimeter length. The equatorial circumference is simply the circle perimeter: C_e=2πa, in terms of the equatorial radius, a. The polar circumference equals C_p=4m_p, four times the quarter meridian m_p=aE(e), where the polar radius b enters via the eccentricity, e=(1−b²/a²)^0.5; see Ellipse#Circumference for details.

Arc length of more general surface curves, such as meridian arcs and geodesics, can also be derived from Earth's equatorial and polar radii.

Likewise for surface area, either based on a map projection or a geodesic polygon.

Earth's volume, or that of the reference ellipsoid, is V = 4/3πa²b. Using the parameters from WGS84 ellipsoid of revolution, a = 6,378.137 km and b = 6356.7523142 km, V = 1.08321×10¹² km³ (2.5988×10¹¹ cu mi).

History

Main article: History of geodesy

The first published reference to the Earth's size appeared around 350 BC, when Aristotle reported in his book On the Heavens that mathematicians had guessed the circumference of the Earth to be 400,000 stadia. Scholars have interpreted Aristotle's figure to be anywhere from highly accurate to almost double the true value. The first known scientific measurement and calculation of the circumference of the Earth was performed by Eratosthenes in about 240 BC. Estimates of the accuracy of Eratosthenes's measurement range from 0.5% to 17%. For both Aristotle and Eratosthenes, uncertainty in the accuracy of their estimates is due to modern uncertainty over which stadion length they meant.

Around 100 BC, Posidonius of Apamea recomputed Earth's radius, and found it to be close to that by Eratosthenes, but later Strabo incorrectly attributed him a value about 3/4 of the actual size. Claudius Ptolemy around 150 AD gave empirical evidence supporting a spherical Earth, but he accepted the lesser value attributed to Posidonius. His highly influential work, the Almagest, left no doubt among medieval scholars that Earth is spherical, but they were wrong about its size.

By 1490, Christopher Columbus believed that traveling 3,000 miles west from the west coast of the Iberian peninsula would let him reach the eastern coasts of Asia. However, the 1492 enactment of that voyage brought his fleet to the Americas. The Magellan expedition (1519–1522), which was the first circumnavigation of the World, soundly demonstrated the sphericity of the Earth, and affirmed the original measurement of 40,000 km (25,000 mi) by Eratosthenes.

Around 1690, Isaac Newton and Christiaan Huygens argued that Earth was closer to an oblate spheroid than to a sphere. However, around 1730, Jacques Cassini argued for a prolate spheroid instead, due to different interpretations of the Newtonian mechanics involved. To settle the matter, the French Geodesic Mission (1735–1739) measured one degree of latitude at two locations, one near the Arctic Circle and the other near the equator. The expedition found that Newton's conjecture was correct: the Earth is flattened at the poles due to rotation's centrifugal force.

Catalysis

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Catalysis

A range of industrial catalysts in pellet form

An air filter that uses a low-temperature oxidation catalyst to convert carbon monoxide to less toxic carbon dioxide at room temperature. It can also remove formaldehyde from the air.

Catalysis (/kəˈtæləsɪs/) is the process of change in rate of a chemical reaction by adding a substance known as a catalyst (/ˈkætəlɪst/). Catalysts are not consumed by the reaction and remain unchanged after it. If the reaction is rapid and the catalyst recycles quickly, very small amounts of catalyst often suffice; mixing, surface area, and temperature are important factors in reaction rate. Catalysts generally react with one or more reactants to form intermediates that subsequently give the final reaction product, in the process of regenerating the catalyst.

Catalysis may be classified as either homogeneous, whose components are dispersed in the same phase (usually gaseous or liquid) as the reactant, or heterogeneous, whose components are not in the same phase. Enzymes and other biocatalysts are often considered as a third category.

Catalysis is ubiquitous in chemical industry of all kinds. Estimates are that 90% of all commercially produced chemical products involve catalysts at some stage in the process of their manufacture.

The term "catalyst" is derived from Greek καταλύειν, kataluein, meaning "loosen" or "untie". The concept of catalysis was invented by chemist Elizabeth Fulhame, based on her novel work in oxidation-reduction experiments.

General principles

Example

An illustrative example is the effect of catalysts to speed the decomposition of hydrogen peroxide into water and oxygen:

2 H₂O₂ → 2 H₂O + O₂

This reaction proceeds because the reaction products are more stable than the starting compound, but this decomposition is so slow that hydrogen peroxide solutions are commercially available. In the presence of a catalyst such as manganese dioxide this reaction proceeds much more rapidly. This effect is readily seen by the effervescence of oxygen. The catalyst is not consumed in the reaction, and may be recovered unchanged and re-used indefinitely. Accordingly, manganese dioxide is said to catalyze this reaction. In living organisms, this reaction is catalyzed by enzymes (proteins that serve as catalysts) such as catalase.

Units

The SI derived unit for measuring the catalytic activity of a catalyst is the katal, which is quantified in moles per second. The productivity of a catalyst can be described by the turnover number (or TON) and the catalytic activity by the turn over frequency (TOF), which is the TON per time unit. The biochemical equivalent is the enzyme unit. For more information on the efficiency of enzymatic catalysis, see the article on enzymes.

Catalytic reaction mechanisms

Main article: catalytic cycle

In general, chemical reactions occur faster in the presence of a catalyst because the catalyst provides an alternative reaction mechanism (reaction pathway) having a lower activation energy than the non-catalyzed mechanism. In catalyzed mechanisms, the catalyst usually reacts to form an intermediate, which then regenerates the original catalyst in the process.

As a simple example occurring in the gas phase, the reaction 2 SO₂ + O₂ → 2 SO₃ can be catalyzed by adding nitric oxide. The reaction occurs in two steps:

2 NO + O₂ → 2 NO₂ (rate-determining)

NO₂ + SO₂ → NO + SO₃ (fast)

The NO catalyst is regenerated. The overall rate is the rate of the slow step

v = 2k₁[NO]²[O₂].

An example of heterogeneous catalysis is the reaction of oxygen and hydrogen on the surface of titanium dioxide (TiO₂, or titania) to produce water. Scanning tunneling microscopy showed that the molecules undergo adsorption and dissociation. The dissociated, surface-bound O and H atoms diffuse together. The intermediate reaction states are: HO₂, H₂O₂, then H₃O₂ and the reaction product (water molecule dimers), after which the water molecule desorbs from the catalyst surface.

Reaction energetics

Generic potential energy diagram showing the effect of a catalyst in a hypothetical exothermic chemical reaction X + Y to give Z. The presence of the catalyst opens a different reaction pathway (shown in red) with lower activation energy. The final result and the overall thermodynamics are the same.

Catalysts enable pathways that differ from the uncatalyzed reactions. These pathways have lower activation energy. Consequently, more molecular collisions have the energy needed to reach the transition state. Hence, catalysts can enable reactions that would otherwise be blocked or slowed by a kinetic barrier. The catalyst may increase the reaction rate or selectivity, or enable the reaction at lower temperatures. This effect can be illustrated with an energy profile diagram.

In the catalyzed elementary reaction, catalysts do not change the extent of a reaction: they have no effect on the chemical equilibrium of a reaction. The ratio of the forward and the reverse reaction rates is unaffected (see also thermodynamics). The second law of thermodynamics describes why a catalyst does not change the chemical equilibrium of a reaction. Suppose there was such a catalyst that shifted an equilibrium. Introducing the catalyst to the system would result in a reaction to move to the new equilibrium, producing energy. Production of energy is a necessary result since reactions are spontaneous only if Gibbs free energy is produced, and if there is no energy barrier, there is no need for a catalyst. Then, removing the catalyst would also result in a reaction, producing energy; i.e. the addition and its reverse process, removal, would both produce energy. Thus, a catalyst that could change the equilibrium would be a perpetual motion machine, a contradiction to the laws of thermodynamics. Thus, catalysts do not alter the equilibrium constant. (A catalyst can however change the equilibrium concentrations by reacting in a subsequent step. It is then consumed as the reaction proceeds, and thus it is also a reactant. Illustrative is the base-catalyzed hydrolysis of esters, where the produced carboxylic acid immediately reacts with the base catalyst and thus the reaction equilibrium is shifted towards hydrolysis.)

The catalyst stabilizes the transition state more than it stabilizes the starting material. It decreases the kinetic barrier by decreasing the difference in energy between starting material and the transition state. It does not change the energy difference between starting materials and products (thermodynamic barrier), or the available energy (this is provided by the environment as heat or light).

Related concepts

Some so-called catalysts are really precatalysts. Precatalysts convert to catalysts in the reaction. For example, Wilkinson's catalyst RhCl(PPh₃)₃ loses one triphenylphosphine ligand before entering the true catalytic cycle. Precatalysts are easier to store but are easily activated in situ. Because of this preactivation step, many catalytic reactions involve an induction period.

In cooperative catalysis, chemical species that improve catalytic activity are called cocatalysts or promoters.

In tandem catalysis two or more different catalysts are coupled in a one-pot reaction.

In autocatalysis, the catalyst is a product of the overall reaction, in contrast to all other types of catalysis considered in this article. The simplest example of autocatalysis is a reaction of type A + B → 2 B, in one or in several steps. The overall reaction is just A → B, so that B is a product. But since B is also a reactant, it may be present in the rate equation and affect the reaction rate. As the reaction proceeds, the concentration of B increases and can accelerate the reaction as a catalyst. In effect, the reaction accelerates itself or is autocatalyzed. An example is the hydrolysis of an ester such as aspirin to a carboxylic acid and an alcohol. In the absence of added acid catalysts, the carboxylic acid product catalyzes the hydrolysis.

A true catalyst can work in tandem with a sacrificial catalyst. The true catalyst is consumed in the elementary reaction and turned into a deactivated form. The sacrificial catalyst regenerates the true catalyst for another cycle. The sacrificial catalyst is consumed in the reaction, and as such, it is not really a catalyst, but a reagent. For example, osmium tetroxide (OsO₄) is a good reagent for dihydroxylation, but it is highly toxic and expensive. In Upjohn dihydroxylation, the sacrificial catalyst N-methylmorpholine N-oxide (NMMO) regenerates OsO₄, and only catalytic quantities of OsO₄ are needed.

Classification

Catalysis may be classified as either homogeneous or heterogeneous. A homogeneous catalysis is one whose components are dispersed in the same phase (usually gaseous or liquid) as the reactant's molecules. A heterogeneous catalysis is one where the reaction components are not in the same phase. Enzymes and other biocatalysts are often considered as a third category. Similar mechanistic principles apply to heterogeneous, homogeneous, and biocatalysis.

Heterogeneous catalysis

Main article: Heterogeneous catalysis

The microporous molecular structure of the zeolite ZSM-5 is exploited in catalysts used in refineries

Zeolites are extruded as pellets for easy handling in catalytic reactors.

Heterogeneous catalysts act in a different phase than the reactants. Most heterogeneous catalysts are solids that act on substrates in a liquid or gaseous reaction mixture. Important heterogeneous catalysts include zeolites, alumina, higher-order oxides, graphitic carbon, transition metal oxides, metals such as Raney nickel for hydrogenation, and vanadium(V) oxide for oxidation of sulfur dioxide into sulfur trioxide by the contact process.

Diverse mechanisms for reactions on surfaces are known, depending on how the adsorption takes place (Langmuir-Hinshelwood, Eley-Rideal, and Mars-van Krevelen). The total surface area of a solid has an important effect on the reaction rate. The smaller the catalyst particle size, the larger the surface area for a given mass of particles.

A heterogeneous catalyst has active sites, which are the atoms or crystal faces where the reaction actually occurs. Depending on the mechanism, the active site may be either a planar exposed metal surface, a crystal edge with imperfect metal valence, or a complicated combination of the two. Thus, not only most of the volume but also most of the surface of a heterogeneous catalyst may be catalytically inactive. Finding out the nature of the active site requires technically challenging research. Thus, empirical research for finding out new metal combinations for catalysis continues.

For example, in the Haber process, finely divided iron serves as a catalyst for the synthesis of ammonia from nitrogen and hydrogen. The reacting gases adsorb onto active sites on the iron particles. Once physically adsorbed, the reagents undergo chemisorption that results in dissociation into adsorbed atomic species, and new bonds between the resulting fragments form in part due to their closeness. In this way the particularly strong triple bond in nitrogen is broken, which would be extremely uncommon in the gas phase due to its high activation energy. Thus, the activation energy of the overall reaction is lowered, and the rate of reaction increases. Another place where a heterogeneous catalyst is applied is in the oxidation of sulfur dioxide on vanadium(V) oxide for the production of sulfuric acid.

Heterogeneous catalysts are typically "supported," which means that the catalyst is dispersed on a second material that enhances the effectiveness or minimizes its cost. Supports prevent or minimize agglomeration and sintering of small catalyst particles, exposing more surface area, thus catalysts have a higher specific activity (per gram) on support. Sometimes the support is merely a surface on which the catalyst is spread to increase the surface area. More often, the support and the catalyst interact, affecting the catalytic reaction. Supports can also be used in nanoparticle synthesis by providing sites for individual molecules of catalyst to chemically bind. Supports are porous materials with a high surface area, most commonly alumina, zeolites or various kinds of activated carbon. Specialized supports include silicon dioxide, titanium dioxide, calcium carbonate, and barium sulfate.

In slurry reactions, heterogeneous catalysts can be lost by dissolving.

Many heterogeneous catalysts are in fact nanomaterials. Nanomaterial-based catalysts with enzyme-mimicking activities are collectively called as nanozymes.

Electrocatalysts

Main article: Electrocatalyst

In the context of electrochemistry, specifically in fuel cell engineering, various metal-containing catalysts are used to enhance the rates of the half reactions that comprise the fuel cell. One common type of fuel cell electrocatalyst is based upon nanoparticles of platinum that are supported on slightly larger carbon particles. When in contact with one of the electrodes in a fuel cell, this platinum increases the rate of oxygen reduction either to water or to hydroxide or hydrogen peroxide.

Homogeneous catalysis

Main article: Homogeneous catalysis

Homogeneous catalysts function in the same phase as the reactants. Typically homogeneous catalysts are dissolved in a solvent with the substrates. One example of homogeneous catalysis involves the influence of H⁺ on the esterification of carboxylic acids, such as the formation of methyl acetate from acetic acid and methanol. High-volume processes requiring a homogeneous catalyst include hydroformylation, hydrosilylation, hydrocyanation. For inorganic chemists, homogeneous catalysis is often synonymous with organometallic catalysts. Many homogeneous catalysts are however not organometallic, illustrated by the use of cobalt salts that catalyze the oxidation of p-xylene to terephthalic acid.

Organocatalysis

Main article: Organocatalysis

Whereas transition metals sometimes attract most of the attention in the study of catalysis, small organic molecules without metals can also exhibit catalytic properties, as is apparent from the fact that many enzymes lack transition metals. Typically, organic catalysts require a higher loading (amount of catalyst per unit amount of reactant, expressed in mol% amount of substance) than transition metal(-ion)-based catalysts, but these catalysts are usually commercially available in bulk, helping to lower costs. In the early 2000s, these organocatalysts were considered "new generation" and are competitive to traditional metal(-ion)-containing catalysts. Organocatalysts are supposed to operate akin to metal-free enzymes utilizing, e.g., non-covalent interactions such as hydrogen bonding. The discipline organocatalysis is divided into the application of covalent (e.g., proline, DMAP) and non-covalent (e.g., thiourea organocatalysis) organocatalysts referring to the preferred catalyst-substrate binding and interaction, respectively. The Nobel Prize in Chemistry 2021 was awarded jointly to Benjamin List and David W.C. MacMillan "for the development of asymmetric organocatalysis."

Photocatalysts

Main article: Photocatalysis

Photocatalysis is the phenomenon where the catalyst can receive light to generate an excited state that effect redox reactions. Singlet oxygen is usually produced by photocatalysis. Photocatalysts are components of dye-sensitized solar cells.

Enzymes and biocatalysts

Main article: enzyme catalysis

In biology, enzymes are protein-based catalysts in metabolism and catabolism. Most biocatalysts are enzymes, but other non-protein-based classes of biomolecules also exhibit catalytic properties including ribozymes, and synthetic deoxyribozymes.

Biocatalysts can be thought of as an intermediate between homogeneous and heterogeneous catalysts, although strictly speaking soluble enzymes are homogeneous catalysts and membrane-bound enzymes are heterogeneous. Several factors affect the activity of enzymes (and other catalysts) including temperature, pH, the concentration of enzymes, substrate, and products. A particularly important reagent in enzymatic reactions is water, which is the product of many bond-forming reactions and a reactant in many bond-breaking processes.

In biocatalysis, enzymes are employed to prepare many commodity chemicals including high-fructose corn syrup and acrylamide.

Some monoclonal antibodies whose binding target is a stable molecule that resembles the transition state of a chemical reaction can function as weak catalysts for that chemical reaction by lowering its activation energy. Such catalytic antibodies are sometimes called "abzymes".

Significance

Left: Partially caramelized cube sugar, Right: burning cube sugar with ash as catalyst

Estimates are that 90% of all commercially produced chemical products involve catalysts at some stage in the process of their manufacture. In 2005, catalytic processes generated about $900 billion in products worldwide. Catalysis is so pervasive that subareas are not readily classified. Some areas of particular concentration are surveyed below.

Energy processing

Petroleum refining makes intensive use of catalysis for alkylation, catalytic cracking (breaking long-chain hydrocarbons into smaller pieces), naphtha reforming and steam reforming (conversion of hydrocarbons into synthesis gas). Even the exhaust from the burning of fossil fuels is treated via catalysis: Catalytic converters, typically composed of platinum and rhodium, break down some of the more harmful byproducts of automobile exhaust.

2 CO + 2 NO → 2 CO₂ + N₂

With regard to synthetic fuels, an old but still important process is the Fischer-Tropsch synthesis of hydrocarbons from synthesis gas, which itself is processed via water-gas shift reactions, catalyzed by iron. The Sabatier reaction produces methane from carbon dioxide and hydrogen. Biodiesel and related biofuels require processing via both inorganic and biocatalysts.

Fuel cells rely on catalysts for both the anodic and cathodic reactions.

Catalytic heaters generate flameless heat from a supply of combustible fuel.

Bulk chemicals

Typical vanadium pentoxide catalyst used in sulfuric acid production for an intermediate reaction to convert sulfur dioxide to sulfur trioxide.

Some of the largest-scale chemicals are produced via catalytic oxidation, often using oxygen. Examples include nitric acid (from ammonia), sulfuric acid (from sulfur dioxide to sulfur trioxide by the contact process), terephthalic acid from p-xylene, acrylic acid from propylene or propane and acrylonitrile from propane and ammonia.

The production of ammonia is one of the largest-scale and most energy-intensive processes. In the Haber process nitrogen is combined with hydrogen over an iron oxide catalyst. Methanol is prepared from carbon monoxide or carbon dioxide but using copper-zinc catalysts.

Bulk polymers derived from ethylene and propylene are often prepared via Ziegler-Natta catalysis. Polyesters, polyamides, and isocyanates are derived via acid-base catalysis.

Most carbonylation processes require metal catalysts, examples include the Monsanto acetic acid process and hydroformylation.

Fine chemicals

Many fine chemicals are prepared via catalysis; methods include those of heavy industry as well as more specialized processes that would be prohibitively expensive on a large scale. Examples include the Heck reaction, and Friedel–Crafts reactions. Because most bioactive compounds are chiral, many pharmaceuticals are produced by enantioselective catalysis (catalytic asymmetric synthesis). (R)-1,2-Propandiol, the precursor to the antibacterial levofloxacin, can be synthesized efficiently from hydroxyacetone by using catalysts based on BINAP-ruthenium complexes, in Noyori asymmetric hydrogenation:

Food processing

One of the most obvious applications of catalysis is the hydrogenation (reaction with hydrogen gas) of fats using nickel catalyst to produce margarine. Many other foodstuffs are prepared via biocatalysis (see below).

Environment

Catalysis affects the environment by increasing the efficiency of industrial processes, but catalysis also plays a direct role in the environment. A notable example is the catalytic role of chlorine free radicals in the breakdown of ozone. These radicals are formed by the action of ultraviolet radiation on chlorofluorocarbons (CFCs).

Cl^· + O₃ → ClO^· + O₂

ClO^· + O^· → Cl^· + O₂

History

The term "catalyst", broadly defined as anything that increases the rate of a process, is derived from Greek καταλύειν, meaning "to annul," or "to untie," or "to pick up". The concept of catalysis was invented by chemist Elizabeth Fulhame and described in a 1794 book, based on her novel work in oxidation–reduction reactions. The first chemical reaction in organic chemistry that knowingly used a catalyst was studied in 1811 by Gottlieb Kirchhoff, who discovered the acid-catalyzed conversion of starch to glucose. The term catalysis was later used by Jöns Jakob Berzelius in 1835 to describe reactions that are accelerated by substances that remain unchanged after the reaction. Fulhame, who predated Berzelius, did work with water as opposed to metals in her reduction experiments. Other 18th century chemists who worked in catalysis were Eilhard Mitscherlich who referred to it as contact processes, and Johann Wolfgang Döbereiner who spoke of contact action. He developed Döbereiner's lamp, a lighter based on hydrogen and a platinum sponge, which became a commercial success in the 1820s that lives on today. Humphry Davy discovered the use of platinum in catalysis. In the 1880s, Wilhelm Ostwald at Leipzig University started a systematic investigation into reactions that were catalyzed by the presence of acids and bases, and found that chemical reactions occur at finite rates and that these rates can be used to determine the strengths of acids and bases. For this work, Ostwald was awarded the 1909 Nobel Prize in Chemistry. Vladimir Ipatieff performed some of the earliest industrial scale reactions, including the discovery and commercialization of oligomerization and the development of catalysts for hydrogenation.

Inhibitors, poisons, and promoters

An added substance that lowers the rate is called a reaction inhibitor if reversible and catalyst poisons if irreversible. Promoters are substances that increase the catalytic activity, even though they are not catalysts by themselves.

Inhibitors are sometimes referred to as "negative catalysts" since they decrease the reaction rate. However the term inhibitor is preferred since they do not work by introducing a reaction path with higher activation energy; this would not lower the rate since the reaction would continue to occur by the non-catalyzed path. Instead, they act either by deactivating catalysts or by removing reaction intermediates such as free radicals. In heterogeneous catalysis, coking inhibits the catalyst, which becomes covered by polymeric side products.

The inhibitor may modify selectivity in addition to rate. For instance, in the hydrogenation of alkynes to alkenes, a palladium (Pd) catalyst partly "poisoned" with lead(II) acetate (Pb(CH₃CO₂)₂) can be used. Without the deactivation of the catalyst, the alkene produced would be further hydrogenated to alkane.

The inhibitor can produce this effect by, e.g., selectively poisoning only certain types of active sites. Another mechanism is the modification of surface geometry. For instance, in hydrogenation operations, large planes of metal surface function as sites of hydrogenolysis catalysis while sites catalyzing hydrogenation of unsaturates are smaller. Thus, a poison that covers the surface randomly will tend to lower the number of uncontaminated large planes but leave proportionally smaller sites free, thus changing the hydrogenation vs. hydrogenolysis selectivity. Many other mechanisms are also possible.

Promoters can cover up the surface to prevent the production of a mat of coke, or even actively remove such material (e.g., rhenium on platinum in platforming). They can aid the dispersion of the catalytic material or bind to reagents.