Temperature

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Temperature

 

Temperature
Thermal vibration of a segment of protein alpha helix. Its amplitude increases with temperature
Common symbols	T
SI unit	K
Other units	°C, °F, °R, °Rø, °Ré, °N, °D, °L, °W
Intensive?	Yes
Derivations from other quantities	${\displaystyle \frac{pV}{nR}}$, ${\displaystyle \frac{d{q}_{\text{rev}}}{dS}}$
Dimension	${\displaystyle \mathsf{\Theta }}$

Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer.

Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called centigrade), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI).

Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature.

Temperature is important in all fields of natural science, including physics, chemistry, Earth science, astronomy, medicine, biology, ecology, material science, metallurgy, mechanical engineering and geography as well as most aspects of daily life.

Effects

Average daily variation in human body temperature

Many physical processes are related to temperature; some of them are given below:

• the physical properties of materials including the phase (solid, liquid, gaseous or plasma), density, solubility, vapor pressure, electrical conductivity, hardness, wear resistance, thermal conductivity, corrosion resistance, strength
• the rate and extent to which chemical reactions occur
• the amount and properties of thermal radiation emitted from the surface of an object
• air temperature affects all living organisms
• the speed of sound, which in a gas is proportional to the square root of the absolute temperature

Scales

Main article: Scale of temperature

Two thermometers showing temperature in Celsius and Fahrenheit

Temperature scales need two values for definition: the point chosen as zero degrees and the magnitudes of the incremental unit of temperature.

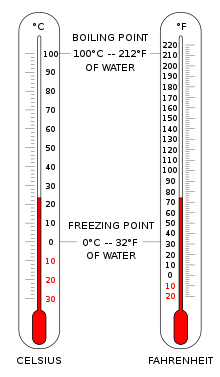
The Celsius scale (°C) is used for common temperature measurements in most of the world. It is an empirical scale that developed historically, which led to its zero point 0 °C being defined as the freezing point of water, and 100 °C as the boiling point of water, both at atmospheric pressure at sea level. It was called a centigrade scale because of the 100-degree interval. Since the standardization of the kelvin in the International System of Units, it has subsequently been redefined in terms of the equivalent fixing points on the Kelvin scale, so that a temperature increment of one degree Celsius is the same as an increment of one kelvin, though numerically the scales differ by an exact offset of 273.15.

The Fahrenheit scale is in common use in the United States. Water freezes at 32 °F and boils at 212 °F at sea-level atmospheric pressure.

Absolute zero

At the absolute zero of temperature, no energy can be removed from matter as heat, a fact expressed in the third law of thermodynamics. At this temperature, matter contains no macroscopic thermal energy, but still has quantum-mechanical zero-point energy as predicted by the uncertainty principle, although this does not enter into the definition of absolute temperature. Experimentally, absolute zero can be approached only very closely; it can never be reached (the lowest temperature attained by experiment is 38 pK). Theoretically, in a body at a temperature of absolute zero, all classical motion of its particles has ceased and they are at complete rest in this classical sense. The absolute zero, defined as 0 K, is exactly equal to −273.15 °C, or −459.67 °F.

Absolute scales

Referring to the Boltzmann constant, to the Maxwell–Boltzmann distribution, and to the Boltzmann statistical mechanical definition of entropy, as distinct from the Gibbs definition, for independently moving microscopic particles, disregarding interparticle potential energy, by international agreement, a temperature scale is defined and said to be absolute because it is independent of the characteristics of particular thermometric substances and thermometer mechanisms. Apart from the absolute zero, it does not have a reference temperature. It is known as the Kelvin scale, widely used in science and technology. The kelvin (the unit name is spelled with a lower-case 'k') is the unit of temperature in the International System of Units (SI). The temperature of a body in a state of thermodynamic equilibrium is always positive relative to the absolute zero.

Besides the internationally agreed Kelvin scale, there is also a thermodynamic temperature scale, invented by Lord Kelvin, also with its numerical zero at the absolute zero of temperature, but directly relating to purely macroscopic thermodynamic concepts, including the macroscopic entropy, though microscopically referable to the Gibbs statistical mechanical definition of entropy for the canonical ensemble, that takes interparticle potential energy into account, as well as independent particle motion so that it can account for measurements of temperatures near absolute zero. This scale has a reference temperature at the triple point of water, the numerical value of which is defined by measurements using the aforementioned internationally agreed Kelvin scale.

Kelvin scale

Many scientific measurements use the Kelvin temperature scale (unit symbol: K), named in honor of the physicist who first defined it. It is an absolute scale. Its numerical zero point, 0 K, is at the absolute zero of temperature. Since May, 2019, the kelvin has been defined through particle kinetic theory, and statistical mechanics. In the International System of Units (SI), the magnitude of the kelvin is defined in terms of the Boltzmann constant, the value of which is defined as fixed by international convention.

Statistical mechanical versus thermodynamic temperature scales

Since May 2019, the magnitude of the kelvin is defined in relation to microscopic phenomena, characterized in terms of statistical mechanics. Previously, but since 1954, the International System of Units defined a scale and unit for the kelvin as a thermodynamic temperature, by using the reliably reproducible temperature of the triple point of water as a second reference point, the first reference point being 0 K at absolute zero.

Historically, the temperature of the triple point of water was defined as exactly 273.16 K. Today it is an empirically measured quantity. The freezing point of water at sea-level atmospheric pressure occurs at very close to 273.15 K (0 °C).

Classification of scales

There are various kinds of temperature scale. It may be convenient to classify them as empirically and theoretically based. Empirical temperature scales are historically older, while theoretically based scales arose in the middle of the nineteenth century.

Empirical scales

Empirically based temperature scales rely directly on measurements of simple macroscopic physical properties of materials. For example, the length of a column of mercury, confined in a glass-walled capillary tube, is dependent largely on temperature and is the basis of the very useful mercury-in-glass thermometer. Such scales are valid only within convenient ranges of temperature. For example, above the boiling point of mercury, a mercury-in-glass thermometer is impracticable. Most materials expand with temperature increase, but some materials, such as water, contract with temperature increase over some specific range, and then they are hardly useful as thermometric materials. A material is of no use as a thermometer near one of its phase-change temperatures, for example, its boiling-point.

In spite of these limitations, most generally used practical thermometers are of the empirically based kind. Especially, it was used for calorimetry, which contributed greatly to the discovery of thermodynamics. Nevertheless, empirical thermometry has serious drawbacks when judged as a basis for theoretical physics. Empirically based thermometers, beyond their base as simple direct measurements of ordinary physical properties of thermometric materials, can be re-calibrated, by use of theoretical physical reasoning, and this can extend their range of adequacy.

Theoretical scales

Theoretically based temperature scales are based directly on theoretical arguments, especially those of kinetic theory and thermodynamics. They are more or less ideally realized in practically feasible physical devices and materials. Theoretically based temperature scales are used to provide calibrating standards for practical empirically based thermometers.

Microscopic statistical mechanical scale

In physics, the internationally agreed conventional temperature scale is called the Kelvin scale. It is calibrated through the internationally agreed and prescribed value of the Boltzmann constant, referring to motions of microscopic particles, such as atoms, molecules, and electrons, constituent in the body whose temperature is to be measured. In contrast with the thermodynamic temperature scale invented by Kelvin, the presently conventional Kelvin temperature is not defined through comparison with the temperature of a reference state of a standard body, nor in terms of macroscopic thermodynamics.

Apart from the absolute zero of temperature, the Kelvin temperature of a body in a state of internal thermodynamic equilibrium is defined by measurements of suitably chosen of its physical properties, such as have precisely known theoretical explanations in terms of the Boltzmann constant. That constant refers to chosen kinds of motion of microscopic particles in the constitution of the body. In those kinds of motion, the particles move individually, without mutual interaction. Such motions are typically interrupted by inter-particle collisions, but for temperature measurement, the motions are chosen so that, between collisions, the non-interactive segments of their trajectories are known to be accessible to accurate measurement. For this purpose, interparticle potential energy is disregarded.

In an ideal gas, and in other theoretically understood bodies, the Kelvin temperature is defined to be proportional to the average kinetic energy of non-interactively moving microscopic particles, which can be measured by suitable techniques. The proportionality constant is a simple multiple of the Boltzmann constant. If molecules, atoms, or electrons, are emitted from material and their velocities are measured, the spectrum of their velocities often nearly obeys a theoretical law called the Maxwell–Boltzmann distribution, which gives a well-founded measurement of temperatures for which the law holds. There have not yet been successful experiments of this same kind that directly use the Fermi–Dirac distribution for thermometry, but perhaps that will be achieved in the future.

The speed of sound in a gas can be calculated theoretically from the molecular character of the gas, from its temperature and pressure, and from the value of the Boltzmann constant. For a gas of known molecular character and pressure, this provides a relation between temperature and the Boltzmann constant. Those quantities can be known or measured more precisely than can the thermodynamic variables that define the state of a sample of water at its triple point. Consequently, taking the value of the Boltzmann constant as a primarily defined reference of exactly defined value, a measurement of the speed of sound can provide a more precise measurement of the temperature of the gas.

Measurement of the spectrum of electromagnetic radiation from an ideal three-dimensional black body can provide an accurate temperature measurement because the frequency of maximum spectral radiance of black-body radiation is directly proportional to the temperature of the black body; this is known as Wien's displacement law and has a theoretical explanation in Planck's law and the Bose–Einstein law.

Measurement of the spectrum of noise-power produced by an electrical resistor can also provide accurate temperature measurement. The resistor has two terminals and is in effect a one-dimensional body. The Bose-Einstein law for this case indicates that the noise-power is directly proportional to the temperature of the resistor and to the value of its resistance and to the noise bandwidth. In a given frequency band, the noise-power has equal contributions from every frequency and is called Johnson noise. If the value of the resistance is known then the temperature can be found.

Macroscopic thermodynamic scale

Historically, till May 2019, the definition of the Kelvin scale was that invented by Kelvin, based on a ratio of quantities of energy in processes in an ideal Carnot engine, entirely in terms of macroscopic thermodynamics. That Carnot engine was to work between two temperatures, that of the body whose temperature was to be measured, and a reference, that of a body at the temperature of the triple point of water. Then the reference temperature, that of the triple point, was defined to be exactly 273.16 K. Since May 2019, that value has not been fixed by definition but is to be measured through microscopic phenomena, involving the Boltzmann constant, as described above. The microscopic statistical mechanical definition does not have a reference temperature.

Ideal gas

A material on which a macroscopically defined temperature scale may be based is the ideal gas. The pressure exerted by a fixed volume and mass of an ideal gas is directly proportional to its temperature. Some natural gases show so nearly ideal properties over suitable temperature range that they can be used for thermometry; this was important during the development of thermodynamics and is still of practical importance today. The ideal gas thermometer is, however, not theoretically perfect for thermodynamics. This is because the entropy of an ideal gas at its absolute zero of temperature is not a positive semi-definite quantity, which puts the gas in violation of the third law of thermodynamics. In contrast to real materials, the ideal gas does not liquefy or solidify, no matter how cold it is. Alternatively thinking, the ideal gas law, refers to the limit of infinitely high temperature and zero pressure; these conditions guarantee non-interactive motions of the constituent molecules.

Kinetic theory approach

The magnitude of the kelvin is now defined in terms of kinetic theory, derived from the value of the Boltzmann constant.

Kinetic theory provides a microscopic account of temperature for some bodies of material, especially gases, based on macroscopic systems' being composed of many microscopic particles, such as molecules and ions of various species, the particles of a species being all alike. It explains macroscopic phenomena through the classical mechanics of the microscopic particles. The equipartition theorem of kinetic theory asserts that each classical degree of freedom of a freely moving particle has an average kinetic energy of k_BT/2 where k_B denotes the Boltzmann constant. The translational motion of the particle has three degrees of freedom, so that, except at very low temperatures where quantum effects predominate, the average translational kinetic energy of a freely moving particle in a system with temperature T will be 3k_BT/2.

Molecules, such as oxygen (O₂), have more degrees of freedom than single spherical atoms: they undergo rotational and vibrational motions as well as translations. Heating results in an increase of temperature due to an increase in the average translational kinetic energy of the molecules. Heating will also cause, through equipartitioning, the energy associated with vibrational and rotational modes to increase. Thus a diatomic gas will require more energy input to increase its temperature by a certain amount, i.e. it will have a greater heat capacity than a monatomic gas.

As noted above, the speed of sound in a gas can be calculated from the molecular character of the gas, from its temperature and pressure, and from the value of the Boltzmann constant. Taking the value of the Boltzmann constant as a primarily defined reference of exactly defined value, a measurement of the speed of sound can provide a more precise measurement of the temperature of the gas.

It is possible to measure the average kinetic energy of constituent microscopic particles if they are allowed to escape from the bulk of the system, through a small hole in the containing wall. The spectrum of velocities has to be measured, and the average calculated from that. It is not necessarily the case that the particles that escape and are measured have the same velocity distribution as the particles that remain in the bulk of the system, but sometimes a good sample is possible.

Thermodynamic approach

Temperature is one of the principal quantities in the study of thermodynamics. Formerly, the magnitude of the kelvin was defined in thermodynamic terms, but nowadays, as mentioned above, it is defined in terms of kinetic theory.

The thermodynamic temperature is said to be absolute for two reasons. One is that its formal character is independent of the properties of particular materials. The other reason is that its zero is, in a sense, absolute, in that it indicates absence of microscopic classical motion of the constituent particles of matter, so that they have a limiting specific heat of zero for zero temperature, according to the third law of thermodynamics. Nevertheless, a thermodynamic temperature does in fact have a definite numerical value that has been arbitrarily chosen by tradition and is dependent on the property of particular materials; it is simply less arbitrary than relative "degrees" scales such as Celsius and Fahrenheit. Being an absolute scale with one fixed point (zero), there is only one degree of freedom left to arbitrary choice, rather than two as in relative scales. For the Kelvin scale since May 2019, by international convention, the choice has been made to use knowledge of modes of operation of various thermometric devices, relying on microscopic kinetic theories about molecular motion. The numerical scale is settled by a conventional definition of the value of the Boltzmann constant, which relates macroscopic temperature to average microscopic kinetic energy of particles such as molecules. Its numerical value is arbitrary, and an alternate, less widely used absolute temperature scale exists called the Rankine scale, made to be aligned with the Fahrenheit scale as Kelvin is with Celsius.

The thermodynamic definition of temperature is due to Kelvin. It is framed in terms of an idealized device called a Carnot engine, imagined to run in a fictive continuous cycle of successive processes that traverse a cycle of states of its working body. The engine takes in a quantity of heat Q₁ from a hot reservoir and passes out a lesser quantity of waste heat Q₂ < 0 to a cold reservoir. The net heat energy absorbed by the working body is passed, as thermodynamic work, to a work reservoir, and is considered to be the output of the engine. The cycle is imagined to run so slowly that at each point of the cycle the working body is in a state of thermodynamic equilibrium. The successive processes of the cycle are thus imagined to run reversibly with no entropy production. Then the quantity of entropy taken in from the hot reservoir when the working body is heated is equal to that passed to the cold reservoir when the working body is cooled. Then the absolute or thermodynamic temperatures, T₁ and T₂, of the reservoirs are defined such that

${\displaystyle \frac{T_1}{T_2}=-\frac{Q_1}{Q_2}.}$

(1)

The zeroth law of thermodynamics allows this definition to be used to measure the absolute or thermodynamic temperature of an arbitrary body of interest, by making the other heat reservoir have the same temperature as the body of interest.

Kelvin's original work postulating absolute temperature was published in 1848. It was based on the work of Carnot, before the formulation of the first law of thermodynamics. Carnot had no sound understanding of heat and no specific concept of entropy. He wrote of 'caloric' and said that all the caloric that passed from the hot reservoir was passed into the cold reservoir. Kelvin wrote in his 1848 paper that his scale was absolute in the sense that it was defined "independently of the properties of any particular kind of matter". His definitive publication, which sets out the definition just stated, was printed in 1853, a paper read in 1851.

Numerical details were formerly settled by making one of the heat reservoirs a cell at the triple point of water, which was defined to have an absolute temperature of 273.16 K. Nowadays, the numerical value is instead obtained from measurement through the microscopic statistical mechanical international definition, as above.

Intensive variability

In thermodynamic terms, temperature is an intensive variable because it is equal to a differential coefficient of one extensive variable with respect to another, for a given body. It thus has the dimensions of a ratio of two extensive variables. In thermodynamics, two bodies are often considered as connected by contact with a common wall, which has some specific permeability properties. Such specific permeability can be referred to a specific intensive variable. An example is a diathermic wall that is permeable only to heat; the intensive variable for this case is temperature. When the two bodies have been connected through the specifically permeable wall for a very long time, and have settled to a permanent steady state, the relevant intensive variables are equal in the two bodies; for a diathermal wall, this statement is sometimes called the zeroth law of thermodynamics.

In particular, when the body is described by stating its internal energy U, an extensive variable, as a function of its entropy S, also an extensive variable, and other state variables V, N, with U = U (S, V, N), then the temperature is equal to the partial derivative of the internal energy with respect to the entropy:

${\displaystyle T={\left(\frac{\mathrm{\partial }U}{\mathrm{\partial }S}\right)}_{V,N}.}$

(2)

Likewise, when the body is described by stating its entropy S as a function of its internal energy U, and other state variables V, N, with S = S (U, V, N), then the reciprocal of the temperature is equal to the partial derivative of the entropy with respect to the internal energy:

${\displaystyle \frac{1}{T}={\left(\frac{\mathrm{\partial }S}{\mathrm{\partial }U}\right)}_{V,N}.}$

(3)

The above definition, equation (1), of the absolute temperature, is due to Kelvin. It refers to systems closed to the transfer of matter and has a special emphasis on directly experimental procedures. A presentation of thermodynamics by Gibbs starts at a more abstract level and deals with systems open to the transfer of matter; in this development of thermodynamics, the equations (2) and (3) above are actually alternative definitions of temperature.

Local thermodynamic equilibrium

Real-world bodies are often not in thermodynamic equilibrium and not homogeneous. For the study by methods of classical irreversible thermodynamics, a body is usually spatially and temporally divided conceptually into 'cells' of small size. If classical thermodynamic equilibrium conditions for matter are fulfilled to good approximation in such a 'cell', then it is homogeneous and a temperature exists for it. If this is so for every 'cell' of the body, then local thermodynamic equilibrium is said to prevail throughout the body.

It makes good sense, for example, to say of the extensive variable U, or of the extensive variable S, that it has a density per unit volume or a quantity per unit mass of the system, but it makes no sense to speak of the density of temperature per unit volume or quantity of temperature per unit mass of the system. On the other hand, it makes no sense to speak of the internal energy at a point, while when local thermodynamic equilibrium prevails, it makes good sense to speak of the temperature at a point. Consequently, the temperature can vary from point to point in a medium that is not in global thermodynamic equilibrium, but in which there is local thermodynamic equilibrium.

Thus, when local thermodynamic equilibrium prevails in a body, the temperature can be regarded as a spatially varying local property in that body, and this is because the temperature is an intensive variable.

Basic theory

Temperature is a measure of a quality of a state of a material. The quality may be regarded as a more abstract entity than any particular temperature scale that measures it, and is called hotness by some writers. The quality of hotness refers to the state of material only in a particular locality, and in general, apart from bodies held in a steady state of thermodynamic equilibrium, hotness varies from place to place. It is not necessarily the case that a material in a particular place is in a state that is steady and nearly homogeneous enough to allow it to have a well-defined hotness or temperature. Hotness may be represented abstractly as a one-dimensional manifold. Every valid temperature scale has its own one-to-one map into the hotness manifold.

When two systems in thermal contact are at the same temperature no heat transfers between them. When a temperature difference does exist heat flows spontaneously from the warmer system to the colder system until they are in thermal equilibrium. Such heat transfer occurs by conduction or by thermal radiation.

Experimental physicists, for example Galileo and Newton, found that there are indefinitely many empirical temperature scales. Nevertheless, the zeroth law of thermodynamics says that they all measure the same quality. This means that for a body in its own state of internal thermodynamic equilibrium, every correctly calibrated thermometer, of whatever kind, that measures the temperature of the body, records one and the same temperature. For a body that is not in its own state of internal thermodynamic equilibrium, different thermometers can record different temperatures, depending respectively on the mechanisms of operation of the thermometers.

Bodies in thermodynamic equilibrium

For experimental physics, hotness means that, when comparing any two given bodies in their respective separate thermodynamic equilibria, any two suitably given empirical thermometers with numerical scale readings will agree as to which is the hotter of the two given bodies, or that they have the same temperature. This does not require the two thermometers to have a linear relation between their numerical scale readings, but it does require that the relation between their numerical readings shall be strictly monotonic. A definite sense of greater hotness can be had, independently of calorimetry, of thermodynamics, and of properties of particular materials, from Wien's displacement law of thermal radiation: the temperature of a bath of thermal radiation is proportional, by a universal constant, to the frequency of the maximum of its frequency spectrum; this frequency is always positive, but can have values that tend to zero. Thermal radiation is initially defined for a cavity in thermodynamic equilibrium. These physical facts justify a mathematical statement that hotness exists on an ordered one-dimensional manifold. This is a fundamental character of temperature and thermometers for bodies in their own thermodynamic equilibrium.

Except for a system undergoing a first-order phase change such as the melting of ice, as a closed system receives heat, without a change in its volume and without a change in external force fields acting on it, its temperature rises. For a system undergoing such a phase change so slowly that departure from thermodynamic equilibrium can be neglected, its temperature remains constant as the system is supplied with latent heat. Conversely, a loss of heat from a closed system, without phase change, without change of volume, and without a change in external force fields acting on it, decreases its temperature.

Bodies in a steady state but not in thermodynamic equilibrium

While for bodies in their own thermodynamic equilibrium states, the notion of temperature requires that all empirical thermometers must agree as to which of two bodies is the hotter or that they are at the same temperature, this requirement is not safe for bodies that are in steady states though not in thermodynamic equilibrium. It can then well be that different empirical thermometers disagree about which is hotter, and if this is so, then at least one of the bodies does not have a well-defined absolute thermodynamic temperature. Nevertheless, any one given body and any one suitable empirical thermometer can still support notions of empirical, non-absolute, hotness, and temperature, for a suitable range of processes. This is a matter for study in non-equilibrium thermodynamics.

Bodies not in a steady state

When a body is not in a steady-state, then the notion of temperature becomes even less safe than for a body in a steady state not in thermodynamic equilibrium. This is also a matter for study in non-equilibrium thermodynamics.

Thermodynamic equilibrium axiomatics

For the axiomatic treatment of thermodynamic equilibrium, since the 1930s, it has become customary to refer to a zeroth law of thermodynamics. The customarily stated minimalist version of such a law postulates only that all bodies, which when thermally connected would be in thermal equilibrium, should be said to have the same temperature by definition, but by itself does not establish temperature as a quantity expressed as a real number on a scale. A more physically informative version of such a law views empirical temperature as a chart on a hotness manifold. While the zeroth law permits the definitions of many different empirical scales of temperature, the second law of thermodynamics selects the definition of a single preferred, absolute temperature, unique up to an arbitrary scale factor, whence called the thermodynamic temperature. If internal energy is considered as a function of the volume and entropy of a homogeneous system in thermodynamic equilibrium, thermodynamic absolute temperature appears as the partial derivative of internal energy with respect the entropy at constant volume. Its natural, intrinsic origin or null point is absolute zero at which the entropy of any system is at a minimum. Although this is the lowest absolute temperature described by the model, the third law of thermodynamics postulates that absolute zero cannot be attained by any physical system.

Heat capacity

See also: Heat capacity and Calorimetry

When an energy transfer to or from a body is only as heat, the state of the body changes. Depending on the surroundings and the walls separating them from the body, various changes are possible in the body. They include chemical reactions, increase of pressure, increase of temperature and phase change. For each kind of change under specified conditions, the heat capacity is the ratio of the quantity of heat transferred to the magnitude of the change.

For example, if the change is an increase in temperature at constant volume, with no phase change and no chemical change, then the temperature of the body rises and its pressure increases. The quantity of heat transferred, ΔQ, divided by the observed temperature change, ΔT, is the body's heat capacity at constant volume:

${\displaystyle C_V=\frac{\mathrm{\Delta }Q}{\mathrm{\Delta }T}.}$

If heat capacity is measured for a well-defined amount of substance, the specific heat is the measure of the heat required to increase the temperature of such a unit quantity by one unit of temperature. For example, raising the temperature of water by one kelvin (equal to one degree Celsius) requires 4186 joules per kilogram (J/kg).

Measurement

A typical Celsius thermometer measures a winter day temperature of −17 °C

See also: Timeline of temperature and pressure measurement technology, International Temperature Scale of 1990, and Comparison of temperature scales

Temperature measurement using modern scientific thermometers and temperature scales goes back at least as far as the early 18th century, when Daniel Gabriel Fahrenheit adapted a thermometer (switching to mercury) and a scale both developed by Ole Christensen Rømer. Fahrenheit's scale is still in use in the United States for non-scientific applications.

Temperature is measured with thermometers that may be calibrated to a variety of temperature scales. In most of the world (except for Belize, Myanmar, Liberia and the United States), the Celsius scale is used for most temperature measuring purposes. Most scientists measure temperature using the Celsius scale and thermodynamic temperature using the Kelvin scale, which is the Celsius scale offset so that its null point is 0 K = −273.15 °C, or absolute zero. Many engineering fields in the US, notably high-tech and US federal specifications (civil and military), also use the Kelvin and Celsius scales. Other engineering fields in the US also rely upon the Rankine scale (a shifted Fahrenheit scale) when working in thermodynamic-related disciplines such as combustion.

Units

The basic unit of temperature in the International System of Units (SI) is the kelvin. It has the symbol K.

For everyday applications, it is often convenient to use the Celsius scale, in which 0 °C corresponds very closely to the freezing point of water and 100 °C is its boiling point at sea level. Because liquid droplets commonly exist in clouds at sub-zero temperatures, 0 °C is better defined as the melting point of ice. In this scale, a temperature difference of 1 degree Celsius is the same as a 1kelvin increment, but the scale is offset by the temperature at which ice melts (273.15 K).

By international agreement, until May 2019, the Kelvin and Celsius scales were defined by two fixing points: absolute zero and the triple point of Vienna Standard Mean Ocean Water, which is water specially prepared with a specified blend of hydrogen and oxygen isotopes. Absolute zero was defined as precisely 0 K and −273.15 °C. It is the temperature at which all classical translational motion of the particles comprising matter ceases and they are at complete rest in the classical model. Quantum-mechanically, however, zero-point motion remains and has an associated energy, the zero-point energy. Matter is in its ground state, and contains no thermal energy. The temperatures 273.16 K and 0.01 °C were defined as those of the triple point of water. This definition served the following purposes: it fixed the magnitude of the kelvin as being precisely 1 part in 273.16 parts of the difference between absolute zero and the triple point of water; it established that one kelvin has precisely the same magnitude as one degree on the Celsius scale; and it established the difference between the null points of these scales as being 273.15 K (0 K = −273.15 °C and 273.16 K = 0.01 °C). Since 2019, there has been a new definition based on the Boltzmann constant, but the scales are scarcely changed.

In the United States, the Fahrenheit scale is the most widely used. On this scale the freezing point of water corresponds to 32 °F and the boiling point to 212 °F. The Rankine scale, still used in fields of chemical engineering in the US, is an absolute scale based on the Fahrenheit increment.

Historical scales

See also: Conversion of scales of temperature

The following temperature scales are in use or have historically been used for measuring temperature:

• Kelvin scale
• Celsius scale
• Fahrenheit scale
• Rankine scale
• Delisle scale
• Newton scale
• Réaumur scale
• Rømer scale

Plasma physics

The field of plasma physics deals with phenomena of electromagnetic nature that involve very high temperatures. It is customary to express temperature as energy in a unit related to the electronvolt or kiloelectronvolt (eV/k_B or keV/k_B). The corresponding energy, which is dimensionally distinct from temperature, is then calculated as the product of the Boltzmann constant and temperature, ${\displaystyle E=k_{\text{B}}T}$. Then, 1 eV/k_B is 11605 K. In the study of QCD matter one routinely encounters temperatures of the order of a few hundred MeV/k_B, equivalent to about 10¹² K.

Continuous or discrete

When one measures the variation of temperature across a region of space or time, do the temperature measurements turn out to be continuous or discrete? There is a widely held misconception that such temperature measurements must always be continuous. This misconception partly originates from the historical view associated with the continuity of classical physical quantities, which states that physical quantities must assume every intermediate value between a starting value and a final value. However, the classical picture is only true in the cases where temperature is measured in a system that is in equilibrium, that is, temperature may not be continuous outside these conditions. For systems outside equilibrium, such as at interfaces between materials (e.g., a metal/non-metal interface or a liquid-vapour interface) temperature measurements may show steep discontinuities in time and space. For instance, Fang and Ward were some of the first authors to successfully report temperature discontinuities of as much as 7.8 K at the surface of evaporating water droplets. This was reported at inter-molecular scales, or at the scale of the mean free path of molecules which is typically of the order of a few micrometers in gases at room temperature. Generally speaking, temperature discontinuities are considered to be norms rather than exceptions in cases of interfacial heat transfer. This is due to the abrupt change in the vibrational or thermal properties of the materials across such interfaces which prevent instantaneous transfer of heat and the establishment of thermal equilibrium (a prerequisite for having a uniform equilibrium temperature across the interface). Further, temperature measurements at the macro-scale (typical observational scale) may be too coarse-grained as they average out the microscopic thermal information based on the scale of the representative sample volume of the control system, and thus it is likely that temperature discontinuities at the micro-scale may be overlooked in such averages. Such an averaging may even produce incorrect or misleading results in many cases of temperature measurements, even at macro-scales, and thus it is prudent that one examines the micro-physical information carefully before averaging out or smoothing out any potential temperature discontinuities in a system as such discontinuities cannot always be averaged or smoothed out. Temperature discontiuities, rather than merely being anomalies, have actually substantially improved our understanding and predictive abilities pertaining to heat transfer at small scales.

Theoretical foundation

See also: Thermodynamic temperature

Historically, there are several scientific approaches to the explanation of temperature: the classical thermodynamic description based on macroscopic empirical variables that can be measured in a laboratory; the kinetic theory of gases which relates the macroscopic description to the probability distribution of the energy of motion of gas particles; and a microscopic explanation based on statistical physics and quantum mechanics. In addition, rigorous and purely mathematical treatments have provided an axiomatic approach to classical thermodynamics and temperature. Statistical physics provides a deeper understanding by describing the atomic behavior of matter and derives macroscopic properties from statistical averages of microscopic states, including both classical and quantum states. In the fundamental physical description, the temperature may be measured directly in units of energy. However, in the practical systems of measurement for science, technology, and commerce, such as the modern metric system of units, the macroscopic and the microscopic descriptions are interrelated by the Boltzmann constant, a proportionality factor that scales temperature to the microscopic mean kinetic energy.

The microscopic description in statistical mechanics is based on a model that analyzes a system into its fundamental particles of matter or into a set of classical or quantum-mechanical oscillators and considers the system as a statistical ensemble of microstates. As a collection of classical material particles, the temperature is a measure of the mean energy of motion, called translational kinetic energy, of the particles, whether in solids, liquids, gases, or plasmas. The kinetic energy, a concept of classical mechanics, is half the mass of a particle times its speed squared. In this mechanical interpretation of thermal motion, the kinetic energies of material particles may reside in the velocity of the particles of their translational or vibrational motion or in the inertia of their rotational modes. In monatomic perfect gases and, approximately, in most gas and in simple metals, the temperature is a measure of the mean particle translational kinetic energy, 3/2 k_BT. It also determines the probability distribution function of energy. In condensed matter, and particularly in solids, this purely mechanical description is often less useful and the oscillator model provides a better description to account for quantum mechanical phenomena. Temperature determines the statistical occupation of the microstates of the ensemble. The microscopic definition of temperature is only meaningful in the thermodynamic limit, meaning for large ensembles of states or particles, to fulfill the requirements of the statistical model.

Kinetic energy is also considered as a component of thermal energy. The thermal energy may be partitioned into independent components attributed to the degrees of freedom of the particles or to the modes of oscillators in a thermodynamic system. In general, the number of these degrees of freedom that are available for the equipartitioning of energy depends on the temperature, i.e. the energy region of the interactions under consideration. For solids, the thermal energy is associated primarily with the vibrations of its atoms or molecules about their equilibrium position. In an ideal monatomic gas, the kinetic energy is found exclusively in the purely translational motions of the particles. In other systems, vibrational and rotational motions also contribute degrees of freedom.

Kinetic theory of gases

A theoretical understanding of temperature in a hard-sphere model of a gas can be obtained from the Kinetic theory.

Maxwell and Boltzmann developed a kinetic theory that yields a fundamental understanding of temperature in gases. This theory also explains the ideal gas law and the observed heat capacity of monatomic (or 'noble') gases.

Plots of pressure vs temperature for three different gas samples extrapolated to absolute zero

The ideal gas law is based on observed empirical relationships between pressure (p), volume (V), and temperature (T), and was recognized long before the kinetic theory of gases was developed (see Boyle's and Charles's laws). The ideal gas law states:

${\displaystyle pV=nRT,}$

where n is the number of moles of gas and R = 8.314462618... J⋅mol⁻¹⋅K⁻¹ is the gas constant.

This relationship gives us our first hint that there is an absolute zero on the temperature scale, because it only holds if the temperature is measured on an absolute scale such as Kelvin's. The ideal gas law allows one to measure temperature on this absolute scale using the gas thermometer. The temperature in kelvins can be defined as the pressure in pascals of one mole of gas in a container of one cubic meter, divided by the gas constant.

Although it is not a particularly convenient device, the gas thermometer provides an essential theoretical basis by which all thermometers can be calibrated. As a practical matter, it is not possible to use a gas thermometer to measure absolute zero temperature since the gases condense into a liquid long before the temperature reaches zero. It is possible, however, to extrapolate to absolute zero by using the ideal gas law, as shown in the figure.

The kinetic theory assumes that pressure is caused by the force associated with individual atoms striking the walls, and that all energy is translational kinetic energy. Using a sophisticated symmetry argument, Boltzmann deduced what is now called the Maxwell–Boltzmann probability distribution function for the velocity of particles in an ideal gas. From that probability distribution function, the average kinetic energy (per particle) of a monatomic ideal gas is

${\displaystyle E_{\text{k}}=\frac{1}{2}m{v}_{\text{rms}}^2=\frac{3}{2}{k}_{\text{B}}T,}$

where the Boltzmann constant k_B is the ideal gas constant divided by the Avogadro number, and $v_{\text{rms}}=\sqrt{⟨v^2⟩}=\sqrt{⟨\mathbf{v}\cdot \mathbf{v}⟩}$ is the root-mean-square speed. This direct proportionality between temperature and mean molecular kinetic energy is a special case of the equipartition theorem, and holds only in the classical limit of a perfect gas. It does not hold exactly for most substances.

Zeroth law of thermodynamics

Main article: Zeroth law of thermodynamics

When two otherwise isolated bodies are connected together by a rigid physical path impermeable to matter, there is the spontaneous transfer of energy as heat from the hotter to the colder of them. Eventually, they reach a state of mutual thermal equilibrium, in which heat transfer has ceased, and the bodies' respective state variables have settled to become unchanging.

One statement of the zeroth law of thermodynamics is that if two systems are each in thermal equilibrium with a third system, then they are also in thermal equilibrium with each other.

This statement helps to define temperature but it does not, by itself, complete the definition. An empirical temperature is a numerical scale for the hotness of a thermodynamic system. Such hotness may be defined as existing on a one-dimensional manifold, stretching between hot and cold. Sometimes the zeroth law is stated to include the existence of a unique universal hotness manifold, and of numerical scales on it, so as to provide a complete definition of empirical temperature. To be suitable for empirical thermometry, a material must have a monotonic relation between hotness and some easily measured state variable, such as pressure or volume, when all other relevant coordinates are fixed. An exceptionally suitable system is the ideal gas, which can provide a temperature scale that matches the absolute Kelvin scale. The Kelvin scale is defined on the basis of the second law of thermodynamics.

Second law of thermodynamics

Main article: Second law of thermodynamics

As an alternative to considering or defining the zeroth law of thermodynamics, it was the historical development in thermodynamics to define temperature in terms of the second law of thermodynamics which deals with entropy. The second law states that any process will result in either no change or a net increase in the entropy of the universe. This can be understood in terms of probability.

For example, in a series of coin tosses, a perfectly ordered system would be one in which either every toss comes up heads or every toss comes up tails. This means the outcome is always 100% the same result. In contrast, many mixed (disordered) outcomes are possible, and their number increases with each toss. Eventually, the combinations of ~50% heads and ~50% tails dominate, and obtaining an outcome significantly different from 50/50 becomes increasingly unlikely. Thus the system naturally progresses to a state of maximum disorder or entropy.

As temperature governs the transfer of heat between two systems and the universe tends to progress toward a maximum of entropy, it is expected that there is some relationship between temperature and entropy. A heat engine is a device for converting thermal energy into mechanical energy, resulting in the performance of work. An analysis of the Carnot heat engine provides the necessary relationships. According to energy conservation and energy being a state function that does not change over a full cycle, the work from a heat engine over a full cycle is equal to the net heat, i.e. the sum of the heat put into the system at high temperature, q_H > 0, and the waste heat given off at the low temperature, q_C < 0.

The efficiency is the work divided by the heat input:

${\displaystyle \text{efficiency}=\frac{w_{\text{cy}}}{q_{\text{H}}}=\frac{q_{\text{H}}+q_{\text{C}}}{q_{\text{H}}}=1-\frac{|q_{\text{C}}|}{q_{\text{H}}},}$

(4)

where w_cy is the work done per cycle. The efficiency depends only on |q_C|/q_H. Because q_C and q_H correspond to heat transfer at the temperatures T_C and T_H, respectively, |q_C|/q_H should be some function of these temperatures:

${\displaystyle \frac{|q_{\text{C}}|}{q_{\text{H}}}=f\left(T_{\text{H}},T_{\text{C}}\right).}$

(5)

Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, a heat engine operating between T₁ and T₃ must have the same efficiency as one consisting of two cycles, one between T₁ and T₂, and the second between T₂ and T₃. This can only be the case if

${\displaystyle q_{13}=\frac{q_1{q}_2}{q_2{q}_3},}$

which implies

${\displaystyle q_{13}=f\left(T_1,T_3\right)=f\left(T_1,T_2\right)f\left(T_2,T_3\right).}$

Since the first function is independent of T₂, this temperature must cancel on the right side, meaning f(T₁, T₃) is of the form g(T₁)/g(T₃) (i.e. f(T₁, T₃) = f(T₁, T₂)f(T₂, T₃) = g(T₁)/g(T₂) · g(T₂)/g(T₃) = g(T₁)/g(T₃)), where g is a function of a single temperature. A temperature scale can now be chosen with the property that

${\displaystyle \frac{|q_{\text{C}}|}{q_{\text{H}}}=\frac{T_{\text{C}}}{T_{\text{H}}}.}$

(6)

Substituting (6) back into (4) gives a relationship for the efficiency in terms of temperature:

${\displaystyle \text{efficiency}=1-\frac{|q_{\text{C}}|}{q_{\text{H}}}=1-\frac{T_{\text{C}}}{T_{\text{H}}}.}$

(7)

For T_C = 0 K the efficiency is 100% and that efficiency becomes greater than 100% below 0 K. Since an efficiency greater than 100% violates the first law of thermodynamics, this implies that 0 K is the minimum possible temperature. In fact, the lowest temperature ever obtained in a macroscopic system was 20 nK, which was achieved in 1995 at NIST. Subtracting the right hand side of (5) from the middle portion and rearranging gives

${\displaystyle \frac{q_{\text{H}}}{T_{\text{H}}}+\frac{q_{\text{C}}}{T_{\text{C}}}=0,}$

where the negative sign indicates heat ejected from the system. This relationship suggests the existence of a state function, S, whose change characteristically vanishes for a complete cycle if it is defined by

${\displaystyle dS=\frac{d{q}_{\text{rev}}}{T},}$

(8)

where the subscript indicates a reversible process. This function corresponds to the entropy of the system, which was described previously. Rearranging (8) gives a formula for temperature in terms of fictive infinitesimal quasi-reversible elements of entropy and heat:

${\displaystyle T=\frac{d{q}_{\text{rev}}}{dS}.}$

(9)

For a constant-volume system where entropy S(E) is a function of its energy E, dE = dq_rev and (9) gives

${\displaystyle T^{-1}=\frac{d}{dE}S(E),}$

(10)

i.e. the reciprocal of the temperature is the rate of increase of entropy with respect to energy at constant volume.

Definition from statistical mechanics

Statistical mechanics defines temperature based on a system's fundamental degrees of freedom. Eq.(10) is the defining relation of temperature, where the entropy ${\displaystyle S}$ is defined (up to a constant) by the logarithm of the number of microstates of the system in the given macrostate (as specified in the microcanonical ensemble):

${\displaystyle S=k_{\mathrm{B}}\ln (W)}$

where ${\displaystyle k_{\mathrm{B}}}$ is the Boltzmann constant and W is the number of microstates with the energy E of the system (degeneracy).

When two systems with different temperatures are put into purely thermal connection, heat will flow from the higher temperature system to the lower temperature one; thermodynamically this is understood by the second law of thermodynamics: The total change in entropy following a transfer of energy ${\displaystyle \mathrm{\Delta }E}$ from system 1 to system 2 is:

${\displaystyle \mathrm{\Delta }S=-(dS/dE{)}_1\cdot \mathrm{\Delta }E+(dS/dE{)}_2\cdot \mathrm{\Delta }E=\left(\frac{1}{T_2}-\frac{1}{T_1}\right)\mathrm{\Delta }E}$

and is thus positive if ${\displaystyle T_1>T_2}$

From the point of view of statistical mechanics, the total number of microstates in the combined system 1 + system 2 is ${\displaystyle N_1\cdot N_2}$, the logarithm of which (times the Boltzmann constant) is the sum of their entropies; thus a flow of heat from high to low temperature, which brings an increase in total entropy, is more likely than any other scenario (normally it is much more likely), as there are more microstates in the resulting macrostate.

Generalized temperature from single-particle statistics

It is possible to extend the definition of temperature even to systems of few particles, like in a quantum dot. The generalized temperature is obtained by considering time ensembles instead of configuration-space ensembles given in statistical mechanics in the case of thermal and particle exchange between a small system of fermions (N even less than 10) with a single/double-occupancy system. The finite quantum grand canonical ensemble, obtained under the hypothesis of ergodicity and orthodicity, allows expressing the generalized temperature from the ratio of the average time of occupation ${\displaystyle {\tau }_1}$ and ${\displaystyle {\tau }_2}$ of the single/double-occupancy system:

${\displaystyle T=\frac{E-E_{\text{F}}\left(1+\frac{3}{2N}\right)}{k_{\text{B}}\ln \left(2\frac{{\tau }_2}{{\tau }_1}\right)},}$

where E_F is the Fermi energy. This generalized temperature tends to the ordinary temperature when N goes to infinity.

Negative temperature

Main article: Negative temperature

On the empirical temperature scales that are not referenced to absolute zero, a negative temperature is one below the zero-point of the scale used. For example, dry ice has a sublimation temperature of −78.5 °C which is equivalent to −109.3 °F. On the absolute Kelvin scale this temperature is 194.6 K. No body can be brought to exactly 0 K (the temperature of the ideally coldest possible body) by any finite practicable process; this is a consequence of the third law of thermodynamics.

The international kinetic theory temperature of a body cannot take negative values. The thermodynamic temperature scale, however, is not so constrained.

For a body of matter, there can sometimes be conceptually defined, in terms of microscopic degrees of freedom, namely particle spins, a subsystem, with a temperature other than that of the whole body. When the body is in its own state of internal thermodynamic equilibrium, the temperatures of the whole body and of the subsystem must be the same. The two temperatures can differ when, by work through externally imposed force fields, energy can be transferred to and from the subsystem, separately from the rest of the body; then the whole body is not in its own state of internal thermodynamic equilibrium. There is an upper limit of energy such a spin subsystem can attain.

Considering the subsystem to be in a temporary state of virtual thermodynamic equilibrium, it is possible to obtain a negative temperature on the thermodynamic scale. Thermodynamic temperature is the inverse of the derivative of the subsystem's entropy with respect to its internal energy. As the subsystem's internal energy increases, the entropy increases for some range, but eventually attains a maximum value and then begins to decrease as the highest energy states begin to fill. At the point of maximum entropy, the temperature function shows the behavior of a singularity, because the slope of the entropy as a function of energy decreases to zero and then turns negative. As the subsystem's entropy reaches its maximum, its thermodynamic temperature goes to positive infinity, switching to negative infinity as the slope turns negative. Such negative temperatures are hotter than any positive temperature. Over time, when the subsystem is exposed to the rest of the body, which has a positive temperature, energy is transferred as heat from the negative temperature subsystem to the positive temperature system. The kinetic theory temperature is not defined for such subsystems.

Old Testament messianic prophecies quoted in the New Testament

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Old_Testament_messianic_prophecies_quoted_in_the_New_Testament 

The books of the New Testament frequently cite Jewish scripture to support the claim of the Early Christians that Jesus was the promised Jewish Messiah. Scholars have observed that few of these citations are actual predictions in context; the majority of these quotations and references are taken from the prophetic Book of Isaiah, but they range over the entire corpus of Jewish writings.

Jews do not regard any of these as having been fulfilled by Jesus, and in some cases do not regard them as messianic prophecies at all. Old Testament prophecies that were regarded as referring to the arrival of Christ are either not thought to be prophecies by biblical scholars, as the verses make no stated claim of being predictions, or are seen as having no correlation as they do not explicitly refer to the Messiah. Historical criticism has been agreed to be a field that is unable to argue for the evidential fulfillment of prophecy, or that Jesus was indeed the Messiah because he fulfilled messianic prophecies, as it cannot "construct such an argument" within that academic method, since it is a theological claim.

No view of the Messiah as based on the Old Testament predicted a Messiah who would suffer and die for the sins of all people. The story of Jesus' death, therefore, involved a profound shift in meaning from the Old Testament tradition.

Overview: prophecy and biblical scholarship

The Hebrew scriptures were an important source for the New Testament authors. There are 27 direct quotations in the Gospel of Mark, 54 in Matthew, 24 in Luke, and 14 in John, and the influence of the scriptures is vastly increased when allusions and echoes are included, with half of Mark's gospel being made up of allusions to and citations of the scriptures.  Matthew contains all Mark's quotations and introduces around 30 more, sometimes in the mouth of Jesus, sometimes as his own commentary on the narrative, and Luke makes allusions to all but three of the Old Testament books.

Gospel of Matthew

The Gospel of Matthew has the largest number of messianic quotations from the Old Testament.

An example of one is Matthew 1:23: "'Look, the virgin shall conceive and bear a son, and they shall name him Emmanuel,' which means, 'God is with us.'". This references Isaiah 7:14: "therefore the Lord himself shall give you a sign: the maiden is with child and she will bear a son, and will call his name Immanuel".

The word translated here as "maiden" is almah, meaning a young woman of childbearing age rather than a virgin. Matthew, however, used the Greek translation of Isaiah rather than the Hebrew original, and the word that appears there is parthenos, meaning virgin.

Prophecies Christians consider fulfilled

Daniel 9:24–27

Main article: Prophecy of Seventy Weeks

Seventy weeks are decreed for your people and your holy city: to finish the transgression, to put an end to sin, and to atone for iniquity, to bring in everlasting righteousness, to seal both vision and prophet, and to anoint a most holy place. Know therefore and understand: from the time that the word went out to restore and rebuild Jerusalem until the time of an anointed prince, there shall be seven weeks; and for sixty-two weeks it shall be built again with streets and moat, but in a troubled time. After the sixty-two weeks, an anointed one shall be cut off and shall have nothing, and the troops of the prince who is to come shall destroy the city and the sanctuary. Its end shall come with a flood, and to the end there shall be war. Desolations are decreed. He shall make a strong covenant with many for one week, and for half of the week he shall make sacrifice and offering cease; and in their place shall be an abomination that desolates, until the decreed end is poured out upon the desolator.

— Daniel 9:24–27

The general scholarly view is that the author of Daniel is writing a contemporaneous account of the Maccabean Revolt c. 167 BCE and the "an anointed one shall be cut off" refers to the murder of the high priest Onias III; the "abomination that desolates" refers to Antiochus IV Epiphanes erecting a statue of Zeus in the Temple. References to "most holy", "anointed one" and "prince" have been interpreted by Christians as speaking of Jesus, and the phrase "anointed one shall be cut off" as pointing to his crucifixion, the "troops of the prince who is to come" being taken to refer to the Romans who destroyed Jerusalem and the Temple in 70 AD.

Deuteronomy 18:15

Deuteronomy 18 speaks of a prophet who would be raised up from among the Jewish nation:

The LORD will raise up for you a prophet like me from among yourselves, from your own kinsmen. You are to pay attention to him ... I will raise up for them a prophet like you from among their kinsmen. I will put my words in his mouth, and he will tell them everything I order him. (CJB)

By the time of Jesus, this promise of Moses was understood to refer to a special individual. In John 6:14, after the multiplication of the loaves, people are quoted as saying, "This is truly the Prophet, the one who is to come into the world." In John 7:40, On the last day of the feast (tabernacles/Booths), the great day...Many of the people, therefore, when they heard this saying, said, Of a truth this is the Prophet. In Acts 3:18–22, Peter said that Jesus was the fulfillment of this promise.

Ezekiel 37:24, 25–27

And David my servant [shall be] king over them; and they all shall have one shepherd: they shall also walk in my judgments, and observe my statutes, and do them.

— Ezekiel 37:24, KJV

Ezekiel 37:24 refers to a person coming from the House of David as the servant of God, unique Shepherd of Israel, which will rule over the House of Judah (v. 16) and over the Tribe of Joseph (v. 17) so that he will "make them one stick, and they shall be one in mine hand" (v. 19), in a unique nation of Israel.

Verses from to 15 to 24 cannot be referring to King David, since the united monarchy of Israel was divided in two reigns after the death of his son Solomon (999–931 BCE), son of David. Furthermore, Ezekiel (622–570 BCE) wrote in the seventh century BCE, four centuries after this subject of the biblical narration, nevertheless adopting a prophecy that is by its nature usually referred to future happenings. Therefore, as the "stick of Judah" stands for the House of Judah, and the "stick of Joseph" stands for his tribe (verse 19), the expression "David my servant shall be king over them" (verse 24) may be read as a prophecy about a person of the House of David, which would have ruled over one nation in one land, gathered upon the mountains of Israel on every side of the earth.

The narration continues as follows:

They will live in the land I gave to Ya'akov my servant, where your ancestors lived; they will live there – they, their children, and their grandchildren, forever; and David my servant will be their leader forever. I will make a covenant of peace with them, an everlasting covenant. I will give to them, increase their numbers, and set my Sanctuary among them forever. My dwelling place will be with them; I will be their God, and they will be my people. (CJB)

They will "live" ('made for thee to dwell' [KJV/ESV] in Song of The Sea Exodus 15:17) in the land. The "dwelling place" (Hebrew mishkan מִשְׁכָּן Exodus 25:9) recalls the wilderness tabernacle. The Sanctuary (Hebrew miqdash מִקְדָּשׁ Exodus 15:17) points rather to the Temple, in particular the renewed Temple, which will occupy Ezekiel's attention in the last chapters of 40–48.

Christianity believes that Ezekiel's Temple is more glorious than the Tabernacle of Moses (Exodus 25–40) and the Temple of Solomon (1 Kings 5–8), pointing forward to several beliefs:

• (1) the glory in which God dwells with man in the Messiah, John 1:14: "The Word became a human being and lived with us, and we saw his Sh'khinah" (שָׁכֵחַ Exodus 25:8) (CJB)
• (2) The Messiah's body is the Temple, John 2:19–21: "Yeshua answered them, 'Destroy this temple, and in three days I will raise it up again.' The Judeans said, 'It took 46 years to build this Temple, and you're going to raise it in three days?' But the 'temple' he had spoken of was his body." (CJB)
• (3) the messianic community as the Temple, 1 Corinthians 3:16: "Don't you know that you people are God's Temple and that God's Spirit lives in you?", Ephesians 2:20–22 "You have been built on the foundation of the emissaries and the prophets, with the cornerstone being Yeshua the Messiah himself. In union with him the whole building is held together, and it is growing into a holy temple in union with the Lord. Yes, in union with him, you yourselves are being built together into a spiritual dwelling-place for God!", 1 Peter 2:5 "...you yourselves, as living stones, are being built into a spiritual house to be cohanim set apart for God to offer spiritual sacrifices acceptable to him through Yeshua the Messiah." (CJB)
• (4) the body of the individual believer, 1 Corinthians 6:19: "Or don't you know that your body is a Temple for the Ruach HaKodesh who lives inside you, whom you received from God? The fact is, you don't belong to yourselves" (CJB)
• (5) the heavenly Jerusalem, Revelation 21:9-22:5

Judaism holds that the Messiah has not yet arrived namely because of the belief that the Messianic Age has not started yet. Jews believe that the Messiah will completely change life on earth and that pain and suffering will be conquered, thus initiating the Kingdom of God and the Messianic Age on earth. Christian belief varies, with one segment holding that the Kingdom of God is not worldly at all, while another believe that the Kingdom is both spiritual and will be of this world in a Messianic Age where Jesus will rule on the throne of David. Most Jews hold that the Kingdom of God will be on earth and the Messiah will occupy the throne of David. Christians (in particular Evangelicals) believe that it is both, and claim that it is spiritual (the historical Jesus completed salvation) and within right now, and physical and outward at the return of the Messiah (Second Coming of Jesus as "New Jerusalem, coming down out of heaven from God" Revelation 21:1–4).

While Christians have cited the following as prophecies referencing the life, status, and legacy of Jesus, Jewish scholars maintain that these passages are not messianic prophecies and are based on mistranslations or misunderstanding of the Hebrew texts.

Hosea 11:1

Main article: Flight into Egypt § Prophecy of Hosea

When Israel was a child, I loved him, and out of Egypt I called my son.

In its original context, this text from Hosea referred to the deliverance of the people of Israel from bondage in Egypt. The Gospel of Matthew chapter 2 applies it to the return from Egypt of Jesus and his family as a messianic prophecy:

An angel of the Lord appeared to Joseph in a dream and said, "Rise, take the child and his mother, and flee to Egypt, and remain there till I tell you; for Herod is about to search for the child to destroy him." And he rose and took the child and his mother by night, and departed to Egypt, and remained there until the death of Herod. This was to fulfill what the Lord had spoken by the prophet, "Out of Egypt have I called my son."

— Matthew 2:13–15

Isaiah

The Vision of Isaiah is depicted in this 1860 woodcut by Julius Schnorr von Karolsfeld

Isaiah 7:14

Therefore the Lord himself shall give you a sign; Behold, the young woman shall conceive, and bear a son, and shall call his name Immanuel

Early Christian tradition interpreted this verse as a reference to the mother of Jesus. The prophet Isaiah, addressing king Ahaz of Judah, promises the king that God will destroy his enemies, and as a sign that his oracle is a true one he predicts that a "young woman" ("almah") standing nearby will shortly give birth to a child whose name will be Immanuel, "God is with us", and that the threat from the enemy kings will be ended before the child grows up. The almah might be the mother of Hezekiah or a daughter of Isaiah, although there are problems with both candidates – Hezekiah, for example, was apparently born nine years before the prophecy was given – but the biblical chronology for Hezekiah is confused, and his identity as the prophesied child is strongly suggested by the reference to Immanuel's "land" in 8.8 and 10.

The Gospel of Matthew references this verse to support its claim of the supernatural origins of Jesus. In the time of Jesus, however, the Jews of Palestine no longer spoke Hebrew, and Isaiah had to be translated into Greek and Aramaic, the two commonly used languages. In the original Hebrew, the word almah means a young woman of childbearing age or who is a mother, but the Greek translation of Isaiah 7:14 rendered almah as parthenos, the Greek word for "virgin". Scholars agree that almah has nothing to do with virginity, but many conservative American Christians still judge the acceptability of new Bible translations by the way they deal with Isaiah 7:14.

Isaiah 8:14

And he shall be for a sanctuary; but for a stone of stumbling and for a rock of offence to both the houses of Israel, for a gin and for a snare to the inhabitants of Jerusalem. (KJV)

1 Peter 2:8 interprets the stone as Christ, quoting Isaiah 8:14 along with Psalm 118:22 and Isaiah 28:16 which mention a stone and a cornerstone.

Isaiah 8:22–9:1 (9:1–2)

Nevertheless, there will be no more gloom for those who were in distress. In the past he humbled the land of Zebulun and the land of Naphtali, but in the future he will honor Galilee of the nations, by the Way of the Sea, beyond the Jordan...

— ISA 8:23 (9:1)^[34]

According to both Jewish and Christian interpretation, the prophet Isaiah was commanded to inform the people of Israel in a prophecy that Sennacherib's plunder of the Ten Tribes was at hand, and that Nebuchadnezzar's spoil of Jerusalem, in later years, was coming nearer.

During the Syro-Ephraimite War, Isaiah opposed an alliance with Assyria, and counseled Ahaz to rely instead on the assurances of the Davidic covenant. This view was not well received at court. Assyria absorbed the lands of Zebulon and Naphtali to form the provinces of Galilee, Dor, and Gilead. Judah became a vassal kingdom of the Assyrians.

The reign of Hezekiah saw a notable increase in the power of the Judean state.Hezekiah was successful in his wars against the Philistines, driving them back in a series of victorious battles as far as Gaza. He thus not only retook all the cities that his father had lost, but even conquered others belonging to the Philistines. He also looked to attempting to reincorporate some of the desolate northern territories into the kingdom of Judah and thus restore the boundaries of the country as it was under David. At this time Judah was the strongest nation on the Assyrian-Egyptian frontier. The "messianic oracle" ("The people walking in darkness have seen a great light; Upon those living in the land of deep darkness a light has dawned.") may have coincided with the coronation of Hezekiah and looked toward the deliverance of the Israelites living in the northern provinces.

According to Jewish tradition, the salvation of which he speaks is the miraculous end of Sennacherib's siege of Jerusalem (see Isaiah 36 and 37) in the days of the Prince of Peace, King Hezekiah, a son of King Ahaz.

Matthew cites the messianic oracle, when Jesus began his ministry in Galilee:

And leaving Nazareth, He came and dwelt in Capernaum, which is by the sea, in the regions of Zebulun and Naphtali, that it might be fulfilled which was spoken by Isaiah the prophet, saying: "The land of Zebulun and the land of Naphtali, By the way of the sea, beyond the Jordan, Galilee of the Gentiles: The people who sat in darkness have seen a great light, And upon those who sat in the region and shadow of death Light has dawned."

— Matthew 4:12–16

The interpretation of Isaiah 9:1–2 by the author of the Gospel of Matthew has led Christian authors to hint at its messianic applications.

While the Gospel of Matthew modifies a Greek Septuagint interpretation of scripture (Isaiah 8:23–9:2), in the Masoretic text it refers to the "region of the nations".

Isaiah 9:6,7 (Masoretic 9:5,6)

Main article: Pele-joez-el-gibbor-abi-ad-sar-shalom

For a child has been born to us, a son given to us, and the authority is upon his shoulder, and the wondrous adviser, the mighty God, the everlasting Father, called his name, "the prince of peace."

— Isaiah 9:5 JPS

In Jewish translations of the Hebrew Bible the verse numbering is different (9:6 in the Christian Old Testament is numbered 9:5 in Hebrew Bible versions).

Newer Jewish versions do not translate the verse as follows:

• Isaiah 9:6 (Masoretic 9:5) "For a child is born unto us, a son hath been given unto us, and the government is placed on his shoulders; and his name is called, Wonderful, counsellor of the mighty God, of the everlasting Father, the prince of peace", (Lesser)
• Isaiah 9:6 (Masoretic 9:5) "For a child is born unto us, a son is given unto us; and the government is upon his shoulder; and his name is called Pele- joez-el-gibbor-Abi-ad-sar-shalom"; (JPS 1917)

This verse is expressly applied to the Messiah in the Targum, i.e. Aramaic commentary on the Hebrew Bible.

Some Christians believe that this verse refers to the birth of Jesus as the Messiah. The verse reads in Christian bible versions:

For a child will be born to us, a son will be given to us; And the government will rest on His shoulders; And His name will be called Wonderful, Counselor, The Mighty God, The Everlasting Father, The Prince of Peace.

— Isaiah 9:6

Isaiah 11:12

And he shall set up a banner for the nations, and shall assemble the outcasts of Israel, and gather together the dispersed of Judah from the four corners of the earth.

— Isaiah 11:12

Some commentators view this as an unfulfilled prophecy, arguing that the Jewish people have not all been gathered in Israel. Some Christians refer to the foundation of the State of Israel as fulfillment of this prophecy. Others argue that the fulfillment is that Jesus as Messiah brings all nations to himself (cf. 11:10 "Nations will seek his counsel / And his abode will be honored.") citing John 12:32 ("And I, when I am lifted up from the earth, will draw all people to myself.") and Paul in Romans 15:12 when he quotes Isaiah 11:10, emphasizing the inclusion of the gentiles into the people of God.

Some Christians also believe that Isaiah 2:2 is to be understood in connection with Isaiah 11:10,12.

In the days to come, The Mount of the Lord’s house Shall stand firm above the mountains And tower above the hills; And all the nations Shall gaze on it with joy.

— Isaiah 2:2

Some Christians believe that Jesus the Messiah is the ultimate "house" or dwelling place of God, as is told in John 1:14 ("And the Word became flesh and dwelt among us, and we have seen his glory") and 2:19–21 ("Jesus answered them, 'Destroy this temple, and in three days I will raise it up.' The Jews then said, 'It has taken forty-six years to build this temple, and will you raise it up in three days?' But he was speaking about the temple of his body."). Through him the messianic community becomes a temple in 1 Corinthians 3:16 ("Do you not know that you all are God's temple and that God's Spirit dwells in you?") and Ephesians 2:20–22 ("...built on the foundation of the apostles and prophets, the Messiah Jesus himself being the cornerstone, in whom the whole structure, being joined together, grows into a holy temple in the Lord. In him you also are being built together into a dwelling place for God by the Spirit."). It is through the Messiah's exaltation all nations are drawn to him, as in Luke 24:47 ("...and that repentance and forgiveness of sins should be proclaimed in his name to all nations, beginning from Jerusalem.").

Isaiah 28:16

Therefore thus saith the Lord God, Behold, I lay in Zion for a foundation a stone, a tried stone, a precious corner stone, a sure foundation: he that believeth shall not make haste. (KJV)

1 Peter 2:8 interprets the stone mentioned as Christ, quoting Isaiah 28:16 along with Psalm 118:22 and Isaiah 8:14 which mention a stone of stumbling and a cornerstone.

Isaiah 53:5

Main article: Isaiah 53

But he was wounded for our transgressions, he was bruised for our iniquities: the chastisement of our peace was upon him, and with his stripes we are healed.

— Isaiah 53:5 (KJV)

But he was pained because of our transgressions, crushed because of our iniquities; the chastisement of our welfare was upon him, and with his wound we were healed.

— Isaiah 53:5 (JPS The Judaica Press Tanakh with Rashi's commentary

Isaiah 53 is probably the most famous example claimed by Christians to be a messianic prophecy fulfilled by Jesus. It speaks of one known as the "suffering servant," who suffers because of the sins of others. Jesus is said to fulfill this prophecy through his death on the cross. The verse from Isaiah 53:5 has traditionally been understood by many Christians to speak of Jesus as the Messiah. The claim frequently advanced by Christian apologists is that the noted Jewish commentator, Rashi (1040 CE – 1105 CE), was the first to identify the suffering servant of Isaiah 53 with the nation of Israel. The consensus among Jewish is that the "servant" in Isaiah 52-53 refers to the nation of Israel is misleading as by the implication then, the pagan nations would essentially be healed by making Jewish nation suffer and the more they strike them,the more they are to be healed. However, many still view the "suffering servant" as a reference to the whole Jewish people, regarded as one individual, and more specifically to the Jewish people deported to Babylon. However, in aggadic midrash on the books of Samuel, a compendium of rabbinic folklore, historical anecdotes and moral exhortations, Isa 53:5 is messianically interpreted.

One of the first claims in the New Testament that Isaiah 53 is a prophecy of Jesus comes from the Book of Acts chapter 8 verses 26–36, which describes a scene in which God commands Philip the Apostle to approach an Ethiopian eunuch who is sitting in a chariot, reading aloud to himself from the Book of Isaiah. The eunuch comments that he does not understand what he is reading (Isaiah 53) and Philip explains to him that the passage refers to Jesus: "And the eunuch answered Philip, and said, I pray thee, of whom speaketh the prophet this? Of himself, or of some other man? Then Philip opened his mouth, and began at the same scripture, and preached unto him Jesus."

The (suffering) Servant, as referring to the Jewish people, suffering from the cruelties of the nations, is a theme in the Servant songs and is mentioned previously.

Jeremiah 31:15

Thus saith the Lord; A voice was heard in Ramah, lamentation, and bitter weeping; Rahel weeping for her children refused to be comforted for her children, because they were not.

— Jeremiah 31:15 (KJV)

Matthew 2:17–18 gives the Massacre of the Innocents by Herod the Great as the fulfillment of a prophecy allegedly given by this verse in Jeremiah.

The phrase "because her children are no more" is believed to refer to the captivity of Rachel's children in Assyria. The subsequent verses describe their return to Israel.

Micah 5:2 (Micah 5:1 in Hebrew)

See also: Census of Quirinius

But thou, Beth-lehem Ephrathah, which art little to be among the thousands of Judah, out of thee shall one come forth unto Me that is to be ruler in Israel; whose goings forth are from of old, from ancient days. (Micah 5:1)

This verse near the end of Micah's prophecy on the Babylonian captivity has been interpreted by Christian apologists, and by Pharisees mentioned in the Gospel of John (John 7:42), as a prophecy that the Messiah would be born in Bethlehem.

The verse describes the clan of Bethlehem, who was the son of Caleb's second wife, Ephrathah. (1 Chr. 2:18, 2:50–52, 4:4) Bethlehem Ephrathah is the town and clan from which king David was born, and this passage refers to the future birth of a new Davidic heir.

Although the Gospel of Matthew and the Gospel of Luke give different accounts of the birth of Jesus, they both place the birth in Bethlehem. The Gospel of Matthew describes Herod the Great as asking the chief priests and scribes of Jerusalem where the Messiah was to be born. They respond by quoting Micah, "In Beit-Lechem of Y'hudah," they replied, "because the prophet wrote, 'And you, Beit-Lechem in the land of Y'hudah, are by no means the least among the rulers of Y'hudah; for from you will come a Ruler who will shepherd my people Isra'el.'" (Matthew 2:4–6)

The idea that Bethlehem was to be the birthplace of the Messiah appears in no Jewish source before the 4th century CE. Jewish tradition appears to have emphasised the idea that the birthplace of the Messiah was not known.

Some modern scholars consider the birth stories as inventions by the gospel writers, created to glorify Jesus and present his birth as the fulfillment of prophecy.

Psalms

Some portions of the Psalms are considered prophetic in Judaism, even though they are listed among the Ketuvim (Writings) and not the Nevi'im (Prophets).

The words Messiah and Christ mean "anointed one". In ancient times Jewish leaders were anointed with olive oil when they assumed their position (e.g. David, Saul, Isaac, Jacob). And Messiah is used as a name for kings in the Hebrew Bible: in 2 Samuel 1:14 David finds King Saul's killer and asks, "Why were you not afraid to lift your hand to destroy the LORD's anointed?"

In many Psalms, whose authorship are traditionally ascribed to King David (i.e. Messiah David), the author writes about his life in third person, referring to himself as "the/God's/your messiah" while clearly discussing his military exploits. Thus it can be argued that many of the portions that are asserted to be prophetic Psalms may not be.

Psalm 2

Main article: Psalm 2

Why do the nations conspire, and the peoples plot in vain? The kings of the earth set themselves, and the rulers take counsel together, against the LORD and his Anointed, saying, "Let us burst their bonds asunder, and cast their cords from us." He who sits in the heavens laughs; the LORD has them in derision. Then he will speak to them in his wrath, and terrify them in his fury, saying, "I have set my king on Zion, my holy hill." I will tell of the decree of the LORD: He said to me, "You are my son, today I have begotten you. Ask of me, and I will make the nations your heritage, and the ends of the earth your possession. You shall break them with a rod of iron, and dash them in pieces like a potter's vessel."

— Psalm 2: 1–9

Psalm 2 can be argued to be about David; the authors of Acts and the Epistle to the Hebrews interpreted it as relating to Jesus. Saint Augustine identifies "the nations [that] conspire, and the peoples [that] plot in vain" as the enemies referred to in Psalm 110: "Sit at my right hand, until I make your enemies your footstool."

Verse 7. The LORD is the messiah's father. In Judaism the phrase "Son of God" has very different connotations than in Christianity, not referring to literal descent but to the righteous who have become conscious of God's father of mankind.

Christians cite Herod and Pontius Pilate setting themselves against Jesus as evidence that Psalm 2 refers to him. Acts 13:33 interprets Jesus' rising from the dead as confirmation of verse 7 ("You are my son, today I have begotten you").

Hebrews 1:5 employs verse 7 in order to argue that Jesus is superior to the angels, i.e., Jesus is superior as a mediator between God and man. "For to what angel did God ever say, Thou art my Son, today I have begotten thee?" However, the phrase "son of God" appears in the Hebrew Bible to describe others than the coming Messiah, including David and Jacob.

Texts vary in the exact wording of the phrase beginning Psalm 2:12, with "kiss his foot", and "kiss the Son" being most common in various languages for centuries (including the King James Version), though not in original Hebrew Manuscripts such as the Dead Sea Scrolls. The proper noun was reduced to "son" in the Revised Version. The marginal interpretation accompanying the latter reads, "Worship in purity," which according to Joseph Hertz, "is in agreement with Jewish authorities."

Psalm 16

I bless the Lord who has given me understanding, because even in the night, my heart warns me. I keep the Lord always within my sight; for he is at my right hand, I shall not be moved. For this reason my heart is glad and my soul rejoices; moreover, my body also will rest secure, for thou wilt not leave my soul in the abode of the dead, nor permit thy holy one to see corruption. Thou wilt show me the path of life, the fullness of joys in thy presence, and delights at thy right hand forever.

— Psalm 16:7–11

The interpretation of Psalm 16 as a messianic prophecy is common among Christian evangelical hermeneutics.

According to the preaching of Peter, this prophecy is about the messiah's triumph over death, i.e., the resurrection of Jesus.

God raised Jesus up, having loosed the pangs of death, because it was not possible for him to be held by it. For David says concerning him, "I saw the Lord always before me, for he is at my right hand that I may not be shaken… For thou wilt not abandon my soul to Hades, nor let thy Holy One see corruption… Thou wilt make me full of gladness with thy presence." Brethren, I may say to you confidently of the patriarch David that he both died and was buried, and his tomb is with us to this day. Being therefore a prophet, and knowing that God had sworn with an oath to him that he would set one of his descendants upon his throne, he foresaw and spoke of the resurrection of the Christ, that he was not abandoned to Hades, nor did his flesh see corruption. This Jesus God raised up, and we are all witnesses of it.

— Acts 2: 24–32

Also of note is what Paul said in the synagogue at Antioch. "And as for the fact that he raised him from the dead, no more to return to corruption, he spoke in this way, 'I will give you the holy and sure blessings of David.' Therefore, he also says in another psalm, 'Thou wilt not let thy Holy One see corruption.' For David, after he had served the counsel of God in his own generation, fell asleep, and saw corruption; but he whom God raised up saw no corruption" (Acts 13: 34–37).

Psalm 22

See also: Sayings of Jesus on the cross

1 My God, my God, why hast thou forsaken me? why art thou so far from helping me, and from the words of my roaring? 2 O my God, I cry in the day time, but thou hearest not; and in the night season, and am not silent. ... (KJV)

Two of the Gospels (Matthew 27:46 and Mark 15:34) quote Jesus as speaking these words of Psalm 22 from the cross;

And about three o’clock Jesus cried with a loud voice, "Eli, Eli, lema sabachthani?" that is, "My God, my God, why have you forsaken me?"

— Matthew 27:46

The other two canonical Gospels give different accounts of the words of Jesus. Luke 23:46 quotes Psalm 31:5 ("Into your hands I commit my spirit") while John has Jesus say "It is finished" (John 19:30). Some scholars see this as evidence that the words of Jesus were not part of a pre-Gospel Passion narrative, but were added later by the Gospel writers.

In most Hebrew manuscripts, such as the Masoretic, Psalm 22:16 (verse 17 in the Hebrew verse numbering) reads כארי ידי ורגלי ("like a lion my hands and my feet"). Many Modern English translations render this as "they have pierced my hands and my feet", starting with the Coverdale Bible which translated Luther's durchgraben (dig through, penetrate) as pearsed, with durchgraben being a variation of the Septuagint's ωρυξαν "dug". While this translation is highly controversial, it is asserted in Christian apologetics that the Dead Sea Scrolls lend weight to the translation as "They have pierced my hands and my feet", by lengthening the ending yud in the Hebrew word כארי (like a lion) into a vav כארו "Kaaru", which is not a word in the Hebrew language but when the aleph is omitted becomes כרו, dig, similar to the Septuagint translation. However, this view is contested considering the Nahal Hever scribe's other numerous misspellings, such as one in the very same sentence, where ידיה is written instead of the correct ידי, making the Hebrew word ידי yadai "hands" into ידיה yadehah, "her hands". Christian apologists argue that this passage refers to Jesus.

Psalm 34

Many are the afflictions of the just man; but the Lord delivers him from all of them. He guards all his bones: not even one of them shall be broken.

— Psalms 34:20

Ray Pritchard has described Psalm 34:20 as a messianic prophecy. In its account of the crucifixion of Jesus, the Gospel of John interprets it as a prophecy (John 19:36) and presents some of the details as fulfillment.

So the soldiers came and broke the legs of the first, and of the other who had been crucified with Jesus; but when they came to Jesus and saw that he was already dead, they did not break his legs. But one of the soldiers pierced his side with a spear, and at once there came out blood and water… For these things took place that the scripture might be fulfilled, "Not a bone of him shall be broken." And again another scripture says, "They shall look on him whom they have pierced"

— John 19:32–37

Psalm 69

They gave me also gall for my meat; and in my thirst they gave me vinegar to drink

— Psalm 69:21

Christians believe that this verse refers to Jesus' time on the cross in which he was given a sponge soaked in vinegar to drink, as seen in Matthew 27:34, Mark 15:23, and John 19:29.

Psalm 110

Main article: Psalm 110

The Lord said unto my Lord, Sit thou at my right hand, until I make thine enemies thy footstool. The Lord shall send the rod of thy strength out of Zion: rule thou in the midst of thine enemies. Thy people shall be willing in the day of thy power, in the beauties of holiness from the womb of the morning: thou hast the dew of thy youth. The Lord hath sworn, and will not repent, Thou art a priest for ever after the order of Melchizedek. The Lord at thy right hand shall strike through kings in the day of his wrath. He shall judge among the heathen, he shall fill the places with the dead bodies; he shall wound the heads over many countries. He shall drink of the brook in the way: therefore shall he lift up the head. (KJV)

"A royal psalm (see Psalm 2 intro). It is quite difficult because verse 3 is totally obscure, and the psalm speakers often. In Christian interpretation, it is understood as a reference to Jesus, as a messianic and sometimes eschatological psalm; Radak polemicizes against this view" 1. Here God is speaking to the king, called my lord; Perhaps these are the words spoken by a prophet. The king is very proximate to God, in a position of privilege, imagined as being on His right hand in the Divine Council. The second-in-command was seated to the right of the king in the ancient Near East. Such images are rare in psalms, but see Psalm 45:7. If the king trods on the back of his enemies (see Joshua 10:24), they poetically become his "Footstool" 2. In contrast to v.1, God is spoken of in the third person. The Zion tradition (see Isaiah 2:1–4; 60:1–22) and royal tradition are here connected. While v.1-2 express the great power of the king, they also emphasize it comes from God" (YHWH).

Psalm 110 is viewed as messianic in both Jewish and Christian tradition. Christian authors have interpreted this psalm as a messianic passage in light of several New Testament passages. Pope Benedict XVI noted, "The royal glorification expressed at the beginning of the Psalm was adopted by the New Testament as a messianic prophecy. For this reason the verse is among those most frequently used by New Testament authors, either as an explicit quotation or as an allusion." He further connects this image to the concept of Christ the King.

In Acts 2:29–35, Peter refers to the similar glorification of Jesus in the context of the resurrection.

The gospel writers interpret the psalm as a messianic prophecy:

while the Pharisees were gathered together, Jesus asked them a question, saying, "What do you think of the Christ? Whose son is he?" They said to him, "The son of David." He said to them, "How is it then that David in the Spirit calls him Lord, saying, The Lord said to my Lord: Sit at my right hand, till I put thy enemies under thy feet? If David thus calls him Lord, how is he his son?" And no one was able to answer him a word

— Matthew 22:41–46

According to Augustine of Hippo,: "It was necessary that all this should be prophesied, announced in advance. We needed to be told so that our minds might be prepared. He did not will to come so suddenly that we would shrink from him in fear; rather are we meant to expect him as the one in whom we have believed."

2 Samuel 7:14

I will be his father, and he shall be my son. If he commit iniquity, I will chasten him with the rod of men, and with the stripes of the children of men: (KJV)

Hebrews 1:5 quotes this verse as, "I will be his Father, and he will be my Son." In Samuel, the verse continues: "When he does wrong, I will punish him with the rod of men, with floggings inflicted by men." This is, however, not reflected in the comparable section in 1 Chronicles 17:13. The phrase as quoted in Hebrews is generally seen as a reference to the Davidic covenant, whereby God assures the king of his continued mercy to him and his descendants. It is in this context that Charles James Butler sees Psalm 41 as quoted by Jesus in John 13:18 as also messianic.

Wisdom 2:12–20

See also: Book of Wisdom § Themes

The Wisdom of Solomon is one of the Deuterocanonical books of the Old Testament. The Deuterocanonical books are considered canonical by Catholics, Eastern Orthodox and Oriental Orthodox, but are considered non-canonical by Jews and Protestants.

Let us lie in wait for the righteous man,

because he is inconvenient to us and opposes our actions;

he reproaches us for sins against the law,

and accuses us of sins against our training.

He professes to have knowledge of God,

and calls himself a child of the Lord.

He became to us a reproof of our thoughts;

the very sight of him is a burden to us,

because his manner of life is unlike that of others,

and his ways are strange.

We are considered by him as something base,

and he avoids our ways as unclean;

he calls the last end of the righteous happy,

and boasts that God is his father.

Let us see if his words are true,

and let us test what will happen at the end of his life;

for if the righteous man is God’s son, he will help him,

and will deliver him from the hand of his adversaries.

Let us test him with insult and torture,

that we may find out how gentle he is,

and make trial of his forbearance.

Let us condemn him to a shameful death,

for, according to what he says, he will be protected.

— Wisdom 2:12–20

Zechariah

Zechariah 9:9

Rejoice greatly, O daughter of Zion! Shout in triumph, O daughter of Jerusalem! Behold, your king is coming to you; He is just and endowed with salvation, Humble, and mounted on a donkey, Even on a colt, the foal of a donkey.

— Zechariah 9:9

Christian authors have interpreted Zechariah 9:9 as a prophecy of an act of messianic self-humiliation. The Gospel of John links this verse to the account of Jesus' entry into Jerusalem:

took the branches of the palm trees and went out to meet Him, and began to shout, "Hosanna! BLESSED IS HE WHO COMES IN THE NAME OF THE LORD, even the King of Israel." Jesus, finding a young donkey, sat on it; as it is written, "FEAR NOT, DAUGHTER OF ZION; BEHOLD, YOUR KING IS COMING, SEATED ON A DONKEY'S COLT."

— John 12:13–15

The Synoptic Gospels make clear that Jesus arranged this event, thus consciously fulfilling the prophecy.^[79]

The Gospel of Matthew describes Jesus' triumphant entry on Palm Sunday as a fulfillment of this verse in Zechariah. Matthew describes the prophecy in terms of a colt and a separate donkey, whereas the original only mentions the colt; the reference in Zechariah is a Jewish parallelism referring only to a single animal, and the gospels of Mark, Luke, and John state Jesus sent his disciples after only one animal. Several explanations have been suggested, such as that Matthew misread the original, the existence of the foal is implied, or he wanted to create a deliberate echo of a reference in 2 Samuel 16:1–4, where there are two asses for David's household to ride on.

In the most ancient Jewish writings Zechariah 9:9 is applied to the Messiah. According to the Talmud, so firm was the belief in the ass on which the Messiah is to ride that "if anyone saw an ass in his dream, he will see salvation". The verse is also Messianically quoted in Sanh. 98 a, in Pirqé de R. Eliez. c. 31, and in several of the Midrashim.

Zechariah 12:10

And I will pour upon the house of David, and upon the inhabitants of Jerusalem, the spirit of grace and of supplication; and they shall look unto Me because they have thrust him through; and they shall mourn for him, as one mourneth for his only son, and shall be in bitterness for him, as one that is in bitterness for his first-born.

— Zechariah 12:10

Zechariah 12:10 is another verse commonly cited by Christian authors as a messianic prophecy fulfilled by Jesus.

In some of the most ancient Jewish writings, Zechariah 12:10 is applied to the Messiah Ben Joseph in the Talmud, and so is verse 12 ("The land will wail, each family by itself: The family of the House of David by themselves, and their women by themselves; the family of the House of Nathan by themselves, and their women by themselves"), there being, however, a difference of opinion whether the mourning is caused by the death of the Messiah Ben Joseph, or else on account of the evil concupiscence (Yetzer hara).

The Gospel of John makes reference to this prophecy when referring to the crucifixion of Jesus, as can be seen in the following account:

So the soldiers came, and broke the legs of the first man and of the other who was crucified with Him; but coming to Jesus, when they saw that He was already dead, they did not break His legs. But one of the soldiers pierced His side with a spear, and immediately blood and water came out. And he who has seen has testified, and his testimony is true; and he knows that he is telling the truth, so that you also may believe. For these things came to pass to fulfill the Scripture, "NOT A BONE OF HIM SHALL BE BROKEN." And again another Scripture says, "THEY SHALL LOOK ON HIM WHOM THEY PIERCED."

— John 19:32–37

Zechariah 12:10 is often regarded as mistranslated by modern-day adherents to Judaism. It is often translated by Jews as follows:

And I will pour out upon the house of David and upon the inhabitants of Jerusalem a spirit of grace and supplications. And they shall look to me because of those who have been thrust through [with swords], and they shall mourn over it as one mourns over an only son and shall be in bitterness, therefore, as one is embittered over a firstborn son.

The Jewish-Christian debate on the correct rendering of Zechariah 12:10 oftentimes come down to the translation of the Hebrew phrase "את אשר (’êṯ-’ă·šer or et-asher)" which can mean either "whom" or "about" depending on the context.

Verses read as Davidic line prophecies

Main article: Davidic dynasty in Bible prophecy

Debate about prophecy fulfillment

Among Christian believers, opinion varies as to which Old Testament passages are messianic prophecies and which are not, and whether the prophecies they claim to have been fulfilled are intended to be prophecies. The authors of these Old Testament prophecies often appear to be describing events that had already occurred. For example, the New Testament verse states:

So he got up, took the child and his mother during the night and left for Egypt, 15 where he stayed until the death of Herod. And so was fulfilled what the Lord had said through the prophet: 'Out of Egypt I called my son.

— Matthew 2:14

This is referring to the Old Testament verse Hosea 11:1. However, that passage reads,

When Israel was a child, I loved him, and out of Egypt I called my son.

Skeptics say that the Hosea passage clearly is talking about a historical event and therefore the passage clearly is not a prophecy.

According to modern scholarship, the suffering servant described in Isaiah chapter 53 is actually the Jewish people. According to some, the rabbinic response, e.g., Rashi and Maimonides, is that, although the suffering servant passage is clearly prophetic and even if Psalm 22 is prophetic, the Messiah has not come yet; therefore, the passages could not be talking about Jesus. As noted above, there is some controversy about the phrase "they have pierced my hands and my feet".

For modern Bible scholars, either the verses make no claim of predicting future events, or the verses make no claim of speaking about the Messiah. They view the argument that Jesus is the Messiah because he has fulfilled prophecy as a fallacy, i.e. it is a confession of faith masquerading as objective rational argumentation. As Christian-turned-atheist Farrell Till argues in his Skeptical Review,

What is the rationale for distorting the scriptures so flagrantly? Well, the answer, of course, is obvious: the gospel writers were desperate to prove that their man Jesus was the Messiah who had been promised in the Old Testament. Since there really were no prophecies of a virgin-born, crucified, resurrected Messiah in the Old Testament, they had to twist and distort to give the appearance that Jesus was the long-awaited one.