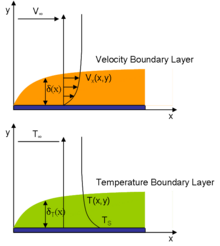
In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition (zero velocity at the wall). The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.
The air next to a human is heated resulting in gravity-induced convective airflow, airflow which results in both a velocity and thermal boundary layer. A breeze disrupts the boundary layer, and hair and clothing protect it, making the human feel cooler or warmer. On an aircraft wing, the velocity boundary layer is the part of the flow close to the wing, where viscous forces distort the surrounding non-viscous flow. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) near the ground. It is affected by the surface; day-night heat flows caused by the sun heating the ground, moisture, or momentum transfer to or from the surface.
Types of boundary layer

Laminar boundary layers can be loosely classified according to their structure and the circumstances under which they are created. The thin shear layer which develops on an oscillating body is an example of a Stokes boundary layer, while the Blasius boundary layer refers to the well-known similarity solution near an attached flat plate held in an oncoming unidirectional flow and Falkner–Skan boundary layer, a generalization of Blasius profile. When a fluid rotates and viscous forces are balanced by the Coriolis effect (rather than convective inertia), an Ekman layer forms. In the theory of heat transfer, a thermal boundary layer occurs. A surface can have multiple types of boundary layer simultaneously.
The viscous nature of airflow reduces the local velocities on a surface and is responsible for skin friction. The layer of air over the wing's surface that is slowed down or stopped by viscosity, is the boundary layer. There are two different types of boundary layer flow: laminar and turbulent.
Laminar boundary layer flow
The laminar boundary is a very smooth flow, while the turbulent boundary layer contains swirls or "eddies." The laminar flow creates less skin friction drag than the turbulent flow, but is less stable. Boundary layer flow over a wing surface begins as a smooth laminar flow. As the flow continues back from the leading edge, the laminar boundary layer increases in thickness.
Turbulent boundary layer flow
At some distance back from the leading edge, the smooth laminar flow breaks down and transitions to a turbulent flow. From a drag standpoint, it is advisable to have the transition from laminar to turbulent flow as far aft on the wing as possible, or have a large amount of the wing surface within the laminar portion of the boundary layer. The low energy laminar flow, however, tends to break down more suddenly than the turbulent layer.
The Prandtl boundary layer concept


The aerodynamic boundary layer was first hypothesized by Ludwig Prandtl in a paper presented on August 12, 1904 at the third International Congress of Mathematicians in Heidelberg, Germany. It simplifies the equations of fluid flow by dividing the flow field into two areas: one inside the boundary layer, dominated by viscosity and creating the majority of drag experienced by the boundary body; and one outside the boundary layer, where viscosity can be neglected without significant effects on the solution. This allows a closed-form solution for the flow in both areas by making significant simplifications of the full Navier–Stokes equations. The same hypothesis is applicable to other fluids (besides air) with moderate to low viscosity such as water. For the case where there is a temperature difference between the surface and the bulk fluid, it is found that the majority of the heat transfer to and from a body takes place in the vicinity of the velocity boundary layer. This again allows the equations to be simplified in the flow field outside the boundary layer. The pressure distribution throughout the boundary layer in the direction normal to the surface (such as an airfoil) remains relatively constant throughout the boundary layer, and is the same as on the surface itself.
The thickness of the velocity boundary layer is normally defined as the distance from the solid body to the point at which the viscous flow velocity is 99% of the freestream velocity (the surface velocity of an inviscid flow). Displacement thickness is an alternative definition stating that the boundary layer represents a deficit in mass flow compared to inviscid flow with slip at the wall. It is the distance by which the wall would have to be displaced in the inviscid case to give the same total mass flow as the viscous case. The no-slip condition requires the flow velocity at the surface of a solid object be zero and the fluid temperature be equal to the temperature of the surface. The flow velocity will then increase rapidly within the boundary layer, governed by the boundary layer equations, below.
The thermal boundary layer thickness is similarly the distance from the body at which the temperature is 99% of the freestream temperature. The ratio of the two thicknesses is governed by the Prandtl number. If the Prandtl number is 1, the two boundary layers are the same thickness. If the Prandtl number is greater than 1, the thermal boundary layer is thinner than the velocity boundary layer. If the Prandtl number is less than 1, which is the case for air at standard conditions, the thermal boundary layer is thicker than the velocity boundary layer.
In high-performance designs, such as gliders and commercial aircraft, much attention is paid to controlling the behavior of the boundary layer to minimize drag. Two effects have to be considered. First, the boundary layer adds to the effective thickness of the body, through the displacement thickness, hence increasing the pressure drag. Secondly, the shear forces at the surface of the wing create skin friction drag.
At high Reynolds numbers, typical of full-sized aircraft, it is desirable to have a laminar boundary layer. This results in a lower skin friction due to the characteristic velocity profile of laminar flow. However, the boundary layer inevitably thickens and becomes less stable as the flow develops along the body, and eventually becomes turbulent, the process known as boundary layer transition. One way of dealing with this problem is to suck the boundary layer away through a porous surface (see Boundary layer suction). This can reduce drag, but is usually impractical due to its mechanical complexity and the power required to move the air and dispose of it. Natural laminar flow (NLF) techniques push the boundary layer transition aft by reshaping the airfoil or fuselage so that its thickest point is more aft and less thick. This reduces the velocities in the leading part and the same Reynolds number is achieved with a greater length.
At lower Reynolds numbers, such as those seen with model aircraft, it is relatively easy to maintain laminar flow. This gives low skin friction, which is desirable. However, the same velocity profile which gives the laminar boundary layer its low skin friction also causes it to be badly affected by adverse pressure gradients. As the pressure begins to recover over the rear part of the wing chord, a laminar boundary layer will tend to separate from the surface. Such flow separation causes a large increase in the pressure drag, since it greatly increases the effective size of the wing section. In these cases, it can be advantageous to deliberately trip the boundary layer into turbulence at a point prior to the location of laminar separation, using a turbulator. The fuller velocity profile of the turbulent boundary layer allows it to sustain the adverse pressure gradient without separating. Thus, although the skin friction is increased, overall drag is decreased. This is the principle behind the dimpling on golf balls, as well as vortex generators on aircraft. Special wing sections have also been designed which tailor the pressure recovery so laminar separation is reduced or even eliminated. This represents an optimum compromise between the pressure drag from flow separation and skin friction from induced turbulence.
When using half-models in wind tunnels, a peniche is sometimes used to reduce or eliminate the effect of the boundary layer.
Boundary layer equations
The deduction of the boundary layer equations was one of the most important advances in fluid dynamics. Using an order of magnitude analysis, the well-known governing Navier–Stokes equations of viscous fluid flow can be greatly simplified within the boundary layer. Notably, the characteristic of the partial differential equations (PDE) becomes parabolic, rather than the elliptical form of the full Navier–Stokes equations. This greatly simplifies the solution of the equations. By making the boundary layer approximation, the flow is divided into an inviscid portion (which is easy to solve by a number of methods) and the boundary layer, which is governed by an easier to solve PDE. The continuity and Navier–Stokes equations for a two-dimensional steady incompressible flow in Cartesian coordinates are given by
where and are the velocity components, is the density, is the pressure, and is the kinematic viscosity of the fluid at a point.
The approximation states that, for a sufficiently high Reynolds number the flow over a surface can be divided into an outer region of inviscid flow unaffected by viscosity (the majority of the flow), and a region close to the surface where viscosity is important (the boundary layer). Let and be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysis, it can be shown that the above equations of motion reduce within the boundary layer to become
and if the fluid is incompressible (as liquids are under standard conditions):
The order of magnitude analysis assumes the streamwise length scale significantly larger than the transverse length scale inside the boundary layer. It follows that variations in properties in the streamwise direction are generally much lower than those in the wall normal direction. Apply this to the continuity equation shows that , the wall normal velocity, is small compared with the streamwise velocity.
Since the static pressure is independent of , then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let be the fluid velocity outside the boundary layer, where and are both parallel. This gives upon substituting for the following result
For a flow in which the static pressure also does not change in the direction of the flow
so remains constant.
Therefore, the equation of motion simplifies to become
These approximations are used in a variety of practical flow problems of scientific and engineering interest. The above analysis is for any instantaneous laminar or turbulent boundary layer, but is used mainly in laminar flow studies since the mean flow is also the instantaneous flow because there are no velocity fluctuations present. This simplified equation is a parabolic PDE and can be solved using a similarity solution often referred to as the Blasius boundary layer.
Prandtl's transposition theorem
Prandtl observed that from any solution which satisfies the boundary layer equations, further solution , which is also satisfying the boundary layer equations, can be constructed by writing
where is arbitrary. Since the solution is not unique from mathematical perspective, to the solution can added any one of an infinite set of eigenfunctions as shown by Stewartson and Paul A. Libby.
Von Kármán momentum integral
Von Kármán derived the integral equation by integrating the boundary layer equation across the boundary layer in 1921. The equation is
where
- is the wall shear stress, is the suction/injection velocity at the wall, is the displacement thickness and is the momentum thickness. Kármán–Pohlhausen Approximation is derived from this equation.
Energy integral
The energy integral was derived by Wieghardt.
where
- is the energy dissipation rate due to viscosity across the boundary layer and is the energy thickness.
Von Mises transformation
For steady two-dimensional boundary layers, von Mises introduced a transformation which takes and (stream function) as independent variables instead of and and uses a dependent variable instead of . The boundary layer equation then become
The original variables are recovered from
This transformation is later extended to compressible boundary layer by von Kármán and HS Tsien.
Crocco's transformation
For steady two-dimensional compressible boundary layer, Luigi Crocco introduced a transformation which takes and as independent variables instead of and and uses a dependent variable (shear stress) instead of . The boundary layer equation then becomes
The original coordinate is recovered from
Turbulent boundary layers
The treatment of turbulent boundary layers is far more difficult due to the time-dependent variation of the flow properties. One of the most widely used techniques in which turbulent flows are tackled is to apply Reynolds decomposition. Here the instantaneous flow properties are decomposed into a mean and fluctuating component with the assumption that the mean of the fluctuating component is always zero. Applying this technique to the boundary layer equations gives the full turbulent boundary layer equations not often given in literature:
Using a similar order-of-magnitude analysis, the above equations can be reduced to leading order terms. By choosing length scales for changes in the transverse-direction, and for changes in the streamwise-direction, with , the x-momentum equation simplifies to:
This equation does not satisfy the no-slip condition at the wall. Like Prandtl did for his boundary layer equations, a new, smaller length scale must be used to allow the viscous term to become leading order in the momentum equation. By choosing as the y-scale, the leading order momentum equation for this "inner boundary layer" is given by:
In the limit of infinite Reynolds number, the pressure gradient term can be shown to have no effect on the inner region of the turbulent boundary layer. The new "inner length scale" is a viscous length scale, and is of order , with being the velocity scale of the turbulent fluctuations, in this case a friction velocity.
Unlike the laminar boundary layer equations, the presence of two regimes governed by different sets of flow scales (i.e. the inner and outer scaling) has made finding a universal similarity solution for the turbulent boundary layer difficult and controversial. To find a similarity solution that spans both regions of the flow, it is necessary to asymptotically match the solutions from both regions of the flow. Such analysis will yield either the so-called log-law or power-law.
Similar approaches to the above analysis has also been applied for thermal boundary layers, using the energy equation in compressible flows.
The additional term in the turbulent boundary layer equations is known as the Reynolds shear stress and is unknown a priori. The solution of the turbulent boundary layer equations therefore necessitates the use of a turbulence model, which aims to express the Reynolds shear stress in terms of known flow variables or derivatives. The lack of accuracy and generality of such models is a major obstacle in the successful prediction of turbulent flow properties in modern fluid dynamics.
A constant stress layer exists in the near wall region. Due to the damping of the vertical velocity fluctuations near the wall, the Reynolds stress term will become negligible and we find that a linear velocity profile exists. This is only true for the very near wall region.
Heat and mass transfer
In 1928, the French engineer André Lévêque observed that convective heat transfer in a flowing fluid is affected only by the velocity values very close to the surface. For flows of large Prandtl number, the temperature/mass transition from surface to freestream temperature takes place across a very thin region close to the surface. Therefore, the most important fluid velocities are those inside this very thin region in which the change in velocity can be considered linear with normal distance from the surface. In this way, for
when , then
where θ is the tangent of the Poiseuille parabola intersecting the wall. Although Lévêque's solution was specific to heat transfer into a Poiseuille flow, his insight helped lead other scientists to an exact solution of the thermal boundary-layer problem. Schuh observed that in a boundary-layer, u is again a linear function of y, but that in this case, the wall tangent is a function of x. He expressed this with a modified version of Lévêque's profile,
This results in a very good approximation, even for low numbers, so that only liquid metals with much less than 1 cannot be treated this way. In 1962, Kestin and Persen published a paper describing solutions for heat transfer when the thermal boundary layer is contained entirely within the momentum layer and for various wall temperature distributions. For the problem of a flat plate with a temperature jump at , they propose a substitution that reduces the parabolic thermal boundary-layer equation to an ordinary differential equation. The solution to this equation, the temperature at any point in the fluid, can be expressed as an incomplete gamma function. Schlichting proposed an equivalent substitution that reduces the thermal boundary-layer equation to an ordinary differential equation whose solution is the same incomplete gamma function.
Convective transfer constants from boundary layer analysis
Paul Richard Heinrich Blasius derived an exact solution to the above laminar boundary layer equations. The thickness of the boundary layer is a function of the Reynolds number for laminar flow.
- = the thickness of the boundary layer: the region of flow where the velocity is less than 99% of the far field velocity ; is position along the semi-infinite plate, and is the Reynolds Number given by ( density and dynamic viscosity).
The Blasius solution uses boundary conditions in a dimensionless form:
- at
- at and
Note that in many cases, the no-slip boundary condition holds that , the fluid velocity at the surface of the plate equals the velocity of the plate at all locations. If the plate is not moving, then . A much more complicated derivation is required if fluid slip is allowed.
In fact, the Blasius solution for laminar velocity profile in the boundary layer above a semi-infinite plate can be easily extended to describe Thermal and Concentration boundary layers for heat and mass transfer respectively. Rather than the differential x-momentum balance (equation of motion), this uses a similarly derived Energy and Mass balance:
Energy:
Mass:
For the momentum balance, kinematic viscosity can be considered to be the momentum diffusivity. In the energy balance this is replaced by thermal diffusivity , and by mass diffusivity in the mass balance. In thermal diffusivity of a substance, is its thermal conductivity, is its density and is its heat capacity. Subscript AB denotes diffusivity of species A diffusing into species B.
Under the assumption that , these equations become equivalent to the momentum balance. Thus, for Prandtl number and Schmidt number the Blasius solution applies directly.
Accordingly, this derivation uses a related form of the boundary conditions, replacing with or (absolute temperature or concentration of species A). The subscript S denotes a surface condition.
- at
- at and
Using the streamline function Blasius obtained the following solution for the shear stress at the surface of the plate.
And via the boundary conditions, it is known that
We are given the following relations for heat/mass flux out of the surface of the plate
So for
where are the regions of flow where and are less than 99% of their far field values.
Because the Prandtl number of a particular fluid is not often unity, German engineer E. Polhausen who worked with Ludwig Prandtl attempted to empirically extend these equations to apply for . His results can be applied to as well. He found that for Prandtl number greater than 0.6, the thermal boundary layer thickness was approximately given by:

- and therefore
From this solution, it is possible to characterize the convective heat/mass transfer constants based on the region of boundary layer flow. Fourier's law of conduction and Newton's Law of Cooling are combined with the flux term derived above and the boundary layer thickness.
This gives the local convective constant at one point on the semi-infinite plane. Integrating over the length of the plate gives an average
Following the derivation with mass transfer terms ( = convective mass transfer constant, = diffusivity of species A into species B, ), the following solutions are obtained:
These solutions apply for laminar flow with a Prandtl/Schmidt number greater than 0.6.
Many of the principles that apply to aircraft also apply to ships, submarines, and offshore platforms.
For ships, unlike aircraft, one deals with incompressible flows, where change in water density is negligible (a pressure rise close to 1000kPa leads to a change of only 2–3 kg/m3). This field of fluid dynamics is called hydrodynamics. A ship engineer designs for hydrodynamics first, and for strength only later. The boundary layer development, breakdown, and separation become critical because the high viscosity of water produces high shear stresses.
Boundary layer turbine
This effect was exploited in the Tesla turbine, patented by Nikola Tesla in 1913. It is referred to as a bladeless turbine because it uses the boundary layer effect and not a fluid impinging upon the blades as in a conventional turbine. Boundary layer turbines are also known as cohesion-type turbine, bladeless turbine, and Prandtl layer turbine (after Ludwig Prandtl).
Predicting transient boundary layer thickness in a cylinder using dimensional analysis
By using the transient and viscous force equations for a cylindrical flow you can predict the transient boundary layer thickness by finding the Womersley Number ().
Transient Force =
Viscous Force =
Setting them equal to each other gives:
Solving for delta gives:
In dimensionless form:
where = Womersley Number; = density; = velocity; ?; = length of transient boundary layer; = viscosity; = characteristic length.
Predicting convective flow conditions at the boundary layer in a cylinder using dimensional analysis
By using the convective and viscous force equations at the boundary layer for a cylindrical flow you can predict the convective flow conditions at the boundary layer by finding the dimensionless Reynolds Number ().
Convective force:
Viscous force:
Setting them equal to each other gives:
Solving for delta gives:
In dimensionless form:
where = Reynolds Number; = density; = velocity; = length of convective boundary layer; = viscosity; = characteristic length.
Boundary layer ingestion
Boundary layer ingestion promises an increase in aircraft fuel efficiency with an aft-mounted propulsor ingesting the slow fuselage boundary layer and re-energising the wake to reduce drag and improve propulsive efficiency. To operate in distorted airflow, the fan is heavier and its efficiency is reduced, and its integration is challenging. It is used in concepts like the Aurora D8 or the French research agency Onera’s Nova, saving 5% in cruise by ingesting 40% of the fuselage boundary layer.
Airbus presented the Nautilius concept at the ICAS congress in September 2018: to ingest all the fuselage boundary layer, while minimizing the azimuthal flow distortion, the fuselage splits into two spindles with 13-18:1 bypass ratio fans. Propulsive efficiencies are up to 90% like counter-rotating open rotors with smaller, lighter, less complex and noisy engines. It could lower fuel burn by over 10% compared to a usual underwing 15:1 bypass ratio engine.



































![{\displaystyle {\begin{aligned}&\mu \rho u{\frac {\partial }{\partial x}}\left({\frac {1}{\tau }}\right)+{\frac {\partial ^{2}\tau }{\partial u^{2}}}-\mu {\frac {dp}{dx}}{\frac {\partial }{\partial u}}\left({\frac {1}{\tau }}\right)=0,\\[5pt]&{\text{if }}{\frac {dp}{dx}}=0,{\text{ then }}{\frac {\mu \rho }{\tau ^{2}}}{\frac {\partial \tau }{\partial x}}={\frac {1}{u}}{\frac {\partial ^{2}\tau }{\partial u^{2}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4fb1fe61083afecdabf54fe54eb101ba820a717)














![{\displaystyle u(y)=U\left[1-{\frac {(y-h)^{2}}{h^{2}}}\right]=U{\frac {y}{h}}\left[2-{\frac {y}{h}}\right]\;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/823f8f75f57cfdb9b46572e46a4f5b04ebf97e00)