Adenosine

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Adenosine

Adenosine

Clinical data
Trade names	Adenocard; Adenocor; Adenic; Adenoco; Adeno-Jec; Adenoscan; Adenosin; Adrekar; Krenosin
Other names	SR-96225 (developmental code name)
AHFS/Drugs.com	Monograph
Pregnancy category	C (adenosine may be safe to the fetus in pregnant women)
Routes of administration	Intravenous
ATC code	C01EB10 (WHO)
Legal status
Legal status	In general: ℞ (Prescription only)
Pharmacokinetic data
Bioavailability	Rapidly cleared from circulation via cellular uptake
Protein binding	No
Metabolism	Rapidly converted to inosine and adenosine monophosphate
Elimination half-life	cleared plasma <30 seconds; half-life <10 seconds
Excretion	can leave cell intact or can be degraded to hypoxanthine, xanthine, and ultimately uric acid
Identifiers

IUPAC name
CAS Number	58-61-7
PubChem CID	60961
IUPHAR/BPS	2844
DrugBank	DB00640
ChemSpider	54923
UNII	K72T3FS567
KEGG	C00212
ChEBI	CHEBI:16335
ChEMBL	ChEMBL477
CompTox Dashboard (EPA)	DTXSID1022558
ECHA InfoCard	100.000.354
Chemical and physical data
Formula	C10H13N5O4
Molar mass	267.245 g·mol−1

Adenosine (symbol A) is an organic compound that occurs widely in nature in the form of diverse derivatives. The molecule consists of an adenine attached to a ribose via a β-N₉-glycosidic bond. Adenosine is one of the four nucleoside building blocks of RNA (and its derivative deoxyadenosine is a building block of DNA), which are essential for all life on earth. Its derivatives include the energy carriers adenosine mono-, di-, and triphosphate, also known as AMP/ADP/ATP. Cyclic adenosine monophosphate (cAMP) is pervasive in signal transduction. Adenosine is used as an intravenous medication for some cardiac arrhythmias.

Adenosyl (abbreviated Ado or 5'-dAdo) is the chemical group formed by removal of the 5′-hydroxy (OH) group. It is found in adenosylcobalamin (an active form of vitamin B12) and as a radical in the radical SAM enzymes.

Medical uses

Supraventricular tachycardia

In individuals with supraventricular tachycardia (SVT), adenosine is used to help identify and convert the rhythm.

Certain SVTs can be successfully terminated with adenosine. This includes any re-entrant arrhythmias that require the AV node for the re-entry, e.g., AV reentrant tachycardia (AVRT) and AV nodal reentrant tachycardia (AVNRT). In addition, atrial tachycardia can sometimes be terminated with adenosine.

Fast rhythms of the heart that are confined to the atria (e.g., atrial fibrillation and atrial flutter) or ventricles (e.g., monomorphic ventricular tachycardia), and do not involve the AV node as part of the re-entrant circuit, are not typically converted by adenosine. However, the ventricular response rate is temporarily slowed with adenosine in such cases.

Because of the effects of adenosine on AV node-dependent SVTs, adenosine is considered a class V antiarrhythmic agent. When adenosine is used to cardiovert an abnormal rhythm, it is normal for the heart to enter ventricular asystole for a few seconds. This can be disconcerting to a normally conscious patient, and is associated with angina-like sensations in the chest.

Nuclear stress test

Adenosine is used as an adjunct to thallium (TI 201) or technetium (Tc99m) myocardial perfusion scintigraphy (nuclear stress test) in patients unable to undergo adequate stress testing with exercise.

Dosage

When given for the evaluation or treatment of a supraventricular tachycardia (SVT), the initial dose is 6 mg to 12 mg, depending on standing orders or provider preference, given as a rapid parenteral infusion. Due to adenosine's extremely short half-life, the IV line is started as proximal (near) to the heart as possible, such as the antecubital fossa. The IV push is often followed with a flush of 10–20 mL of normal saline. If this has no effect (i.e., no evidence of transient AV block), a dose of 12 mg can be given 1–2 minutes after the first dose. When given to dilate the arteries, such as in a "stress test", the dosage is typically 0.14 mg/kg/min, administered for 4 or 6 minutes, depending on the protocol.

The recommended dose may be increased in patients on theophylline since methylxanthines prevent binding of adenosine at receptor sites. The dose is often decreased in patients on dipyridamole (Persantine) and diazepam (Valium) because adenosine potentiates the effects of these drugs. The recommended dose is also reduced by half in patients presenting congestive heart failure, myocardial infarction, shock, hypoxia, and/or chronic liver disease or chronic kidney disease, and in elderly patients.

Drug interactions

Dipyridamole potentiates the action of adenosine, requiring the use of lower doses.

Caffeine's principal mode of action is as an antagonist of adenosine receptors in the brain.

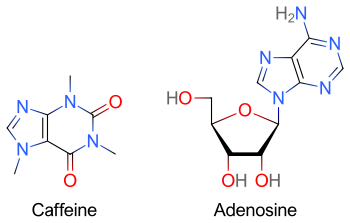
Methylxanthines (e.g. caffeine found in coffee, theophylline found in tea, or theobromine found in chocolate) have a purine structure and bind to some of the same receptors as adenosine. Methylxanthines act as competitive antagonists of adenosine and can blunt its pharmacological effects. Individuals taking large quantities of methylxanthines may require increased doses of adenosine.

Caffeine acts by blocking binding of adenosine to the adenosine A₁ receptor, which enhances release of the neurotransmitter acetylcholine. Caffeine also increases cyclic AMP levels through nonselective inhibition of phosphodiesterase. "Caffeine has a three-dimensional structure similar to that of adenosine," which allows it to bind and block its receptors.

Contraindications

Common contraindications for adenosine include

• Asthma, traditionally considered an absolute contraindication. This is being contended, and it is now considered a relative contraindication (however, selective adenosine antagonists are being investigated for use in treatment of asthma)

Pharmacological effects

Adenosine is an endogenous purine nucleoside that modulates many physiological processes. Cellular signaling by adenosine occurs through four known adenosine receptor subtypes (A₁, A_2A, A_2B, and A₃).

Extracellular adenosine concentrations from normal cells are approximately 300 nM; however, in response to cellular damage (e.g., in inflammatory or ischemic tissue), these concentrations are quickly elevated (600–1,200 nM). Thus, in regard to stress or injury, the function of adenosine is primarily that of cytoprotection preventing tissue damage during instances of hypoxia, ischemia, and seizure activity. Activation of A_2A receptors produces a constellation of responses that in general can be classified as anti-inflammatory. Enzymatic production of adenosine can be anti-inflammatory or immunosuppressive.

Adenosine receptors

Main article: Adenosine receptor

All adenosine receptor subtypes (A₁, A_2A, A_2B, and A₃) are G-protein-coupled receptors. The four receptor subtypes are further classified based on their ability to either stimulate or inhibit adenylate cyclase activity. The A₁ receptors couple to G_i/o and decrease cAMP levels, while the A₂ adenosine receptors couple to G_s, which stimulates adenylate cyclase activity. In addition, A₁ receptors couple to G_o, which has been reported to mediate adenosine inhibition of Ca²⁺ conductance, whereas A_2B and A₃ receptors also couple to G_q and stimulate phospholipase activity. Researchers at Cornell University have recently shown adenosine receptors to be key in opening the blood-brain barrier (BBB). Mice dosed with adenosine have shown increased transport across the BBB of amyloid plaque antibodies and prodrugs associated with Parkinson's disease, Alzheimer's, multiple sclerosis, and cancers of the central nervous system.

Ghrelin/growth hormone secretagogue receptor

Adenosine is an endogenous agonist of the ghrelin/growth hormone secretagogue receptor. However, while it is able to increase appetite, unlike other agonists of this receptor, adenosine is unable to induce the secretion of growth hormone and increase its plasma levels.

Mechanism of action

When it is administered intravenously, adenosine causes transient heart block in the atrioventricular (AV) node. This is mediated via the A₁ receptor, inhibiting adenylyl cyclase, reducing cAMP and so causing cell hyperpolarization by increasing K⁺ efflux via inward rectifier K⁺ channels, subsequently inhibiting Ca²⁺ current. It also causes endothelial-dependent relaxation of smooth muscle as is found inside the artery walls. This causes dilation of the "normal" segments of arteries, i.e. where the endothelium is not separated from the tunica media by atherosclerotic plaque. This feature allows physicians to use adenosine to test for blockages in the coronary arteries, by exaggerating the difference between the normal and abnormal segments.

The administration of adenosine also reduces blood flow to coronary arteries past the occlusion. Other coronary arteries dilate when adenosine is administered while the segment past the occlusion is already maximally dilated, which is a process called coronary steal. This leads to less blood reaching the ischemic tissue, which in turn produces the characteristic chest pain.

Metabolism

Adenosine used as a second messenger can be the result of de novo purine biosynthesis via adenosine monophosphate (AMP), though it is possible other pathways exist.

When adenosine enters the circulation, it is broken down by adenosine deaminase, which is present in red blood cells and the vessel wall.

Dipyridamole, an inhibitor of adenosine nucleoside transporter, allows adenosine to accumulate in the blood stream. This causes an increase in coronary vasodilatation.

Adenosine deaminase deficiency is a known cause of immunodeficiency.

Research

Viruses

See also: Nucleoside analogue

The adenosine analog NITD008 has been reported to directly inhibit the recombinant RNA-dependent RNA polymerase of the dengue virus by terminating its RNA chain synthesis. This interaction suppresses peak viremia and rise in cytokines and prevents lethality in infected animals, raising the possibility of a new treatment for this flavivirus. The 7-deaza-adenosine analog has been shown to inhibit the replication of the hepatitis C virus. BCX4430 is protective against Ebola and Marburg viruses. Such adenosine analogs are potentially clinically useful since they can be taken orally.

Anti-inflammatory properties

Adenosine is believed to be an anti-inflammatory agent at the A_2A receptor. Topical treatment of adenosine to foot wounds in diabetes mellitus has been shown in lab animals to drastically increase tissue repair and reconstruction. Topical administration of adenosine for use in wound-healing deficiencies and diabetes mellitus in humans is currently under clinical investigation.

Methotrexate's anti-inflammatory effect may be due to its stimulation of adenosine release.

Central nervous system

In general, adenosine has an inhibitory effect in the central nervous system (CNS). Caffeine's stimulatory effects are credited primarily (although not entirely) to its capacity to block adenosine receptors, thereby reducing the inhibitory tonus of adenosine in the CNS. This reduction in adenosine activity leads to increased activity of the neurotransmitters dopamine and glutamate. Experimental evidence suggests that adenosine and adenosine agonists can activate Trk receptor phosphorylation through a mechanism that requires the adenosine A_2A receptor.

Hair

Adenosine has been shown to promote thickening of hair on people with thinning hair. A 2013 study compared topical adenosine with minoxidil in male androgenetic alopecia, finding it was as potent as minoxidil (in overall treatment outcomes) but with higher satisfaction rate with patients due to “faster prevention of hair loss and appearance of the newly grown hairs” (further trials were called for to clarify the findings).

Sleep

Adenosine is a key factor in regulating the body's sleep-wake cycle. Adenosine levels rise during periods of wakefulness and lowers during sleep. Higher adenosine levels correlate with a stronger feeling of sleepiness, also known as sleep drive or sleep pressure. Cognitive behavioral therapy for insomnia (CBT-I), which is considered one of the most effective treatments for insomnia, utilizes short-term sleep deprivation to raise and regulate adenosine levels in the body, for the intended promotion of consistent and sustained sleep in the long term.

A principal component of cannabis delta-9-tetrahydrocannabinol (THC) and the endocannabinoid anandamide (AEA) induces sleep in rats by increasing adenosine levels in the basal forebrain. These components also significantly increase slow-wave sleep during the sleep cycle, mediated by CB1 receptor activation. These findings identify a potential therapeutic use of cannabinoids to induce sleep in conditions where sleep may be severely attenuated.

Vasodilation

It also plays a role in regulation of blood flow to various organs through vasodilation.

Limb-sparing techniques

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Limb-sparing_techniques

Limb-sparing techniques, also known as limb-saving or limb-salvage techniques, are performed in order to preserve the look and function of limbs. Limb-sparing techniques are used to preserve limbs affected by trauma, arthritis, cancers such as high-grade bone sarcomas, and vascular conditions such as diabetic foot ulcers. As the techniques for chemotherapy, radiation, and diagnostic modalities improve, there has been a trend toward limb-sparing procedures to avoid amputation, which has been associated with a lower 5-year survival rate and cost-effectiveness compared to limb salvage in the long-run. There are many different types of limb-sparing techniques, including arthrodesis, arthroplasty, endoprosthetic reconstruction, various types of implants, rotationplasty, osseointegration limb replacement, fasciotomy, and revascularization.

Arthrodesis

X-ray of a wrist that has undergone carpal arthrodesis (fusion of the wrist joint). In this case, this means that screws have been inserted through multiple wrist bones so they are now immobilized. Over time, these bones will fuse together, preventing them from rubbing against each other and causing pain.

Arthrodesis is the surgical immobilization of bones within a joint to promote fusion of the joint. Arthrodesis is performed most commonly on joints of the feet, hands, and spine. Arthrodesis can relieve pain from arthritis and fractures. This is accomplished through the use of orthobiologics such as allografts and autografts. Allografts are done by creating bone grafts from a donor bone bank, whereas autografts are bone grafts from other bones in a patient's body. Patient-reported outcomes following this procedure are typically positive in terms of long-term pain relief; however, the procedure also results in decreased range of motion.

Arthroplasty

Diagrams of the most common joints that undergo arthroplasty (joint replacement): shoulders, hips, and knees. Notice that the articular surface of each joint has been removed and replaced with metal and plastic implants to recreate the normal joint interface.

Arthroplasty, otherwise known as joint replacement, is a surgical procedure which involves resurfacing, realignment, or removal of bone at a joint interface to restore the joint's function. Arthroplasty is often performed on hips, knees, shoulders, and ankles to improve range of motion and relieve pain from arthritis or trauma. Arthroplasty of the shoulder is one of the most common of these procedures, although it has only been widely used since 1955. Themistocles Gluck is thought to have created the first shoulder arthroplasty in the 1800s. Since Gluck never published any results or notes on the procedure, Jules-Emile Pean is credited with performing the first shoulder arthroplasty in 1893.

Implants

Alloprosthetic composites

Alloprosthetic composites are a combination of multiple limb-sparing techniques, namely allografts and prosthesis. Allografts are used to replace the bone that has been "resected" using arthroplasty techniques, and then prosthesis is used to support and strengthen the allografts. Alloprosthetic composites are flexible in that surgeons can adapt the implants for any situation.

Prosthetic implants

Prosthetic implants are used when sections of bone must be replaced and no further growth is expected. Implants are mostly made from metals, but the possibility of using ceramic material has been discussed among surgeons. Prosthetics can be temporary or permanent. Temporary implants remain in place until the bone has healed and are then removed. The temporary implants take most of the burden off of the fracture, causing the bone to become less dense. This can lead to re-fracturing of the bone after the implant is removed. The implants can also cause stress concentrations as a result of the material difference between the bone and the plate. With the permanent prostheses, a putty-like substance is injected into the implant site to keep the body, mainly the immune system, from fighting off the implant. This substance can deteriorate bony tissue and cause serious bone problems for the patient. Prosthetic limbs have been used for many years.

Diagram of workflow describing the basic process of 3D-printing an implant for the skull. Notice the use of the advanced computer software to create a 3-dimensional rendering of the part of the skull that will be printed. The rightmost photo depicts the 3D-printed implant placed on the actual skull.

3D-printed implants

3D-printing leverages the power of computer rendering of advanced imaging to tailor implants to each patient, which can then be used to create a physical realization of that implant to use in that individual's surgery. 3D-printing of medical devices was first used in the 1990s for dental implants and custom prosthetics but has since been used for various bones and organs such as urinary bladders.

Rotationplasty

Rotationplasty, more commonly known as Van-Nes or Borggreve Rotation, is a limb-sparing medical procedure performed when a patient's leg is amputated at the knee. The ankle joint is then rotated 180 degrees and is attached to the former knee joint, becoming a new knee joint. This allows patients to have two fully functional feet, as opposed to losing one leg completely to amputation.

Reasons for rotationplasty

Originally, rotationplasty was performed to treat infections and tumors around the knee, especially osteosarcoma of the knee. While it is still being used to treat their complications, rotationplasty is also used to treat growing children who have been diagnosed with tumors around the knee. Rotationplasty is also performed on children with congenital femoral deficiencies, such as those that cause unstable hip joints or limb-length discrepancy of the femur. This procedure gives patients the ability to retain the use of both feet, allowing them to continue living an active lifestyle.

History of rotationplasty

Rotationplasty was first performed by Borggreve in the early 1900s on a 12-year-old boy with tuberculosis. However, the procedure was not well known until 1950. At that time, physician Van Nes reported the results of rotationplasty procedures and became well known for founding the procedure. Since then, many surgeons have performed modified versions of rotationplasty and have had great success.

Rotationplasty procedure

In the actual procedure, the bone affected by the tumor, as well as a small part of the healthy femur and occasionally tibia bone, is removed. The ankle joint is then turned 180 degrees and is reattached to the thigh. They are held together by plates and screws until they have healed naturally. The surgery can take anywhere from 6–10 hours, with a day or two in intensive care. The leg is kept in a cast for 6–12 weeks. After the leg has sufficiently healed, the leg can be fitted for a prosthetic.

Advantages and disadvantages of rotationplasty

In the same scenario, amputation would not leave a knee joint. Rotationplasty retains the use of a knee joint. Furthermore, it provides a better position for a prosthetic limb compared to amputation. As a result, children who have had rotationplasty can return to their previous activities such as playing sports and avoid undergoing additional surgeries throughout their lives. Rotationplasty is also durable and has been associated with enhanced quality of life and life contentment. Unfortunately, not every case turns out favorably. Rotationplasty can result in problems with blood supply to the leg, infection, nerve injuries, problems with bone healing, and fracture of the leg.

Orientability

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Orientability

A torus is an orientable surface

The Möbius strip is a non-orientable surface. Note that the fiddler crab moving around it has left and right flipped with every complete circulation. This would not happen if the crab were on the torus.

The Roman surface is non-orientable

In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space.

Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds often employ methods of homology theory, whereas for differentiable manifolds more structure is present, allowing a formulation in terms of differential forms. A generalization of the notion of orientability of a space is that of orientability of a family of spaces parameterized by some other space (a fiber bundle) for which an orientation must be selected in each of the spaces which varies continuously with respect to changes in the parameter values.

Orientable surfaces

In this animation, a simple analogy is made using a gear that rotates according to the right-hand rule on a surface's normal vector. The orientation of the curves given by the boundaries is given by the direction in which the dots move as they are pushed by the moving gear. On a non-orientable surface, such as the Möbius strip, the boundary would have to move in both directions at once, which is not possible.

A surface S in the Euclidean space R³ is orientable if a chiral two-dimensional figure (for example, ) cannot be moved around the surface and back to where it started so that it looks like its own mirror image (). Otherwise the surface is non-orientable. An abstract surface (i.e., a two-dimensional manifold) is orientable if a consistent concept of clockwise rotation can be defined on the surface in a continuous manner. That is to say that a loop going around one way on the surface can never be continuously deformed (without overlapping itself) to a loop going around the opposite way. This turns out to be equivalent to the question of whether the surface contains no subset that is homeomorphic to the Möbius strip. Thus, for surfaces, the Möbius strip may be considered the source of all non-orientability.

For an orientable surface, a consistent choice of "clockwise" (as opposed to counter-clockwise) is called an orientation, and the surface is called oriented. For surfaces embedded in Euclidean space, an orientation is specified by the choice of a continuously varying surface normal n at every point. If such a normal exists at all, then there are always two ways to select it: n or −n. More generally, an orientable surface admits exactly two orientations, and the distinction between an oriented surface and an orientable surface is subtle and frequently blurred. An orientable surface is an abstract surface that admits an orientation, while an oriented surface is a surface that is abstractly orientable, and has the additional datum of a choice of one of the two possible orientations.

Examples

Most surfaces encountered in the physical world are orientable. Spheres, planes, and tori are orientable, for example. But Möbius strips, real projective planes, and Klein bottles are non-orientable. They, as visualized in 3-dimensions, all have just one side. The real projective plane and Klein bottle cannot be embedded in R³, only immersed with nice intersections.

Note that locally an embedded surface always has two sides, so a near-sighted ant crawling on a one-sided surface would think there is an "other side". The essence of one-sidedness is that the ant can crawl from one side of the surface to the "other" without going through the surface or flipping over an edge, but simply by crawling far enough.

In general, the property of being orientable is not equivalent to being two-sided; however, this holds when the ambient space (such as R³ above) is orientable. For example, a torus embedded in

${\displaystyle K^2\times S^1}$

can be one-sided, and a Klein bottle in the same space can be two-sided; here ${\displaystyle K^2}$ refers to the Klein bottle.

Orientation by triangulation

Any surface has a triangulation: a decomposition into triangles such that each edge on a triangle is glued to at most one other edge. Each triangle is oriented by choosing a direction around the perimeter of the triangle, associating a direction to each edge of the triangle. If this is done in such a way that, when glued together, neighboring edges are pointing in the opposite direction, then this determines an orientation of the surface. Such a choice is only possible if the surface is orientable, and in this case there are exactly two different orientations.

If the figure can be consistently positioned at all points of the surface without turning into its mirror image, then this will induce an orientation in the above sense on each of the triangles of the triangulation by selecting the direction of each of the triangles based on the order red-green-blue of colors of any of the figures in the interior of the triangle.

This approach generalizes to any n-manifold having a triangulation. However, some 4-manifolds do not have a triangulation, and in general for n > 4 some n-manifolds have triangulations that are inequivalent.

Orientability and homology

If H₁(S) denotes the first homology group of a surface S, then S is orientable if and only if H₁(S) has a trivial torsion subgroup. More precisely, if S is orientable then H₁(S) is a free abelian group, and if not then H₁(S) = F + Z/2Z where F is free abelian, and the Z/2Z factor is generated by the middle curve in a Möbius band embedded in S.

Orientability of manifolds

Let M be a connected topological n-manifold. There are several possible definitions of what it means for M to be orientable. Some of these definitions require that M has extra structure, like being differentiable. Occasionally, n = 0 must be made into a special case. When more than one of these definitions applies to M, then M is orientable under one definition if and only if it is orientable under the others.

Orientability of differentiable manifolds

The most intuitive definitions require that M be a differentiable manifold. This means that the transition functions in the atlas of M are C¹-functions. Such a function admits a Jacobian determinant. When the Jacobian determinant is positive, the transition function is said to be orientation preserving. An oriented atlas on M is an atlas for which all transition functions are orientation preserving. M is orientable if it admits an oriented atlas. When n > 0, an orientation of M is a maximal oriented atlas. (When n = 0, an orientation of M is a function M → {±1}.)

Orientability and orientations can also be expressed in terms of the tangent bundle. The tangent bundle is a vector bundle, so it is a fiber bundle with structure group GL(n, R). That is, the transition functions of the manifold induce transition functions on the tangent bundle which are fiberwise linear transformations. If the structure group can be reduced to the group GL⁺(n, R) of positive determinant matrices, or equivalently if there exists an atlas whose transition functions determine an orientation preserving linear transformation on each tangent space, then the manifold M is orientable. Conversely, M is orientable if and only if the structure group of the tangent bundle can be reduced in this way. Similar observations can be made for the frame bundle.

Another way to define orientations on a differentiable manifold is through volume forms. A volume form is a nowhere vanishing section ω of ⋀ⁿ T^∗M, the top exterior power of the cotangent bundle of M. For example, Rⁿ has a standard volume form given by dx¹ ∧ ⋯ ∧ dxⁿ. Given a volume form on M, the collection of all charts U → Rⁿ for which the standard volume form pulls back to a positive multiple of ω is an oriented atlas. The existence of a volume form is therefore equivalent to orientability of the manifold.

Volume forms and tangent vectors can be combined to give yet another description of orientability. If X₁, …, X_n is a basis of tangent vectors at a point p, then the basis is said to be right-handed if ω(X₁, …, X_n) > 0. A transition function is orientation preserving if and only if it sends right-handed bases to right-handed bases. The existence of a volume form implies a reduction of the structure group of the tangent bundle or the frame bundle to GL⁺(n, R). As before, this implies the orientability of M. Conversely, if M is orientable, then local volume forms can be patched together to create a global volume form, orientability being necessary to ensure that the global form is nowhere vanishing.

Homology and the orientability of general manifolds

At the heart of all the above definitions of orientability of a differentiable manifold is the notion of an orientation preserving transition function. This raises the question of what exactly such transition functions are preserving. They cannot be preserving an orientation of the manifold because an orientation of the manifold is an atlas, and it makes no sense to say that a transition function preserves or does not preserve an atlas of which it is a member.

This question can be resolved by defining local orientations. On a one-dimensional manifold, a local orientation around a point p corresponds to a choice of left and right near that point. On a two-dimensional manifold, it corresponds to a choice of clockwise and counter-clockwise. These two situations share the common feature that they are described in terms of top-dimensional behavior near p but not at p. For the general case, let M be a topological n-manifold. A local orientation of M around a point p is a choice of generator of the group

${\displaystyle H_n\left(M,M\setminus \{p\};\mathbf{Z}\right).}$

To see the geometric significance of this group, choose a chart around p. In that chart there is a neighborhood of p which is an open ball B around the origin O. By the excision theorem, ${\displaystyle H_n\left(M,M\setminus \{p\};\mathbf{Z}\right)}$ is isomorphic to ${\displaystyle H_n\left(B,B\setminus \{O\};\mathbf{Z}\right)}$. The ball B is contractible, so its homology groups vanish except in degree zero, and the space B \ O is an (n − 1)-sphere, so its homology groups vanish except in degrees n − 1 and 0. A computation with the long exact sequence in relative homology shows that the above homology group is isomorphic to ${\displaystyle H_{n-1}\left(S^{n-1};\mathbf{Z}\right)\cong \mathbf{Z}}$. A choice of generator therefore corresponds to a decision of whether, in the given chart, a sphere around p is positive or negative. A reflection of Rⁿ through the origin acts by negation on ${\displaystyle H_{n-1}\left(S^{n-1};\mathbf{Z}\right)}$, so the geometric significance of the choice of generator is that it distinguishes charts from their reflections.

On a topological manifold, a transition function is orientation preserving if, at each point p in its domain, it fixes the generators of ${\displaystyle H_n\left(M,M\setminus \{p\};\mathbf{Z}\right)}$. From here, the relevant definitions are the same as in the differentiable case. An oriented atlas is one for which all transition functions are orientation preserving, M is orientable if it admits an oriented atlas, and when n > 0, an orientation of M is a maximal oriented atlas.

Intuitively, an orientation of M ought to define a unique local orientation of M at each point. This is made precise by noting that any chart in the oriented atlas around p can be used to determine a sphere around p, and this sphere determines a generator of ${\displaystyle H_n\left(M,M\setminus \{p\};\mathbf{Z}\right)}$. Moreover, any other chart around p is related to the first chart by an orientation preserving transition function, and this implies that the two charts yield the same generator, whence the generator is unique.

Purely homological definitions are also possible. Assuming that M is closed and connected, M is orientable if and only if the nth homology group ${\displaystyle H_n(M;\mathbf{Z})}$ is isomorphic to the integers Z. An orientation of M is a choice of generator α of this group. This generator determines an oriented atlas by fixing a generator of the infinite cyclic group ${\displaystyle H_n(M;\mathbf{Z})}$ and taking the oriented charts to be those for which α pushes forward to the fixed generator. Conversely, an oriented atlas determines such a generator as compatible local orientations can be glued together to give a generator for the homology group ${\displaystyle H_n(M;\mathbf{Z})}$.

Orientation and cohomology

A manifold M is orientable if and only if the first Stiefel–Whitney class ${\displaystyle w_1(M)\in H^1(M;\mathbf{Z}/2)}$ vanishes. In particular, if the first cohomology group with Z/2 coefficients is zero, then the manifold is orientable. Moreover, if M is orientable and w₁ vanishes, then ${\displaystyle H^0(M;\mathbf{Z}/2)}$ parametrizes the choices of orientations. This characterization of orientability extends to orientability of general vector bundles over M, not just the tangent bundle.

The orientation double cover

Around each point of M there are two local orientations. Intuitively, there is a way to move from a local orientation at a point p to a local orientation at a nearby point p′: when the two points lie in the same coordinate chart U → Rⁿ, that coordinate chart defines compatible local orientations at p and p′. The set of local orientations can therefore be given a topology, and this topology makes it into a manifold.

More precisely, let O be the set of all local orientations of M. To topologize O we will specify a subbase for its topology. Let U be an open subset of M chosen such that ${\displaystyle H_n(M,M\setminus U;\mathbf{Z})}$ is isomorphic to Z. Assume that α is a generator of this group. For each p in U, there is a pushforward function ${\displaystyle H_n(M,M\setminus U;\mathbf{Z})\to H_n\left(M,M\setminus \{p\};\mathbf{Z}\right)}$. The codomain of this group has two generators, and α maps to one of them. The topology on O is defined so that

${\displaystyle \{\text{Image of }\alpha \text{ in }{H}_n\left(M,M\setminus \{p\};\mathbf{Z}\right):p\in U\}}$

is open.

There is a canonical map π : O → M that sends a local orientation at p to p. It is clear that every point of M has precisely two preimages under π. In fact, π is even a local homeomorphism, because the preimages of the open sets U mentioned above are homeomorphic to the disjoint union of two copies of U. If M is orientable, then M itself is one of these open sets, so O is the disjoint union of two copies of M. If M is non-orientable, however, then O is connected and orientable. The manifold O is called the orientation double cover.

Manifolds with boundary

If M is a manifold with boundary, then an orientation of M is defined to be an orientation of its interior. Such an orientation induces an orientation of ∂M. Indeed, suppose that an orientation of M is fixed. Let U → Rⁿ₊ be a chart at a boundary point of M which, when restricted to the interior of M, is in the chosen oriented atlas. The restriction of this chart to ∂M is a chart of ∂M. Such charts form an oriented atlas for ∂M.

When M is smooth, at each point p of ∂M, the restriction of the tangent bundle of M to ∂M is isomorphic to T_p∂M ⊕ R, where the factor of R is described by the inward pointing normal vector. The orientation of T_p∂M is defined by the condition that a basis of T_p∂M is positively oriented if and only if it, when combined with the inward pointing normal vector, defines a positively oriented basis of T_pM.

Orientable double cover

A closely related notion uses the idea of covering space. For a connected manifold M take M^∗, the set of pairs (x, o) where x is a point of M and o is an orientation at x; here we assume M is either smooth so we can choose an orientation on the tangent space at a point or we use singular homology to define orientation. Then for every open, oriented subset of M we consider the corresponding set of pairs and define that to be an open set of M^∗. This gives M^∗ a topology and the projection sending (x, o) to x is then a 2-to-1 covering map. This covering space is called the orientable double cover, as it is orientable. M^∗ is connected if and only if M is not orientable.

Another way to construct this cover is to divide the loops based at a basepoint into either orientation-preserving or orientation-reversing loops. The orientation preserving loops generate a subgroup of the fundamental group which is either the whole group or of index two. In the latter case (which means there is an orientation-reversing path), the subgroup corresponds to a connected double covering; this cover is orientable by construction. In the former case, one can simply take two copies of M, each of which corresponds to a different orientation.

Orientation of vector bundles

Main article: Orientation of a vector bundle

A real vector bundle, which a priori has a GL(n) structure group, is called orientable when the structure group may be reduced to ${\displaystyle G{L}^{+}(n)}$, the group of matrices with positive determinant. For the tangent bundle, this reduction is always possible if the underlying base manifold is orientable and in fact this provides a convenient way to define the orientability of a smooth real manifold: a smooth manifold is defined to be orientable if its tangent bundle is orientable (as a vector bundle). Note that as a manifold in its own right, the tangent bundle is always orientable, even over nonorientable manifolds.

See also: Euler class

Related concepts

Lorentzian geometry

In Lorentzian geometry, there are two kinds of orientability: space orientability and time orientability. These play a role in the causal structure of spacetime. In the context of general relativity, a spacetime manifold is space orientable if, whenever two right-handed observers head off in rocket ships starting at the same spacetime point, and then meet again at another point, they remain right-handed with respect to one another. If a spacetime is time-orientable then the two observers will always agree on the direction of time at both points of their meeting. In fact, a spacetime is time-orientable if and only if any two observers can agree which of the two meetings preceded the other.

Formally, the pseudo-orthogonal group O(p,q) has a pair of characters: the space orientation character σ₊ and the time orientation character σ₋,

${\displaystyle {\sigma }_{\pm }:\mathrm{O}(p,q)\to \{-1,+1\}.}$

Their product σ = σ₊σ₋ is the determinant, which gives the orientation character. A space-orientation of a pseudo-Riemannian manifold is identified with a section of the associated bundle

${\displaystyle \mathrm{O}(M){\times }_{{\sigma }_{+}}\{-1,+1\}}$

where O(M) is the bundle of pseudo-orthogonal frames. Similarly, a time orientation is a section of the associated bundle

${\displaystyle \mathrm{O}(M){\times }_{{\sigma }_{-}}\{-1,+1\}.}$

Open aortic surgery

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Open_aortic_surgery

 

Open aortic surgery
Drawing of an open infrarenal aortic aneurysm repair using a tube graft
Other names	Open aortic repair
Specialty	Vascular Surgery

Open aortic surgery (OAS), also known as open aortic repair (OAR), describes a technique whereby an abdominal, thoracic or retroperitoneal surgical incision is used to visualize and control the aorta for purposes of treatment, usually by the replacement of the affected segment with a prosthetic graft. OAS is used to treat aneurysms of the abdominal and thoracic aorta, aortic dissection, acute aortic syndrome, and aortic ruptures. Aortobifemoral bypass is also used to treat atherosclerotic disease of the abdominal aorta below the level of the renal arteries. In 2003, OAS was surpassed by endovascular aneurysm repair (EVAR) as the most common technique for repairing abdominal aortic aneurysms in the United States.

Depending on the extent of the aorta repaired, an open aortic operation may be called an Infrarenal aortic repair, a Thoracic aortic repair, or a Thoracoabdominal aortic repair. A thoracoabdominal aortic repair is a more extensive operation than either an isolated infrarenal or thoracic aortic repair.

OAS is distinct from aortic valve repair and aortic valve replacement, as OAS describes surgery of the aorta, rather than of the heart valves. When the aortic valve is diseased in addition to the ascending aorta, the Bentall procedure is used to treat the entire aortic root. An axillary-bifemoral bypass is another type of vascular bypass used to treat aortic pathology, however it is not true open aortic surgery as it reconstructs the flow of blood to the legs from the arm, rather than in the native location of the aorta.

Medical uses

Open aortic surgery (OAS) is used to treat patients with aortic aneurysms greater than 5.5 cm in diameter, to treat aortic rupture of an aneurysm any size, to treat aortic dissections, and to treat acute aortic syndrome. It is used to treat infrarenal aneurysms, as well as juxta- and pararenal aneurysm, thoracic and thoracoabdominal aneurysms, and also non-aneurysmal aortic pathology. Disease of the aorta proximal to the left subclavian artery in the chest lies within the specialty of cardiac surgery, and is treated via procedures such as the valve-sparing aortic root replacement.

Prior to the advent of endovascular aneurysm repair (EVAR), OAS was the only surgical treatment available for aortic aneurysms. It is still preferred at some institutions and by some patients as it may be more durable than EVAR, and does not require post-operative surveillance CT scans.

OAS is sometimes required for patients who have previously undergone EVAR but need further treatment, such as for degeneration of the EVAR seal zones leading to continued aneurysm growth. OAS is also sometimes required in cases of EVAR graft infection where the stent graft is removed to treat the infection.

Open repair versus endovascular repair

The shift away from open aortic surgery towards endovascular surgery since 2003 has been driven by worse perioperative mortality associated with OAS, particularly in patients in relatively frail health. Unlike endovascular repair, there are no strict anatomic contra-indications to open repair; Rather, open repair is viewed as the fall back option for patients with unfavorable anatomy for endovascular repair. The main drawback of open repair is the larger physiologic demand of the operation, which is associated with increased rates of short term mortality in most studies.

Patients younger than 50 years with descending and thoracoabdominal aortic aneurysm have low surgical risks, and open repairs can be performed with excellent short-term and durable long-term results. Open surgical repairs should be considered initially in younger patients requiring descending and thoracoabdominal aortic aneurysm repairs. Heritable thoracic aortic disease (HTAD) warrants closer postoperative surveillance.

Technique

Simulated open aortic surgery for an infrarenal aortic aneurysm. The clamp seen is above the aneurysm and below the renal arteries

Simulated clamp placement for open repair of an infrarenal aortic aneurysm

Simulated proximal suture line using "parachute" technique for an open infrarenal aortic aneurysm repair

Completed proximal suture line of a simulated infrarenal open aortic repair with a dacron bifurcated graft

Open surgery typically involves exposure of the dilated portion of the aorta and insertion of a synthetic (Dacron or Gore-Tex) graft (tube). Once the graft is sewn into the proximal (toward the patient's head) and distal (toward the patient's foot) portions of the aorta, the aneurysmal sac is closed around the graft. Alternatively, the anastomosis can be carried out with expandable devices, a simpler and quicker procedure 

The aorta and its branching arteries are cross-clamped during open surgery. This can lead to inadequate blood supply to the spinal cord, resulting in paraplegia, when repairing thoracic aneurysms. A 2004 systematic review and meta analysis found that cerebrospinal fluid drainage (CFSD), when performed in experienced centers, reduces the risk of ischemic spinal cord injury by increasing the perfusion pressure to the spinal cord. A 2012 Cochrane systematic review noted that further research regarding the effectiveness of CFSD for preventing a spinal cord injury is required.

Approach

The infrarenal aorta can be approached via a transabdominal midline or paramedian incision, or via a retroperitoneal approach.

The paravisceral and thoracic aorta are approached via a left-sided posteriolateral thoracotomy incision in approximately the 9th intercostal space. For a thoracoabdominal aortic aneurysm, this approach can be extended to a median or paramedian abdominal incision to allow access to the iliac arteries.

Sequential aortic clamping

At medical centers with a high volume of open aortic surgery, the fastest option for open aortic surgery was sequential aortic clamping or "clamp-and-sew", whereby the aorta was clamped proximally and distally to the diseased segment, and a graft sewn into the intervening segment. This technique leaves the branches of the aorta un-perfused during the time it takes to sew in the graft, potentially increasing the risk of ischemia to the organs which derive their arterial supply from the clamped segment. Critics of this technique advocate intra-operative aortic perfusion. In infrarenal aneurysms, the relative tolerance of the lower extremities to ischemia allows surgeons to clamp distally with low risk of ill effect.

Techniques to limit ischemia

A number of techniques exist for maintaining perfusion to the viscera and spinal cord during open thoracoabdominal aortic aneurysm repair, including left heart bypass, balloon perfusion catheter placement in the visceral arteries, selective spinal drainage and cold crystalloid renal perfusion. There is limited evidence supporting these techniques.

Graft configuration

The abdominal aorta is anastomosed preferentially to the main limb of a tube or bifurcated graft in an end-to-end fashion to minimize turbulent flow at the proximal anastomosis. If normal aorta exists superior to the iliac bifurcation, a tube graft can be sewn distally to that normal aorta. If the distal aorta is diseased, a bifurcated graft can be used in an aorto-billiac or aorto-bifemoral configuration. If visceral vessels are involved in the diseased aortic segment, a branched graft can be used with branches sewn directly to visceral vessels, or the visceral vessels can be separately revascularized.

Reimplantation of the inferior mesenteric artery

Because of collateral blood flow from the superior mesenteric artery (SMA) via the marginal artery, the inferior mesenteric artery usually does not have to be reimplanted into the aortic graft when performing an open abdominal aortic aneurysm repair.

Risks and complications

OAS is widely recognized as having higher rates of perioperative morbidity and mortality than endovascular procedures for comparable segments of the aorta. For example, in infrarenal aneurysms, perioperative mortality with endovascular surgery is approximately 0.5%, against 3% with open repair.

Besides the risk of death, other risks and complications with OAS depend on the segment of aorta involved, and may include renal failure, spinal cord ischemia leading to paralysis, buttock claudication, ischemic colitis, embolization leading to acute limb ischemia, infection, and bleeding. Development of spinal cord injury is associated with increased perioperative mortality after the complex aortic repair.

Recovery after OAS

Recovery time after OAS is substantial. Immediately following surgery, patients can expect to spend 1–3 days in the intensive care unit, followed by 4–10 days on the hospital ward. After discharge, patients will take 3–6 months to fully recover their energy and return to their pre-operative daily activities. However, enhanced recovery after surgery (ERAS) protocols can improve recovery following surgery.

TAAA repair requires a very large incision that cuts through muscles and bones making recovery very difficult and painful for the patient. Intraoperative intercostal nerve cryoanalgesia has been used during procedure to help reduce pain after TAAA.

History

The history of aortic surgery dates back to Greek surgeon Antyllus, who first performed surgeries for various aneurysms in the second century AD. Many advancements of OAS have been developed in the past century.

In 1955, cardiovascular surgeons, Drs. Michael DeBakey and Denton Cooley performed the first replacement of a thoracic aneurysm with a homograft. In 1958, they began using the Dacron graft, resulting in a revolution for surgeons in the surgical repair of aortic aneurysms. DeBakey was first to perform cardiopulmonary bypass to repair the ascending aorta, using antegrade perfusion of the brachiocephalic artery.

By the mid-1960s, at Baylor College of Medicine, DeBakey’s group began performing surgery on thoracoabdominal aortic aneurysms (TAAA), which presented formidable surgical challenges, often fraught with serious complications, such as paraplegia, paraparesis and renal failure. DeBakey protégé and vascular Surgeon, E. Stanley Crawford, in particular, began dedicating most of his time to TAAAs. In 1986, he classified TAAA open surgery cases into four types: Extent I, extending from the left subclavian artery to just below the renal artery; Extent II, from the left subclavian to below the renal artery; Extent III, from the sixth intercostal space to below the renal artery; and Extent IV, from the twelfth intercostal space to the iliac bifurcation (i.e. total abdominal).

In 1992, another classification, Extent V, characterized by Hazim J. Safi, MD, identified aneurysmal disease extending from the sixth intercostal space to above the renal arteries. Safi's group used experimental animal models for a prospective study on the use distal aortic perfusion, cerebrospinal fluid drainage, moderate hypothermia and sequential clamping to decrease in the incidence of neurological deficit. In 1994, they presented their experiences, showing that the incidence for Extent I and II dropped from 25% to 5%. This marked a new era for protecting the spinal cord, brain, kidneys, heart and lungs during OAS on TAAA.

Progress and future challenges

Postoperative paraplegia and paraparesis have been the scourge of thoracoabdominal aortic repair since the inception of the procedure. However, with evolving surgical strategies, identification of predictors, and use of various adjuncts over the years, the incidence of spinal cord injury after thoracic/thoracoabdominal aortic repair has declined. Embracing a multimodality approach offers a good insight into combating this grave complication.