Affine space

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Affine_space

In ${\displaystyle {\mathbb{R}}^3,}$ the upper plane (in blue)${\displaystyle P_2}$ is not a vector subspace, since ${\displaystyle \mathbf{0}\notin P_2}$ and ${\displaystyle \mathbf{a}+\mathbf{b}\notin P_2;}$ it is an affine subspace. Its direction (the linear subspace associated with this affine subspace) is the lower (green) plane ${\displaystyle P_1,}$ which is a vector subspace. Although ${\displaystyle \mathbf{a}}$ and ${\displaystyle \mathbf{b}}$ are in ${\displaystyle P_2,}$ their difference is a displacement vector, which does not belong to ${\displaystyle P_2,}$ but belongs to vector space ${\displaystyle P_1.}$

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.

In an affine space, there is no distinguished point that serves as an origin. Hence, no vector has a fixed origin and no vector can be uniquely associated to a point. In an affine space, there are instead displacement vectors, also called translation vectors or simply translations, between two points of the space. Thus it makes sense to subtract two points of the space, giving a translation vector, but it does not make sense to add two points of the space. Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector.

Any vector space may be viewed as an affine space; this amounts to forgetting the special role played by the zero vector. In this case, elements of the vector space may be viewed either as points of the affine space or as displacement vectors or translations. When considered as a point, the zero vector is called the origin. Adding a fixed vector to the elements of a linear subspace (vector subspace) of a vector space produces an affine subspace. One commonly says that this affine subspace has been obtained by translating (away from the origin) the linear subspace by the translation vector (the vector added to all the elements of the linear space). In finite dimensions, such an affine subspace is the solution set of an inhomogeneous linear system. The displacement vectors for that affine space are the solutions of the corresponding homogeneous linear system, which is a linear subspace. Linear subspaces, in contrast, always contain the origin of the vector space.

The dimension of an affine space is defined as the dimension of the vector space of its translations. An affine space of dimension one is an affine line. An affine space of dimension 2 is an affine plane. An affine subspace of dimension n – 1 in an affine space or a vector space of dimension n is an affine hyperplane.

Informal description

Origins from Alice's and Bob's perspectives. Vector computation from Alice's perspective is in red, whereas that from Bob's is in blue.

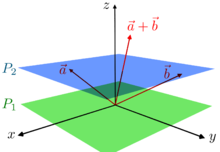
The following characterization may be easier to understand than the usual formal definition: an affine space is what is left of a vector space after one has forgotten which point is the origin (or, in the words of the French mathematician Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps"). Imagine that Alice knows that a certain point is the actual origin, but Bob believes that another point—call it p—is the origin. Two vectors, a and b, are to be added. Bob draws an arrow from point p to point a and another arrow from point p to point b, and completes the parallelogram to find what Bob thinks is a + b, but Alice knows that he has actually computed

p + (a − p) + (b − p).

Similarly, Alice and Bob may evaluate any linear combination of a and b, or of any finite set of vectors, and will generally get different answers. However, if the sum of the coefficients in a linear combination is 1, then Alice and Bob will arrive at the same answer.

If Alice travels to

λa + (1 − λ)b

then Bob can similarly travel to

p + λ(a − p) + (1 − λ)(b − p) = λa + (1 − λ)b.

Under this condition, for all coefficients λ + (1 − λ) = 1, Alice and Bob describe the same point with the same linear combination, despite using different origins.

While only Alice knows the "linear structure", both Alice and Bob know the "affine structure"—i.e. the values of affine combinations, defined as linear combinations in which the sum of the coefficients is 1. A set with an affine structure is an affine space.

Definition

An affine space is a set A together with a vector space ${\displaystyle \overrightarrow{A}}$, and a transitive and free action of the additive group of ${\displaystyle \overrightarrow{A}}$ on the set A. The elements of the affine space A are called points. The vector space ${\displaystyle \overrightarrow{A}}$ is said to be associated to the affine space, and its elements are called vectors, translations, or sometimes free vectors.

Explicitly, the definition above means that the action is a mapping, generally denoted as an addition,

${\displaystyle \begin{array}{rl}A\times \overrightarrow{A}& \to A\\ (a,v)& \mapsto a+v,\end{array}}$

that has the following properties.

1. Right identity:

   ${\displaystyle \mathrm{\forall }a\in A,a+0=a}$, where 0 is the zero vector in ${\displaystyle \overrightarrow{A}}$

2. Associativity:

   ${\displaystyle \mathrm{\forall }v,w\in \overrightarrow{A},\mathrm{\forall }a\in A,(a+v)+w=a+(v+w)}$ (here the last + is the addition in ${\displaystyle \overrightarrow{A}}$)

3. Free and transitive action:

   For every ${\displaystyle a\in A}$, the mapping ${\displaystyle \overrightarrow{A}\to A:v\mapsto a+v}$ is a bijection.

The first two properties are simply defining properties of a (right) group action. The third property characterizes free and transitive actions, the onto character coming from transitivity, and then the injective character follows from the action being free. There is a fourth property that follows from 1, 2 above:

4. Existence of one-to-one translations

For all ${\displaystyle v\in \overrightarrow{A}}$, the mapping ${\displaystyle A\to A:a\mapsto a+v}$ is a bijection.

Property 3 is often used in the following equivalent form (the 5th property).

5. Subtraction:

For every a, b in A, there exists a unique ${\displaystyle v\in \overrightarrow{A}}$, denoted b – a, such that ${\displaystyle b=a+v}$.

Another way to express the definition is that an affine space is a principal homogeneous space for the action of the additive group of a vector space. Homogeneous spaces are by definition endowed with a transitive group action, and for a principal homogeneous space such a transitive action is by definition free.

Subtraction and Weyl's axioms

The properties of the group action allows for the definition of subtraction for any given ordered pair (b, a) of points in A, producing a vector of ${\displaystyle \overrightarrow{A}}$. This vector, denoted ${\displaystyle b-a}$ or ${\displaystyle \overrightarrow{ab}}$, is defined to be the unique vector in ${\displaystyle \overrightarrow{A}}$ such that

${\displaystyle a+(b-a)=b.}$

Existence follows from the transitivity of the action, and uniqueness follows because the action is free.

This subtraction has the two following properties, called Weyl's axioms:

1. ${\displaystyle \mathrm{\forall }a\in A,\mathrm{\forall }v\in \overrightarrow{A}}$, there is a unique point ${\displaystyle b\in A}$ such that ${\displaystyle b-a=v.}$
2. ${\displaystyle \mathrm{\forall }a,b,c\in A,(c-b)+(b-a)=c-a.}$

A feature of affine spaces that are Euclidean is the parallelogram property of vectors.

Affine spaces can be equivalently defined as a point set A, together with a vector space ${\displaystyle \overrightarrow{A}}$, and a subtraction satisfying Weyl's axioms. In this case, the addition of a vector to a point is defined from the first of Weyl's axioms.

Affine subspaces and parallelism

An affine subspace (also called, in some contexts, a linear variety, a flat, or, over the real numbers, a linear manifold) B of an affine space A is a subset of A such that, given a point ${\displaystyle a\in B}$, the set of vectors ${\displaystyle \overrightarrow{B}=\{b-a\mid b\in B\}}$ is a linear subspace of ${\displaystyle \overrightarrow{A}}$. This property, which does not depend on the choice of a, implies that B is an affine space, which has ${\displaystyle \overrightarrow{B}}$ as its associated vector space.

The affine subspaces of A are the subsets of A of the form

${\displaystyle a+V=\{a+w:w\in V\},}$

where a is a point of A, and V a linear subspace of ${\displaystyle \overrightarrow{A}}$.

The linear subspace associated with an affine subspace is often called its direction, and two subspaces that share the same direction are said to be parallel.

This implies the following generalization of Playfair's axiom: Given a direction V, for any point a of A there is one and only one affine subspace of direction V, which passes through a, namely the subspace a + V.

Every translation ${\displaystyle A\to A:a\mapsto a+v}$ maps any affine subspace to a parallel subspace.

The term parallel is also used for two affine subspaces such that the direction of one is included in the direction of the other.

Affine map

Given two affine spaces A and B whose associated vector spaces are ${\displaystyle \overrightarrow{A}}$ and ${\displaystyle \overrightarrow{B}}$, an affine map or affine homomorphism from A to B is a map

${\displaystyle f:A\to B}$

such that

${\displaystyle \begin{array}{rl}\overrightarrow{f}:\overrightarrow{A}& \to \overrightarrow{B}\\ b-a& \mapsto f(b)-f(a)\end{array}}$

is a well defined linear map. By ${\displaystyle f}$ being well defined is meant that b – a = d – c implies f(b) – f(a) = f(d) – f(c).

This implies that, for a point ${\displaystyle a\in A}$ and a vector ${\displaystyle v\in \overrightarrow{A}}$, one has

${\displaystyle f(a+v)=f(a)+\overrightarrow{f}(v).}$

Therefore, since for any given b in A, b = a + v for a unique v, f is completely defined by its value on a single point and the associated linear map ${\displaystyle \overrightarrow{f}}$.

Endomorphisms

Main articles: Affine transformation and Affine group

An affine transformation or endomorphism of an affine space ${\displaystyle A}$ is an affine map from that space to itself. One important family of examples is the translations: given a vector ${\displaystyle \overrightarrow{v}}$, the translation map ${\displaystyle T_{\overrightarrow{v}}:A\to A}$ that sends ${\displaystyle a\mapsto a+\overrightarrow{v}}$ for every ${\displaystyle a}$ in ${\displaystyle A}$ is an affine map. Another important family of examples are the linear maps centred at an origin: given a point ${\displaystyle b}$ and a linear map ${\displaystyle M}$, one may define an affine map ${\displaystyle L_{M,b}:A\to A}$ by

$${\displaystyle L_{M,b}(a)=b+M(a-b)}$$

for every ${\displaystyle a}$ in ${\displaystyle A}$.

After making a choice of origin ${\displaystyle b}$, any affine map may be written uniquely as a combination of a translation and a linear map centred at ${\displaystyle b}$.

Vector spaces as affine spaces

Every vector space V may be considered as an affine space over itself. This means that every element of V may be considered either as a point or as a vector. This affine space is sometimes denoted (V, V) for emphasizing the double role of the elements of V. When considered as a point, the zero vector is commonly denoted o (or O, when upper-case letters are used for points) and called the origin.

If A is another affine space over the same vector space (that is ${\displaystyle V=\overrightarrow{A}}$) the choice of any point a in A defines a unique affine isomorphism, which is the identity of V and maps a to o. In other words, the choice of an origin a in A allows us to identify A and (V, V) up to a canonical isomorphism. The counterpart of this property is that the affine space A may be identified with the vector space V in which "the place of the origin has been forgotten".

Relation to Euclidean spaces

Definition of Euclidean spaces

Euclidean spaces (including the one-dimensional line, two-dimensional plane, and three-dimensional space commonly studied in elementary geometry, as well as higher-dimensional analogues) are affine spaces.

Indeed, in most modern definitions, a Euclidean space is defined to be an affine space, such that the associated vector space is a real inner product space of finite dimension, that is a vector space over the reals with a positive-definite quadratic form q(x). The inner product of two vectors x and y is the value of the symmetric bilinear form

${\displaystyle x\cdot y=\frac{1}{2}(q(x+y)-q(x)-q(y)).}$

The usual Euclidean distance between two points A and B is

${\displaystyle d(A,B)=\sqrt{q(B-A)}.}$

In older definition of Euclidean spaces through synthetic geometry, vectors are defined as equivalence classes of ordered pairs of points under equipollence (the pairs (A, B) and (C, D) are equipollent if the points A, B, D, C (in this order) form a parallelogram). It is straightforward to verify that the vectors form a vector space, the square of the Euclidean distance is a quadratic form on the space of vectors, and the two definitions of Euclidean spaces are equivalent.

Affine properties

In Euclidean geometry, the common phrase "affine property" refers to a property that can be proved in affine spaces, that is, it can be proved without using the quadratic form and its associated inner product. In other words, an affine property is a property that does not involve lengths and angles. Typical examples are parallelism, and the definition of a tangent. A non-example is the definition of a normal.

Equivalently, an affine property is a property that is invariant under affine transformations of the Euclidean space.

Affine combinations and barycenter

Let a₁, ..., a_n be a collection of n points in an affine space, and ${\displaystyle {\lambda }_1,\dots ,{\lambda }_n}$ be n elements of the ground field.

Suppose that ${\displaystyle {\lambda }_1+\cdots +{\lambda }_n=0}$. For any two points o and o' one has

${\displaystyle {\lambda }_1\overrightarrow{o{a}_1}+\cdots +{\lambda }_n\overrightarrow{o{a}_n}={\lambda }_1\overrightarrow{o^{\prime }{a}_1}+\cdots +{\lambda }_n\overrightarrow{o^{\prime }{a}_n}.}$

Thus, this sum is independent of the choice of the origin, and the resulting vector may be denoted

${\displaystyle {\lambda }_1{a}_1+\cdots +{\lambda }_n{a}_n.}$

When ${\displaystyle n=2,{\lambda }_1=1,{\lambda }_2=-1}$, one retrieves the definition of the subtraction of points.

Now suppose instead that the field elements satisfy ${\displaystyle {\lambda }_1+\cdots +{\lambda }_n=1}$. For some choice of an origin o, denote by ${\displaystyle g}$ the unique point such that

${\displaystyle {\lambda }_1\overrightarrow{o{a}_1}+\cdots +{\lambda }_n\overrightarrow{o{a}_n}=\overrightarrow{og}.}$

One can show that ${\displaystyle g}$ is independent from the choice of o. Therefore, if

${\displaystyle {\lambda }_1+\cdots +{\lambda }_n=1,}$

one may write

${\displaystyle g={\lambda }_1{a}_1+\cdots +{\lambda }_n{a}_n.}$

The point ${\displaystyle g}$ is called the barycenter of the ${\displaystyle a_i}$ for the weights ${\displaystyle {\lambda }_i}$. One says also that ${\displaystyle g}$ is an affine combination of the ${\displaystyle a_i}$ with coefficients ${\displaystyle {\lambda }_i}$.

Examples

• When children find the answers to sums such as 4 + 3 or 4 − 2 by counting right or left on a number line, they are treating the number line as a one-dimensional affine space.
• The space of energies is an affine space for ${\displaystyle \mathbb{R}}$, since it is often not meaningful to talk about absolute energy, but it is meaningful to talk about energy differences. The vacuum energy when it is defined picks out a canonical origin.
• Physical space is often modelled as an affine space for ${\displaystyle {\mathbb{R}}^3}$ in non-relativistic settings and ${\displaystyle {\mathbb{R}}^{1,3}}$ in the relativistic setting. To distinguish them from the vector space these are sometimes called Euclidean spaces ${\displaystyle \text{E}(3)}$ and ${\displaystyle \text{E}(1,3)}$.
• Any coset of a subspace V of a vector space is an affine space over that subspace.
• If T is a matrix and b lies in its column space, the set of solutions of the equation Tx = b is an affine space over the subspace of solutions of Tx = 0.
• The solutions of an inhomogeneous linear differential equation form an affine space over the solutions of the corresponding homogeneous linear equation.
• Generalizing all of the above, if T : V → W is a linear map and y lies in its image, the set of solutions x ∈ V to the equation Tx = y is a coset of the kernel of T , and is therefore an affine space over Ker T .
• The space of (linear) complementary subspaces of a vector subspace V in a vector space W is an affine space, over Hom(W/V, V). That is, if 0 → V → W → X → 0 is a short exact sequence of vector spaces, then the space of all splittings of the exact sequence naturally carries the structure of an affine space over Hom(X, V).
• The space of connections (viewed from the vector bundle ${\displaystyle E\stackrel{\pi }{\to }M}$, where ${\displaystyle M}$ is a smooth manifold) is an affine space for the vector space of ${\displaystyle \text{End}(E)}$ valued 1-forms. The space of connections (viewed from the principal bundle ${\displaystyle P\stackrel{\pi }{\to }M}$) is an affine space for the vector space of ${\displaystyle \text{ad}(P)}$-valued 1-forms, where ${\displaystyle \text{ad}(P)}$ is the associated adjoint bundle.

Affine span and bases

For any non-empty subset X of an affine space A, there is a smallest affine subspace that contains it, called the affine span of X. It is the intersection of all affine subspaces containing X, and its direction is the intersection of the directions of the affine subspaces that contain X.

The affine span of X is the set of all (finite) affine combinations of points of X, and its direction is the linear span of the x − y for x and y in X. If one chooses a particular point x₀, the direction of the affine span of X is also the linear span of the x – x₀ for x in X.

One says also that the affine span of X is generated by X and that X is a generating set of its affine span.

A set X of points of an affine space is said to be affinely independent or, simply, independent, if the affine span of any strict subset of X is a strict subset of the affine span of X. An affine basis or barycentric frame (see § Barycentric coordinates, below) of an affine space is a generating set that is also independent (that is a minimal generating set).

Recall that the dimension of an affine space is the dimension of its associated vector space. The bases of an affine space of finite dimension n are the independent subsets of n + 1 elements, or, equivalently, the generating subsets of n + 1 elements. Equivalently, {x₀, ..., x_n} is an affine basis of an affine space if and only if {x₁ − x₀, ..., x_n − x₀} is a linear basis of the associated vector space.

Coordinates

There are two strongly related kinds of coordinate systems that may be defined on affine spaces.

Barycentric coordinates

See also: Barycentric coordinate system

Let A be an affine space of dimension n over a field k, and ${\displaystyle \{x_0,\dots ,x_n\}}$ be an affine basis of A. The properties of an affine basis imply that for every x in A there is a unique (n + 1)-tuple ${\displaystyle ({\lambda }_0,\dots ,{\lambda }_n)}$ of elements of k such that

${\displaystyle {\lambda }_0+\cdots +{\lambda }_n=1}$

and

${\displaystyle x={\lambda }_0{x}_0+\cdots +{\lambda }_n{x}_n.}$

The ${\displaystyle {\lambda }_i}$ are called the barycentric coordinates of x over the affine basis ${\displaystyle \{x_0,\dots ,x_n\}}$. If the x_i are viewed as bodies that have weights (or masses) ${\displaystyle {\lambda }_i}$, the point x is thus the barycenter of the x_i, and this explains the origin of the term barycentric coordinates.

The barycentric coordinates define an affine isomorphism between the affine space A and the affine subspace of k^{n + 1} defined by the equation ${\displaystyle {\lambda }_0+\cdots +{\lambda }_n=1}$.

For affine spaces of infinite dimension, the same definition applies, using only finite sums. This means that for each point, only a finite number of coordinates are non-zero.

Affine coordinates

An affine frame of an affine space consists of a point, called the origin, and a linear basis of the associated vector space. More precisely, for an affine space A with associated vector space ${\displaystyle \overrightarrow{A}}$, the origin o belongs to A, and the linear basis is a basis (v₁, ..., v_n) of ${\displaystyle \overrightarrow{A}}$ (for simplicity of the notation, we consider only the case of finite dimension, the general case is similar).

For each point p of A, there is a unique sequence ${\displaystyle {\lambda }_1,\dots ,{\lambda }_n}$ of elements of the ground field such that

${\displaystyle p=o+{\lambda }_1{v}_1+\cdots +{\lambda }_n{v}_n,}$

or equivalently

${\displaystyle \overrightarrow{op}={\lambda }_1{v}_1+\cdots +{\lambda }_n{v}_n.}$

The ${\displaystyle {\lambda }_i}$ are called the affine coordinates of p over the affine frame (o, v₁, ..., v_n).

Example: In Euclidean geometry, Cartesian coordinates are affine coordinates relative to an orthonormal frame, that is an affine frame (o, v₁, ..., v_n) such that (v₁, ..., v_n) is an orthonormal basis.

Relationship between barycentric and affine coordinates

Barycentric coordinates and affine coordinates are strongly related, and may be considered as equivalent.

In fact, given a barycentric frame

${\displaystyle (x_0,\dots ,x_n),}$

one deduces immediately the affine frame

${\displaystyle (x_0,\overrightarrow{x_0{x}_1},\dots ,\overrightarrow{x_0{x}_n})=\left(x_0,x_1-x_0,\dots ,x_n-x_0\right),}$

and, if

${\displaystyle \left({\lambda }_0,{\lambda }_1,\dots ,{\lambda }_n\right)}$

are the barycentric coordinates of a point over the barycentric frame, then the affine coordinates of the same point over the affine frame are

${\displaystyle \left({\lambda }_1,\dots ,{\lambda }_n\right).}$

Conversely, if

${\displaystyle \left(o,v_1,\dots ,v_n\right)}$

is an affine frame, then

${\displaystyle \left(o,o+v_1,\dots ,o+v_n\right)}$

is a barycentric frame. If

${\displaystyle \left({\lambda }_1,\dots ,{\lambda }_n\right)}$

are the affine coordinates of a point over the affine frame, then its barycentric coordinates over the barycentric frame are

${\displaystyle \left(1-{\lambda }_1-\cdots -{\lambda }_n,{\lambda }_1,\dots ,{\lambda }_n\right).}$

Therefore, barycentric and affine coordinates are almost equivalent. In most applications, affine coordinates are preferred, as involving less coordinates that are independent. However, in the situations where the important points of the studied problem are affinely independent, barycentric coordinates may lead to simpler computation, as in the following example.

Example of the triangle

The vertices of a non-flat triangle form an affine basis of the Euclidean plane. The barycentric coordinates allows easy characterization of the elements of the triangle that do not involve angles or distances:

The vertices are the points of barycentric coordinates (1, 0, 0), (0, 1, 0) and (0, 0, 1). The lines supporting the edges are the points that have a zero coordinate. The edges themselves are the points that have one zero coordinate and two nonnegative coordinates. The interior of the triangle are the points whose coordinates are all positive. The medians are the points that have two equal coordinates, and the centroid is the point of coordinates (1/3, 1/3, 1/3).

Change of coordinates

Case of affine coordinates

Case of barycentric coordinates

Properties of affine homomorphisms

Matrix representation

Image and fibers

Let

${\displaystyle f:E\to F}$

be an affine homomorphism, with

${\displaystyle \overrightarrow{f}:\overrightarrow{E}\to \overrightarrow{F}}$

its associated linear map. The image of f is the affine subspace ${\displaystyle f(E)=\{f(a)\mid a\in E\}}$ of F, which has ${\displaystyle \overrightarrow{f}(\overrightarrow{E})}$ as associated vector space. As an affine space does not have a zero element, an affine homomorphism does not have a kernel. However, the linear map ${\displaystyle \overrightarrow{f}}$ does, and if we denote by ${\displaystyle K=\{v\in \overrightarrow{E}\mid \overrightarrow{f}(v)=0\}}$ its kernel, then for any point x of ${\displaystyle f(E)}$, the inverse image ${\displaystyle f^{-1}(x)}$ of x is an affine subspace of E whose direction is ${\displaystyle K}$. This affine subspace is called the fiber of x.

Projection

See also: Projection (mathematics)

An important example is the projection parallel to some direction onto an affine subspace. The importance of this example lies in the fact that Euclidean spaces are affine spaces, and that these kinds of projections are fundamental in Euclidean geometry.

More precisely, given an affine space E with associated vector space ${\displaystyle \overrightarrow{E}}$, let F be an affine subspace of direction ${\displaystyle \overrightarrow{F}}$, and D be a complementary subspace of ${\displaystyle \overrightarrow{F}}$ in ${\displaystyle \overrightarrow{E}}$ (this means that every vector of ${\displaystyle \overrightarrow{E}}$ may be decomposed in a unique way as the sum of an element of ${\displaystyle \overrightarrow{F}}$ and an element of D). For every point x of E, its projection to F parallel to D is the unique point p(x) in F such that

${\displaystyle p(x)-x\in D.}$

This is an affine homomorphism whose associated linear map ${\displaystyle \overrightarrow{p}}$ is defined by

${\displaystyle \overrightarrow{p}(x-y)=p(x)-p(y),}$

for x and y in E.

The image of this projection is F, and its fibers are the subspaces of direction D.

Quotient space

Although kernels are not defined for affine spaces, quotient spaces are defined. This results from the fact that "belonging to the same fiber of an affine homomorphism" is an equivalence relation.

Let E be an affine space, and D be a linear subspace of the associated vector space ${\displaystyle \overrightarrow{E}}$. The quotient E/D of E by D is the quotient of E by the equivalence relation such that x and y are equivalent if

${\displaystyle x-y\in D.}$

This quotient is an affine space, which has ${\displaystyle \overrightarrow{E}/D}$ as associated vector space.

For every affine homomorphism ${\displaystyle E\to F}$, the image is isomorphic to the quotient of E by the kernel of the associated linear map. This is the first isomorphism theorem for affine spaces.

Axioms

Affine spaces are usually studied by analytic geometry using coordinates, or equivalently vector spaces. They can also be studied as synthetic geometry by writing down axioms, though this approach is much less common. There are several different systems of axioms for affine space.

Coxeter (1969, p. 192) axiomatizes the special case of affine geometry over the reals as ordered geometry together with an affine form of Desargues's theorem and an axiom stating that in a plane there is at most one line through a given point not meeting a given line.

Affine planes satisfy the following axioms (Cameron 1991, chapter 2): (in which two lines are called parallel if they are equal or disjoint):

• Any two distinct points lie on a unique line.
• Given a point and line there is a unique line which contains the point and is parallel to the line
• There exist three non-collinear points.

As well as affine planes over fields (or division rings), there are also many non-Desarguesian planes satisfying these axioms. (Cameron 1991, chapter 3) gives axioms for higher-dimensional affine spaces.

Purely axiomatic affine geometry is more general than affine spaces and is treated in a separate article.

Relation to projective spaces

An affine space is a subspace of a projective space, which is in turn the quotient of a vector space by an equivalence relation (not by a linear subspace)

Affine spaces are contained in projective spaces. For example, an affine plane can be obtained from any projective plane by removing one line and all the points on it, and conversely any affine plane can be used to construct a projective plane as a closure by adding a line at infinity whose points correspond to equivalence classes of parallel lines. Similar constructions hold in higher dimensions.

Further, transformations of projective space that preserve affine space (equivalently, that leave the hyperplane at infinity invariant as a set) yield transformations of affine space. Conversely, any affine linear transformation extends uniquely to a projective linear transformation, so the affine group is a subgroup of the projective group. For instance, Möbius transformations (transformations of the complex projective line, or Riemann sphere) are affine (transformations of the complex plane) if and only if they fix the point at infinity.

Affine algebraic geometry

In algebraic geometry, an affine variety (or, more generally, an affine algebraic set) is defined as the subset of an affine space that is the set of the common zeros of a set of so-called polynomial functions over the affine space. For defining a polynomial function over the affine space, one has to choose an affine frame. Then, a polynomial function is a function such that the image of any point is the value of some multivariate polynomial function of the coordinates of the point. As a change of affine coordinates may be expressed by linear functions (more precisely affine functions) of the coordinates, this definition is independent of a particular choice of coordinates.

The choice of a system of affine coordinates for an affine space ${\displaystyle {\mathbb{A}}_k^n}$ of dimension n over a field k induces an affine isomorphism between ${\displaystyle {\mathbb{A}}_k^n}$ and the affine coordinate space kⁿ. This explains why, for simplification, many textbooks write ${\displaystyle {\mathbb{A}}_k^n=k^n}$, and introduce affine algebraic varieties as the common zeros of polynomial functions over kⁿ.

As the whole affine space is the set of the common zeros of the zero polynomial, affine spaces are affine algebraic varieties.

Ring of polynomial functions

By the definition above, the choice of an affine frame of an affine space ${\displaystyle {\mathbb{A}}_k^n}$ allows one to identify the polynomial functions on ${\displaystyle {\mathbb{A}}_k^n}$ with polynomials in n variables, the ith variable representing the function that maps a point to its ith coordinate. It follows that the set of polynomial functions over ${\displaystyle {\mathbb{A}}_k^n}$ is a k-algebra, denoted ${\displaystyle k\left[{\mathbb{A}}_k^n\right]}$, which is isomorphic to the polynomial ring ${\displaystyle k\left[X_1,\dots ,X_n\right]}$.

When one changes coordinates, the isomorphism between ${\displaystyle k\left[{\mathbb{A}}_k^n\right]}$ and ${\displaystyle k[X_1,\dots ,X_n]}$ changes accordingly, and this induces an automorphism of ${\displaystyle k\left[X_1,\dots ,X_n\right]}$, which maps each indeterminate to a polynomial of degree one. It follows that the total degree defines a filtration of ${\displaystyle k\left[{\mathbb{A}}_k^n\right]}$, which is independent from the choice of coordinates. The total degree defines also a graduation, but it depends on the choice of coordinates, as a change of affine coordinates may map indeterminates on non-homogeneous polynomials.

Zariski topology

See also: Zariski topology

Affine spaces over topological fields, such as the real or the complex numbers, have a natural topology. The Zariski topology, which is defined for affine spaces over any field, allows use of topological methods in any case. Zariski topology is the unique topology on an affine space whose closed sets are affine algebraic sets (that is sets of the common zeros of polynomial functions over the affine set). As, over a topological field, polynomial functions are continuous, every Zariski closed set is closed for the usual topology, if any. In other words, over a topological field, Zariski topology is coarser than the natural topology.

There is a natural injective function from an affine space into the set of prime ideals (that is the spectrum) of its ring of polynomial functions. When affine coordinates have been chosen, this function maps the point of coordinates ${\displaystyle \left(a_1,\dots ,a_n\right)}$ to the maximal ideal ${\displaystyle ⟨X_1-a_1,\dots ,X_n-a_n⟩}$. This function is a homeomorphism (for the Zariski topology of the affine space and of the spectrum of the ring of polynomial functions) of the affine space onto the image of the function.

The case of an algebraically closed ground field is especially important in algebraic geometry, because, in this case, the homeomorphism above is a map between the affine space and the set of all maximal ideals of the ring of functions (this is Hilbert's Nullstellensatz).

This is the starting idea of scheme theory of Grothendieck, which consists, for studying algebraic varieties, of considering as "points", not only the points of the affine space, but also all the prime ideals of the spectrum. This allows gluing together algebraic varieties in a similar way as, for manifolds, charts are glued together for building a manifold.

Cohomology

Like all affine varieties, local data on an affine space can always be patched together globally: the cohomology of affine space is trivial. More precisely, ${\displaystyle H^i\left({\mathbb{A}}_k^n,\mathbf{F}\right)=0}$ for all coherent sheaves F, and integers ${\displaystyle i>0}$. This property is also enjoyed by all other affine varieties. But also all of the étale cohomology groups on affine space are trivial. In particular, every line bundle is trivial. More generally, the Quillen–Suslin theorem implies that every algebraic vector bundle over an affine space is trivial.

Family farm

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Family_farm 

Historical farming estate Stoffl in Radenthein, Carinthia, with an 18th-century arrangement of a main building, a granary and two buildings used as stables and barns.

Barn of a Wisconsin family farm, inscribed with the foundational year (1911).

The Scharmoos estate in Schwarzenberg in the Swiss canton of Lucerne, owned by the Schofer family during c. 1670–1918.

A family farm is generally understood to be a farm owned and/or operated by a family; it is sometimes considered to be an estate passed down by inheritance.

Although a recurring conceptual and archetypal distinction is that of a family farm as a smallholding versus corporate farming as large-scale agribusiness, that notion does not accurately describe the realities of farm ownership in many countries. Family farm businesses can take many forms, from smallholder farms to larger farms operated under intensive farming practices. In various countries, most farm families have structured their farm businesses as corporations (such as limited liability companies) or trusts, for liability, tax, and business purposes. Thus, the idea of a family farm as a unitary concept or definition does not easily translate across languages, cultures, or centuries, as there are substantial differences in agricultural traditions and histories between countries and between centuries within a country. For example, in U.S. agriculture, a family farm can be of any size, as long as the ownership is held within a family. A 2014 USDA report shows that family farms operate 90 percent of the nation’s farmland, and account for 85 percent of the country’s agricultural production value.^[4] However, that does not at all imply that corporate farming is a small presence in U.S. agriculture; rather, it simply reflects the fact that many corporations are closely held. In contrast, in Brazilian agriculture, the official definition of a family farm (agricultura familiar) is limited to small farms worked primarily by members of a single family; but again, this fact does not imply that corporate farming is a small presence in Brazilian agriculture; rather, it simply reflects the fact that large farms with many workers cannot be legally classified under the family farm label because that label is legally reserved for smallholdings in that country.

Farms that would not be considered family farms would be those operated as collectives, non-family corporations, or in other institutionalised forms. At least 500 million of the world's [estimated] 570 million farms are managed by families, making family farms predominant in global agriculture.

Definitions

An "informal discussion of the concepts and definitions" in a working paper published by Food and Agriculture Organization of the United Nations in 2014 reviewed English, Spanish and French definitions of the concept of "family farm". Definitions referred to one or more of labor, management, size, provision of family livelihood, residence, family ties and generational aspects, community and social networks, subsistence orientation, patrimony, land ownership and family investment. The disparity of definitions reflects national and geographical differences in cultures, rural land tenure, and rural economies, as well as the different purposes for which definitions are coined.

The 2012 United States Census of Agriculture defines a family farm as "any farm where the majority of the business is owned by the operator and individuals related to the operator, including relatives who do not live in the operator’s household"; it defines a farm as "any place from which $1,000 or more of agricultural products were produced and sold, or normally would have been sold, during a given year."

The Food and Agriculture Organization of the United Nations defines a "family farm" as one that relies primarily on family members for labour and management.

In some usages, "family farm" implies that the farm remains within the ownership of a family over a number of generations.

Being special-purpose definitions, the definitions found in laws or regulations may differ substantially from commonly understood meanings of "family farm". For example, In the United States, under federal Farm Ownership loan regulations, the definition of a "family farm" does not specify the nature of farm ownership, and management of the farm is either by the borrower, or by members operating the farm when a loan is made to a corporation, co-operative or other entity. The complete definition can be found in the US Code of Federal Regulations 7 CFR 1943.4.

History

Dispersed settlement landscape in Carinthia.

Mountain farms in South Tyrol.

In the Roman Republic, latifundia, great landed estates, specialised in agriculture destined for export, producing grain, olive oil, or wine, corresponding largely to modern industrialized agriculture but depending on slave labour instead of mechanization, developed after the Second Punic War and increasingly replaced the former system of family-owned small or intermediate farms in the Roman Empire period. The basis of the latifundia in Spain and Sicily was the ager publicus that fell to the dispensation of the state through Rome's policy of war in the 1st century BC and the 1st century AD.

In the collapse of the Western Roman Empire, the largely self-sufficient villa-system of the latifundia remained among the few political-cultural centres of a fragmented Europe. These latifundia had been of great importance economically, until the long-distance shipping of wine and oil, grain and garum disintegrated, but extensive lands controlled in a single pair of hands still constituted power: it can be argued that the latifundia formed part of the economic basis of the European social feudal system, taking the form of Manorialism, the essential element of feudal society, and the organizing principle of rural economy in medieval Europe. Manorialism was characterised by the vesting of legal and economic power in a Lord of the Manor, supported economically from his own direct landholding in a manor (sometimes called a fief), and from the obligatory contributions of a legally subject part of the peasant population under the jurisdiction of himself and his manorial court. Manorialism died slowly and piecemeal, along with its most vivid feature in the landscape, the open field system. It outlasted serfdom as it outlasted feudalism: "primarily an economic organization, it could maintain a warrior, but it could equally well maintain a capitalist landlord. It could be self-sufficient, yield produce for the market, or it could yield a money rent." The last feudal dues in France were abolished at the French Revolution. In parts of eastern Germany, the Rittergut manors of Junkers remained until World War II. The common law of the leasehold estate relation evolved in medieval England. That law still retains many archaic terms and principles pertinent to a feudal social order. Under the tenant system, a farm may be worked by the same family over many generations, but what is inherited is not the farm's estate itself but the lease on the estate. In much of Europe, serfdom was abolished only in the modern period, in Western Europe after the French Revolution, in Russia as late as in 1861.

In contrast to the Roman system of latifundia and the derived system of manoralism, the Germanic peoples had a system based on heritable estates owned by individual families or clans. The Germanic term for "heritable estate, allodium" was *ōþalan (Old English ēþel), which incidentally was also used as a rune name; the gnomic verse on this term in the Anglo-Saxon rune poem reads:

[Ēðel] byþ oferleof æghwylcum men, gif he mot ðær rihtes and gerysena on brucan on bolde bleadum oftast.

"[An estate] is very dear to every man, if he can enjoy there in his house whatever is right and proper in constant prosperity."

In the inheritance system known as Salic patrimony (also gavelkind in its exceptional survival in medieval Kent) refers to this clan-based possession of real estate property, particularly in Germanic context. Terra salica could not be sold or otherwise disposed; it was not alienable. Much of Germanic Europe has a history of overlap or conflict between the feudal system of manoralism, where the estate is owned by noblemen and leased to the tenants or worked by serfs, and the Germanic system of free farmers working landed estates heritable within their clan or family. Historical prevalence of the Germanic system of independent estates or Höfe resulted in dispersed settlement (Streusiedlung) structure, as opposed to the village-centered settlements of manoralism.

Mention of "hofe" in Beowulf

In German-speaking Europe, a farmyard is known as a Hof; in modern German this word designates the area enclosed by the farm buildings, not the fields around them, and it is also used in other everyday situations for courtyards of any type (Hinterhof = 'back yard', etc.). The recharacterized compound Bauernhof was formed in the early modern period to designate family farming estates and today is the most common word for 'farm', while the archaic Meierhof designated a manorial estate. Historically, the unmarked term Hof was increasingly used for the royal or noble court. The estate as a whole is referred to by the collective Gehöft (15th century); the corresponding Slavic concept being Khutor. Höfeordnung is the German legal term for the inheritance laws regarding family farms, deriving from inheritance under medieval Saxon law. In England, the title of yeoman was applied to such land-owning commoners from the 15th century.

In the early modern and modern period, the dissolution of manoralism went parallel to the development of intensive farming parallel to the Industrial Revolution. Mechanization enabled the cultivation of much larger areas than what was typical for the traditional estates aimed at subsistence farming, resulting in the emergence of a smaller number of large farms, with the displaced population partly contributing to the new class of industrial wage-labourers and partly emigrating to the New World or the Russian Empire (following the 1861 emancipation of the serfs). The family farms established in Imperial Russia were again collectivized under the Soviet Union, but the emigration of European farmers displaced by the Industrial Revolution contributed to the emergence of a system of family estates in the Americas (Homestead Act of 1862).

Thomas Jefferson's argument that a large number of family estates are a factor in ensuring the stability of democracy was repeatedly used in support of subsidies.

Developed world

Perceptions of the family farm

In developed countries the family farm is viewed sentimentally, as a lifestyle to be preserved for tradition's sake, or as a birthright. It is in these nations very often a political rallying cry against change in agricultural policy, most commonly in France, Japan, and the United States, where rural lifestyles are often regarded as desirable. In these countries, strange bedfellows can often be found arguing for similar measures despite otherwise vast differences in political ideology. For example, Pat Buchanan and Ralph Nader, both candidates for the office of President of the United States, held rural rallies together and spoke for measures to preserve the so-called family farm. On other economic matters they were seen as generally opposed, but found common ground on this one.

The social roles of family farms are much changed today. Until recently, staying in line with traditional and conservative sociology, the heads of the household were usually the oldest man followed closely by his oldest sons. The wife generally took care of the housework, child rearing, and financial matters pertaining to the farm. However, agricultural activities have taken on many forms and change over time. Agronomy, horticulture, aquaculture, silviculture, and apiculture, along with traditional plants and animals, all make up aspects of today's family farm. Farm wives often need to find work away from the farm to supplement farm income and children sometimes have no interest in farming as their chosen field of work.

Bolder promoters argue that as agriculture has become more efficient with the application of modern management and new technologies in each generation, the idealized classic family farm is now simply obsolete, or more often, unable to compete without the economies of scale available to larger and more modern farms. Advocates argue that family farms in all nations need to be protected, as the basis of rural society and social stability.

Viability

According to the United States Department of Agriculture, ninety-eight percent of all farms in the U.S. are family farms. Two percent of farms are not family farms, and those two percent make up fourteen percent of total agricultural output in the United States, although half of them have total sales of less than $50,000 per year. Overall, ninety-one percent of farms in the United States are considered "small family farms" (with sales of less than $250,000 per year), and those farms produce twenty-seven percent of U.S. agricultural output.

Depending on the type and size of independently owned operation, some limiting factors are:

• Economies of scale: Larger farms are able to bargain more competitively, purchase more competitively, profit from economic highs, and weather lows more readily through monetary inertia than smaller farms.
• Cost of inputs: fertilizer and other agrichemicals can fluctuate dramatically from season to season, partially based on oil prices, a range of 25% to 200% is common over a period of a few years.
• oil prices: Directly (for farm machinery) and somewhat less directly (long distance transport; production cost of agrichemicals), the cost of oil significantly impacts the year-to-year viability of all mechanized conventional farms.
• commodity futures: the predicted price of commodity crops, hogs, grain, etc., can determine ahead of a season what seems economically viable to grow.
• technology user agreements: a less publicly known factor, patented GE seed that is widely used for many crops, like cotton and soy, comes with restrictions on use, which can even include who the crop can be sold to.
• wholesale infrastructure: A farmer growing larger quantities of a crop than can be sold directly to consumers has to meet a range of criteria for sale into the wholesale market, which include harvest timing and graded quality, and may also include variety, therefore, the market channel really determines most aspects of the farm decisionmaking.
• availability of financing: Larger farms today often rely on lines of credit, typically from banks, to purchase the agrichemicals, and other supplies needed for each growing year. These lines are heavily affected by almost all of the other constraining factors.
• government economic intervention: In some countries, notably the US and EU, government subsidies to farmers, intended to mitigate the impact on domestic farmers of economic and political activities in other areas of the economy, can be a significant source of farm income. Bailouts, when crises such as drought or the "mad cow disease" problems hit agricultural sectors, are also relied on. To some large degree, this situation is a result of the large-scale global markets farms have no alternative but to participate in.
• government and industry regulation: A wide range of quotas, marketing boards and legislation governing agriculture impose complicated limits, and often require significant resources to navigate. For example, on the small farming end, in many jurisdictions, there are severe limits or prohibitions on the sale of livestock, dairy and eggs. These have arisen from pressures from all sides: food safety, environmental, industry marketing.
• real estate prices: The growth of urban centers around the world, and the resulting urban sprawl have caused the price of centrally located farmland to skyrocket, while reducing the local infrastructure necessary to support farming, putting effectively intense pressure on many farmers to sell out.

Over the 20th century, the people of developed nations have collectively taken most of the steps down the path to this situation. Individual farmers opted for successive waves of new technology, happily "trading in their horses for a tractor", increasing their debt and their production capacity. This in turn required larger, more distant markets, and heavier and more complex financing. The public willingly purchased increasingly commoditized, processed, shipped and relatively inexpensive food. The availability of an increasingly diverse supply of fresh, uncured, unpreserved produce and meat in all seasons of the year (oranges in January, freshly killed steers in July, fresh pork rather than salted, smoked, or potassium-impregnated ham) opened an entirely new cuisine and an unprecedented healthy diet to millions of consumers who had never enjoyed such produce before. These abilities also brought to market an unprecedented variety of processed foods, such as corn syrup and bleached flour. For the family farm this new technology and increasingly complex marketing strategy has presented new and unprecedented challenges, and not all family farmers have been able to effectively cope with the changing market conditions.

Intensive wheat farming in western North Dakota.

Local food and the organic movement

In the last few decades there has been a resurgence of interest in organic and free range foods. A percentage of consumers have begun to question the viability of industrial agriculture practices and have turned to organic groceries that sell products produced on family farms including not only meat and produce but also such things as wheat germ breads and natural lye soaps (as opposed to bleached white breads and petroleum based detergent bars). Others buy these products direct from family farms. The "new family farm" provides an alternative market in some localities with an array of traditionally and naturally produced products.

Such "organic" and "free-range" farming is attainable where a significant number of affluent urban and suburban consumers willingly pay a premium for the ideals of "locally produced produce" and "humane treatment of animals". Sometimes, these farms are hobby or part-time ventures, or supported by wealth from other sources. Viable farms on a scale sufficient to support modern families at an income level commensurate with urban and suburban upper-middle-class families are often large scale operations, both in area and capital requirements. These farms, family owned and operated in a technologically and economically conventional manner, produce crops and animal products oriented to national and international markets, rather than to local markets. In assessing this complex economic situation, it is important to consider all sources of income available to these farms; for instance, the millions of dollars in farm subsidies which the United States government offers each year. As fuel prices rise, foods shipped to national and international markets are already rising in price.

United States

In 2012, the United States had 2,039,093 family farms (as defined by USDA), accounting for 97 percent of all farms and 89 percent of census farm area in the United States. In 1988 Mark Friedberger warned, "The farm family is a unique institution, perhaps the last remnant, in an increasingly complex world, of a simpler social order in which economic and domestic activities were inextricably bound together. In the past few years, however, American agriculture has suffered huge losses, and family farmers have seen their way of life threatened by economic forces beyond their control." However by 1981 Ingolf Vogeler argued it was too late—the American family farm had been replaced by large agribusiness corporations pretending to be family operated.

A USDA survey conducted in 2011 estimated that family farms account for 85 percent of US farm production and 85 percent of US gross farm income. Mid-size and larger family farms account for 60 percent of US farm production and dominate US production of cotton, cash grain and hogs. Small family farms account for 26 percent of US farm production overall, and higher percentages of production of poultry, beef cattle, some other livestock and hay.

Several kinds of US family farms are recognized in USDA farm typology:

Small family farms are defined as those with annual gross cash farm income (GCFI) of less than $350,000; in 2011, these accounted for 90 percent of all US farms. Because low net farm incomes tend to predominate on such farms, most farm families on small family farms are extremely dependent on off-farm income. Small family farms in which the principal operator was mostly employed off-farm accounted for 42 percent of all farms and 15 percent of total US farm area; median net farm income was $788. Retirement family farms were small farms accounting for 16 percent of all farms and 7 percent of total US farm area; median net farm income was $5,002.

The other small family farm categories are those in which farming occupies at least 50 percent of the principal operator’s working time. These are:

Low-sales small family farms (with GCFI less than $150,000); 26 percent of all US farms, 18 percent of total US farm area, median net farm income $3,579.

Moderate-sales small family farms (with GCFI of $150,000 to $349,999); 5.44 percent of all US farms, 13 percent of total US farm area, median net farm income $67,986.

Mid-size family farms (GCFI of $350,000 to $999,999); 6 percent of all US farms, 22 percent of total US farm area; median net farm income $154,538.

Large family farms (GCFI $1,000,000 to $4,999,999); 2 percent of all US farms, 14 percent of total US farm area; median net farm income $476,234.

Very large family farms (GCFI over $5,000,000); <1 percent of all US farms, 2 percent of total US farm area; median net farm income $1,910,454.

Family farms include not only sole proprietorships and family partnerships, but also family corporations. Family-owned corporations account for 5 percent of all farms and 89 percent of corporate farms in the United States. About 98 percent of US family corporations owning farms are small, with no more than 10 shareholders; average net farm income of family corporate farms was $189,400 in 2012. (In contrast, 90 percent of US non-family corporations owning farms are small, having no more than 10 shareholders; average net cash farm income for US non-family corporate farms was $270,670 in 2012.)

Canada

In Canada, the number of "family farms" cannot be inferred closely, because of the nature of census data, which do not distinguish family and non-family farm partnerships. In 2011, of Canada’s 205,730 farms, 55 percent were sole proprietorships, 25 percent were partnerships, 17 percent were family corporations, 2 percent were non-family corporations and <1 percent were other categories. Because some but not all partnerships involve family members, these data suggest that family farms account for between about 73 and 97 percent of Canadian farms. The family farm percentage is likely to be near the high end of this range, for two reasons. The partners in a [Canadian] farm partnership are typically spouses, often forming the farm partnership for tax reasons. Also, as in the US, family farm succession planning can use a partnership as a means of apportioning family farm tenure among family members when a sole proprietor is ready to transfer some or all of ownership and operation of a farm to offspring. Conversion of a sole proprietorship family farm to a family corporation may also be influenced by legal and financial, e.g. tax, considerations. The Canadian Encyclopedia estimates that more than 90 percent of Canadian farms are family operations. In 2006, of Canadian farms with more than one million dollars in annual gross farm receipts, about 63 percent were family corporations and 13 percent were non-family corporations.

Europe

Analysis of data for 59,000 farms in the 12 member states of the European Community found that in 1989, about three-quarters of the farms were family farms, producing just over half of total agricultural output.

As of 2010, there were approximately 139,900 family farms in Ireland, with an average size of 35.7 hectares per holding. (Nearly all farms in Ireland are family farms.) In Ireland, average family farm income was 25,483 euros in 2012. Analysis by Teagasc (Ireland’s Agriculture and Food Development Authority) estimates that 37 percent of Irish farms are economically viable and an additional 30 percent are sustainable due to income from off-farm sources; 33 percent meet neither criterion and are considered economically vulnerable.

Newly industrialized countries

A family farm in Urubici, Santa Catarina State in Brazil.

In Brazil, there are about 4.37 million family farms. These account for 84.4 percent of farms, 24.3 percent of farmland area and 37.5 percent of the value of agricultural production.

Developing countries

In sub-Saharan Africa, 80% of farms are family owned and worked.

Sub-Saharan agriculture was mostly defined by slash-and-burn subsistence farming, historically spread by the Bantu expansion. Permanent farming estates were established during colonialism, in the 19th to 20th century. After decolonisation, white farmers in some African countries have tended to be attacked, killed or evicted, notably in South Africa and Zimbabwe.

In southern Africa, "On peasant family farms ..., cash input costs are very low, non‐household labour is sourced largely from communal work groups through kinship ties, and support services needed to sustain production are minimal." On commercial family farms, "cash input costs are high, little non‐family labour is used and strong support services are necessary."

International Year of Family Farming

Logo of International Year of Family Farming 2014

At the 66th session of the United Nations General Assembly, 2014 was formally declared to be the "International Year of Family Farming" (IYFF). The Food and Agriculture Organization of the United Nations was invited to facilitate its implementation, in collaboration with Governments, International Development Agencies, farmers' organizations and other relevant organizations of the United Nations system as well as relevant non-governmental organizations.

The goal of the 2014 IYFF is to reposition family farming at the centre of agricultural, environmental and social policies in the national agendas by identifying gaps and opportunities to promote a shift towards a more equal and balanced development. The 2014 IYFF will promote broad discussion and cooperation at the national, regional and global levels to increase awareness and understanding of the challenges faced by smallholders and help identify efficient ways to support family farmers.