A Medley of Potpourri

Sunday, October 22, 2023

Flame detector

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Flame_detector

A flame detector is a sensor designed to detect and respond to the presence of a flame or fire, allowing flame detection. Responses to a detected flame depend on the installation, but can include sounding an alarm, deactivating a fuel line (such as a propane or a natural gas line), and activating a fire suppression system. When used in applications such as industrial furnaces, their role is to provide confirmation that the furnace is working properly; it can be used to turn off the ignition system though in many cases they take no direct action beyond notifying the operator or control system. A flame detector can often respond faster and more accurately than a smoke or heat detector due to the mechanisms it uses to detect the flame.

Optical flame detectors

Ultraviolet detector

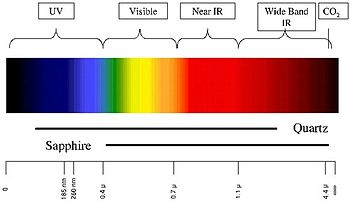
Ultraviolet (UV) detectors work by detecting the UV radiation emitted at the instant of ignition. While capable of detecting fires and explosions within 3–4 milliseconds, a time delay of 2–3 seconds is often included to minimize false alarms which can be triggered by other UV sources such as lightning, arc welding, radiation, and sunlight. UV detectors typically operate with wavelengths shorter than 300 nm to minimize the effects of natural background radiation. The solar blind UV wavelength band is also easily blinded by oily contaminants.

Near IR array

Near infrared (IR) array flame detectors (0.7 to 1.1 μm), also known as visual flame detectors, employ flame recognition technology to confirm fire by analyzing near IR radiation using a charge-coupled device (CCD). A near infrared (IR) sensor is especially able to monitor flame phenomena, without too much hindrance from water and water vapour. Pyroelectric sensors operating at this wavelength can be relatively cheap. Multiple channel or pixel array sensors monitoring flames in the near IR band are arguably the most reliable technologies available for detection of fires. Light emission from a fire forms an image of the flame at a particular instant. Digital image processing can be utilized to recognize flames through analysis of the video created from the near IR images.

Infrared

Infrared (IR) or wideband infrared (1.1 μm and higher) flame detectors monitor the infrared spectral band for specific patterns given off by hot gases. These are sensed using a specialized fire-fighting thermal imaging camera (TIC), a type of thermographic camera. False alarms can be caused by other hot surfaces and background thermal radiation in the area. Water on the detector's lens will greatly reduce the accuracy of the detector, as will exposure to direct sunlight. A special frequency range is 4.3 to 4.4 μm. This is a resonance frequency of CO₂. During burning of a hydrocarbon (for example, wood or fossil fuels such as oil and natural gas) much heat and CO₂ is released. The hot CO₂ emits much energy at its resonance frequency of 4.3 μm. This causes a peak in the total radiation emission and can be well detected. Moreover, the "cold" CO₂ in the air is taking care that the sunlight and other IR radiation is filtered. This makes the sensor in this frequency "solar blind"; however, sensitivity is reduced by sunlight. By observing the flicker frequency of a fire (1 to 20 Hz) the detector is made less sensitive to false alarms caused by heat radiation, for example caused by hot machinery.

A severe disadvantage is that almost all radiation can be absorbed by water or water vapour; this is particularly valid for infrared flame detection in the 4.3 to 4.4 μm region. From approx. 3.5 μm and higher the absorption by water or ice is practically 100%. This makes infrared sensors for use in outdoor applications very unresponsive to fires. The biggest problem is our ignorance; some infrared detectors have an (automatic) detector window self test, but this self test only monitors the occurrence of water or ice on the detector window.

A salt film is also harmful, because salt absorbs water. However, water vapour, fog or light rain also makes the sensor almost blind, without the user knowing. The cause is similar to what a fire fighter does if he approaches a hot fire: he protects himself by means of a water vapour screen against the enormous infrared heat radiation. The presence of water vapor, fog, or light rain will then also "protect" the monitor causing it to not see the fire. Visible light will, however be transmitted through the water vapour screen, as can easily been seen by the fact that a human can still see the flames through the water vapour screen.

The usual response time of an IR detector is 3–5 seconds.

Infrared thermal cameras

MWIR infrared (IR) cameras can be used to detect heat and with particular algorithms can detect hot-spots within a scene as well as flames for both detection and prevention of fire and risks of fire. These cameras can be used in complete darkness and operate both inside and outside.

UV/IR

These detectors are sensitive to both UV and IR wavelengths, and detect flame by comparing the threshold signal of both ranges. This helps minimize false alarms.

IR/IR flame detection

Dual IR (IR/IR) flame detectors compare the threshold signal in two infrared ranges. Often one sensor looks at the 4.4 micrometer carbon dioxide (CO₂), while the other sensor looks at a reference frequency. Sensing the CO₂ emission is appropriate for hydrocarbon fuels; for non-carbon based fuels, e.g., hydrogen, the broadband water bands are sensed.

IR3 flame detection

Multi-infrared detectors make use of algorithms to suppress the effects of background radiation (blackbody radiation), again sensitivity is reduced by this radiation.

Triple-IR flame detectors compare three specific wavelength bands within the IR spectral region and their ratio to each other. In this case one sensor looks at the 4.4 micrometer range while the other sensors look at reference wavelengths both above and below 4.4. This allows the detector to distinguish between non-flame IR sources and actual flames which emit hot CO₂ in the combustion process. As a result, both detection range and immunity to false alarms can be significantly increased. IR3 detectors can detect a 0.1m² (1 ft²) gasoline pan fire at up to 65 m (215 ft) in less than 5 seconds. Triple IRs, like other IR detector types, are susceptible to blinding by a layer of water on the detector's window.

Most IR detectors are designed to ignore constant background IR radiation, which is present in all environments. Instead they are designed to detect suddenly changing or increasing sources of the radiation. When exposed to changing patterns of non-flame IR radiation, IR and UV/IR detectors become more prone to false alarms, while IR3 detectors become somewhat less sensitive but are more immune to false alarms.

3IR+UV flame detection

Multi-Infrared (Multi-IR/3IR) detectors use algorithms to determine the presence of fire and tell them apart from background noise known to as black-body radiation, which in generally reduce the range and accuracy of the detector. Black-body radiation is constantly present in all environments , but is given off especially strongly by objects at high temperature. this makes high temperature environments, or areas where high temperature material is handled especially challenging for IR only detectors. Thus, one additional UV-C band sensor is sometimes included in flame detectors to add another layer of confirmation, as black-body radiation does not impact UV sensors unless the temperature is extremely high, such as the plasma glow from an Arc welding machine.

Multi-wavelength detectors vary in sensor configuration. 1 IR+UV, or UVIR being the most common and low cost. 2 IR + UV being a compromise between cost and False alarm immunity and 3 IR + UV, which combines past 3IR technology with the additional layer of identification from the UV sensor.

Multi-Wavelength or Multi-spectral detectors such as 3IR+UV and UVIR are an improvement over their IR-only detectors counterparts which have been known to either false alarm or lose sensitivity and range in the presence of strong background noise such as direct or reflected light sources or even sun exposure. IR detectors have often relied on Infrared bulk energy growth to as their primary determining factor for fire detection, declaring an alarm when the sensors exceed a given range and ratio. This approach however is prone to trigger from non-fire noise. whether from blackbody radiation, high temperature environments, or simply changes in the ambient lighting. alternatively in another design approach, IR-only detectors may only alarm given perfect conditions and clear signal matches, which results in missing the fire when there is too much noise, such as looking into the sunset.

Modern Flame detectors may also make use of high speed sensors, which allow the capture of the flickering movement of flame, and monitor the pattern and ratios of the spectral output for patterns unique to fire. Higher speed sensors allow for not only faster reaction times, but also more data per second, increasing the level of confidence in fire identification, or false alarm rejection.

Visible sensors

A visible light sensor (for example a camera: 0.4 to 0.7 μm) is able to present an image, which can be understood by a human being. Furthermore, complex image processing analysis can be executed by computers, which can recognize a flame or even smoke. Unfortunately, a camera can be blinded, like a human, by heavy smoke and by fog. It is also possible to mix visible light information (monitor) with UV or infrared information, in order to better discriminate against false alarms or to improve the detection range. The corona camera is an example of this equipment. In this equipment the information of a UV camera mixed with visible image information. It is used for tracing defects in high voltage equipment and fire detection over high distances.

In some detectors, a sensor for visible radiation (light) is added to the design.

Video

Closed-circuit television or a web camera can be used for visual detection of (wavelengths between 0.4 and 0.7 μm). Smoke or fog can limit the effective range of these, since they operate solely in the visible spectrum.

Other types

Ionization current flame detection

The intense ionization within the body of a flame can be measured by means by the phenomena of flame rectification whereby an AC current flows more easily in one direction when a voltage is applied. This current can be used to verify flame presence and quality. Such detectors can be used in large industrial process gas heaters and are connected to the flame control system. They usually act as both flame quality monitors and for flame failure detection. They are also common in a variety of household gas furnaces and boilers.

Problems with boilers failing to stay lit can often be due to dirty flame sensors or to a poor burner surface with which to complete the electrical circuit. A poor flame or one that is lifting off the burner may also interrupt the continuity.

Thermocouple flame detection

Thermocouples are used extensively for monitoring flame presence in combustion heating systems and gas cookers. A common use in these installations is to cut off the supply of fuel if the flame fails, in order to prevent unburned fuel from accumulating. These sensors measure heat and therefore are commonly used to determine the absence of a flame. This can be used to verify the presence of a pilot flame.

Applications

UV/IR flame detectors are used in:

Hydrogen stations.
Gas-fueled cookers
Industrial heating and drying systems
Domestic heating systems
Industrial gas turbines

Emission of radiation

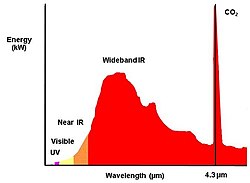
A fire emits radiation, which human eye experiences as the visible yellow red flames and heat. In fact, during a fire, relatively sparsely UV energy and visible light energy is emitted, as compared to the emission of Infrared radiation. A non-hydrocarbon fire, for example, one from hydrogen, does not show a CO₂ peak on 4.3 μm because during the burning of hydrogen no CO₂ is released. The 4.3 μm CO₂ peak in the picture is exaggerated, and is in reality less than 2% of the total energy of the fire. A multi-frequency-detector with sensors for UV, visible light, near IR and/or wideband IR thus have much more "sensor data" to calculate with and therefore are able to detect more types of fires and to detect these types of fires better: hydrogen, methanol, ether or sulphur. It looks like a static picture, but in reality the energy fluctuates, or flickers. This flickering is caused by the fact that the aspirated oxygen and the present combustible are burning and concurrently aspirate new oxygen and new combustible material. These little explosions cause the flickering of the flame.

Sunlight

The sun emits an enormous amount of energy, which would be harmful to human beings if not for the vapours and gases in the atmosphere, like water (clouds), ozone, and others, through which the sunlight is filtered. In the figure it can clearly be seen that "cold" CO₂ filters the solar radiation around 4.3 μm. An Infrared detector which uses this frequency is therefore solar blind. Not all manufacturers of flame detectors use sharp filters for the 4.3 μm radiation and thus still pick up quite an amount of sunlight. These cheap flame detectors are hardly usable for outdoor applications. Between 0.7 μm and approx. 3 μm there is relatively large absorption of sunlight. Hence, this frequency range is used for flame detection by a few flame detector manufacturers (in combination with other sensors like ultraviolet, visible light, or near infrared). The big economical advantage is that detector windows can be made of quartz instead of expensive sapphire. These electro-optical sensor combinations also enable the detection of non-hydrocarbons like hydrogen fires without the risk of false alarms caused by artificial light or electrical welding.

Heat radiation

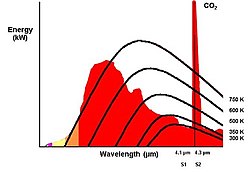
Infrared flame detectors suffer from Infrared heat radiation which is not emitted by the possible fire. One could say that the fire can be masked by other heat sources. All objects which have a temperature higher than the absolute minimum temperature (0 kelvins or −273.15 °C) emit energy and at room temperature (300 K) this heat is already a problem for the infrared flame detectors with the highest sensitivity. Sometimes a moving hand is sufficient to trigger an IR flame detector. At 700 K a hot object (black body) starts to emit visible light (glow). Dual- or multi-infrared detectors suppress the effects of heat radiation by means of sensors which detect just off the CO₂ peak; for example at 4.1 μm. Here it is necessary that there is a large difference in output between the applied sensors (for example sensor S1 and S2 in the picture). A disadvantage is that the radiation energy of a possible fire must be much bigger than the present background heat radiation. In other words, the flame detector becomes less sensitive. Every multi infrared flame detector is negatively influenced by this effect, regardless how expensive it is.

Cone of vision

The cone of vision of a flame detector is determined by the shape and size of the window and the housing and the location of the sensor in the housing. For infrared sensors also the lamination of the sensor material plays a part; it limits the cone of vision of the flame detector. A wide cone of vision does not automatically mean that the flame detector is better. For some applications the flame detector needs to be aligned precisely to take care that it does not detect potential background radiation sources. The cone of vision of the flame detector is three dimensional and is not necessarily perfectly round. The horizontal angle of vision and the vertical angle of vision often differ; this is mostly caused by the shape of the housing and by mirroring parts (meant for the self test). Different combustibles can even have a different angle of vision in the same flame detector. Very important is the sensitivity at angles of 45°. Here at least 50% of the maximum sensitivity at the central axis must be achieved. Some flame detectors here achieve 70% or more. In fact these flame detectors have a total horizontal angle of vision of more than 90°, but most of the manufacturers do not mention this. A high sensitivity on the edges of the angle of vision provides advantages for the projection of a flame detector.

The detection range

The range of a flame detector is highly determined by the mounting location. In fact, when making a projection, one should imagine in what the flame detector "sees". A rule of thumb is, that the mounting height of the flame detector is twice as high as the highest object in the field of view. Also the accessibility of the flame detector must be taken into account, because of maintenance and/or repairs. A rigid light-mast with a pivot point is for this reason recommendable. A "roof" on top of the flame detector (30 x 30 cm, 1 x 1-foot) prevents quick pollution in outdoor applications. Also the shadow effect must be considered. The shadow effect can be minimized by mounting a second flame detector in the opposite of the first detector. A second advantage of this approach is, that the second flame detector is a redundant one, in case the first one is not working or is blinded. In general, when mounting several flame detectors, one should let them "look" to each other not let them look to the walls. Following this procedure blind spots (caused by the shadow effect) can be avoided and a better redundancy can be achieved than if the flame detectors would "look" from the central position into the area to be protected. The range of flame detectors to the 30 x 30 cm, 1 x 1-foot industry standard fire is stated within the manufacturers data sheets and manuals, this range can be affected by the previously stated de-sensitizing effects of sunlight, water, fog, steam and blackbody radiation.

The square law

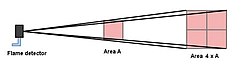
If the distance between the flame and the flame detector is large compared to the dimension of the fire then the square law applies: If a flame detector can detect a fire with an area A on a certain distance, then a 4 times bigger flame area is necessary if the distance between the flame detector and the fire is doubled. In short:

Double distance = four times bigger flame area (fire).

This law is equally valid for all optical flame detectors, including video based ones. The maximum sensitivity can be estimated by dividing the maximum flame area A by the square of the distance between the fire and the flame detector: c = A/d². With this constant c can, for the same flame detector and the same type of fire, the maximum distance or the minimum fire area be calculated: $A = cd 2$ and $d = \sqrt A / c$

It must be emphasized, however, that the square root in reality is not valid anymore at very high distances. At long distances other parameters are playing a significant part; like the occurrence of water vapour and of cold CO₂ in the air. In the case of a very small flame, on the other hand, the decreasing flickering of the flame will play an increasing part.

A more exact relation - valid when the distance between the flame and the flame detector is small - between the radiation density, E, at the detector and the distance, D, between the detector and a flame of effective radius, R, emitting energy density, M, is given by

$E = 2π MR 2 / (R 2 + D 2)$

When R<<D then the relation reduces to the (inverse) square law

$E = 2π MR 2 / D 2$

Shock wave

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Shock_wave

In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a medium but is characterized by an abrupt, nearly discontinuous, change in pressure, temperature, and density of the medium.

For the purpose of comparison, in supersonic flows, additional increased expansion may be achieved through an expansion fan, also known as a Prandtl–Meyer expansion fan. The accompanying expansion wave may approach and eventually collide and recombine with the shock wave, creating a process of destructive interference. The sonic boom associated with the passage of a supersonic aircraft is a type of sound wave produced by constructive interference.

Unlike solitons (another kind of nonlinear wave), the energy and speed of a shock wave alone dissipates relatively quickly with distance. When a shock wave passes through matter, energy is preserved but entropy increases. This change in the matter's properties manifests itself as a decrease in the energy which can be extracted as work, and as a drag force on supersonic objects; shock waves are strongly irreversible processes.

Terminology

Shock waves can be:

Normal: At 90° (perpendicular) to the shock medium's flow direction.
Oblique: At an angle to the direction of flow.
Bow: Occurs upstream of the front (bow) of a blunt object when the upstream flow velocity exceeds Mach 1.

Some other terms:

Shock front: The boundary over which the physical conditions undergo an abrupt change because of a shock wave.
Contact front: In a shock wave caused by a driver gas (for example the "impact" of a high explosive on the surrounding air), the boundary between the driver (explosive products) and the driven (air) gases. The contact front trails the shock front.

In supersonic flows

The abruptness of change in the features of the medium, that characterize shock waves, can be viewed as a phase transition: the pressure-time diagram of a supersonic object propagating shows how the transition induced by a shock wave is analogous to a dynamic phase transition.

When an object (or disturbance) moves faster than the information can propagate into the surrounding fluid, then the fluid near the disturbance cannot react or "get out of the way" before the disturbance arrives. In a shock wave the properties of the fluid (density, pressure, temperature, flow velocity, Mach number) change almost instantaneously. Measurements of the thickness of shock waves in air have resulted in values around 200 nm (about 10⁻⁵ in), which is on the same order of magnitude as the mean free path of gas molecules. In reference to the continuum, this implies the shock wave can be treated as either a line or a plane if the flow field is two-dimensional or three-dimensional, respectively.

Shock waves are formed when a pressure front moves at supersonic speeds and pushes on the surrounding air. At the region where this occurs, sound waves travelling against the flow reach a point where they cannot travel any further upstream and the pressure progressively builds in that region; a high pressure shock wave rapidly forms.

Shock waves are not conventional sound waves; a shock wave takes the form of a very sharp change in the gas properties. Shock waves in air are heard as a loud "crack" or "snap" noise. Over longer distances, a shock wave can change from a nonlinear wave into a linear wave, degenerating into a conventional sound wave as it heats the air and loses energy. The sound wave is heard as the familiar "thud" or "thump" of a sonic boom, commonly created by the supersonic flight of aircraft.

The shock wave is one of several different ways in which a gas in a supersonic flow can be compressed. Some other methods are isentropic compressions, including Prandtl–Meyer compressions. The method of compression of a gas results in different temperatures and densities for a given pressure ratio which can be analytically calculated for a non-reacting gas. A shock wave compression results in a loss of total pressure, meaning that it is a less efficient method of compressing gases for some purposes, for instance in the intake of a scramjet. The appearance of pressure-drag on supersonic aircraft is mostly due to the effect of shock compression on the flow.

Normal shocks

In elementary fluid mechanics utilizing ideal gases, a shock wave is treated as a discontinuity where entropy increases abruptly as the shock passes. Since no fluid flow is discontinuous, a control volume is established around the shock wave, with the control surfaces that bound this volume parallel to the shock wave (with one surface on the pre-shock side of the fluid medium and one on the post-shock side). The two surfaces are separated by a very small depth such that the shock itself is entirely contained between them. At such control surfaces, momentum, mass flux and energy are constant; within combustion, detonations can be modelled as heat introduction across a shock wave. It is assumed the system is adiabatic (no heat exits or enters the system) and no work is being done. The Rankine–Hugoniot conditions arise from these considerations.

Taking into account the established assumptions, in a system where the downstream properties are becoming subsonic: the upstream and downstream flow properties of the fluid are considered isentropic. Since the total amount of energy within the system is constant, the stagnation enthalpy remains constant over both regions. Though, entropy is increasing; this must be accounted for by a drop in stagnation pressure of the downstream fluid.

Other shocks

Oblique shocks

When analyzing shock waves in a flow field, which are still attached to the body, the shock wave which is deviating at some arbitrary angle from the flow direction is termed oblique shock. These shocks require a component vector analysis of the flow; doing so allows for the treatment of the flow in an orthogonal direction to the oblique shock as a normal shock.

Bow shocks

When an oblique shock is likely to form at an angle which cannot remain on the surface, a nonlinear phenomenon arises where the shock wave will form a continuous pattern around the body. These are termed bow shocks. In these cases, the 1d flow model is not valid and further analysis is needed to predict the pressure forces which are exerted on the surface.

Shock waves due to nonlinear steepening

Shock waves can form due to steepening of ordinary waves. The best-known example of this phenomenon is ocean waves that form breakers on the shore. In shallow water, the speed of surface waves is dependent on the depth of the water. An incoming ocean wave has a slightly higher wave speed near the crest of each wave than near the troughs between waves, because the wave height is not infinitesimal compared to the depth of the water. The crests overtake the troughs until the leading edge of the wave forms a vertical face and spills over to form a turbulent shock (a breaker) that dissipates the wave's energy as sound and heat.

Similar phenomena affect strong sound waves in gas or plasma, due to the dependence of the sound speed on temperature and pressure. Strong waves heat the medium near each pressure front, due to adiabatic compression of the air itself, so that high pressure fronts outrun the corresponding pressure troughs. There is a theory that the sound pressure levels in brass instruments such as the trombone become high enough for steepening to occur, forming an essential part of the bright timbre of the instruments. While shock formation by this process does not normally happen to unenclosed sound waves in Earth's atmosphere, it is thought to be one mechanism by which the solar chromosphere and corona are heated, via waves that propagate up from the solar interior.

Analogies

A shock wave may be described as the furthest point upstream of a moving object which "knows" about the approach of the object. In this description, the shock wave position is defined as the boundary between the zone having no information about the shock-driving event and the zone aware of the shock-driving event, analogous with the light cone described in the theory of special relativity.

To produce a shock wave, an object in a given medium (such as air or water) must travel faster than the local speed of sound. In the case of an aircraft travelling at high subsonic speed, regions of air around the aircraft may be travelling at exactly the speed of sound, so that the sound waves leaving the aircraft pile up on one another, similar to a traffic jam on a motorway. When a shock wave forms, the local air pressure increases and then spreads out sideways. Because of this amplification effect, a shock wave can be very intense, more like an explosion when heard at a distance (not coincidentally, since explosions create shock waves).

Analogous phenomena are known outside fluid mechanics. For example, charged particles accelerated beyond the speed of light in a refractive medium (such as water, where the speed of light is less than that in a vacuum) create visible shock effects, a phenomenon known as Cherenkov radiation.

Phenomenon types

Below are a number of examples of shock waves, broadly grouped with similar shock phenomena:

Moving shock

Usually consists of a shock wave propagating into a stationary medium
In this case, the gas ahead of the shock is stationary (in the laboratory frame) and the gas behind the shock can be supersonic in the laboratory frame. The shock propagates with a wavefront which is normal (at right angles) to the direction of flow. The speed of the shock is a function of the original pressure ratio between the two bodies of gas.
Moving shocks are usually generated by the interaction of two bodies of gas at different pressure, with a shock wave propagating into the lower pressure gas and an expansion wave propagating into the higher pressure gas.
Examples: Balloon bursting, Shock tube, shock wave from explosion.

Detonation wave

A detonation wave is essentially a shock supported by a trailing exothermic reaction. It involves a wave travelling through a highly combustible or chemically unstable medium, such as an oxygen-methane mixture or a high explosive. The chemical reaction of the medium occurs following the shock wave, and the chemical energy of the reaction drives the wave forward.
A detonation wave follows slightly different rules from an ordinary shock since it is driven by the chemical reaction occurring behind the shock wavefront. In the simplest theory for detonations, an unsupported, self-propagating detonation wave proceeds at the Chapman-Jouguet flow velocity. A detonation will also cause a shock to propagate into the surrounding air due to the overpressure induced by the explosion.
When a shock wave is created by high explosives such as TNT (which has a detonation velocity of 6,900 m/s), it will always travel at high, supersonic velocity from its point of origin.

Shadowgram of shock waves from a supersonic bullet fired from a rifle. The shadowgraph optical technique reveals that the bullet is moving at about a Mach number of 1.9. Left- and right-running bow waves and tail waves stream back from the bullet and its turbulent wake is also visible. Patterns at the far right are from unburned gunpowder particles ejected by the rifle.

Bow shock (detached shock)

These shocks are curved and form a small distance in front of the body. Directly in front of the body, they stand at 90 degrees to the oncoming flow and then curve around the body. Detached shocks allow the same type of analytic calculations as for the attached shock, for the flow near the shock. They are a topic of continuing interest, because the rules governing the shock's distance ahead of the blunt body are complicated and are a function of the body's shape. Additionally, the shock standoff distance varies drastically with the temperature for a non-ideal gas, causing large differences in the heat transfer to the thermal protection system of the vehicle. See the extended discussion on this topic at Atmospheric reentry. These follow the "strong-shock" solutions of the analytic equations, meaning that for some oblique shocks very close to the deflection angle limit, the downstream Mach number is subsonic. See also bow shock or oblique shock
Such a shock occurs when the maximum deflection angle is exceeded. A detached shock is commonly seen on blunt bodies, but may also be seen on sharp bodies at low Mach numbers.
Examples: Space return vehicles (Apollo, Space shuttle), bullets, the boundary (Bow shock) of a magnetosphere. The name "bow shock" comes from the example of a bow wave, the detached shock formed at the bow (front) of a ship or boat moving through water, whose slow surface wave speed is easily exceeded (see ocean surface wave).

Attached shock

These shocks appear as attached to the tip of sharp bodies moving at supersonic speeds.
Examples: Supersonic wedges and cones with small apex angles.
The attached shock wave is a classic structure in aerodynamics because, for a perfect gas and inviscid flow field, an analytic solution is available, such that the pressure ratio, temperature ratio, angle of the wedge and the downstream Mach number can all be calculated knowing the upstream Mach number and the shock angle. Smaller shock angles are associated with higher upstream Mach numbers, and the special case where the shock wave is at 90° to the oncoming flow (Normal shock), is associated with a Mach number of one. These follow the "weak-shock" solutions of the analytic equations.

In rapid granular flows

Shock waves can also occur in rapid flows of dense granular materials down inclined channels or slopes. Strong shocks in rapid dense granular flows can be studied theoretically and analyzed to compare with experimental data. Consider a configuration in which the rapidly moving material down the chute impinges on an obstruction wall erected perpendicular at the end of a long and steep channel. Impact leads to a sudden change in the flow regime from a fast moving supercritical thin layer to a stagnant thick heap. This flow configuration is particularly interesting because it is analogous to some hydraulic and aerodynamic situations associated with flow regime changes from supercritical to subcritical flows.

In astrophysics

Astrophysical environments feature many different types of shock waves. Some common examples are supernovae shock waves or blast waves travelling through the interstellar medium, the bow shock caused by the Earth's magnetic field colliding with the solar wind and shock waves caused by galaxies colliding with each other. Another interesting type of shock in astrophysics is the quasi-steady reverse shock or termination shock that terminates the ultra relativistic wind from young pulsars.

Meteor entering events

Shock waves are generated by meteoroids when they enter the Earth's atmosphere. The Tunguska event and the 2013 Russian meteor event are the best documented evidence of the shock wave produced by a massive meteoroid.

When the 2013 meteor entered into the Earth's atmosphere with an energy release equivalent to 100 or more kilotons of TNT, dozens of times more powerful than the atomic bomb dropped on Hiroshima, the meteor's shock wave produced damages as in a supersonic jet's flyby (directly underneath the meteor's path) and as a detonation wave, with the circular shock wave centred at the meteor explosion, causing multiple instances of broken glass in the city of Chelyabinsk and neighbouring areas (pictured).

Technological applications

In the examples below, the shock wave is controlled, produced by (ex. airfoil) or in the interior of a technological device, like a turbine.

Recompression shock

These shocks appear when the flow over a transonic body is decelerated to subsonic speeds.
Examples: Transonic wings, turbines
Where the flow over the suction side of a transonic wing is accelerated to a supersonic speed, the resulting re-compression can be by either Prandtl–Meyer compression or by the formation of a normal shock. This shock is of particular interest to makers of transonic devices because it can cause separation of the boundary layer at the point where it touches the transonic profile. This can then lead to full separation and stall on the profile, higher drag, or shock-buffet, a condition where the separation and the shock interact in a resonance condition, causing resonating loads on the underlying structure.

Pipe flow

This shock appears when supersonic flow in a pipe is decelerated.
Examples:
- In supersonic propulsion: ramjet, scramjet, unstart.
- In flow control: needle valve, choked venturi.
In this case the gas ahead of the shock is supersonic (in the laboratory frame), and the gas behind the shock system is either supersonic (oblique shocks) or subsonic (a normal shock) (Although for some oblique shocks very close to the deflection angle limit, the downstream Mach number is subsonic.) The shock is the result of the deceleration of the gas by a converging duct, or by the growth of the boundary layer on the wall of a parallel duct.

Combustion engines

The wave disk engine (also named "Radial Internal Combustion Wave Rotor") is a kind of pistonless rotary engine that utilizes shock waves to transfer energy between a high-energy fluid to a low-energy fluid, thereby increasing both temperature and pressure of the low-energy fluid.

Memristors

In memristors, under externally-applied electric field, shock waves can be launched across the transition-metal oxides, creating fast and non-volatile resistivity changes.

Shock capturing and detection

Advanced techniques are needed to capture shock waves and to detect shock waves in both numerical computations and experimental observations.

Computational fluid dynamics is commonly used to obtain the flow field with shock waves. Though shock waves are sharp discontinuities, in numerical solutions of fluid flow with discontinuities (shock wave, contact discontinuity or slip line), the shock wave can be smoothed out by low-order numerical method (due to numerical dissipation) or there are spurious oscillations near shock surface by high-order numerical method (due to Gibbs phenomena).

There exist some other discontinuities in fluid flow than the shock wave. The slip surface (3D) or slip line (2D) is a plane across which the tangent velocity is discontinuous, while pressure and normal velocity are continuous. Across the contact discontinuity, the pressure and velocity are continuous and the density is discontinuous. A strong expansion wave or shear layer may also contain high gradient regions which appear to be a discontinuity. Some common features of these flow structures and shock waves and the insufficient aspects of numerical and experimental tools lead to two important problems in practices: (1) some shock waves can not be detected or their positions are detected wrong, (2) some flow structures which are not shock waves are wrongly detected to be shock waves.

In fact, correct capturing and detection of shock waves are important since shock waves have the following influences: (1) causing loss of total pressure, which may be a concern related to scramjet engine performance, (2) providing lift for wave-rider configuration, as the oblique shock wave at lower surface of the vehicle can produce high pressure to generate lift, (3) leading to wave drag of high-speed vehicle which is harmful to vehicle performance, (4) inducing severe pressure load and heat flux, e.g. the Type IV shock–shock interference could yield a 17 times heating increase at vehicle surface, (5) interacting with other structures, such as boundary layers, to produce new flow structures such as flow separation, transition, etc.

Sonic boom

From Wikipedia, the free encyclopedia

The sound source is travelling at 1.4 times the speed of sound (Mach 1.4). Since the source is moving faster than the sound waves it creates, it leads the advancing wavefront.

A sonic boom is a sound associated with shock waves created when an object travels through the air faster than the speed of sound. Sonic booms generate enormous amounts of sound energy, sounding similar to an explosion or a thunderclap to the human ear.

The crack of a supersonic bullet passing overhead or the crack of a bullwhip are examples of a sonic boom in miniature.

Sonic booms due to large supersonic aircraft can be particularly loud and startling, tend to awaken people, and may cause minor damage to some structures. This led to prohibition of routine supersonic flight overland. Although they cannot be completely prevented, research suggests that with careful shaping of the vehicle, the nuisance due to the sonic booms may be reduced to the point that overland supersonic flight may become a feasible option.

A sonic boom does not occur only at the moment an object crosses the sound barrier and neither is it heard in all directions emanating from the supersonic object. Rather, the boom is a continuous effect that occurs while the object is travelling at supersonic speeds and affects only observers that are positioned at a point that intersects a region in the shape of a geometrical cone behind the object. As the object moves, this conical region also moves behind it and when the cone passes over the observer, they will briefly experience the "boom".

Causes

When an aircraft passes through the air, it creates a series of pressure waves in front of the aircraft and behind it, similar to the bow and stern waves created by a boat. These waves travel at the speed of sound and, as the speed of the object increases, the waves are forced together, or compressed, because they cannot get out of each other's way quickly enough. Eventually they merge into a single shock wave, which travels at the speed of sound, a critical speed known as Mach 1, and is approximately 1,192 km/h (741 mph) at sea level and 20 °C (68 °F).

In smooth flight, the shock wave starts at the nose of the aircraft and ends at the tail. Because the different radial directions around the aircraft's direction of travel are equivalent (given the "smooth flight" condition), the shock wave forms a Mach cone, similar to a vapour cone, with the aircraft at its tip. The half-angle $α$ between the direction of flight and the shock wave is given by:

\sin (α) = \frac{v_{sound}}{v_{object}}

where $\frac{v_{sound}}{v_{object}}$ is the inverse $(\frac{1}{M a})$ of the plane's Mach number ( $M a = \frac{v_{object}}{v_{sound}}$ ). Thus the faster the plane travels, the finer and more pointed the cone is.

There is a rise in pressure at the nose, decreasing steadily to a negative pressure at the tail, followed by a sudden return to normal pressure after the object passes. This "overpressure profile" is known as an N-wave because of its shape. The "boom" is experienced when there is a sudden change in pressure; therefore, an N-wave causes two booms – one when the initial pressure-rise reaches an observer, and another when the pressure returns to normal. This leads to a distinctive "double boom" from a supersonic aircraft. When the aircraft is maneuvering, the pressure distribution changes into different forms, with a characteristic U-wave shape.

Since the boom is being generated continually as long as the aircraft is supersonic, it fills out a narrow path on the ground following the aircraft's flight path, a bit like an unrolling red carpet, and hence known as the boom carpet. Its width depends on the altitude of the aircraft. The distance from the point on the ground where the boom is heard to the aircraft depends on its altitude and the angle $α$ .

For today's supersonic aircraft in normal operating conditions, the peak overpressure varies from less than 50 to 500 Pa (1 to 10 psf (pound per square foot)) for an N-wave boom. Peak overpressures for U-waves are amplified two to five times the N-wave, but this amplified overpressure impacts only a very small area when compared to the area exposed to the rest of the sonic boom. The strongest sonic boom ever recorded was 7,000 Pa (144 psf) and it did not cause injury to the researchers who were exposed to it. The boom was produced by an F-4 flying just above the speed of sound at an altitude of 100 feet (30 m). In recent tests, the maximum boom measured during more realistic flight conditions was 1,010 Pa (21 psf). There is a probability that some damage—shattered glass, for example—will result from a sonic boom. Buildings in good condition should suffer no damage by pressures of 530 Pa (11 psf) or less. And, typically, community exposure to sonic boom is below 100 Pa (2 psf). Ground motion resulting from sonic boom is rare and is well below structural damage thresholds accepted by the U.S. Bureau of Mines and other agencies.

The power, or volume, of the shock wave depends on the quantity of air that is being accelerated, and thus the size and shape of the aircraft. As the aircraft increases speed the shock cone gets tighter around the craft and becomes weaker to the point that at very high speeds and altitudes no boom is heard. The "length" of the boom from front to back depends on the length of the aircraft to a power of 3/2. Longer aircraft therefore "spread out" their booms more than smaller ones, which leads to a less powerful boom.

Several smaller shock waves can and usually do form at other points on the aircraft, primarily at any convex points, or curves, the leading wing edge, and especially the inlet to engines. These secondary shockwaves are caused by the air being forced to turn around these convex points, which generates a shock wave in supersonic flow.

The later shock waves are somewhat faster than the first one, travel faster and add to the main shockwave at some distance away from the aircraft to create a much more defined N-wave shape. This maximizes both the magnitude and the "rise time" of the shock which makes the boom seem louder. On most aircraft designs the characteristic distance is about 40,000 feet (12,000 m), meaning that below this altitude the sonic boom will be "softer". However, the drag at this altitude or below makes supersonic travel particularly inefficient, which poses a serious problem.

Supersonic aircraft

Supersonic aircraft are any aircraft that can achieve flight faster than Mach 1, which is supersonic. "Supersonic includes speeds up to five times Mach than the speed of sound, or Mach 5." (Dunbar, 2015) The top mileage per hour for a supersonic aircraft normally ranges anywhere from 700 to 1,500 miles per hour (1,100 to 2,400 km/h). Typically, most aircraft do not exceed 1,500 mph (2,414 km/h). There are many variations of supersonic aircraft. Some models of a supersonic aircraft make use of better engineered aerodynamics that allow a few sacrifices in the aerodynamics of the model for thruster power. Other models use the efficiency and power of the thruster to allow a less aerodynamic model to achieve greater speeds. Typical model found in United States military use ranges from an average of $13 million to $35 million U.S. dollars.

Measurement and examples

The pressure from sonic booms caused by aircraft is often a few pounds per square foot. A vehicle flying at greater altitude will generate lower pressures on the ground, because the shock wave reduces in intensity as it spreads out away from the vehicle, but the sonic booms are less affected by vehicle speed.

Aircraft	Speed	Altitude	Pressure (lbf/ft²)	Pressure (Pa)
SR-71 Blackbird	Mach 3+	80,000 feet (24,000 m)	0.9	43
Concorde (SST)	Mach 2	52,000 feet (16,000 m)	1.94	93
F-104 Starfighter	Mach 1.93	48,000 feet (15,000 m)	0.8	38
Space Shuttle	Mach 1.5	60,000 feet (18,000 m)	1.25	60

Abatement

In the late 1950s when supersonic transport (SST) designs were being actively pursued, it was thought that although the boom would be very large, the problems could be avoided by flying higher. This assumption was proven false when the North American XB-70 Valkyrie first flew, and it was found that the boom was a problem even at 70,000 feet (21,000 m). It was during these tests that the N-wave was first characterized.

Richard Seebass and his colleague Albert George at Cornell University studied the problem extensively and eventually defined a "figure of merit" (FM) to characterize the sonic boom levels of different aircraft. FM is a function of the aircraft weight and the aircraft length. The lower this value, the less boom the aircraft generates, with figures of about 1 or lower being considered acceptable. Using this calculation, they found FMs of about 1.4 for Concorde and 1.9 for the Boeing 2707. This eventually doomed most SST projects as public resentment, mixed with politics, eventually resulted in laws that made any such aircraft less useful (flying supersonically only over water for instance). Small aeroplane designs like business jets are favoured and tend to produce minimal to no audible booms.

Seebass and George also worked on the problem from a different angle, trying to spread out the N-wave laterally and temporally (longitudinally), by producing a strong and downwards-focused (SR-71 Blackbird, Boeing X-43) shock at a sharp, but wide angle nose cone, which will travel at slightly supersonic speed (bow shock), and using a swept back flying wing or an oblique flying wing to smooth out this shock along the direction of flight (the tail of the shock travels at sonic speed). To adapt this principle to existing planes, which generate a shock at their nose cone and an even stronger one at their wing leading edge, the fuselage below the wing is shaped according to the area rule. Ideally this would raise the characteristic altitude from 40,000 feet (12,000 m) to 60,000 feet (from 12,000 m to 18,000 m), which is where most SST aircraft were expected to fly.

This remained untested for decades, until DARPA started the Quiet Supersonic Platform project and funded the Shaped Sonic Boom Demonstration (SSBD) aircraft to test it. SSBD used an F-5 Freedom Fighter. The F-5E was modified with a highly refined shape which lengthened the nose to that of the F-5F model. The fairing extended from the nose all the way back to the inlets on the underside of the aircraft. The SSBD was tested over a two-year period culminating in 21 flights and was an extensive study on sonic boom characteristics. After measuring the 1,300 recordings, some taken inside the shock wave by a chase plane, the SSBD demonstrated a reduction in boom by about one-third. Although one-third is not a huge reduction, it could have reduced Concorde's boom to an acceptable level below FM = 1.

As a follow-on to SSBD, in 2006 a NASA-Gulfstream Aerospace team tested the Quiet Spike on NASA-Dryden's F-15B aircraft 836. The Quiet Spike is a telescoping boom fitted to the nose of an aircraft specifically designed to weaken the strength of the shock waves forming on the nose of the aircraft at supersonic speeds. Over 50 test flights were performed. Several flights included probing of the shockwaves by a second F-15B, NASA's Intelligent Flight Control System testbed, aircraft 837.

There are theoretical designs that do not appear to create sonic booms at all, such as the Busemann biplane. However, creating a shockwave is inescapable if they generate aerodynamic lift.

In 2018, NASA awarded Lockheed Martin a $247.5 million contract to construct a design known as the Low Boom Flight Demonstrator, which aims to reduce the boom to the sound of a car door closing. As of November 2022, the first flight was expected in 2023.

Perception, noise and other concerns

The sound of a sonic boom depends largely on the distance between the observer and the aircraft shape producing the sonic boom. A sonic boom is usually heard as a deep double "boom" as the aircraft is usually some distance away. The sound is much like that of mortar bombs, commonly used in firework displays. It is a common misconception that only one boom is generated during the subsonic to supersonic transition; rather, the boom is continuous along the boom carpet for the entire supersonic flight. As a former Concorde pilot puts it, "You don't actually hear anything on board. All we see is the pressure wave moving down the aeroplane – it gives an indication on the instruments. And that's what we see around Mach 1. But we don't hear the sonic boom or anything like that. That's rather like the wake of a ship – it's behind us."

In 1964, NASA and the Federal Aviation Administration began the Oklahoma City sonic boom tests, which caused eight sonic booms per day over a period of six months. Valuable data was gathered from the experiment, but 15,000 complaints were generated and ultimately entangled the government in a class-action lawsuit, which it lost on appeal in 1969.

Sonic booms were also a nuisance in North Cornwall and North Devon in the UK as these areas were underneath the flight path of Concorde. Windows would rattle and in some cases the "torching" (pointing underneath roof slates) would be dislodged with the vibration.

There has been recent work in this area, notably under DARPA's Quiet Supersonic Platform studies. Research by acoustics experts under this program began looking more closely at the composition of sonic booms, including the frequency content. Several characteristics of the traditional sonic boom "N" wave can influence how loud and irritating it can be perceived by listeners on the ground. Even strong N-waves such as those generated by Concorde or military aircraft can be far less objectionable if the rise time of the over-pressure is sufficiently long. A new metric has emerged, known as perceived loudness, measured in PLdB. This takes into account the frequency content, rise time, etc. A well-known example is the snapping of one's fingers in which the "perceived" sound is nothing more than an annoyance.

The energy range of sonic boom is concentrated in the 0.1–100 hertz frequency range that is considerably below that of subsonic aircraft, gunfire and most industrial noise. Duration of sonic boom is brief; less than a second, 100 milliseconds (0.1 second) for most fighter-sized aircraft and 500 milliseconds for the space shuttle or Concorde jetliner. The intensity and width of a sonic boom path depends on the physical characteristics of the aircraft and how it is operated. In general, the greater an aircraft's altitude, the lower the over-pressure on the ground. Greater altitude also increases the boom's lateral spread, exposing a wider area to the boom. Over-pressures in the sonic boom impact area, however, will not be uniform. Boom intensity is greatest directly under the flight path, progressively weakening with greater horizontal distance away from the aircraft flight track. Ground width of the boom exposure area is approximately 1 statute mile (1.6 km) for each 1,000 feet (300 m) of altitude (the width is about five times the altitude); that is, an aircraft flying supersonic at 30,000 feet (9,100 m) will create a lateral boom spread of about 30 miles (48 km). For steady supersonic flight, the boom is described as a carpet boom since it moves with the aircraft as it maintains supersonic speed and altitude. Some maneuvers, diving, acceleration or turning, can cause focusing of the boom. Other maneuvers, such as deceleration and climbing, can reduce the strength of the shock. In some instances weather conditions can distort sonic booms.

Depending on the aircraft's altitude, sonic booms reach the ground 2 to 60 seconds after flyover. However, not all booms are heard at ground level. The speed of sound at any altitude is a function of air temperature. A decrease or increase in temperature results in a corresponding decrease or increase in sound speed. Under standard atmospheric conditions, air temperature decreases with increased altitude. For example, when sea-level temperature is 59 degrees Fahrenheit (15 °C), the temperature at 30,000 feet (9,100 m) drops to minus 49 degrees Fahrenheit (−45 °C). This temperature gradient helps bend the sound waves upward. Therefore, for a boom to reach the ground, the aircraft speed relative to the ground must be greater than the speed of sound at the ground. For example, the speed of sound at 30,000 feet (9,100 m) is about 670 miles per hour (1,080 km/h), but an aircraft must travel at least 750 miles per hour (1,210 km/h) (Mach 1.12) for a boom to be heard on the ground.

The composition of the atmosphere is also a factor. Temperature variations, humidity, atmospheric pollution, and winds can all have an effect on how a sonic boom is perceived on the ground. Even the ground itself can influence the sound of a sonic boom. Hard surfaces such as concrete, pavement, and large buildings can cause reflections which may amplify the sound of a sonic boom. Similarly, grassy fields and profuse foliage can help attenuate the strength of the over-pressure of a sonic boom.

Currently there are no industry-accepted standards for the acceptability of a sonic boom. However, work is underway to create metrics that will help in understanding how humans respond to the noise generated by sonic booms. Until such metrics can be established, either through further study or supersonic overflight testing, it is doubtful that legislation will be enacted to remove the current prohibition on supersonic overflight in place in several countries, including the United States.

Bullwhip

The cracking sound a bullwhip makes when properly wielded is, in fact, a small sonic boom. The end of the whip, known as the "cracker", moves faster than the speed of sound, thus creating a sonic boom.

A bullwhip tapers down from the handle section to the cracker. The cracker has much less mass than the handle section. When the whip is sharply swung, the momentum is transferred down the length of the tapering whip, the declining mass being made up for with increasing speed. Goriely and McMillen showed that the physical explanation is complex, involving the way that a loop travels down a tapered filament under tension.

Search This Blog

Sunday, October 22, 2023

Flame detector

Optical flame detectors

Ultraviolet detector

Near IR array

Infrared

Infrared thermal cameras

UV/IR

IR/IR flame detection

IR3 flame detection

3IR+UV flame detection

Visible sensors

Video

Other types

Ionization current flame detection

Thermocouple flame detection

Applications

Emission of radiation

Sunlight

Heat radiation

Cone of vision

The detection range

The square law

Shock wave

Terminology

In supersonic flows

Normal shocks

Other shocks

Oblique shocks

Bow shocks

Shock waves due to nonlinear steepening

Analogies

Phenomenon types

Moving shock

Detonation wave

Bow shock (detached shock)

Attached shock

In rapid granular flows

In astrophysics

Meteor entering events

Technological applications

Recompression shock

Pipe flow

Combustion engines

Memristors

Shock capturing and detection

Sonic boom

Causes

Supersonic aircraft

Measurement and examples

Abatement

Perception, noise and other concerns

Bullwhip

Introduction to entropy