From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Magnetic_nanoparticles
Magnetic nanoparticles are a class of nanoparticle that can be manipulated using magnetic fields. Such particles commonly consist of two components, a magnetic material, often iron, nickel and cobalt, and a chemical component that has functionality. While nanoparticles are smaller than 1 micrometer in diameter (typically 1–100 nanometers), the larger microbeads are 0.5–500 micrometer in diameter. Magnetic nanoparticle clusters that are composed of a number of individual magnetic nanoparticles are known as magnetic nanobeads with a diameter of 50–200 nanometers. Magnetic nanoparticle clusters are a basis for their further magnetic assembly into magnetic nanochains. The magnetic nanoparticles have been the focus of much research recently because they possess attractive properties which could see potential use in catalysis including nanomaterial-based catalysts, biomedicine and tissue specific targeting, magnetically tunable colloidal photonic crystals, microfluidics, magnetic resonance imaging, magnetic particle imaging, data storage, environmental remediation, nanofluids, optical filters, defect sensor, magnetic cooling and cation sensors.
Properties
The physical and chemical properties of magnetic nanoparticles largely depend on the synthesis method and chemical structure. In most cases, the particles range from 1 to 100 nm in size and may display superparamagnetism.
Types of magnetic nanoparticles
Oxides: ferrites
Ferrite nanoparticles or iron oxide nanoparticles (iron oxides in crystal structure of maghemite or magnetite) are the most explored magnetic nanoparticles up to date. Once the ferrite particles become smaller than 128 nm they become superparamagnetic which prevents self agglomeration since they exhibit their magnetic behavior only when an external magnetic field is applied. The magnetic moment of ferrite nanoparticles can be greatly increased by controlled clustering of a number of individual superparamagnetic nanoparticles into superparamagnetic nanoparticle clusters, namely magnetic nanobeads. With the external magnetic field switched off, the remanence falls back to zero. Just like non-magnetic oxide nanoparticles, the surface of ferrite nanoparticles is often modified by surfactants, silica, silicones or phosphoric acid derivatives to increase their stability in solution.
Ferrites with a shell

The surface of a maghemite or magnetite magnetic nanoparticle is relatively inert and does not usually allow strong covalent bonds with functionalization molecules. However, the reactivity of the magnetic nanoparticles can be improved by coating a layer of silica onto their surface. The silica shell can be easily modified with various surface functional groups via covalent bonds between organo-silane molecules and silica shell. In addition, some fluorescent dye molecules can be covalently bonded to the functionalized silica shell.
Ferrite nanoparticle clusters with narrow size distribution consisting of superparamagnetic oxide nanoparticles (~ 80 maghemite superparamagnetic nanoparticles per bead) coated with a silica shell have several advantages over metallic nanoparticles:
- Higher chemical stability (crucial for biomedical applications)
- Narrow size distribution (crucial for biomedical applications)
- Higher colloidal stability since they do not magnetically agglomerate
- Magnetic moment can be tuned with the nanoparticle cluster size
- Retained superparamagnetic properties (independent of the nanoparticle cluster size)
- Silica surface enables straightforward covalent functionalization
Metallic
Metallic nanoparticles may be beneficial for some technical applications due to their higher magnetic moment whereas oxides (maghemite, magnetite) would be beneficial for biomedical applications. This also implies that for the same moment, metallic nanoparticles can be made smaller than their oxide counterparts. On the other hand, metallic nanoparticles have the great disadvantage of being pyrophoric and reactive to oxidizing agents to various degrees. This makes their handling difficult and enables unwanted side reactions which makes them less appropriate for biomedical applications. Colloid formation for metallic particles is also much more challenging.
Metallic with a shell

The metallic core of magnetic nanoparticles may be passivated by gentle oxidation, surfactants, polymers and precious metals. In an oxygen environment, Co nanoparticles form an anti-ferromagnetic CoO layer on the surface of the Co nanoparticle. Recently, work has explored the synthesis and exchange bias effect in these Co core CoO shell nanoparticles with a gold outer shell. Nanoparticles with a magnetic core consisting either of elementary Iron or Cobalt with a nonreactive shell made of graphene have been synthesized recently. The advantages compared to ferrite or elemental nanoparticles are:
- Higher magnetization
- Higher stability in acidic and basic solution as well as organic solvents
- Chemistry[28] on the graphene surface via methods already known for carbon nanotubes
Synthesis
Several methods exist for preparing magnetic nanoparticle.
Co-precipitation
Co-precipitation is a facile and convenient way to synthesize iron oxides (either Fe3O4 or γ-Fe2O3) from aqueous Fe2+/Fe3+ salt solutions by the addition of a base under inert atmosphere at room temperature or at elevated temperature. The size, shape, and composition of the magnetic nanoparticles very much depends on the type of salts used (e.g.chlorides, sulfates, nitrates), the Fe2+/Fe3+ ratio, the reaction temperature, the pH value and ionic strength of the media, and the mixing rate with the base solution used to provoke the precipitation. The co-precipitation approach has been used extensively to produce ferrite nanoparticles of controlled sizes and magnetic properties. A variety of experimental arrangements have been reported to facilitate continuous and large–scale co–precipitation of magnetic particles by rapid mixing. Recently, the growth rate of the magnetic nanoparticles was measured in real-time during the precipitation of magnetite nanoparticles by an integrated AC magnetic susceptometer within the mixing zone of the reactants.
Thermal decomposition
Magnetic nanocrystals with smaller size can essentially be synthesized through the thermal decomposition of alkaline organometallic compounds in high-boiling organic solvents containing stabilizing surfactants.
Microemulsion
Using the microemulsion technique, metallic cobalt, cobalt/platinum alloys, and gold-coated cobalt/platinum nanoparticles have been synthesized in reverse micelles of cetyltrimethlyammonium bromide, using 1-butanol as the cosurfactant and octane as the oil phase.
Flame spray synthesis
Using flame spray pyrolysis and varying the reaction conditions, oxides, metal or carbon coated nanoparticles are produced at a rate of > 30 g/h .
 Various flame spray conditions and their impact on the resulting nanoparticles |
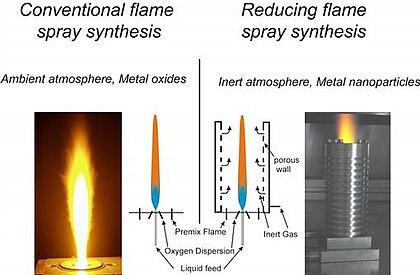 Operational layout differences between conventional and reducing flame spray synthesis |
Potential applications
A wide variety of potential applications have been envisaged. Since magnetic nanoparticles are expensive to produce, there is interest in their recycling or for highly specialized applications.
The potential and versatility of magnetic chemistry arises from the fast and easy separation of the magnetic nanoparticles, eliminating tedious and costly separation processes usually applied in chemistry. Furthermore, the magnetic nanoparticles can be guided via a magnetic field to the desired location which could, for example, enable pinpoint precision in fighting cancer.
Medical diagnostics and treatments
Magnetic nanoparticles have been examined for use in an experimental cancer treatment called magnetic hyperthermia in which an alternating magnetic field (AMF) is used to heat the nanoparticles. To achieve sufficient magnetic nanoparticle heating, the AMF typically has a frequency between 100–500 kHz, although significant research has been done at lower frequencies as well as frequencies as high as 10 MHz, with the amplitude of the field usually between 8-16kAm−1.
Affinity ligands such as epidermal growth factor (EGF), folic acid, aptamers, lectins etc. can be attached to the magnetic nanoparticle surface with the use of various chemistries. This enables targeting of magnetic nanoparticles to specific tissues or cells. This strategy is used in cancer research to target and treat tumors in combination with magnetic hyperthermia or nanoparticle-delivered cancer drugs. Despite research efforts, however, the accumulation of nanoparticles inside of cancer tumors of all types is sub-optimal, even with affinity ligands. Willhelm et al. conducted a broad analysis of nanoparticle delivery to tumors and concluded that the median amount of injected dose reaching a solid tumor is only 0.7%. The challenge of accumulating large amounts of nanoparticles inside of tumors is arguably the biggest obstacle facing nanomedicine in general. While direct injection is used in some cases, intravenous injection is most often preferred to obtain a good distribution of particles throughout the tumor. Magnetic nanoparticles have a distinct advantage in that they can accumulate in desired regions via magnetically guided delivery, although this technique still needs further development to achieve optimal delivery to solid tumors.
Another potential treatment of cancer includes attaching magnetic nanoparticles to free-floating cancer cells, allowing them to be captured and carried out of the body. The treatment has been tested in the laboratory on mice and will be looked at in survival studies.
Magnetic nanoparticles can be used for the detection of cancer. Blood can be inserted onto a microfluidic chip with magnetic nanoparticles in it. These magnetic nanoparticles are trapped inside due to an externally applied magnetic field as the blood is free to flow through. The magnetic nanoparticles are coated with antibodies targeting cancer cells or proteins. The magnetic nanoparticles can be recovered and the attached cancer-associated molecules can be assayed to test for their existence.
Magnetic nanoparticles can be conjugated with carbohydrates and used for detection of bacteria. Iron oxide particles have been used for the detection of Gram negative bacteria like Escherichia coli and for detection of Gram positive bacteria like Streptococcus suis
Core-shell magnetic nanoparticles, particularly cobalt ferrite, possess antimicrobial properties against hazardous prokaryotic (E. coli, Staphylococcus aureus) and eukaryotic (Candida parapsilosis, Candida albicans) microorganisms. It is known that the size of the magnetic nanoparticles performs a critical role, as the smaller the particles, the more significant the antimicrobial effect.
Other diagnostic uses can be achieved by conjugation of the nanoparticles with oligonucleotides that can either be complementary to a DNA or RNA sequence of interest to detect them, such as pathogenic DNA or products of DNA amplification reactions in the presence of pathogenic DNA, or an aptamer recognizing a molecule of interest. This can lead to detection of pathogens such as virus or bacteria in humans or dangerous chemicals or other substances in the body.
Magnetic immunoassay
Magnetic immunoassay (MIA) is a novel type of diagnostic immunoassay utilizing magnetic nanobeads as labels in lieu of conventional, enzymes, radioisotopes or fluorescent moieties. This assay involves the specific binding of an antibody to its antigen, where a magnetic label is conjugated to one element of the pair. The presence of magnetic nanobeads is then detected by a magnetic reader (magnetometer) which measures the magnetic field change induced by the beads. The signal measured by the magnetometer is proportional to the analyte (virus, toxin, bacteria, cardiac marker, etc.) quantity in the initial sample.
Waste water treatment
Thanks to the easy separation by applying a magnetic field and the very large surface to volume ratio, magnetic nanoparticles have a potential for treatment of contaminated water. In this method, attachment of EDTA-like chelators to carbon coated metal nanomagnets results in a magnetic reagent for the rapid removal of heavy metals from solutions or contaminated water by three orders of magnitude to concentrations as low as micrograms per Litre. Magnetic nanobeads or nanoparticle clusters composed of FDA-approved oxide superparamagnetic nanoparticles (e.g. maghemite, magnetite) hold much potential for waste water treatment since they express excellent biocompatibility which concerning the environmental impacts of the material is an advantage compared to metallic nanoparticles.
Electrochemical sensing
Magneto-electrochemical assays are based on the use of magnetic nanoparticles in electrochemical sensing either by being distributed through a sample where they can collect and preconcentrate the analyte and handled by a magnetic field or by modifying an electrode surface enhancing its conductivity and the affinity with the analyte. Coated-magnetic nanoparticles have a key aspect in electrochemical sensing not only because it facilitates the collecting of analyte but also it allows MNPs to be part of the sensor transduction mechanism. For the manipulation of MNPs in electrochemical sensing has been used magnetic electrode shafts or disposable screen-printed electrodes integrating permanent bonded magnets, aiming to replace magnetic supports or any external magnetic field.
Supported enzymes and peptides
Enzymes, proteins, and other biologically and chemically active substances have been immobilized on magnetic nanoparticles. The immobilization of enzymes on inexpensive, non-toxic and easily synthesized iron magnetic nanoparticles (MNP) has shown great promise due to more stable proteins, better product yield, ease of protein purification and multiple usage as a result of their magnetic susceptibility. They are of interest as possible supports for solid phase synthesis.
This technology is potentially relevant to cellular labelling/cell separation, detoxification of biological fluids, tissue repair, drug delivery, magnetic resonance imaging, hyperthermia and magnetofection.
Random versus site-directed enzyme immobilization
Enzymes immobilized on magnetic nanoparticles (MNP) via random multipoint attachment, result in a heterogeneous protein population with reduced activity due to restriction of substrate access to the active site. Methods based on chemical modifications are now available where MNP can be linked to a protein molecule via a single specific amino acid (such as N- or C- termini), thus avoiding reduction in activity due to the free access of the substrate to the active site. Moreover, site-directed immobilization also avoids modifying catalytic residues. One such common method involves using Alkyne-Azide Click chemistry as both groups are absent in proteins.
Catalyst support
Magnetic nanoparticles are of potential use as a catalyst or catalyst supports. In chemistry, a catalyst support is the material, usually a solid with a high surface area, to which a catalyst is affixed. The reactivity of heterogeneous catalysts occurs at the surface atoms. Consequently, great effort is made to maximize the surface area of a catalyst by distributing it over the support. The support may be inert or participate in the catalytic reactions. Typical supports include various kinds of carbon, alumina, and silica. Immobilizing the catalytic center on top of nanoparticles with a large surface to volume ratio addresses this problem. In the case of magnetic nanoparticles it adds the property of facile a separation. An early example involved a rhodium catalysis attached to magnetic nanoparticles.

In another example, the stable radical TEMPO was attached to the graphene-coated cobalt nanoparticles via a diazonium reaction. The resulting catalyst was then used for the chemoselective oxidation of primary and secondary alcohols.

The catalytic reaction can be conducted in a continuous flow reactor instead of a batch reactor with no remains of the catalyst in the end product. Graphene coated cobalt nanoparticles have been used for that experiment since they exhibit a higher magnetization than Ferrite nanoparticles, which is essential for a fast and clean separation via external magnetic field.

Biomedical imaging
There are many applications for iron-oxide based nanoparticles in concert with magnetic resonance imaging. Magnetic CoPt nanoparticles are being used as an MRI contrast agent for transplanted neural stem cell detection.
Cancer therapy
In magnetic fluid hyperthermia, nanoparticles of different types like Iron oxide, magnetite, maghemite or even gold are injected in tumor and then subjected under a high frequency magnetic field. These nanoparticles produce heat that typically increases tumor temperature to 40-46 °C, which can kill cancer cells. Another major potential of magnetic nanoparticles is the ability to combine heat (hyperthermia) and drug release for a cancer treatment. Numerous studies have shown particle constructs that can be loaded with a drug cargo and magnetic nanoparticles. The most prevalent construct is the "Magnetoliposome", which is a liposome with magnetic nanoparticles typically embedded in the lipid bilayer. Under an alternating magnetic field, the magnetic nanoparticles are heated, and this heat permeabilizes the membrane. This causes release of the loaded drug. This treatment option has a lot of potential as the combination of hyperthermia and drug release is likely to treat tumors better than either option alone, but it is still under development.
Information storage
A promising candidate for high-density storage is the face-centered tetragonal phase FePt alloy. Grain sizes can be as small as 3 nanometers. If it's possible to modify the MNPs at this small scale, the information density that can be achieved with this media could easily surpass 1 Terabyte per square inch.
Genetic engineering
Magnetic nanoparticles can be used for a variety of genetics applications. One application is the rapid isolation of DNA and mRNA. In one application, the magnetic bead is attached to a poly T tail. When mixed with mRNA, the poly A tail of the mRNA will attach to the bead's poly T tail and the isolation takes place simply by placing a magnet on the side of the tube and pouring out the liquid. Magnetic beads have also been used in plasmid assembly. Rapid genetic circuit construction has been achieved by the sequential addition of genes onto a growing genetic chain, using nanobeads as an anchor. This method has been shown to be much faster than previous methods, taking less than an hour to create functional multi-gene constructs in vitro.






















