Algebraic curve

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Algebraic_curve

The Tschirnhausen cubic is an algebraic curve of degree three.

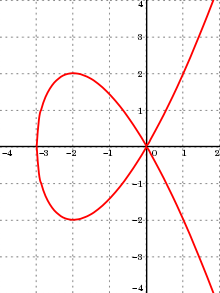
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.

More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for such a birational equivalence.

These birational equivalences reduce most of the study of algebraic curves to the study of algebraic plane curves. However, some properties are not kept under birational equivalence and must be studied on non-plane curves. This is, in particular, the case for the degree and smoothness. For example, there exist smooth curves of genus 0 and degree greater than two, but any plane projection of such curves has singular points (see Genus–degree formula).

A non-plane curve is often called a space curve or a skew curve.

In Euclidean geometry

An algebraic curve in the Euclidean plane is the set of the points whose coordinates are the solutions of a bivariate polynomial equation p(x, y) = 0. This equation is often called the implicit equation of the curve, in contrast to the curves that are the graph of a function defining explicitly y as a function of x.

With a curve given by such an implicit equation, the first problems are to determine the shape of the curve and to draw it. These problems are not as easy to solve as in the case of the graph of a function, for which y may easily be computed for various values of x. The fact that the defining equation is a polynomial implies that the curve has some structural properties that may help in solving these problems.

Every algebraic curve may be uniquely decomposed into a finite number of smooth monotone arcs (also called branches) sometimes connected by some points sometimes called "remarkable points", and possibly a finite number of isolated points called acnodes. A smooth monotone arc is the graph of a smooth function which is defined and monotone on an open interval of the x-axis. In each direction, an arc is either unbounded (usually called an infinite arc) or has an endpoint which is either a singular point (this will be defined below) or a point with a tangent parallel to one of the coordinate axes.

For example, for the Tschirnhausen cubic, there are two infinite arcs having the origin (0,0) as of endpoint. This point is the only singular point of the curve. There are also two arcs having this singular point as one endpoint and having a second endpoint with a horizontal tangent. Finally, there are two other arcs each having one of these points with horizontal tangent as the first endpoint and having the unique point with vertical tangent as the second endpoint. In contrast, the sinusoid is certainly not an algebraic curve, having an infinite number of monotone arcs.

To draw an algebraic curve, it is important to know the remarkable points and their tangents, the infinite branches and their asymptotes (if any) and the way in which the arcs connect them. It is also useful to consider the inflection points as remarkable points. When all this information is drawn on a sheet of paper, the shape of the curve usually appears rather clearly. If not, it suffices to add a few other points and their tangents to get a good description of the curve.

The methods for computing the remarkable points and their tangents are described below in the section Remarkable points of a plane curve.

Plane projective curves

It is often desirable to consider curves in the projective space. An algebraic curve in the projective plane or plane projective curve is the set of the points in a projective plane whose projective coordinates are zeros of a homogeneous polynomial in three variables P(x, y, z).

Every affine algebraic curve of equation p(x, y) = 0 may be completed into the projective curve of equation ${\displaystyle {}^{h}p(x,y,z)=0,}$ where

$${\displaystyle {}^{h}p(x,y,z)=z^{\mathrm{deg}(p)}p\left(\frac{x}{z},\frac{y}{z}\right)}$$

is the result of the homogenization of p. Conversely, if P(x, y, z) = 0 is the homogeneous equation of a projective curve, then P(x, y, 1) = 0 is the equation of an affine curve, which consists of the points of the projective curve whose third projective coordinate is not zero. These two operations are reciprocal one to the other, as ${\displaystyle {}^{h}p(x,y,1)=p(x,y)}$ and, if p is defined by ${\displaystyle p(x,y)=P(x,y,1)}$, then ${\displaystyle {}^{h}p(x,y,z)=P(x,y,z),}$ as soon as the homogeneous polynomial P is not divisible by z.

For example, the projective curve of equation x² + y² − z² is the projective completion of the unit circle of equation x² + y² − 1 = 0.

This implies that an affine curve and its projective completion are the same curves, or, more precisely that the affine curve is a part of the projective curve that is large enough to well define the "complete" curve. This point of view is commonly expressed by calling "points at infinity" of the affine curve the points (in finite number) of the projective completion that do not belong to the affine part.

Projective curves are frequently studied for themselves. They are also useful for the study of affine curves. For example, if p(x, y) is the polynomial defining an affine curve, beside the partial derivatives ${\displaystyle p_x^{\prime }}$ and ${\displaystyle p_y^{\prime }}$, it is useful to consider the derivative at infinity

$${\displaystyle p_{\mathrm{\infty }}^{\prime }(x,y)={}^h{p}_z^{\prime }(x,y,1).}$$

For example, the equation of the tangent of the affine curve of equation p(x, y) = 0 at a point (a, b) is

$${\displaystyle x{p}_x^{\prime }(a,b)+y{p}_y^{\prime }(a,b)+p_{\mathrm{\infty }}^{\prime }(a,b)=0.}$$

Remarkable points of a plane curve

See also: Plane curve

In this section, we consider a plane algebraic curve defined by a bivariate polynomial p(x, y) and its projective completion, defined by the homogenization ${\displaystyle P(x,y,z)={}^{h}p(x,y,z)}$ of p.

Intersection with a line

Knowing the points of intersection of a curve with a given line is frequently useful. The intersection with the axes of coordinates and the asymptotes are useful to draw the curve. Intersecting with a line parallel to the axes allows one to find at least a point in each branch of the curve. If an efficient root-finding algorithm is available, this allows to draw the curve by plotting the intersection point with all the lines parallel to the y-axis and passing through each pixel on the x-axis.

If the polynomial defining the curve has a degree d, any line cuts the curve in at most d points. Bézout's theorem asserts that this number is exactly d, if the points are searched in the projective plane over an algebraically closed field (for example the complex numbers), and counted with their multiplicity. The method of computation that follows proves again this theorem, in this simple case.

To compute the intersection of the curve defined by the polynomial p with the line of equation ax+by+c = 0, one solves the equation of the line for x (or for y if a = 0). Substituting the result in p, one gets a univariate equation q(y) = 0 (or q(x) = 0, if the equation of the line has been solved in y), each of whose roots is one coordinate of an intersection point. The other coordinate is deduced from the equation of the line. The multiplicity of an intersection point is the multiplicity of the corresponding root. There is an intersection point at infinity if the degree of q is lower than the degree of p; the multiplicity of such an intersection point at infinity is the difference of the degrees of p and q.

Tangent at a point

The tangent at a point (a, b) of the curve is the line of equation ${\displaystyle (x-a)p_x^{\prime }(a,b)+(y-b)p_y^{\prime }(a,b)=0}$, like for every differentiable curve defined by an implicit equation. In the case of polynomials, another formula for the tangent has a simpler constant term and is more symmetric:

$${\displaystyle x{p}_x^{\prime }(a,b)+y{p}_y^{\prime }(a,b)+p_{\mathrm{\infty }}^{\prime }(a,b)=0,}$$

where ${\displaystyle p_{\mathrm{\infty }}^{\prime }(x,y)=P_z^{\prime }(x,y,1)}$ is the derivative at infinity. The equivalence of the two equations results from Euler's homogeneous function theorem applied to P.

If ${\displaystyle p_x^{\prime }(a,b)=p_y^{\prime }(a,b)=0,}$ the tangent is not defined and the point is a singular point.

This extends immediately to the projective case: The equation of the tangent of at the point of projective coordinates (a:b:c) of the projective curve of equation P(x, y, z) = 0 is

$${\displaystyle x{P}_x^{\prime }(a,b,c)+y{P}_y^{\prime }(a,b,c)+z{P}_z^{\prime }(a,b,c)=0,}$$

and the points of the curves that are singular are the points such that

$${\displaystyle P_x^{\prime }(a,b,c)=P_y^{\prime }(a,b,c)=P_z^{\prime }(a,b,c)=0.}$$

(The condition P(a, b, c) = 0 is implied by these conditions, by Euler's homogeneous function theorem.)

Asymptotes

Every infinite branch of an algebraic curve corresponds to a point at infinity on the curve, that is a point of the projective completion of the curve that does not belong to its affine part. The corresponding asymptote is the tangent of the curve at that point. The general formula for a tangent to a projective curve may apply, but it is worth to make it explicit in this case.

Let ${\displaystyle p=p_d+\cdots +p_0}$ be the decomposition of the polynomial defining the curve into its homogeneous parts, where p_i is the sum of the monomials of p of degree i. It follows that

$${\displaystyle P={}^{h}p=p_d+z{p}_{d-1}+\cdots +z^d{p}_0}$$

and

$${\displaystyle P_z^{\prime }(a,b,0)=p_{d-1}(a,b).}$$

A point at infinity of the curve is a zero of p of the form (a, b, 0). Equivalently, (a, b) is a zero of p_d. The fundamental theorem of algebra implies that, over an algebraically closed field (typically, the field of complex numbers), p_d factors into a product of linear factors. Each factor defines a point at infinity on the curve: if bx − ay is such a factor, then it defines the point at infinity (a, b, 0). Over the reals, p_d factors into linear and quadratic factors. The irreducible quadratic factors define non-real points at infinity, and the real points are given by the linear factors. If (a, b, 0) is a point at infinity of the curve, one says that (a, b) is an asymptotic direction. Setting q = p_d the equation of the corresponding asymptote is

$${\displaystyle x{q}_x^{\prime }(a,b)+y{q}_y^{\prime }(a,b)+p_{d-1}(a,b)=0.}$$

If ${\displaystyle q_x^{\prime }(a,b)=q_y^{\prime }(a,b)=0}$ and ${\displaystyle p_{d-1}(a,b)\ne 0,}$ the asymptote is the line at infinity, and, in the real case, the curve has a branch that looks like a parabola. In this case one says that the curve has a parabolic branch. If

$${\displaystyle q_x^{\prime }(a,b)=q_y^{\prime }(a,b)=p_{d-1}(a,b)=0,}$$

the curve has a singular point at infinity and may have several asymptotes. They may be computed by the method of computing the tangent cone of a singular point.

Singular points

The singular points of a curve of degree d defined by a polynomial p(x,y) of degree d are the solutions of the system of equations:

$${\displaystyle p_x^{\prime }(x,y)=p_y^{\prime }(x,y)=p(x,y)=0.}$$

In characteristic zero, this system is equivalent to

$${\displaystyle p_x^{\prime }(x,y)=p_y^{\prime }(x,y)=p_{\mathrm{\infty }}^{\prime }(x,y)=0,}$$

where, with the notation of the preceding section, ${\displaystyle p_{\mathrm{\infty }}^{\prime }(x,y)=P_z^{\prime }(x,y,1).}$ The systems are equivalent because of Euler's homogeneous function theorem. The latter system has the advantage of having its third polynomial of degree d-1 instead of d.

Similarly, for a projective curve defined by a homogeneous polynomial P(x,y,z) of degree d, the singular points have the solutions of the system

$${\displaystyle P_x^{\prime }(x,y,z)=P_y^{\prime }(x,y,z)=P_z^{\prime }(x,y,z)=0}$$

as homogeneous coordinates. (In positive characteristic, the equation ${\displaystyle P(x,y,z)}$ has to be added to the system.)

This implies that the number of singular points is finite as long as p(x,y) or P(x,y,z) is square free. Bézout's theorem implies thus that the number of singular points is at most (d − 1)², but this bound is not sharp because the system of equations is overdetermined. If reducible polynomials are allowed, the sharp bound is d(d − 1)/2, this value is reached when the polynomial factors in linear factors, that is if the curve is the union of d lines. For irreducible curves and polynomials, the number of singular points is at most (d − 1)(d − 2)/2, because of the formula expressing the genus in term of the singularities (see below). The maximum is reached by the curves of genus zero whose all singularities have multiplicity two and distinct tangents (see below).

The equation of the tangents at a singular point is given by the nonzero homogeneous part of the lowest degree in the Taylor series of the polynomial at the singular point. When one changes the coordinates to put the singular point at the origin, the equation of the tangents at the singular point is thus the nonzero homogeneous part of the lowest degree of the polynomial, and the multiplicity of the singular point is the degree of this homogeneous part.

Analytic structure

The study of the analytic structure of an algebraic curve in the neighborhood of a singular point provides accurate information of the topology of singularities. In fact, near a singular point, a real algebraic curve is the union of a finite number of branches that intersect only at the singular point and look either as a cusp or as a smooth curve.

Near a regular point, one of the coordinates of the curve may be expressed as an analytic function of the other coordinate. This is a corollary of the analytic implicit function theorem, and implies that the curve is smooth near the point. Near a singular point, the situation is more complicated and involves Puiseux series, which provide analytic parametric equations of the branches.

For describing a singularity, it is worth to translate the curve for having the singularity at the origin. This consists of a change of variable of the form ${\displaystyle X=x-a,Y=y-b,}$ where ${\displaystyle a,b}$ are the coordinates of the singular point. In the following, the singular point under consideration is always supposed to be at the origin.

The equation of an algebraic curve is ${\displaystyle f(x,y)=0,}$ where f is a polynomial in x and y. This polynomial may be considered as a polynomial in y, with coefficients in the algebraically closed field of the Puiseux series in x. Thus f may be factored in factors of the form ${\displaystyle y-P(x),}$ where P is a Puiseux series. These factors are all different if f is an irreducible polynomial, because this implies that f is square-free, a property which is independent of the field of coefficients.

The Puiseux series that occur here have the form

$${\displaystyle P(x)=\sum _{n=n_0}^{\mathrm{\infty }}{a}_n{x}^{n/d},}$$

where d is a positive integer, and ${\displaystyle n_0}$ is an integer that may also be supposed to be positive, because we consider only the branches of the curve that pass through the origin. Without loss of generality, we may suppose that d is coprime with the greatest common divisor of the n such that ${\displaystyle a_n\ne 0}$ (otherwise, one could choose a smaller common denominator for the exponents).

Let ${\displaystyle {\omega }_d}$ be a primitive dth root of unity. If the above Puiseux series occurs in the factorization of ${\displaystyle f(x,y)=0}$, then the d series

$${\displaystyle P_i(x)=\sum _{n=n_0}^{\mathrm{\infty }}{a}_n{\omega }_d^i{x}^{n/d}}$$

occur also in the factorization (a consequence of Galois theory). These d series are said conjugate, and are considered as a single branch of the curve, of ramification index d.

In the case of a real curve, that is a curve defined by a polynomial with real coefficients, three cases may occur. If none ${\displaystyle P_i(x)}$ has real coefficients, then one has a non-real branch. If some ${\displaystyle P_i(x)}$ has real coefficients, then one may choose it as ${\displaystyle P_0(x)}$. If d is odd, then every real value of x provides a real value of ${\displaystyle P_0(x)}$, and one has a real branch that looks regular, although it is singular if d > 1. If d is even, then ${\displaystyle P_0(x)}$ and ${\displaystyle P_{d/2}(x)}$ have real values, but only for x ≥ 0. In this case, the real branch looks as a cusp (or is a cusp, depending on the definition of a cusp that is used).

For example, the ordinary cusp has only one branch. If it is defined by the equation ${\displaystyle y^2-x^3=0,}$ then the factorization is ${\displaystyle (y-x^{3/2})(y+x^{3/2});}$ the ramification index is 2, and the two factors are real and define each a half branch. If the cusp is rotated, it equation becomes ${\displaystyle y^3-x^2=0,}$ and the factorization is ${\displaystyle (y-x^{2/3})(y-j^2{x}^{2/3})(y-(j^2{)}^2{x}^{2/3}),}$ with ${\displaystyle j=(1+\sqrt{-3})/2}$ (the coefficient ${\displaystyle (j^2{)}^2}$ has not been simplified to j for showing how the above definition of ${\displaystyle P_i(x)}$ is specialized). Here the ramification index is 3, and only one factor is real; this shows that, in the first case, the two factors must be considered as defining the same branch.

Non-plane algebraic curves

An algebraic curve is an algebraic variety of dimension one. This implies that an affine curve in an affine space of dimension n is defined by, at least, n − 1 polynomials in n variables. To define a curve, these polynomials must generate a prime ideal of Krull dimension 1. This condition is not easy to test in practice. Therefore, the following way to represent non-plane curves may be preferred.

Let ${\displaystyle f,g_0,g_3,\dots ,g_n}$ be n polynomials in two variables x₁ and x₂ such that f is irreducible. The points in the affine space of dimension n such whose coordinates satisfy the equations and inequations

$${\displaystyle \begin{array}{rl}& f(x_1,x_2)=0\\ & g_0(x_1,x_2)\ne 0\\ x_3& =\frac{g_3(x_1,x_2)}{g_0(x_1,x_2)}\\ & ⋮\\ x_n& =\frac{g_n(x_1,x_2)}{g_0(x_1,x_2)}\end{array}}$$

are all the points of an algebraic curve in which a finite number of points have been removed. This curve is defined by a system of generators of the ideal of the polynomials h such that it exists an integer k such ${\displaystyle g_0^{k}h}$ belongs to the ideal generated by ${\displaystyle f,x_3{g}_0-g_3,\dots ,x_n{g}_0-g_n}$. This representation is a birational equivalence between the curve and the plane curve defined by f. Every algebraic curve may be represented in this way. However, a linear change of variables may be needed in order to make almost always injective the projection on the two first variables. When a change of variables is needed, almost every change is convenient, as soon as it is defined over an infinite field.

This representation allows us to deduce easily any property of a non-plane algebraic curve, including its graphical representation, from the corresponding property of its plane projection.

For a curve defined by its implicit equations, above representation of the curve may easily deduced from a Gröbner basis for a block ordering such that the block of the smaller variables is (x₁, x₂). The polynomial f is the unique polynomial in the base that depends only of x₁ and x₂. The fractions g_i/g₀ are obtained by choosing, for i = 3, ..., n, a polynomial in the basis that is linear in x_i and depends only on x₁, x₂ and x_i. If these choices are not possible, this means either that the equations define an algebraic set that is not a variety, or that the variety is not of dimension one, or that one must change of coordinates. The latter case occurs when f exists and is unique, and, for i = 3, …, n, there exist polynomials whose leading monomial depends only on x₁, x₂ and x_i.

Algebraic function fields

The study of algebraic curves can be reduced to the study of irreducible algebraic curves: those curves that cannot be written as the union of two smaller curves. Up to birational equivalence, the irreducible curves over a field F are categorically equivalent to algebraic function fields in one variable over F. Such an algebraic function field is a field extension K of F that contains an element x which is transcendental over F, and such that K is a finite algebraic extension of F(x), which is the field of rational functions in the indeterminate x over F.

For example, consider the field C of complex numbers, over which we may define the field C(x) of rational functions in C. If y² = x³ − x − 1, then the field C(x, y) is an elliptic function field. The element x is not uniquely determined; the field can also be regarded, for instance, as an extension of C(y). The algebraic curve corresponding to the function field is simply the set of points (x, y) in C² satisfying y² = x³ − x − 1.

If the field F is not algebraically closed, the point of view of function fields is a little more general than that of considering the locus of points, since we include, for instance, "curves" with no points on them. For example, if the base field F is the field R of real numbers, then x² + y² = −1 defines an algebraic extension field of R(x), but the corresponding curve considered as a subset of R² has no points. The equation x² + y² = −1 does define an irreducible algebraic curve over R in the scheme sense (an integral, separated one-dimensional schemes of finite type over R). In this sense, the one-to-one correspondence between irreducible algebraic curves over F (up to birational equivalence) and algebraic function fields in one variable over F holds in general.

Two curves can be birationally equivalent (i.e. have isomorphic function fields) without being isomorphic as curves. The situation becomes easier when dealing with nonsingular curves, i.e. those that lack any singularities. Two nonsingular projective curves over a field are isomorphic if and only if their function fields are isomorphic.

Tsen's theorem is about the function field of an algebraic curve over an algebraically closed field.

Complex curves and real surfaces

A complex projective algebraic curve resides in n-dimensional complex projective space CPⁿ. This has complex dimension n, but topological dimension, as a real manifold, 2n, and is compact, connected, and orientable. An algebraic curve over C likewise has topological dimension two; in other words, it is a surface.

The topological genus of this surface, that is the number of handles or donut holes, is equal to the geometric genus of the algebraic curve that may be computed by algebraic means. In short, if one consider a plane projection of a nonsingular curve that has degree d and only ordinary singularities (singularities of multiplicity two with distinct tangents), then the genus is (d − 1)(d − 2)/2 − k, where k is the number of these singularities.

Compact Riemann surfaces

A Riemann surface is a connected complex analytic manifold of one complex dimension, which makes it a connected real manifold of two dimensions. It is compact if it is compact as a topological space.

There is a triple equivalence of categories between the category of smooth irreducible projective algebraic curves over C (with non-constant regular maps as morphisms), the category of compact Riemann surfaces (with non-constant holomorphic maps as morphisms), and the opposite of the category of algebraic function fields in one variable over C (with field homomorphisms that fix C as morphisms). This means that in studying these three subjects we are in a sense studying one and the same thing. It allows complex analytic methods to be used in algebraic geometry, and algebraic-geometric methods in complex analysis and field-theoretic methods to be used in both. This is characteristic of a much wider class of problems in algebraic geometry.

See also algebraic geometry and analytic geometry for a more general theory.

Singularities

Using the intrinsic concept of tangent space, points P on an algebraic curve C are classified as smooth (synonymous: non-singular), or else singular. Given n − 1 homogeneous polynomials in n + 1 variables, we may find the Jacobian matrix as the (n − 1)×(n + 1) matrix of the partial derivatives. If the rank of this matrix is n − 1, then the polynomials define an algebraic curve (otherwise they define an algebraic variety of higher dimension). If the rank remains n − 1 when the Jacobian matrix is evaluated at a point P on the curve, then the point is a smooth or regular point; otherwise it is a singular point. In particular, if the curve is a plane projective algebraic curve, defined by a single homogeneous polynomial equation f(x,y,z) = 0, then the singular points are precisely the points P where the rank of the 1×(n + 1) matrix is zero, that is, where

$${\displaystyle \frac{\mathrm{\partial }f}{\mathrm{\partial }x}(P)=\frac{\mathrm{\partial }f}{\mathrm{\partial }y}(P)=\frac{\mathrm{\partial }f}{\mathrm{\partial }z}(P)=0.}$$

Since f is a polynomial, this definition is purely algebraic and makes no assumption about the nature of the field F, which in particular need not be the real or complex numbers. It should, of course, be recalled that (0,0,0) is not a point of the curve and hence not a singular point.

Similarly, for an affine algebraic curve defined by a single polynomial equation f(x,y) = 0, then the singular points are precisely the points P of the curve where the rank of the 1×n Jacobian matrix is zero, that is, where

$${\displaystyle f(P)=\frac{\mathrm{\partial }f}{\mathrm{\partial }x}(P)=\frac{\mathrm{\partial }f}{\mathrm{\partial }y}(P)=0.}$$

The singularities of a curve are not birational invariants. However, locating and classifying the singularities of a curve is one way of computing the genus, which is a birational invariant. For this to work, we should consider the curve projectively and require F to be algebraically closed, so that all the singularities which belong to the curve are considered.

Classification of singularities

"Delta invariant" redirects here. For another notion of delta invariant in K-stability of Fano varieties, see K-stability of Fano varieties § Delta invariant.

x³ = y²

Singular points include multiple points where the curve crosses over itself, and also various types of cusp, for example that shown by the curve with equation x³ = y² at (0,0).

A curve C has at most a finite number of singular points. If it has none, it can be called smooth or non-singular. Commonly, this definition is understood over an algebraically closed field and for a curve C in a projective space (i.e., complete in the sense of algebraic geometry). For example, the plane curve of equation ${\displaystyle y-x^3=0}$ is considered as singular, as having a singular point (a cusp) at infinity.

In the remainder of this section, one considers a plane curve C defined as the zero set of a bivariate polynomial f(x, y). Some of the results, but not all, may be generalized to non-plane curves.

The singular points are classified by means of several invariants. The multiplicity m is defined as the maximum integer such that the derivatives of f to all orders up to m – 1 vanish (also the minimal intersection number between the curve and a straight line at P). Intuitively, a singular point has delta invariant δ if it concentrates δ ordinary double points at P. To make this precise, the blow up process produces so-called infinitely near points, and summing m(m − 1)/2 over the infinitely near points, where m is their multiplicity, produces δ. For an irreducible and reduced curve and a point P we can define δ algebraically as the length of ${\displaystyle {\tilde{\mathcal{O}}}_P/{\mathcal{O}}_P}$ where ${\displaystyle {\mathcal{O}}_P}$ is the local ring at P and ${\displaystyle {\tilde{\mathcal{O}}}_P}$ is its integral closure.

The Milnor number μ of a singularity is the degree of the mapping grad f(x,y)/|grad f(x,y)| on the small sphere of radius ε, in the sense of the topological degree of a continuous mapping, where grad f is the (complex) gradient vector field of f. It is related to δ and r by the Milnor–Jung formula,

μ = 2δ − r + 1.

Here, the branching number r of P is the number of locally irreducible branches at P. For example, r = 1 at an ordinary cusp, and r = 2 at an ordinary double point. The multiplicity m is at least r, and that P is singular if and only if m is at least 2. Moreover, δ is at least m(m-1)/2.

Computing the delta invariants of all of the singularities allows the genus g of the curve to be determined; if d is the degree, then

$${\displaystyle g=\frac{1}{2}(d-1)(d-2)-\sum _P{\delta }_P,}$$

where the sum is taken over all singular points P of the complex projective plane curve. It is called the genus formula.

Assign the invariants [m, δ, r] to a singularity, where m is the multiplicity, δ is the delta-invariant, and r is the branching number. Then an ordinary cusp is a point with invariants [2,1,1] and an ordinary double point is a point with invariants [2,1,2], and an ordinary m-multiple point is a point with invariants [m, m(m − 1)/2, m].

Examples of curves

Rational curves

A rational curve, also called a unicursal curve, is any curve which is birationally equivalent to a line, which we may take to be a projective line; accordingly, we may identify the function field of the curve with the field of rational functions in one indeterminate F(x). If F is algebraically closed, this is equivalent to a curve of genus zero; however, the field of all real algebraic functions defined on the real algebraic variety x² + y² = −1 is a field of genus zero which is not a rational function field.

Concretely, a rational curve embedded in an affine space of dimension n over F can be parameterized (except for isolated exceptional points) by means of n rational functions of a single parameter t; by reducing these rational functions to the same denominator, the n+1 resulting polynomials define a polynomial parametrization of the projective completion of the curve in the projective space. An example is the rational normal curve, where all these polynomials are monomials.

Any conic section defined over F with a rational point in F is a rational curve. It can be parameterized by drawing a line with slope t through the rational point, and an intersection with the plane quadratic curve; this gives a polynomial with F-rational coefficients and one F-rational root, hence the other root is F-rational (i.e., belongs to F) also.

x² + xy + y² = 1

For example, consider the ellipse x² + xy + y² = 1, where (−1, 0) is a rational point. Drawing a line with slope t from (−1,0), y = t(x + 1), substituting it in the equation of the ellipse, factoring, and solving for x, we obtain

$${\displaystyle x=\frac{1-t^2}{1+t+t^2}.}$$

Then the equation for y is

$${\displaystyle y=t(x+1)=\frac{t(t+2)}{1+t+t^2},}$$

which defines a rational parameterization of the ellipse and hence shows the ellipse is a rational curve. All points of the ellipse are given, except for (−1,1), which corresponds to t = ∞; the entire curve is parameterized therefore by the real projective line.

Such a rational parameterization may be considered in the projective space by equating the first projective coordinates to the numerators of the parameterization and the last one to the common denominator. As the parameter is defined in a projective line, the polynomials in the parameter should be homogenized. For example, the projective parameterization of the above ellipse is

$${\displaystyle X=U^2-T^2,Y=T(T+2U),Z=T^2+TU+U^2.}$$

Eliminating T and U between these equations we get again the projective equation of the ellipse

$${\displaystyle X^2+XY+Y^2=Z^2,}$$

which may be easily obtained directly by homogenizing the above equation.

Many of the curves on Wikipedia's list of curves are rational and hence have similar rational parameterizations.

Rational plane curves

Rational plane curves are rational curves embedded into ${\displaystyle {\mathbb{P}}^2}$. Given generic sections ${\displaystyle s_1,s_2,s_3\in \mathrm{\Gamma }({\mathbb{P}}^1,\mathcal{O}(d))}$ of degree ${\displaystyle d}$ homogeneous polynomials in two coordinates, ${\displaystyle x,y}$, there is a map

$${\displaystyle s:{\mathbb{P}}^1\to {\mathbb{P}}^2}$$

given by

$${\displaystyle s([x:y])=[s_1([x:y]):s_2([x:y]):s_3([x:y])]}$$

defining a rational plane curve of degree ${\displaystyle d}$. There is an associated moduli space ${\displaystyle \mathcal{M}={\overline{\mathcal{M}}}_{0,0}({\mathbb{P}}^2,d\cdot [H])}$ (where ${\displaystyle [H]}$ is the hyperplane class) parametrizing all such stable curves. A dimension count can be made to determine the moduli spaces dimension: There are ${\displaystyle d+1}$ parameters in ${\displaystyle \mathrm{\Gamma }({\mathbb{P}}^1,\mathcal{O}(d))}$ giving ${\displaystyle 3d+3}$ parameters total for each of the sections. Then, since they are considered up to a projective quotient in ${\displaystyle {\mathbb{P}}^2}$ there is ${\displaystyle 1}$ less parameter in ${\displaystyle \mathcal{M}}$. Furthermore, there is a three dimensional group of automorphisms of ${\displaystyle {\mathbb{P}}^1}$, hence ${\displaystyle \mathcal{M}}$ has dimension ${\displaystyle 3d+3-1-3=3d-1}$. This moduli space can be used to count the number ${\displaystyle N_d}$ of degree ${\displaystyle d}$ rational plane curves intersecting ${\displaystyle 3d-1}$ points using Gromov–Witten theory. It is given by the recursive relation

$${\displaystyle N_d=\sum _{d_A+d_B=d}{N}_{d_A}{N}_{d_B}{d}_A^2{d}_B\left(d_B(\genfrac{}{}{0ex}{}{3d-4}{3d_A-2})-d_A(\genfrac{}{}{0ex}{}{3d-4}{3d_A-1})\right)}$$

where ${\displaystyle N_1=N_2=1}$.

Elliptic curves

An elliptic curve may be defined as any curve of genus one with a rational point: a common model is a nonsingular cubic curve, which suffices to model any genus one curve. In this model the distinguished point is commonly taken to be an inflection point at infinity; this amounts to requiring that the curve can be written in Tate-Weierstrass form, which in its projective version is

$${\displaystyle y^{2}z+a_{1}xyz+a_{3}y{z}^2=x^3+a_2{x}^{2}z+a_{4}x{z}^2+a_6{z}^3.}$$

If the characteristic of the field is different from 2 and 3, then a linear change of coordinates allows putting ${\displaystyle a_1=a_2=a_3=0,}$ which gives the classical Weierstrass form

$${\displaystyle y^2=x^3+px+q.}$$

Elliptic curves carry the structure of an abelian group with the distinguished point as the identity of the group law. In a plane cubic model three points sum to zero in the group if and only if they are collinear. For an elliptic curve defined over the complex numbers the group is isomorphic to the additive group of the complex plane modulo the period lattice of the corresponding elliptic functions.

The intersection of two quadric surfaces is, in general, a nonsingular curve of genus one and degree four, and thus an elliptic curve, if it has a rational point. In special cases, the intersection either may be a rational singular quartic or is decomposed in curves of smaller degrees which are not always distinct (either a cubic curve and a line, or two conics, or a conic and two lines, or four lines).

Curves of genus greater than one

Curves of genus greater than one differ markedly from both rational and elliptic curves. Such curves defined over the rational numbers, by Faltings's theorem, can have only a finite number of rational points, and they may be viewed as having a hyperbolic geometry structure. Examples are the hyperelliptic curves, the Klein quartic curve, and the Fermat curve xⁿ + yⁿ = zⁿ when n is greater than three. Also projective plane curves in ${\displaystyle {\mathbb{P}}^2}$ and curves in ${\displaystyle {\mathbb{P}}^1\times {\mathbb{P}}^1}$ provide many useful examples.

Projective plane curves

Plane curves ${\displaystyle C\subset {\mathbb{P}}^2}$ of degree ${\displaystyle k}$, which can be constructed as the vanishing locus of a generic section ${\displaystyle s\in \mathrm{\Gamma }({\mathbb{P}}^2,\mathcal{O}(k))}$, has genus

$${\displaystyle \frac{(k-1)(k-2)}{2}}$$

which can be computed using Coherent sheaf cohomology. Here's a brief summary of the curves genera relative to their degree

degree	1	2	3	4	5	6	7
genus	0	0	1	3	6	10	15

For example, the curve ${\displaystyle x^4+y^4+z^4}$ defines a curve of genus ${\displaystyle 3}$ which is smooth since the differentials ${\displaystyle 4x^3,4y^3,4z^3}$ have no common zeros with the curve.. A non-example of a generic section is the curve ${\displaystyle x(x^2+y^2+z^2)}$ which, by Bezouts theorem, should intersect at most ${\displaystyle 2}$ points, is the union of two rational curves ${\displaystyle C_1\cup C_2}$ intersecting at two points. Note ${\displaystyle C_1}$ is given by the vanishing locus of ${\displaystyle x}$ and ${\displaystyle C_2}$ is given by the vanishing locus of ${\displaystyle x^2+y^2+z^2}$. These can be found explicitly: a point lies in both if ${\displaystyle x=0}$. So the two solutions are the points ${\displaystyle [0:y:z]}$ such that ${\displaystyle y^2+z^2=0}$, which are ${\displaystyle [0:1:-\sqrt{-1}]}$ and ${\displaystyle [0:1:\sqrt{-1}]}$.

Curves in product of projective lines

Curve ${\displaystyle C\subset {\mathbb{P}}^1\times {\mathbb{P}}^1}$ given by the vanishing locus of ${\displaystyle s\in \mathrm{\Gamma }({\mathbb{P}}^1\times {\mathbb{P}}^1,\mathcal{O}(a,b))}$, for ${\displaystyle a,b\ge 2}$, give curves of genus

$${\displaystyle ab-a-b+1}$$

which can be checked using Coherent sheaf cohomology. If ${\displaystyle a=2}$, then they define curves of genus ${\displaystyle 2b-2-b+1=b-1}$, hence a curve of any genus can be constructed as a curve in ${\displaystyle {\mathbb{P}}^1\times {\mathbb{P}}^1}$. Their genera can be summarized in the table

bidegree	${\displaystyle (2,2)}$	${\displaystyle (2,3)}$	${\displaystyle (2,4)}$	${\displaystyle (2,5)}$
genus	1	2	3	4

and for ${\displaystyle a=3}$, this is

bidegree	${\displaystyle (3,2)}$	${\displaystyle (3,3)}$	${\displaystyle (3,4)}$	${\displaystyle (3,5)}$
genus	2	4	6	8

Digital imaging

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Digital_imaging

Digital imaging or digital image acquisition is the creation of a digital representation of the visual characteristics of an object, such as a physical scene or the interior structure of an object. The term is often assumed to imply or include the processing, compression, storage, printing and display of such images. A key advantage of a digital image, versus an analog image such as a film photograph, is the ability to digitally propagate copies of the original subject indefinitely without any loss of image quality.

Digital imaging can be classified by the type of electromagnetic radiation or other waves whose variable attenuation, as they pass through or reflect off objects, conveys the information that constitutes the image. In all classes of digital imaging, the information is converted by image sensors into digital signals that are processed by a computer and made output as a visible-light image. For example, the medium of visible light allows digital photography (including digital videography) with various kinds of digital cameras (including digital video cameras). X-rays allow digital X-ray imaging (digital radiography, fluoroscopy, and CT), and gamma rays allow digital gamma ray imaging (digital scintigraphy, SPECT, and PET). Sound allows ultrasonography (such as medical ultrasonography) and sonar, and radio waves allow radar. Digital imaging lends itself well to image analysis by software, as well as to image editing (including image manipulation).

History

Before digital imaging, the first photograph ever produced, View from the Window at Le Gras, was in 1826 by Frenchman Joseph Nicéphore Niépce. When Joseph was 28, he was discussing with his brother Claude about the possibility of reproducing images with light. His focus on his new innovations began in 1816. He was in fact more interested in creating an engine for a boat. Joseph and his brother focused on that for quite some time and Claude successfully promoted his innovation moving and advancing him to England. Joseph was able to focus on the photograph and finally in 1826, he was able to produce his first photograph of a view through his window. This took 8 hours or more of exposure to light.

The first digital image was produced in 1920, by the Bartlane cable picture transmission system. British inventors, Harry G. Bartholomew and Maynard D. McFarlane, developed this method. The process consisted of "a series of negatives on zinc plates that were exposed for varying lengths of time, thus producing varying densities,". The Bartlane cable picture transmission system generated at both its transmitter and its receiver end a punched data card or tape that was recreated as an image.

In 1957, Russell A. Kirsch produced a device that generated digital data that could be stored in a computer; this used a drum scanner and photomultiplier tube.

Digital imaging was developed in the 1960s and 1970s, largely to avoid the operational weaknesses of film cameras, for scientific and military missions including the KH-11 program. As digital technology became cheaper in later decades, it replaced the old film methods for many purposes.

In the early 1960s, while developing compact, lightweight, portable equipment for the onboard nondestructive testing of naval aircraft, Frederick G. Weighart and James F. McNulty (U.S. radio engineer) at Automation Industries, Inc., then, in El Segundo, California co-invented the first apparatus to generate a digital image in real-time, which image was a fluoroscopic digital radiograph. Square wave signals were detected on the fluorescent screen of a fluoroscope to create the image.

Digital image sensors

Main article: Image sensor

The charge-coupled device was invented by Willard S. Boyle and George E. Smith at Bell Labs in 1969. While researching MOS technology, they realized that an electric charge was the analogy of the magnetic bubble and that it could be stored on a tiny MOS capacitor. As it was fairly straightforward to fabricate a series of MOS capacitors in a row, they connected a suitable voltage to them so that the charge could be stepped along from one to the next. The CCD is a semiconductor circuit that was later used in the first digital video cameras for television broadcasting.

Early CCD sensors suffered from shutter lag. This was largely resolved with the invention of the pinned photodiode (PPD). It was invented by Nobukazu Teranishi, Hiromitsu Shiraki and Yasuo Ishihara at NEC in 1980. It was a photodetector structure with low lag, low noise, high quantum efficiency and low dark current. In 1987, the PPD began to be incorporated into most CCD devices, becoming a fixture in consumer electronic video cameras and then digital still cameras. Since then, the PPD has been used in nearly all CCD sensors and then CMOS sensors.

The NMOS active-pixel sensor (APS) was invented by Olympus in Japan during the mid-1980s. This was enabled by advances in MOS semiconductor device fabrication, with MOSFET scaling reaching smaller micron and then sub-micron levels. The NMOS APS was fabricated by Tsutomu Nakamura's team at Olympus in 1985. The CMOS active-pixel sensor (CMOS sensor) was later developed by Eric Fossum's team at the NASA Jet Propulsion Laboratory in 1993. By 2007, sales of CMOS sensors had surpassed CCD sensors.

Digital image compression

Main article: Image compression

An important development in digital image compression technology was the discrete cosine transform (DCT). DCT compression is used in JPEG, which was introduced by the Joint Photographic Experts Group in 1992. JPEG compresses images down to much smaller file sizes, and has become the most widely used image file format on the Internet.

Digital cameras

Main article: Digital camera

These different scanning ideas were the basis of the first designs of digital camera. Early cameras took a long time to capture an image and were poorly suited for consumer purposes. It was not until the adoption of the CCD (charge-coupled device) that the digital camera really took off. The CCD became part of the imaging systems used in telescopes, the first black-and-white digital cameras in the 1980s. Color was eventually added to the CCD and is a usual feature of cameras today.

Changing environment

Great strides have been made in the field of digital imaging. Negatives and exposure are foreign concepts to many, and the first digital image in 1920 led eventually to cheaper equipment, increasingly powerful yet simple software, and the growth of the Internet.

The constant advancement and production of physical equipment and hardware related to digital imaging has affected the environment surrounding the field. From cameras and webcams to printers and scanners, the hardware is becoming sleeker, thinner, faster, and cheaper. As the cost of equipment decreases, the market for new enthusiasts widens, allowing more consumers to experience the thrill of creating their own images.

Everyday personal laptops, family desktops, and company computers are able to handle photographic software. Our computers are more powerful machines with increasing capacities for running programs of any kind—especially digital imaging software. And that software is quickly becoming both smarter and simpler. Although functions on today's programs reach the level of precise editing and even rendering 3-D images, user interfaces are designed to be friendly to advanced users as well as first-time fans.

The Internet allows editing, viewing, and sharing digital photos and graphics. A quick browse around the web can easily turn up graphic artwork from budding artists, news photos from around the world, corporate images of new products and services, and much more. The Internet has clearly proven itself a catalyst in fostering the growth of digital imaging.

Online photo sharing of images changes the way we understand photography and photographers. Online sites such as Flickr, Shutterfly, and Instagram give billions the capability to share their photography, whether they are amateurs or professionals. Photography has gone from being a luxury medium of communication and sharing to more of a fleeting moment in time. Subjects have also changed. Pictures used to be primarily taken of people and family. Now, we take them of anything. We can document our day and share it with everyone with the touch of our fingers.

In 1826 Niepce was the first to develop a photo which used lights to reproduce images, the advancement of photography has drastically increased over the years. Everyone is now a photographer in their own way, whereas during the early 1800s and 1900s the expense of lasting photos was highly valued and appreciated by consumers and producers. According to the magazine article on five ways digital camera changed us states the following:The impact on professional photographers has been dramatic. Once upon a time a photographer wouldn't dare waste a shot unless they were virtually certain it would work."The use of digital imaging( photography) has changed the way we interacted with our environment over the years. Part of the world is experienced differently through visual imagining of lasting memories, it has become a new form of communication with friends, family and love ones around the world without face to face interactions. Through photography it is easy to see those that you have never seen before and feel their presence without them being around, for example Instagram is a form of social media where anyone is allowed to shoot, edit, and share photos of whatever they want with friends and family. Facebook, snapshot, vine and twitter are also ways people express themselves with little or no words and are able to capture every moment that is important. Lasting memories that were hard to capture, is now easy because everyone is now able to take pictures and edit it on their phones or laptops. Photography has become a new way to communicate and it is rapidly increasing as time goes by, which has affected the world around us.

A study done by Basey, Maines, Francis, and Melbourne found that drawings used in class have a significant negative effect on lower-order content for student's lab reports, perspectives of labs, excitement, and time efficiency of learning. Documentation style learning has no significant effects on students in these areas. He also found that students were more motivated and excited to learn when using digital imaging.

Field advancements

In the field of education.

• As digital projectors, screens, and graphics find their way to the classroom, teachers and students alike are benefitting from the increased convenience and communication they provide, although their theft can be a common problem in schools. In addition acquiring a basic digital imaging education is becoming increasingly important for young professionals. Reed, a design production expert from Western Washington University, stressed the importance of using "digital concepts to familiarize students with the exciting and rewarding technologies found in one of the major industries of the 21st century".

The field of medical imaging

• A branch of digital imaging that seeks to assist in the diagnosis and treatment of diseases, is growing at a rapid rate. A recent study by the American Academy of Pediatrics suggests that proper imaging of children who may have appendicitis may reduce the amount of appendectomies needed. Further advancements include amazingly detailed and accurate imaging of the brain, lungs, tendons, and other parts of the body—images that can be used by health professionals to better serve patients.
• According to Vidar, as more countries take on this new way of capturing an image, it has been found that image digitalization in medicine has been increasingly beneficial for both patient and medical staff. Positive ramifications of going paperless and heading towards digitization includes the overall reduction of cost in medical care, as well as an increased global, real-time, accessibility of these images. (http://www.vidar.com/film/images/stories/PDFs/newsroom/Digital%20Transition%20White%20Paper%20hi-res%20GFIN.pdf)
• There is a program called Digital Imaging in Communications and Medicine (DICOM) that is changing the medical world as we know it. DICOM is not only a system for taking high quality images of the aforementioned internal organs, but also is helpful in processing those images. It is a universal system that incorporates image processing, sharing, and analyzing for the convenience of patient comfort and understanding. This service is all encompassing and is beginning a necessity.

In the field of technology, digital image processing has become more useful than analog image processing when considering the modern technological advancement.

• Image sharpen & reinstatement –
  • Image sharpens & reinstatement is the procedure of images which is capture by the contemporary camera making them an improved picture or manipulating the pictures in the way to get chosen product. This comprises the zooming process, the blurring process, the sharpening process, the gray scale to color translation process, the picture recovery process and the picture identification process.
• Facial Recognition –
  • Face recognition is a PC innovation that decides the positions and sizes of human faces in self-assertive digital pictures. It distinguishes facial components and overlooks whatever, for example, structures, trees & bodies.
• Remote detection –
  • Remote detecting is little or substantial scale procurement of data of article or occurrence, with the utilization of recording or ongoing detecting apparatus which is not in substantial or close contact with an article. Practically speaking, remote detecting is face-off accumulation using an assortment of gadgets for collecting data on particular article or location.
• Pattern detection –
  • The pattern detection is the study or investigation from picture processing. In the pattern detection, image processing is utilized for recognizing elements in the images and after that machine study is utilized to instruct a framework for variation in pattern. The pattern detection is utilized in computer-aided analysis, detection of calligraphy, identification of images, and many more.
• Color processing –
  • The color processing comprises processing of colored pictures and diverse color locations which are utilized. This moreover involves study of transmit, store, and encode of the color pictures.

Augmented reality

Digital Imaging for Augmented Reality (DIAR) is a comprehensive field within the broader context of Augmented Reality (AR) technologies. It involves the creation, manipulation, and interpretation of digital images for use in augmented reality environments. DIAR plays a significant role in enhancing the user experience, providing realistic overlays of digital information onto the real world, thereby bridging the gap between the physical and the virtual realms.

DIAR is employed in numerous sectors including entertainment, education, healthcare, military, and retail. In entertainment, DIAR is used to create immersive gaming experiences and interactive movies. In education, it provides a more engaging learning environment, while in healthcare, it assists in complex surgical procedures. The military uses DIAR for training purposes and battlefield visualization. In retail, customers can virtually try on clothes or visualize furniture in their home before making a purchase.

With continuous advancements in technology, the future of DIAR is expected to witness more realistic overlays, improved 3D object modeling, and seamless integration with the Internet of Things (IoT). The incorporation of haptic feedback in DIAR systems could further enhance the user experience by adding a sense of touch to the visual overlays. Additionally, advancements in artificial intelligence and machine learning are expected to further improve the context-appropriateness and realism of the overlaid digital images.

Theoretical application

Although theories are quickly becoming realities in today's technological society, the range of possibilities for digital imaging is wide open. One major application that is still in the works is that of child safety and protection. How can we use digital imaging to better protect our kids? Kodak's program, Kids Identification Digital Software (KIDS) may answer that question. The beginnings include a digital imaging kit to be used to compile student identification photos, which would be useful during medical emergencies and crimes. More powerful and advanced versions of applications such as these are still developing, with increased features constantly being tested and added.

But parents and schools aren't the only ones who see benefits in databases such as these. Criminal investigation offices, such as police precincts, state crime labs, and even federal bureaus have realized the importance of digital imaging in analyzing fingerprints and evidence, making arrests, and maintaining safe communities. As the field of digital imaging evolves, so does our ability to protect the public.

Digital imaging can be closely related to the social presence theory especially when referring to the social media aspect of images captured by our phones. There are many different definitions of the social presence theory but two that clearly define what it is would be "the degree to which people are perceived as real" (Gunawardena, 1995), and "the ability to project themselves socially and emotionally as real people" (Garrison, 2000). Digital imaging allows one to manifest their social life through images in order to give the sense of their presence to the virtual world. The presence of those images acts as an extension of oneself to others, giving a digital representation of what it is they are doing and who they are with. Digital imaging in the sense of cameras on phones helps facilitate this effect of presence with friends on social media. Alexander (2012) states, "presence and representation is deeply engraved into our reflections on images...this is, of course, an altered presence...nobody confuses an image with the representation reality. But we allow ourselves to be taken in by that representation, and only that 'representation' is able to show the liveliness of the absentee in a believable way." Therefore, digital imaging allows ourselves to be represented in a way so as to reflect our social presence.

Photography is a medium used to capture specific moments visually. Through photography our culture has been given the chance to send information (such as appearance) with little or no distortion. The Media Richness Theory provides a framework for describing a medium's ability to communicate information without loss or distortion. This theory has provided the chance to understand human behavior in communication technologies. The article written by Daft and Lengel (1984,1986) states the following:

Communication media fall along a continuum of richness. The richness of a medium comprises four aspects: the availability of instant feedback, which allows questions to be asked and answered; the use of multiple cues, such as physical presence, vocal inflection, body gestures, words, numbers and graphic symbols; the use of natural language, which can be used to convey an understanding of a broad set of concepts and ideas; and the personal focus of the medium (pp. 83).

The more a medium is able to communicate the accurate appearance, social cues and other such characteristics the more rich it becomes. Photography has become a natural part of how we communicate. For example, most phones have the ability to send pictures in text messages. Apps Snapchat and Vine have become increasingly popular for communicating. Sites like Instagram and Facebook have also allowed users to reach a deeper level of richness because of their ability to reproduce information. Sheer, V. C. (January–March 2011). Teenagers' use of MSN features, discussion topics, and online friendship development: the impact of media richness and communication control. Communication Quarterly, 59(1).

Methods

A digital photograph may be created directly from a physical scene by a camera or similar device. Alternatively, a digital image may be obtained from another image in an analog medium, such as photographs, photographic film, or printed paper, by an image scanner or similar device. Many technical images—such as those acquired with tomographic equipment, side-scan sonar, or radio telescopes—are actually obtained by complex processing of non-image data. Weather radar maps as seen on television news are a commonplace example. The digitalization of analog real-world data is known as digitizing, and involves sampling (discretization) and quantization. Projectional imaging of digital radiography can be done by X-ray detectors that directly convert the image to digital format. Alternatively, phosphor plate radiography is where the image is first taken on a photostimulable phosphor (PSP) plate which is subsequently scanned by a mechanism called photostimulated luminescence.

Finally, a digital image can also be computed from a geometric model or mathematical formula. In this case, the name image synthesis is more appropriate, and it is more often known as rendering.

Digital image authentication is an issue for the providers and producers of digital images such as health care organizations, law enforcement agencies, and insurance companies. There are methods emerging in forensic photography to analyze a digital image and determine if it has been altered.

Previously digital imaging depended on chemical and mechanical processes, now all these processes have converted to electronic. A few things need to take place for digital imaging to occur, the light energy converts to electrical energy – think of a grid with millions of little solar cells. Each condition generates a specific electrical charge. Charges for each of these "solar cells" are transported and communicated to the firmware to be interpreted. The firmware is what understands and translates the color and other light qualities. Pixels are what is noticed next, with varying intensities they create and cause different colors, creating a picture or image. Finally, the firmware records the information for a future date and for reproduction.

Advantages

There are several benefits of digital imaging. First, the process enables easy access of photographs and word documents. Google is at the forefront of this 'revolution,' with its mission to digitize the world's books. Such digitization will make the books searchable, thus making participating libraries, such as Stanford University and the University of California Berkeley, accessible worldwide. Digital imaging also benefits the medical world because it "allows the electronic transmission of images to third-party providers, referring dentists, consultants, and insurance carriers via a modem". The process "is also environmentally friendly since it does not require chemical processing". Digital imaging is also frequently used to help document and record historical, scientific and personal life events.

Benefits also exist regarding photographs. Digital imaging will reduce the need for physical contact with original images. Furthermore, digital imaging creates the possibility of reconstructing the visual contents of partially damaged photographs, thus eliminating the potential that the original would be modified or destroyed. In addition, photographers will be "freed from being 'chained' to the darkroom," will have more time to shoot and will be able to cover assignments more effectively. Digital imaging 'means' that "photographers no longer have to rush their film to the office, so they can stay on location longer while still meeting deadlines".

Another advantage to digital photography is that it has been expanded to camera phones. We are able to take cameras with us wherever as well as send photos instantly to others. It is easy for people to us as well as help in the process of self-identification for the younger generation.

Criticisms

Critics of digital imaging cite several negative consequences. An increased "flexibility in getting better quality images to the readers" will tempt editors, photographers and journalists to manipulate photographs. In addition, "staff photographers will no longer be photojournalists, but camera operators... as editors have the power to decide what they want 'shot'". Legal constraints, including copyright, pose another concern: will copyright infringement occur as documents are digitized and copying becomes easier?