In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space.
The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions.
Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quantities include the average value of the process over a range of times and the error in estimating the average using sample values at a small set of times. While exact models often scale poorly as the amount of data increases, multiple approximation methods have been developed which often retain good accuracy while drastically reducing computation time.
Definition
A time continuous stochastic process is Gaussian if and only if for every finite set of indices in the index set
is a multivariate Gaussian random variable. That is the same as saying every linear combination of has a univariate normal (or Gaussian) distribution.
Using characteristic functions of random variables, the Gaussian property can be formulated as follows: is Gaussian if and only if, for every finite set of indices , there are real-valued , with such that the following equality holds for all
where denotes the imaginary unit such that .
The numbers and can be shown to be the covariances and means of the variables in the process.
Variance
The variance of a Gaussian process is finite at any time , formally
Stationarity
For general stochastic processes strict-sense stationarity implies wide-sense stationarity but not every wide-sense stationary stochastic process is strict-sense stationary. However, for a Gaussian stochastic process the two concepts are equivalent.
A Gaussian stochastic process is strict-sense stationary if, and only if, it is wide-sense stationary.
Example
There is an explicit representation for stationary Gaussian processes. A simple example of this representation is
where and are independent random variables with the standard normal distribution.
Covariance functions
A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. Thus, if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loève expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity.
Stationarity refers to the process' behaviour regarding the separation of any two points and . If the process is stationary, the covariance function depends only on . For example, the Ornstein–Uhlenbeck process is stationary.
If the process depends only on , the Euclidean distance (not the direction) between and , then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer.
Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. If we expect that for "near-by" input points and their corresponding output points and to be "near-by" also, then the assumption of continuity is present. If we wish to allow for significant displacement then we might choose a rougher covariance function. Extreme examples of the behaviour is the Ornstein–Uhlenbeck covariance function and the squared exponential where the former is never differentiable and the latter infinitely differentiable.
Periodicity refers to inducing periodic patterns within the behaviour of the process. Formally, this is achieved by mapping the input to a two dimensional vector .
Usual covariance functions

There are a number of common covariance functions:
- Constant :
- Linear:
- white Gaussian noise:
- Squared exponential:
- Ornstein–Uhlenbeck:
- Matérn:
- Periodic:
- Rational quadratic:
Here . The parameter is the characteristic length-scale of the process (practically, "how close" two points and have to be to influence each other significantly), is the Kronecker delta and the standard deviation of the noise fluctuations. Moreover, is the modified Bessel function of order and is the gamma function evaluated at . Importantly, a complicated covariance function can be defined as a linear combination of other simpler covariance functions in order to incorporate different insights about the data-set at hand.
The inferential results are dependent on the values of the hyperparameters (e.g. and ) defining the model's behaviour. A popular choice for is to provide maximum a posteriori (MAP) estimates of it with some chosen prior. If the prior is very near uniform, this is the same as maximizing the marginal likelihood of the process; the marginalization being done over the observed process values . This approach is also known as maximum likelihood II, evidence maximization, or empirical Bayes.
Continuity
For a Gaussian process, continuity in probability is equivalent to mean-square continuity, and continuity with probability one is equivalent to sample continuity. The latter implies, but is not implied by, continuity in probability. Continuity in probability holds if and only if the mean and autocovariance are continuous functions. In contrast, sample continuity was challenging even for stationary Gaussian processes (as probably noted first by Andrey Kolmogorov), and more challenging for more general processes. As usual, by a sample continuous process one means a process that admits a sample continuous modification.
Stationary case
For a stationary Gaussian process some conditions on its spectrum are sufficient for sample continuity, but fail to be necessary. A necessary and sufficient condition, sometimes called Dudley–Fernique theorem, involves the function defined by
does not follow from continuity of and the evident relations (for all ) and
Theorem 1 — Let be continuous and satisfy (*). Then the condition is necessary and sufficient for sample continuity of
Some history. Sufficiency was announced by Xavier Fernique in 1964, but the first proof was published by Richard M. Dudley in 1967. Necessity was proved by Michael B. Marcus and Lawrence Shepp in 1970.
There exist sample continuous processes such that they violate condition (*). An example found by Marcus and Shepp is a random lacunary Fourier series
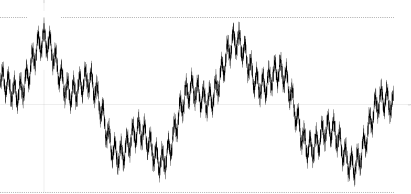
Its autocovariation function
Brownian motion as the integral of Gaussian processes
A Wiener process (also known as Brownian motion) is the integral of a white noise generalized Gaussian process. It is not stationary, but it has stationary increments.
The Ornstein–Uhlenbeck process is a stationary Gaussian process.
The Brownian bridge is (like the Ornstein–Uhlenbeck process) an example of a Gaussian process whose increments are not independent.
The fractional Brownian motion is a Gaussian process whose covariance function is a generalisation of that of the Wiener process.
Driscoll's zero-one law
Driscoll's zero-one law is a result characterizing the sample functions generated by a Gaussian process.
Let be a mean-zero Gaussian process with non-negative definite covariance function . Let be a Reproducing kernel Hilbert space with positive definite kernel .
Then
Moreover,
This has significant implications when , as
As such, almost all sample paths of a mean-zero Gaussian process with positive definite kernel will lie outside of the Hilbert space .
Linearly constrained Gaussian processes
For many applications of interest some pre-existing knowledge about the system at hand is already given. Consider e.g. the case where the output of the Gaussian process corresponds to a magnetic field; here, the real magnetic field is bound by Maxwell's equations and a way to incorporate this constraint into the Gaussian process formalism would be desirable as this would likely improve the accuracy of the algorithm.
A method on how to incorporate linear constraints into Gaussian processes already exists:
Consider the (vector valued) output function which is known to obey the linear constraint (i.e. is a linear operator)
Applications

A Gaussian process can be used as a prior probability distribution over functions in Bayesian inference. Given any set of N points in the desired domain of your functions, take a multivariate Gaussian whose covariance matrix parameter is the Gram matrix of your N points with some desired kernel, and sample from that Gaussian. For solution of the multi-output prediction problem, Gaussian process regression for vector-valued function was developed. In this method, a 'big' covariance is constructed, which describes the correlations between all the input and output variables taken in N points in the desired domain. This approach was elaborated in detail for the matrix-valued Gaussian processes and generalised to processes with 'heavier tails' like Student-t processes.
Inference of continuous values with a Gaussian process prior is known as Gaussian process regression, or kriging; extending Gaussian process regression to multiple target variables is known as cokriging. Gaussian processes are thus useful as a powerful non-linear multivariate interpolation tool.
Gaussian processes are also commonly used to tackle numerical analysis problems such as numerical integration, solving differential equations, or optimisation in the field of probabilistic numerics.
Gaussian processes can also be used in the context of mixture of experts models, for example. The underlying rationale of such a learning framework consists in the assumption that a given mapping cannot be well captured by a single Gaussian process model. Instead, the observation space is divided into subsets, each of which is characterized by a different mapping function; each of these is learned via a different Gaussian process component in the postulated mixture.
In the natural sciences, Gaussian processes have found use as probabilistic models of astronomical time series and as predictors of molecular properties.
Gaussian process prediction, or Kriging

When concerned with a general Gaussian process regression problem (Kriging), it is assumed that for a Gaussian process observed at coordinates , the vector of values is just one sample from a multivariate Gaussian distribution of dimension equal to number of observed coordinates . Therefore, under the assumption of a zero-mean distribution, , where is the covariance matrix between all possible pairs for a given set of hyperparameters θ. As such the log marginal likelihood is:
and maximizing this marginal likelihood towards θ provides the complete specification of the Gaussian process f. One can briefly note at this point that the first term corresponds to a penalty term for a model's failure to fit observed values and the second term to a penalty term that increases proportionally to a model's complexity. Having specified θ, making predictions about unobserved values at coordinates x* is then only a matter of drawing samples from the predictive distribution where the posterior mean estimate A is defined as
Often, the covariance has the form , where is a scaling parameter. Examples are the Matérn class covariance functions. If this scaling parameter is either known or unknown (i.e. must be marginalized), then the posterior probability, , i.e. the probability for the hyperparameters given a set of data pairs of observations of and , admits an analytical expression.
Bayesian neural networks as Gaussian processes
Bayesian neural networks are a particular type of Bayesian network that results from treating deep learning and artificial neural network models probabilistically, and assigning a prior distribution to their parameters. Computation in artificial neural networks is usually organized into sequential layers of artificial neurons. The number of neurons in a layer is called the layer width. As layer width grows large, many Bayesian neural networks reduce to a Gaussian process with a closed form compositional kernel. This Gaussian process is called the Neural Network Gaussian Process (NNGP). It allows predictions from Bayesian neural networks to be more efficiently evaluated, and provides an analytic tool to understand deep learning models.
Computational issues
In practical applications, Gaussian process models are often evaluated on a grid leading to multivariate normal distributions. Using these models for prediction or parameter estimation using maximum likelihood requires evaluating a multivariate Gaussian density, which involves calculating the determinant and the inverse of the covariance matrix. Both of these operations have cubic computational complexity which means that even for grids of modest sizes, both operations can have a prohibitive computational cost. This drawback led to the development of multiple approximation methods.













![{\displaystyle \operatorname {var} [X(t)]=\operatorname {E} \left[\left|X(t)-\operatorname {E} [X(t)]\right|^{2}\right]<\infty \quad {\text{for all }}t\in T.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ab3cbcddd4821c14ffe316a48ab782a4c467763)















































![{\displaystyle [0,\varepsilon ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09b79b1e11f2a6c9b36a919ddbbf91204fe7a1df)



















![{\displaystyle \lim _{n\to \infty }\operatorname {tr} [K_{n}R_{n}^{-1}]<\infty ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc1d1379312a0e78525fce2f2e4404c8069abd48)



![{\displaystyle \Pr[f\in {\mathcal {H}}(R)]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c967b1fdbe5cdad6c678a7022bbfdd6a17901bb)
![{\displaystyle \lim _{n\to \infty }\operatorname {tr} [K_{n}R_{n}^{-1}]=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e133d11ae8a4dc2825314c86ec4c86df1aabb0fe)
![{\displaystyle \Pr[f\in {\mathcal {H}}(R)]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3b6ef001cb269a0cbb38ff83d802da1ad908639)

![{\displaystyle \lim _{n\to \infty }\operatorname {tr} [R_{n}R_{n}^{-1}]=\lim _{n\to \infty }\operatorname {tr} [I]=\lim _{n\to \infty }n=\infty .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ecb16aa9321bb328f2529628314558edb19b482)