Hippocampal prosthesis

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Hippocampal_prosthesis

A hippocampus prosthesis is a type of cognitive prosthesis (a prosthesis implanted into the nervous system in order to improve or replace the function of damaged brain tissue). Prosthetic devices replace normal function of a damaged body part; this can be simply a structural replacement (e.g. reconstructive surgery or glass eye) or a rudimentary, functional replacement (e.g. a pegleg or hook).

However, prosthetics involving the brain have some special categories and requirements. "Input" prosthetics, such as retinal or cochlear implant, supply signals to the brain that the patient eventually learns to interpret as sight or sound. "Output" prosthetics use brain signals to drive a bionic arm, hand or computer device, and require considerable training during which the patient learns to generate the desired action via their thoughts. Both of these types of prosthetics rely on the plasticity of the brain to adapt to the requirement of the prosthesis, thus allowing the user to "learn" the use of his new body part.

A cognitive or "brain-to-brain" prosthesis involves neither learned input nor output signals, but the native signals used normally by the area of the brain to be replaced (or supported). Thus, such a device must be able to fully replace the function of a small section of the nervous system—using that section's normal mode of operation. In order to achieve this, developers require a deep understanding of the functioning of the nervous system. The scope of design must include a reliable mathematical model as well as the technology in order to properly manufacture and install a cognitive prosthesis. The primary goal of an artificial hippocampus is to provide a cure for Alzheimer's disease and other hippocampus—related problems. To do so, the prosthesis has to be able to receive information directly from the brain, analyze the information and give an appropriate output to the cerebral cortex; in other words, it must behave just like a natural hippocampus. At the same time, the artificial organ must be completely autonomous, since any exterior power source will greatly increase the risk of infection.

Hippocampus

Role

The hippocampus is part of the human limbic system, which interacts with the neocortex and other parts of the brain to produce emotions. As a part of the limbic system, the hippocampus plays its part in the formation of emotion in addition to its other roles, such as consolidation of new memories, navigation, and spatial orientation. The hippocampus is responsible for the formation of long term recognition memories. In other words, this is the part of the brain that allows us to associate a face with a name. Because of its close relationship with memory formation, damage to the hippocampus is closely related to Alzheimer's disease.

Anatomy

For more anatomical information, see Hippocampus anatomy.

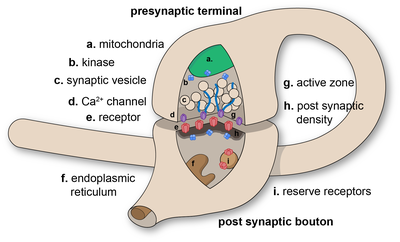
The hippocampus is a bilateral structure, situated under the neocortex. Each hippocampus is "composed of several different subsystem[s] that form a closed feedback loop, with input from the neocortex entering via the entorhinal cortex, propagating through the intrinsic subregions of the hippocampus and returning to the neocortex." In an electronic sense, the hippocampus is composed of a slice of parallel circuits.

Essential requirements

Biocompatibility

Since the prosthesis will be permanently implanted inside the brain, long term biocompatibility is required. We must also take into account the tendency for supporting braincells like astrocytes to encapsulate the implant. (This is a natural response for braincells, in order to protect neurons), thus impairing its function.

Bio-mimetic

Being biomimetic means that the implant must be able to fulfill the properties a real biological neuron. To do so we must have an in–depth understanding of brain behavior to build a solid mathematical model to be based upon. The field of computational neuroscience has made headway in this endeavor.

First, we must take into account that, like most of biological processes, the behaviors of neurons are highly nonlinear and depend on many factors: input frequency patterns, etc. Also, a good model must take into account the fact that the expression of a single nerve cell is negligible, since the processes are carried by groups of neurons interacting in network. Once installed, the device must assume all (or at least most) of the function of the damaged hippocampus for a prolonged period of time. First, the artificial neurons must be able to work together in network just like real neurons. Then, they must be able, working and effective synaptics connections with the existing neurons of the brain; therefore a model for silicon/neurons interface will be required.

Size

The implant must be small enough to be implantable while minimizing collateral damage during and after the implantation.

Bidirectional communication

In order to fully assume the function of the damaged hippocampus, the prosthesis must be able to communicate with the existing tissue in a bidirectional manner. in other words, the implant must be able to receive information from the brain and give an appropriate and compressible feedback to the surrounding nerve cell.

Personalized

The structural and functional characteristic of the brain varies greatly between individuals; therefore any neural implant has to be specific to each individual, which requires a precise model of the hippocampus and the use of advanced brain imagery to determine individual variance.

Surgical requirement

Since the prosthesis will be installed inside the brain, the operation itself will be much like a tumor removal operation. Although collateral damage will be inevitable, the effect on the patient will be minimal.

Model

"In order to incorporate the nonlinear dynamics of biological neurons into neuron models to develop a prosthesis, it is first necessary to measure them accurately. We have developed and applied methods for quantifying the nonlinear dynamics of hippocampal neurons (Berger et al., 1988a,b, 1991, 1992, 1994; Dalal et al., 1997) using principles of nonlinear systems theory (Lee and Schetzen, 1965; Krausz, 1975; P. Z. Marmarelis and Marmarelis, 1978; Rugh, 1981; Sclabassi et al., 1988). In this approach, properties of neurons are assessed experimentally by applying a random interval train of electrical impulses as an input and electrophysiologically recording the evoked output of the target neuron during stimulation (figure 12.2A). The input train consists of a series of impulses (as many as 4064), with interimpulse intervals varying according to a Poisson process having a mean of 500 ms and a range of 0.2–5000 ms. Thus, the input is "broadband" and stimulates the neuron over most of its operating range; that is, the statistical properties of the random train are highly consistent with the known physiological properties of hippocampal neurons. Nonlinear response properties are expressed in terms of the relation between progressively higher-order temporal properties of a sequence of input events and the probability of neuronal output, and are modeled as the kernels of a functional power series."

Technology involved

Imaging

Technology such as EEG, MEG, fMRI and other type of imaging technology are essential to the installation of the implant, which requires a high precision in order to minimize collateral damage (since the hippocampus is situated inside the cortex), as well as the proper function of the device.

Silicon/neuron interface

A silicon/neuron interface will be needed for the proper interaction of the silicon neurons of the prosthesis and the biological neurons of the brain.

Neuron network processor

In the brain, tasks are carried out by groups of interconnected neuronal network rather than a single cell, which means that any prosthesis must be able to simulate this network behavior. To do so, we will need a high number and density of silicon neurons to produce an effective prosthesis; therefore, a High-density Hippocampal Neuron Network Processor will be required in order for the prosthesis to carry out the task of a biological hippocampus. In addition, a neuron/silicon interface will be essential to the bidirectional communication of the implanted prosthesis. The choice of material and the design must ensure long term viability and bio compatibility while ensuring the density and the specificity of the interconnections.

Power supply

Appropriate power supply is still a major issue for any neural implant. Because the prostheses are implanted inside the brain, long term biocompatibility aside, the power supply will require several specification. First, the power supply must be self recharging. Unlike other prostheses, infection is a much greater issue for neural implant, due to the sensitivity of the brain; therefore an external power source is not envisagable. Because the brain is also highly heat sensitive, the power and the device itself must not generate too much heat to avoid disrupting brain function.

Prosthetic neuronal memory silicon chips

A prosthetic neuronal memory silicon chip is a device that imitates the brain's process of creating long-term memories. A prototype for this device was designed by Theodore Berger, a biomedical engineer and neurologist at University of Southern California. Berger started to work on the design in the early 1990s. He partnered with research colleagues that have been able to implant electrodes into rats and monkeys to test restoration of memory function. Recent work shows that the system can form long-term memories in many different behavioral situations. Berger and colleagues hope to eventually use these chips as electronic implants for humans whose brains that suffer from diseases such as Alzheimer's that disrupt neuronal networks.

Technology and medical application

To begin making a brain prosthesis, Berger and his collaborator Vasilis Marmarelis, a biomedical engineer at USC, worked with the hippocampus slices of rats. Since they knew that neuronal signals travel from one side of the hippocampus to the other, the researchers sent random pulses into the hippocampus, recorded the signals at specific locales to see how they were changed, and then derived equations representing the changes. They then programmed those equations into the computer chips.

Next, they had to determine whether a chip could be used as a prosthesis, or implant, for a damaged region in the hippocampus. To do this, they had to figure out whether they could avoid a central component of the pathway in the brain slices. They put electrodes in the region, which carried electrical pulses to an external chip. The chip then executed the transformations that are normally carried out in the hippocampus, and other electrodes sent the signals back to the slice of brain.

Memory codes

In 1996, Dr. Sam A. Deadwyler of Wake Forest Baptist Medical Center in Winston-Salem, NC, studied the activity patterns of collections of hippocampal neurons while rats performed a task requiring short-term memory.  These 'ensembles' or collections of neurons fired in different patterns in both time and 'space' (in this case, space referred to different neurons distributed throughout the hippocampus) depending on the type of behavior required in the task.  More importantly, Deadwyler and his colleagues could identify patterns that clearly distinguished between the various stimuli in the task including position (similar to place cells), behavioral responses, and what part of the task was occurring.  Analyses based on the neural ensemble activity alone without looking at those variables could identify and even 'predict' some of those variables even before they occurred.  In fact, the patterns would even identify when the rat was about to make an error in the task. Over the following ten years, Deadwyler's laboratory refined the analysis to identify the 'codes' and improved the ability to predict correct and error responses, even to the point of being able to have untrained rats perform the memory task using hippocampal stimulation with codes obtained from fully trained rats. The discovery of the memory codes in hippocampus led Deadwyler to join efforts with Berger for future studies in which Berger's team would develop models of memory function in hippocampus, and Deadwyler's team would test the models in rats and monkeys, and eventually move into human studies.

Trials on rats and monkeys

To transition to awake, behaving animals, Berger partnered with Deadwyler and Dr. Robert E. Hampson of Wake Forest to test a prototype of the memory prosthetic connected to rat and monkey brains via electrodes to analyze information just like the actual hippocampus. The prosthetic model allowed even a damaged hippocampus to generate new memories. In one demonstration, Deadwyler and Hampson impaired the rats' ability to form long-term memories by using pharmacological agents. These disrupted the neural circuitry that transfers messages between two subregions of the hippocampus. These subregions, CA1 and CA3, interact to create long-term memories. The rats were unable to remember which lever they needed to pull to obtain the reward. The researchers then developed an artificial hippocampus that could duplicate the pattern of interaction between CA3-CA1 interactions by analyzing the neural spikes in the cells with an electrode array, and then playing back the same pattern on the same array. After stimulating the rat hippocampi using the mathematical model of the prosthesis, their ability to identify the correct lever to pull improved dramatically. This artificial hippocampus played a significant role in the developmental stage of a memory prosthetic, as it went on to show that if a prosthetic device and its associated electrodes were implanted in the animals with a malfunctioning hippocampus, the device could potentially restore the memory capability to that of normal rats.

Goals for the future

The research teams at USC and Wake Forest are working to possibly make this system applicable to humans whose brains suffer damage from Alzheimer's, stroke, or injury, the disruption of neural networks often stops long-term memories from forming. The system designed by Berger and implemented by Deadwyler and Hampson allows the signal processing to take place that would occur naturally in undamaged neurons. Ultimately, they hope to restore the ability to create long-term memories by implanting chips such as these into the brain.

Recent development

Theodore Berger and his colleagues at the University of Southern California in Los Angeles have developed a working hippocampal prosthesis that passed the live tissue test in slices of brain tissue in 2004,. In 2011, in collaboration with Drs. Sam A. Deadwyler and Robert E. Hampson at Wake Forest Baptist Medical Center successfully tested a proof-of-concept hippocampal prosthesis in awake, behaving rats. The prosthesis was in the form of multisite electrodes positioned to record from both the input and output "sides" of the damaged hippocampus, the input is gathered and analyzed by external computation chips, an appropriate feedback is computed, then used to stimulate the appropriate output pattern in the brain so that the prosthesis functioned like a real hippocampus. In 2012, the team tested a further implementation in macaques prefrontal cortex, further developing the neural prosthesis technology. In 2013, Hampson et al. successfully tested a hippocampal prosthesis on non-human primates. While the device does not yet consist of a fully implantable "chip," these tests, from rat to monkey, demonstrate the effectiveness of the device as a neural prosthetic, and supports application to human trials.

Proof of concept for a human hippocampal prosthetic

In 2018, a team led by Robert E. Hampson at Wake Forest Baptist Medical, and including Berger and Deadwyler, became the first to demonstrate effectiveness of the prosthetic model in human patients. The subjects underwent implantation of electrodes in the brain at Wake Forest as part of a medical diagnostic procedure for epilepsy. While in the hospital, patients with electrodes in hippocampus volunteered to perform a memory task on computer while hippocampal neural activity was recorded in order for Berger and his team at USC team to customize the hippocampal prosthetic model for that patient. With model in hand, the Wake Forest team was able to demonstrate up to 37% improvement in memory function in patients with memory impaired by disease. The improvement was demonstrated for memories up to 75 minutes after stimulation by the hippocampal prosthetic model. As of 2018, studies are planned to test memory codes for additional attributes and features of items to be remembered as well as duration of memory facilitation in excess of 24 hours.

Synapse

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Synapse

Diagram of a chemical synaptic connection.

In the nervous system, a synapse is a structure that permits a neuron (or nerve cell) to pass an electrical or chemical signal to another neuron or to the target effector cell.

Synapses are essential to the transmission of nervous impulses from one neuron to another, playing a key role in enabling rapid and direct communication by creating circuits. In addition, a synapse serves as a junction where both the transmission and processing of information occur, making it a vital means of communication between neurons. Neurons are specialized to pass signals to individual target cells, and synapses are the means by which they do so. At a synapse, the plasma membrane of the signal-passing neuron (the presynaptic neuron) comes into close apposition with the membrane of the target (postsynaptic) cell. Both the presynaptic and postsynaptic sites contain extensive arrays of molecular machinery that link the two membranes together and carry out the signaling process. In many synapses, the presynaptic part is located on an axon and the postsynaptic part is located on a dendrite or soma. Astrocytes also exchange information with the synaptic neurons, responding to synaptic activity and, in turn, regulating neurotransmission. Synapses (at least chemical synapses) are stabilized in position by synaptic adhesion molecules (SAMs) projecting from both the pre- and post-synaptic neuron and sticking together where they overlap; SAMs may also assist in the generation and functioning of synapses. Moreover, SAMs coordinate the formation of synapses, with various types working together to achieve the remarkable specificity of synapses. In essence, SAMs function in both excitatory and inhibitory synapses, likely serving as devices for signal transmission.

History

Santiago Ramón y Cajal proposed that neurons are not continuous throughout the body, yet still communicate with each other, an idea known as the neuron doctrine. The word "synapse" was introduced in 1897 by the English neurophysiologist Charles Sherrington in Michael Foster's Textbook of Physiology. Sherrington struggled to find a good term that emphasized a union between two separate elements, and the actual term "synapse" was suggested by the English classical scholar Arthur Woollgar Verrall, a friend of Foster. The word was derived from the Greek synapsis (σύναψις), meaning "conjunction", which in turn derives from synaptein (συνάπτειν), from syn (σύν) "together" and haptein (ἅπτειν) "to fasten".

However, while the synaptic gap remained a theoretical construct, and was sometimes reported as a discontinuity between contiguous axonal terminations and dendrites or cell bodies, histological methods using the best light microscopes of the day could not visually resolve their separation which is now known to be about 20 nm. It needed the electron microscope in the 1950s to show the finer structure of the synapse with its separate, parallel pre- and postsynaptic membranes and processes, and the cleft between the two.

Types

An example of chemical synapse by the release of neurotransmitters like acetylcholine or glutamic acid.

Chemical and electrical synapses are two ways of synaptic transmission.

• In a chemical synapse, electrical activity in the presynaptic neuron is converted (via the activation of voltage-gated calcium channels) into the release of a chemical called a neurotransmitter that binds to receptors located in the plasma membrane of the postsynaptic cell. The neurotransmitter may initiate an electrical response or a secondary messenger pathway that may either excite or inhibit the postsynaptic neuron. Chemical synapses can be classified according to the neurotransmitter released: glutamatergic (often excitatory), GABAergic (often inhibitory), cholinergic (e.g. vertebrate neuromuscular junction), and adrenergic (releasing norepinephrine). Because of the complexity of receptor signal transduction, chemical synapses can have complex effects on the postsynaptic cell.
• In an electrical synapse, the presynaptic and postsynaptic cell membranes are connected by special channels called gap junctions that are capable of passing an electric current, causing voltage changes in the presynaptic cell to induce voltage changes in the postsynaptic cell.In fact, gap junctions facilitate the direct flow of electrical current without the need for neurotransmitters, as well as small molecules like calcium. Thus, the main advantage of an electrical synapse is the rapid transfer of signals from one cell to the next.
• Mixed chemical electrical synapses are synaptic sites that feature both a gap junction and neurotransmitter release. This combination allows a signal to have both a fast component (electrical) and a slow component (chemical).

The formation of neural circuits in nervous systems, appears to heavily depend on the crucial interactions between chemical and electrical synapses. Thus, these interactions govern the generation of synaptic transmission. Synaptic communication is distinct from an ephaptic coupling, in which communication between neurons occurs via indirect electric fields. An autapse is a chemical or electrical synapse that forms when the axon of one neuron synapses onto dendrites of the same neuron.

Excitatory and inhibitory

1. Excitatory synapse: Enhances the probability of depolarization in postsynaptic neurons and the initiation of an action potential.
2. Inhibitory Synapse: Diminishes the probability of depolarization in postsynaptic neurons and the initiation of an action potential.

An influx of Na+ driven by excitatory neurotransmitters opens cation channels, depolarizing the postsynaptic membrane toward the action potential threshold. In contrast, inhibitory neurotransmitters cause the postsynaptic membrane to become less depolarized by opening either Cl- or K+ channels, reducing firing. Depending on their release location, the receptors they bind to, and the ionic circumstances they encounter, various transmitters can be either excitatory or inhibitory. For instance, acetylcholine can either excite or inhibit depending on the type of receptors it binds to. For example, glutamate serves as an excitatory neurotransmitter, in contrast to GABA, which acts as an inhibitory neurotransmitter. Additionally, dopamine is a neurotransmitter that exerts dual effects, displaying both excitatory and inhibitory impacts through binding to distinct receptors.

The membrane potential prevents Cl- from entering the cell, even when its concentration is much higher outside than inside. The resting potential for Cl- in many neurons is quite negative, nearly equal to the resting potential. Opening Cl- channels tends to buffer the membrane potential, but this effect is countered when the membrane starts to depolarize, allowing more negatively charged Cl- ions to enter the cell. Consequently, it becomes more difficult to depolarize the membrane and excite the cell when Cl- channels are open. Similar effects result from the opening of K+ channels. The significance of inhibitory neurotransmitters is evident from the effects of toxins that impede their activity. For instance, strychnine binds to glycine receptors, blocking the action of glycine and leading to muscle spasms, convulsions, and death.

Interfaces

Synapses can be classified by the type of cellular structures serving as the pre- and post-synaptic components. The vast majority of synapses in the mammalian nervous system are classical axo-dendritic synapses (axon synapsing upon a dendrite), however, a variety of other arrangements exist. These include but are not limited to axo-axonic, dendro-dendritic, axo-secretory, axo-ciliary, somato-dendritic, dendro-somatic, and somato-somatic synapses.

In fact, the axon can synapse onto a dendrite, onto a cell body, or onto another axon or axon terminal, as well as into the bloodstream or diffusely into the adjacent nervous tissue.

Different types of synapses

Conversion of chemical into electrical signals

Neurotransmitters are tiny signal molecules stored in membrane-enclosed synaptic vesicles and released via exocytosis. Indeed, a change in electrical potential in the presynaptic cell triggers the release of these molecules. By attaching to transmitter-gated ion channels, the neurotransmitter causes an electrical alteration in the postsynaptic cell and rapidly diffuses across the synaptic cleft. Once released, the neurotransmitter is swiftly eliminated, either by being absorbed by the nerve terminal that produced it, taken up by nearby glial cells, or broken down by specific enzymes in the synaptic cleft. Numerous Na+-dependent neurotransmitter carrier proteins recycle the neurotransmitters and enable the cells to maintain rapid rates of release.

At chemical synapses, transmitter-gated ion channels play a vital role in rapidly converting extracellular chemical impulses into electrical signals. These channels are located in the postsynaptic cell's plasma membrane at the synapse region, and they temporarily open in response to neurotransmitter molecule binding, causing a momentary alteration in the membrane's permeability. Additionally, transmitter-gated channels are comparatively less sensitive to the membrane potential than voltage-gated channels, which is why they are unable to generate self-amplifying excitement on their own. However, they result in graded variations in membrane potential due to local permeability, influenced by the amount and duration of neurotransmitter released at the synapse.

Release of neurotransmitters

Neurotransmitters bind to ionotropic receptors on postsynaptic neurons, either causing their opening or closing. The variations in the quantities of neurotransmitters released from the presynaptic neuron may play a role in regulating the effectiveness of synaptic transmission. In fact, the concentration of cytoplasmic calcium is involved in regulating the release of neurotransmitters from presynaptic neurons.

The chemical transmission involves several sequential processes:

1. Synthesizing neurotransmitters within the presynaptic neuron.
2. Loading the neurotransmitters into secretory vesicles.
3. Controlling the release of neurotransmitters into the synaptic cleft.
4. Binding of neurotransmitters to postsynaptic receptors.
5. Ceasing the activity of the released neurotransmitters.

Synaptic polarization

The function of neurons depends upon cell polarity. The distinctive structure of nerve cells allows action potentials to travel directionally (from dendrites to cell body down the axon), and for these signals to then be received and carried on by post-synaptic neurons or received by effector cells. Nerve cells have long been used as models for cellular polarization, and of particular interest are the mechanisms underlying the polarized localization of synaptic molecules. PIP2 signaling regulated by IMPase plays an integral role in synaptic polarity.

Phosphoinositides (PIP, PIP2, and PIP3) are molecules that have been shown to affect neuronal polarity. A gene (ttx-7) was identified in Caenorhabditis elegans that encodes myo-inositol monophosphatase (IMPase), an enzyme that produces inositol by dephosphorylating inositol phosphate. Organisms with mutant ttx-7 genes demonstrated behavioral and localization defects, which were rescued by expression of IMPase. This led to the conclusion that IMPase is required for the correct localization of synaptic protein components. The egl-8 gene encodes a homolog of phospholipase Cβ (PLCβ), an enzyme that cleaves PIP2. When ttx-7 mutants also had a mutant egl-8 gene, the defects caused by the faulty ttx-7 gene were largely reversed. These results suggest that PIP2 signaling establishes polarized localization of synaptic components in living neurons.

Presynaptic modulation

Modulation of neurotransmitter release by G-protein-coupled receptors (GPCRs) is a prominent presynaptic mechanism for regulation of synaptic transmission. The activation of GPCRs located at the presynaptic terminal, can decrease the probability of neurotransmitter release. This presynaptic depression involves activation of Gi/o-type G-proteins that mediate different inhibitory mechanisms, including inhibition of voltage-gated calcium channels, activation of potassium channels, and direct inhibition of the vesicle fusion process. Endocannabinoids, synthesized in and released from postsynaptic neuronal elements, and their cognate receptors, including the (GPCR) CB1 receptor, located at the presynaptic terminal, are involved in this modulation by an retrograde signaling process, in which these compounds are synthesized in and released from postsynaptic neuronal elements, and travel back to the presynaptic terminal to act on the CB1 receptor for short-term or long-term synaptic depression, that cause a short or long lasting decrease in neurotransmitter release.

Effects of drugs on ligand-gated ion channels

Drugs have long been considered crucial targets for transmitter-gated ion channels. The majority of medications utilized to treat schizophrenia, anxiety, depression, and sleeplessness work at chemical synapses, and many of these pharmaceuticals function by binding to transmitter-gated channels. For instance, some drugs like barbiturates and tranquilizers bind to GABA receptors and enhance the inhibitory effect of GABA neurotransmitter. Thus, reduced concentration of GABA enables the opening of Cl- channels.

Furthermore, psychoactive drugs could potentially target many other synaptic signalling machinery components. In fact, numerous neurotransmitters are released by Na+-driven carriers and are subsequently removed from the synaptic cleft. By inhibiting such carriers, synaptic transmission is strengthened as the action of the transmitter is prolonged. For example, Prozac is one of antidepressant medications that works by preventing the absorption of serotonin neurotransmitter. Also, other antidepressants operate by inhibiting the reabsorption of both serotonin and norepinephrine.

Biogenesis

In nerve terminals, synaptic vesicles are produced quickly to compensate for their rapid depletion during neurotransmitter release. Their biogenesis involves segregating synaptic vesicle membrane proteins from other cellular proteins and packaging those distinct proteins into vesicles of appropriate size. Besides, it entails the endocytosis of synaptic vesicle membrane proteins from the plasma membrane.

Synaptoblastic and synaptoclastic refer to synapse-producing and synapse-removing activities within the biochemical signalling chain. This terminology is associated with the Bredesen Protocol for treating Alzheimer's disease, which conceptualizes Alzheimer's as an imbalance between these processes. As of October 2023, studies concerning this protocol remain small and few results have been obtained within a standardized control framework.

Role in memory

Main article: Hebbian theory

Potentiation and depression

It is widely accepted that the synapse plays a key role in the formation of memory. The stability of long-term memory can persist for many years; nevertheless, synapses, the neurological basis of memory, are very dynamic. The formation of synaptic connections significantly depends on activity-dependent synaptic plasticity observed in various synaptic pathways. Indeed, the connection between memory formation and alterations in synaptic efficacy enables the reinforcement of neuronal interactions between neurons. As neurotransmitters activate receptors across the synaptic cleft, the connection between the two neurons is strengthened when both neurons are active at the same time, as a result of the receptor's signaling mechanisms. The strength of two connected neural pathways is thought to result in the storage of information, resulting in memory. This process of synaptic strengthening is known as long-term potentiation (LTP).

By altering the release of neurotransmitters, the plasticity of synapses can be controlled in the presynaptic cell. The postsynaptic cell can be regulated by altering the function and number of its receptors. Changes in postsynaptic signaling are most commonly associated with a N-methyl-d-aspartic acid receptor (NMDAR)-dependent LTP and long-term depression (LTD) due to the influx of calcium into the post-synaptic cell, which are the most analyzed forms of plasticity at excitatory synapses.

Mechanism of protein kinase

Moreover, Ca2+/calmodulin (CaM)-dependent protein kinase II (CaMKII) is best recognized for its roles in the brain, particularly in the neocortex and hippocampal regions because it serves as a ubiquitous mediator of cellular Ca2+ signals. CaMKII is abundant in the nervous system, mainly concentrated in the synapses in the nerve cells. Indeed, CaMKII has been definitively identified as a key regulator of cognitive processes, such as learning, and neural plasticity. The first concrete experimental evidence for the long-assumed function of CaMKII in memory storage was demonstrated

While Ca2+/CaM binding stimulates CaMKII activity, Ca2+-independent autonomous CaMKII activity can also be produced by a number of other processes. CaMKII becomes active by autophosphorylating itself upon Ca2+/calmodulin binding. CaMKII is still active and phosphorylates itself even after Ca2+ is cleaved; as a result, the brain stores long-term memories using this mechanism. Nevertheless, when the CaMKII enzyme is dephosphorylated by a phosphatase enzyme, it becomes inactive, and memories are lost. Hence, CaMKII plays a vital role in both the induction and maintenance of LTP. 

Experimental models

For technical reasons, synaptic structure and function have been historically studied at unusually large model synapses, for example:

• Squid giant synapse
• Neuromuscular junction (NMJ), a cholinergic synapse in vertebrates, glutamatergic in insects
• Ciliary calyx in the ciliary ganglion of chicks
• Calyx of Held in the brainstem
• Ribbon synapse in the retina
• Schaffer collateral synapses in the hippocampus. These synapses are small, but their pre- and postsynaptic neurons are well separated (CA3 and CA1, respectively).

Synapses and Diseases

Synapses function as ensembles within particular brain networks to control the amount of neuronal activity, which is essential for memory, learning, and behavior. Consequently, synaptic disruptions might have negative effects. In fact, alterations in cell-intrinsic molecular systems or modifications to environmental biochemical processes can lead to synaptic dysfunction. The synapse is the primary unit of information transfer in the nervous system, and correct synaptic contact creation during development is essential for normal brain function. In addition, several mutations have been connected to neurodevelopmental disorders, and that compromised function at different synapse locations is a hallmark of neurodegenerative diseases.

Synaptic defects are causally associated with early appearing neurological diseases, including autism spectrum disorders (ASD), schizophrenia (SCZ), and bipolar disorder (BP). On the other hand, in late-onset degenerative pathologies, such as Alzheimer's (AD), Parkinson's (PD), and Huntington's (HD) diseases, synaptopathy is thought to be the inevitable end-result of an ongoing pathophysiological cascade. These diseases are identified by a gradual loss in cognitive and behavioral function and a steady loss of brain tissue. Moreover, these deteriorations have been mostly linked to the gradual build-up of protein aggregates in neurons, the composition of which may vary based on the pathology; all have the same deleterious effects on neuronal integrity. Furthermore, the high number of mutations linked to synaptic structure and function, as well as dendritic spine alterations in post-mortem tissue, has led to the association between synaptic defects and neurodevelopmental disorders, such as ASD and SCZ, characterized by abnormal behavioral or cognitive phenotypes.

Nevertheless, due to limited access to human tissue at late stages and a lack of thorough assessment of the essential components of human diseases in the available experimental animal models, it has been difficult to fully grasp the origin and role of synaptic dysfunction in neurological disorders. 

Additional images

• 
  Diagram of the synapse. Please see learnbio.org for interactive version
  
  
• 
  A typical central nervous system synapse
  
  
• 
  The synapse and synaptic vesicle cycle
   
• 
  Major elements in chemical synaptic transmission

Brain connectivity estimators

From Wikipedia, the free encyclopedia

Brain connectivity estimators represent patterns of links in the brain. Connectivity can be considered at different levels of the brain's organisation: from neurons, to neural assemblies and brain structures. Brain connectivity involves different concepts such as: neuroanatomical or structural connectivity (pattern of anatomical links), functional connectivity (usually understood as statistical dependencies) and effective connectivity (referring to causal interactions).

Neuroanatomical connectivity is inherently difficult to define given the fact that at the microscopic scale of neurons, new synaptic connections or elimination of existing ones are formed dynamically and are largely dependent on the function executed, but may be considered as pathways extending over regions of the brain, which are in accordance with general anatomical knowledge. Diffusion Weighted Imaging (DWI) can be used to provide such information. The distinction between functional and effective connectivity is not always sharp; sometimes causal or directed connectivity is called functional connectivity. Functional connectivity, may be defined as the temporal correlation (in terms of statistically significant dependence between distant brain regions) among the activity of different neural assemblies, whereas effective connectivity may be defined as the direct or indirect influence that one neural system exerts over another. Some brain connectivity estimators evaluate connectivity from brain activity time series such as Electroencephalography (EEG), Local field potential (LFP) or spike trains, with an effect on the directed connectivity. These estimators can be applied to fMRI data, if the required image sequences are available. Among estimators of connectivity, there are linear and non-linear, bivariate and multivariate measures. Certain estimators also indicate directionality. Different methods of connectivity estimation vary in their effectiveness. This article provides an overview of these measures, with an emphasis on the most effective methods.

Bi-variate estimators

Classical methods

Classical estimators of connectivity are correlation and coherence. The above measures provide information on the directionality of interactions in terms of delay (correlation) or coherence (phase), however the information does not imply causal interaction. Moreover, it may be ambiguous, since phase is determined modulo 2π. It is also not possible to identify by means of correlation or coherence.

Non-linear methods

The most frequently used nonlinear estimators of connectivity are mutual information, transfer entropy, generalised synchronisation, the continuity measure, synchronization likelihood, and phase synchronization. Mutual information and transfer entropy rely on the construction of histograms for probability estimates. The continuity measure, generalized synchronisations, and synchronisation likelihood are very similar methods based on phase space reconstruction. Among these measures, only transfer entropy allows for the determination of directionality. Nonlinear measures require long stationary segments of signals, are prone to systematic errors, and above all are very sensitive to noise. The comparison of nonlinear methods with linear correlation in the presence of noise reveals the poorer performance of non-linear estimators. In the authors conclude that there must be good reason to think that there is non-linearity in the data to apply non-linear methods. In fact it was demonstrated by means of surrogate data test, and time series forecasting  that nonlinearity in EEG and LFP is the exception rather than the norm. On the other hand, linear methods perform quite well for non-linear signals. Finally, non-linear methods are bivariate (calculated pair-wise), which has serious implication on their performance.

Bivariate versus multivariate estimators

Comparison of performance of bivariate and multivariate estimators of connectivity may be found in, where it was demonstrated that in case of interrelated system of channels, greater than two, bivariate methods supply misleading information, even reversal of true propagation may be found. Consider the very common situation that the activity from a given source is measured at electrodes positioned at different distances, hence different delays between the recorded signals.

When a bivariate measure is applied, propagation is always obtained when there is a delay between channels, which results in a lot of spurious flows. When we have two or three sources acting simultaneously, which is a common situation, we shall get dense and disorganized structure of connections, similar to random structure (at best some "small world" structure may be identified). This kind of pattern is usually obtained in case of application of bivariate measures. In fact, effective connectivity patterns yielded by EEG or LFP measurements are far from randomness, when proper multivariate measures are applied, as we shall demonstrate below.

Multivariate methods based on Granger causality

The testable definition of causality was introduced by Granger. Granger causality principle states that if some series Y(t) contains information in past terms that helps in the prediction of series X(t), then Y(t) is said to cause X(t). Granger causality principle can be expressed in terms of two-channel multivariate autoregressive model (MVAR). Granger in his later work  pointed out that the determination of causality is not possible when the system of considered channels is not complete. The measures based on Granger causality principle are: Granger Causality Index (GCI), Directed Transfer Function (DTF) and Partial Directed Coherence (PDC). These measures are defined in the framework of Multivariate Autoregressive Model.

Multivariate Autoregressive Model

The AR model assumes that X(t)—a sample of data at a time t—can be expressed as a sum of p previous values of the samples from the set of k-signals weighted by model coefficients A plus a random value E(t):

${\displaystyle X(t)=\sum _{j=1}^{p}A(j)X(t-j)+E(t)}$

(1)

The p is called the model order. For a k-channel process X(t) and E(t) are vectors of size k and the coefficients A are k×k-sized matrices. The model order may be determined by means of criteria developed in the framework of information theory and the coefficients of the model are found by means of the minimalization of the residual noise. In the procedure correlation matrix between signals is calculated. By the transformation to the frequency domain we get:

${\displaystyle \begin{array}{l}E(f)=A(f)X(f)\\ X(f)=A^{-1}(f)E(f)=H(f)E(f)\end{array}}$

(2)

H(f) is a transfer matrix of the system, it contains information about the relationships between signals and their spectral characteristics. H(f) is non-symmetric, so it allows for finding causal dependencies. Model order may be found by means of criteria developed in the framework of information theory, e.g. AIC criterion.

Granger Causality Index

Granger causality index showing the driving of channel x by channel y is defined as the logarithm of the ratio of residual variance for one channel to the residual variance of the two-channel model: GCI_y→x = ln (e/e₁) This definition can be extended to the multichannel system by considering how the inclusion of the given channel changes the residual variance ratios. To quantify directed influence from a channel x_j to x_i for n channel autoregressive process in time domain we consider n and n−1 dimensional MVAR models. First, the model is fitted to whole n-channel system, leading to the residual variance V_i,n(t) = var(E_i,n(t)) for signal x_i. Next, a n−1 dimensional MVAR model is fitted for n−1 channels, excluding channel j, which leads to the residual variance V_i,n−1(t) = var (E_i,n−1(t)). Then Granger causality is defined as:

${\displaystyle {\mathrm{G}\mathrm{C}\mathrm{I}}_{j\to i}(t)=\ln \left(\frac{V_{i,n}(t)}{V_{i,n-1}(t)}\right)}$

GCI is smaller or equal 1, since the variance of n-dimensional system is lower than the residual variance of a smaller, n−1 dimensional system. GCI(t) estimates causality relations in time domain. For brain signals the spectral characteristics of the signals is of interest, because for a given task the increase of propagation in certain frequency band may be accompanied by the decrease in another frequency band. DTF or PDC are the estimators defined in the frequency domain.

Directed Transfer Function

Directed Transfer Function (DTF) was introduced by Kaminski and Blinowska  in the form:

${\displaystyle {\mathrm{D}\mathrm{T}\mathrm{F}}_{j\to i}^2(f)=\frac{{\left|H_{ij}(f)\right|}^2}{\sum _{m=1}^k{\left|H_{im}(f)\right|}^2}}$

(3)

Where H_ij(f) is an element of a transfer matrix of MVAR model. DTF describes causal influence of channel j on channel i at frequency f. The above equation (3) defines a normalized version of DTF, which takes values from 0 to 1 producing a ratio between the inflow from channel j to channel i to all the inflows to channel i. The non-normalized DTF which is directly related to the coupling strength  is defined as:

${\displaystyle {\mathrm{N}\mathrm{D}\mathrm{T}\mathrm{F}}_{j\to i}^2(f)={\left|H_{ij}(f)\right|}^2}$

(4)

DTF shows not only direct, but also cascade flows, namely in case of propagation 1→2→3 it shows also propagation 1→3. In order to distinguish direct from indirect flows direct Directed Transfer Function (dDTF) was introduced.^[25] The dDTF is defined as a multiplication of a modified DTF by partial coherence. The modification of DTF concerned normalization of the function in such a way as to make the denominator independent of frequency. The dDTF_j→i showing direct propagation from channel j to i is defined as:

${\displaystyle \begin{array}{l}{\mathrm{d}\mathrm{D}\mathrm{T}\mathrm{F}}_{j\to i}^2(f)=F_{ij}^2(f)C_{ij}^2(f)\\ F_{ij}^2(f)={\displaystyle \frac{{\left|H_{ij}(f)\right|}^2}{\sum _f\sum _{m=1}^k{\left|H_{im}(f)\right|}^2}}\end{array}}$

(5)

Where C_ij(f) is partial coherence. The dDTF_j→i has a nonzero value when both functions F_ij(f) and C_ij(f) are non-zero, in that case there exists a direct causal relation between channels j→i. Distinguishing direct from indirect transmission is essential in case of signals from implanted electrodes, for EEG signals recorded by scalp electrodes it is not really important.

DTF may be used for estimation of propagation in case of point processes e.g. spike trains or for the estimation of causal relations between spike trains and Local Field Potentials.

Partial Directed Coherence

The partial directed coherence (PDC) was defined by Baccala and Sameshima  in the following form:

${\displaystyle P_{ij}(f)=\frac{A_{ij}(f)}{\sqrt{{\mathbf{a}}_j^{\ast }(f){\mathbf{a}}_j(f)}}}$

(6)

In the above equation A_ij(f) is an element of A(f)—a Fourier transform of MVAR model coefficients A(t), where a_j(f) is j-th column of A(f) and the asterisk denotes the transpose and complex conjugate operation. Although it is a function operating in the frequency domain, the dependence of A(f) on the frequency has not a direct correspondence to the power spectrum. From normalization condition it follows that PDC takes values from the interval [0,1]. PDC shows only direct flows between channels. Unlike DTF, PDC is normalized to show a ratio between the outflow from channel j to channel i to all the outflows from the source channel j, so it emphasizes rather the sinks, not the sources. The normalization of PDC affects the detected intensities of flow as was pointed out in. Namely, adding further variables that are influenced by a source variable decreases PDC, although the relationship between source and target processes remains unchanged. In other words: the flow emitted in one direction will be enhanced in comparison to the flows of the same intensity emitted from a given source in several directions.

Time-varying estimators of effective connectivity

In order to account for the dynamic changes of propagation, the method of adaptive filtering or the method based on the sliding window may be applied to estimators of connectivity. Both methods require multiple repetition of the experiment to obtain statistically satisfactory results and they produce similar results. The adaptive methods, e.g. Kalman filtering, are more computationally demanding, therefore methods based on sliding window may be recommended.

In the case of parametric model the number of data points kN_T (k—number of channels, N_T—number of points in the data window) has to be bigger (preferably by order of magnitude) than the number of parameters, which in case of MVAR is equal to k²p (p—model order). In order to evaluate dynamics of the process, a short data window has to be applied, which requires an increase of the number of the data points, which may be achieved by means of a repetition of the experiment. A non-stationary recording may be divided into shorter time windows, short enough to treat the data within a window as quasi-stationary. Estimation of MVAR coefficients is based on calculation of the correlation matrix between channels R_ij of k signals X_i from multivariate set, separately for each trial. The resulting model coefficients are based on the correlation matrix averaged over trials. The correlation matrix has the form:

${\displaystyle {\tilde{R}}_{ij}(s)=\frac{1}{N_T}\sum _{r=1}^{N_T}{R}_{ij}^{(r)}(s)=\frac{1}{N_T}\sum _{r=1}^{N_T}\frac{1}{N_S}\sum _{t=1}^{N_S}{X}_i^{(r)}(t)X_j^{(r)}(t+s)}$

(7)

The averaging concerns correlation matrices (model is fitted independently for each short data window); the data are not averaged in the process. The choice of window size is always a compromise between quality of the fit and time resolution.

The errors of the SDTF may be evaluated by means of bootstrap method. This procedure corresponds to simulations of other realizations of the experiment. The variance of the function value is obtained by repeated calculation of the results for a randomly selected (with repetitions) pool of the original data trials.

Applications

The estimation of brain connectivity has found numerous and notable applications, namely when investigating brain changes associated with the treatment of psychopathology like schizophrenia and depression, or following structural damage like in hemorrhage or tumor. The methods applied benefit from a parcellation approach, where regions of the brain are defined from atlases or DWI data, with connectivity metrics then extracted to compare changes within standardized regions.

Specifically, DTF found multiple applications, the early ones involved: localization of epileptic foci, estimation of EEG propagation in different sleep stages and wakefulness, determination of transmission between brain structures of an animal during a behavioral test.

One may observe the shifting of sources toward the front in transition from wakefulness to the deeper sleep stages. In the deep sleep the source is over corpus callosum, presumably it is connected with feeding the cortex from the sub-cortical structures.

One of the first applications of SDTF was determination of the dynamic propagation during performance of finger movement and its imagination,. The results corresponded very well with the known phenomena of event related synchronization and desynchronization such as decrease of the activity in alpha and beta band and brief increase of activity in the gamma band during movement in the areas corresponding to primary motor cortex, beta rebound after movement and so-called surround effect. Especially interesting was comparison of real finger movement and its imagination. In case of real movement the short burst of gamma propagation was observed from the electrode positioned over finger primary motor cortex . In case of movement imagination this propagation started later and a cross-talk between different sites overlying motor area and supplementary motor area (SMA) was found. (The dynamics of propagation may be observed in animations).

Another applications of SDTF concerned evaluation of transmission during cognitive experiments. The results of the Continuous Attention Test (CAT)  confirmed the engagement of prefrontal and frontal structures in the task and supported the hypothesis of an active inhibition by pre-SMA and right inferior frontal cortex. Animations of propagation during CAT test are available.

The results obtained by means of SDTF in experiments involving working memory were compatible with fMRI studies on the localization of the active sites and supplied the information concerning the temporal interaction between them. The animation illustrating dynamics of the interaction are available.

Note that care should be taken to avoid spurious connectivity estimates when using EEG channel data. Recent articles highlight that previous claims that DTF and PDC were insensitive to volume conduction were inaccurate. Indeed, DTF results obtained for signals recorded from the scalp are in general affected by volume conduction. Even though the effects of volume conduction might be minimal in specific recording situations, appropriate preprocessing on channel data (such as source identification) should be performed before estimating DTF or PDC.

Conclusions

The existence of well defined sources of brain activity connected with particular experimental conditions are well established in fMRI experiments, by means of inverse solution methods and intracortical measurements. This kind of deterministic structure of brain activity should affect functional connectivity, so reported in some works random or barely distinguished from random connectivity structure may be considered as a surprising phenomenon. This kind of results may be explained by methodological errors: 1) unrobust methods of connectivity estimation and, even more important, 2) application of bivariate methods. When multivariate robust measures of connectivity are applied for EEG analysis a clear picture of functional connectivity emerges.