Square root

 

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Square_root

Notation for the (principal) square root of x.

For example, √25 = 5, since 25 = 5 ⋅ 5, or 5² (5 squared).

In mathematics, a square root of a number x is a number y such that ${\displaystyle y^2=x}$; in other words, a number y whose square (the result of multiplying the number by itself, or ${\displaystyle y\cdot y}$) is x. For example, 4 and −4 are square roots of 16 because ${\displaystyle 4^2=(-4{)}^2=16}$.

Every nonnegative real number x has a unique nonnegative square root, called the principal square root or simply the square root (with a definite article, see below), which is denoted by ${\displaystyle \sqrt{x},}$ where the symbol "${\displaystyle \sqrt{{}^{}}}$" is called the radical sign or radix. For example, to express the fact that the principal square root of 9 is 3, we write ${\displaystyle \sqrt{9}=3}$. The term (or number) whose square root is being considered is known as the radicand. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative x, the principal square root can also be written in exponent notation, as ${\displaystyle x^{1/2}}$.

Every positive number x has two square roots: ${\displaystyle \sqrt{x}}$ (which is positive) and ${\displaystyle -\sqrt{x}}$ (which is negative). The two roots can be written more concisely using the ± sign as ${\displaystyle \pm \sqrt{x}}$. Although the principal square root of a positive number is only one of its two square roots, the designation "the square root" is often used to refer to the principal square root.

Square roots of negative numbers can be discussed within the framework of complex numbers. More generally, square roots can be considered in any context in which a notion of the "square" of a mathematical object is defined. These include function spaces and square matrices, among other mathematical structures.

History

YBC 7289 clay tablet

The Yale Babylonian Collection clay tablet YBC 7289 was created between 1800 BC and 1600 BC, showing ${\displaystyle \sqrt{2}}$ and $\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$ respectively as 1;24,51,10 and 0;42,25,35 base 60 numbers on a square crossed by two diagonals. (1;24,51,10) base 60 corresponds to 1.41421296, which is correct to 5 decimal places (1.41421356...).

The Rhind Mathematical Papyrus is a copy from 1650 BC of an earlier Berlin Papyrus and other texts – possibly the Kahun Papyrus – that shows how the Egyptians extracted square roots by an inverse proportion method.

In Ancient India, the knowledge of theoretical and applied aspects of square and square root was at least as old as the Sulba Sutras, dated around 800–500 BC (possibly much earlier). A method for finding very good approximations to the square roots of 2 and 3 are given in the Baudhayana Sulba Sutra. Apastamba who was dated around 600 BCE has given a strikingly accurate value for ${\displaystyle \sqrt{2}}$ which is correct upto five decimal places as $1+\frac{1}{3}+\frac{1}{3\times 4}-\frac{1}{3\times 4\times 34}$. Aryabhata, in the Aryabhatiya (section 2.4), has given a method for finding the square root of numbers having many digits.

It was known to the ancient Greeks that square roots of positive integers that are not perfect squares are always irrational numbers: numbers not expressible as a ratio of two integers (that is, they cannot be written exactly as ${\displaystyle \frac{m}{n}}$, where m and n are integers). This is the theorem Euclid X, 9, almost certainly due to Theaetetus dating back to c. 380 BC. The discovery of irrational numbers, including the particular case of the square root of 2, is widely associated with the Pythagorean school. Although some accounts attribute the discovery to Hippasus, the specific contributor remains uncertain due to the scarcity of primary sources and the secretive nature of the brotherhood. It is exactly the length of the diagonal of a square with side length 1.

In the Chinese mathematical work Writings on Reckoning, written between 202 BC and 186 BC during the early Han Dynasty, the square root is approximated by using an "excess and deficiency" method, which says to "...combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."

A symbol for square roots, written as an elaborate R, was invented by Regiomontanus (1436–1476). An R was also used for radix to indicate square roots in Gerolamo Cardano's Ars Magna.

According to historian of mathematics D.E. Smith, Aryabhata's method for finding the square root was first introduced in Europe by Cataneo—in 1546.

According to Jeffrey A. Oaks, Arabs used the letter jīm/ĝīm (ج), the first letter of the word "جذر" (variously transliterated as jaḏr, jiḏr, ǧaḏr or ǧiḏr, "root"), placed in its initial form (ﺟ) over a number to indicate its square root. The letter jīm resembles the present square root shape. Its usage goes as far as the end of the twelfth century in the works of the Moroccan mathematician Ibn al-Yasamin.

The symbol "√" for the square root was first used in print in 1525, in Christoph Rudolff's Coss.

Properties and uses

The graph of the function f(x) = √x, made up of half a parabola with a vertical directrix

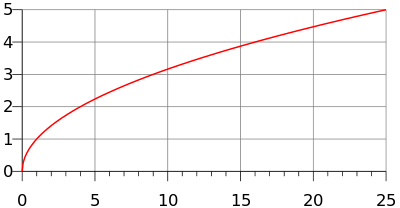
The principal square root function ${\displaystyle f(x)=\sqrt{x}}$ (usually just referred to as the "square root function") is a function that maps the set of nonnegative real numbers onto itself. In geometrical terms, the square root function maps the area of a square to its side length.

The square root of x is rational if and only if x is a rational number that can be represented as a ratio of two perfect squares. (See square root of 2 for proofs that this is an irrational number, and quadratic irrational for a proof for all non-square natural numbers.) The square root function maps rational numbers into algebraic numbers, the latter being a superset of the rational numbers).

For all real numbers x,

$${\displaystyle \sqrt{x^2}=\left|x\right|=\{\begin{array}{ll}x,& \text{if }x\ge 0\\ -x,& \text{if }x<0.\end{array}}$$

(see absolute value).

For all nonnegative real numbers x and y,

$${\displaystyle \sqrt{xy}=\sqrt{x}\sqrt{y}}$$

and

$${\displaystyle \sqrt{x}=x^{1/2}.}$$

The square root function is continuous for all nonnegative x, and differentiable for all positive x. If f denotes the square root function, whose derivative is given by:

$${\displaystyle f^{\prime }(x)=\frac{1}{2\sqrt{x}}.}$$

The Taylor series of ${\displaystyle \sqrt{1+x}}$ about x = 0 converges for |x| ≤ 1, and is given by

$${\displaystyle \sqrt{1+x}=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(2n)!}{(1-2n)(n!{)}^2(4^n)}{x}^n=1+\frac{1}{2}x-\frac{1}{8}{x}^2+\frac{1}{16}{x}^3-\frac{5}{128}{x}^4+\cdots ,}$$

The square root of a nonnegative number is used in the definition of Euclidean norm (and distance), as well as in generalizations such as Hilbert spaces. It defines an important concept of standard deviation used in probability theory and statistics. It has a major use in the formula for roots of a quadratic equation; quadratic fields and rings of quadratic integers, which are based on square roots, are important in algebra and have uses in geometry. Square roots frequently appear in mathematical formulas elsewhere, as well as in many physical laws.

Square roots of positive integers

A positive number has two square roots, one positive, and one negative, which are opposite to each other. When talking of the square root of a positive integer, it is usually the positive square root that is meant.

The square roots of an integer are algebraic integers—more specifically quadratic integers.

The square root of a positive integer is the product of the roots of its prime factors, because the square root of a product is the product of the square roots of the factors. Since $\sqrt{p^{2k}}=p^k,$ only roots of those primes having an odd power in the factorization are necessary. More precisely, the square root of a prime factorization is

$${\displaystyle \sqrt{p_1^{2e_1+1}\cdots p_k^{2e_k+1}{p}_{k+1}^{2e_{k+1}}\dots p_n^{2e_n}}=p_1^{e_1}\dots p_n^{e_n}\sqrt{p_1\dots p_k}.}$$

As decimal expansions

The square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and hence have non-repeating decimals in their decimal representations. Decimal approximations of the square roots of the first few natural numbers are given in the following table.

n	${\displaystyle \sqrt{n},}$ truncated to 50 decimal places
0	0
1	1
2	1.41421356237309504880168872420969807856967187537694
3	1.73205080756887729352744634150587236694280525381038
4	2
5	2.23606797749978969640917366873127623544061835961152
6	2.44948974278317809819728407470589139196594748065667
7	2.64575131106459059050161575363926042571025918308245
8	2.82842712474619009760337744841939615713934375075389
9	3
10	3.16227766016837933199889354443271853371955513932521

As expansions in other numeral systems

As with before, the square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and therefore have non-repeating digits in any standard positional notation system.

The square roots of small integers are used in both the SHA-1 and SHA-2 hash function designs to provide nothing up my sleeve numbers.

As periodic continued fractions

One of the most intriguing results from the study of irrational numbers as continued fractions was obtained by Joseph Louis Lagrange c. 1780. Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction is periodic. That is, a certain pattern of partial denominators repeats indefinitely in the continued fraction. In a sense these square roots are the very simplest irrational numbers, because they can be represented with a simple repeating pattern of integers.

${\displaystyle \sqrt{2}}$	= [1; 2, 2, ...]
${\displaystyle \sqrt{3}}$	= [1; 1, 2, 1, 2, ...]
${\displaystyle \sqrt{4}}$	= [2]
${\displaystyle \sqrt{5}}$	= [2; 4, 4, ...]
${\displaystyle \sqrt{6}}$	= [2; 2, 4, 2, 4, ...]
${\displaystyle \sqrt{7}}$	= [2; 1, 1, 1, 4, 1, 1, 1, 4, ...]
${\displaystyle \sqrt{8}}$	= [2; 1, 4, 1, 4, ...]
${\displaystyle \sqrt{9}}$	= [3]
${\displaystyle \sqrt{10}}$	= [3; 6, 6, ...]
${\displaystyle \sqrt{11}}$	= [3; 3, 6, 3, 6, ...]
${\displaystyle \sqrt{12}}$	= [3; 2, 6, 2, 6, ...]
${\displaystyle \sqrt{13}}$	= [3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, ...]
${\displaystyle \sqrt{14}}$	= [3; 1, 2, 1, 6, 1, 2, 1, 6, ...]
${\displaystyle \sqrt{15}}$	= [3; 1, 6, 1, 6, ...]
${\displaystyle \sqrt{16}}$	= [4]
${\displaystyle \sqrt{17}}$	= [4; 8, 8, ...]
${\displaystyle \sqrt{18}}$	= [4; 4, 8, 4, 8, ...]
${\displaystyle \sqrt{19}}$	= [4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, ...]
${\displaystyle \sqrt{20}}$	= [4; 2, 8, 2, 8, ...]

The square bracket notation used above is a short form for a continued fraction. Written in the more suggestive algebraic form, the simple continued fraction for the square root of 11, [3; 3, 6, 3, 6, ...], looks like this:

$${\displaystyle \sqrt{11}=3+\frac{1}{3+\frac{1}{6+\frac{1}{3+\frac{1}{6+\frac{1}{3+\ddots }}}}}}$$

where the two-digit pattern {3, 6} repeats over and over again in the partial denominators. Since 11 = 3² + 2, the above is also identical to the following generalized continued fractions:

$${\displaystyle \sqrt{11}=3+\frac{2}{6+\frac{2}{6+\frac{2}{6+\frac{2}{6+\frac{2}{6+\ddots }}}}}=3+\frac{6}{20-1-\frac{1}{20-\frac{1}{20-\frac{1}{20-\frac{1}{20-\ddots }}}}}.}$$

Computation

Main article: Methods of computing square roots

Square roots of positive numbers are not in general rational numbers, and so cannot be written as a terminating or recurring decimal expression. Therefore in general any attempt to compute a square root expressed in decimal form can only yield an approximation, though a sequence of increasingly accurate approximations can be obtained.

Most pocket calculators have a square root key. Computer spreadsheets and other software are also frequently used to calculate square roots. Pocket calculators typically implement efficient routines, such as the Newton's method (frequently with an initial guess of 1), to compute the square root of a positive real number. When computing square roots with logarithm tables or slide rules, one can exploit the identities

$${\displaystyle \sqrt{a}=e^{(\ln a)/2}={10}^{({\log }_{10}a)/2},}$$

where ln and log₁₀ are the natural and base-10 logarithms.

By trial-and-error, one can square an estimate for ${\displaystyle \sqrt{a}}$ and raise or lower the estimate until it agrees to sufficient accuracy. For this technique it is prudent to use the identity

$${\displaystyle (x+c{)}^2=x^2+2xc+c^2,}$$

as it allows one to adjust the estimate x by some amount c and measure the square of the adjustment in terms of the original estimate and its square. Furthermore, ${\displaystyle (x+c{)}^2\approx x^2+2xc}$ when c is close to 0, because the tangent line to the graph of ${\displaystyle x^2+2xc+c^2}$ at ${\displaystyle c=0}$, as a function of c alone, is ${\displaystyle y=2xc+x^2}$. Thus, small adjustments to x can be planned out by setting ${\displaystyle 2xc}$ to a, or ${\displaystyle c=\frac{a}{2x}}$.

The most common iterative method of square root calculation by hand is known as the "Babylonian method" or "Heron's method" after the first-century Greek philosopher Heron of Alexandria, who first described it. The method uses the same iterative scheme as the Newton–Raphson method yields when applied to the function y = f(x) = x² − a, using the fact that its slope at any point is dy/dx = f′(x) = 2x, but predates it by many centuries. The algorithm is to repeat a simple calculation that results in a number closer to the actual square root each time it is repeated with its result as the new input. The motivation is that if x is an overestimate to the square root of a nonnegative real number a then a/x will be an underestimate and so the average of these two numbers is a better approximation than either of them. However, the inequality of arithmetic and geometric means shows this average is always an overestimate of the square root (as noted below), and so it can serve as a new overestimate with which to repeat the process, which converges as a consequence of the successive overestimates and underestimates being closer to each other after each iteration. To find x:

1. Start with an arbitrary positive start value x. The closer to the square root of a, the fewer the iterations that will be needed to achieve the desired precision.
2. Replace x by the average (x + a/x) / 2 between x and a/x.
3. Repeat from step 2, using this average as the new value of x.

That is, if an arbitrary guess for ${\displaystyle \sqrt{a}}$ is x₀, and x_{n + 1} = (x_n + a/x_n) / 2, then each x_n is an approximation of ${\displaystyle \sqrt{a}}$ which is better for large n than for small n. If a is positive, the convergence is quadratic, which means that in approaching the limit, the number of correct digits roughly doubles in each next iteration. If a = 0, the convergence is only linear; however, ${\displaystyle \sqrt{0}=0}$ so in this case no iteration is needed.

Using the identity

$${\displaystyle \sqrt{a}=2^{-n}\sqrt{4^{n}a},}$$

the computation of the square root of a positive number can be reduced to that of a number in the range [1, 4). This simplifies finding a start value for the iterative method that is close to the square root, for which a polynomial or piecewise-linear approximation can be used.

The time complexity for computing a square root with n digits of precision is equivalent to that of multiplying two n-digit numbers.

Another useful method for calculating the square root is the shifting nth root algorithm, applied for n = 2.

The name of the square root function varies from programming language to programming language, with sqrt (often pronounced "squirt" ) being common, used in C and derived languages like C++, JavaScript, PHP, and Python.

Square roots of negative and complex numbers

First leaf of the complex square root

 

Second leaf of the complex square root

 

Using the Riemann surface of the square root, it is shown how the two leaves fit together

The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have a real square root. However, it is possible to work with a more inclusive set of numbers, called the complex numbers, that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted by i (sometimes by j, especially in the context of electricity where i traditionally represents electric current) and called the imaginary unit, which is defined such that i² = −1. Using this notation, we can think of i as the square root of −1, but we also have (−i)² = i² = −1 and so −i is also a square root of −1. By convention, the principal square root of −1 is i, or more generally, if x is any nonnegative number, then the principal square root of −x is

$${\displaystyle \sqrt{-x}=i\sqrt{x}.}$$

The right side (as well as its negative) is indeed a square root of −x, since

$${\displaystyle (i\sqrt{x}{)}^2=i^2(\sqrt{x}{)}^2=(-1)x=-x.}$$

For every non-zero complex number z there exist precisely two numbers w such that w² = z: the principal square root of z (defined below), and its negative.

Principal square root of a complex number

Geometric representation of the 2nd to 6th roots of a complex number z, in polar form re^iφ  where r = |z | and φ = arg z. If z is real, φ = 0 or π. Principal roots are shown in black.

To find a definition for the square root that allows us to consistently choose a single value, called the principal value, we start by observing that any complex number ${\displaystyle x+iy}$ can be viewed as a point in the plane, ${\displaystyle (x,y),}$ expressed using Cartesian coordinates. The same point may be reinterpreted using polar coordinates as the pair ${\displaystyle (r,\phi ),}$ where ${\displaystyle r\ge 0}$ is the distance of the point from the origin, and ${\displaystyle \phi }$ is the angle that the line from the origin to the point makes with the positive real (${\displaystyle x}$) axis. In complex analysis, the location of this point is conventionally written ${\displaystyle r{e}^{i\phi }.}$ If

$${\displaystyle z=r{e}^{i\phi }\text{ with }-\pi <\phi \le \pi ,}$$

then the principal square root of ${\displaystyle z}$ is defined to be the following:

$${\displaystyle \sqrt{z}=\sqrt{r}{e}^{i\phi /2}.}$$

The principal square root function is thus defined using the non-positive real axis as a branch cut. If ${\displaystyle z}$ is a non-negative real number (which happens if and only if ${\displaystyle \phi =0}$) then the principal square root of ${\displaystyle z}$ is ${\displaystyle \sqrt{r}{e}^{i(0)/2}=\sqrt{r};}$ in other words, the principal square root of a non-negative real number is just the usual non-negative square root. It is important that ${\displaystyle -\pi <\phi \le \pi }$ because if, for example, ${\displaystyle z=-2i}$ (so ${\displaystyle \phi =-\pi /2}$) then the principal square root is

$${\displaystyle \sqrt{-2i}=\sqrt{2e^{i\phi }}=\sqrt{2}{e}^{i\phi /2}=\sqrt{2}{e}^{i(-\pi /4)}=1-i}$$

but using ${\displaystyle \tilde{\phi }:=\phi +2\pi =3\pi /2}$ would instead produce the other square root ${\displaystyle \sqrt{2}{e}^{i\tilde{\phi }/2}=\sqrt{2}{e}^{i(3\pi /4)}=-1+i=-\sqrt{-2i}.}$

The principal square root function is holomorphic everywhere except on the set of non-positive real numbers (on strictly negative reals it is not even continuous). The above Taylor series for ${\displaystyle \sqrt{1+x}}$ remains valid for complex numbers ${\displaystyle x}$ with ${\displaystyle |x|<1.}$

The above can also be expressed in terms of trigonometric functions:

$${\displaystyle \sqrt{r\left(\cos \phi +i\sin \phi \right)}=\sqrt{r}\left(\cos \frac{\phi }{2}+i\sin \frac{\phi }{2}\right).}$$

Algebraic formula

The square roots of i

When the number is expressed using its real and imaginary parts, the following formula can be used for the principal square root:

$${\displaystyle \sqrt{x+iy}=\sqrt{\frac{1}{2}(\sqrt{x^2+y^2}+x)}+i\mathrm{sgn}(y)\sqrt{\frac{1}{2}(\sqrt{x^2+y^2}-x)},}$$

where sgn(y) = 1 if y ≥ 0 and sgn(y) = −1 otherwise. In particular, the imaginary parts of the original number and the principal value of its square root have the same sign. The real part of the principal value of the square root is always nonnegative.

For example, the principal square roots of ±i are given by:

$${\displaystyle \sqrt{i}=\frac{1+i}{\sqrt{2}},\sqrt{-i}=\frac{1-i}{\sqrt{2}}.}$$

Notes

In the following, the complex z and w may be expressed as:

• ${\displaystyle z=|z|e^{i{\theta }_z}}$
• ${\displaystyle w=|w|e^{i{\theta }_w}}$

where ${\displaystyle -\pi <{\theta }_z\le \pi }$ and ${\displaystyle -\pi <{\theta }_w\le \pi }$.

Because of the discontinuous nature of the square root function in the complex plane, the following laws are not true in general.

• ${\displaystyle \sqrt{zw}=\sqrt{z}\sqrt{w}}$
  Counterexample for the principal square root: z = −1 and w = −1
  This equality is valid only when ${\displaystyle -\pi <{\theta }_z+{\theta }_w\le \pi }$
• ${\displaystyle \frac{\sqrt{w}}{\sqrt{z}}=\sqrt{\frac{w}{z}}}$
  Counterexample for the principal square root: w = 1 and z = −1
  This equality is valid only when ${\displaystyle -\pi <{\theta }_w-{\theta }_z\le \pi }$
• ${\displaystyle \sqrt{z^{\ast }}={\left(\sqrt{z}\right)}^{\ast }}$
  Counterexample for the principal square root: z = −1)
  This equality is valid only when ${\displaystyle {\theta }_z\ne \pi }$

A similar problem appears with other complex functions with branch cuts, e.g., the complex logarithm and the relations logz + logw = log(zw) or log(z^*) = log(z)^* which are not true in general.

Wrongly assuming one of these laws underlies several faulty "proofs", for instance the following one showing that −1 = 1:

$${\displaystyle \begin{array}{rl}-1& =i\cdot i\\ & =\sqrt{-1}\cdot \sqrt{-1}\\ & =\sqrt{\left(-1\right)\cdot \left(-1\right)}\\ & =\sqrt{1}\\ & =1.\end{array}}$$

The third equality cannot be justified (see invalid proof). It can be made to hold by changing the meaning of √ so that this no longer represents the principal square root (see above) but selects a branch for the square root that contains ${\displaystyle \sqrt{1}\cdot \sqrt{-1}.}$ The left-hand side becomes either

$${\displaystyle \sqrt{-1}\cdot \sqrt{-1}=i\cdot i=-1}$$

if the branch includes +i or

$${\displaystyle \sqrt{-1}\cdot \sqrt{-1}=(-i)\cdot (-i)=-1}$$

if the branch includes −i, while the right-hand side becomes

$${\displaystyle \sqrt{\left(-1\right)\cdot \left(-1\right)}=\sqrt{1}=-1,}$$

where the last equality, ${\displaystyle \sqrt{1}=-1,}$ is a consequence of the choice of branch in the redefinition of √.

N-th roots and polynomial roots

The definition of a square root of ${\displaystyle x}$ as a number ${\displaystyle y}$ such that ${\displaystyle y^2=x}$ has been generalized in the following way.

A cube root of ${\displaystyle x}$ is a number ${\displaystyle y}$ such that ${\displaystyle y^3=x}$; it is denoted ${\displaystyle \sqrt[3]{x}.}$

If n is an integer greater than two, a n-th root of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle x} is a number ${\displaystyle y}$ such that ${\displaystyle y^n=x}$; it is denoted ${\displaystyle \sqrt[n]{x}.}$

Given any polynomial p, a root of p is a number y such that p(y) = 0. For example, the nth roots of x are the roots of the polynomial (in y) ${\displaystyle y^n-x.}$

Abel–Ruffini theorem states that, in general, the roots of a polynomial of degree five or higher cannot be expressed in terms of n-th roots.

Square roots of matrices and operators

Main article: Square root of a matrix

See also: Square root of a 2 by 2 matrix

If A is a positive-definite matrix or operator, then there exists precisely one positive definite matrix or operator B with B² = A; we then define A^1/2 = B. In general matrices may have multiple square roots or even an infinitude of them. For example, the 2 × 2 identity matrix has an infinity of square roots, though only one of them is positive definite.

In integral domains, including fields

Each element of an integral domain has no more than 2 square roots. The difference of two squares identity u² − v² = (u − v)(u + v) is proved using the commutativity of multiplication. If u and v are square roots of the same element, then u² − v² = 0. Because there are no zero divisors this implies u = v or u + v = 0, where the latter means that two roots are additive inverses of each other. In other words if an element a square root u of an element a exists, then the only square roots of a are u and −u. The only square root of 0 in an integral domain is 0 itself.

In a field of characteristic 2, an element either has one square root or does not have any at all, because each element is its own additive inverse, so that −u = u. If the field is finite of characteristic 2 then every element has a unique square root. In a field of any other characteristic, any non-zero element either has two square roots, as explained above, or does not have any.

Given an odd prime number p, let q = p^e for some positive integer e. A non-zero element of the field F_q with q elements is a quadratic residue if it has a square root in F_q. Otherwise, it is a quadratic non-residue. There are (q − 1)/2 quadratic residues and (q − 1)/2 quadratic non-residues; zero is not counted in either class. The quadratic residues form a group under multiplication. The properties of quadratic residues are widely used in number theory.

In rings in general

Unlike in an integral domain, a square root in an arbitrary (unital) ring need not be unique up to sign. For example, in the ring ${\displaystyle \mathbb{Z}/8\mathbb{Z}}$ of integers modulo 8 (which is commutative, but has zero divisors), the element 1 has four distinct square roots: ±1 and ±3.

Another example is provided by the ring of quaternions ${\displaystyle \mathbb{H},}$ which has no zero divisors, but is not commutative. Here, the element −1 has infinitely many square roots, including ±i, ±j, and ±k. In fact, the set of square roots of −1 is exactly

$${\displaystyle \{ai+bj+ck\mid a^2+b^2+c^2=1\}.}$$

A square root of 0 is either 0 or a zero divisor. Thus in rings where zero divisors do not exist, it is uniquely 0. However, rings with zero divisors may have multiple square roots of 0. For example, in ${\displaystyle \mathbb{Z}/n^2\mathbb{Z},}$ any multiple of n is a square root of 0.

Geometric construction of the square root

Constructing the length ${\displaystyle x=\sqrt{a}}$, given the ${\displaystyle a}$ and the unit length

The Spiral of Theodorus up to the triangle with a hypotenuse of √4

The square root of a positive number is usually defined as the side length of a square with the area equal to the given number. But the square shape is not necessary for it: if one of two similar planar Euclidean objects has the area a times greater than another, then the ratio of their linear sizes is ${\displaystyle \sqrt{a}}$.

A square root can be constructed with a compass and straightedge. In his Elements, Euclid (fl. 300 BC) gave the construction of the geometric mean of two quantities in two different places: Proposition II.14 and Proposition VI.13. Since the geometric mean of a and b is ${\displaystyle \sqrt{ab}}$, one can construct ${\displaystyle \sqrt{a}}$ simply by taking b = 1.

The construction is also given by Descartes in his La Géométrie, see figure 2 on page 2. However, Descartes made no claim to originality and his audience would have been quite familiar with Euclid.

Euclid's second proof in Book VI depends on the theory of similar triangles. Let AHB be a line segment of length a + b with AH = a and HB = b. Construct the circle with AB as diameter and let C be one of the two intersections of the perpendicular chord at H with the circle and denote the length CH as h. Then, using Thales' theorem and, as in the proof of Pythagoras' theorem by similar triangles, triangle AHC is similar to triangle CHB (as indeed both are to triangle ACB, though we don't need that, but it is the essence of the proof of Pythagoras' theorem) so that AH:CH is as HC:HB, i.e. a/h = h/b, from which we conclude by cross-multiplication that h² = ab, and finally that ${\displaystyle h=\sqrt{ab}}$. When marking the midpoint O of the line segment AB and drawing the radius OC of length (a + b)/2, then clearly OC > CH, i.e. $\frac{a+b}{2}\ge \sqrt{ab}$ (with equality if and only if a = b), which is the arithmetic–geometric mean inequality for two variables and, as noted above, is the basis of the Ancient Greek understanding of "Heron's method".

Another method of geometric construction uses right triangles and induction: ${\displaystyle \sqrt{1}}$ can be constructed, and once ${\displaystyle \sqrt{x}}$ has been constructed, the right triangle with legs 1 and ${\displaystyle \sqrt{x}}$ has a hypotenuse of ${\displaystyle \sqrt{x+1}}$. Constructing successive square roots in this manner yields the Spiral of Theodorus depicted above.

Time perception

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Time_perception

The study of time perception or chronoception is a field within psychology, cognitive linguistics and neuroscience that refers to the subjective experience, or sense, of time, which is measured by someone's own perception of the duration of the indefinite and unfolding of events. The perceived time interval between two successive events is referred to as perceived duration. Though directly experiencing or understanding another person's perception of time is not possible, perception can be objectively studied and inferred through a number of scientific experiments. Some temporal illusions help to expose the underlying neural mechanisms of time perception.

The ancient Greeks recognized the difference between chronological time (chronos) and subjective time (kairos).

Pioneering work on time perception, emphasizing species-specific differences, was conducted by Karl Ernst von Baer.

Theories

Time perception is typically categorized in three distinct ranges, because different ranges of duration are processed in different areas of the brain:

• Sub-second timing or millisecond timing
• Interval timing or seconds-to-minutes timing
• Circadian timing

There are many theories and computational models for time perception mechanisms in the brain. William J. Friedman (1993) contrasted two theories of the sense of time:

• The strength model of time memory. This posits a memory trace that persists over time, by which one might judge the age of a memory (and therefore how long ago the event remembered occurred) from the strength of the trace. This conflicts with the fact that memories of recent events may fade more quickly than more distant memories.
• The inference model suggests the time of an event is inferred from information about relations between the event in question and other events whose date or time is known.

Another hypothesis involves the brain's subconscious tallying of "pulses" during a specific interval, forming a biological stopwatch. This theory proposes that the brain can run multiple biological stopwatches independently depending on the type of tasks being tracked. The source and nature of the pulses is unclear. They are as yet a metaphor whose correspondence to brain anatomy or physiology is unknown.

Philosophical perspectives

Main article: Specious present

The specious present is the time duration wherein a state of consciousness is experienced as being in the present. The term was first introduced by the philosopher E. R. Clay in 1882 (E. Robert Kelly), and was further developed by William James. James defined the specious present to be "the prototype of all conceived times... the short duration of which we are immediately and incessantly sensible". In "Scientific Thought" (1930), C. D. Broad further elaborated on the concept of the specious present and considered that the specious present may be considered as the temporal equivalent of a sensory datum. A version of the concept was used by Edmund Husserl in his works and discussed further by Francisco Varela based on the writings of Husserl, Heidegger, and Merleau-Ponty.

Although the perception of time is not associated with a specific sensory system, psychologists and neuroscientists suggest that humans do have a system, or several complementary systems, governing the perception of time. Time perception is handled by a highly distributed system involving the cerebral cortex, cerebellum and basal ganglia. One particular component, the suprachiasmatic nucleus, is responsible for the circadian (or daily) rhythm, while other cell clusters appear to be capable of shorter (ultradian) timekeeping. There is some evidence that very short (millisecond) durations are processed by dedicated neurons in early sensory parts of the brain.

Warren Meck devised a physiological model for measuring the passage of time. He found the representation of time to be generated by the oscillatory activity of cells in the upper cortex. The frequency of these cells' activity is detected by cells in the dorsal striatum at the base of the forebrain. His model separated explicit timing and implicit timing. Explicit timing is used in estimating the duration of a stimulus. Implicit timing is used to gauge the amount of time separating one from an impending event that is expected to occur in the near future. These two estimations of time do not involve the same neuroanatomical areas. For example, implicit timing often occurs to achieve a motor task, involving the cerebellum, left parietal cortex, and left premotor cortex. Explicit timing often involves the supplementary motor area and the right prefrontal cortex.

Two visual stimuli, inside someone's field of view, can be successfully regarded as simultaneous up to five milliseconds.

In the popular essay "Brain Time", David Eagleman explains that different types of sensory information (auditory, tactile, visual, etc.) are processed at different speeds by different neural architectures. The brain must learn how to overcome these speed disparities if it is to create a temporally unified representation of the external world:

if the visual brain wants to get events correct timewise, it may have only one choice: wait for the slowest information to arrive. To accomplish this, it must wait about a tenth of a second. In the early days of television broadcasting, engineers worried about the problem of keeping audio and video signals synchronized. Then they accidentally discovered that they had around a hundred milliseconds of slop: As long as the signals arrived within this window, viewers' brains would automatically resynchronize the signals. He goes on to say, "This brief waiting period allows the visual system to discount the various delays imposed by the early stages; however, it has the disadvantage of pushing perception into the past. There is a distinct survival advantage to operating as close to the present as possible; an animal does not want to live too far in the past. Therefore, the tenth-of-a-second window may be the smallest delay that allows higher areas of the brain to account for the delays created in the first stages of the system while still operating near the border of the present. This window of delay means that awareness is retroactive, incorporating data from a window of time after an event and delivering a delayed interpretation of what happened."

Experiments have shown that rats can successfully estimate a time interval of approximately 40 seconds, despite having their cortex entirely removed. This suggests that time estimation may be a low-level process.

Ecological perspectives

In recent history, ecologists and psychologists have been interested in whether and how time is perceived by non-human animals, as well as which functional purposes are served by the ability to perceive time. Studies have demonstrated that many species of animals, including both vertebrates and invertebrates, have cognitive abilities that allow them to estimate and compare time intervals and durations in a similar way to humans.

There is empirical evidence that metabolic rate has an impact on animals' ability to perceive time. In general, it is true within and across taxa that animals of smaller size (such as flies), which have a fast metabolic rate, experience time more slowly than animals of larger size, which have a slow metabolic rate. Researchers suppose that this could be the reason why small-bodied animals are generally better at perceiving time on a small scale, and why they are more agile than larger animals.

Time perception in vertebrates

Examples in fish

In a lab experiment, goldfish were conditioned to receive a light stimulus followed shortly by an aversive electric shock, with a constant time interval between the two stimuli. Test subjects showed an increase in general activity around the time of the electric shock. This response persisted in further trials in which the light stimulus was kept but the electric shock was removed. This suggests that goldfish are able to perceive time intervals and to initiate an avoidance response at the time when they expect the distressing stimulus to happen.

In two separate studies, golden shiners and dwarf inangas demonstrated the ability to associate the availability of food sources to specific locations and times of day, called time-place learning. In contrast, when tested for time-place learning based on predation risk, inangas were unable to associate spatiotemporal patterns to the presence or absence of predators.

In June 2022, researchers reported in Physical Review Letters that salamanders were demonstrating counter-intuitive responses to the arrow of time in how their eyes perceived different stimuli.

Examples in birds

When presented with the choice between obtaining food at regular intervals (with a fixed delay between feedings) or at stochastic intervals (with a variable delay between feedings), starlings can discriminate between the two types of intervals and consistently prefer getting food at variable intervals. This is true whether the total amount of food is the same for both options or if the total amount of food is unpredictable in the variable option. This suggests that starlings have an inclination for risk-prone behavior.

Pigeons are able to discriminate between different times of day and show time-place learning. After training, lab subjects were successfully able to peck specific keys at different times of day (morning or afternoon) in exchange for food, even after their sleep/wake cycle was artificially shifted. This suggests that to discriminate between different times of day, pigeons can use an internal timer (or circadian timer) that is independent of external cues. However, a more recent study on time-place learning in pigeons suggests that for a similar task, test subjects will switch to a non-circadian timing mechanism when possible to save energy resources. Experimental tests revealed that pigeons are also able to discriminate between cues of various durations (on the order of seconds), but that they are less accurate when timing auditory cues than when timing visual cues.

Examples in mammals

A study on privately owned dogs revealed that dogs are able to perceive durations ranging from minutes to several hours differently. Dogs reacted with increasing intensity to the return of their owners when they were left alone for longer durations, regardless of the owners' behavior.

After being trained with food reinforcement, female wild boars are able to correctly estimate time intervals of days by asking for food at the end of each interval, but they are unable to accurately estimate time intervals of minutes with the same training method.

When trained with positive reinforcement, rats can learn to respond to a signal of a certain duration, but not to signals of shorter or longer durations, which demonstrates that they can discriminate between different durations. Rats have demonstrated time-place learning, and can also learn to infer correct timing for a specific task by following an order of events, suggesting that they might be able to use an ordinal timing mechanism. Like pigeons, rats are thought to have the ability to use a circadian timing mechanism for discriminating time of day.

Time perception in invertebrates

Forager honey bee flying back to the hive with pollen and nectar

When returning to the hive with nectar, forager honey bees need to know the current ratio of nectar-collecting to nectar-processing rates in the colony. To do so, they estimate the time it takes them to find a food-storer bee, which will unload the forage and store it. The longer it takes them to find one, the busier the food-storer bees are; and therefore the higher the nectar-collecting rate of the colony. Forager bees also assess the quality of nectar by comparing the length of time it takes to unload the forage: a longer unloading time indicates higher quality nectar. They compare their own unloading time to the unloading time of other foragers present in the hive, and adjust their recruiting behavior accordingly. For instance, honey bees reduce the duration of their waggle dance if they judge their own yield to be inferior. Scientists have demonstrated that anesthesia disrupts the circadian clock and impairs the time perception of honey bees, as observed in humans. Experiments revealed that a six-hour-long general anesthesia significantly delayed the start of the foraging behaviour of honeybees if induced during daytime, but not if induced during nighttime.

Bumble bees can be successfully trained to respond to a stimulus after a certain time interval has elapsed (usually several seconds after the start signal). Studies have shown that they can also learn to simultaneously time multiple interval durations.

In a single study, colonies from three species of ants from the genus Myrmica were trained to associate feeding sessions with different times. The trainings lasted several days, where each day the feeding time was delayed by 20 minutes compared to the previous day. In all three species, at the end of the training, most individuals were present at the feeding spot at the correct expected times, suggesting that ants are able to estimate the time running, keep in memory the expected feeding time and to act anticipatively.

Types of temporal illusions

A temporal illusion is a distortion in the perception of time. For example:

• estimating time intervals, e.g., "When did you last see your primary care physician?";
• estimating time duration, e.g., "How long were you waiting at the doctor's office?"; and
• judging the simultaneity of events (see below for examples).

Main types of temporal illusions

• Telescoping effect: People tend to recall recent events as occurring further back in time than they actually did (backward telescoping) and distant events as occurring more recently than they actually did (forward telescoping).
• Vierordt's law: Shorter intervals tend to be overestimated while longer intervals tend to be underestimated
• Time intervals associated with more changes may be perceived as longer than intervals with fewer changes
• Perceived temporal length of a given task may shorten with greater motivation
• Perceived temporal length of a given task may stretch when broken up or interrupted
• Auditory stimuli may appear to last longer than visual stimuli
• Time durations may appear longer with greater stimulus intensity (e.g., auditory loudness or pitch)
• Simultaneity judgments can be manipulated by repeated exposure to non-simultaneous stimuli

Kappa effect

The Kappa effect or perceptual time dilation is a form of temporal illusion verifiable by experiment. The temporal duration between a sequence of consecutive stimuli is thought to be relatively longer or shorter than its actual elapsed time, due to the spatial/auditory/tactile separation between each consecutive stimuli. The kappa effect can be displayed when considering a journey made in two parts that each take an equal amount of time. When mentally comparing these two sub-journeys, the part that covers more distance may appear to take longer than the part covering less distance, even though they take an equal amount of time.

Eye movements and chronostasis

The perception of space and time undergoes distortions during rapid saccadic eye movements. Chronostasis is a type of temporal illusion in which the first impression following the introduction of a new event or task demand to the brain appears to be extended in time. For example, chronostasis temporarily occurs when fixating on a target stimulus, immediately following a saccade (e.g., quick eye movement). This elicits an overestimation in the temporal duration for which that target stimulus (i.e., postsaccadic stimulus) was perceived. This effect can extend apparent durations by up to 500 ms and is consistent with the idea that the visual system models events prior to perception. The most well-known version of this illusion is known as the stopped-clock illusion, wherein a subject's first impression of the second-hand movement of an analog clock, subsequent to one's directed attention (i.e., saccade) to the clock, is the perception of a slower-than-normal second-hand movement rate (the seconds hand of the clock may seemingly temporarily freeze in place after initially looking at it).

The occurrence of chronostasis extends beyond the visual domain into the auditory and tactile domains. In the auditory domain, chronostasis and duration overestimation occur when observing auditory stimuli. One common example is a frequent occurrence when making telephone calls. If, while listening to the phone's dial tone, research subjects move the phone from one ear to the other, the length of time between rings appears longer. In the tactile domain, chronostasis has persisted in research subjects as they reach for and grasp objects. After grasping a new object, subjects overestimate the time in which their hand has been in contact with this object.

Flash-lag effect

Main article: Flash lag illusion

In an experiment, participants were told to stare at an "x" symbol on a computer screen whereby a moving blue doughnut-like ring repeatedly circled the fixed "x" point. Occasionally, the ring would display a white flash for a split second that physically overlapped the ring's interior. However, when asked what was perceived, participants responded that they saw the white flash lagging behind the center of the moving ring. In other words, despite the reality that the two retinal images were actually spatially aligned, the flashed object was usually observed to trail a continuously moving object in space — a phenomenon referred to as the flash-lag effect.

The first proposed explanation, called the "motion extrapolation" hypothesis, is that the visual system extrapolates the position of moving objects but not flashing objects when accounting for neural delays (i.e., the lag time between the retinal image and the observer's perception of the flashing object). The second proposed explanation by David Eagleman and Sejnowski, called the "latency difference" hypothesis, is that the visual system processes moving objects at a faster rate than flashed objects. In the attempt to disprove the first hypothesis, David Eagleman conducted an experiment in which the moving ring suddenly reverses direction to spin in the other way as the flashed object briefly appears. If the first hypothesis were correct, we would expect that, immediately following reversal, the moving object would be observed as lagging behind the flashed object. However, the experiment revealed the opposite — immediately following reversal, the flashed object was observed as lagging behind the moving object. This experimental result supports the "latency difference" hypothesis. A recent study tries to reconcile these different approaches by treating perception as an inference mechanism aiming at describing what is happening at the present time.

Oddball effect

Humans typically overestimate the perceived duration of the initial and final event in a stream of identical events. This oddball effect may serve an evolutionarily adapted "alerting" function and is consistent with reports of time slowing down in threatening situations. The effect seems to be strongest for images that are expanding in size on the retina, in other words, that are "looming" or approaching the viewer, and the effect can be eradicated for oddballs that are contracting or perceived to be receding from the viewer. The effect is also reduced or reversed with a static oddball presented among a stream of expanding stimuli.

Initial studies suggested that this oddball-induced "subjective time dilation" expanded the perceived duration of oddball stimuli by 30–50% but subsequent research has reported more modest expansion of around 10% or less. The direction of the effect, whether the viewer perceives an increase or a decrease in duration, also seems to be dependent upon the stimulus used.

Reversal of temporal order judgment

Numerous experimental findings suggest that temporal order judgments of actions preceding effects can be reversed under special circumstances. Experiments have shown that sensory simultaneity judgments can be manipulated by repeated exposure to non-simultaneous stimuli. In an experiment conducted by David Eagleman, a temporal order judgment reversal was induced in subjects by exposing them to delayed motor consequences. In the experiment, subjects played various forms of video games. Unknown to the subjects, the experimenters introduced a fixed delay between the mouse movements and the subsequent sensory feedback. For example, a subject may not see a movement register on the screen until 150 milliseconds after they had moved the mouse. Participants playing the game quickly adapted to the delay and felt as though there was less delay between their mouse movement and the sensory feedback. Shortly after the experimenters removed the delay, the subjects commonly felt as though the effect on the screen happened just before they commanded it. This work addresses how the perceived timing of effects is modulated by expectations, and the extent to which such predictions are quickly modifiable.

In an experiment conducted by Haggard and colleagues in 2002, participants pressed a button that triggered a flash of light at a distance, after a slight delay of 100 milliseconds. By repeatedly engaging in this act, participants had adapted to the delay (i.e., they experienced a gradual shortening in the perceived time interval between pressing the button and seeing the flash of light). The experimenters then showed the flash of light instantly after the button was pressed. In response, subjects often thought that the flash (the effect) had occurred before the button was pressed (the cause). Additionally, when the experimenters slightly reduced the delay, and shortened the spatial distance between the button and the flash of light, participants had often claimed again to have experienced the effect before the cause.

Several experiments also suggest that temporal order judgment of a pair of tactile stimuli delivered in rapid succession, one to each hand, is noticeably impaired (i.e., misreported) by crossing the hands over the midline. However, congenitally blind subjects showed no trace of temporal order judgment reversal after crossing the arms. These results suggest that tactile signals taken in by the congenitally blind are ordered in time without being referred to a visuospatial representation. Unlike the congenitally blind subjects, the temporal order judgments of the late-onset blind subjects were impaired when crossing the arms to a similar extent as non-blind subjects. These results suggest that the associations between tactile signals and visuospatial representation is maintained once it is accomplished during infancy. Some research studies have also found that the subjects showed reduced deficit in tactile temporal order judgments when the arms were crossed behind their back than when they were crossed in front.

Physiological associations

Tachypsychia

Tachypsychia is a neurological condition that alters the perception of time, usually induced by physical exertion, drug use, or a traumatic event. For someone affected by tachypsychia, time perceived by the individual either lengthens, making events appear to slow down, or contracts, with objects appearing as moving in a speeding blur.

Effects of emotional states

Awe

Research has suggested the feeling of awe has the ability to expand one's perceptions of time availability. Awe can be characterized as an experience of immense perceptual vastness that coincides with an increase in focus. Consequently, it is conceivable that one's temporal perception would slow down when experiencing awe. The perception of time can differ as people choose between savoring moments and deferring gratification.

Fear

Possibly related to the oddball effect, research suggests that time seems to slow down for a person during dangerous events (such as a car accident, a robbery, or when a person perceives a potential predator or mate), or when a person skydives or bungee jumps, where they are capable of complex thoughts in what would normally be the blink of an eye (See Fight-or-flight response). This reported slowing in temporal perception may have been evolutionarily advantageous because it may have enhanced one's ability to intelligibly make quick decisions in moments that were of critical importance to our survival. However, even though observers commonly report that time seems to have moved in slow motion during these events, it is unclear whether this is a function of increased time resolution during the event, or instead an illusion created by the remembering of an emotionally salient event.

A strong time dilation effect has been reported for perception of objects that were looming, but not of those retreating, from the viewer, suggesting that the expanding discs — which mimic an approaching object — elicit self-referential processes which act to signal the presence of a possible danger. Anxious people, or those in great fear, experience greater "time dilation" in response to the same threat stimuli due to higher levels of epinephrine, which increases brain activity (an adrenaline rush). In such circumstances, an illusion of time dilation could assist an effective escape. When exposed to a threat, three-year-old children were observed to exhibit a similar tendency to overestimate elapsed time.

Research suggests that the effect appears only at the point of retrospective assessment, rather than occurring simultaneously with events as they happened. Perceptual abilities were tested during a frightening experience — a free fall — by measuring people's sensitivity to flickering stimuli. The results showed that the subjects' temporal resolution was not improved as the frightening event was occurring. Events appear to have taken longer only in retrospect, possibly because memories were being more densely packed during the frightening situation.

Other researchers suggest that additional variables could lead to a different state of consciousness in which altered time perception does occur during an event. Research does demonstrate that visual sensory processing increases in scenarios involving action preparation. Participants demonstrated a higher detection rate of rapidly presented symbols when preparing to move, as compared to a control without movement.

People shown extracts from films known to induce fear often overestimated the elapsed time of a subsequently presented visual stimulus, whereas people shown emotionally neutral clips (weather forecasts and stock market updates) or those known to evoke feelings of sadness showed no difference. It is argued that fear prompts a state of arousal in the amygdala, which increases the rate of a hypothesized "internal clock". This could be the result of an evolved defensive mechanism triggered by a threatening situation. Individuals experiencing sudden or surprising events, real or imagined (e.g., witnessing a crime, or believing one is seeing a ghost), may overestimate the duration of the event.

Changes with age

Psychologists have found that the subjective perception of the passing of time tends to speed up with increasing age in humans. This often causes people to increasingly underestimate a given interval of time as they age. This fact can likely be attributed to a variety of age-related changes in the aging brain, such as the lowering in dopaminergic levels with older age; however, the details are still being debated.

Very young children will first experience the passing of time when they can subjectively perceive and reflect on the unfolding of a collection of events. A child's awareness of time develops during childhood, when the child's attention and short-term memory capacities form — this developmental process is thought to be dependent on the slow maturation of the prefrontal cortex and hippocampus.

The common explanation is that most external and internal experiences are new for young children but repetitive for adults. Children have to be extremely engaged (i.e. dedicate many neural resources or significant brain power) in the present moment because they must constantly reconfigure their mental models of the world to assimilate it and manage behaviour properly.

Adults, however, may rarely need to step outside mental habits and external routines. When an adult frequently experiences the same stimuli, such stimuli may seem "invisible" as a result of having already been sufficiently mapped by the brain. This phenomenon is known as neural adaptation. Thus, the brain will record fewer densely rich memories during these frequent periods of disengagement from the present moment. Consequently, the subjective perception is often that time passes by at a faster rate with age.

Proportional to the real time

Let S be subjective time, R be real time, and define both to be zero at birth.

One model proposes that the passage of subjective time relative to actual time is inversely proportional to real time:

${\displaystyle \frac{dS}{dR}=\frac{K}{R}}$

When solved, ${\displaystyle S_2-S_1=K(\log R_2-\log R_1)=K\log \left(R_2/R_1\right)}$.

One day would be approximately 1/4,000 of the life of an 11-year-old, but approximately 1/20,000 of the life of a 55-year-old. This helps to explain why a random, ordinary day may therefore appear longer for a young child than an adult. So a year would be experienced by a 55-year-old as passing approximately five times more quickly than a year experienced by an 11-year-old. If long-term time perception is based solely on the proportionality of a person's age, then the following four periods in life would appear to be quantitatively equal: ages 5–10 (1x), ages 10–20 (2x), ages 20–40 (4x), age 40–80 (8x), as the end age is twice the start age. However, this does not work for ages 0–10, which corresponds to ages 10–∞.

Proportional to the subjective time

Lemlich posits that the passage of subjective time relative to actual time is inversely proportional to total subjective time, rather than the total real time:

${\displaystyle \frac{dS}{dR}=\frac{K}{S}}$

When mathematically solved,

${\displaystyle S^2=2KR+C}$

It avoids the issue of infinite subjective time passing from real age 0 to 1 year, as the asymptote can be integrated in an improper integral. Using the initial conditions S = 0 when R = 0 and K > 0,

${\displaystyle S=\sqrt{2KR}}$

${\displaystyle \frac{dS}{dR}=\sqrt{\frac{K}{2R}}}$

This means that time appears to pass in proportion to the square root of the perceiver's real age, rather than directly proportional. Under this model, a 55-year-old would subjectively experience time passing 2+1/4 times more quickly than an 11-year-old, rather than five times under the previous. This means the following periods in life would appear to be quantitatively equal: ages 0–1, 1–4, 4–9, 9–16, 16–25, 25–36, 36–49, 49–64, 64–81, 81–100, 100–121.

In a study, participants consistently provided answers that fit this model when asked about time perception at 1/4 of their age, but were less consistent for 1/2 of their age. Their answers suggest that this model is more accurate than the previous one.

A consequence of this model is that the fraction of subjective life remaining is always less than the fraction of real life remaining, but it is always more than one half of real life remaining. This can be seen for ${\displaystyle 0<S<S_f}$ and ${\displaystyle 0<R<R_f}$:

${\displaystyle \frac{1}{2}\left(1-\frac{R}{R_f}\right)<1-\frac{S}{S_f}<1-\frac{R}{R_f}}$

Effects of drugs on time perception

Stimulants such as thyroxine, caffeine, and amphetamines lead to overestimation of time intervals by both humans and rats, while depressants and anesthetics such as barbiturates and nitrous oxide can have the opposite effect and lead to underestimation of time intervals. The level of activity in the brain of neurotransmitters such as dopamine and norepinephrine may be the reason for this. A research on stimulant-dependent individuals (SDI) showed several abnormal time processing characteristics including larger time differences for effective duration discrimination, and overestimating the duration of a relatively long time interval. Altered time processing and perception in SDI could explain the difficulty SDI have with delaying gratification. Another research studied the dose-dependent effect in methamphetamine dependents with short term abstinence and its effects on time perception. Results shows that motor timing but not perceptual timing, was altered in meth dependents, which persisted for at least three months of abstinence. Dose-dependent effects on time perception were only observed when short-term abstinent meth abusers processed long time intervals. The study concluded that time perception alteration in meth dependents is task specific and dose dependent.

The effect of cannabis on time perception has been studied with inconclusive results mainly due to methodological variations and the paucity of research. Even though 70% of time estimation studies report over-estimation, the findings of time production and time reproduction studies remain inconclusive. Studies show consistently throughout the literature that most cannabis users self-report the experience of a slowed perception of time. In the laboratory, researchers have confirmed the effect of cannabis on the perception of time in both humans and animals. Using PET Scans it was observed that participants who showed a decrease in cerebellar blood flow (CBF) also had a significant alteration in time sense. The relationship between decreased CBF and impaired time sense is of interest as the cerebellum is linked to an internal timing system.

Effects of body temperature

The chemical clock hypothesis implies a causal link between body temperature and the perception of time.

Past work show that increasing body temperature tends to make individuals experience a dilated perception of time and they perceive durations as shorter than they actually were, ultimately leading them to under-estimate time durations. While decreasing body temperature has the opposite effect – causing participants to experience a condensed perception of time leading them to over-estimate time duration – observations of the latter type were rare. Research establishes a parametric effect of body temperature on time perception with higher temperatures generally producing faster subjective time and vice versa. This is especially seen to be true under changes in arousal levels and stressful events.

Applications

Since subjective time is measurable, through information such as heartbeats or actions taken within a time period, there are analytical applications for time perception.

Social networks

Time perception can be used as a tool in social networks to define the subjective experiences of each node within a system. This method can be used to study characters' psychology in dramas, both film and literature, analyzed by social networks. Each character's subjective time may be calculated, with methods as simple as word counting, and compared to the real time of the story to shed light on their internal states.