Butterfly effect

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Butterfly_effect

A plot of Lorenz' strange attractor for values ρ=28, σ = 10, β = 8/3. The butterfly effect or sensitive dependence on initial conditions is the property of a dynamical system that, starting from any of various arbitrarily close alternative initial conditions on the attractor, the iterated points will become arbitrarily spread out from each other.

In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.

The term is closely associated with the work of mathematician and meteorologist Edward Norton Lorenz. He noted that the butterfly effect is derived from the metaphorical example of the details of a tornado (the exact time of formation, the exact path taken) being influenced by minor perturbations such as a distant butterfly flapping its wings several weeks earlier. Lorenz originally used a seagull causing a storm but was persuaded to make it more poetic with the use of a butterfly and tornado by 1972. He discovered the effect when he observed runs of his weather model with initial condition data that were rounded in a seemingly inconsequential manner. He noted that the weather model would fail to reproduce the results of runs with the unrounded initial condition data. A very small change in initial conditions had created a significantly different outcome.

The idea that small causes may have large effects in weather was earlier acknowledged by French mathematician and physicist Henri Poincaré. American mathematician and philosopher Norbert Wiener also contributed to this theory. Lorenz's work placed the concept of instability of the Earth's atmosphere onto a quantitative base and linked the concept of instability to the properties of large classes of dynamic systems which are undergoing nonlinear dynamics and deterministic chaos.

The butterfly effect concept has since been used outside the context of weather science as a broad term for any situation where a small change is supposed to be the cause of larger consequences.

History

See also: Chaos theory § A popular but inaccurate analogy for chaos

In The Vocation of Man (1800), Johann Gottlieb Fichte says "you could not remove a single grain of sand from its place without thereby ... changing something throughout all parts of the immeasurable whole".

Chaos theory and the sensitive dependence on initial conditions were described in numerous forms of literature. This is evidenced by the case of the three-body problem by Poincaré in 1890. He later proposed that such phenomena could be common, for example, in meteorology.

In 1898, Jacques Hadamard noted general divergence of trajectories in spaces of negative curvature. Pierre Duhem discussed the possible general significance of this in 1908.

In 1950, Alan Turing noted: "The displacement of a single electron by a billionth of a centimetre at one moment might make the difference between a man being killed by an avalanche a year later, or escaping."

The idea that the death of one butterfly could eventually have a far-reaching ripple effect on subsequent historical events made its earliest known appearance in "A Sound of Thunder", a 1952 short story by Ray Bradbury. "A Sound of Thunder" features time travel.

More precisely, though, almost the exact idea and the exact phrasing —of a tiny insect's wing affecting the entire atmosphere's winds— was published in a children's book which became extremely successful and well-known globally in 1962, the year before Lorenz published:

"...whatever we do affects everything and everyone else, if even in the tiniest way. Why, when a housefly flaps his wings, a breeze goes round the world."

-- The Princess of Pure Reason

— Norton Juster, The Phantom Tollbooth

In 1961, Lorenz was running a numerical computer model to redo a weather prediction from the middle of the previous run as a shortcut. He entered the initial condition 0.506 from the printout instead of entering the full precision 0.506127 value. The result was a completely different weather scenario.

Lorenz wrote:

At one point I decided to repeat some of the computations in order to examine what was happening in greater detail. I stopped the computer, typed in a line of numbers that it had printed out a while earlier, and set it running again. I went down the hall for a cup of coffee and returned after about an hour, during which time the computer had simulated about two months of weather. The numbers being printed were nothing like the old ones. I immediately suspected a weak vacuum tube or some other computer trouble, which was not uncommon, but before calling for service I decided to see just where the mistake had occurred, knowing that this could speed up the servicing process. Instead of a sudden break, I found that the new values at first repeated the old ones, but soon afterward differed by one and then several units in the last [decimal] place, and then began to differ in the next to the last place and then in the place before that. In fact, the differences more or less steadily doubled in size every four days or so, until all resemblance with the original output disappeared somewhere in the second month. This was enough to tell me what had happened: the numbers that I had typed in were not the exact original numbers, but were the rounded-off values that had appeared in the original printout. The initial round-off errors were the culprits; they were steadily amplifying until they dominated the solution.

— E. N. Lorenz, The Essence of Chaos, U. Washington Press, Seattle (1993), page 134

In 1963, Lorenz published a theoretical study of this effect in a highly cited, seminal paper called Deterministic Nonperiodic Flow (the calculations were performed on a Royal McBee LGP-30 computer). Elsewhere he stated:

One meteorologist remarked that if the theory were correct, one flap of a sea gull's wings would be enough to alter the course of the weather forever. The controversy has not yet been settled, but the most recent evidence seems to favor the sea gulls.

Following proposals from colleagues, in later speeches and papers, Lorenz used the more poetic butterfly. According to Lorenz, when he failed to provide a title for a talk he was to present at the 139th meeting of the American Association for the Advancement of Science in 1972, Philip Merilees concocted Does the flap of a butterfly's wings in Brazil set off a tornado in Texas? as a title. Although a butterfly flapping its wings has remained constant in the expression of this concept, the location of the butterfly, the consequences, and the location of the consequences have varied widely.

The phrase refers to the idea that a butterfly's wings might create tiny changes in the atmosphere that may ultimately alter the path of a tornado or delay, accelerate, or even prevent the occurrence of a tornado in another location. The butterfly does not power or directly create the tornado, but the term is intended to imply that the flap of the butterfly's wings can cause the tornado: in the sense that the flap of the wings is a part of the initial conditions of an interconnected complex web; one set of conditions leads to a tornado, while the other set of conditions doesn't. The flapping wing represents a small change in the initial condition of the system, which cascades to large-scale alterations of events (compare: domino effect). Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different—but it's also equally possible that the set of conditions without the butterfly flapping its wings is the set that leads to a tornado.

The butterfly effect presents an obvious challenge to prediction, since initial conditions for a system such as the weather can never be known to complete accuracy. This problem motivated the development of ensemble forecasting, in which a number of forecasts are made from perturbed initial conditions.

Some scientists have since argued that the weather system is not as sensitive to initial conditions as previously believed. David Orrell argues that the major contributor to weather forecast error is model error, with sensitivity to initial conditions playing a relatively small role. Stephen Wolfram also notes that the Lorenz equations are highly simplified and do not contain terms that represent viscous effects; he believes that these terms would tend to damp out small perturbations. Recent studies using generalized Lorenz models that included additional dissipative terms and nonlinearity suggested that a larger heating parameter is required for the onset of chaos.

While the "butterfly effect" is often explained as being synonymous with sensitive dependence on initial conditions of the kind described by Lorenz in his 1963 paper (and previously observed by Poincaré), the butterfly metaphor was originally applied to work he published in 1969 which took the idea a step further. Lorenz proposed a mathematical model for how tiny motions in the atmosphere scale up to affect larger systems. He found that the systems in that model could only be predicted up to a specific point in the future, and beyond that, reducing the error in the initial conditions would not increase the predictability (as long as the error is not zero). This demonstrated that a deterministic system could be "observationally indistinguishable" from a non-deterministic one in terms of predictability. Recent re-examinations of this paper suggest that it offered a significant challenge to the idea that our universe is deterministic, comparable to the challenges offered by quantum physics.

In the book entitled The Essence of Chaos published in 1993, Lorenz defined butterfly effect as: "The phenomenon that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration." This feature is the same as sensitive dependence of solutions on initial conditions (SDIC) in . In the same book, Lorenz applied the activity of skiing and developed an idealized skiing model for revealing the sensitivity of time-varying paths to initial positions. A predictability horizon is determined before the onset of SDIC.

Illustrations

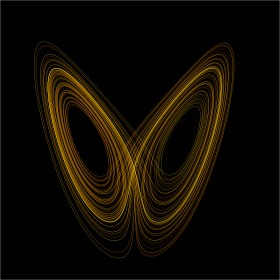
The butterfly effect in the Lorenz attractor
time 0 ≤ t ≤ 30 (larger)		z coordinate (larger)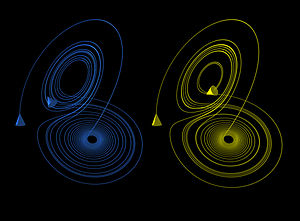
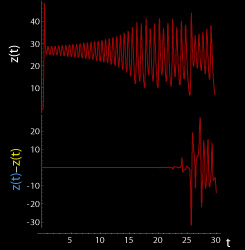
These figures show two segments of the three-dimensional evolution of two trajectories (one in blue, and the other in yellow) for the same period of time in the Lorenz attractor starting at two initial points that differ by only 10−5 in the x-coordinate. Initially, the two trajectories seem coincident, as indicated by the small difference between the z coordinate of the blue and yellow trajectories, but for t > 23 the difference is as large as the value of the trajectory. The final position of the cones indicates that the two trajectories are no longer coincident at t = 30.
An animation of the Lorenz attractor shows the continuous evolution.

Theory and mathematical definition

See also: Chaos theory § Lorenz's pioneering contributions to chaotic modeling

Recurrence, the approximate return of a system toward its initial conditions, together with sensitive dependence on initial conditions, are the two main ingredients for chaotic motion. They have the practical consequence of making complex systems, such as the weather, difficult to predict past a certain time range (approximately a week in the case of weather) since it is impossible to measure the starting atmospheric conditions completely accurately.

A dynamical system displays sensitive dependence on initial conditions if points arbitrarily close together separate over time at an exponential rate. The definition is not topological, but essentially metrical. Lorenz defined sensitive dependence as follows:

The property characterizing an orbit (i.e., a solution) if most other orbits that pass close to it at some point do not remain close to it as time advances.

If M is the state space for the map ${\displaystyle f^t}$, then ${\displaystyle f^t}$ displays sensitive dependence to initial conditions if for any x in M and any δ > 0, there are y in M, with distance d(. , .) such that ${\displaystyle 0<d(x,y)<\delta }$ and such that

${\displaystyle d(f^{\tau }(x),f^{\tau }(y))>{\mathrm{e}}^{a\tau }d(x,y)}$

for some positive parameter a. The definition does not require that all points from a neighborhood separate from the base point x, but it requires one positive Lyapunov exponent. In addition to a positive Lyapunov exponent, boundedness is another major feature within chaotic systems.

The simplest mathematical framework exhibiting sensitive dependence on initial conditions is provided by a particular parametrization of the logistic map:

${\displaystyle x_{n+1}=4x_n(1-x_n),0\le x_0\le 1,}$

which, unlike most chaotic maps, has a closed-form solution:

${\displaystyle x_n={\sin }^2(2^n\theta \pi )}$

where the initial condition parameter ${\displaystyle \theta }$ is given by ${\displaystyle \theta =\frac{1}{\pi }{\sin }^{-1}(x_0^{1/2})}$. For rational ${\displaystyle \theta }$, after a finite number of iterations ${\displaystyle x_n}$ maps into a periodic sequence. But almost all ${\displaystyle \theta }$ are irrational, and, for irrational ${\displaystyle \theta }$, ${\displaystyle x_n}$ never repeats itself – it is non-periodic. This solution equation clearly demonstrates the two key features of chaos – stretching and folding: the factor 2ⁿ shows the exponential growth of stretching, which results in sensitive dependence on initial conditions (the butterfly effect), while the squared sine function keeps ${\displaystyle x_n}$ folded within the range [0, 1].

In physical systems

In weather

Overview

The butterfly effect is most familiar in terms of weather; it can easily be demonstrated in standard weather prediction models, for example. The climate scientists James Annan and William Connolley explain that chaos is important in the development of weather prediction methods; models are sensitive to initial conditions. They add the caveat: "Of course the existence of an unknown butterfly flapping its wings has no direct bearing on weather forecasts, since it will take far too long for such a small perturbation to grow to a significant size, and we have many more immediate uncertainties to worry about. So the direct impact of this phenomenon on weather prediction is often somewhat wrong."

Differentiating types of butterfly effects

The concept of the butterfly effect encompasses several phenomena. The two kinds of butterfly effects, including the sensitive dependence on initial conditions, and the ability of a tiny perturbation to create an organized circulation at large distances, are not exactly the same. A comparison of the two kinds of butterfly effects and the third kind of butterfly effect has been documented. In recent studies, it was reported that both meteorological and non-meteorological linear models have shown that instability plays a role in producing a butterfly effect, which is characterized by brief but significant exponential growth resulting from a small disturbance.

Recent debates on butterfly effects

The first kind of butterfly effect, known as SDIC (Sensitive Dependence on Initial Conditions), is widely recognized and demonstrated through idealized chaotic models. However, opinions differ regarding the second kind of butterfly effect, specifically the impact of a butterfly flapping its wings on tornado formation, as indicated in two 2024 articles. For the third kind of butterfly effect, the limited predictability within the Lorenz 1969 model is explained by scale interactions in one article and by system ill-conditioning in another more recent study.

Finite predictability in chaotic systems

According to Lighthill (1986), the presence of SDIC (commonly known as the butterfly effect) implies that chaotic systems have a finite predictability limit. In a literature review, it was found that Lorenz's perspective on the predictability limit can be condensed into the following statement:

• (A). The Lorenz 1963 model qualitatively revealed the essence of a finite predictability within a chaotic system such as the atmosphere. However, it did not determine a precise limit for the predictability of the atmosphere.
• (B). In the 1960s, the two-week predictability limit was originally estimated based on a doubling time of five days in real-world models. Since then, this finding has been documented in Charney et al. (1966) and has become a consensus.

Recently, a short video has been created to present Lorenz's perspective on predictability limit.

Revised perspectives on chaotic and non-chaotic systems

By revealing coexisting chaotic and non-chaotic attractors within Lorenz models, Shen and his colleagues proposed a revised view that "weather possesses chaos and order", in contrast to the conventional view of "weather is chaotic". As a result, sensitive dependence on initial conditions (SDIC) does not always appear. Namely, SDIC appears when two orbits (i.e., solutions) become the chaotic attractor; it does not appear when two orbits move toward the same point attractor. The above animation for double pendulum motion provides an analogy. For large angles of swing the motion of the pendulum is often chaotic. By comparison, for small angles of swing, motions are non-chaotic. Multistability is defined when a system (e.g., the double pendulum system) contains more than one bounded attractor that depends only on initial conditions. The multistability was illustrated using kayaking in Figure on the right side (i.e., Figure 1 of ) where the appearance of strong currents and a stagnant area suggests instability and local stability, respectively. As a result, when two kayaks move along strong currents, their paths display SDIC. On the other hand, when two kayaks move into a stagnant area, they become trapped, showing no typical SDIC (although a chaotic transient may occur). Such features of SDIC or no SDIC suggest two types of solutions and illustrate the nature of multistability.

By taking into consideration time-varying multistability that is associated with the modulation of large-scale processes (e.g., seasonal forcing) and aggregated feedback of small-scale processes (e.g., convection), the above revised view is refined as follows:

"The atmosphere possesses chaos and order; it includes, as examples, emerging organized systems (such as tornadoes) and time varying forcing from recurrent seasons."

In quantum mechanics

The potential for sensitive dependence on initial conditions (the butterfly effect) has been studied in a number of cases in semiclassical and quantum physics, including atoms in strong fields and the anisotropic Kepler problem. Some authors have argued that extreme (exponential) dependence on initial conditions is not expected in pure quantum treatments; however, the sensitive dependence on initial conditions demonstrated in classical motion is included in the semiclassical treatments developed by Martin Gutzwiller and John B. Delos and co-workers. The random matrix theory and simulations with quantum computers prove that some versions of the butterfly effect in quantum mechanics do not exist.

Other authors suggest that the butterfly effect can be observed in quantum systems. Zbyszek P. Karkuszewski et al. consider the time evolution of quantum systems which have slightly different Hamiltonians. They investigate the level of sensitivity of quantum systems to small changes in their given Hamiltonians. David Poulin et al. presented a quantum algorithm to measure fidelity decay, which "measures the rate at which identical initial states diverge when subjected to slightly different dynamics". They consider fidelity decay to be "the closest quantum analog to the (purely classical) butterfly effect". Whereas the classical butterfly effect considers the effect of a small change in the position and/or velocity of an object in a given Hamiltonian system, the quantum butterfly effect considers the effect of a small change in the Hamiltonian system with a given initial position and velocity. This quantum butterfly effect has been demonstrated experimentally. Quantum and semiclassical treatments of system sensitivity to initial conditions are known as quantum chaos.

In popular culture

Main article: Butterfly effect in popular culture

The butterfly affect has appeared across mediums such as literature (for instance, A Sound of Thunder), films and television (such as The Simpsons), video games (such as Life Is Strange), AI-driven expansive language models, and more.

Catastrophe theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Catastrophe_theory

In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry.

Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analysing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, for example the unpredictable timing and magnitude of a landslide.

Catastrophe theory originated with the work of the French mathematician René Thom in the 1960s, and became very popular due to the efforts of Christopher Zeeman in the 1970s. It considers the special case where the long-run stable equilibrium can be identified as the minimum of a smooth, well-defined potential function (Lyapunov function). Small changes in certain parameters of a nonlinear system can cause equilibria to appear or disappear, or to change from attracting to repelling and vice versa, leading to large and sudden changes of the behaviour of the system. However, examined in a larger parameter space, catastrophe theory reveals that such bifurcation points tend to occur as part of well-defined qualitative geometrical structures.

In the late 1970s, applications of catastrophe theory to areas outside its scope began to be criticized, especially in biology and social sciences. Zahler and Sussmann, in a 1977 article in Nature, referred to such applications as being "characterised by incorrect reasoning, far-fetched assumptions, erroneous consequences, and exaggerated claims". As a result, catastrophe theory has become less popular in applications.

Elementary catastrophes

Catastrophe theory analyzes degenerate critical points of the potential function — points where not just the first derivative, but one or more higher derivatives of the potential function are also zero. These are called the germs of the catastrophe geometries. The degeneracy of these critical points can be unfolded by expanding the potential function as a Taylor series in small perturbations of the parameters.

When the degenerate points are not merely accidental, but are structurally stable, the degenerate points exist as organising centres for particular geometric structures of lower degeneracy, with critical features in the parameter space around them. If the potential function depends on two or fewer active variables, and four or fewer active parameters, then there are only seven generic structures for these bifurcation geometries, with corresponding standard forms into which the Taylor series around the catastrophe germs can be transformed by diffeomorphism (a smooth transformation whose inverse is also smooth). These seven fundamental types are now presented, with the names that Thom gave them.

Potential functions of one active variable

Catastrophe theory studies dynamical systems that describe the evolution of a state variable ${\displaystyle x}$ over time ${\displaystyle t}$:

${\displaystyle \dot{x}={\displaystyle \frac{dx}{dt}}=-{\displaystyle \frac{dV(u,x)}{dx}}}$

In the above equation, ${\displaystyle V}$ is referred to as the potential function, and ${\displaystyle u}$ is often a vector or a scalar which parameterise the potential function. The value of ${\displaystyle u}$ may change over time, and it can also be referred to as the control variable. In the following examples, parameters like ${\displaystyle a,b}$ are such controls.

Fold catastrophe

Fold catastrophe, with surface ${\displaystyle z=-y^2-0.1x^4}$.

Stable and unstable pair of extrema disappear at a fold bifurcation

${\displaystyle V=x^3+ax}$

When a < 0, the potential V has two extrema - one stable, and one unstable. If the parameter a is slowly increased, the system can follow the stable minimum point. But at a = 0 the stable and unstable extrema meet, and annihilate. This is the bifurcation point. At a > 0 there is no longer a stable solution. If a physical system is followed through a fold bifurcation, one therefore finds that as a reaches 0, the stability of the a < 0 solution is suddenly lost, and the system will make a sudden transition to a new, very different behaviour. This bifurcation value of the parameter a is sometimes called the "tipping point".

Cusp catastrophe

Diagram of cusp catastrophe, showing curves (brown, red) of x satisfying dV/dx = 0 for parameters (a,b), drawn for parameter b continuously varied, for several values of parameter a. Outside the cusp locus of bifurcations (blue), for each point (a,b) in parameter space there is only one extremising value of x. Inside the cusp, there are two different values of x giving local minima of V(x) for each (a,b), separated by a value of x giving a local maximum.

Cusp shape in parameter space (a,b) near the catastrophe point, showing the locus of fold bifurcations separating the region with two stable solutions from the region with one.

Pitchfork bifurcation at a = 0 on the surface b = 0

Cusp catastrophe, with surface ${\displaystyle z=-0.1(x^4+y^4)-y^3+xy}$.

${\displaystyle V=x^4+a{x}^2+bx}$

The cusp geometry is very common when one explores what happens to a fold bifurcation if a second parameter, b, is added to the control space. Varying the parameters, one finds that there is now a curve (blue) of points in (a,b) space where stability is lost, where the stable solution will suddenly jump to an alternate outcome.

But in a cusp geometry the bifurcation curve loops back on itself, giving a second branch where this alternate solution itself loses stability, and will make a jump back to the original solution set. By repeatedly increasing b and then decreasing it, one can therefore observe hysteresis loops, as the system alternately follows one solution, jumps to the other, follows the other back, and then jumps back to the first.

However, this is only possible in the region of parameter space a < 0. As a is increased, the hysteresis loops become smaller and smaller, until above a = 0 they disappear altogether (the cusp catastrophe), and there is only one stable solution.

One can also consider what happens if one holds b constant and varies a. In the symmetrical case b = 0, one observes a pitchfork bifurcation as a is reduced, with one stable solution suddenly splitting into two stable solutions and one unstable solution as the physical system passes to a < 0 through the cusp point (0,0) (an example of spontaneous symmetry breaking). Away from the cusp point, there is no sudden change in a physical solution being followed: when passing through the curve of fold bifurcations, all that happens is an alternate second solution becomes available.

A famous suggestion is that the cusp catastrophe can be used to model the behaviour of a stressed dog, which may respond by becoming cowed or becoming angry. The suggestion is that at moderate stress (a > 0), the dog will exhibit a smooth transition of response from cowed to angry, depending on how it is provoked. But higher stress levels correspond to moving to the region (a < 0). Then, if the dog starts cowed, it will remain cowed as it is irritated more and more, until it reaches the 'fold' point, when it will suddenly, discontinuously snap through to angry mode. Once in 'angry' mode, it will remain angry, even if the direct irritation parameter is considerably reduced.

A simple mechanical system, the "Zeeman Catastrophe Machine", nicely illustrates a cusp catastrophe. In this device, smooth variations in the position of the end of a spring can cause sudden changes in the rotational position of an attached wheel.

Catastrophic failure of a complex system with parallel redundancy can be evaluated based on the relationship between local and external stresses. The model of the structural fracture mechanics is similar to the cusp catastrophe behavior. The model predicts reserve ability of a complex system.

Other applications include the outer sphere electron transfer frequently encountered in chemical and biological systems, modelling the dynamics of cloud condensation nuclei in the atmosphere, and modelling real estate prices.

Fold bifurcations and the cusp geometry are by far the most important practical consequences of catastrophe theory. They are patterns which reoccur again and again in physics, engineering and mathematical modelling. They produce the strong gravitational lensing events and provide astronomers with one of the methods used for detecting black holes and the dark matter of the universe, via the phenomenon of gravitational lensing producing multiple images of distant quasars.

The remaining simple catastrophe geometries are very specialised in comparison, and presented here only for curiosity value.

Swallowtail catastrophe

Swallowtail catastrophe, with surface ${\displaystyle z=-y^4-0.1x^4+(1-x^2)y^2+0.4xy}$

Swallowtail catastrophe surface

${\displaystyle V=x^5+a{x}^3+b{x}^2+cx}$

The control parameter space is three-dimensional. The bifurcation set in parameter space is made up of three surfaces of fold bifurcations, which meet in two lines of cusp bifurcations, which in turn meet at a single swallowtail bifurcation point.

As the parameters go through the surface of fold bifurcations, one minimum and one maximum of the potential function disappear. At the cusp bifurcations, two minima and one maximum are replaced by one minimum; beyond them the fold bifurcations disappear. At the swallowtail point, two minima and two maxima all meet at a single value of x. For values of a > 0, beyond the swallowtail, there is either one maximum-minimum pair, or none at all, depending on the values of b and c. Two of the surfaces of fold bifurcations, and the two lines of cusp bifurcations where they meet for a < 0, therefore disappear at the swallowtail point, to be replaced with only a single surface of fold bifurcations remaining. Salvador Dalí's last painting, The Swallow's Tail, was based on this catastrophe.

Butterfly catastrophe

Butterfly catastrophe, with surface ${\displaystyle z=-20x^5+4x^3-2xy-0.5(x^4+y^4)}$.

${\displaystyle V=x^6+a{x}^4+b{x}^3+c{x}^2+dx}$

Depending on the parameter values, the potential function may have three, two, or one different local minima, separated by the loci of fold bifurcations. At the butterfly point, the different 3-surfaces of fold bifurcations, the 2-surfaces of cusp bifurcations, and the lines of swallowtail bifurcations all meet up and disappear, leaving a single cusp structure remaining when a > 0.

Potential functions of two active variables

A surface with a hyperbolic umbilic and its focal surface. The hyperbolic umbilic catastrophe is just the upper part of this image.

A surface with an elliptical umbilic, and its focal surface. The elliptic umbilic catastrophe is just the upper part of this image.

Umbilic catastrophes are examples of corank 2 catastrophes. They can be observed in optics in the focal surfaces created by light reflecting off a surface in three dimensions and are intimately connected with the geometry of nearly spherical surfaces: umbilical point. Thom proposed that the hyperbolic umbilic catastrophe modeled the breaking of a wave and the elliptical umbilic modeled the creation of hair-like structures.

Hyperbolic umbilic catastrophe

${\displaystyle V=x^3+y^3+axy+bx+cy}$

Elliptic umbilic catastrophe

${\displaystyle V=\frac{x^3}{3}-x{y}^2+a(x^2+y^2)+bx+cy}$

Parabolic umbilic catastrophe

${\displaystyle V=x^{2}y+y^4+a{x}^2+b{y}^{2}78+cx+dy}$

Arnold's notation

Vladimir Arnold gave the catastrophes the ADE classification, due to a deep connection with simple Lie groups. 

• A₀ - a non-singular point: ${\displaystyle V=x}$.
• A₁ - a local extremum, either a stable minimum or unstable maximum ${\displaystyle V=\pm x^2+ax}$.
• A₂ - the fold
• A₃ - the cusp
• A₄ - the swallowtail
• A₅ - the butterfly
• A_k - a representative of an infinite sequence of one variable forms ${\displaystyle V=x^{k+1}+\cdots }$
• D₄⁻ - the elliptical umbilic
• D₄⁺ - the hyperbolic umbilic
• D₅ - the parabolic umbilic
• D_k - a representative of an infinite sequence of further umbilic forms
• E₆ - the symbolic umbilic ${\displaystyle V=x^3+y^4+ax{y}^2+bxy+cx+dy+e{y}^2}$
• E₇
• E₈

There are objects in singularity theory which correspond to most of the other simple Lie groups.

Optics

The edge of the rainbow is a fold catastrophe, and so it has a diffraction pattern described by the Airy function. This is generic and stable for any shape of the water droplet.

As predicted by catastrophe theory, singularities are generic, and stable under perturbation. This explains how the bright lines and surfaces are stable under perturbation. The caustics one sees at the bottom of a swimming pool, for example, have a distinctive texture and only has a few types of singular points, even though the surface of the water is ever changing.

The edge of the rainbow, for example, has a fold catastrophe. Due to the wave nature of light, the catastrophe has fine diffraction details described by the Airy function. This is a generic result and does not depend on the precise shape of the water droplet, and so the edge of the rainbow always has the shape of an Airy function. The same Airy function fold catastrophe can be seen in nuclear-nuclear scattering ("nuclear rainbow").

The cusp catastrophe is the next-simplest to observe. Due to the wave nature of light, the catastrophe has fine diffraction details described by the Pearcey function. Higher-order catastrophes, such as the swallowtail and the butterfly, have also been observed.

Punctuated equilibrium

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Richard_Dawkins_bibliography

The punctuated equilibrium model (top) consists of morphological stability followed by rare bursts of evolutionary change via rapid cladogenesis – vertical equilibrium states separated by horizontal "jump" phases. In contrast, phyletic gradualism (below), is a more gradual, continuous model of evolution – with accumulation of small incremental changes represented by slanted bars that split at branch-points, where two separate modes of life are feasible but of which, each prospers best with divergent specializations.

In evolutionary biology, punctuated equilibrium (also called punctuated equilibria) is a theory that proposes that once a species appears in the fossil record, the population will become stable, showing little evolutionary change for most of its geological history. This state of little or no morphological change is called stasis. When significant evolutionary change occurs, the theory proposes that it is generally restricted to rare and geologically rapid events of branching speciation called cladogenesis. Cladogenesis is the process by which a species splits into two distinct species, rather than one species gradually transforming into another.

Punctuated equilibrium is commonly contrasted with phyletic gradualism, the idea that evolution generally occurs uniformly by the steady and gradual transformation of whole lineages (anagenesis).

In 1972, paleontologists Niles Eldredge and Stephen Jay Gould published a landmark paper developing their theory and called it punctuated equilibria. Their paper built upon Ernst Mayr's model of geographic speciation, I. M. Lerner's theories of developmental and genetic homeostasis, and their own empirical research. Eldredge and Gould proposed that the degree of gradualism commonly attributed to Charles Darwin is virtually nonexistent in the fossil record, and that stasis dominates the history of most fossil species.

History

Punctuated equilibrium originated as a logical consequence of Ernst Mayr's concept of genetic revolutions by allopatric and especially peripatric speciation as applied to the fossil record. Although the sudden appearance of species and its relationship to speciation was proposed and identified by Mayr in 1954, historians of science generally recognize the 1972 Eldredge and Gould paper as the basis of the new paleobiological research program. Punctuated equilibrium differs from Mayr's ideas mainly in that Eldredge and Gould placed considerably greater emphasis on stasis, whereas Mayr was concerned with explaining the morphological discontinuity (or "sudden jumps") found in the fossil record. Mayr later complimented Eldredge and Gould's paper, stating that evolutionary stasis had been "unexpected by most evolutionary biologists" and that punctuated equilibrium "had a major impact on paleontology and evolutionary biology."

A year before their 1972 Eldredge and Gould paper, Niles Eldredge published a paper in the journal Evolution which suggested that gradual evolution was seldom seen in the fossil record and argued that Ernst Mayr's standard mechanism of allopatric speciation might suggest a possible resolution.

The Eldredge and Gould paper was presented at the Annual Meeting of the Geological Society of America in 1971. The symposium focused its attention on how modern microevolutionary studies could revitalize various aspects of paleontology and macroevolution. Tom Schopf, who organized that year's meeting, assigned Gould the topic of speciation. Gould recalls that "Eldredge's 1971 publication [on Paleozoic trilobites] had presented the only new and interesting ideas on the paleontological implications of the subject—so I asked Schopf if we could present the paper jointly." According to Gould "the ideas came mostly from Niles, with yours truly acting as a sounding board and eventual scribe. I coined the term punctuated equilibrium and wrote most of our 1972 paper, but Niles is the proper first author in our pairing of Eldredge and Gould." In his book Time Frames Eldredge recalls that after much discussion the pair "each wrote roughly half. Some of the parts that would seem obviously the work of one of us were actually first penned by the other—I remember for example, writing the section on Gould's snails. Other parts are harder to reconstruct. Gould edited the entire manuscript for better consistency. We sent it in, and Schopf reacted strongly against it—thus signaling the tenor of the reaction it has engendered, though for shifting reasons, down to the present day."

John Wilkins and Gareth Nelson have argued that French architect Pierre Trémaux proposed an "anticipation of the theory of punctuated equilibrium of Gould and Eldredge."

Evidence from the fossil record

Main article: Rate of evolution

The fossil record includes well documented examples of both phyletic gradualism and punctuational evolution. As such, much debate persists over the prominence of stasis in the fossil record. Before punctuated equilibrium, most evolution biologists considered stasis to be rare or unimportant. The paleontologist George Gaylord Simpson, for example, believed that phyletic gradual evolution (called horotely in his terminology) comprised 90% of evolution. More modern studies, including a meta-analysis examining 58 published studies on speciation patterns in the fossil record showed that 71% of species exhibited stasis, and 63% were associated with punctuated patterns of evolutionary change. According to Michael Benton, "it seems clear then that stasis is common, and that had not been predicted from modern genetic studies." A paramount example of evolutionary stasis is the fern Osmunda claytoniana. Based on paleontological evidence it has remained unchanged, even at the level of fossilized nuclei and chromosomes, for at least 180 million years.

Theoretical mechanisms

Punctuational change

When Eldredge and Gould published their 1972 paper, allopatric speciation was considered the "standard" model of speciation. This model was popularized by Ernst Mayr in his 1954 paper "Change of genetic environment and evolution," and his classic volume Animal Species and Evolution (1963).

Allopatric speciation suggests that species with large central populations are stabilized by their large volume and the process of gene flow. New and even beneficial mutations are diluted by the population's large size and are unable to reach fixation, due to such factors as constantly changing environments. If this is the case, then the transformation of whole lineages should be rare, as the fossil record indicates. Smaller populations on the other hand, which are isolated from the parental stock, are decoupled from the homogenizing effects of gene flow. In addition, pressure from natural selection is especially intense, as peripheral isolated populations exist at the outer edges of ecological tolerance. If most evolution happens in these rare instances of allopatric speciation then evidence of gradual evolution in the fossil record should be rare. This hypothesis was alluded to by Mayr in the closing paragraph of his 1954 paper:

Rapidly evolving peripherally isolated populations may be the place of origin of many evolutionary novelties. Their isolation and comparatively small size may explain phenomena of rapid evolution and lack of documentation in the fossil record, hitherto puzzling to the palaeontologist.

Although punctuated equilibrium generally applies to sexually reproducing organisms, some biologists have applied the model to non-sexual species like viruses, which cannot be stabilized by conventional gene flow. As time went on biologists like Gould moved away from wedding punctuated equilibrium to allopatric speciation, particularly as evidence accumulated in support of other modes of speciation. Gould, for example, was particularly attracted to Douglas Futuyma's work on the importance of reproductive isolating mechanisms.

Stasis

Many hypotheses have been proposed to explain the putative causes of stasis. Gould was initially attracted to I. Michael Lerner's theories of developmental and genetic homeostasis. However this hypothesis was rejected over time, as evidence accumulated against it. Other plausible mechanisms which have been suggested include: habitat tracking, stabilizing selection, the Stenseth-Maynard Smith stability hypothesis, constraints imposed by the nature of subdivided populations, normalizing clade selection, and koinophilia.

Evidence for stasis has also been corroborated from the genetics of sibling species, species which are morphologically indistinguishable, but whose proteins have diverged sufficiently to suggest they have been separated for millions of years. Fossil evidence of reproductively isolated extant species of sympatric Olive Shells (Amalda sp.) also confirm morphological stasis in multiple lineages over three million years.

According to Gould, "stasis may emerge as the theory's most important contribution to evolutionary science." Philosopher Kim Sterelny in clarifying the meaning of stasis adds, "In claiming that species typically undergo no further evolutionary change once speciation is complete, they are not claiming that there is no change at all between one generation and the next. Lineages do change. But the change between generations does not accumulate. Instead, over time, the species wobbles about its phenotypic mean. Jonathan Weiner's The Beak of the Finch describes this very process."

Hierarchical evolution

Punctuated equilibrium has also been cited as contributing to the hypothesis that species are Darwinian individuals, and not just classes, thereby providing a stronger framework for a hierarchical theory of evolution.

Common misconceptions

Much confusion has arisen over what proponents of punctuated equilibrium actually argued, what mechanisms they advocated, how fast the punctuations were, what taxonomic scale their theory applied to, how revolutionary their claims were intended to be, and how punctuated equilibrium related to other ideas like saltationism, quantum evolution, and mass extinction.

Saltationism

Alternative explanations for the punctuated pattern of evolution observed in the fossil record. Both macromutation and seemingly "rapid" episodes of gradual evolution could give the appearance of instantaneous change, since 10,000 years seldom registers in the geological record.

The punctuational nature of punctuated equilibrium has engendered perhaps the most confusion over Eldredge and Gould's theory. Gould's sympathetic treatment of Richard Goldschmidt, the controversial geneticist who advocated the idea of "hopeful monsters," led some biologists to conclude that Gould's punctuations were occurring in single-generation jumps. This interpretation has frequently been used by creationists to characterize the weakness of the paleontological record, and to portray contemporary evolutionary biology as advancing neo-saltationism.

In an often quoted remark, Gould stated,

"Since we proposed punctuated equilibria to explain trends, it is infuriating to be quoted again and again by creationists – whether through design or stupidity, I do not know – as admitting that the fossil record includes no transitional forms. Transitional forms are generally lacking at the species level, but they are abundant between larger groups."

Although there exist some debate over how long the punctuations last, supporters of punctuated equilibrium generally place the figure between 50,000 and 100,000 years.

Quantum evolution

Quantum evolution was a controversial hypothesis advanced by Columbia University paleontologist George Gaylord Simpson, regarded by Gould as "the greatest and most biologically astute paleontologist of the twentieth century." Simpson's conjecture was that according to the geological record, on very rare occasions evolution would proceed very rapidly to form entirely new families, orders, and classes of organisms. This hypothesis differs from punctuated equilibrium in several respects. First, punctuated equilibrium was more modest in scope, in that it was addressing evolution specifically at the species level. Simpson's idea was principally concerned with evolution at higher taxonomic groups. Second, Eldredge and Gould relied upon a different mechanism. Where Simpson relied upon a synergistic interaction between genetic drift and a shift in the adaptive fitness landscape, Eldredge and Gould relied upon ordinary speciation, particularly Ernst Mayr's concept of allopatric speciation. Lastly, and perhaps most significantly, quantum evolution took no position on the issue of stasis. Although Simpson acknowledged the existence of stasis in what he called the bradytelic mode, he considered it (along with rapid evolution) to be unimportant in the larger scope of evolution. In his Major Features of Evolution Simpson stated, "Evolutionary change is so nearly the universal rule that a state of motion is, figuratively, normal in evolving populations. The state of rest, as in bradytely, is the exception and it seems that some restraint or force must be required to maintain it." Despite such differences between the two models, earlier critiques—from such eminent commentators as Sewall Wright as well as Simpson himself—have argued that punctuated equilibrium is little more than quantum evolution relabeled.

Multiple meanings of gradualism

Punctuated equilibrium is often portrayed to oppose the concept of gradualism, when it is actually a form of gradualism. This is because even though evolutionary change appears instantaneous between geological sedimentary layers, change is still occurring incrementally, with no great change from one generation to the next. To this end, Gould later commented that "Most of our paleontological colleagues missed this insight because they had not studied evolutionary theory and either did not know about allopatric speciation or had not considered its translation to geological time. Our evolutionary colleagues also failed to grasp the implication(s), primarily because they did not think at geological scales".

Richard Dawkins dedicates a chapter in The Blind Watchmaker to correcting, in his view, the wide confusion regarding rates of change. His first point is to argue that phyletic gradualism—understood in the sense that evolution proceeds at a single uniform speed, called "constant speedism" by Dawkins—is a "caricature of Darwinism" and "does not really exist". His second argument, which follows from the first, is that once the caricature of "constant speedism" is dismissed, we are left with one logical alternative, which Dawkins terms "variable speedism". Variable speedism may also be distinguished one of two ways: "discrete variable speedism" and "continuously variable speedism". Eldredge and Gould, proposing that evolution jumps between stability and relative rapidity, are described as "discrete variable speedists", and "in this respect they are genuinely radical." They assert that evolution generally proceeds in bursts, or not at all. "Continuously variable speedists", on the other hand, advance that "evolutionary rates fluctuate continuously from very fast to very slow and stop, with all intermediates. They see no particular reason to emphasize certain speeds more than others. In particular, stasis, to them, is just an extreme case of ultra-slow evolution. To a punctuationist, there is something very special about stasis."

Criticism

See also: Species problem, Species complex, and Push of the past

Richard Dawkins regards the apparent gaps represented in the fossil record as documenting migratory events rather than evolutionary events. According to Dawkins, evolution certainly occurred but "probably gradually" elsewhere. However, the punctuational equilibrium model may still be inferred from both the observation of stasis and examples of rapid and episodic speciation events documented in the fossil record.

Dawkins also emphasizes that punctuated equilibrium has been "oversold by some journalists", but partly due to Eldredge and Gould's "later writings". Dawkins contends that the hypothesis "does not deserve a particularly large measure of publicity". It is a "minor gloss," an "interesting but minor wrinkle on the surface of neo-Darwinian theory," and "lies firmly within the neo-Darwinian synthesis".

In his book Darwin's Dangerous Idea, philosopher Daniel Dennett is especially critical of Gould's presentation of punctuated equilibrium. Dennett argues that Gould alternated between revolutionary and conservative claims, and that each time Gould made a revolutionary statement—or appeared to do so—he was criticized, and thus retreated to a traditional neo-Darwinian position. Gould responded to Dennett's claims in The New York Review of Books, and in his technical volume The Structure of Evolutionary Theory.

English professor Heidi Scott argues that Gould's talent for writing vivid prose, his use of metaphor, and his success in building a popular audience of nonspecialist readers altered the "climate of specialized scientific discourse" favorably in his promotion of punctuated equilibrium. While Gould is celebrated for the color and energy of his prose, as well as his interdisciplinary knowledge, critics such as Scott, Richard Dawkins, and Daniel Dennett have concerns that the theory has gained undeserved credence among non-scientists because of Gould's rhetorical skills. Philosopher John Lyne and biologist Henry Howe believed punctuated equilibrium's success has much more to do with the nature of the geological record than the nature of Gould's rhetoric. They state, a "re-analysis of existing fossil data has shown, to the increasing satisfaction of the paleontological community, that Eldredge and Gould were correct in identifying periods of evolutionary stasis which are interrupted by much shorter periods of evolutionary change."

Evolutionary biologist Robert Trivers accused Gould of being "something of an intellectual fraud" for using claims that were "well known from the time of Darwin" (that evolution displayed "periods of long stasis interspersed with periods of rapid change") to support distinct but more "grandiose" claims regarding species selection, despite the "rate of species turnover [having] nothing to do with the traits within species—only with the relative frequency of species showing these traits".

Some critics jokingly referred to the theory of punctuated equilibrium as "evolution by jerks", which reportedly prompted punctuationists to describe phyletic gradualism as "evolution by creeps."

Darwin's theory

The sudden appearance of most species in the geologic record and the lack of evidence of substantial gradual change in most species—from their initial appearance until their extinction—has long been noted, including by Charles Darwin, who appealed to the imperfection of the record as the favored explanation. When presenting his ideas against the prevailing influences of catastrophism and progressive creationism, which envisaged species being supernaturally created at intervals, Darwin needed to forcefully stress the gradual nature of evolution in accordance with the gradualism promoted by his friend Charles Lyell. He privately expressed concern, noting in the margin of his 1844 Essay, "Better begin with this: If species really, after catastrophes, created in showers world over, my theory false."

It is often incorrectly assumed that he insisted that the rate of change must be constant, or nearly so, but even the first edition of On the Origin of Species states that "Species of different genera and classes have not changed at the same rate, or in the same degree. In the oldest tertiary beds a few living shells may still be found in the midst of a multitude of extinct forms... The Silurian Lingula differs but little from the living species of this genus". Lingula is among the few brachiopods surviving today but also known from fossils over 500 million years old. In the fourth edition (1866) of On the Origin of Species Darwin wrote that "the periods during which species have undergone modification, though long as measured in years, have probably been short in comparison with the periods during which they retain the same form." Thus punctuationism in general is consistent with Darwin's conception of evolution.

According to early versions of punctuated equilibrium, "peripheral isolates" are considered to be of critical importance for speciation. However, Darwin wrote, "I can by no means agree ... that immigration and isolation are necessary elements. ... Although isolation is of great importance in the production of new species, on the whole I am inclined to believe that largeness of area is still more important, especially for the production of species which shall prove capable of enduring for a long period, and of spreading widely."

The importance of isolation in forming species had played a significant part in Darwin's early thinking, as shown in his Essay of 1844. But by the time he wrote the Origin he had downplayed its importance. He explained the reasons for his revised view as follows:

Throughout a great and open area, not only will there be a greater chance of favourable variations, arising from the large number of individuals of the same species there supported, but the conditions of life are much more complex from the large number of already existing species; and if some of these species become modified and improved, others will have to be improved in a corresponding degree, or they will be exterminated. Each new form, also, as soon as it has been improved, will be able to spread over the open and continuous area, and will thus come into competition with many other forms ... the new forms produced on large areas, which have already been victorious over many competitors, will be those that will spread most widely, and will give rise to the greatest number of new varieties and species. They will thus play a more important role in the changing history of the organic world.

Thus punctuated equilibrium is incongruous with some of Darwin's ideas regarding the specific mechanisms of evolution, but generally accords with Darwin's theory of evolution by natural selection.

Supplemental modes of rapid evolution

See also: Rapid modes of evolution

Recent work in developmental biology has identified dynamical and physical mechanisms of tissue morphogenesis that may underlie abrupt morphological transitions during evolution. Consequently, consideration of mechanisms of phylogenetic change that have been found in reality to be non-gradual is increasingly common in the field of evolutionary developmental biology, particularly in studies of the origin of morphological novelty. A description of such mechanisms can be found in the multi-authored volume Origination of Organismal Form (MIT Press; 2003).

Language change

See also: Language change

In linguistics, R. M. W. Dixon has proposed a punctuated equilibrium model for language histories, with reference particularly to the prehistory of the indigenous languages of Australia and his objections to the proposed Pama–Nyungan language family there. Although his model has raised considerable interest, it does not command majority support within linguistics.

Separately, recent work using computational phylogenetic methods claims to show that punctuational bursts play an important factor when languages split from one another, accounting for anywhere from 10 to 33% of the total divergence in vocabulary.

Mythology

Punctuational evolution has been argued to explain changes in folktales and mythology over time.