Molecular orbital theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Molecular_orbital_theory 

 

See also: Molecular orbital

In chemistry, molecular orbital theory (MO theory or MOT) is a method for describing the electronic structure of molecules using quantum mechanics. It was proposed early in the 20th century.

In molecular orbital theory, electrons in a molecule are not assigned to individual chemical bonds between atoms, but are treated as moving under the influence of the atomic nuclei in the whole molecule. Quantum mechanics describes the spatial and energetic properties of electrons as molecular orbitals that surround two or more atoms in a molecule and contain valence electrons between atoms.

Molecular orbital theory revolutionized the study of chemical bonding by approximating the states of bonded electrons—the molecular orbitals—as linear combinations of atomic orbitals (LCAO). These approximations are made by applying the density functional theory (DFT) or Hartree–Fock (HF) models to the Schrödinger equation.

Molecular orbital theory and valence bond theory are the foundational theories of quantum chemistry.

Linear combination of atomic orbitals (LCAO) method

In the LCAO method, each molecule has a set of molecular orbitals. It is assumed that the molecular orbital wave function ψ_j can be written as a simple weighted sum of the n constituent atomic orbitals χ_i, according to the following equation:

$${\displaystyle {\psi }_j=\sum _{i=1}^n{c}_{ij}{\chi }_i.}$$

One may determine c_ij coefficients numerically by substituting this equation into the Schrödinger equation and applying the variational principle. The variational principle is a mathematical technique used in quantum mechanics to build up the coefficients of each atomic orbital basis. A larger coefficient means that the orbital basis is composed more of that particular contributing atomic orbital—hence, the molecular orbital is best characterized by that type. This method of quantifying orbital contribution as a linear combination of atomic orbitals is used in computational chemistry. An additional unitary transformation can be applied on the system to accelerate the convergence in some computational schemes. Molecular orbital theory was seen as a competitor to valence bond theory in the 1930s, before it was realized that the two methods are closely related and that when extended they become equivalent.

Molecular orbital theory is used to interpret ultraviolet-visible spectroscopy (UV-VIS). Changes to the electronic structure of molecules can be seen by the absorbance of light at specific wavelengths. Assignments can be made to these signals indicated by the transition of electrons moving from one orbital at a lower energy to a higher energy orbital. The molecular orbital diagram for the final state describes the electronic nature of the molecule in an excited state.

There are three main requirements for atomic orbital combinations to be suitable as approximate molecular orbitals.

1. The atomic orbital combination must have the correct symmetry, which means that it must belong to the correct irreducible representation of the molecular symmetry group. Using symmetry adapted linear combinations, or SALCs, molecular orbitals of the correct symmetry can be formed.
2. Atomic orbitals must also overlap within space. They cannot combine to form molecular orbitals if they are too far away from one another.
3. Atomic orbitals must be at similar energy levels to combine as molecular orbitals. Because if the energy difference is great, when the molecular orbitals form, the change in energy becomes small. Consequently, there is not enough reduction in energy of electrons to make significant bonding.

History

Molecular orbital theory was developed in the years after valence bond theory had been established (1927), primarily through the efforts of Friedrich Hund, Robert Mulliken, John C. Slater, and John Lennard-Jones. MO theory was originally called the Hund-Mulliken theory. According to physicist and physical chemist Erich Hückel, the first quantitative use of molecular orbital theory was the 1929 paper of Lennard-Jones. This paper predicted a triplet ground state for the dioxygen molecule which explained its paramagnetism (see Molecular orbital diagram § Dioxygen) before valence bond theory, which came up with its own explanation in 1931. The word orbital was introduced by Mulliken in 1932. By 1933, the molecular orbital theory had been accepted as a valid and useful theory.

Erich Hückel applied molecular orbital theory to unsaturated hydrocarbon molecules starting in 1931 with his Hückel molecular orbital (HMO) method for the determination of MO energies for pi electrons, which he applied to conjugated and aromatic hydrocarbons. This method provided an explanation of the stability of molecules with six pi-electrons such as benzene.

The first accurate calculation of a molecular orbital wavefunction was that made by Charles Coulson in 1938 on the hydrogen molecule. By 1950, molecular orbitals were completely defined as eigenfunctions (wave functions) of the self-consistent field Hamiltonian and it was at this point that molecular orbital theory became fully rigorous and consistent. This rigorous approach is known as the Hartree–Fock method for molecules although it had its origins in calculations on atoms. In calculations on molecules, the molecular orbitals are expanded in terms of an atomic orbital basis set, leading to the Roothaan equations. This led to the development of many ab initio quantum chemistry methods. In parallel, molecular orbital theory was applied in a more approximate manner using some empirically derived parameters in methods now known as semi-empirical quantum chemistry methods.

The success of Molecular Orbital Theory also spawned ligand field theory, which was developed during the 1930s and 1940s as an alternative to crystal field theory.

Types of orbitals

MO diagram showing the formation of molecular orbitals of H₂ (centre) from atomic orbitals of two H atoms. The lower-energy MO is bonding with electron density concentrated between the two H nuclei. The higher-energy MO is anti-bonding with electron density concentrated behind each H nucleus.

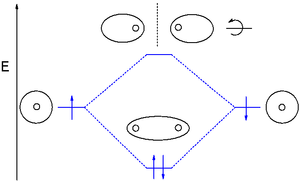
Molecular orbital (MO) theory uses a linear combination of atomic orbitals (LCAO) to represent molecular orbitals resulting from bonds between atoms. These are often divided into three types, bonding, antibonding, and non-bonding. A bonding orbital concentrates electron density in the region between a given pair of atoms, so that its electron density will tend to attract each of the two nuclei toward the other and hold the two atoms together. An anti-bonding orbital concentrates electron density "behind" each nucleus (i.e. on the side of each atom which is farthest from the other atom), and so tends to pull each of the two nuclei away from the other and actually weaken the bond between the two nuclei. Electrons in non-bonding orbitals tend to be associated with atomic orbitals that do not interact positively or negatively with one another, and electrons in these orbitals neither contribute to nor detract from bond strength.

Molecular orbitals are further divided according to the types of atomic orbitals they are formed from. Chemical substances will form bonding interactions if their orbitals become lower in energy when they interact with each other. Different bonding orbitals are distinguished that differ by electron configuration (electron cloud shape) and by energy levels.

The molecular orbitals of a molecule can be illustrated in molecular orbital diagrams.

Common bonding orbitals are sigma (σ) orbitals which are symmetric about the bond axis and pi (π) orbitals with a nodal plane along the bond axis. Less common are delta (δ) orbitals and phi (φ) orbitals with two and three nodal planes respectively along the bond axis. Antibonding orbitals are signified by the addition of an asterisk. For example, an antibonding pi orbital may be shown as π*.

Bond Order

Molecular orbital diagram of He₂

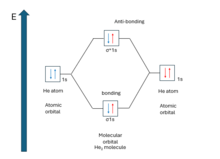
Bond order is the number of chemical bonds between a pair of atoms. The bond order of a molecule can be calculated by subtracting the number of electrons in anti-bonding orbitals from the number of bonding orbitals, and the resulting number is then divided by two. A molecule is expected to be stable if it has bond order larger than zero. It is adequate to consider the valence electron to determine the bond order. Because (for principal quantum number, n>1) when MOs are derived from 1s AOs, the difference in number of electrons in bonding and anti-bonding molecular orbital is zero. So, there is no net effect on bond order if the electron is not the valence one.

Bond Order = 1/2 [(Number of electrons in bonding MO) - (Number of electrons in anti-bonding MO)]

From bond order, one can predict whether a bond between two atoms will form or not. For example, the existence of He₂ molecule. From the molecular orbital diagram, bond order,=1/2*(2-2)=0. That means, no bond formation will occur between two He atoms which is seen experimentally. It can be detected under very low temperature and pressure molecular beam and has binding energy of approximately 0.001 J/mol. 

Besides, the strength of a bond can also be realized from bond order (BO). For example:

H₂ :BO=(2-0)/2=1; Bond Energy= 436 kJ/mol.

H₂⁺ :BO=(1-0)/2=1/2; Bond Energy=171 kJ/mol.

As bond order of H₂⁺ is smaller than H₂, it should be less stable which is observed experimentally and can be seen from the bond energy.

Overview

MOT provides a global, delocalized perspective on chemical bonding. In MO theory, any electron in a molecule may be found anywhere in the molecule, since quantum conditions allow electrons to travel under the influence of an arbitrarily large number of nuclei, as long as they are in eigenstates permitted by certain quantum rules. Thus, when excited with the requisite amount of energy through high-frequency light or other means, electrons can transition to higher-energy molecular orbitals. For instance, in the simple case of a hydrogen diatomic molecule, promotion of a single electron from a bonding orbital to an antibonding orbital can occur under UV radiation. This promotion weakens the bond between the two hydrogen atoms and can lead to photodissociation—the breaking of a chemical bond due to the absorption of light.

Molecular orbital theory is used to interpret ultraviolet-visible spectroscopy (UV-VIS). Changes to the electronic structure of molecules can be seen by the absorbance of light at specific wavelengths. Assignments can be made to these signals indicated by the transition of electrons moving from one orbital at a lower energy to a higher energy orbital. The molecular orbital diagram for the final state describes the electronic nature of the molecule in an excited state.

Although in MO theory some molecular orbitals may hold electrons that are more localized between specific pairs of molecular atoms, other orbitals may hold electrons that are spread more uniformly over the molecule. Thus, overall, bonding is far more delocalized in MO theory, which makes it more applicable to resonant molecules that have equivalent non-integer bond orders than valence bond theory. This makes MO theory more useful for the description of extended systems.

Robert S. Mulliken, who actively participated in the advent of molecular orbital theory, considers each molecule to be a self-sufficient unit. He asserts in his article:

...Attempts to regard a molecule as consisting of specific atomic or ionic units held together by discrete numbers of bonding electrons or electron-pairs are considered as more or less meaningless, except as an approximation in special cases, or as a method of calculation […]. A molecule is here regarded as a set of nuclei, around each of which is grouped an electron configuration closely similar to that of a free atom in an external field, except that the outer parts of the electron configurations surrounding each nucleus usually belong, in part, jointly to two or more nuclei....

An example is the MO description of benzene, C
₆H
₆, which is an aromatic hexagonal ring of six carbon atoms and three double bonds. In this molecule, 24 of the 30 total valence bonding electrons—24 coming from carbon atoms and 6 coming from hydrogen atoms—are located in 12 σ (sigma) bonding orbitals, which are located mostly between pairs of atoms (C-C or C-H), similarly to the electrons in the valence bond description. However, in benzene the remaining six bonding electrons are located in three π (pi) molecular bonding orbitals that are delocalized around the ring. Two of these electrons are in an MO that has equal orbital contributions from all six atoms. The other four electrons are in orbitals with vertical nodes at right angles to each other. As in the VB theory, all of these six delocalized π electrons reside in a larger space that exists above and below the ring plane. All carbon-carbon bonds in benzene are chemically equivalent. In MO theory this is a direct consequence of the fact that the three molecular π orbitals combine and evenly spread the extra six electrons over six carbon atoms.

Structure of benzene

In molecules such as methane, CH
₄, the eight valence electrons are found in four MOs that are spread out over all five atoms. It is possible to transform the MOs into four localized sp³ orbitals. Linus Pauling, in 1931, hybridized the carbon 2s and 2p orbitals so that they pointed directly at the hydrogen 1s basis functions and featured maximal overlap. However, the delocalized MO description is more appropriate for predicting ionization energies and the positions of spectral absorption bands. When methane is ionized, a single electron is taken from the valence MOs, which can come from the s bonding or the triply degenerate p bonding levels, yielding two ionization energies. In comparison, the explanation in valence bond theory is more complicated. When one electron is removed from an sp³ orbital, resonance is invoked between four valence bond structures, each of which has a single one-electron bond and three two-electron bonds. Triply degenerate T₂ and A₁ ionized states (CH₄⁺) are produced from different linear combinations of these four structures. The difference in energy between the ionized and ground state gives the two ionization energies.

As in benzene, in substances such as beta carotene, chlorophyll, or heme, some electrons in the π orbitals are spread out in molecular orbitals over long distances in a molecule, resulting in light absorption in lower energies (the visible spectrum), which accounts for the characteristic colours of these substances. This and other spectroscopic data for molecules are well explained in MO theory, with an emphasis on electronic states associated with multicenter orbitals, including mixing of orbitals premised on principles of orbital symmetry matching. The same MO principles also naturally explain some electrical phenomena, such as high electrical conductivity in the planar direction of the hexagonal atomic sheets that exist in graphite. This results from continuous band overlap of half-filled p orbitals and explains electrical conduction. MO theory recognizes that some electrons in the graphite atomic sheets are completely delocalized over arbitrary distances, and reside in very large molecular orbitals that cover an entire graphite sheet, and some electrons are thus as free to move and therefore conduct electricity in the sheet plane, as if they resided in a metal.

Emerald

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Emerald 

 

Emerald
Emerald crystal from Muzo, Colombia

Main emerald producing countries

Emerald is a gemstone and a variety of the mineral beryl (Be₃Al₂(SiO₃)₆) colored green by trace amounts of chromium or sometimes vanadium. Beryl has a hardness of 7.5–8 on the Mohs scale. Most emeralds have many inclusions, so their toughness (resistance to breakage) is classified as generally poor. Emerald is a cyclosilicate.

Etymology

The word "emerald" is derived (via Old French: esmeraude and Middle English: emeraude), from Vulgar Latin: esmaralda/esmaraldus, a variant of Latin smaragdus, which was via Ancient Greek: σμάραγδος (smáragdos; "green gem"). The Greek word may have a Semitic, Sanskrit or Persian origin. According to Webster's Dictionary the term emerald was first used in the 14th century.

Properties determining value

Cut emeralds

Emeralds, like all colored gemstones, are graded using four basic parameters known as "the four Cs": color, clarity, cut and carat weight. Normally, in grading colored gemstones, color is by far the most important criterion. However, in the grading of emeralds, clarity is considered a close second. A fine emerald must possess not only a pure verdant green hue as described below, but also a high degree of transparency to be considered a top gemstone.

This member of the beryl family ranks among the traditional "big four" gems along with diamonds, rubies and sapphires.

In the 1960s, the American jewelry industry changed the definition of emerald to include the green vanadium-bearing beryl. As a result, vanadium emeralds purchased as emeralds in the United States are not recognized as such in the United Kingdom and Europe. In America, the distinction between traditional emeralds and the new vanadium kind is often reflected in the use of terms such as "Colombian emerald".

Color

In gemology, color is divided into three components: hue, saturation, and tone. Emeralds occur in hues ranging from yellow-green to blue-green, with the primary hue necessarily being green. Yellow and blue are the normal secondary hues found in emeralds. Only gems that are medium to dark in tone are considered emeralds; light-toned gems are known instead by the species name green beryl. The finest emeralds are approximately 75% tone on a scale where 0% tone is colorless and 100% is opaque black. In addition, a fine emerald will be saturated and have a hue that is bright (vivid). Gray is the normal saturation modifier or mask found in emeralds; a grayish-green hue is a dull-green hue.

Clarity

Brazilian emerald (grass-green variety of the mineral beryl) in a quartz-pegmatite matrix with typical hexagonal, prismatic crystals.

Emeralds tend to have numerous inclusions and surface-breaking fissures. Unlike diamonds, where the loupe standard (i.e., 10× magnification) is used to grade clarity, emeralds are graded by eye. Thus, if an emerald has no visible inclusions to the eye (assuming normal visual acuity) it is considered flawless. Stones that lack surface breaking fissures are extremely rare and therefore almost all emeralds are treated ("oiled", see below) to enhance the apparent clarity. The inclusions and fissures within an emerald are sometimes described as jardin (French for garden), because of their mossy appearance. Imperfections are unique for each emerald and can be used to identify a particular stone. Eye-clean stones of a vivid primary green hue (as described above), with no more than 15% of any secondary hue or combination (either blue or yellow) of a medium-dark tone, command the highest prices. The relative non-uniformity motivates the cutting of emeralds in cabochon form, rather than faceted shapes. Faceted emeralds are most commonly given an oval cut, or the signature emerald cut, a rectangular cut with facets around the top edge.

Treatments

Most emeralds are oiled as part of the post-lapidary process, in order to fill in surface-reaching cracks so that clarity and stability are improved. Cedar oil, having a similar refractive index, is often used in this widely adopted practice. Other liquids, including synthetic oils and polymers with refractive indexes close to that of emeralds, such as Opticon, are also used. The least expensive emeralds are often treated with epoxy resins, which are effective for filling stones with many fractures. These treatments are typically applied in a vacuum chamber under mild heat, to open the pores of the stone and allow the fracture-filling agent to be absorbed more effectively. The U.S. Federal Trade Commission requires the disclosure of this treatment when an oil-treated emerald is sold. The use of oil is traditional and largely accepted by the gem trade, although oil-treated emeralds are worth much less than untreated emeralds of similar quality. Untreated emeralds must also be accompanied by a certificate from a licensed, independent gemology laboratory. Other treatments, for example the use of green-tinted oil, are not acceptable in the trade. Gems are graded on a four-step scale; none, minor, moderate and highly enhanced. These categories reflect levels of enhancement, not clarity. A gem graded none on the enhancement scale may still exhibit visible inclusions. Laboratories apply these criteria differently. Some gemologists consider the mere presence of oil or polymers to constitute enhancement. Others may ignore traces of oil if the presence of the material does not improve the look of the gemstone.

Emerald mines

A Colombian trapiche emerald

Emeralds in antiquity were mined in Ancient Egypt at locations on Mount Smaragdus since 1500 BC, and India and Austria since at least the 14th century AD. The Egyptian mines were exploited on an industrial scale by the Roman and Byzantine Empires, and later by Islamic conquerors. Mining in Egypt ceased with the discovery of the Colombian deposits. Today, only ruins remain in Egypt.

Colombia is by far the world's largest producer of emeralds, constituting 50–95% of the world production, with the number depending on the year, source and grade. Emerald production in Colombia has increased drastically in the last decade, increasing by 78% from 2000 to 2010. The three main emerald mining areas in Colombia are Muzo, Coscuez, and Chivor. Rare "trapiche" emeralds are found in Colombia, distinguished by ray-like spokes of dark impurities.

Zambia is the world's second biggest producer, with its Kafubu River area deposits (Kagem Mines) about 45 km (28 mi) southwest of Kitwe responsible for 20% of the world's production of gem-quality stones in 2004. In the first half of 2011, the Kagem Mines produced 3.74 tons of emeralds.

Emeralds are found all over the world in countries such as Afghanistan, Australia, Austria, Brazil, Bulgaria, Cambodia, Canada, China, Egypt, Ethiopia, France, Germany, India, Kazakhstan, Madagascar, Mozambique, Namibia, Nigeria, Norway, Pakistan, Russia, Somalia, South Africa, Spain, Switzerland, Tanzania, the United States, Zambia, and Zimbabwe. In the US, emeralds have been found in Connecticut, Montana, Nevada, North Carolina, and South Carolina. In 1998, emeralds were discovered in the Yukon Territory of Canada.

Origin determinations

Since the onset of concerns regarding diamond origins, research has been conducted to determine if the mining location could be determined for an emerald already in circulation. Traditional research used qualitative guidelines such as an emerald's color, style and quality of cutting, type of fracture filling, and the anthropological origins of the artifacts bearing the mineral to determine the emerald's mine location. More recent studies using energy-dispersive X-ray spectroscopy methods have uncovered trace chemical element differences between emeralds, including ones mined in close proximity to one another. American gemologist David Cronin and his colleagues have extensively examined the chemical signatures of emeralds resulting from fluid dynamics and subtle precipitation mechanisms, and their research demonstrated the chemical homogeneity of emeralds from the same mining location and the statistical differences that exist between emeralds from different mining locations, including those between the three locations: Muzo, Coscuez, and Chivor, in Colombia, South America.

Synthetic emerald

Emerald showing its hexagonal structure

Both hydrothermal and flux-growth synthetics have been produced, and a method has been developed for producing an emerald overgrowth on colorless beryl. The first commercially successful emerald synthesis process was that of Carroll Chatham, likely involving a lithium vanadate flux process, as Chatham's emeralds do not have any water and contain traces of vanadate, molybdenum and vanadium. The other large producer of flux emeralds was Pierre Gilson Sr., whose products have been on the market since 1964. Gilson's emeralds are usually grown on natural colorless beryl seeds, which are coated on both sides. Growth occurs at the rate of 1 mm per month, a typical seven-month growth run produces emerald crystals 7 mm thick.

Hydrothermal synthetic emeralds have been attributed to IG Farben, Nacken, Tairus, and others, but the first satisfactory commercial product was that of Johann Lechleitner of Innsbruck, Austria, which appeared on the market in the 1960s. These stones were initially sold under the names "Emerita" and "Symeralds", and they were grown as a thin layer of emerald on top of natural colorless beryl stones. Later, from 1965 to 1970, the Linde Division of Union Carbide produced completely synthetic emeralds by hydrothermal synthesis. According to their patents (attributable to E.M. Flanigen), acidic conditions are essential to prevent the chromium (which is used as the colorant) from precipitating. Also, it is important that the silicon-containing nutrient be kept away from the other ingredients to prevent nucleation and confine growth to the seed crystals. Growth occurs by a diffusion-reaction process, assisted by convection. The largest producer of hydrothermal emeralds today is Tairus, which has succeeded in synthesizing emeralds with chemical composition similar to emeralds in alkaline deposits in Colombia, and whose products are thus known as “Colombian created emeralds” or “Tairus created emeralds”. Luminescence in ultraviolet light is considered a supplementary test when making a natural versus synthetic determination, as many, but not all, natural emeralds are inert to ultraviolet light. Many synthetics are also UV inert.

Emerald made by hydrothermal synthesis

Synthetic emeralds are often referred to as "created", as their chemical and gemological composition is the same as their natural counterparts. The U.S. Federal Trade Commission (FTC) has very strict regulations as to what can and what cannot be called a "synthetic" stone. The FTC says: "§ 23.23(c) It is unfair or deceptive to use the word "laboratory-grown", "laboratory-created", "[manufacturer name]-created", or "synthetic" with the name of any natural stone to describe any industry product unless such industry product has essentially the same optical, physical, and chemical properties as the stone named."

In culture and lore

Emerald is regarded as the traditional birthstone for May as well as the traditional gemstone for the astrological sign of Taurus.

Traditional alchemical lore ascribes several uses and characteristics to emeralds:

The virtue of the Emerald is to counteract poison. They say that if a venomous animal should look at it, it will become blinded. The gem also acts as a preservative against epilepsy; it cures leprosy, strengthens sight and memory, checks copulation, during which act it will break, if worn at the time on the finger.

According to French writer Brantôme (c. 1540–1614) Hernán Cortés had one of the emeralds which he had looted from Mexico text engraved, Inter Natos Mulierum non surrexit major ("Among those born of woman there hath not arisen a greater," Matthew 11:11), in reference to John the Baptist. Brantôme considered engraving such a beautiful and simple product of nature sacrilegious and considered this act the cause for Cortez's loss in 1541 of an extremely precious pearl (to which he dedicated a work, A beautiful and incomparable pearl), and even for the death of King Charles IX of France, who died (1574) soon afterward.

In American author L. Frank Baum's 1900 children's novel The Wonderful Wizard of Oz, and the 1939 MGM film adaptation, the protagonist must travel to an Emerald City to meet the eponymous character, the Wizard.

The chief deity of one of India's most famous temples, the Meenakshi Amman Temple in Madurai, is the goddess Meenakshi, whose idol is traditionally thought to be made of emerald.

Notable emeralds

Emerald	Origin	Size	Location
Chipembele	Zambia, 2021	7,525 carats (1.505 kg)	Israel Diamond Exchange, Eshed – Gemstar
Bahia Emerald	Brazil, 2001	180,000 carats, crystals in host rock 752 lb (341 kg)	Los Angeles County Sheriff's Department
Carolina Emperor	United States, 2009	310 carats uncut, 64.8 carats cut	North Carolina Museum of Natural Sciences, Raleigh
Chalk Emerald	Colombia	38.40 carats cut, then recut to 37.82 carats	National Museum of Natural History, Washington
Duke of Devonshire Emerald	Colombia, before 1831	1,383.93 carats uncut	Natural History Museum, London
Emerald of Saint Louis	Austria, probably Habachtal	51.60 carats cut	National Museum of Natural History, Paris
Gachalá Emerald	Colombia, 1967	858 carats uncut	National Museum of Natural History, Washington
Mogul Mughal Emerald	Colombia, 1107 A.H. (1695–1696 AD)	217.80 carats cut	Museum of Islamic Art, Doha, Qatar
Rockefeller Emerald	Colombia	18.04 carats Octagonal step-cut	Private collection
Patricia Emerald	Colombia, 1920	632 carats uncut, dihexagonal (12 sided)	American Museum of Natural History, New York
Mim Emerald	Colombia, 2014	1,390 carats uncut, dihexagonal (12 sided)	Mim Museum, Beirut

Gallery

• 
  Emerald on quartz, from Carnaiba Mine, Pindobaçu, Campo Formoso ultramafic complex, Bahia, Brazil
   
• 
  The Chalk Emerald ring, containing a top-quality 37-carat emerald, in the U.S. National Museum of Natural History
   
• 
  Emerald crystals
   
• 
  A 5-carat emerald from Muzo with hexagonal cross-section
   
• 
  Gachalá Emerald, one of the largest gem emeralds in the world, at 858 carats (171.6 g). Found in 1967 at La Vega de San Juan mine in Gachalá, Colombia. Housed at the National Museum of Natural History in Washington, D.C.
   
• 
  Colombian emeralds
   
• 
  Rough emerald crystals from Panjshir Valley Afghanistan
   
• 
  Large, di-hexagonal prismatic crystal of 1,390 carats uncut with a deep green color. It is transparent and features few inclusions in the upper 2/3, and is translucent in the lower part. Housed at the Mim Museum, Beirut, Lebanon.

Molecular term symbol

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Molecular_term_symbol

In molecular physics, the molecular term symbol is a shorthand expression of the group representation and angular momenta that characterize the state of a molecule, i.e. its electronic quantum state which is an eigenstate of the electronic molecular Hamiltonian. It is the equivalent of the term symbol for the atomic case. However, the following presentation is restricted to the case of homonuclear diatomic molecules, or other symmetric molecules with an inversion centre. For heteronuclear diatomic molecules, the u/g symbol does not correspond to any exact symmetry of the electronic molecular Hamiltonian. In the case of less symmetric molecules the molecular term symbol contains the symbol of the group representation to which the molecular electronic state belongs.

It has the general form:

${\displaystyle {}^{2S+1}{\mathrm{\Lambda }}_{\mathrm{\Omega },(g/u)}^{(+/-)}}$

where

• ${\displaystyle S}$ is the total spin quantum number
• ${\displaystyle \mathrm{\Lambda }}$ (Lambda) is the projection of the orbital angular momentum along the internuclear axis
• ${\displaystyle \mathrm{\Omega }}$ (Omega) is the projection of the total angular momentum along the internuclear axis
• ${\displaystyle g/u}$ indicates the symmetry or parity with respect to inversion (${\displaystyle \hat{i}}$) through a centre of symmetry
• ${\displaystyle +/-}$ is the reflection symmetry along an arbitrary plane containing the internuclear axis

Λ quantum number

For atoms, we use S, L, J and M_J to characterize a given state. In linear molecules, however, the lack of spherical symmetry destroys the relationship ${\displaystyle [{\hat{\mathbf{L}}}^2,\hat{H}]=0}$, so L ceases to be a good quantum number. A new set of operators have to be used instead: ${\displaystyle \{{\hat{\mathbf{S}}}^2,{\hat{\mathbf{S}}}_z,{\hat{\mathbf{L}}}_z,{\hat{\mathbf{J}}}_z={\hat{\mathbf{S}}}_z+{\hat{\mathbf{L}}}_z\}}$, where the z-axis is defined along the internuclear axis of the molecule. Since these operators commute with each other and with the Hamiltonian on the limit of negligible spin-orbit coupling, their eigenvalues may be used to describe a molecule state through the quantum numbers S, M_S, M_L and M_J.

The cylindrical symmetry of a linear molecule ensures that positive and negative values of a given ${\displaystyle m_{\ell }}$ for an electron in a molecular orbital will be degenerate in the absence of spin-orbit coupling. Different molecular orbitals are classified with a new quantum number, λ, defined as

${\displaystyle \lambda =|m_{\ell }|}$

Following the spectroscopic notation pattern, molecular orbitals are designated by a lower case Greek letter: for λ = 0, 1, 2, 3,... orbitals are called σ, π, δ, φ... respectively, analogous to the Latin letters s, p, d, f used for atomic orbitals.

Now, the total z-projection of L can be defined as

${\displaystyle M_L=\sum _i{m_{\ell }}_i.}$

As states with positive and negative values of M_L are degenerate, we define

Λ = |M_L|,

and a capital Greek letter is used to refer to each value: Λ = 0, 1, 2, 3... are coded as Σ, Π, Δ, Φ... respectively (analogous to S, P, D, F for atomic states). The molecular term symbol is then defined as

^2S+1Λ

and the number of electron degenerate states (under the absence of spin-orbit coupling) corresponding to this term symbol is given by:

• (2S+1)×2 if Λ is not 0
• (2S+1) if Λ is 0.

Ω and spin–orbit coupling

Spin–orbit coupling lifts the degeneracy of the electronic states. This is because the z-component of spin interacts with the z-component of the orbital angular momentum, generating a total electronic angular momentum along the molecule axis J_z. This is characterized by the M_J quantum number, where

M_J = M_S + M_L.

Again, positive and negative values of M_J are degenerate, so the pairs (M_L, M_S) and (−M_L, −M_S) are degenerate: {(1, 1/2), (−1, −1/2)}, and {(1, −1/2), (−1, 1/2)} represent two different degenerate states. These pairs are grouped together with the quantum number Ω, which is defined as the sum of the pair of values (M_L, M_S) for which M_L is positive. Sometimes the equation

Ω = Λ + M_S

is used (often Σ is used instead of M_S). Note that although this gives correct values for Ω it could be misleading, as obtained values do not correspond to states indicated by a given pair of values (M_L, M_S). For example, a state with (−1, −1/2) would give an Ω value of Ω = |−1| + (−1/2) = 1/2, which is wrong. Choosing the pair of values with M_L positive will give a Ω = 3/2 for that state.

With this, a level is given by

${\displaystyle {}^{2S+1}{\mathrm{\Lambda }}_{\mathrm{\Omega }}}$

Note that Ω can have negative values and subscripts r and i represent regular (normal) and inverted multiplets, respectively. For a ⁴Π term there are four degenerate (M_L, M_S) pairs: {(1, 3/2), (−1, −3/2)}, {(1, 1/2), (−1, −1/2)}, {(1, −1/2), (−1, 1/2)}, {(1, −3/2), (−1, 3/2)}. These correspond to Ω values of 5/2, 3/2, 1/2 and −1/2, respectively. Approximating the spin–orbit Hamiltonian to first order perturbation theory, the energy level is given by

E = A M_L M_S

where A is the spin–orbit constant. For ⁴Π the Ω values 5/2, 3/2, 1/2 and −1/2 correspond to energies of 3A/2, A/2, −A/2 and −3A/2. Despite having the same magnitude of Ω, the levels Ω = ±1/2 have different energies and so are not degenerate. States with different energies are assigned different Ω values. For states with positive values of A (which are said to be regular), increasing values of Ω correspond to increasing values of energies; on the other hand, with A negative (said to be inverted) the energy order is reversed. Including higher-order effects can lead to a spin-orbital levels or energy that do not even follow the increasing value of Ω.

When Λ = 0 there is no spin–orbit splitting to first order in perturbation theory, as the associated energy is zero. So for a given S, all of its M_S values are degenerate. This degeneracy is lifted when spin–orbit interaction is treated to higher order in perturbation theory, but still states with same |M_S| are degenerate in a non-rotating molecule. We can speak of a ⁵Σ₂ substate, a ⁵Σ₁ substate or a ⁵Σ₀ substate. Except for the case Ω = 0, these substates have a degeneracy of 2.

Reflection through a plane containing the internuclear axis

There are an infinite number of planes containing the internuclear axis and hence there are an infinite number of possible reflections. For any of these planes, molecular terms with Λ > 0 always have a state which is symmetric with respect to this reflection and one state that is antisymmetric. Rather than labelling those situations as, e.g., ²Π^±, the ± is omitted.

For the Σ states, however, this two-fold degeneracy disappears, and all Σ states are either symmetric under any plane containing the internuclear axis, or antisymmetric. These two situations are labeled as Σ⁺ or Σ⁻.

Reflection through an inversion center: u and g symmetry

Taking the molecular center of mass as origin of coordinates, consider the change of all electrons' position from (x_i, y_i, z_i) to (−x_i, −y_i, −z_i). If the resulting wave function is unchanged, it is said to be gerade (German for even) or have even parity; if the wave function changes sign then it is said to be ungerade (odd) or have odd parity. For a molecule with a center of inversion, all orbitals will be symmetric or antisymmetric. The resulting wavefunction for the whole multielectron system will be gerade if an even number of electrons are in ungerade orbitals, and ungerade if there are an odd number of electrons in ungerade orbitals, regardless of the number of electrons in gerade orbitals.

An alternative method for determining the symmetry of an MO is to rotate the orbital about the axis joining the two nuclei and then rotate the orbital about a line perpendicular to the axis. If the sign of the lobes remains the same, the orbital is gerade, and if the sign changes, the orbital is ungerade.

Wigner-Witmer correlation rules

In 1928 Eugene Wigner and E.E. Witmer proposed rules to determine the possible term symbols for diatomic molecular states formed by the combination of a pair of atomic states with given atomic term symbols. For example, two like atoms in identical ³S states can form a diatomic molecule in ¹Σ_g⁺, ³Σ_u⁺, or ⁵Σ_g⁺ states. For one like atom in a ¹S_g state and one in a ¹P_u state, the possible diatomic states are ¹Σ_g⁺, ¹Σ_u⁺, ¹Π_g and ¹Π_u. The parity of an atomic term is g if the sum of the individual angular momentum is even, and u if the sum is odd.

Simplified correlation rules for electronic states of diatomic molecules resulting from given states of separated (unlike) atoms

Atomic Term Symbols	Molecular Term Symbols
Sg + Sg or Su + Su	Σ+
Sg + Su	Σ−
Sg + Pg or Su + Pu	Σ−, Π
Sg + Pu or Su + Pg	Σ+, Π
Sg + Dg or Su + Du	Σ+, Π, Δ
Sg + Du or Su + Dg	Σ–, Π, Δ
Sg + Fg or Su + Fu	Σ–, Π, Δ, Φ
Sg + Fu or Su + Fg	Σ+, Π, Δ, Φ
Pg + Pg or Pu + Pu	Σ+(2), Σ–, Π(2), Δ
Pg + Pu	Σ+, Σ–(2), Π(2), Δ
Pg + Dg or Pu + Du	Σ+, Σ−(2), Π(3), Δ(2), Φ
Pg + Du or Pu + Dg	Σ+(2), Σ–, Π(3), Δ(2), Φ
Pg + Fg or Pu + Fu	Σ+(2), Σ–, Π(3), Δ(3), Φ(2), Γ
Pg + Fu or Pu + Fg	Σ+, Σ–(2), Π(3), Δ(3), Φ(2), Γ
Dg + Dg or Du + Du	Σ+(3), Σ–(2), Π(4), Δ(3), Φ(2), Γ
Dg + Du	Σ+(2), Σ–(3), Π(4), Δ(3), Φ(2), Γ
Dg + Fg or Du + Fu	Σ+(2), Σ–(3), Π(5), Δ(4), Φ(3), Γ(2), Η
Dg + Fu or Du + Fg	Σ+(3), Σ–(2), Π(5), Δ(4), Φ(3), Γ(2), Η

Alternative empirical notation

Electronic states are also often identified by an empirical single-letter label. The ground state is labelled X, excited states of the same multiplicity (i.e., having the same spin quantum number) are labelled in ascending order of energy with capital letters A, B, C...; excited states having different multiplicity than the ground state are labelled with lower-case letters a, b, c... In polyatomic molecules (but not in diatomic) it is customary to add a tilde (e.g. ${\displaystyle \tilde{X}}$, ${\displaystyle \tilde{a}}$) to these empirical labels to prevent possible confusion with symmetry labels based on group representations.

Galena

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Galena

 

Galena with minor pyrite

Galena, also called lead glance, is the natural mineral form of lead(II) sulfide (PbS). It is the most important ore of lead and an important source of silver.

Galena is one of the most abundant and widely distributed sulfide minerals. It crystallizes in the cubic crystal system often showing octahedral forms. It is often associated with the minerals sphalerite, calcite and fluorite.

Occurrence

Galena with baryte and pyrite from Cerro de Pasco, Peru; 5.8 cm × 4.8 cm × 4.4 cm (2.3 in × 1.9 in × 1.7 in)

Galena is the main ore of lead, used since ancient times, since lead can be smelted from galena in an ordinary wood fire. Galena typically is found in hydrothermal veins in association with sphalerite, marcasite, chalcopyrite, cerussite, anglesite, dolomite, calcite, quartz, barite, and fluorite. It is also found in association with sphalerite in low-temperature lead-zinc deposits within limestone beds. Minor amounts are found in contact metamorphic zones, in pegmatites, and disseminated in sedimentary rock.

In some deposits, the galena contains up to 0.5% silver, a byproduct that far surpasses the main lead ore in revenue. In these deposits significant amounts of silver occur as included silver sulfide mineral phases or as limited silver in solid solution within the galena structure. These argentiferous galenas have long been an important ore of silver. Silver-bearing galena is almost entirely of hydrothermal origin; galena in lead-zinc deposits contains little silver.

Galena deposits are found worldwide in various environments. Noted deposits include those at Freiberg in Saxony; Cornwall, the Mendips in Somerset, Derbyshire, and Cumberland in England; the Linares mines in Spain were worked from before the Roman times until the end of the 20th century; the Madan and Rhodope Mountains in Bulgaria; the Sullivan Mine of British Columbia; Broken Hill and Mount Isa in Australia; and the ancient mines of Sardinia.

In the United States, it occurs most notably as lead-zinc ore in the Mississippi Valley type deposits of the Lead Belt in southeastern Missouri, which is the largest known deposit, and in the Driftless Area of Illinois, Iowa and Wisconsin, providing the origin of the name of Galena, Illinois, a historical settlement known for the material. Galena also was a major mineral of the zinc-lead mines of the tri-state district around Joplin in southwestern Missouri and the adjoining areas of Kansas and Oklahoma. Galena is also an important ore mineral in the silver mining regions of Colorado, Idaho, Utah and Montana. Of the latter, the Coeur d'Alene district of northern Idaho was most prominent.

Australia is the world's leading producer of lead as of 2021, most of which is extracted as galena. Argentiferous galena was accidentally discovered at Glen Osmond in 1841, and additional deposits were discovered near Broken Hill in 1876 and at Mount Isa in 1923. Most galena in Australia is found in hydrothermal deposits emplaced around 1680 million years ago, which have since been heavily metamorphosed.

The largest documented crystal of galena is composite cubo-octahedra from the Great Laxey Mine, Isle of Man, measuring 25 cm × 25 cm × 25 cm (10 in × 10 in × 10 in).

Importance

Galena is the official state mineral of the U.S. states of Kansas, Missouri, and Wisconsin; the former mining communities of Galena, Kansas, Galena, Illinois, Galena, South Dakota and Galena, Alaska, take their names from deposits of this mineral.

Structure

Galena belongs to the octahedral sulfide group of minerals that have metal ions in octahedral positions, such as the iron sulfide pyrrhotite and the nickel arsenide niccolite. The galena group is named after its most common member, with other isometric members that include manganese bearing alabandite and niningerite.

Divalent lead (Pb) cations and sulfur (S) anions form a close-packed cubic unit cell much like the mineral halite of the halide mineral group. Zinc, cadmium, iron, copper, antimony, arsenic, bismuth and selenium also occur in variable amounts in galena. Selenium substitutes for sulfur in the structure constituting a solid solution series. The lead telluride mineral altaite has the same crystal structure as galena.

Geochemistry

Within the weathering or oxidation zone galena alters to anglesite (lead sulfate) or cerussite (lead carbonate). Galena exposed to acid mine drainage can be oxidized to anglesite by naturally occurring bacteria and archaea, in a process similar to bioleaching.

Uses

Galena "cat's whisker" detector

One of the oldest uses of galena was to produce kohl, an eye cosmetic now regarded as toxic due to the risk of lead poisoning. In Ancient Egypt, this was applied around the eyes to reduce the glare of the desert sun and to repel flies, which were a potential source of disease.

In pre-Columbian North America, galena was used by indigenous peoples as an ingredient in decorative paints and cosmetics, and widely traded throughout the eastern United States. Traces of galena are frequently found at the Mississippian city at Kincaid Mounds in present-day Illinois. The galena used at the site originated from deposits in southeastern and central Missouri and the Upper Mississippi Valley.

Galena is the primary ore of lead, and is often mined for its silver content. It is used as a source of lead in ceramic glaze.

Galena is a semiconductor with a small band gap of about 0.4 eV, which found use in early wireless communication systems. It was used as the crystal in crystal radio receivers, in which it was used as a point-contact diode capable of rectifying alternating current to detect the radio signals. The galena crystal was used with a sharp wire, known as a "cat's whisker", in contact with it.

In modern times, galena is primarily used to extract its constituent minerals. In addition to silver, it is the most important source of lead, for uses such as in lead-acid batteries.