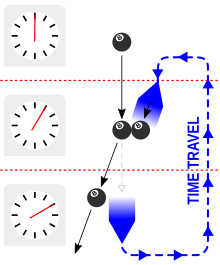
The chronology protection conjecture is a hypothesis first proposed by Stephen Hawking that laws of physics beyond those of standard general relativity prevent time travel on all but microscopic scales—even when the latter theory states that it should be possible (such as in scenarios where faster than light travel is allowed). The permissibility of time travel is represented mathematically by the existence of closed timelike curves in some solutions to the field equations of general relativity. The chronology protection conjecture should be distinguished from chronological censorship under which every closed timelike curve passes through an event horizon, which might prevent an observer from detecting the causal violation (also known as chronology violation).
Etymology
In a 1992 paper, Hawking uses the metaphorical device of a "Chronology Protection Agency" as a personification of the aspects of physics that make time travel impossible at macroscopic scales, thus apparently preventing temporal paradoxes. He says:
It seems that there is a Chronology Protection Agency which prevents the appearance of closed timelike curves and so makes the universe safe for historians.
The idea of the Chronology Protection Agency appears to be drawn playfully from the Time Patrol or Time Police concept, which has been used in many works of science fiction such as Poul Anderson's series of Time Patrol stories or Isaac Asimov's novel The End of Eternity, or in the television series Doctor Who. "The Chronology Protection Case" by Paul Levinson, published after Hawking's paper, posits a universe that goes so far as to murder any scientists who are close to inventing any means of time travel. Larry Niven, in his short story ‘Rotating Cylinders and the possibility of Global Causality Violation’ expands this concept so that the universe causes environmental catastrophe, or global civil war, or the local sun going nova, to any civilisation which shows any sign of successful construction.
General relativity and quantum corrections
Many attempts to generate scenarios for closed timelike curves have been suggested, and the theory of general relativity does allow them in certain circumstances. Some theoretical solutions in general relativity that contain closed timelike curves would require an infinite universe with certain features that our universe does not appear to have, such as the universal rotation of the Gödel metric or the rotating cylinder of infinite length known as a Tipler cylinder. However, some solutions allow for the creation of closed timelike curves in a bounded region of spacetime, with the Cauchy horizon being the boundary between the region of spacetime where closed timelike curves can exist and the rest of spacetime where they cannot. One of the first such bounded time travel solutions found was constructed from a traversable wormhole, based on the idea of taking one of the two "mouths" of the wormhole on a round-trip journey at relativistic speed to create a time difference between it and the other mouth (see the discussion at Wormhole#Time travel).
General relativity does not include quantum effects on its own, and a full integration of general relativity and quantum mechanics would require a theory of quantum gravity, but there is an approximate method for modeling quantum fields in the curved spacetime of general relativity, known as semiclassical gravity. Initial attempts to apply semiclassical gravity to the traversable wormhole time machine indicated that at exactly the moment that wormhole would first allow for closed timelike curves, quantum vacuum fluctuations build up and drive the energy density to infinity in the region of the wormholes. This occurs when the two wormhole mouths, call them A and B, have been moved in such a way that it becomes possible for a particle or wave moving at the speed of light to enter mouth B at some time T2 and exit through mouth A at an earlier time T1, then travel back towards mouth B through ordinary space, and arrive at mouth B at the same time T2 that it entered B on the previous loop; in this way the same particle or wave can make a potentially infinite number of loops through the same regions of spacetime, piling up on itself. Calculations showed that this effect would not occur for an ordinary beam of radiation, because it would be "defocused" by the wormhole so that most of a beam emerging from mouth A would spread out and miss mouth B.[7] But when the calculation was done for vacuum fluctuations, it was found that they would spontaneously refocus on the trip between the mouths, indicating that the pileup effect might become large enough to destroy the wormhole in this case.
Uncertainty about this conclusion remained, because the semiclassical calculations indicated that the pileup would only drive the energy density to infinity for an infinitesimal moment of time, after which the energy density would die down. But semiclassical gravity is considered unreliable for large energy densities or short time periods that reach the Planck scale; at these scales, a complete theory of quantum gravity is needed for accurate predictions. So, it remains uncertain whether quantum-gravitational effects might prevent the energy density from growing large enough to destroy the wormhole. Stephen Hawking conjectured that not only would the pileup of vacuum fluctuations still succeed in destroying the wormhole in quantum gravity, but also that the laws of physics would ultimately prevent any type of time machine from forming; this is the chronology protection conjecture.
Subsequent works in semiclassical gravity provided examples of spacetimes with closed timelike curves where the energy density due to vacuum fluctuations does not approach infinity in the region of spacetime outside the Cauchy horizon. However, in 1997 a general proof was found demonstrating that according to semiclassical gravity, the energy of the quantum field (more precisely, the expectation value of the quantum stress-energy tensor) must always be either infinite or undefined on the horizon itself. Both cases indicate that semiclassical methods become unreliable at the horizon and quantum gravity effects would be important there, consistent with the possibility that such effects would always intervene to prevent time machines from forming.
A definite theoretical decision on the status of the chronology protection conjecture would require a full theory of quantum gravity as opposed to semiclassical methods. There are also some arguments from string theory that seem to support chronology protection, but string theory is not yet a complete theory of quantum gravity. Experimental observation of closed timelike curves would of course demonstrate this conjecture to be false, but short of that, if physicists had a theory of quantum gravity whose predictions had been well-confirmed in other areas, this would give them a significant degree of confidence in the theory's predictions about the possibility or impossibility of time travel.
Other proposals that allow for backwards time travel but prevent time paradoxes, such as the Novikov self-consistency principle, which would ensure the timeline stays consistent, or the idea that a time traveler is taken to a parallel universe while their original timeline remains intact, do not qualify as "chronology protection".
![{\displaystyle \rho _{\text{CTC}}={\text{Tr}}_{A}\left[U\left(\rho _{A}\otimes \rho _{\text{CTC}}\right)U^{\dagger }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/899893034677f871b619e995c8b8b4139f5e0169)


![{\displaystyle \rho _{f}={\frac {C\rho _{i}C^{\dagger }}{{\text{Tr}}\left[C\rho _{i}C^{\dagger }\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66a8d66d08bd0e3ea453d3dae97759fc6cae15f0)
![{\displaystyle C={\text{Tr}}_{\text{CTC}}\left[U\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8a14fd5f6200d9a3e61ef2ccc5cde74dae00af5)




![{\displaystyle {\text{Tr}}\left[C\rho _{i}C^{\dagger }\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5f6bef6c7060324d7bc028c4a2809d8ff7acf90)