Commonsense reasoning

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Commonsense_reasoning

In artificial intelligence (AI), commonsense reasoning is a human-like ability to make presumptions about the type and essence of ordinary situations humans encounter every day. These assumptions include judgments about the nature of physical objects, taxonomic properties, and peoples' intentions. A device that exhibits commonsense reasoning might be capable of drawing conclusions that are similar to humans' folk psychology (humans' innate ability to reason about people's behavior and intentions) and naive physics (humans' natural understanding of the physical world).

Definitions and characterizations

Some definitions and characterizations of common sense from different authors include:

• "Commonsense knowledge includes the basic facts about events (including actions) and their effects, facts about knowledge and how it is obtained, facts about beliefs and desires. It also includes the basic facts about material objects and their properties."
• "Commonsense knowledge differs from encyclopedic knowledge in that it deals with general knowledge rather than the details of specific entities."
• Commonsense knowledge is "real world knowledge that can provide a basis for additional knowledge to be gathered and interpreted automatically".
• The commonsense world consists of "time, space, physical interactions, people, and so on".
• Common sense is "all the knowledge about the world that we take for granted but rarely state out loud".
• Common sense is "broadly reusable background knowledge that's not specific to a particular subject area... knowledge that you ought to have."

NYU professor Ernest Davis characterizes commonsense knowledge as "what a typical seven year old knows about the world", including physical objects, substances, plants, animals, and human society. It usually excludes book-learning, specialized knowledge, and knowledge of conventions; but it sometimes includes knowledge about those topics. For example, knowing how to play cards is specialized knowledge, not "commonsense knowledge"; but knowing that people play cards for fun does count as "commonsense knowledge".

Commonsense reasoning problem

A self-driving car system may use a neural network to determine which parts of the picture seem to match previous training images of pedestrians, and then model those areas as slow-moving but somewhat unpredictable rectangular prisms that must be avoided.

Compared with humans, existing AI lacks several features of human commonsense reasoning; most notably, humans have powerful mechanisms for reasoning about "naïve physics" such as space, time, and physical interactions. This enables even young children to easily make inferences like "If I roll this pen off a table, it will fall on the floor". Humans also have a powerful mechanism of "folk psychology" that helps them to interpret natural-language sentences such as "The city councilmen refused the demonstrators a permit because they advocated violence". (A generic AI has difficulty discerning whether the ones alleged to be advocating violence are the councilmen or the demonstrators.) This lack of "common knowledge" means that AI often makes different mistakes than humans make, in ways that can seem incomprehensible. For example, existing self-driving cars cannot reason about the location nor the intentions of pedestrians in the exact way that humans do, and instead must use non-human modes of reasoning to avoid accidents.

Overlapping subtopics of commonsense reasoning include quantities and measurements, time and space, physics, minds, society, plans and goals, and actions and change.

Commonsense knowledge problem

Main article: Commonsense knowledge (artificial intelligence)

The commonsense knowledge problem is a current project in the sphere of artificial intelligence to create a database that contains the general knowledge most individuals are expected to have, represented in an accessible way to artificial intelligence programs that use natural language. Due to the broad scope of the commonsense knowledge, this issue is considered to be among the most difficult problems in AI research. In order for any task to be done as a human mind would manage it, the machine is required to appear as intelligent as a human being. Such tasks include object recognition, machine translation and text mining. To perform them, the machine has to be aware of the same concepts that an individual, who possess commonsense knowledge, recognizes.

Commonsense in intelligent tasks

In 1961, Bar Hillel first discussed the need and significance of practical knowledge for natural language processing in the context of machine translation. Some ambiguities are resolved by using simple and easy to acquire rules. Others require a broad acknowledgement of the surrounding world, thus they require more commonsense knowledge. For instance, when a machine is used to translate a text, problems of ambiguity arise, which could be easily resolved by attaining a concrete and true understanding of the context. Online translators often resolve ambiguities using analogous or similar words. For example, in translating the sentences "The electrician is working" and "The telephone is working" into German, the machine translates correctly "working" in the means of "laboring" in the first one and as "functioning properly" in the second one. The machine has seen and read in the body of texts that the German words for "laboring" and "electrician" are frequently used in a combination and are found close together. The same applies for "telephone" and "function properly". However, the statistical proxy which works in simple cases often fails in complex ones. Existing computer programs carry out simple language tasks by manipulating short phrases or separate words, but they don't attempt any deeper understanding and focus on short-term results.

Computer vision

Issues of this kind arise in computer vision. For instance when looking at a photograph of a bathroom some items that are small and only partly seen, such as facecloths and bottles, are recognizable due to the surrounding objects (toilet, wash basin, bathtub), which suggest the purpose of the room. In an isolated image they would be difficult to identify. Movies prove to be even more difficult tasks. Some movies contain scenes and moments that cannot be understood by simply matching memorized templates to images. For instance, to understand the context of the movie, the viewer is required to make inferences about characters’ intentions and make presumptions depending on their behavior. In the contemporary state of the art, it is impossible to build and manage a program that will perform such tasks as reasoning, i.e. predicting characters’ actions. The most that can be done is to identify basic actions and track characters.

Robotic manipulation

The need and importance of commonsense reasoning in autonomous robots that work in a real-life uncontrolled environment is evident. For instance, if a robot is programmed to perform the tasks of a waiter at a cocktail party, and it sees that the glass he had picked up is broken, the waiter-robot should not pour the liquid into the glass, but instead pick up another one. Such tasks seem obvious when an individual possesses simple commonsense reasoning, but to ensure that a robot will avoid such mistakes is challenging.

Successes in automated commonsense reasoning

Significant progress in the field of the automated commonsense reasoning is made in the areas of the taxonomic reasoning, actions and change reasoning, reasoning about time. Each of these spheres has a well-acknowledged theory for wide range of commonsense inferences.

Taxonomic reasoning

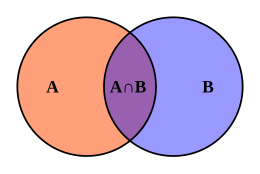
Taxonomy is the collection of individuals and categories and their relations. Three basic relations are:

• An individual is an instance of a category. For example, the individual Tweety is an instance of the category robin.
• One category is a subset of another. For instance robin is a subset of bird.
• Two categories are disjoint. For instance robin is disjoint from penguin.

Transitivity is one type of inference in taxonomy. Since Tweety is an instance of robin and robin is a subset of bird, it follows that Tweety is an instance of bird. Inheritance is another type of inference. Since Tweety is an instance of robin, which is a subset of bird and bird is marked with property canfly, it follows that Tweety and robin have property canfly. When an individual taxonomizes more abstract categories, outlining and delimiting specific categories becomes more problematic. Simple taxonomic structures are frequently used in AI programs. For instance, WordNet is a resource including a taxonomy, whose elements are meanings of English words. Web mining systems used to collect commonsense knowledge from Web documents focus on taxonomic relations and specifically in gathering taxonomic relations.

Action and change

The theory of action, events and change is another range of the commonsense reasoning. There are established reasoning methods for domains that satisfy the constraints listed below:

• Events are atomic, meaning one event occurs at a time and the reasoner needs to consider the state and condition of the world at the start and at the finale of the specific event, but not during the states, while there is still an evidence of on-going changes (progress).
• Every single change is a result of some event
• Events are deterministic, meaning the world's state at the end of the event is defined by the world's state at the beginning and the specification of the event.
• There is a single actor and all events are their actions.
• The relevant state of the world at the beginning is either known or can be calculated.

Temporal reasoning

Further information: Spatial–temporal reasoning

Temporal reasoning is the ability to make presumptions about humans' knowledge of times, durations and time intervals. For example, if an individual knows that Mozart was born after Haydn and died earlier than him, they can use their temporal reasoning knowledge to deduce that Mozart had died younger than Haydn. The inferences involved reduce themselves to solving systems of linear inequalities. To integrate that kind of reasoning with concrete purposes, such as natural language interpretation, is more challenging, because natural language expressions have context dependent interpretation. Simple tasks such as assigning timestamps to procedures cannot be done with total accuracy.

Qualitative reasoning

Qualitative reasoning is the form of commonsense reasoning analyzed with certain success. It is concerned with the direction of change in interrelated quantities. For instance, if the price of a stock goes up, the amount of stocks that are going to be sold will go down. If some ecosystem contains wolves and lambs and the number of wolves decreases, the death rate of the lambs will go down as well. This theory was firstly formulated by Johan de Kleer, who analyzed an object moving on a roller coaster. The theory of qualitative reasoning is applied in many spheres such as physics, biology, engineering, ecology, etc. It serves as the basis for many practical programs, analogical mapping, text understanding.

Challenges in automating commonsense reasoning

As of 2014, there are some commercial systems trying to make the use of commonsense reasoning significant. However, they use statistical information as a proxy for commonsense knowledge, where reasoning is absent. Current programs manipulate individual words, but they don't attempt or offer further understanding. According to Ernest Davis and Gary Marcus, five major obstacles interfere with the producing of a satisfactory "commonsense reasoner".

• First, some of the domains that are involved in commonsense reasoning are only partly understood. Individuals are far from a comprehensive understanding of domains such as communication and knowledge, interpersonal interactions or physical processes.

• Second, situations that seem easily predicted or assumed about could have logical complexity, which humans’ commonsense knowledge does not cover. Some aspects of similar situations are studied and are well understood, but there are many relations that are unknown, even in principle and how they could be represented in a form that is usable by computers.

• Third, commonsense reasoning involves plausible reasoning. It requires coming to a reasonable conclusion given what is already known. Plausible reasoning has been studied for many years and there are a lot of theories developed that include probabilistic reasoning and non-monotonic logic. It takes different forms that include using unreliable data and rules, whose conclusions are not certain sometimes.

• Fourth, there are many domains, in which a small number of examples are extremely frequent, whereas there is a vast number of highly infrequent examples.

• Fifth, when formulating presumptions it is challenging to discern and determine the level of abstraction.

Compared with humans, as of 2018 existing computer programs perform extremely poorly on modern "commonsense reasoning" benchmark tests such as the Winograd Schema Challenge. The problem of attaining human-level competency at "commonsense knowledge" tasks is considered to probably be "AI complete" (that is, solving it would require the ability to synthesize a human-level intelligence). Some researchers believe that supervised learning data is insufficient to produce an artificial general intelligence capable of commonsense reasoning, and have therefore turned to less-supervised learning techniques.

Approaches and techniques

Commonsense's reasoning study is divided into knowledge-based approaches and approaches that are based on machine learning over and using a large data corpora with limited interactions between these two types of approaches. There are also crowdsourcing approaches, attempting to construct a knowledge basis by linking the collective knowledge and the input of non-expert people. Knowledge-based approaches can be separated into approaches based on mathematical logic.

In knowledge-based approaches, the experts are analyzing the characteristics of the inferences that are required to do reasoning in a specific area or for a certain task. The knowledge-based approaches consist of mathematically grounded approaches, informal knowledge-based approaches and large-scale approaches. The mathematically grounded approaches are purely theoretical and the result is a printed paper instead of a program. The work is limited to the range of the domains and the reasoning techniques that are being reflected on. In informal knowledge-based approaches, theories of reasoning are based on anecdotal data and intuition that are results from empirical behavioral psychology. Informal approaches are common in computer programming. Two other popular techniques for extracting commonsense knowledge from Web documents involve Web mining and Crowd sourcing.

COMET (2019), which uses both the OpenAI GPT language model architecture and existing commonsense knowledge bases such as ConceptNet, claims to generate commonsense inferences at a level approaching human benchmarks. Like many other current efforts, COMET over-relies on surface language patterns and is judged to lack deep human-level understanding of many commonsense concepts. Other language-model approaches include training on visual scenes rather than just text, and training on textual descriptions of scenarios involving commonsense physics.

Necessity and sufficiency

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Necessity_and_sufficiency

In logic and mathematics, necessity and sufficiency are terms used to describe a conditional or implicational relationship between two statements. For example, in the conditional statement: "If P then Q", Q is necessary for P, because the truth of Q is guaranteed by the truth of P. (Equivalently, it is impossible to have P without Q, or the falsity of Q ensures the falsity of P.) Similarly, P is sufficient for Q, because P being true always implies that Q is true, but P not being true does not always imply that Q is not true.

In general, a necessary condition is one (possibly one of several conditions) that must be present in order for another condition to occur, while a sufficient condition is one that produces the said condition. The assertion that a statement is a "necessary and sufficient" condition of another means that the former statement is true if and only if the latter is true. That is, the two statements must be either simultaneously true, or simultaneously false.

In ordinary English (also natural language) "necessary" and "sufficient" indicate relations between conditions or states of affairs, not statements. For example, being a man is a necessary condition for being a brother, but it is not sufficient—while being a man sibling is a necessary and sufficient condition for being a brother. Any conditional statement consists of at least one sufficient condition and at least one necessary condition.

In data analytics, necessity and sufficiency can refer to different causal logics, where necessary condition analysis and qualitative comparative analysis can be used as analytical techniques for examining necessity and sufficiency of conditions for a particular outcome of interest.

Definitions

In the conditional statement, "if S, then N", the expression represented by S is called the antecedent, and the expression represented by N is called the consequent. This conditional statement may be written in several equivalent ways, such as "N if S", "S only if N", "S implies N", "N is implied by S", S → N , S ⇒ N and "N whenever S".

In the above situation of "N whenever S," N is said to be a necessary condition for S. In common language, this is equivalent to saying that if the conditional statement is a true statement, then the consequent N must be true—if S is to be true (see third column of "truth table" immediately below). In other words, the antecedent S cannot be true without N being true. For example, in order for someone to be called Socrates, it is necessary for that someone to be Named. Similarly, in order for human beings to live, it is necessary that they have air.

One can also say S is a sufficient condition for N (refer again to the third column of the truth table immediately below). If the conditional statement is true, then if S is true, N must be true; whereas if the conditional statement is true and N is true, then S may be true or be false. In common terms, "the truth of S guarantees the truth of N". For example, carrying on from the previous example, one can say that knowing that someone is called Socrates is sufficient to know that someone has a Name.

A necessary and sufficient condition requires that both of the implications ${\displaystyle S\Rightarrow N}$ and ${\displaystyle N\Rightarrow S}$ (the latter of which can also be written as ${\displaystyle S\Leftarrow N}$) hold. The first implication suggests that S is a sufficient condition for N, while the second implication suggests that S is a necessary condition for N. This is expressed as "S is necessary and sufficient for N ", "S if and only if N ", or ${\displaystyle S\iff N}$.

Truth table

S	N	${\displaystyle S\Rightarrow N}$	${\displaystyle S\Leftarrow N}$	${\displaystyle S\iff N}$
T	T	T	T	T
T	F	F	T	F
F	T	T	F	F
F	F	T	T	T

Necessity

The sun being above the horizon is a necessary condition for direct sunlight; but it is not a sufficient condition, as something else may be casting a shadow, e.g., the moon in the case of an eclipse.

The assertion that Q is necessary for P is colloquially equivalent to "P cannot be true unless Q is true" or "if Q is false, then P is false". By contraposition, this is the same thing as "whenever P is true, so is Q".

The logical relation between P and Q is expressed as "if P, then Q" and denoted "P ⇒ Q" (P implies Q). It may also be expressed as any of "P only if Q", "Q, if P", "Q whenever P", and "Q when P". One often finds, in mathematical prose for instance, several necessary conditions that, taken together, constitute a sufficient condition (i.e., individually necessary and jointly sufficient), as shown in Example 5.

Example 1

For it to be true that "John is a bachelor", it is necessary that it be also true that he is

1. unmarried,
2. male,
3. adult,

since to state "John is a bachelor" implies John has each of those three additional predicates.

Example 2

For the whole numbers greater than two, being odd is necessary to being prime, since two is the only whole number that is both even and prime.

Example 3

Consider thunder, the sound caused by lightning. One says that thunder is necessary for lightning, since lightning never occurs without thunder. Whenever there is lightning, there is thunder. The thunder does not cause the lightning (since lightning causes thunder), but because lightning always comes with thunder, we say that thunder is necessary for lightning. (That is, in its formal sense, necessity doesn't imply causality.)

Example 4

Being at least 30 years old is necessary for serving in the U.S. Senate. If you are under 30 years old, then it is impossible for you to be a senator. That is, if you are a senator, it follows that you must be at least 30 years old.

Example 5

In algebra, for some set S together with an operation ${\displaystyle \star }$ to form a group, it is necessary that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle \star} be associative. It is also necessary that S include a special element e such that for every x in S, it is the case that e ${\displaystyle \star }$ x and x ${\displaystyle \star }$ e both equal x. It is also necessary that for every x in S there exist a corresponding element x″, such that both x ${\displaystyle \star }$ x″ and x″ ${\displaystyle \star }$ x equal the special element e. None of these three necessary conditions by itself is sufficient, but the conjunction of the three is.

Sufficiency

That a train runs on schedule is a sufficient condition for arriving on time (if one boards the train and it departs on time, then one will arrive on time); but it is not a necessary condition, since there are other ways to travel (if the train does not run to time, one could still arrive on time through other means of transport).

If P is sufficient for Q, then knowing P to be true is adequate grounds to conclude that Q is true; however, knowing P to be false does not meet a minimal need to conclude that Q is false.

The logical relation is, as before, expressed as "if P, then Q" or "P ⇒ Q". This can also be expressed as "P only if Q", "P implies Q" or several other variants. It may be the case that several sufficient conditions, when taken together, constitute a single necessary condition (i.e., individually sufficient and jointly necessary), as illustrated in example 5.

Example 1

"John is a king" implies that John is male. So knowing that John is a king is sufficient to knowing that he is a male.

Example 2

A number's being divisible by 4 is sufficient (but not necessary) for it to be even, but being divisible by 2 is both sufficient and necessary for it to be even.

Example 3

An occurrence of thunder is a sufficient condition for the occurrence of lightning in the sense that hearing thunder, and unambiguously recognizing it as such, justifies concluding that there has been a lightning bolt.

Example 4

If the U.S. Congress passes a bill, the president's signing of the bill is sufficient to make it law. Note that the case whereby the president did not sign the bill, e.g. through exercising a presidential veto, does not mean that the bill has not become a law (for example, it could still have become a law through a congressional override).

Example 5

That the center of a playing card should be marked with a single large spade (♠) is sufficient for the card to be an ace. Three other sufficient conditions are that the center of the card be marked with a single diamond (♦), heart (♥), or club (♣). None of these conditions is necessary to the card's being an ace, but their disjunction is, since no card can be an ace without fulfilling at least (in fact, exactly) one of these conditions.

Relationship between necessity and sufficiency

Being in the purple region is sufficient for being in A, but not necessary. Being in A is necessary for being in the purple region, but not sufficient. Being in A and being in B is necessary and sufficient for being in the purple region.

A condition can be either necessary or sufficient without being the other. For instance, being a mammal (N) is necessary but not sufficient to being human (S), and that a number ${\displaystyle x}$ is rational (S) is sufficient but not necessary to ${\displaystyle x}$ being a real number (N) (since there are real numbers that are not rational).

A condition can be both necessary and sufficient. For example, at present, "today is the Fourth of July" is a necessary and sufficient condition for "today is Independence Day in the United States". Similarly, a necessary and sufficient condition for invertibility of a matrix M is that M has a nonzero determinant.

Mathematically speaking, necessity and sufficiency are dual to one another. For any statements S and N, the assertion that "N is necessary for S" is equivalent to the assertion that "S is sufficient for N". Another facet of this duality is that, as illustrated above, conjunctions (using "and") of necessary conditions may achieve sufficiency, while disjunctions (using "or") of sufficient conditions may achieve necessity. For a third facet, identify every mathematical predicate N with the set T(N) of objects, events, or statements for which N holds true; then asserting the necessity of N for S is equivalent to claiming that T(N) is a superset of T(S), while asserting the sufficiency of S for N is equivalent to claiming that T(S) is a subset of T(N).

Psychologically speaking, necessity and sufficiency are both key aspects of the classical view of concepts. Under the classical theory of concepts, how human minds represent a category X, gives rise to a set of individually necessary conditions that define X. Together, these individually necessary conditions are sufficient to be X. This contrasts with the probabilistic theory of concepts which states that no defining feature is necessary or sufficient, rather that categories resemble a family tree structure.

Simultaneous necessity and sufficiency

See also: Material equivalence

To say that P is necessary and sufficient for Q is to say two things:

1. that P is necessary for Q, ${\displaystyle P\Leftarrow Q}$, and that P is sufficient for Q, ${\displaystyle P\Rightarrow Q}$.
2. equivalently, it may be understood to say that P and Q is necessary for the other, ${\displaystyle P\Rightarrow Q\wedge Q\Rightarrow P}$, which can also be stated as each is sufficient for or implies the other.

One may summarize any, and thus all, of these cases by the statement "P if and only if Q", which is denoted by ${\displaystyle P\iff Q}$, whereas cases tell us that ${\displaystyle P\iff Q}$ is identical to ${\displaystyle P\Rightarrow Q\wedge Q\Rightarrow P}$.

For example, in graph theory a graph G is called bipartite if it is possible to assign to each of its vertices the color black or white in such a way that every edge of G has one endpoint of each color. And for any graph to be bipartite, it is a necessary and sufficient condition that it contain no odd-length cycles. Thus, discovering whether a graph has any odd cycles tells one whether it is bipartite and conversely. A philosopher might characterize this state of affairs thus: "Although the concepts of bipartiteness and absence of odd cycles differ in intension, they have identical extension.

In mathematics, theorems are often stated in the form "P is true if and only if Q is true".

Because, as explained in previous section, necessity of one for the other is equivalent to sufficiency of the other for the first one, e.g. ${\displaystyle P\Leftarrow Q}$ is equivalent to ${\displaystyle Q\Rightarrow P}$, if P is necessary and sufficient for Q, then Q is necessary and sufficient for P. We can write ${\displaystyle P\iff Q\equiv Q\iff P}$ and say that the statements "P is true if and only if Q, is true" and "Q is true if and only if P is true" are equivalent.

Eternity of the world

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Eternity_of_the_world 

 

Time

The eternity of the world is the question of whether the world has a beginning in time or has existed for eternity. It was a concern for ancient philosophers as well as theologians and philosophers of the 13th century, and is also of interest to modern philosophers and scientists. The problem became a focus of a dispute in the 13th century, when some of the works of Aristotle, who believed in the eternity of the world, were rediscovered in the Latin West. This view conflicted with the view of the Catholic Church that the world had a beginning in time. The Aristotelian view was prohibited in the Condemnations of 1210–1277.

Aristotle

The ancient Greek philosopher Aristotle argued that the world must have existed from eternity in his Physics as follows. In Book I, he argues that everything that comes into existence does so from a substratum. Therefore, if the underlying matter of the universe came into existence, it would come into existence from a substratum. But the nature of matter is precisely to be the substratum from which other things arise. Consequently, the underlying matter of the universe could have come into existence only from an already existing matter exactly like itself; to assume that the underlying matter of the universe came into existence would require assuming that an underlying matter already existed. As this assumption is self-contradictory, Aristotle argued, matter must be eternal.

In Book VIII, his argument from motion is that if an absolute beginning of motion should be assumed, the object to undergo the first motion must either:

1. have come into existence and begun to move, or
2. have existed in an eternal state of rest before beginning to move.

Option A is self-contradictory because an object cannot move before it comes into existence, and the act of coming into existence is itself a "movement," so that the first movement requires a movement before it, that is, the act of coming into existence. Option B is also unsatisfactory for two reasons:

• First, if the world began at a state of rest, the coming into existence of that state of rest would itself have been motion.
• Second, if the world changed from a state of rest to a state of motion, the cause of that change to motion would itself have been a motion.

He concludes that motion is necessarily eternal.

Aristotle argued that a "vacuum" (that is, a place where there is no matter) is impossible. Material objects can come into existence only in place, that is, occupy space. Were something to come from nothing, "the place to be occupied by what comes into existence would previously have been occupied by a vacuum, inasmuch as no body existed." But a vacuum is impossible, and matter must be eternal.

The Greek philosopher Critolaus (c. 200-c. 118 BC) of Phaselis defended Aristotle's doctrine of the eternity of the world, and of the human race in general, against the Stoics. There is no observed change in the natural order of things; mankind recreates itself in the same manner according to the capacity given by Nature, and the various ills to which it is heir, though fatal to individuals, do not avail to modify the whole. Just as it is absurd to suppose that humans are merely earth-born, so the possibility of their ultimate destruction is inconceivable. The world, as the manifestation of eternal order, must itself be eternal.

The Neo-Platonists

The Neoplatonist philosopher Proclus (412 – 485 AD) advanced in his De Aeternitate Mundi (On the Eternity of the World) eighteen proofs for the eternity of the world, resting on the divinity of its creator.

John Philoponus in 529 wrote his critique Against Proclus On the Eternity of the World in which he systematically argued against every proposition put forward for the eternity of the world. The intellectual battle against eternalism became one of Philoponus’ major preoccupations and dominated several of his publications (some now lost) over the following decade.

Philoponus originated the argument now known as the Traversal of the infinite. If the existence of something requires that something else exist before it, then the first thing cannot come into existence without the thing before it existing. An infinite number cannot actually exist, nor be counted through or 'traversed,' or be increased. Something cannot come into existence if this requires an infinite number of other things existing before it. Therefore, the world cannot be infinite.

The Aristotelian commentator Simplicius of Cilicia and contemporary of Philoponus held that Philoponus’ arguments relied on a fundamental misunderstanding of Aristotelian physics: “To my mind I have demonstrated that when this man objected against these demonstrations he did not comprehend a thing of what Aristotle said.” Simplicius adhered to the Aristotelian doctrine of the eternity of the world and strongly opposed Philoponus, who asserted the beginning of the world through divine creation.

Philoponus' arguments

Philoponus' arguments for temporal finitism were severalfold. Contra Aristotlem has been lost, and is chiefly known through the citations used by Simplicius of Cilicia in his commentaries on Aristotle's Physics and De Caelo. Philoponus' refutation of Aristotle extended to six books, the first five addressing De Caelo and the sixth addressing Physics, and from comments on Philoponus made by Simplicius can be deduced to have been quite lengthy.

A full exposition of Philoponus' several arguments, as reported by Simplicius, can be found in Sorabji. One such argument was based upon Aristotle's own theorem that there were not multiple infinities, and ran as follows: If time were infinite, then as the universe continued in existence for another hour, the infinity of its age since creation at the end of that hour must be one hour greater than the infinity of its age since creation at the start of that hour. But since Aristotle holds that such treatments of infinity are impossible and ridiculous, the world cannot have existed for infinite time.

Philoponus's works were adopted by many; his first argument against an infinite past being the "argument from the impossibility of the existence of an actual infinite", which states:

"An actual infinite cannot exist."

"An infinite temporal regress of events is an actual infinite."

"Thus an infinite temporal regress of events cannot exist."

This argument defines event as equal increments of time. Philoponus argues that the second premise is not controversial since the number of events prior to today would be an actual infinite without beginning if the universe is eternal. The first premise is defended by a reductio ad absurdum where Philoponus shows that actual infinites can not exist in the actual world because they would lead to contradictions albeit being a possible mathematical enterprise. Since an actual infinite in reality would create logical contradictions, it can not exist including the actual infinite set of past events. The second argument, the "argument from the impossibility of completing an actual infinite by successive addition", states:

"An actual infinite cannot be completed by successive addition."

"The temporal series of past events has been completed by successive addition."

"Thus the temporal series of past events cannot be an actual infinite."

The first statement states, correctly, that a finite (number) cannot be made into an infinite one by the finite addition of more finite numbers. The second skirts around this; the analogous idea in mathematics, that the (infinite) sequence of negative integers "..-3, -2, -1" may be extended by appending zero, then one, and so forth; is perfectly valid.

Medieval period

Avicenna argued that prior to a thing's coming into actual existence, its existence must have been 'possible.' Were its existence necessary, the thing would already have existed, and were its existence impossible, the thing would never exist. The possibility of the thing must therefore in some sense have its own existence. Possibility cannot exist in itself, but must reside within a subject. If an already existent matter must precede everything coming into existence, clearly nothing, including matter, can come into existence ex nihilo, that is, from absolute nothingness. An absolute beginning of the existence of matter is therefore impossible.

The Aristotelian commentator Averroes supported Aristotle's view, particularly in his work The Incoherence of the Incoherence (Tahafut al-tahafut), in which he defended Aristotelian philosophy against al-Ghazali's claims in The Incoherence of the Philosophers (Tahafut al-falasifa).

Averroes' contemporary Maimonides challenged Aristotle's assertion that "everything in existence comes from a substratum," on that basis that his reliance on induction and analogy is a fundamentally flawed means of explaining unobserved phenomenon. According to Maimonides, to argue that "because I have never observed something coming into existence without coming from a substratum it cannot occur" is equivalent to arguing that "because I cannot empirically observe eternity it does not exist."

Maimonides himself held that neither creation nor Aristotle's infinite time were provable, or at least that no proof was available. (According to scholars of his work, he didn't make a formal distinction between unprovability and the simple absence of proof.) However, some of Maimonides' Jewish successors, including Gersonides and Crescas, conversely held that the question was decidable, philosophically.

In the West, the 'Latin Averroists' were a group of philosophers writing in Paris in the middle of the thirteenth century, who included Siger of Brabant, Boethius of Dacia. They supported Aristotle's doctrine of the eternity of the world against conservative theologians such as John Pecham and Bonaventure. The conservative position is that the world can be logically proved to have begun in time, of which the classic exposition is Bonaventure's argument in the second book of his commentary on Peter Lombard's sentences, where he repeats Philoponus' case against a traversal of the infinite.

Thomas Aquinas, like Maimonides, argued against both the conservative theologians and the Averroists, claiming that neither the eternity nor the finite nature of the world could be proved by logical argument alone. According to Aquinas the possible eternity of the world and its creation would be contradictory if an efficient cause were to precede its effect in duration or if non-existence precedes existence in duration. But an efficient cause, such as God, which instantaneously produces its effect would not necessarily precede its effect in duration. God can also be distinguished from a natural cause which produces its effect by motion, for a cause that produces motion must precede its effect. God could be an instantaneous and motionless creator, and could have created the world without preceding it in time. To Aquinas, that the world began was an article of faith.

The position of the Averroists was condemned by Stephen Tempier in 1277.

Giordano Bruno, famously, believed in eternity of the world (and this was one of the heretical beliefs for which he was burned at the stake).

Modernity

The question of the eternity of the world remains unsettled; Alexander Vilenkin is a famous proponent of the view that the world had a beginning, while it is also known that its eternity is a physically consistent possibility.

Zeno's paradoxes

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Zeno%27s_paradoxes

Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through the works of Plato, Aristotle, and later commentators like Simplicius of Cilicia. Zeno devised these paradoxes to support his teacher Parmenides's philosophy of monism, which posits that despite our sensory experiences, reality is singular and unchanging. The paradoxes famously challenge the notions of plurality (the existence of many things), motion, space, and time by suggesting they lead to logical contradictions.

Zeno's work, primarily known from second-hand accounts since his original texts are lost, comprises forty "paradoxes of plurality," which argue against the coherence of believing in multiple existences, and several arguments against motion and change. Of these, only a few are definitively known today, including the renowned "Achilles Paradox", which illustrates the problematic concept of infinite divisibility in space and time. In this paradox, Zeno argues that a swift runner like Achilles cannot overtake a slower moving tortoise with a head start, because the distance between them can be infinitely subdivided, implying Achilles would require an infinite number of steps to catch the tortoise.

These paradoxes have stirred extensive philosophical and mathematical discussion throughout history, particularly regarding the nature of infinity and the continuity of space and time. Initially, Aristotle's interpretation, suggesting a potential rather than actual infinity, was widely accepted. However, modern solutions leveraging the mathematical framework of calculus have provided a different perspective, highlighting Zeno's significant early insight into the complexities of infinity and continuous motion. Zeno's paradoxes remain a pivotal reference point in the philosophical and mathematical exploration of reality, motion, and the infinite, influencing both ancient thought and modern scientific understanding.

History

The origins of the paradoxes are somewhat unclear, but they are generally thought to have been developed to support Parmenides' doctrine of monism, that all of reality is one, and that all change is impossible, that is, that nothing ever changes in location or in any other respect. Diogenes Laërtius, citing Favorinus, says that Zeno's teacher Parmenides was the first to introduce the paradox of Achilles and the tortoise. But in a later passage, Laërtius attributes the origin of the paradox to Zeno, explaining that Favorinus disagrees. Modern academics attribute the paradox to Zeno.

Many of these paradoxes argue that contrary to the evidence of one's senses, motion is nothing but an illusion. In Plato's Parmenides (128a–d), Zeno is characterized as taking on the project of creating these paradoxes because other philosophers claimed paradoxes arise when considering Parmenides' view. Zeno's arguments may then be early examples of a method of proof called reductio ad absurdum, also known as proof by contradiction. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point. They are also credited as a source of the dialectic method used by Socrates.

Paradoxes

Some of Zeno's nine surviving paradoxes (preserved in Aristotle's Physics and Simplicius's commentary thereon) are essentially equivalent to one another. Aristotle offered a response to some of them. Popular literature often misrepresents Zeno's arguments. For example, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the sum, but rather with finishing a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?

Paradoxes of motion

Three of the strongest and most famous—that of Achilles and the tortoise, the Dichotomy argument, and that of an arrow in flight—are presented in detail below.

Dichotomy paradox

The dichotomy

That which is in locomotion must arrive at the half-way stage before it arrives at the goal.

— as recounted by Aristotle, Physics VI:9, 239b10

Suppose Atalanta wishes to walk to the end of a path. Before she can get there, she must get halfway there. Before she can get halfway there, she must get a quarter of the way there. Before traveling a quarter, she must travel one-eighth; before an eighth, one-sixteenth; and so on.

The resulting sequence can be represented as:

${\displaystyle \left\{\cdots ,\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1\right\}}$

This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.

This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can be neither completed nor begun, and so all motion must be an illusion.

This argument is called the "Dichotomy" because it involves repeatedly splitting a distance into two parts. An example with the original sense can be found in an asymptote. It is also known as the Race Course paradox.

Achilles and the tortoise

"Achilles and the Tortoise" redirects here. For other uses, see Achilles and the Tortoise (disambiguation).

 

See also: Infinity § Zeno: Achilles and the tortoise

Achilles and the tortoise

In a race, the quickest runner can never over­take the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.

— as recounted by Aristotle, Physics VI:9, 239b15

In the paradox of Achilles and the tortoise, Achilles is in a footrace with a tortoise. Achilles allows the tortoise a head start of 100 meters, for example. Suppose that each racer starts running at some constant speed, one faster than the other. After some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say 2 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles arrives somewhere the tortoise has been, he still has some distance to go before he can even reach the tortoise. As Aristotle noted, this argument is similar to the Dichotomy. It lacks, however, the apparent conclusion of motionlessness.

Arrow paradox

The arrow

Not to be confused with other paradoxes of the same name.

If everything when it occupies an equal space is at rest at that instant of time, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless at that instant of time and at the next instant of time but if both instants of time are taken as the same instant or continuous instant of time then it is in motion.

— as recounted by Aristotle, Physics VI:9, 239b5

In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that at any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not. It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.

Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.

Other paradoxes

Aristotle gives three other paradoxes.

Paradox of place

From Aristotle:

If everything that exists has a place, place too will have a place, and so on ad infinitum.

Paradox of the grain of millet

Description of the paradox from the Routledge Dictionary of Philosophy:

The argument is that a single grain of millet makes no sound upon falling, but a thousand grains make a sound. Hence a thousand nothings become something, an absurd conclusion.

Aristotle's response:

Zeno's reasoning is false when he argues that there is no part of the millet that does not make a sound: for there is no reason why any such part should not in any length of time fail to move the air that the whole bushel moves in falling. In fact it does not of itself move even such a quantity of the air as it would move if this part were by itself: for no part even exists otherwise than potentially.

Description from Nick Huggett:

This is a Parmenidean argument that one cannot trust one's sense of hearing. Aristotle's response seems to be that even inaudible sounds can add to an audible sound.

The moving rows (or stadium)

The moving rows

From Aristotle:

... concerning the two rows of bodies, each row being composed of an equal number of bodies of equal size, passing each other on a race-course as they proceed with equal velocity in opposite directions, the one row originally occupying the space between the goal and the middle point of the course and the other that between the middle point and the starting-post. This...involves the conclusion that half a given time is equal to double that time.

An expanded account of Zeno's arguments, as presented by Aristotle, is given in Simplicius's commentary On Aristotle's Physics.

According to Angie Hobbs of Sheffield university, this paradox is intended to be considered together with the paradox of Achilles and the Tortoise, problematizing the concept of discrete space & time where the other problematizes the concept of infinitely divisible space & time.

Proposed solutions

In classical antiquity

According to Simplicius, Diogenes the Cynic said nothing upon hearing Zeno's arguments, but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions. To fully solve any of the paradoxes, however, one needs to show what is wrong with the argument, not just the conclusions. Throughout history several solutions have been proposed, among the earliest recorded being those of Aristotle and Archimedes.

Aristotle (384 BC–322 BC) remarked that as the distance decreases, the time needed to cover those distances also decreases, so that the time needed also becomes increasingly small. Aristotle also distinguished "things infinite in respect of divisibility" (such as a unit of space that can be mentally divided into ever smaller units while remaining spatially the same) from things (or distances) that are infinite in extension ("with respect to their extremities"). Aristotle's objection to the arrow paradox was that "Time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles." Thomas Aquinas, commenting on Aristotle's objection, wrote "Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points, as we have already proved. Hence it does not follow that a thing is not in motion in a given time, just because it is not in motion in any instant of that time."

In modern mathematics

Some mathematicians and historians, such as Carl Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus provides a mathematical solution. Infinite processes remained theoretically troublesome in mathematics until the late 19th century. With the epsilon-delta definition of limit, Weierstrass and Cauchy developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes.

Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp) remain relevant metaphysical problems. While mathematics can calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Kevin Brown and Francis Moorcroft hold that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise. Brown concludes "Given the history of 'final resolutions', from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of 'Rorschach image' onto which people can project their most fundamental phenomenological concerns (if they have any)."

Henri Bergson

An alternative conclusion, proposed by Henri Bergson in his 1896 book Matter and Memory, is that, while the path is divisible, the motion is not.

Peter Lynds

In 2003, Peter Lynds argued that all of Zeno's motion paradoxes are resolved by the conclusion that instants in time and instantaneous magnitudes do not physically exist. Lynds argues that an object in relative motion cannot have an instantaneous or determined relative position (for if it did, it could not be in motion), and so cannot have its motion fractionally dissected as if it does, as is assumed by the paradoxes. Nick Huggett argues that Zeno is assuming the conclusion when he says that objects that occupy the same space as they do at rest must be at rest.

Bertrand Russell

Based on the work of Georg Cantor, Bertrand Russell offered a solution to the paradoxes, what is known as the "at-at theory of motion". It agrees that there can be no motion "during" a durationless instant, and contends that all that is required for motion is that the arrow be at one point at one time, at another point another time, and at appropriate points between those two points for intervening times. In this view motion is just change in position over time.

Hermann Weyl

Another proposed solution is to question one of the assumptions Zeno used in his paradoxes (particularly the Dichotomy), which is that between any two different points in space (or time), there is always another point. Without this assumption there are only a finite number of distances between two points, hence there is no infinite sequence of movements, and the paradox is resolved. According to Hermann Weyl, the assumption that space is made of finite and discrete units is subject to a further problem, given by the "tile argument" or "distance function problem". According to this, the length of the hypotenuse of a right angled triangle in discretized space is always equal to the length of one of the two sides, in contradiction to geometry. Jean Paul Van Bendegem has argued that the Tile Argument can be resolved, and that discretization can therefore remove the paradox.

Applications

Quantum Zeno effect

Main article: Quantum Zeno effect

In 1977, physicists E. C. George Sudarshan and B. Misra discovered that the dynamical evolution (motion) of a quantum system can be hindered (or even inhibited) through observation of the system. This effect is usually called the "Quantum Zeno effect" as it is strongly reminiscent of Zeno's arrow paradox. This effect was first theorized in 1958.

Zeno behaviour

In the field of verification and design of timed and hybrid systems, the system behaviour is called Zeno if it includes an infinite number of discrete steps in a finite amount of time. Some formal verification techniques exclude these behaviours from analysis, if they are not equivalent to non-Zeno behaviour. In systems design these behaviours will also often be excluded from system models, since they cannot be implemented with a digital controller.

Similar paradoxes

School of Names

Diagram of Hui Shi's stick paradox

Roughly contemporaneously during the Warring States period (475–221 BCE), ancient Chinese philosophers from the School of Names, a school of thought similarly concerned with logic and dialectics, developed paradoxes similar to those of Zeno. The works of the School of Names have largely been lost, with the exception of portions of the Gongsun Longzi. The second of the Ten Theses of Hui Shi suggests knowledge of infinitesimals:That which has no thickness cannot be piled up; yet it is a thousand li in dimension. Among the many puzzles of his recorded in the Zhuangzi is one very similar to Zeno's Dichotomy:

"If from a stick a foot long you every day take the half of it, in a myriad ages it will not be exhausted."

— Zhuangzi, chapter 33 (Legge translation)

The Mohist canon appears to propose a solution to this paradox by arguing that in moving across a measured length, the distance is not covered in successive fractions of the length, but in one stage. Due to the lack of surviving works from the School of Names, most of the other paradoxes listed are difficult to interpret.

Lewis Carroll's "What the Tortoise Said to Achilles"

Main article: What the Tortoise Said to Achilles

 

"What the Tortoise Said to Achilles", written in 1895 by Lewis Carroll, describes a paradoxical infinite regress argument in the realm of pure logic. It uses Achilles and the Tortoise as characters in a clear reference to Zeno's paradox of Achilles.