From Wikipedia, the free encyclopedia
In the physical sciences, subatomic particles are particles much smaller than atoms.[1] There are two types of subatomic particles: elementary particles, which according to current theories are not made of other particles; and composite particles.[2] Particle physics and nuclear physics study these particles and how they interact.[3]
In particle physics, the concept of a particle is one of several concepts inherited from classical physics. But it also reflects the modern understanding that at the quantum scale matter and energy behave very differently from what much of everyday experience would lead us to expect.
The idea of a particle underwent serious rethinking when experiments showed that light could behave like a stream of particles (called photons) as well as exhibit wave-like properties. This led to the new concept of wave–particle duality to reflect that quantum-scale "particles" behave like both particles and waves (also known as wavicles). Another new concept, the uncertainty principle, states that some of their properties taken together, such as their simultaneous position and momentum, cannot be measured exactly.[4] In more recent times, wave–particle duality has been shown to apply not only to photons but to increasingly massive particles as well.[5]
Interactions of particles in the framework of quantum field theory are understood as creation and annihilation of quanta of corresponding fundamental interactions. This blends particle physics with field theory.

Any subatomic particle, like any particle in the 3-dimensional space that obeys laws of quantum mechanics, can be either a boson (an integer spin) or a fermion (a half-integer spin).
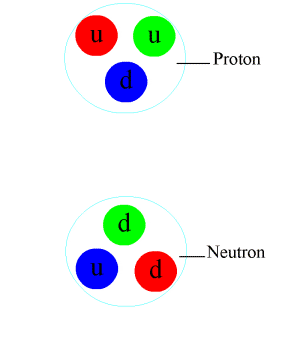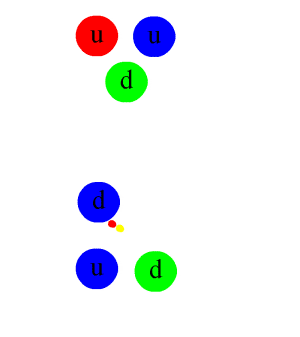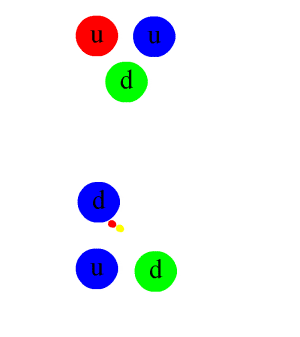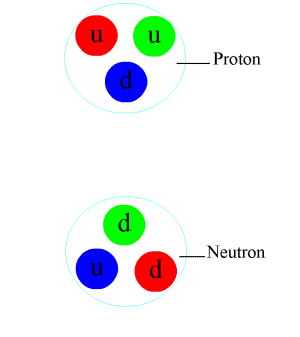
Composite subatomic particles (such as protons or atomic nuclei) are bound states of two or more elementary particles. For example, a proton is made of two up quarks and one down quark, while the atomic nucleus of helium-4 is composed of two protons and two neutrons. Composite particles include all hadrons: these include baryons (such as protons and neutrons) and mesons (such as pions and kaons).
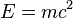 ). That is, mass can be expressed in terms of energy and vice versa. If a particle has a frame of reference where it lies at rest, then it has a positive rest mass and is referred to as massive.
). That is, mass can be expressed in terms of energy and vice versa. If a particle has a frame of reference where it lies at rest, then it has a positive rest mass and is referred to as massive.
All composite particles are massive. Baryons (meaning "heavy") tend to have greater mass than mesons (meaning "intermediate"), which in turn tend to be heavier than leptons (meaning "lightweight"), but the heaviest lepton (the tau particle) is heavier than the two lightest flavours of baryons (nucleons). It is also certain that any particle with an electric charge is massive.
All massless particles (particles whose invariant mass is zero) are elementary. These include the photon and gluon, although the latter cannot be isolated.
The question of the masses of neutrinos is uncertain.
Interactions between particles have been scrutinized for many centuries, and a few simple laws underpin how particles behave in collisions and interactions. The most fundamental of these are the laws of conservation of energy and conservation of momentum, which let us make calculations of particle interactions on scales of magnitude that range from stars to quarks.[9] These are the prerequisite basics of Newtonian mechanics, a series of statements and equations in Philosophiae Naturalis Principia Mathematica, originally published in 1687.
Chemistry concerns itself with how electron sharing binds atoms into structures such as crystals and molecules. Nuclear physics deals with how protons and neutrons arrange themselves in nuclei. The study of subatomic particles, atoms and molecules, and their structure and interactions, requires quantum mechanics. Analyzing processes that change the numbers and types of particles requires quantum field theory. The study of subatomic particles per se is called particle physics. The term high-energy physics is nearly synonymous to "particle physics" since creation of particles requires high energies: it occurs only as a result of cosmic rays, or in particle accelerators.
Particle phenomenology systematizes the knowledge about subatomic particles obtained from these experiments.
A list of important discoveries follows:
In particle physics, the concept of a particle is one of several concepts inherited from classical physics. But it also reflects the modern understanding that at the quantum scale matter and energy behave very differently from what much of everyday experience would lead us to expect.
The idea of a particle underwent serious rethinking when experiments showed that light could behave like a stream of particles (called photons) as well as exhibit wave-like properties. This led to the new concept of wave–particle duality to reflect that quantum-scale "particles" behave like both particles and waves (also known as wavicles). Another new concept, the uncertainty principle, states that some of their properties taken together, such as their simultaneous position and momentum, cannot be measured exactly.[4] In more recent times, wave–particle duality has been shown to apply not only to photons but to increasingly massive particles as well.[5]
Interactions of particles in the framework of quantum field theory are understood as creation and annihilation of quanta of corresponding fundamental interactions. This blends particle physics with field theory.
Classification
By statistics

The Standard Model classification of particles
Any subatomic particle, like any particle in the 3-dimensional space that obeys laws of quantum mechanics, can be either a boson (an integer spin) or a fermion (a half-integer spin).
By composition
The elementary particles of the Standard Model include:[6]- Six "flavors" of quarks: up, down, bottom, top, strange, and charm;
- Six types of leptons: electron, electron neutrino, muon, muon neutrino, tau, tau neutrino;
- Twelve gauge bosons (force carriers): the photon of electromagnetism, the three W and Z bosons of the weak force, and the eight gluons of the strong force;
- The Higgs boson.
Composite subatomic particles (such as protons or atomic nuclei) are bound states of two or more elementary particles. For example, a proton is made of two up quarks and one down quark, while the atomic nucleus of helium-4 is composed of two protons and two neutrons. Composite particles include all hadrons: these include baryons (such as protons and neutrons) and mesons (such as pions and kaons).
By mass
In special relativity, the energy of a particle at rest equals its mass times the speed of light squared (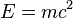 ). That is, mass can be expressed in terms of energy and vice versa. If a particle has a frame of reference where it lies at rest, then it has a positive rest mass and is referred to as massive.
). That is, mass can be expressed in terms of energy and vice versa. If a particle has a frame of reference where it lies at rest, then it has a positive rest mass and is referred to as massive.All composite particles are massive. Baryons (meaning "heavy") tend to have greater mass than mesons (meaning "intermediate"), which in turn tend to be heavier than leptons (meaning "lightweight"), but the heaviest lepton (the tau particle) is heavier than the two lightest flavours of baryons (nucleons). It is also certain that any particle with an electric charge is massive.
All massless particles (particles whose invariant mass is zero) are elementary. These include the photon and gluon, although the latter cannot be isolated.
The question of the masses of neutrinos is uncertain.
Other properties
Through the work of Albert Einstein, Louis de Broglie, and many others, current scientific theory holds that all particles also have a wave nature.[7] This has been verified not only for elementary particles but also for compound particles like atoms and even molecules. In fact, according to traditional formulations of non-relativistic quantum mechanics, wave–particle duality applies to all objects, even macroscopic ones; although the wave properties of macroscopic objects cannot be detected due to their small wavelengths.[8]Interactions between particles have been scrutinized for many centuries, and a few simple laws underpin how particles behave in collisions and interactions. The most fundamental of these are the laws of conservation of energy and conservation of momentum, which let us make calculations of particle interactions on scales of magnitude that range from stars to quarks.[9] These are the prerequisite basics of Newtonian mechanics, a series of statements and equations in Philosophiae Naturalis Principia Mathematica, originally published in 1687.
Dividing an atom
The negatively-charged electron has a mass equal to 1⁄1836 of that of a hydrogen atom. The remainder of the hydrogen atom's mass comes from the positively charged proton. The atomic number of an element is the number of protons in its nucleus. Neutrons are neutral particles having a mass slightly greater than that of the proton. Different isotopes of the same element contain the same number of protons but differing numbers of neutrons. The mass number of an isotope is the total number of nucleons (neutrons and protons collectively).Chemistry concerns itself with how electron sharing binds atoms into structures such as crystals and molecules. Nuclear physics deals with how protons and neutrons arrange themselves in nuclei. The study of subatomic particles, atoms and molecules, and their structure and interactions, requires quantum mechanics. Analyzing processes that change the numbers and types of particles requires quantum field theory. The study of subatomic particles per se is called particle physics. The term high-energy physics is nearly synonymous to "particle physics" since creation of particles requires high energies: it occurs only as a result of cosmic rays, or in particle accelerators.
Particle phenomenology systematizes the knowledge about subatomic particles obtained from these experiments.
History
The term "subatomic particle" is largely a retronym of 1960s made to distinguish a big number of baryons and mesons (that comprise hadrons) from particles that are now thought to be truly elementary. Before that hadrons were usually classified as "elementary" because their composition was unknown.A list of important discoveries follows:
| Particle | Composition | Theorized | Discovered | Comments |
|---|---|---|---|---|
| Electron e− | elementary (lepton) | G. Johnstone Stoney (1874) | J. J. Thomson (1897) | Minimum unit of electrical charge, for which Stoney suggested the name in 1891.[10] |
| alpha particle α | composite (atomic nucleus) | never | Ernest Rutherford (1899) | Proven by Rutherford and Thomas Royds in 1907 to be helium nuclei. |
| Photon γ | elementary (quantum) | Max Planck (1900) | Albert Einstein (1905) or Ernest Rutherford (1899) as γ rays |
Necessary to solve the problem of black body radiation in thermodynamics. |
| Proton p | composite (baryon) | Long ago | Ernest Rutherford (1919, named 1920) | The nucleus of 1H. |
| Neutron n | composite (baryon) | Ernest Rutherford (c.1918) | James Chadwick (1932) | The second nucleon. |
| Antiparticles | Paul Dirac (1928) | Carl D. Anderson (e+, 1932) | Now explained with CPT symmetry. | |
| Pions π | composite (mesons) | Hideki Yukawa (1935) | César Lattes, Giuseppe Occhialini (1947) and Cecil Powell | Explains the nuclear force between nucleons. The first meson (by modern definition) to be discovered. |
| Muon μ− | elementary (lepton) | never | Carl D. Anderson (1936) | The first named meson; today considered a lepton. |
| Kaons K | composite (mesons) | never | 1947 | Discovered in cosmic rays. The first strange particle. |
| Lambda baryons Λ | composite (baryons) | never | University of Melbourne (Λ0, 1950)[11] | The first hyperon discovered. |
| Neutrino ν | elementary (lepton) | Wolfgang Pauli (1930), named by Enrico Fermi | Clyde Cowan, Frederick Reines (ν e, 1956) |
Solved the problem of energy spectrum of beta decay. |
| Quarks (u, d, s) |
elementary | Murray Gell-Mann, George Zweig (1964) | No particular confirmation event for the quark model. | |
| charm quark c | elementary (quark) | 1970 | 1974 | |
| bottom quark b | elementary (quark) | 1973 | 1977 | |
| Weak gauge bosons | elementary (quantum) | Glashow, Weinberg, Salam (1968) | CERN (1983) | Properties verified through the 1990s. |
| top quark t | elementary (quark) | 1973 | 1995 | Does not hadronize, but is necessary to complete the Standard Model. |
| Higgs boson | elementary (quantum) | Peter Higgs et al. (1964) | CERN (2012) | Thought to be confirmed in 2013. More evidence found in 2014.[12] |
| Tetraquark | composite | ? | Zc(3900), 2013, to be confirmed as a tetraquark | A new class of hadrons. |
| Graviton | elementary (quantum) | Albert Einstein (1916) | Not discovered | Interpretation of a gravitational wave (also hypothetical) as a particle is controversial. |
| Magnetic monopole | elementary (unclassified) | Paul Dirac (1931) | Not discovered | |


 .
.

 .
.