Atlantic multidecadal oscillation

From Wikipedia, the free encyclopedia

AMO spatial pattern.

Atlantic Multidecadal Oscillation index computed as the linearly detrended North Atlantic sea surface temperature anomalies 1856-2013.

The Atlantic Multidecadal Oscillation (AMO) is an ocean current, with different modes on multi-decadal time-scales, affecting the North Atlantic Ocean, in particular its sea surface temperature.^[1] While there is some support for this mode in models and in historical observations, controversy exists with regard to its amplitude, and in particular, the attribution of sea surface temperature change to natural or anthropogenic causes, especially in tropical Atlantic areas important for hurricane development.^[2]

Definition

The Atlantic multidecadal oscillation (AMO) was identified by Schlesinger and Ramankutty in 1994.^[3]

The AMO signal is usually defined from the patterns of SST variability in the North Atlantic once any linear trend has been removed. This detrending is intended to remove the influence of greenhouse gas-induced global warming from the analysis. However, if the global warming signal is significantly non-linear in time (i.e. not just a smooth linear increase), variations in the forced signal will leak into the AMO definition. Consequently, correlations with the AMO index may mask effects of global warming.

Atlantic Multidecadal Oscillation according to the methodology proposed by van Oldenborgh et al.

Several methods have been proposed to remove the global trend and ENSO influence over the North Atlantic SST. Trenberth and Shea, assuming that the effect of global forcing over the North Atlantic is similar to the global ocean, subtracted the global (60°N-60°S) mean SST from the North Atlantic SST to derive a revised AMO index.^[4]

Ting et al. however argue that the forced SST pattern is not spatially uniform; they separated the forced and internally generated variability using signal to noise maximizing EOF analysis.^[2]

Van Oldenborgh et al. derived an AMO index as the SST averaged over the extra-tropical North Atlantic (to remove the influence of ENSO that is greater at tropical latitude) minus the regression on global mean temperature.^[5]

Guan and Nigam removed the non stationary global trend and Pacific natural variability before applying an EOF analysis to the residual North Atlantic SST.^[6]

The linearly detrended index suggests that the North Atlantic SST anomaly at the end of the twentieth century is equally divided between the externally forced component and internally generated variability, and that the current peak is similar to middle twentieth century; by contrast the others methodology suggest that a large portion of the North Atlantic anomaly at the end of the twentieth century is externally forced.^[2]

Mechanisms

In models, AMO-like variability is associated with small changes in the North Atlantic branch of the Thermohaline Circulation. However, historical oceanic observations are not sufficient to associate the derived AMO index to present-day circulation anomalies.^{[citation needed]}

The Atlantic Multidecadal Oscillation (AMO) is important for how external forcings are linked with North Atlantic SSTs.^[7]

Climate impacts worldwide

The AMO index is correlated to air temperatures and rainfall over much of the Northern Hemisphere, in particular, North America and Europe such as North Eastern Brazilian and African Sahel rainfall and North American and European summer climate. It is also associated with changes in the frequency of North American droughts and is reflected in the frequency of severe Atlantic hurricanes.^[4]

Recent research suggests that the AMO is related to the past occurrence of major droughts in the US Midwest and the Southwest. When the AMO is in its warm phase, these droughts tend to be more frequent or prolonged. Two of the most severe droughts of the 20th century occurred during the positive AMO between 1925 and 1965: The Dust Bowl of the 1930s and the 1950s drought. Florida and the Pacific Northwest tend to be the opposite—warm AMO, more rainfall.^[8]

Climate models suggest that a warm phase of the AMO strengthens the summer rainfall over India and Sahel and the North Atlantic tropical cyclone activity.^[9] Paleoclimatologic studies have confirmed this pattern—increased rainfall in AMO warmphase, decreased in cold phase—for the Sahel over the past 3,000 years.^[10]

Relation to Atlantic hurricanes

Atlantic basin cyclone intensity by accumulated cyclone energy, timeseries 1895–2007

In viewing actual data on a short time horizon, sparse experience would suggest the frequency of major hurricanes is not strongly correlated with the AMO. During warm phases of the AMO, the number of minor hurricanes (category 1 and 2) saw a modest increase.^[11] With full consideration of meteorological science, the number of tropical storms that can mature into severe hurricanes is much greater during warm phases of the AMO than during cool phases, at least twice as many; the AMO is reflected in the frequency of severe Atlantic hurricanes.^[8] The hurricane activity index is found to be highly correlated with the Atlantic multidecadal oscillation.^[11] If there is an increase in hurricane activity connected to global warming, it is currently obscured by the AMO quasi-periodic cycle.^[11] The AMO alternately obscures and exaggerates the global increase in temperatures due to human-induced global warming.^[8] Based on the typical duration of negative and positive phases of the AMO, the current warm regime is expected to persist at least until 2015 and possibly as late as 2035. Enfield et al. assume a peak around 2020.^[12]

Florida rainfall

The AMO has a strong effect on Florida rainfall. Rainfall in central and south Florida becomes more plentiful when the Atlantic is in its warm phase and droughts and wildfires are more frequent in the cool phase. As a result of these variations, the inflow to Lake Okeechobee—the reservoir for South Florida’s water supply—changes by as much as 40% between AMO extremes. In northern Florida the relationship begins to reverse—less rainfall when the Atlantic is warm.^[8]

Periodicity and prediction of AMO shifts

There are only about 130–150 years of data based on instrument data, which are too few samples for conventional statistical approaches. With the aid of multi-century proxy reconstruction, a longer period of 424 years was used by Enfield and Cid–Serrano as an illustration of an approach as described in their paper called "The Probabilistic Projection of Climate Risk".^[13] Their histogram of zero crossing intervals from a set of five re-sampled and smoothed version of Gray et al. (2004) index together with the Maximum Likelihood Estimate gamma distribution fit to the histogram, showed that the largest frequency of regime interval was around 10–20 year. The cumulative probability for all intervals 20 years or less was about 70%.

There is no demonstrated predictability for when the AMO will switch, in any deterministic sense. Computer models, such as those that predict El Niño, are far from being able to do this. Enfield and colleagues have calculated the probability that a change in the AMO will occur within a given future time frame, assuming that historical variability persists. Probabilistic projections of this kind may prove to be useful for long-term planning in climate sensitive applications, such as water management.

Assuming that the AMO continues with its quasi-cycle of roughly 70 years, the peak of the current warm phase would be expected in c. 2020,^[14] or based on its 50–90 year quasi-cycle, between 2000 and 2040 (after peaks in c. 1880 and c. 1950).^{[12][relevant? – discuss]}

El Niño Southern Oscillation

From Wikipedia, the free encyclopedia

Southern Oscillation Index timeseries 1876–2012.

El Niño Southern Oscillation (ENSO) is an irregularly periodical climate change caused by variations in sea surface temperatures over the tropical eastern Pacific Ocean, affecting much of the tropics and subtropics. The warming phase is known as El Niño and the cooling phase as La Niña. The two variations are coupled: El Niño is accompanied with high, and La Niña with low air surface pressure in the tropical western Pacific.^[1][2] The two periods last several years each (typically three to four) and their effects vary in intensity.^[3]

The two phases relate to the Walker circulation, discovered by Gilbert Walker during the early twentieth century. The Walker circulation is caused by the pressure gradient force that results from a high pressure system over the eastern Pacific ocean, and a low pressure system over Indonesia. When the Walker circulation weakens or reverses, an El Niño results, causing the ocean surface to be warmer than average, as upwelling of cold water occurs less or not at all. An especially strong Walker circulation causes a La Niña, resulting in cooler ocean temperatures due to increased upwelling.

Mechanisms that cause the oscillation remain under study. The extremes of this climate pattern's oscillations cause extreme weather (such as floods and droughts) in many regions of the world. Developing countries dependent upon agriculture and fishing, particularly those bordering the Pacific Ocean, are the most affected.

Gilbert Walker

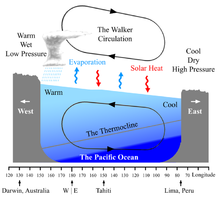
Diagram of the quasi-equilibrium and La Niña phase of the Southern Oscillation. The Walker circulation is seen at the surface as easterly trade winds which move water and air warmed by the sun towards the west. The western side of the equatorial Pacific is characterized by warm, wet low pressure weather as the collected moisture is dumped in the form of typhoons and thunderstorms. The ocean is some 60 centimetres (24 in) higher in the western Pacific as the result of this motion. The water and air are returned to the east. Both are now much cooler, and the air is much drier. An El Niño episode is characterised by a breakdown of this water and air cycle, resulting in relatively warm water and moist air in the eastern Pacific.

Gilbert Walker was an established applied mathematician at the University of Cambridge when he became director-general of observatories in India in 1904.^[4] While there, he studied the characteristics of the Indian Ocean monsoon, the failure of whose rains had brought severe famine to the country in 1899. Analyzing vast amounts of weather data from India and lands beyond, over the next fifteen years he published the first descriptions of the great seesaw oscillation of atmospheric pressure between the Indian and Pacific Ocean, and its correlation to temperature and rainfall patterns across much of the Earth's tropical regions, including India. He also worked with the Indian Meteorological Department especially in linking the monsoon with Southern Oscillation phenomenon. He was made a Companion of the Order of the Star of India in 1911.^[4]

Southern Oscillation

Normal Pacific pattern: Equatorial winds gather warm water pool toward the west. Cold water upwells along South American coast. (NOAA / PMEL / TAO)

The Southern Oscillation is the atmospheric component of El Niño. This component is an oscillation in surface air pressure between the tropical eastern and the western Pacific Ocean waters. The strength of the Southern Oscillation is measured by the Southern Oscillation Index (SOI). The SOI is computed from fluctuations in the surface air pressure difference between Tahiti (in the Pacific) and Darwin, Australia (on the Indian Ocean).^[5]

• El Niño episodes have negative SOI, meaning there is lower pressure over Tahiti and higher pressure in Darwin.
• La Niña episodes have positive SOI, meaning there is higher pressure in Tahiti and lower in Darwin.

Low atmospheric pressure tends to occur over warm water and high pressure occurs over cold water, in part because of deep convection over the warm water. El Niño episodes are defined as sustained warming of the central and eastern tropical Pacific Ocean, thus resulting in a decrease in the strength of the Pacific trade winds, and a reduction in rainfall over eastern and northern Australia. La Niña episodes are defined as sustained cooling of the central and eastern tropical Pacific Ocean, thus resulting in an increase in the strength of the Pacific trade winds, and the opposite effects in Australia when compared to El Niño.

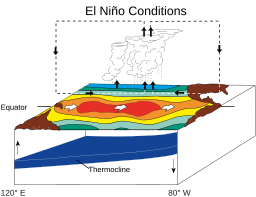
El Niño conditions: Warm water pool approaches the South American coast. The absence of cold upwelling increases warming.

La Niña conditions: Warm water is farther west than usual.

Although the Southern Oscillation Index has a long station record going back to the 1800s, its reliability is limited due to the presence of both Darwin and Tahiti well south of the Equator, resulting in the surface air pressure at both locations being less directly related to ENSO.^[6] To overcome this question, a new index was created, being named Equatorial Southern Oscillation Index (EQSOI).^[6][6] To generate this index data, two new regions, centered on the Equator, were delimited to create a new index: The western one is located over Indonesia and the eastern one is located over equatorial Pacific, close to the South American coast.^[6] However, data on EQSOI goes back only to 1949.^[6]

Walker circulation

The Walker circulation is caused by the pressure gradient force that results from a high pressure system over the eastern Pacific ocean, and a low pressure system over Indonesia. The Walker Circulations of the tropical Indian, Pacific, and Atlantic basins result in westerly surface winds in Northern Summer in the first basin and easterly winds in the second and third basins. As a result the temperature structure of the three oceans display dramatic asymmetries. The equatorial Pacific and Atlantic both have cool surface temperatures in Northern Summer in the east, while cooler surface temperatures prevail only in the western Indian Ocean.^[7] These changes in surface temperature reflect changes in the depth of the thermocline.^[8]
Changes in the Walker Circulation with time occur in conjunction with changes in surface temperature. Some of these changes are forced externally, such as the seasonal shift of the Sun into the Northern Hemisphere in summer. Other changes appear to be the result of coupled ocean-atmosphere feedback in which, for example, easterly winds cause the sea surface temperature to fall in the east, enhancing the zonal heat contrast and hence intensifying easterly winds across the basin. These anomalous easterlies induce more equatorial upwelling and raise the thermocline in the east, amplifying the initial cooling by the southerlies. This coupled ocean-atmosphere feedback was originally proposed by Bjerknes. From an oceanographic point of view, the equatorial cold tongue is caused by easterly winds. Were the earth climate symmetric about the equator, cross-equatorial wind would vanish, and the cold tongue would be much weaker and have a very different zonal structure than is observed today.^[9]

During non-El Niño conditions, the Walker circulation is seen at the surface as easterly trade winds that move water and air warmed by the sun toward the west. This also creates ocean upwelling off the coasts of Peru and Ecuador and brings nutrient-rich cold water to the surface, increasing fishing stocks.^[10] The western side of the equatorial Pacific is characterized by warm, wet, low-pressure weather as the collected moisture is dumped in the form of typhoons and thunderstorms. The ocean is some 60 cm (24 in) higher in the western Pacific as the result of this motion.^{[11][12][13][14]}

Madden–Julian oscillation

A Hovmöller diagram of the 5-day running mean of outgoing longwave radiation showing the MJO. Time increases from top to bottom in the figure, so contours that are oriented from upper-left to lower-right represent movement from west to east.

The Madden–Julian oscillation, or (MJO), is the largest element of the intraseasonal (30–90 day) variability in the tropical atmosphere, and was discovered by Roland Madden and Paul Julian of the National Center for Atmospheric Research (NCAR) in 1971. It is a large-scale coupling between atmospheric circulation and tropical deep convection.^[15][16] Rather than being a standing pattern like the El Niño Southern Oscillation (ENSO), the MJO is a traveling pattern that propagates eastward at approximately 4 to 8 m/s (9 to 18 mph), through the atmosphere above the warm parts of the Indian and Pacific oceans. This overall circulation pattern manifests itself in various ways, most clearly as anomalous rainfall. The wet phase of enhanced convection and precipitation is followed by a dry phase where thunderstorm activity is suppressed. Each cycle lasts approximately 30–60 days.^[17] Because of this pattern, The MJO is also known as the 30–60 day oscillation, 30–60 day wave, or intraseasonal oscillation.

There is strong year-to-year (interannual) variability in MJO activity, with long periods of strong activity followed by periods in which the oscillation is weak or absent. This interannual variability of the MJO is partly linked to the El Niño-Southern Oscillation (ENSO) cycle. In the Pacific, strong MJO activity is often observed 6 – 12 months prior to the onset of an El Niño episode, but is virtually absent during the maxima of some El Niño episodes, while MJO activity is typically greater during a La Niña episode. Strong events in the Madden–Julian oscillation over a series of months in the western Pacific can speed the development of an El Niño or La Niña but usually do not in themselves lead to the onset of a warm or cold ENSO event.^[18] However, observations suggest that the 1982-1983 El Niño developed rapidly during July 1982 in direct response to a Kelvin wave triggered by an MJO event during late May.^[19] Further, changes in the structure of the MJO with the seasonal cycle and ENSO might facilitate more substantial impacts of the MJO on ENSO. For example, the surface westerly winds associated with active MJO convection are stronger during advancement toward El Niño and the surface easterly winds associated with the suppressed convective phase are stronger during advancement toward La Nina.^[20]

How the phase is determined

The various "Niño regions" where sea surface temperatures are monitored to determine the current ENSO phase (warm or cold)

Within the National Oceanic and Atmospheric Administration in the United States, sea surface temperatures in the Niño 3.4 region, which stretches from the 120th to 150th meridians west longitude astride the equator five degrees of latitude on either side, is monitored. This region is approximately 3,000 kilometres (1,900 mi) to the southeast of Hawaii. The most recent three-month average for the area is computed, and if the region is more than 0.5 °C (0.9 °F) above (or below) normal for that period, then an El Niño (or La Niña) is considered in progress.^[21] The United Kingdom's MetOffice also uses a several month period to determine ENSO state.^[22] When this warming or cooling occurs for only seven to nine months, it is classified as El Niño/La Niña "conditions"; when it occurs for more than that period, it is classified as El Niño/La Niña "episodes".^[23]

Neutral phase

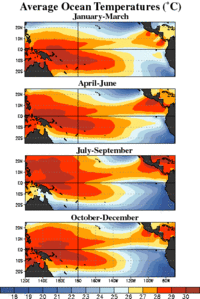
Average equatorial Pacific temperatures

If the temperature variation from climatology is within 0.5 °C (0.9 °F), ENSO conditions are described as neutral. Neutral conditions are the transition between warm and cold phases of ENSO. Ocean temperatures (by definition), tropical precipitation, and wind patterns are near average conditions during this phase.^[24] Close to half of all years are within neutral periods.^[25] During the neutral ENSO phase, other climate anomalies/patterns such as the sign of the North Atlantic Oscillation or the Pacific–North American teleconnection pattern exert more influence.^[26]

The 1997 El Niño observed by TOPEX/Poseidon

Warm phase

When the Walker circulation weakens or reverses and the Hadley circulation strengthens an El Niño results,^[27] causing the ocean surface to be warmer than average, as upwelling of cold water occurs less or not at all offshore northwestern South America. El Niño (/ɛlˈniːnjoʊ/, /-ˈnɪn-/, Spanish pronunciation: [el ˈniɲo]) is associated with a band of warmer than average ocean water temperatures that periodically develops off the Pacific coast of South America. El niño is Spanish for "the boy", and the capitalized term El Niño refers to the Christ child, Jesus, because periodic warming in the Pacific near South America is usually noticed around Christmas.^[28] It is a phase of 'El Niño–Southern Oscillation' (ENSO), which refers to variations in the temperature of the surface of the tropical eastern Pacific Ocean and in air surface pressure in the tropical western Pacific. The warm oceanic phase, El Niño, accompanies high air surface pressure in the western Pacific.^[1][29] Mechanisms that cause the oscillation remain under study.

Cold phase

An especially strong Walker circulation causes a La Niña, resulting in cooler ocean temperatures due to increased upwelling. La Niña (/lɑːˈniːnjə/, Spanish pronunciation: [la ˈniɲa]) is a coupled ocean-atmosphere phenomenon that is the counterpart of El Niño as part of the broader El Niño Southern Oscillation climate pattern. The name La Niña originates from Spanish, meaning "the girl", analogous to El Niño meaning "the boy". It has also in the past been called anti-El Niño, and El Viejo (meaning "the old man").^[30] During a period of La Niña, the sea surface temperature across the equatorial eastern central Pacific will be lower than normal by 3–5 °C. In the United States, an appearance of La Niña happens for at least five months of La Niña conditions. La Niña, sometimes informally called "anti-El Niño", is the opposite of El Niño, with a sea surface temperature anomaly of at least 0.5 °C (0.9 °F) below normal and its effects are often the reverse of those of El Niño.

Impacts

On precipitation

Regional impacts of La Niña.

Developing countries dependent upon agriculture and fishing, particularly those bordering the Pacific Ocean, are the most affected by ENSO. The effects of El Niño in South America are direct and strong. An El Niño is associated with warm and very wet weather months in April–October along the coasts of northern Peru and Ecuador, causing major flooding whenever the event is strong or extreme.^[31] La Niña causes a drop in sea surface temperatures over Southeast Asia and heavy rains over Malaysia, the Philippines, and Indonesia.^[32]

To the north across Alaska, La Niña events lead to drier than normal conditions, while El Niño events do not have a correlation towards dry or wet conditions. During El Niño events, increased precipitation is expected in California due to a more southerly, zonal, storm track.^[33] During La Niña, increased precipitation is diverted into the Pacific Northwest due to a more northerly storm track.^[34] During La Niña events, the storm track shifts far enough northward to bring wetter than normal winter conditions (in the form of increased snowfall) to the Midwestern states, as well as hot and dry summers.^[35] During the El Niño portion of ENSO, increased precipitation falls along the Gulf coast and Southeast due to a stronger than normal, and more southerly, polar jet stream.^[36] In the late winter and spring during El Niño events, drier than average conditions can be expected in Hawaii.^[37] On Guam during El Niño years, dry season precipitation averages below normal. However, the threat of a tropical cyclone is over triple what is normal during El Niño years, so extreme shorter duration rainfall events are possible.^[38] On American Samoa during El Niño events, precipitation averages about 10 percent above normal, while La Niña events lead to precipitation amounts which average close to 10 percent below normal.^[39] ENSO is linked to rainfall over Puerto Rico.^[40] During an El Niño, snowfall is greater than average across the southern Rockies and Sierra Nevada mountain range, and is well-below normal across the Upper Midwest and Great Lakes states. During a La Niña, snowfall is above normal across the Pacific Northwest and western Great Lakes.^[41]

On Tehuantepecers

The synoptic condition for the Tehuantepecer, a violent mountain-gap wind in between the mountains of Mexico and Guatemala, is associated with high-pressure system forming in Sierra Madre of Mexico in the wake of an advancing cold front, which causes winds to accelerate through the Isthmus of Tehuantepec. Tehuantepecers primarily occur during the cold season months for the region in the wake of cold fronts, between October and February, with a summer maximum in July caused by the westward extension of the Azores-Bermuda high pressure system. Wind magnitude is greater during El Niño years than during La Niña years, due to the more frequent cold frontal incursions during El Niño winters.^[42] Tehuantepec winds reach 20 knots (40 km/h) to 45 knots (80 km/h), and on rare occasions 100 knots (200 km/h). The wind’s direction is from the north to north-northeast.^[43] It leads to a localized acceleration of the trade winds in the region, and can enhance thunderstorm activity when it interacts with the Intertropical Convergence Zone.^[44] The effects can last from a few hours to six days.^[45]

On global warming

NOAA graph of Global Annual Temperature Anomalies 1950–2012, showing ENSO

During the last several decades, the number of El Niño events increased, and the number of La Niña events decreased,^[46] although observation of ENSO for much longer is needed to detect robust changes.^[47] The question is whether this is a random fluctuation or a normal instance of variation for that phenomenon or the result of global climate changes toward global warming.

The studies of historical data show the recent El Niño variation is most likely linked to global warming. For example, one of the most recent results, even after subtracting the positive influence of decadal variation, is shown to be possibly present in the ENSO trend,^[48] the amplitude of the ENSO variability in the observed data still increases, by as much as 60% in the last 50 years.^[49]

The exact changes happening to ENSO in the future is uncertain:^[50] Different models make different predictions.^[51][52] It may be that the observed phenomenon of more frequent and stronger El Niño events occurs only in the initial phase of the global warming, and then (e.g., after the lower layers of the ocean get warmer, as well), El Niño will become weaker than it was.^[53] It may also be that the stabilizing and destabilizing forces influencing the phenomenon will eventually compensate for each other.^[54] More research is needed to provide a better answer to that question. The ENSO is considered to be a potential tipping element in Earth's climate.^[55]

ENSO diversity

The traditional ENSO (El Niño Southern Oscillation), also called Eastern Pacific (EP) ENSO,^[56] involves temperature anomalies in the eastern pacific. However, in the 1990s and 2000s, nontraditional ENSO conditions were observed, in which the usual place of the temperature anomaly (Niño 1 and 2) is not affected, but an anomaly arises in the central Pacific (Niño 3.4).^[57] The phenomenon is called Central Pacific (CP) ENSO,^[56] "dateline" ENSO (because the anomaly arises near the dateline), or ENSO "Modoki" (Modoki is Japanese for "similar, but different").^[58][59] There are flavors of ENSO additional to EP and CP types and some scientists argue that ENSO exists as a continuum often with hybrid types.^[60]

The effects of the CP ENSO are different from those of the traditional EP ENSO. The El Niño Modoki leads to more hurricanes more frequently making landfall in the Atlantic.^[61] La Niña Modoki leads to a rainfall increase over northwestern Australia and northern Murray-Darling basin, rather than over the east as in a conventional La Niña.^[59] Also, La Niña Modoki increases the frequency of cyclonic storms over Bay of Bengal, but decreases the occurrence of severe storms in the Indian Ocean.^[62]

The recent discovery of ENSO Modoki has some scientists believing it to be linked to global warming.^[63] However, comprehensive satellite data go back only to 1979. More research must be done to find the correlation and study past El Niño episodes. More generally, there is no scientific consensus on how/if climate change may affect ENSO.^[50]

There is also a scientific debate on the very existence of this "new" ENSO. Indeed, a number of studies dispute the reality of this statistical distinction or its increasing occurrence, or both, either arguing the reliable record is too short to detect such a distinction,^[64][65] finding no distinction or trend using other statistical approaches,^{[66][67][68][69][70]} or that other types should be distinguished, such as standard and extreme ENSO.^[71][72] Following the asymmetric nature of the warm and cold phases of ENSO, some studies could not identify such distinctions for La Niña, both in observations and in the climate models,^[73] but some sources indicate that there is a variation on La Niña with cooler waters on central Pacific and average or warmer water temperatures on both eastern and western Pacific, also showing eastern Pacific ocean currents going to the opposite direction compared to the currents in traditional La Niñas.^[58][74][75]

Fresnel equations

From Wikipedia, the free encyclopedia

Partial transmission and reflection amplitudes of a wave travelling from a low to high refractive index medium.

The Fresnel equations (or Fresnel conditions), deduced by Augustin-Jean Fresnel /frɛˈnɛl/, describe the behaviour of light when moving between media of differing refractive indices. The reflection of light that the equations predict is known as Fresnel reflection.

Overview

When light moves from a medium of a given refractive index n₁ into a second medium with refractive index n₂, both reflection and refraction of the light may occur. The Fresnel equations describe what fraction of the light is reflected and what fraction is refracted (i.e., transmitted). They also describe the phase shift of the reflected light.
The equations assume the interface between the media is flat and that the media are homogeneous. The incident light is assumed to be a plane wave, and effects of edges are neglected.

S and p polarizations

The calculations below depend on polarisation of the incident ray. Two cases are analyzed:

1. The incident light is polarized with its electric field perpendicular to the plane containing the incident, reflected, and refracted rays. This plane is called the plane of incidence; it is the plane of the diagram below. The light is said to be s-polarized, from the German senkrecht (perpendicular).
2. The incident light is polarized with its electric field parallel to the plane of incidence. Such light is described as p-polarized, from parallel.

Power or intensity equations

Variables used in the Fresnel equations.

In the diagram on the right, an incident light ray IO strikes the interface between two media of refractive indices n₁ and n₂ at point O. Part of the ray is reflected as ray OR and part refracted as ray OT. The angles that the incident, reflected and refracted rays make to the normal of the interface are given as θ_i, θ_r and θ_t, respectively.

The relationship between these angles is given by the law of reflection:

and Snell's law:

The fraction of the incident power that is reflected from the interface is given by the reflectance or reflectivity R and the fraction that is refracted is given by the transmittance or transmissivity T (unrelated to the transmission through a medium).^[1]

The reflectance for s-polarized light is

while the reflectance for p-polarized light is

where Z₁ and Z₂ are the wave impedances of media 1 and 2, respectively.

For non-magnetic media, we have μ₁ = μ₂ = μ₀, so that

Then, the reflectance for s-polarized light becomes

while the reflectance for p-polarized light becomes

The second form of each equation is derived from the first by eliminating θ_t using Snell's law and trigonometric identities.

As a consequence of the conservation of energy, the transmittances are given by^[2]

and

These relationships hold only for power or intensity, not for complex amplitude transmission and reflection coefficients as defined below.

If the incident light is unpolarised (containing an equal mix of s- and p-polarisations), the reflectance is

For common glass, with n₂ around 1.5, the reflectance at θ_i = 0 is about 4%. Note that reflection by a window is from the front side as well as the back side, and that some of the light bounces back and forth a number of times between the two sides. The combined reflectance for this case is 2R/(1 + R), when interference can be neglected (see below).

The discussion given here assumes that the permeability μ is equal to the vacuum permeability μ₀ in both media, embodying the assumption that the material is non-magnetic. This is approximately true for most dielectric materials, but not for some other types of material. The completely general Fresnel equations are more complicated.

For low-precision applications where polarization may be ignored, such as computer graphics, Schlick's approximation may be used.

Special angles

At one particular angle for a given n₁ and n₂, the value of R_p goes to zero and a p-polarised incident ray is purely refracted. This angle is known as Brewster's angle, and is around 56° for a glass medium in air or vacuum. Note that this statement is only true when the refractive indices of both materials are real numbers, as is the case for materials like air and glass. For materials that absorb light, like metals and semiconductors, n is complex, and R_p does not generally go to zero.

When moving from a denser medium into a less dense one (i.e., n₁ > n₂), above an incidence angle known as the critical angle, all light is reflected and R_s = R_p =1. This phenomenon is known as total internal reflection. The critical angle is approximately 41° for glass in air.

Amplitude or field equations

Equations for coefficients corresponding to ratios of the electric field complex-valued amplitudes of the waves (not necessarily real-valued magnitudes) are also called "Fresnel equations". These take several different forms, depending on the choice of formalism and sign convention used. The amplitude coefficients are usually represented by lower case r and t.

Amplitude ratios: air to glass

Amplitude ratios: glass to air

Conventions used here

In this treatment, the coefficient r is the ratio of the reflected wave's complex electric field amplitude to that of the incident wave. The coefficient t is the ratio of the transmitted wave's electric field amplitude to that of the incident wave. The light is split into s and p polarizations as defined above. (In the figures to the right, s polarization is denoted "" and p is denoted "".)

For s-polarization, a positive r or t means that the electric fields of the incoming and reflected or transmitted wave are parallel, while negative means anti-parallel. For p-polarization, a positive r or t means that the magnetic fields of the waves are parallel, while negative means anti-parallel.^[3] It is also assumed that the magnetic permeability µ of both media is equal to the permeability of free space µ₀.

(Be aware that some authors say instead use the opposite sign convention for r_p, so that r_p is positive when the incoming and reflected magnetic fields are antiparallel, and negative when they are parallel. This latter convention has the convenient advantage that the s- and p- sign conventions are the same at normal incidence. However, either convention, when used consistently, gives the right answers.)

Formulas

Using the arbitrary sign conventions above,^[3]

Notice that t_s = 1 + r_s but t_p ≠ 1 + r_p.^[4]

Because the reflected and incident waves propagate in the same medium and make the same angle with the normal to the surface, the amplitude reflection coefficient is related to the reflectance R by ^[5]

The transmittance T is generally not equal to |t|², since the light travels with different direction and speed in the two media. The transmittance is related to t by:^[6]

The factor of n₂/n₁ occurs from the ratio of intensities (closely related to irradiance). The factor of cos θ_t/cos θ_i represents the change in area m of the pencil of rays, needed since T, the ratio of powers, is equal to the ratio of (intensity × area). In terms of the ratio of refractive indices,

and of the magnification m of the beam cross section occurring at the interface,

Multiple surfaces

When light makes multiple reflections between two or more parallel surfaces, the multiple beams of light generally interfere with one another, resulting in net transmission and reflection amplitudes that depend on the light's wavelength. The interference, however, is seen only when the surfaces are at distances comparable to or smaller than the light's coherence length, which for ordinary white light is few micrometers; it can be much larger for light from a laser.

An example of interference between reflections is the iridescent colours seen in a soap bubble or in thin oil films on water. Applications include Fabry–Pérot interferometers, antireflection coatings, and optical filters. A quantitative analysis of these effects is based on the Fresnel equations, but with additional calculations to account for interference.

The transfer-matrix method, or the recursive Rouard method^[7] can be used to solve multiple-surface problems.