From Wikipedia, the free encyclopedia

Frequency distribution of climate sensitivity, based on model simulations.[1] Few of the simulations result in less than 2 °C of warming—near the low end of estimates by the Intergovernmental Panel on Climate Change (IPCC).[1] Some simulations result in significantly more than the 4 °C, which is at the high end of the IPCC estimates.[1] This pattern (statisticians call it a "right-skewed distribution") suggests that if carbon dioxide concentrations double, the probability of very large increases in temperature is greater than the probability of very small increases.[1]
Climate sensitivity is the equilibrium temperature change in response to changes of the radiative forcing.[2] Therefore climate sensitivity depends on the initial climate state, but potentially can be accurately inferred from precise palaeoclimate data. Slow climate feedbacks, especially changes of ice sheet size and atmospheric CO2, amplify the total Earth system sensitivity by an amount that depends on the time scale considered.[3]
Although climate sensitivity is usually used in the context of radiative forcing by carbon dioxide (CO2), it is thought of as a general property of the climate system: the change in surface air temperature (ΔTs) following a unit change in radiative forcing (RF), and thus is expressed in units of °C/(W/m2). For this to be useful, the measure must be independent of the nature of the forcing (e.g. from greenhouse gases or solar variation); to first order this is indeed found to be so[citation needed].
The climate sensitivity specifically due to CO2 is often expressed as the temperature change in °C associated with a doubling of the concentration of carbon dioxide in Earth's atmosphere.
For coupled atmosphere-ocean global climate models (e.g. CMIP5) the climate sensitivity is an emergent property: it is not a model parameter, but rather a result of a combination of model physics and parameters. By contrast, simpler energy-balance models may have climate sensitivity as an explicit parameter.
The terms represented in the equation relate radiative forcing (RF) to linear changes in global surface temperature change (ΔTs) via the climate sensitivity λ.
It is also possible to estimate climate sensitivity from observations; however, this is difficult due to uncertainties in the forcing and temperature histories.
Equilibrium and transient climate sensitivity
The equilibrium climate sensitivity (ECS) refers to the equilibrium change in global mean near-surface air temperature that would result from a sustained doubling of the atmospheric (equivalent) carbon dioxide concentration (ΔTx2). As estimated by the IPCC Fifth Assessment Report (AR5) "there is high confidence that ECS is extremely unlikely less than 1°C and medium confidence that the ECS is likely between 1.5°C and 4.5°C and very unlikely greater than 6°C."[4] This is a change from the IPCC Fourth Assessment Report (AR4), which said it was likely to be in the range 2 to 4.5 °C with a best estimate of about 3 °C, and is very unlikely to be less than 1.5 °C. Values substantially higher than 4.5 °C cannot be excluded, but agreement of models with observations is not as good for those values.[5] The IPCC Third Assessment Report (TAR) said it was "likely to be in the range of 1.5 to 4.5 °C".[6] Other estimates of climate sensitivity are discussed later on.A model estimate of equilibrium sensitivity thus requires a very long model integration; fully equilibrating ocean temperatures requires integrations of thousands of model years. A measure requiring shorter integrations is the transient climate response (TCR) which is defined as the average temperature response over a twenty-year period centered at CO2 doubling in a transient simulation with CO2 increasing at 1% per year.[7] The transient response is lower than the equilibrium sensitivity, due to the "inertia" of ocean heat uptake.
Over the 50–100 year timescale, the climate response to forcing is likely to follow the TCR; for considerations of climate stabilization, the ECS is more useful.
An estimate of the equilibrium climate sensitivity may be made from combining the transient climate sensitivity with the known properties of the ocean reservoirs and the surface heat fluxes; this is the effective climate sensitivity. This "may vary with forcing history and climate state".[8] [9]
A less commonly used concept, the Earth system sensitivity (ESS), can be defined which includes the effects of slower feedbacks, such as the albedo change from melting the large ice sheets that covered much of the northern hemisphere during the last glacial maximum. These extra feedbacks make the ESS larger than the ECS — possibly twice as large — but also mean that it may well not apply to current conditions.[10]
Sensitivity to carbon dioxide forcing
Climate sensitivity is often evaluated in terms of the change in equilibrium temperature due to radiative forcing due to the greenhouse effect. According to the Arrhenius relation,[11] the radiative forcing (and hence the change in temperature) is proportional to the logarithm of the concentration of infrared-absorbing gasses in the atmosphere. Thus, the sensitivity of temperature to gasses in the atmosphere (most notably carbon dioxide) is often expressed in terms of the change in temperature per doubling of the concentration of the gas.Radiative forcing due to doubled CO2
CO2 climate sensitivity has a component directly due to radiative forcing by CO2, and a further contribution arising from climate feedbacks, both positive and negative. "Without any feedbacks, a doubling of CO2 (which amounts to a forcing of 3.7 W/m2) would result in 1 °C global warming, which is easy to calculate and is undisputed. The remaining uncertainty is due entirely to feedbacks in the system, namely, the water vapor feedback, the ice-albedo feedback, the cloud feedback, and the lapse rate feedback";[12] addition of these feedbacks leads to a value of the sensitivity to CO2 doubling of approximately 3 °C ± 1.5 °C, which corresponds to a value of λ of 0.8 K/(W/m2).In the earlier 1979 NAS report[13] (p. 7), the radiative forcing due to doubled CO2 is estimated to be 4 W/m2, as calculated (for example) in Ramanathan et al. (1979).[14] In 2001 the IPCC adopted the revised value of 3.7 W/m2, the difference attributed to a "stratospheric temperature adjustment".[15] More recently an intercomparison of radiative transfer codes (Collins et al., 2006)[16] showed discrepancies among climate models and between climate models and more exact radiation codes in the forcing attributed to doubled CO2 even in cloud-free sky; presumably the differences would be even greater if forcing were evaluated in the presence of clouds because of differences in the treatment of clouds in different models. Undoubtedly the difference in forcing attributed to doubled CO2 in different climate models contributes to differences in apparent sensitivities of the models, although this effect is thought to be small relative to the intrinsic differences in sensitivities of the models themselves.[17]

Frequency distribution of climate sensitivity, based on model simulations.[1] Few of the simulations result in less than 2 °C of warming—near the low end of estimates by the Intergovernmental Panel on Climate Change (IPCC).[1] Some simulations result in significantly more than the 4 °C, which is at the high end of the IPCC estimates.[1] This pattern (statisticians call it a "right-skewed distribution") suggests that if carbon dioxide concentrations double, the probability of very large increases in temperature is greater than the probability of very small increases.[1]
Consensus estimates
A committee on anthropogenic global warming convened in 1979 by the National Academy of Sciences and chaired by Jule Charney[13] estimated climate sensitivity to be 3 °C, plus or minus 1.5 °C. Only two sets of models were available; one, due to Syukuro Manabe, exhibited a climate sensitivity of 2 °C, the other, due to James E. Hansen, exhibited a climate sensitivity of 4 °C. "According to Manabe, Charney chose 0.5 °C as a not-unreasonable margin of error, subtracted it from Manabe’s number, and added it to Hansen’s. Thus was born the 1.5 °C-to-4.5 °C range of likely climate sensitivity that has appeared in every greenhouse assessment since..."[18]Chapter 4 of the "Charney report" compares the predictions of the models: "We conclude that the predictions ... are basically consistent and mutually supporting. The differences in model results are relatively small and may be accounted for by differences in model characteristics and simplifying assumptions."[13]
In 2008 climatologist Stefan Rahmstorf wrote, regarding the Charney report's original range of uncertainty: "At that time, this range was on very shaky ground. Since then, many vastly improved models have been developed by a number of climate research centers around the world. Current state-of-the-art climate models span a range of 2.6–4.1 °C, most clustering around 3 °C."[12]
Intergovernmental Panel on Climate Change
The 1990 IPCC First Assessment Report estimated that equilibrium climate sensitivity to CO2 doubling lay between 1.5 and 4.5 °C, with a "best guess in the light of current knowledge" of 2.5 °C.[19] This used models with strongly simplified representations of the ocean dynamics. The IPCC supplementary report, 1992 which used full ocean GCMs nonetheless saw "no compelling reason to warrant changing" from this estimate [20] and the IPCC Second Assessment Report found that "No strong reasons have emerged to change" these estimates,[21] with much of the uncertainty attributed to cloud processes. As noted above, the IPCC TAR retained the likely range 1.5 to 4.5 °C.[6]Authors of the IPCC Fourth Assessment Report (Meehl et al., 2007)[22] stated that confidence in estimates of equilibrium climate sensitivity had increased substantially since the TAR. AR4's assessment was based on a combination of several independent lines of evidence, including observed climate change and the strength of known "feedbacks" simulated in general circulation models.[23] IPCC authors concluded that the global mean equilibrium warming for doubling CO2 (to a concentration of 560 ppmv), or equilibrium climate sensitivity, very likely is greater than 1.5 °C (2.7 °F) and likely to lie in the range 2 to 4.5 °C (4 to 8.1 °F), with a most likely value of about 3 °C (5 °F). For fundamental physical reasons, as well as data limitations, the IPCC states a climate sensitivity higher than 4.5 °C (8.1 °F) cannot be ruled out, but that agreement for these values with observations and "proxy" climate data is generally worse compared to values in the 2 to 4.5 °C (4 to 8.1 °F) range.[23]
The TAR uses the word "likely" in a qualitative sense to describe the likelihood of the 1.5 to 4.5 °C range being correct.[22] AR4, however, quantifies the probable range of climate sensitivity estimates:[24]
- 2-4.5 °C is "likely", = greater than 66% chance of being correct
- less than 1.5 °C is "very unlikely" = less than 10%
These are Bayesian probabilities, which are based on an expert assessment of the available evidence.[24]
Calculations of CO2 sensitivity from observational data
Sample calculation using industrial-age data
Rahmstorf (2008)[12] provides an informal example of how climate sensitivity might be estimated empirically, from which the following is modified. Denote the sensitivity, i.e. the equilibrium increase in global mean temperature including the effects of feedbacks due to a sustained forcing by doubled CO2 (taken as 3.7 W/m2), as x °C. If Earth were to experience an equilibrium temperature change of ΔT (°C) due to a sustained forcing of ΔF (W/m2), then one might say that x/(ΔT) = (3.7 W/m2)/(ΔF), i.e. that x = ΔT * (3.7 W/m2)/ΔF. The global temperature increase since the beginning of the industrial period (taken as 1750) is about 0.8 °C, and the radiative forcing due to CO2 and other long-lived greenhouse gases (mainly methane, nitrous oxide, and chlorofluorocarbons) emitted since that time is about 2.6 W/m2. Neglecting other forcings and considering the temperature increase to be an equilibrium increase would lead to a sensitivity of about 1.1 °C. However, ΔF also contains contributions due to solar activity (+0.3 W/m2), aerosols (-1 W/m2), ozone (0.3 W/m2) and other lesser influences, bringing the total forcing over the industrial period to 1.6 W/m2 according to best estimate of the IPCC AR4, albeit with substantial uncertainty. Additionally the fact that the climate system is not at equilibrium must be accounted for; this is done by subtracting the planetary heat uptake rate H from the forcing; i.e., x = ΔT * (3.7 W/m2)/(ΔF-H). Taking planetary heat uptake rate as the rate of ocean heat uptake, estimated by the IPCC AR4 as 0.2 W/m2, yields a value for x of 2.1 °C. (All numbers are approximate and quite uncertain.)Sample calculation using ice-age data
In 2008, Farley wrote: "... examine the change in temperature and solar forcing between glaciation (ice age) and interglacial (no ice age) periods. The change in temperature, revealed in ice core samples, is 5 °C, while the change in solar forcing is 7.1 W/m2. The computed climate sensitivity is therefore 5/7.1 = 0.7 K(W/m2)−1. We can use this empirically derived climate sensitivity to predict the temperature rise from a forcing of 4 W/m2, arising from a doubling of the atmospheric CO2 from pre-industrial levels. The result is a predicted temperature increase of 3 °C."[25]Based on analysis of uncertainties in total forcing, in Antarctic cooling, and in the ratio of global to Antarctic cooling of the last glacial maximum relative to the present, Ganopolski and Schneider von Deimling (2008) infer a range of 1.3 to 6.8 °C for climate sensitivity determined by this approach.[26]
A lower figure was calculated in a 2011 Science paper by Schmittner et al., who combined temperature reconstructions of the Last Glacial Maximum with climate model simulations to suggest a rate of global warming from doubling of atmospheric carbon dioxide of a median of 2.3 °C and uncertainty 1.7–2.6 °C (66% probability range), less than the earlier estimates of 2 to 4.5 °C as the 66% probability range. Schmittner et al. said their "results imply less probability of extreme climatic change than previously thought." Their work suggests that climate sensitivities >6 °C "cannot be reconciled with paleoclimatic and geologic evidence, and hence should be assigned near-zero probability."[27][28]
Other experimental estimates
Idso (1998)[29] calculated based on eight natural experiments a λ of 0.1 °C/(Wm−2) resulting in a climate sensitivity of only 0.4 °C for a doubling of the concentration of CO2 in the atmosphere.Andronova and Schlesinger (2001) found that the climate sensitivity could lie between 1 and 10 °C, with a 54 percent likelihood that it lies outside the IPCC range.[30] The exact range depends on which factors are most important during the instrumental period: "At present, the most likely scenario is one that includes anthropogenic sulfate aerosol forcing but not solar variation. Although the value of the climate sensitivity in that case is most uncertain, there is a 70 percent chance that it exceeds the maximum IPCC value. This is not good news," said Schlesinger.
Forest, et al. (2002)[31] using patterns of change and the MIT EMIC estimated a 95% confidence interval of 1.4–7.7 °C for the climate sensitivity, and a 30% probability that sensitivity was outside the 1.5 to 4.5 °C range.
Gregory, et al. (2002)[32] estimated a lower bound of 1.6 °C by estimating the change in Earth's radiation budget and comparing it to the global warming observed over the 20th century.
Shaviv (2005)[33] carried out a similar analysis for 6 different time scales, ranging from the 11-yr solar cycle to the climate variations over geological time scales. He found a typical sensitivity of 0.54±0.12 K/(W m−2) or 2.1 °C (ranging between 1.6 °C and 2.5 °C at 99% confidence) if there is no cosmic-ray climate connection, or a typical sensitivity of 0.35±0.09 K/(W m−2) or 1.3 °C (between 1.0 °C and 1.7 °C at 99% confidence), if the cosmic-ray climate link is real. (Note Shaviv quotes a radiative forcing equivalent of 3.8 Wm−2. [ΔTx2=3.8 Wm−2 λ].)
Frame, et al. (2005)[34] noted that the range of the confidence limits is dependent on the nature of the prior assumptions made.
Annan and Hargreaves (2006)[35] presented an estimate that resulted from combining prior estimates based on analyses of paleoclimate, responses to volcanic eruptions, and the temperature change in response to forcings over the twentieth century. They also introduced a triad notation (L, C, H) to convey the probability distribution function (pdf) of the sensitivity, where the central value C indicates the maximum likelihood estimate in degrees Celsius and the outer values L and H represent the limits of the 95% confidence interval for a pdf, or 95% of the area under the curve for a likelihood function. In this notation their estimate of sensitivity was (1.7, 2.9, 4.9) °C.
Forster and Gregory (2006)[36] presented a new independent estimate based on the slope of a plot of calculated greenhouse gas forcing minus top-of-atmosphere energy imbalance, as measured by satellite borne radiometers, versus global mean surface temperature. In the triad notation of Annan and Hargreaves their estimate of sensitivity was (1.0, 1.6, 4.1) °C.
Royer, et al. (2007)[37] determined climate sensitivity within a major part of the Phanerozoic. The range of values—1.5 °C minimum, 2.8 °C best estimate, and 6.2 °C maximum—is, given various uncertainties, consistent with sensitivities of current climate models and with other determinations.[38]
Lindzen and Choi (2011) find the equilibrium climate sensitivity to be 0.7 C, implying a negative feedback of clouds.[39]
Ring et all (2012) find the equilibrium climate sensitivity to be in the range 1.45 C- 2.01 C, depending on the data set used as an input in model simulations.[40]
Skeie et al (2013) use the Bayesian analysis of the OHC data and conclude that the equilibrium climate sensitivity is 1.8 C, far lower than previous best estimate relied upon by the IPCC.[41]
Aldrin et al (2012)use simple deterministic climate model, modelling yearly hemispheric surface temperature and global ocean heat content as a function of historical radiative forcing and combine it with an empirical, stochastic model. By using a Bayesian framework they estimate the equilibrium climate sensitivity to be 1.98 C.[42]
Lewis (2013) estimates by using the Bayesian framework that the equilibrium climate sensitivity is 1.6 K, with the likely range (90% confidence level) 1.2-2.2 K.[43]
ScienceDaily reported on a study by Fasullo and Trenberth (2012),[44] who tested model estimates of climate sensitivity based on their ability to reproduce observed relative humidity in the tropics and subtropics. The best performing models tended to project relatively high climate sensitivities, of around 4 °C.[44]
Previdi et al. 2013 reviewed the 2×CO2 Earth system sensitivity, and concluded it is higher if the ice sheet and the vegetation albedo feedback is included in addition to the fast feedbacks, being ∼4–6 °C, and higher still if climate–GHG feedbacks are also included.[45]
Lewis and Curry (2014) estimated that equilibrium climate sensitivity was 1.64 °C, based on the 1750-2011 time series and "the uncertainty ranges for forcing components" in the IPCC's Fifth Assessment Report.[46]


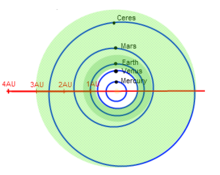
 , or 0.5, the distance from the star, corresponding to a distance of 0.67 AU. Various complicating factors, though, including the individual characteristics of stars themselves, mean that extrasolar extrapolation of the CHZ concept is more complex.
, or 0.5, the distance from the star, corresponding to a distance of 0.67 AU. Various complicating factors, though, including the individual characteristics of stars themselves, mean that extrasolar extrapolation of the CHZ concept is more complex.