From Wikipedia, the free encyclopedia
The shapes of the first five atomic orbitals are: 1s, 2s, 2p
x, 2p
y, and 2p
z. The two colors show the phase or sign of the wave function in each region. These are graphs of
ψ(x, y, z) functions which depend on the coordinates of one electron. To see the elongated shape of
ψ(x, y, z)2 functions that show
probability density more directly, see the graphs of d-orbitals below.
In
quantum mechanics, an
atomic orbital is a
mathematical function that describes the wave-like behavior of either one
electron or a pair of electrons in an
atom.
[1] This function can be used to calculate the
probability of finding any electron of an atom in any specific region around the
atom's nucleus.
The term, atomic orbital, may also refer to the physical region or
space where the electron can be calculated to be present, as defined by
the particular mathematical form of the orbital.
[2]
Each orbital in an atom is characterized by a unique set of values of the three
quantum numbers n,
ℓ, and
m, which respectively correspond to the electron's
energy,
angular momentum, and an angular momentum
vector component (the
magnetic quantum number). Each such orbital can be occupied by a maximum of two electrons, each with its own
spin quantum number s. The simple names
s orbital,
p orbital,
d orbital and
f orbital refer to orbitals with angular momentum quantum number
ℓ = 0, 1, 2 and
3 respectively. These names, together with the value of
n, are used to describe the
electron configurations of atoms. They are derived from the description by early spectroscopists of certain series of
alkali metal spectroscopic lines as
sharp,
principal,
diffuse, and
fundamental. Orbitals for
ℓ > 3 continue alphabetically, omitting j (g, h, i, k, …)
[3][4][5] because some languages do not distinguish between the letters "i" and "j".
[6]
Atomic orbitals are the basic building blocks of the
atomic orbital model
(alternatively known as the electron cloud or wave mechanics model), a
modern framework for visualizing the submicroscopic behavior of
electrons in matter. In this model the electron cloud of a
multi-electron atom may be seen as being built up (in approximation) in
an electron configuration that is a product of simpler
hydrogen-like atomic orbitals. The repeating
periodicity of the blocks of 2, 6, 10, and 14
elements within sections of the
periodic table arises naturally from the total number of electrons that occupy a complete set of
s,
p,
d and
f atomic orbitals, respectively, although for higher values of the quantum number
n,
particularly when the atom in question bears a positive charge, the
energies of certain sub-shells become very similar and so the
order in which they are said to be populated by electrons (e.g. Cr = [Ar]4
s13
d5 and Cr
2+ = [Ar]3
d4) can only be rationalized somewhat arbitrarily.
Electron properties
With the development of
quantum mechanics
and experimental findings (such as the two slits diffraction of
electrons), it was found that the orbiting electrons around a nucleus
could not be fully described as particles, but needed to be explained by
the
wave-particle duality. In this sense, the electrons have the following properties:
Wave-like properties:
- The electrons do not orbit the nucleus in the manner of a planet orbiting the sun, but instead exist as standing waves.
The lowest possible energy an electron can take is therefore analogous
to the fundamental frequency of a wave on a string. Higher energy states
are then similar to harmonics of the fundamental frequency.
- The electrons are never in a single point location, although the
probability of interacting with the electron at a single point can be
found from the wave function of the electron.
Particle-like properties:
- There is always an integer number of electrons orbiting the nucleus.
- Electrons jump between orbitals in a particle-like fashion. For example, if a single photon strikes the electrons, only a single electron changes states in response to the photon.
- The electrons retain particle-like properties such as: each wave
state has the same electrical charge as the electron particle. Each wave
state has a single discrete spin (spin up or spin down). This can
depend upon its superposition.
Thus, despite the popular analogy to planets revolving around the
Sun, electrons cannot be described simply as solid particles. In
addition, atomic orbitals do not closely resemble a planet's elliptical
path in ordinary atoms. A more accurate analogy might be that of a large
and often oddly shaped "atmosphere" (the electron), distributed around a
relatively tiny planet (the atomic nucleus). Atomic orbitals exactly
describe the shape of this "atmosphere" only when a single electron is
present in an atom. When more electrons are added to a single atom, the
additional electrons tend to more evenly fill in a volume of space
around the nucleus so that the resulting collection (sometimes termed
the atom’s “electron cloud”
[7])
tends toward a generally spherical zone of probability describing where
the atom’s electrons will be found. This is due to the uncertainty
principle.
Formal quantum mechanical definition
Atomic orbitals may be defined more precisely in formal
quantum mechanical language. Specifically, in quantum mechanics, the state of an atom, i.e., an
eigenstate of the atomic
Hamiltonian, is approximated by an expansion (see
configuration interaction expansion and
basis set) into
linear combinations of anti-symmetrized products (
Slater determinants)
of one-electron functions. The spatial components of these one-electron
functions are called atomic orbitals. (When one considers also their
spin component, one speaks of
atomic spin orbitals.)
A state is actually a function of the coordinates of all the electrons,
so that their motion is correlated, but this is often approximated by
this
independent-particle model of products of single electron wave functions.
[8] (The
London dispersion force, for example, depends on the correlations of the motion of the electrons.)
In
atomic physics, the
atomic spectral lines correspond to transitions (
quantum leaps) between
quantum states of an atom. These states are labeled by a set of
quantum numbers summarized in the
term symbol and usually associated with particular electron configurations, i.e., by occupation schemes of atomic orbitals (for example, 1s
2 2s
2 2p
6 for the ground state of
neon—term symbol:
1S
0).
This notation means that the corresponding Slater determinants have a clear higher weight in the
configuration interaction
expansion. The atomic orbital concept is therefore a key concept for
visualizing the excitation process associated with a given
transition.
For example, one can say for a given transition that it corresponds to
the excitation of an electron from an occupied orbital to a given
unoccupied orbital. Nevertheless, one has to keep in mind that electrons
are
fermions ruled by the
Pauli exclusion principle
and cannot be distinguished from the other electrons in the atom.
Moreover, it sometimes happens that the configuration interaction
expansion converges very slowly and that one cannot speak about simple
one-determinant wave function at all. This is the case when
electron correlation is large.
Fundamentally, an atomic orbital is a one-electron wave function,
even though most electrons do not exist in one-electron atoms, and so
the one-electron view is an approximation. When thinking about orbitals,
we are often given an orbital vision which (even if it is not spelled
out) is heavily influenced by this
Hartree–Fock approximation, which is one way to reduce the complexities of
molecular orbital theory.
Types of orbitals
False-color density images of some
hydrogen-like atomic orbitals (
f orbitals and higher are not shown)
Atomic orbitals can be the hydrogen-like "orbitals" which are exact solutions to the
Schrödinger equation for a
hydrogen-like "atom"
(i.e., an atom with one electron). Alternatively, atomic orbitals refer
to functions that depend on the coordinates of one electron (i.e.,
orbitals) but are used as starting points for approximating wave
functions that depend on the simultaneous coordinates of all the
electrons in an atom or molecule. The
coordinate systems chosen for atomic orbitals are usually
spherical coordinates (r, θ, φ) in atoms and
cartesians (x, y, z)
in polyatomic molecules. The advantage of spherical coordinates (for
atoms) is that an orbital wave function is a product of three factors
each dependent on a single coordinate:
ψ(r, θ, φ) = R(r) Θ(θ) Φ(φ). The angular factors of atomic orbitals
Θ(θ) Φ(φ) generate s, p, d, etc. functions as
real combinations of
spherical harmonics Yℓm(θ, φ) (where
ℓ and
m are quantum numbers). There are typically three mathematical forms for the radial functions
R(r) which can be chosen as a starting point for the calculation of the properties of atoms and molecules with many electrons:
- The hydrogen-like atomic orbitals are derived from the exact solution of the Schrödinger Equation for one electron and a nucleus, for a hydrogen-like atom. The part of the function that depends on the distance r from the nucleus has nodes (radial nodes) and decays as e−(constant × distance).
- The Slater-type orbital (STO) is a form without radial nodes but decays from the nucleus as does the hydrogen-like orbital.
- The form of the Gaussian type orbital (Gaussians) has no radial nodes and decays as
 .
.
Although hydrogen-like orbitals are still used as pedagogical tools,
the advent of computers has made STOs preferable for atoms and diatomic
molecules since combinations of STOs can replace the nodes in
hydrogen-like atomic orbital. Gaussians are typically used in molecules
with three or more atoms. Although not as accurate by themselves as
STOs, combinations of many Gaussians can attain the accuracy of
hydrogen-like orbitals.
History
The term "orbital" was coined by
Robert Mulliken in 1932 as an abbreviation for
one-electron orbital wave function.
[9]
However, the idea that electrons might revolve around a compact nucleus
with definite angular momentum was convincingly argued at least 19
years earlier by
Niels Bohr,
[10] and the Japanese physicist
Hantaro Nagaoka published an orbit-based hypothesis for electronic behavior as early as 1904.
[11] Explaining the behavior of these electron "orbits" was one of the driving forces behind the development of
quantum mechanics.
[12]
Early models
With
J.J. Thomson's discovery of the electron in 1897,
[13]
it became clear that atoms were not the smallest building blocks of
nature, but were rather composite particles. The newly discovered
structure within atoms tempted many to imagine how the atom's
constituent parts might interact with each other. Thomson theorized that
multiple electrons revolved in orbit-like rings within a positively
charged jelly-like substance,
[14] and between the electron's discovery and 1909, this "
plum pudding model" was the most widely accepted explanation of atomic structure.
Shortly after Thomson's discovery,
Hantaro Nagaoka predicted a different model for electronic structure.
[11]
Unlike the plum pudding model, the positive charge in Nagaoka's
"Saturnian Model" was concentrated into a central core, pulling the
electrons into circular orbits reminiscent of Saturn's rings. Few people
took notice of Nagaoka's work at the time,
[15]
and Nagaoka himself recognized a fundamental defect in the theory even
at its conception, namely that a classical charged object cannot sustain
orbital motion because it is accelerating and therefore loses energy
due to electromagnetic radiation.
[16] Nevertheless, the
Saturnian model turned out to have more in common with modern theory than any of its contemporaries.
Bohr atom
In 1909,
Ernest Rutherford
discovered that the bulk of the atomic mass was tightly condensed into a
nucleus, which was also found to be positively charged. It became clear
from his analysis in 1911 that the plum pudding model could not explain
atomic structure. In 1913 as Rutherford's post-doctoral student,
Niels Bohr
proposed a new model of the atom, wherein electrons orbited the nucleus
with classical periods, but were only permitted to have discrete values
of angular momentum, quantized in units
h/2π.
[10] This constraint automatically permitted only certain values of electron energies. The
Bohr model
of the atom fixed the problem of energy loss from radiation from a
ground state (by declaring that there was no state below this), and more
importantly explained the origin of spectral lines.
After Bohr's use of
Einstein's explanation of the
photoelectric effect
to relate energy levels in atoms with the wavelength of emitted light,
the connection between the structure of electrons in atoms and the
emission and
absorption spectra
of atoms became an increasingly useful tool in the understanding of
electrons in atoms. The most prominent feature of emission and
absorption spectra (known experimentally since the middle of the 19th
century), was that these atomic spectra contained discrete lines. The
significance of the Bohr model was that it related the lines in emission
and absorption spectra to the energy differences between the orbits
that electrons could take around an atom. This was, however,
not achieved by Bohr through giving the electrons some kind of wave-like properties, since the idea that electrons could behave as
matter waves
was not suggested until eleven years later. Still, the Bohr model's use
of quantized angular momenta and therefore quantized energy levels was a
significant step towards the understanding of electrons in atoms, and
also a significant step towards the development of
quantum mechanics in suggesting that quantized restraints must account for all discontinuous energy levels and spectra in atoms.
With
de Broglie's suggestion of the existence of electron matter waves in 1924, and for a short time before the full 1926
Schrödinger equation treatment of
hydrogen-like atom,
a Bohr electron "wavelength" could be seen to be a function of its
momentum, and thus a Bohr orbiting electron was seen to orbit in a
circle at a multiple of its half-wavelength (this physically incorrect
Bohr model is still often taught to beginning students). The Bohr model
for a short time could be seen as a classical model with an additional
constraint provided by the 'wavelength' argument. However, this period
was immediately superseded by the full three-dimensional wave mechanics
of 1926. In our current understanding of physics, the Bohr model is
called a semi-classical model because of its quantization of angular
momentum, not primarily because of its relationship with electron
wavelength, which appeared in hindsight a dozen years after the Bohr
model was proposed.
The Bohr model was able to explain the emission and absorption spectra of
hydrogen. The energies of electrons in the
n
= 1, 2, 3, etc. states in the Bohr model match those of current
physics. However, this did not explain similarities between different
atoms, as expressed by the periodic table, such as the fact that
helium (two electrons), neon (10 electrons), and
argon (18 electrons) exhibit similar chemical inertness. Modern
quantum mechanics explains this in terms of
electron shells and subshells which can each hold a number of electrons determined by the
Pauli exclusion principle. Thus the
n = 1 state can hold one or two electrons, while the
n = 2 state can hold up to eight electrons in 2s and 2p subshells. In helium, all
n = 1 states are fully occupied; the same for
n = 1 and
n
= 2 in neon. In argon the 3s and 3p subshells are similarly fully
occupied by eight electrons; quantum mechanics also allows a 3d subshell
but this is at higher energy than the 3s and 3p in argon (contrary to
the situation in the hydrogen atom) and remains empty.
Modern conceptions and connections to the Heisenberg Uncertainty Principle
Immediately after
Heisenberg discovered his
uncertainty principle,
[17] Bohr noted that the existence of any sort of
wave packet implies uncertainty in the wave frequency and wavelength, since a spread of frequencies is needed to create the packet itself.
[18]
In quantum mechanics, where all particle momenta are associated with
waves, it is the formation of such a wave packet which localizes the
wave, and thus the particle, in space. In states where a quantum
mechanical particle is bound, it must be localized as a wave packet, and
the existence of the packet and its minimum size implies a spread and
minimal value in particle wavelength, and thus also momentum and energy.
In quantum mechanics, as a particle is localized to a smaller region in
space, the associated compressed wave packet requires a larger and
larger range of momenta, and thus larger kinetic energy. Thus, the
binding energy to contain or trap a particle in a smaller region of
space, increases without bound, as the region of space grows smaller.
Particles cannot be restricted to a geometric point in space, since this
would require an infinite particle momentum.
In chemistry,
Schrödinger,
Pauling,
Mulliken
and others noted that the consequence of Heisenberg's relation was that
the electron, as a wave packet, could not be considered to have an
exact location in its orbital.
Max Born suggested that the electron's position needed to be described by a
probability distribution
which was connected with finding the electron at some point in the
wave-function which described its associated wave packet. The new
quantum mechanics did not give exact results, but only the probabilities
for the occurrence of a variety of possible such results. Heisenberg
held that the path of a moving particle has no meaning if we cannot
observe it, as we cannot with electrons in an atom.
In the quantum picture of Heisenberg, Schrödinger and others, the Bohr atom number
n for each orbital became known as an
n-sphere[citation needed]
in a three dimensional atom and was pictured as the mean energy of the
probability cloud of the electron's wave packet which surrounded the
atom.
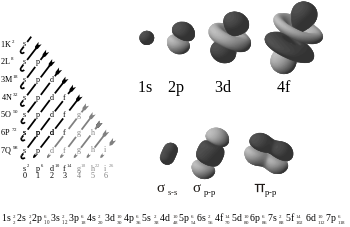
Orbital names
Orbitals are given names in the form:

where
X is the energy level corresponding to the
principal quantum number n,
type is a lower-case letter denoting the shape or
subshell of the orbital and it corresponds to the
angular quantum number ℓ, and
y is the number of electrons in that orbital.
For example, the orbital 1s
2 (pronounced "one ess two") has two electrons and is the lowest energy level (
n = 1) and has an angular quantum number of
ℓ = 0. In
X-ray notation, the principal quantum number is given a letter associated with it. For
n = 1, 2, 3, 4, 5, …, the letters associated with those numbers are K, L, M, N, O, … respectively.
Hydrogen-like orbitals
The simplest atomic orbitals are those that are calculated for systems with a single electron, such as the
hydrogen atom. An atom of any other element
ionized
down to a single electron is very similar to hydrogen, and the orbitals
take the same form. In the Schrödinger equation for this system of one
negative and one positive particle, the atomic orbitals are the
eigenstates of the
Hamiltonian operator
for the energy. They can be obtained analytically, meaning that the
resulting orbitals are products of a polynomial series, and exponential
and trigonometric functions. (see
hydrogen atom).
For atoms with two or more electrons, the governing equations can
only be solved with the use of methods of iterative approximation.
Orbitals of multi-electron atoms are
qualitatively similar to
those of hydrogen, and in the simplest models, they are taken to have
the same form. For more rigorous and precise analysis, the numerical
approximations must be used.
A given (hydrogen-like) atomic orbital is identified by unique values of three quantum numbers:
n,
ℓ, and
mℓ.
The rules restricting the values of the quantum numbers, and their
energies (see below), explain the electron configuration of the atoms
and the
periodic table.
The stationary states (
quantum states) of the hydrogen-like atoms are its atomic orbitals.
[clarification needed]
However, in general, an electron's behavior is not fully described by a
single orbital. Electron states are best represented by time-depending
"mixtures" (
linear combinations) of multiple orbitals. See
Linear combination of atomic orbitals molecular orbital method.
The quantum number
n first appeared in the
Bohr model where it determines the radius of each circular electron orbit. In modern quantum mechanics however,
n determines the mean distance of the electron from the nucleus; all electrons with the same value of
n lie at the same average distance. For this reason, orbitals with the same value of
n are said to comprise a "
shell". Orbitals with the same value of
n and also the same value of
ℓ are even more closely related, and are said to comprise a "
subshell".
Quantum numbers
Because of the quantum mechanical nature of the electrons around a
nucleus, atomic orbitals can be uniquely defined by a set of integers
known as quantum numbers. These quantum numbers only occur in certain
combinations of values, and their physical interpretation changes
depending on whether real or complex versions of the atomic orbitals are
employed.
Complex orbitals
In
physics, the most common orbital descriptions are based on the
solutions to the hydrogen atom, where orbitals are given by the product
between a radial function and a pure spherical harmonic. The quantum
numbers, together with the rules governing their possible values, are as
follows:
The
principal quantum number n describes the energy of the electron and is always a
positive integer.
In fact, it can be any positive integer, but for reasons discussed
below, large numbers are seldom encountered. Each atom has, in general,
many orbitals associated with each value of
n; these orbitals together are sometimes called
electron shells.
The
azimuthal quantum number ℓ describes the orbital angular momentum of each electron and is a non-negative integer. Within a shell where
n is some integer
n0,
ℓ ranges across all (integer) values satisfying the relation

. For instance, the
n = 1 shell has only orbitals with

, and the
n = 2 shell has only orbitals with

, and

. The set of orbitals associated with a particular value of
ℓ are sometimes collectively called a
subshell.
The
magnetic quantum number,

,
describes the magnetic moment of an electron in an arbitrary direction,
and is also always an integer. Within a subshell where

is some integer

,

ranges thus:

.
The above results may be summarized in the following table. Each cell represents a subshell, and lists the values of

available in that subshell. Empty cells represent subshells that do not exist.
|
ℓ = 0 |
ℓ = 1 |
ℓ = 2 |
ℓ = 3 |
ℓ = 4 |
… |
| n = 1 |
 |
|
|
|
|
|
| n = 2 |
0 |
−1, 0, 1 |
|
|
|
|
| n = 3 |
0 |
−1, 0, 1 |
−2, −1, 0, 1, 2 |
|
|
|
| n = 4 |
0 |
−1, 0, 1 |
−2, −1, 0, 1, 2 |
−3, −2, −1, 0, 1, 2, 3 |
|
|
| n = 5 |
0 |
−1, 0, 1 |
−2, −1, 0, 1, 2 |
−3, −2, −1, 0, 1, 2, 3 |
−4, −3, −2, −1, 0, 1, 2, 3, 4 |
|
| … |
… |
… |
… |
… |
… |
… |
Subshells are usually identified by their

- and

-values.

is represented by its numerical value, but

is represented by a letter as follows: 0 is represented by 's', 1 by
'p', 2 by 'd', 3 by 'f', and 4 by 'g'. For instance, one may speak of
the subshell with

and

as a '2s subshell'.
Each electron also has a
spin quantum number,
s, which describes the spin of each electron (spin up or spin down). The number
s can be +
1/2 or −
1/2.
The
Pauli exclusion principle
states that no two electrons can occupy the same quantum state: every
electron in an atom must have a unique combination of quantum numbers.
The above conventions imply a preferred axis (for example, the
z
direction in Cartesian coordinates), and they also imply a preferred
direction along this preferred axis. Otherwise there would be no sense
in distinguishing
m = +1 from
m = −1. As such, the model is most useful when applied to physical systems that share these symmetries. The
Stern–Gerlach experiment — where an atom is exposed to a magnetic field — provides one such example.
[19]
Real orbitals
An
atom that is embedded in a crystalline solid feels multiple preferred
axes, but no preferred direction. Instead of building atomic orbitals
out of the product of radial functions and a single
spherical harmonic,
linear combinations of spherical harmonics are typically used, designed
so that the imaginary part of the spherical harmonics cancel out. These
real orbitals are the building blocks most commonly shown in orbital visualizations.
In the real hydrogen-like orbitals, for example,
n and
ℓ have the same interpretation and significance as their complex counterparts, but
m
is no longer a good quantum number (though its absolute value is). The
orbitals are given new names based on their shape with respect to a
standardized Cartesian basis. The real hydrogen-like p orbitals are
given by the following
[20][21]



where
p0 = Rn 1 Y1 0,
p1 = Rn 1 Y1 1, and
p−1 = Rn 1 Y1 −1, are the complex orbitals corresponding to
ℓ = 1.
The equations for the p
x and p
y orbitals depend
on the phase convention used for the spherical harmonics. The above
equations suppose that the spherical harmonics are defined by

. However some quantum physicists
[22][23] include a phase factor (-1)
m in these definitions, which has the effect of relating the p
x orbital to a
difference of spherical harmonics and the p
y orbital to the corresponding
sum. (For more detail, see
Spherical harmonics#Conventions).
Shapes of orbitals
Cross-section of computed hydrogen atom orbital (ψ(r, θ, φ)2) for the 6s (n = 6, ℓ = 0, m = 0) orbital. Note that s orbitals, though spherically symmetrical, have radially placed wave-nodes for n > 1. However, only s orbitals invariably have a center anti-node; the other types never do.
Simple pictures showing orbital shapes are intended to describe the
angular forms of regions in space where the electrons occupying the
orbital are likely to be found. The diagrams cannot, however, show the
entire region where an electron can be found, since according to quantum
mechanics there is a non-zero probability of finding the electron
(almost) anywhere in space. Instead the diagrams are approximate
representations of boundary or
contour surfaces where the probability density
| ψ(r, θ, φ) |2
has a constant value, chosen so that there is a certain probability
(for example 90%) of finding the electron within the contour. Although
| ψ |2 as the square of an
absolute value is everywhere non-negative, the sign of the
wave function ψ(r, θ, φ) is often indicated in each subregion of the orbital picture.
Sometimes the
ψ function will be graphed to show its phases, rather than the
| ψ(r, θ, φ) |2 which shows probability density but has no phases (which have been lost in the process of taking the absolute value, since
ψ(r, θ, φ) is a complex number).
| ψ(r, θ, φ) |2 orbital graphs tend to have less spherical, thinner lobes than
ψ(r, θ, φ)
graphs, but have the same number of lobes in the same places, and
otherwise are recognizable. This article, in order to show wave function
phases, shows mostly
ψ(r, θ, φ) graphs.
The lobes can be viewed as
standing wave interference patterns between the two counter rotating, ring resonant
travelling wave "
m" and "
−m" modes, with the projection of the orbital onto the xy plane having a resonant "
m"
wavelengths around the circumference. Though rarely depicted the
travelling wave solutions can be viewed as rotating banded tori, with
the bands representing phase information. For each
m there are two standing wave solutions
⟨m⟩+⟨−m⟩ and
⟨m⟩−⟨−m⟩. For the case where
m = 0 the orbital is vertical, counter rotating information is unknown, and the orbital is z-axis symmetric. For the case where
ℓ = 0 there are no counter rotating modes. There are only radial modes and the shape is spherically symmetric. For any given
n, the smaller
ℓ is, the more radial nodes there are. Loosely speaking
n is energy,
ℓ is analogous to
eccentricity, and
m
is orientation. For the record, in the classical case, a ring resonant
travelling wave, for example in a circular transmission line, unless
actively forced, will spontaneously decay into a ring resonant standing
wave because reflections will build up over time at even the smallest
imperfection or discontinuity.
Generally speaking, the number
n determines the size and energy of the orbital for a given nucleus: as
n increases, the size of the orbital increases. However, in comparing different elements, the higher nuclear charge
Z
of heavier elements causes their orbitals to contract by comparison to
lighter ones, so that the overall size of the whole atom remains very
roughly constant, even as the number of electrons in heavier elements
(higher
Z) increases.
Experimentally imaged 1
s and 2
p core-electron orbitals of
Sr, including the effects of atomic thermal vibrations and excitation
broadening, retrieved from energy dispersive x-ray spectroscopy (EDX) in
scanning transmission electron microscopy (STEM).
[24]
Also in general terms,
ℓ determines an orbital's shape, and
mℓ its orientation. However, since some orbitals are described by equations in
complex numbers, the shape sometimes depends on
mℓ also. Together, the whole set of orbitals for a given
ℓ and
n fill space as symmetrically as possible, though with increasingly complex sets of lobes and nodes.
The single s-orbitals (

) are shaped like spheres. For
n = 1 it is roughly a
solid ball (it is most dense at the center and fades exponentially outwardly), but for
n = 2
or more, each single s-orbital is composed of spherically symmetric
surfaces which are nested shells (i.e., the "wave-structure" is radial,
following a sinusoidal radial component as well). See illustration of a
cross-section of these nested shells, at right. The s-orbitals for all
n
numbers are the only orbitals with an anti-node (a region of high wave
function density) at the center of the nucleus. All other orbitals (p,
d, f, etc.) have angular momentum, and thus avoid the nucleus (having a
wave node
at the nucleus). Recently, there has been an effort to experimentally image the 1
s and 2
p orbitials in a SrTiO
3 crystal using scanning transmission electron microscopy with energy dispersive x-ray spectroscopy.
[24]
Because the imaging was conducted using an electron beam, Coulombic
beam-orbital interaction that is often termed as the impact parameter
effect is included in the final outcome (see the figure at right).
The shapes of p, d and f-orbitals are described verbally here and shown graphically in the
Orbitals table below. The three p-orbitals for
n = 2 have the form of two
ellipsoids with a
point of tangency at the
nucleus (the two-lobed shape is sometimes referred to as a "
dumbbell"—there are two lobes pointing in opposite directions from each other). The three p-orbitals in each
shell are oriented at right angles to each other, as determined by their respective linear combination of values of
mℓ. The overall result is a lobe pointing along each direction of the primary axes.
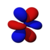
Four of the five d-orbitals for
n = 3
look similar, each with four pear-shaped lobes, each lobe tangent at
right angles to two others, and the centers of all four lying in one
plane. Three of these planes are the xy-, xz-, and yz-planes—the lobes
are between the pairs of primary axes—and the fourth has the centres
along the x and y axes themselves. The fifth and final d-orbital
consists of three regions of high probability density: a
torus
with two pear-shaped regions placed symmetrically on its z axis. The
overall total of 18 directional lobes point in every primary axis
direction and between every pair.
There are seven f-orbitals, each with shapes more complex than those of the d-orbitals.
Additionally, as is the case with the s orbitals, individual p, d, f and g orbitals with
n
values higher than the lowest possible value, exhibit an additional
radial node structure which is reminiscent of harmonic waves of the same
type, as compared with the lowest (or fundamental) mode of the wave. As
with s orbitals, this phenomenon provides p, d, f, and g orbitals at
the next higher possible value of
n (for example, 3p orbitals vs. the fundamental 2p), an additional node in each lobe. Still higher values of
n further increase the number of radial nodes, for each type of orbital.
The shapes of atomic orbitals in one-electron atom are related to 3-dimensional
spherical harmonics. These shapes are not unique, and any linear combination is valid, like a transformation to
cubic harmonics, in fact it is possible to generate sets where all the d's are the same shape, just like the
px, py, and
pz are the same shape.
[25][26]
Orbitals table
This
table shows all orbital configurations for the real hydrogen-like wave
functions up to 7s, and therefore covers the simple electronic
configuration for all elements in the periodic table up to
radium. "ψ" graphs are shown with
− and
+ wave function phases shown in two different colors (arbitrarily red and blue). The
pz orbital is the same as the
p0 orbital, but the
px and
py are formed by taking linear combinations of the
p+1 and
p−1 orbitals (which is why they are listed under the
m = ±1 label). Also, the
p+1 and
p−1 are not the same shape as the
p0, since they are pure
spherical harmonics.
|
s (ℓ = 0) |
p (ℓ = 1) |
d (ℓ = 2) |
f (ℓ = 3) |
|
m = 0 |
m = 0 |
m = ±1 |
m = 0 |
m = ±1 |
m = ±2 |
m = 0 |
m = ±1 |
m = ±2 |
m = ±3 |
|
s |
pz |
px |
py |
dz2 |
dxz |
dyz |
dxy |
dx2−y2 |
fz3 |
fxz2 |
fyz2 |
fxyz |
fz(x2−y2) |
fx(x2−3y2) |
fy(3x2−y2) |
| n = 1 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n = 2 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
| n = 3 |
 |
 |
 |
 |
 |
 |
 |
 |
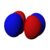 |
|
|
|
|
|
|
|
| n = 4 |
 |
 |
 |
 |
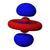 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| n = 5 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
| n = 6 |
 |
 |
 |
 |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
| n = 7 |
 |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
Qualitative understanding of shapes
The shapes of atomic orbitals can be understood qualitatively by considering the analogous case of
standing waves on a circular drum.
[27]
To see the analogy, the mean vibrational displacement of each bit of
drum membrane from the equilibrium point over many cycles (a measure of
average drum membrane velocity and momentum at that point) must be
considered relative to that point's distance from the center of the drum
head. If this displacement is taken as being analogous to the
probability of finding an electron at a given distance from the nucleus,
then it will be seen that the many modes of the vibrating disk form
patterns that trace the various shapes of atomic orbitals. The basic
reason for this correspondence lies in the fact that the distribution of
kinetic energy and momentum in a matter-wave is predictive of where the
particle associated with the wave will be. That is, the probability of
finding an electron at a given place is also a function of the
electron's average momentum at that point, since high electron momentum
at a given position tends to "localize" the electron in that position,
via the properties of electron wave-packets (see the
Heisenberg uncertainty principle for details of the mechanism).
This relationship means that certain key features can be observed in
both drum membrane modes and atomic orbitals. For example, in all of the
modes analogous to
s orbitals (the top row in the animated
illustration below), it can be seen that the very center of the drum
membrane vibrates most strongly, corresponding to the
antinode in all
s orbitals
in an atom. This antinode means the electron is most likely to be at
the physical position of the nucleus (which it passes straight through
without scattering or striking it), since it is moving (on average) most
rapidly at that point, giving it maximal momentum.
A mental "planetary orbit" picture closest to the behavior of electrons in
s orbitals, all of which have no angular momentum, might perhaps be that of a
Keplerian orbit with the
orbital eccentricity of 1 but a finite major axis, not physically possible (because
particles were to collide), but can be imagined as a
limit of orbits with equal major axes but increasing eccentricity.
Below, a number of drum membrane vibration modes and the respective
wave functions of the hydrogen atom are shown. A correspondence can be
considered where the wave functions of a vibrating drum head are for a
two-coordinate system
ψ(r, θ) and the wave functions for a vibrating sphere are three-coordinate
ψ(r, θ, φ).
- s-type drum modes and wave functions
-
Drum mode

-
Drum mode

-
Drum mode

-
Wave function of 1s orbital (real part, 2D-cut,

)
-
Wave function of 2s orbital (real part, 2D-cut,

)
-
Wave function of 3s orbital (real part, 2D-cut,

)
None of the other sets of modes in a drum membrane have a central
antinode, and in all of them the center of the drum does not move. These
correspond to a node at the nucleus for all non-
s orbitals in an
atom. These orbitals all have some angular momentum, and in the
planetary model, they correspond to particles in orbit with eccentricity
less than 1.0, so that they do not pass straight through the center of
the primary body, but keep somewhat away from it.
In addition, the drum modes analogous to
p and
d modes
in an atom show spatial irregularity along the different radial
directions from the center of the drum, whereas all of the modes
analogous to
s modes are perfectly symmetrical in radial direction. The non radial-symmetry properties of non-
s
orbitals are necessary to localize a particle with angular momentum and
a wave nature in an orbital where it must tend to stay away from the
central attraction force, since any particle localized at the point of
central attraction could have no angular momentum. For these modes,
waves in the drum head tend to avoid the central point. Such features
again emphasize that the shapes of atomic orbitals are a direct
consequence of the wave nature of electrons.
- p-type drum modes and wave functions
-
Drum mode

-
Drum mode

-
Drum mode

-
Wave function of 2p orbital (real part, 2D-cut,

)
-
Wave function of 3p orbital (real part, 2D-cut,

)
-
Wave function of 4p orbital (real part, 2D-cut,

)
- d-type drum modes
-
Mode

(3d orbital)
-
Mode

(4d orbital)
-
Mode

(5d orbital)
Orbital energy
In atoms with a single electron (
hydrogen-like atoms), the energy of an orbital (and, consequently, of any electrons in the orbital) is determined exclusively by

. The

orbital has the lowest possible energy in the atom. Each successively higher value of

has a higher level of energy, but the difference decreases as

increases. For high

,
the level of energy becomes so high that the electron can easily escape
from the atom. In single electron atoms, all levels with different

within a given

are (to a good approximation) degenerate, and have the same energy.
This approximation is broken to a slight extent by the effect of the
magnetic field of the nucleus, and by
quantum electrodynamics effects. The latter induce tiny binding energy differences especially for
s electrons
that go nearer the nucleus, since these feel a very slightly different
nuclear charge, even in one-electron atoms; see
Lamb shift.
In atoms with multiple electrons, the energy of an electron depends
not only on the intrinsic properties of its orbital, but also on its
interactions with the other electrons. These interactions depend on the
detail of its spatial probability distribution, and so the
energy levels of orbitals depend not only on

but also on

. Higher values of

are associated with higher values of energy; for instance, the 2p state is higher than the 2s state. When

,
the increase in energy of the orbital becomes so large as to push the
energy of orbital above the energy of the s-orbital in the next higher
shell; when

the energy is pushed into the shell two steps higher. The filling of
the 3d orbitals does not occur until the 4s orbitals have been filled.
The increase in energy for subshells of increasing angular momentum
in larger atoms is due to electron–electron interaction effects, and it
is specifically related to the ability of low angular momentum electrons
to penetrate more effectively toward the nucleus, where they are
subject to less screening from the charge of intervening electrons.
Thus, in atoms of higher atomic number, the

of electrons becomes more and more of a determining factor in their energy, and the principal quantum numbers

of electrons becomes less and less important in their energy placement.
The energy sequence of the first 35 subshells (e.g., 1s, 2p, 3d,
etc.) is given in the following table. Each cell represents a subshell
with

and

given by its row and column indices, respectively. The number in the
cell is the subshell's position in the sequence. For a linear listing of
the subshells in terms of increasing energies in multielectron atoms,
see the section below.
|
s |
p |
d |
f |
g |
h |
| 1 |
1 |
|
|
|
|
|
| 2 |
2 |
3 |
|
|
|
|
| 3 |
4 |
5 |
7 |
|
|
|
| 4 |
6 |
8 |
10 |
13 |
|
|
| 5 |
9 |
11 |
14 |
17 |
21 |
|
| 6 |
12 |
15 |
18 |
22 |
26 |
31 |
| 7 |
16 |
19 |
23 |
27 |
32 |
37 |
| 8 |
20 |
24 |
28 |
33 |
38 |
44 |
| 9 |
25 |
29 |
34 |
39 |
45 |
51 |
| 10 |
30 |
35 |
40 |
46 |
52 |
59 |
Note: empty cells indicate non-existent sublevels, while numbers
in italics indicate sublevels that could (potentially) exist, but which
do not hold electrons in any element currently known.
Electron placement and the periodic table
Electron atomic and
molecular orbitals. The chart of orbitals (
left) is arranged by increasing energy (see
Madelung rule).
Note that atomic orbits are functions of three variables (two angles, and the distance r
from the nucleus). These images are faithful to the angular component
of the orbital, but not entirely representative of the orbital as a
whole.
Several rules govern the placement of electrons in orbitals (
electron configuration). The first dictates that no two electrons in an atom may have the same set of values of quantum numbers (this is the
Pauli exclusion principle). These quantum numbers include the three that define orbitals, as well as
s, or
spin quantum number. Thus, two electrons may occupy a single orbital, so long as they have different values of
s. However,
only two electrons, because of their spin, can be associated with each orbital.
Additionally, an electron always tends to fall to the lowest possible
energy state. It is possible for it to occupy any orbital so long as it
does not violate the Pauli exclusion principle, but if lower-energy
orbitals are available, this condition is unstable. The electron will
eventually lose energy (by releasing a
photon) and drop into the lower orbital. Thus, electrons fill orbitals in the order specified by the energy sequence given above.
This behavior is responsible for the structure of the
periodic table.
The table may be divided into several rows (called 'periods'), numbered
starting with 1 at the top. The presently known elements occupy seven
periods. If a certain period has number
i, it consists of elements whose outermost electrons fall in the
ith shell.
Niels Bohr was the first to propose (1923) that the
periodicity
in the properties of the elements might be explained by the periodic
filling of the electron energy levels, resulting in the electronic
structure of the atom.
[28]
The periodic table may also be divided into several numbered rectangular '
blocks'. The elements belonging to a given block have this common feature: their highest-energy electrons all belong to the same
ℓ-state (but the
n associated with that
ℓ-state depends upon the period). For instance, the leftmost two columns constitute the 's-block'. The outermost electrons of
Li and
Be respectively belong to the 2s subshell, and those of
Na and
Mg to the 3s subshell.
The following is the order for filling the "subshell" orbitals, which
also gives the order of the "blocks" in the periodic table:
- 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p
The "periodic" nature of the filling of orbitals, as well as emergence of the
s,
p,
d and
f
"blocks", is more obvious if this order of filling is given in matrix
form, with increasing principal quantum numbers starting the new rows
("periods") in the matrix. Then, each subshell (composed of the first
two quantum numbers) is repeated as many times as required for each pair
of electrons it may contain. The result is a compressed periodic table,
with each entry representing two successive elements:
1s
2s 2p 2p 2p
3s 3p 3p 3p
4s 3d 3d 3d 3d 3d 4p 4p 4p
5s 4d 4d 4d 4d 4d 5p 5p 5p
6s 4f 4f 4f 4f 4f 4f 4f 5d 5d 5d 5d 5d 6p 6p 6p
7s 5f 5f 5f 5f 5f 5f 5f 6d 6d 6d 6d 6d 7p 7p 7p
|
Although this is the general order of orbital filling according to
the Madelung rule, there are exceptions, and the actual electronic
energies of each element are also dependent upon additional details of
the atoms (see
Electron configuration#Atoms: Aufbau principle and Madelung rule).
The number of electrons in an electrically neutral atom increases with the
atomic number. The electrons in the outermost shell, or
valence electrons,
tend to be responsible for an element's chemical behavior. Elements
that contain the same number of valence electrons can be grouped
together and display similar chemical properties.
Relativistic effects
For elements with high atomic number
Z,
the effects of relativity become more pronounced, and especially so for
s electrons, which move at relativistic velocities as they penetrate
the screening electrons near the core of high-
Z
atoms. This relativistic increase in momentum for high speed electrons
causes a corresponding decrease in wavelength and contraction of 6s
orbitals relative to 5d orbitals (by comparison to corresponding s and d
electrons in lighter elements in the same column of the periodic
table); this results in 6s valence electrons becoming lowered in energy.
Examples of significant physical outcomes of this effect include the lowered melting temperature of
mercury (which results from 6s electrons not being available for metal bonding) and the golden color of
gold and
caesium (which results from narrowing of 6s to 5d transition energy to the point that visible light begins to be absorbed).
[29]
In the
Bohr Model, an
n = 1 electron has a velocity given by

, where
Z is the atomic number,

is the
fine-structure constant, and
c
is the speed of light. In non-relativistic quantum mechanics,
therefore, any atom with an atomic number greater than 137 would require
its 1s electrons to be traveling faster than the speed of light. Even
in the
Dirac equation, which accounts for relativistic effects, the wave function of the electron for atoms with
Z > 137 is oscillatory and
unbounded. The significance of element 137, also known as
untriseptium, was first pointed out by the physicist
Richard Feynman. Element 137 is sometimes informally called
feynmanium (symbol Fy)
[citation needed]. However, Feynman's approximation fails to predict the exact critical value of
Z
due to the non-point-charge nature of the nucleus and very small
orbital radius of inner electrons, resulting in a potential seen by
inner electrons which is effectively less than
Z. The critical
Z value
which makes the atom unstable with regard to high-field breakdown of
the vacuum and production of electron-positron pairs, does not occur
until
Z is
about 173. These conditions are not seen except transiently in
collisions of very heavy nuclei such as lead or uranium in accelerators,
where such electron-positron production from these effects has been
claimed to be observed.
There are no nodes in relativistic orbital densities, although individual components of the wave function will have nodes.
[30]
Transitions between orbitals
Bound quantum states have discrete energy levels. When applied to
atomic orbitals, this means that the energy differences between states
are also discrete. A transition between these states (i.e., an electron
absorbing or emitting a photon) can thus only happen if the photon has
an energy corresponding with the exact energy difference between said
states.
Consider two states of the hydrogen atom:
State 1)
n = 1,
ℓ = 0,
mℓ = 0 and
s = +1/2
State 2)
n = 2,
ℓ = 0,
mℓ = 0 and
s = +1/2
By quantum theory, state 1 has a fixed energy of
E1, and state 2 has a fixed energy of
E2.
Now, what would happen if an electron in state 1 were to move to
state 2? For this to happen, the electron would need to gain an energy
of exactly
E2 − E1.
If the electron receives energy that is less than or greater than this
value, it cannot jump from state 1 to state 2. Now, suppose we irradiate
the atom with a broad-spectrum of light. Photons that reach the atom
that have an energy of exactly
E2 − E1
will be absorbed by the electron in state 1, and that electron will
jump to state 2. However, photons that are greater or lower in energy
cannot be absorbed by the electron, because the electron can only jump
to one of the orbitals, it cannot jump to a state between orbitals. The
result is that only photons of a specific frequency will be absorbed by
the atom. This creates a line in the spectrum, known as an absorption
line, which corresponds to the energy difference between states 1 and 2.
The atomic orbital model thus predicts line spectra, which are
observed experimentally. This is one of the main validations of the
atomic orbital model.
The atomic orbital model is nevertheless an approximation to the full
quantum theory, which only recognizes many electron states. The
predictions of line spectra are qualitatively useful but are not
quantitatively accurate for atoms and ions other than those containing
only one electron.