From Wikipedia, the free encyclopedia
Entropy
is the only quantity in the physical sciences (apart from certain rare
interactions in particle physics; see below) that requires a particular
direction for time, sometimes called an
arrow of time. As one goes "forward" in time, the
second law of thermodynamics
says, the entropy of an isolated system can increase, but not decrease.
Hence, from one perspective, entropy measurement is a way of
distinguishing the past from the future. However, in thermodynamic
systems that are not closed, entropy can decrease with time: many
systems, including
living systems,
reduce local entropy at the expense of an environmental increase,
resulting in a net increase in entropy. Examples of such systems and
phenomena include the formation of typical crystals, the workings of a
refrigerator and living organisms, used in thermodynamics.
Entropy, like
temperature,
is an abstract concept, yet, like temperature, everyone has an
intuitive sense of the effects of entropy. Watching a movie, it is
usually easy to determine whether it is being run forward or in reverse.
When run in reverse, broken glasses spontaneously reassemble; smoke
goes down a chimney; wood "unburns", cooling the environment; and ice
"unmelts", warming the environment. No physical laws are broken in the
reverse movie except the
second law of thermodynamics,
which reflects the time-asymmetry of entropy. An intuitive
understanding of the irreversibility of certain physical phenomena (and
subsequent creation of entropy) allows one to make this determination.
By contrast, all physical processes occurring at the atomic level,
such as mechanics, do not pick out an arrow of time. Going forward in
time, an atom might move to the left, whereas going backward in time the
same atom might move to the right; the behavior of the atom is not
qualitatively different in either case. It would, however, be an astronomically improbable event if a
macroscopic amount of gas that originally filled a container evenly spontaneously shrunk to occupy only half the container.
Certain subatomic interactions involving the
weak nuclear force violate the
conservation of parity, but only very rarely,
[citation needed] According to the
CPT theorem, this means they should also be
time irreversible, and so establish an
arrow of time.
This, however, is neither linked to the thermodynamic arrow of time,
nor has anything to do with our daily experience of time
irreversibility.
[1]
 |
Unsolved problem in physics:
|
Overview
The
Second Law of Thermodynamics allows for the entropy to
remain the same
regardless of the direction of time. If the entropy is constant in
either direction of time, there would be no preferred direction.
However, the entropy can only be a constant if the system is in the
highest possible state of disorder, such as a gas that always was, and
always will be, uniformly spread out in its container. The existence of a
thermodynamic arrow of time implies that the system is highly ordered
in one time direction only, which would by definition be the "past".
Thus this law is about the
boundary conditions rather than the
equations of motion of our world.
The Second Law of Thermodynamics is
statistical
in nature, and therefore its reliability arises from the huge number of
particles present in macroscopic systems. It is not impossible, in
principle, for all 6 × 10
23 atoms in a
mole of a gas to spontaneously migrate to one half of a container; it is only
fantastically unlikely—so unlikely that no macroscopic violation of the Second Law has ever been observed.
T Symmetry
is the symmetry of physical laws under a time reversal transformation.
Although in restricted contexts one may find this symmetry, the
observable universe itself does not show symmetry under time reversal,
primarily due to the second law of thermodynamics.
The thermodynamic arrow is often linked to the cosmological arrow of time, because it is ultimately about the
boundary conditions of the early universe. According to the
Big Bang theory, the
Universe was initially very hot with energy distributed uniformly. For a system in which
gravity
is important, such as the universe, this is a low-entropy state
(compared to a high-entropy state of having all matter collapsed into
black holes,
a state to which the system may eventually evolve). As the Universe
grows, its temperature drops, which leaves less energy available to
perform work in the future than was available in the past. Additionally,
perturbations in the energy density grow (eventually forming
galaxies and
stars).
Thus the Universe itself has a well-defined thermodynamic arrow of
time. But this does not address the question of why the initial state of
the universe was that of low entropy. If cosmic expansion were to halt
and reverse due to gravity, the temperature of the Universe would once
again grow hotter, but its entropy would also continue to increase due
to the continued growth of perturbations and the eventual
black hole formation,
[2] until the latter stages of the
Big Crunch when entropy would be lower than now.
[citation needed]
An example of apparent irreversibility
Consider
the situation in which a large container is filled with two separated
liquids, for example a dye on one side and water on the other. With no
barrier between the two liquids, the random jostling of their
molecules
will result in them becoming more mixed as time passes. However, if the
dye and water are mixed then one does not expect them to separate out
again when left to themselves. A movie of the mixing would seem
realistic when played forwards, but unrealistic when played backwards.
If the large container is observed early on in the mixing process, it
might be found only partially mixed. It would be reasonable to conclude
that, without outside intervention, the liquid reached this state
because it was more ordered in the past, when there was greater
separation, and will be more disordered, or mixed, in the future.
Now imagine that the experiment is repeated, this time with only a
few molecules, perhaps ten, in a very small container. One can easily
imagine that by watching the random jostling of the molecules it might
occur — by chance alone — that the molecules became neatly segregated,
with all dye molecules on one side and all water molecules on the other.
That this can be expected to occur from time to time can be concluded
from the
fluctuation theorem;
thus it is not impossible for the molecules to segregate themselves.
However, for a large numbers of molecules it is so unlikely that one
would have to wait, on average, many times longer than the age of the
universe for it to occur. Thus a movie that showed a large number of
molecules segregating themselves as described above would appear
unrealistic and one would be inclined to say that the movie was being
played in reverse. See Boltzmann's
Second Law as a law of disorder.
Mathematics of the arrow
The
mathematics behind the
arrow of time,
entropy, and basis of the
second law of thermodynamics derive from the following set-up, as detailed by Carnot (1824), Clapeyron (1832), and Clausius (1854):
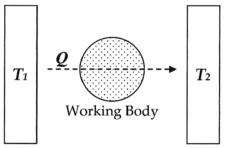
Here, as common experience demonstrates, when a
hot body
T1, such as a furnace, is put into physical contact, such as being connected via a body of fluid (
working body), with a cold body
T2, such as a stream of cold water,
energy will invariably flow from hot to cold in the form of
heat Q, and given
time the system will reach
equilibrium. Entropy, defined as Q/T, was conceived by
Rudolf Clausius as a function to measure the molecular
irreversibility of this process, i.e. the dissipative work the atoms and molecules do on each other during the transformation.
In this diagram, one can calculate the entropy change Δ
S for the passage of the quantity of heat
Q from the
temperature T1, through the "working body" of fluid (see
heat engine), which was typically a body of steam, to the temperature
T2. Moreover, one could assume, for the sake of argument, that the working body contains only two molecules of water.
Next, if we make the assignment, as originally done by Clausius:

Then the entropy change or "equivalence-value" for this transformation is:

which equals:

and by factoring out Q, we have the following form, as was derived by Clausius:

Thus, for example, if Q was 50 units,
T1 was initially 100 degrees, and
T2
was initially 1 degree, then the entropy change for this process would
be 49.5. Hence, entropy increased for this process, the process took a
certain amount of "time", and one can correlate entropy increase with
the passage of time. For this system configuration, subsequently, it is
an "absolute rule". This rule is based on the fact that all natural
processes are
irreversible
by virtue of the fact that molecules of a system, for example two
molecules in a tank, not only do external work (such as to push a
piston), but also do internal work on each other, in proportion to the
heat used to do work (see:
Mechanical equivalent of heat) during the process. Entropy accounts for the fact that internal inter-molecular friction exists.
Maxwell's demon
In 1867,
James Clerk Maxwell introduced a now-famous
thought experiment
that highlighted the contrast between the statistical nature of entropy
and the deterministic nature of the underlying physical processes. This
experiment, known as
Maxwell's demon,
consists of a hypothetical "demon" that guards a trapdoor between two
containers filled with gases at equal temperatures. By allowing fast
molecules through the trapdoor in only one direction and only slow
molecules in the other direction, the demon raises the temperature of
one gas and lowers the temperature of the other, apparently violating
the Second Law.
Maxwell's thought experiment was only resolved in the 20th century by
Leó Szilárd,
Charles H. Bennett,
Seth Lloyd
and others. The key idea is that the demon itself necessarily possesses
a non-negligible amount of entropy that increases even as the gases
lose entropy, so that the entropy of the system as a whole increases.
This is because the demon has to contain many internal "parts"
(essentially: a
memory space to store information on the gas molecules) if it is to perform its job reliably, and therefore must be considered a
macroscopic system with non-vanishing entropy. An equivalent way of saying this is that the
information possessed by the demon on which atoms are considered
fast or
slow, can be considered a form of entropy known as
information entropy.
Correlations
An
important difference between the past and the future is that in any
system (such as a gas of particles) its initial conditions are usually
such that its different parts are uncorrelated, but as the system
evolves and its different parts interact with each other, they become
correlated.
[3]
For example, whenever dealing with a gas of particles, it is always
assumed that its initial conditions are such that there is no
correlation between the states of different particles (i.e. the speeds
and locations of the different particles are completely random, up to
the need to conform with the
macrostate of the system). This is closely related to the Second Law of Thermodynamics.
Take for example (experiment A) a closed box that is, at the
beginning, half-filled with ideal gas. As time passes, the gas obviously
expands to fill the whole box, so that the final state is a box full of
gas. This is an irreversible process, since if the box is full at the
beginning (experiment B), it does not become only half-full later,
except for the very unlikely situation where the gas particles have very
special locations and speeds. But this is precisely because we always
assume that the initial conditions are such that the particles have
random locations and speeds. This is not correct for the final
conditions of the system, because the particles have interacted between
themselves, so that their locations and speeds have become dependent on
each other, i.e. correlated. This can be understood if we look at
experiment A backwards in time, which we'll call experiment C: now we
begin with a box full of gas, but the particles do not have random
locations and speeds; rather, their locations and speeds are so
particular, that after some time they all move to one half of the box,
which is the final state of the system (this is the initial state of
experiment A, because now we're looking at the same experiment
backwards!). The interactions between particles now do not create
correlations between the particles, but in fact turn them into (at least
seemingly) random, "canceling" the pre-existing correlations. The only
difference between experiment C (which defies the Second Law of
Thermodynamics) and experiment B (which obeys the Second Law of
Thermodynamics) is that in the former the particles are uncorrelated at
the end, while in the latter the particles are uncorrelated at the
beginning.
[citation needed]
In fact, if all the microscopic physical processes are reversible
(see discussion below), then the Second Law of Thermodynamics can be
proven for any isolated system of particles with initial conditions in
which the particles states are uncorrelated. To do this, one must
acknowledge the difference between the measured entropy of a
system—which depends only on its
macrostate (its volume, temperature etc.)—and its
information entropy (also called
Kolmogorov complexity),
[4] which is the amount of information (number of computer bits) needed to describe the exact
microstate
of the system. The measured entropy is independent of correlations
between particles in the system, because they do not affect its
macrostate, but the information entropy
does depend on them,
because correlations lower the randomness of the system and thus lowers
the amount of information needed to describe it.
[5]
Therefore, in the absence of such correlations the two entropies are
identical, but otherwise the information entropy is smaller than the
measured entropy, and the difference can be used as a measure of the
amount of correlations.
Now, by
Liouville's theorem, time-reversal of all microscopic processes implies that the amount of information needed to describe the exact
microstate of an isolated system (its information-theoretic
joint entropy)
is constant in time. This joint entropy is equal to the marginal
entropy (entropy assuming no correlations) plus the entropy of
correlation (mutual entropy, or its negative
mutual information).
If we assume no correlations between the particles initially, then this
joint entropy is just the marginal entropy, which is just the initial
thermodynamic entropy of the system, divided by
Boltzmann's constant.
However, if these are indeed the initial conditions (and this is a
crucial assumption), then such correlations form with time. In other
words, there is a decreasing mutual entropy (or increasing mutual
information), and for a time that is not too long—the correlations
(mutual information) between particles only increase with time.
Therefore, the thermodynamic entropy, which is proportional to the
marginal entropy, must also increase with time
[6]
(note that "not too long" in this context is relative to the time
needed, in a classical version of the system, for it to pass through all
its possible microstates—a time that can be roughly estimated as

, where

is the time between particle collisions and S is the system's entropy.
In any practical case this time is huge compared to everything else).
Note that the correlation between particles is not a fully objective
quantity. One cannot measure the mutual entropy, one can only measure
its change, assuming one can measure a microstate. Thermodynamics is
restricted to the case where microstates cannot be distinguished, which
means that only the marginal entropy, proportional to the thermodynamic
entropy, can be measured, and, in a practical sense, always increases.
The arrow of time in various phenomena
All phenomena that behave differently in one time direction can ultimately be linked to the
Second Law of Thermodynamics.
This includes the fact that ice cubes melt in hot coffee rather than
assembling themselves out of the coffee, that a block sliding on a rough
surface slows down rather than speeding up, and that we can remember
the past rather than the future. This last phenomenon, called the
"psychological arrow of time", has deep connections with
Maxwell's demon
and the physics of information; In fact, it is easy to understand its
link to the Second Law of Thermodynamics if one views memory as
correlation between brain cells (or computer bits) and the outer world.
Since the Second Law of Thermodynamics is equivalent to the growth with
time of such correlations, then it states that memory is created as we
move towards the future (rather than towards the past).
Current research
Current
research focuses mainly on describing the thermodynamic arrow of time
mathematically, either in classical or quantum systems, and on
understanding its origin from the point of view of
cosmological boundary conditions.
Dynamical systems
Some current research in
dynamical systems indicates a possible "explanation" for the arrow of time.
[citation needed] There are several ways to describe the time evolution of a dynamical system. In the classical framework, one considers a
differential equation,
where one of the parameters is explicitly time. By the very nature of
differential equations, the solutions to such systems are inherently
time-reversible. However, many of the interesting cases are either
ergodic or
mixing, and it is strongly suspected that mixing and ergodicity somehow underlie the fundamental mechanism of the arrow of time.
Mixing and ergodic systems do not have exact solutions, and thus
proving time irreversibility in a mathematical sense is (as of 2006) impossible. Some progress can be made by studying discrete-time models or
difference equations. Many discrete-time models, such as the
iterated functions
considered in popular fractal-drawing programs, are explicitly not
time-reversible, as any given point "in the present" may have several
different "pasts" associated with it: indeed, the set of all pasts is
known as the
Julia set. Since such systems have a built-in irreversibility, it is inappropriate to use them to explain why time is not reversible.
There are other systems that are chaotic, and are also explicitly time-reversible: among these is the
baker's map,
which is also exactly solvable. An interesting avenue of study is to
examine solutions to such systems not by iterating the dynamical system
over time, but instead, to study the corresponding
Frobenius-Perron operator or
transfer operator for the system. For some of these systems, it can be explicitly, mathematically shown that the transfer operators are not
trace-class. This means that these operators do not have a unique
eigenvalue
spectrum that is independent of the choice of basis. In the case of the
baker's map, it can be shown that several unique and inequivalent
diagonalizations or bases exist, each with a different set of
eigenvalues. It is this phenomenon that can be offered as an
"explanation" for the arrow of time. That is, although the iterated,
discrete-time system is explicitly time-symmetric, the transfer operator
is not. Furthermore, the transfer operator can be diagonalized in one
of two inequivalent ways: one that describes the forward-time evolution
of the system, and one that describes the backwards-time evolution.
As of 2006, this type of time-symmetry breaking has been demonstrated
for only a very small number of exactly-solvable, discrete-time
systems. The transfer operator for more complex systems has not been
consistently formulated, and its precise definition is mired in a
variety of subtle difficulties. In particular, it has not been shown
that it has a broken symmetry for the simplest exactly-solvable
continuous-time ergodic systems, such as
Hadamard's billiards, or the
Anosov flow on the tangent space of
PSL(2,R).
Quantum mechanics
Research on irreversibility in quantum mechanics takes several different directions. One avenue is the study of
rigged Hilbert spaces, and in particular, how discrete and continuous eigenvalue spectra intermingle
[citation needed]. For example, the
rational numbers are completely intermingled with the
real numbers,
and yet have a unique, distinct set of properties. It is hoped that the
study of Hilbert spaces with a similar inter-mingling will provide
insight into the arrow of time.
Another distinct approach is through the study of
quantum chaos by which attempts are made to quantize systems as classically chaotic, ergodic or mixing.
[citation needed]
The results obtained are not dissimilar from those that come from the
transfer operator method. For example, the quantization of the
Boltzmann gas,
that is, a gas of hard (elastic) point particles in a rectangular box
reveals that the eigenfunctions are space-filling fractals that occupy
the entire box, and that the energy eigenvalues are very closely spaced
and have an "almost continuous" spectrum (for a finite number of
particles in a box, the spectrum must be, of necessity, discrete). If
the initial conditions are such that all of the particles are confined
to one side of the box, the system very quickly evolves into one where
the particles fill the entire box. Even when all of the particles are
initially on one side of the box, their wave functions do, in fact,
permeate the entire box: they constructively interfere on one side, and
destructively interfere on the other. Irreversibility is then argued by
noting that it is "nearly impossible" for the wave functions to be
"accidentally" arranged in some unlikely state: such arrangements are a
set of zero
measure.
Because the eigenfunctions are fractals, much of the language and
machinery of entropy and statistical mechanics can be imported to
discuss and argue the quantum case.
[citation needed]
Cosmology
Some processes that involve high energy particles and are governed by the
weak force (such as
K-meson decay) defy the symmetry between time directions. However, all known physical processes
do preserve a more complicated symmetry (
CPT symmetry), and are therefore unrelated to the
second law of thermodynamics, or to our day-to-day experience of the arrow of time. A notable exception is the
wave function collapse in
quantum mechanics,
which is an irreversible process. It has been conjectured that the
collapse of the wave function may be the reason for the Second Law of
Thermodynamics. However it is more accepted today that the opposite is
correct, namely that the (possibly merely apparent)
wave function collapse is a consequence of
quantum decoherence, a process that is ultimately an outcome of the Second Law of Thermodynamics.
The
universe was in a uniform, high density state at its very early stages, shortly after the
big bang. The hot gas in the early universe was near thermodynamic equilibrium (giving rise to the
horizon problem) and hence in a state of
maximum entropy,
given its volume. Expansion of a gas increases its entropy, however,
and expansion of the universe has therefore enabled an ongoing increase
in entropy. Viewed from later eras, the early universe can thus be
considered to be highly ordered. The uniformity of this early
near-equilibrium state has been explained by the theory of
cosmic inflation.
According to this theory our universe (or, rather, its accessible
part, a radius of 46 billion light years around our location) evolved
from a tiny, totally uniform volume (a portion of a much bigger
universe), which expanded greatly; hence it was highly ordered.
Fluctuations were then created by quantum processes related to its
expansion, in a manner supposed to be such that these fluctuations are
uncorrelated for any practical use. This is supposed to give the desired
initial conditions needed for the Second Law of Thermodynamics.
Our universe is apparently an
open universe, so that its expansion will never terminate, but it is an interesting
thought experiment to imagine what would have happened had our universe been
closed.
In such a case, its expansion would stop at a certain time in the
distant future, and then begin to shrink. Moreover, a closed universe is
finite. It is unclear what would happen to the
Second Law of Thermodynamics
in such a case. One could imagine at least three different scenarios
(in fact, only the third one is plausible, since the first two require a
smooth cosmic evolution, contrary to what is observed):
- A highly controversial view is that in such a case the arrow of time will reverse.[7] The quantum fluctuations—which in the meantime have evolved into galaxies and stars—will be in superposition in such a way that the whole process described above is reversed—i.e., the fluctuations are erased by destructive interference and total uniformity is achieved once again. Thus the universe ends in a big crunch, which is similar to its beginning in the big bang.
Because the two are totally symmetric, and the final state is very
highly ordered, entropy must decrease close to the end of the universe,
so that the Second Law of Thermodynamics reverses when the universe
shrinks. This can be understood as follows: in the very early universe,
interactions between fluctuations created entanglement (quantum correlations)
between particles spread all over the universe; during the expansion,
these particles became so distant that these correlations became
negligible (see quantum decoherence).
At the time the expansion halts and the universe starts to shrink, such
correlated particles arrive once again at contact (after circling
around the universe), and the entropy starts to decrease—because highly
correlated initial conditions may lead to a decrease in entropy. Another
way of putting it, is that as distant particles arrive, more and more
order is revealed because these particles are highly correlated with
particles that arrived earlier.
- It could be that this is the crucial point where the wavefunction collapse
is important: if the collapse is real, then the quantum fluctuations
will not be in superposition any longer; rather they had collapsed to a
particular state (a particular arrangement of galaxies and stars), thus
creating a big crunch, which is very different from the big bang. Such a scenario may be viewed as adding boundary conditions (say, at the distant future) that dictate the wavefunction collapse.[8]
- The broad consensus among the scientific community today is that
smooth initial conditions lead to a highly non-smooth final state, and
that this is in fact the source of the thermodynamic arrow of time.[9] Highly non-smooth gravitational systems tend to collapse to black holes, so the wavefunction of the whole universe evolves from a superposition of small fluctuations to a superposition of states with many black holes
in each. It may even be that it is impossible for the universe to have
both a smooth beginning and a smooth ending. Note that in this scenario
the energy density of the universe in the final stages of its shrinkage
is much larger than in the corresponding initial stages of its expansion
(there is no destructive interference, unlike in the first scenario described above), and consists of mostly black holes rather than free particles.
In the first scenario, the cosmological
arrow of time
is the reason for both the thermodynamic arrow of time and the quantum
arrow of time. Both will slowly disappear as the universe will come to a
halt, and will later be reversed.
In the second and third scenarios, it is the difference between the
initial state and the final state of the universe that is responsible
for the thermodynamic arrow of time. This is independent of the
cosmological arrow of time. In the second scenario, the quantum arrow of
time may be seen as the deep reason for this.
.
. (This is the same amount of entropy absorbed in step 1, as can be seen from the Clausius inequality.)
,
.
 and
and  are both lower and in fact are in the same ratio as
are both lower and in fact are in the same ratio as  .
. is defined to be:
is defined to be:is the work done by the system (energy exiting the system as work),
is the heat taken from the system (heat energy leaving the system),
is the heat put into the system (heat energy entering the system),
is the absolute temperature of the cold reservoir, and
is the absolute temperature of the hot reservoir.
is the maximum system entropy
is the minimum system entropy
 and
and  , none can exceed the efficiency of a Carnot cycle.
, none can exceed the efficiency of a Carnot cycle.