Tunguska event

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Tunguska_event 

 

Tunguska event

Trees knocked over by the Tunguska blast. Photograph from the Soviet Academy of Science 1927 expedition led by Leonid Kulik.
Date	30 June 1908
Time	07:17
Location	Podkamennaya Tunguska River, Siberia, Russian Empire
Coordinates	60°53′09″N 101°53′40″ECoordinates: 60°53′09″N 101°53′40″E
Cause	Probable air burst of small asteroid or comet
Outcome	Flattening 2,150 km2 (830 sq mi) of forest Devastation to local plants and animals
Deaths	0 confirmed, 3 possible
Property damage	A few damaged buildings

The Tunguska event was a massive ~12 Mt explosion that occurred near the Podkamennaya Tunguska River in Yeniseysk Governorate (now Krasnoyarsk Krai), Russia, on the morning of June 30, 1908. The explosion over the sparsely populated Eastern Siberian Taiga flattened an estimated 80 million trees over an area of 2,150 km² (830 sq mi) of forest, and eyewitness reports suggest that at least three people may have died in the event. The explosion is generally attributed to the air burst of a stony meteoroid about 50–60 metres (160–200 feet) in size. The meteoroid approached from the ESE, and therefore likely with a relatively high speed of about 27 km/s. It is classified as an impact event, even though no impact crater has been found; the object is thought to have disintegrated at an altitude of 5 to 10 kilometres (3 to 6 miles) rather than to have hit the surface of the Earth.

The Tunguska event is the largest impact event on Earth in recorded history, though much larger impacts have occurred in prehistoric times. An explosion of this magnitude would be capable of destroying a large metropolitan area. It has been mentioned numerous times in popular culture, and has also inspired real-world discussion of asteroid impact avoidance.

Description

Location of the event in Siberia (modern map)

On 30 June 1908 (N. S.) (cited in Russia as 17 June 1908, O. S., before the implementation of the Soviet calendar in 1918), at around 07:17 local time, Evenki natives and Russian settlers in the hills northwest of Lake Baikal observed a bluish light, nearly as bright as the sun, moving across the sky and leaving a thin trail. Closer to the horizon, there was a flash producing a billowing cloud, followed by a pilar of fire that cast a red light on the landscape. The pilar split in two and faded, turning to black. About ten minutes later, there was a sound similar to artillery fire. Eyewitnesses closer to the explosion reported that the source of the sound moved from the east to the north of them. The sounds were accompanied by a shock wave that knocked people off their feet and broke windows hundreds of kilometres away.

The explosion registered at seismic stations across Eurasia, and air waves from the blast were detected in Germany, Denmark, Croatia, and the United Kingdom—and as far away as Batavia, Dutch East Indies, and Washington, D.C. It is estimated that, in some places, the resulting shock wave was equivalent to an earthquake measuring 5.0 on the Richter magnitude scale. Over the next few days, night skies in Asia and Europe were aglow. There are contemporaneous reports of brightly lit photographs being successfully taken at midnight (without the aid of flashbulbs) in Sweden and Scotland. It has been theorized that this sustained glowing effect was due to light passing through high-altitude ice particles that had formed at extremely low temperatures as a result of the explosion—a phenomenon that many years later was reproduced by space shuttles. In the United States, a Smithsonian Astrophysical Observatory program at the Mount Wilson Observatory in California observed a months-long decrease in atmospheric transparency consistent with an increase in suspended dust particles.

Selected eyewitness reports

Tunguska marshes, around the area where it fell. This photo is from the magazine Around the World, 1931. The original photo was taken between 1927 and 1930 (presumptively no later than 14 September 1930).

Though the region of Siberia in which the explosion occurred was very sparsely populated in 1908, there are accounts of the event from eyewitnesses who were in the surrounding area at the time, and regional newspapers reported the event shortly after it occurred.

According to the testimony of S. Semenov, as recorded by Russian mineralogist Leonid Kulik's expedition in 1930:

At breakfast time I was sitting by the house at Vanavara Trading Post [approximately 65 kilometres (40 mi) south of the explosion], facing north. […] I suddenly saw that directly to the north, over Onkoul's Tunguska Road, the sky split in two and fire appeared high and wide over the forest [as Semenov showed, about 50 degrees up—expedition note]. The split in the sky grew larger, and the entire northern side was covered with fire. At that moment I became so hot that I couldn't bear it as if my shirt was on fire; from the northern side, where the fire was, came strong heat. I wanted to tear off my shirt and throw it down, but then the sky shut closed, and a strong thump sounded, and I was thrown a few metres. I lost my senses for a moment, but then my wife ran out and led me to the house. After that such noise came, as if rocks were falling or cannons were firing, the Earth shook, and when I was on the ground, I pressed my head down, fearing rocks would smash it. When the sky opened up, hot wind raced between the houses, like from cannons, which left traces in the ground like pathways, and it damaged some crops. Later we saw that many windows were shattered, and in the barn, a part of the iron lock snapped.

Testimony of Chuchan of Shanyagir tribe, as recorded by I. M. Suslov in 1926:

We had a hut by the river with my brother Chekaren. We were sleeping. Suddenly we both woke up at the same time. Somebody shoved us. We heard whistling and felt strong wind. Chekaren said 'Can you hear all those birds flying overhead?' We were both in the hut, couldn't see what was going on outside. Suddenly, I got shoved again, this time so hard I fell into the fire. I got scared. Chekaren got scared too. We started crying out for father, mother, brother, but no one answered. There was noise beyond the hut, we could hear trees falling down. Chekaren and I got out of our sleeping bags and wanted to run out, but then the thunder struck. This was the first thunder. The Earth began to move and rock, the wind hit our hut and knocked it over. My body was pushed down by sticks, but my head was in the clear. Then I saw a wonder: trees were falling, the branches were on fire, it became mighty bright, how can I say this, as if there was a second sun, my eyes were hurting, I even closed them. It was like what the Russians call lightning. And immediately there was a loud thunderclap. This was the second thunder. The morning was sunny, there were no clouds, our Sun was shining brightly as usual, and suddenly there came a second one!

Chekaren and I had some difficulty getting out from under the remains of our hut. Then we saw that above, but in a different place, there was another flash, and loud thunder came. This was the third thunder strike. Wind came again, knocked us off our feet, struck the fallen trees.

We looked at the fallen trees, watched the tree tops get snapped off, watched the fires. Suddenly Chekaren yelled "Look up" and pointed with his hand. I looked there and saw another flash, and it made another thunder. But the noise was less than before. This was the fourth strike, like normal thunder.

Now I remember well there was also one more thunder strike, but it was small, and somewhere far away, where the Sun goes to sleep.

Sibir newspaper, 2 July 1908:

On the morning of 17th of June, around 9:00, we observed an unusual natural occurrence. In the north Karelinski village [200 verst (213 km (132 mi)) north of Kirensk] the peasants saw to the northwest, rather high above the horizon, some strangely bright (impossible to look at) bluish-white heavenly body, which for 10 minutes moved downwards. The body appeared as a "pipe", i.e., a cylinder. The sky was cloudless, only a small dark cloud was observed in the general direction of the bright body. It was hot and dry. As the body neared the ground (forest), the bright body seemed to smudge, and then turned into a giant billow of black smoke, and a loud knocking (not thunder) was heard as if large stones were falling, or artillery was fired. All buildings shook. At the same time the cloud began emitting flames of uncertain shapes. All villagers were stricken with panic and took to the streets, women cried, thinking it was the end of the world. The author of these lines was meantime in the forest about 6 versts [6.4 km] north of Kirensk and heard to the north east some kind of artillery barrage, that repeated in intervals of 15 minutes at least 10 times. In Kirensk in a few buildings in the walls facing north-east window glass shook.

Siberian Life newspaper, 27 July 1908:

When the meteorite fell, strong tremors in the ground were observed, and near the Lovat village of the Kansk uezd two strong explosions were heard, as if from large-calibre artillery.

Krasnoyaretz newspaper, 13 July 1908:

Kezhemskoye village. On the 17th an unusual atmospheric event was observed. At 7:43 the noise akin to a strong wind was heard. Immediately afterward a horrific thump sounded, followed by an earthquake that literally shook the buildings as if they were hit by a large log or a heavy rock. The first thump was followed by a second, and then a third. Then the interval between the first and the third thumps was accompanied by an unusual underground rattle, similar to a railway upon which dozens of trains are travelling at the same time. Afterward, for 5 to 6 minutes an exact likeness of artillery fire was heard: 50 to 60 salvoes in short, equal intervals, which got progressively weaker. After 1.5–2 minutes after one of the "barrages" six more thumps were heard, like cannon firing, but individual, loud and accompanied by tremors. The sky, at the first sight, appeared to be clear. There was no wind and no clouds. Upon closer inspection to the north, i.e. where most of the thumps were heard, a kind of an ashen cloud was seen near the horizon, which kept getting smaller and more transparent and possibly by around 2–3 p.m. completely disappeared.

Tunguska's trajectory and the locations of five villages projected onto a plane normal to the Earth's surface and passing through the fireball's approach path. The scale is given by an adopted beginning height of 100 km. Three zenith angles ZR of the apparent radiant are assumed and the trajectories plotted by the solid, dashed, and dotted lines, respectively. The parenthesized data are the distances of the locations from the plane of projection: a plus sign indicates the location is south-south west of the plane; a minus sign, north-north east of it. The transliteration of the village names in this figure and the text is consistent with that of Paper I and differs somewhat from the transliteration in the current world atlases.

Scientific investigation

Since the 1908 event, there have been an estimated 1,000 scholarly papers (most in Russian) published about the Tunguska explosion. Owing to the remoteness of the site and the limited instrumentation available at the time of the event, modern scientific interpretations of its cause and magnitude have relied chiefly on damage assessments and geological studies conducted many years after the event. Estimates of its energy have ranged from 3–30 megatons of TNT (13–126 petajoules).

It was not until more than a decade after the event that any scientific analysis of the region took place, in part due to the isolation of the area and significant political upheaval affecting Russia in the 1910s. In 1921, the Russian mineralogist Leonid Kulik led a team to the Podkamennaya Tunguska River basin to conduct a survey for the Soviet Academy of Sciences. Although they never visited the central blast area, the many local accounts of the event led Kulik to believe that the explosion had been caused by a giant meteorite impact. Upon returning, he persuaded the Soviet government to fund an expedition to the suspected impact zone, based on the prospect of salvaging meteoric iron.

Photograph from Kulik's 1929 expedition taken near the Hushmo River

Kulik led a scientific expedition to the Tunguska blast site in 1927. He hired local Evenki hunters to guide his team to the centre of the blast area, where they expected to find an impact crater. To their surprise, there was no crater to be found at ground zero. Instead they found a zone, roughly 8 kilometres (5.0 mi) across, where the trees were scorched and devoid of branches, but still standing upright. Trees more distant from the centre had been partly scorched and knocked down in a direction away from the centre, creating a large radial pattern of downed trees.

In the 1960s, it was established that the zone of levelled forest occupied an area of 2,150 km² (830 sq mi), its shape resembling a gigantic spread-eagled butterfly with a "wingspan" of 70 km (43 mi) and a "body length" of 55 km (34 mi). Upon closer examination, Kulik located holes that he erroneously concluded were meteorite holes; he did not have the means at that time to excavate the holes.

During the following 10 years, there were three more expeditions to the area. Kulik found several dozens of little "pothole" bogs, each 10 to 50 metres (33 to 164 feet) in diameter, that he thought might be meteoric craters. After a laborious exercise in draining one of these bogs (the so-called "Suslov's crater", 32 m (105 ft) in diameter), he found an old tree stump on the bottom, ruling out the possibility that it was a meteoric crater. In 1938, Kulik arranged for an aerial photographic survey of the area covering the central part of the leveled forest (250 square kilometres (97 sq mi)). The original negatives of these aerial photographs (1,500 negatives, each 18 by 18 centimetres (7.1 by 7.1 inches)) were burned in 1975 by order of Yevgeny Krinov, then Chairman of the Committee on Meteorites of the USSR Academy of Sciences, as part of an initiative to dispose of flammable nitrate film. Positive prints were preserved for further study in the Russian city of Tomsk.

Expeditions sent to the area in the 1950s and 1960s found microscopic silicate and magnetite spheres in siftings of the soil. Similar spheres were predicted to exist in the felled trees, although they could not be detected by contemporary means. Later expeditions did identify such spheres in the resin of the trees. Chemical analysis showed that the spheres contained high proportions of nickel relative to iron, which is also found in meteorites, leading to the conclusion they were of extraterrestrial origin. The concentration of the spheres in different regions of the soil was also found to be consistent with the expected distribution of debris from a meteoroid air burst. Later studies of the spheres found unusual ratios of numerous other metals relative to the surrounding environment, which was taken as further evidence of their extraterrestrial origin.

Chemical analysis of peat bogs from the area also revealed numerous anomalies considered consistent with an impact event. The isotopic signatures of carbon, hydrogen, and nitrogen at the layer of the bogs corresponding to 1908 were found to be inconsistent with the isotopic ratios measured in the adjacent layers, and this abnormality was not found in bogs located outside the area. The region of the bogs showing these anomalous signatures also contains an unusually high proportion of iridium, similar to the iridium layer found in the Cretaceous–Paleogene boundary. These unusual proportions are believed to result from debris from the falling body that deposited in the bogs. The nitrogen is believed to have been deposited as acid rain, a suspected fallout from the explosion.

However other scientists disagree: "Some papers report that hydrogen, carbon and nitrogen isotopic compositions with signatures similar to those of CI and CM carbonaceous chondrites were found in Tunguska peat layers dating from the TE (Kolesnikov et al. 1999, 2003) and that iridium anomalies were also observed (Hou et al. 1998, 2004). Measurements performed in other laboratories have not confirmed these results (Rocchia et al. 1990; Tositti et al. 2006).".

Researcher John Anfinogenov has suggested that a boulder found at the event site, known as John's stone, is a remnant of the meteorite, but oxygen isotope analysis of the quartzite suggests that it is of hydrothermal origin, and probably related to Permian-Triassic Siberian Traps magmatism.

In 2013, a team of researchers published the results of an analysis of micro-samples from a peat bog near the centre of the affected area, which show fragments that may be of extraterrestrial origin.

Earth impactor model

Comparison of possible sizes of Tunguska (TM mark) and Chelyabinsk (CM) meteoroids to the Eiffel Tower and Empire State Building

The leading scientific explanation for the explosion is the air burst of an asteroid 6–10 km (4–6 mi) above the Earth's surface.

Meteoroids enter Earth's atmosphere from outer space every day, travelling at a speed of at least 11 km/s (7 mi/s). The heat generated by compression of air in front of the body (ram pressure) as it travels through the atmosphere is immense and most meteoroids burn up or explode before they reach the ground. Early estimates of the energy of the Tunguska air burst ranged from 10–15 megatons of TNT (42–63 petajoules) to 30 megatons of TNT (130 PJ), depending on the exact height of the burst as estimated when the scaling laws from the effects of nuclear weapons are employed. More recent calculations that include the effect of the object's momentum find that more of the energy was focused downward than would be the case from a nuclear explosion and estimate that the air burst had an energy range from 3 to 5 megatons of TNT (13 to 21 PJ). The 15-megaton (Mt) estimate represents an energy about 1,000 times greater than that of Hiroshima bomb, and roughly equal to that of the United States' Castle Bravo nuclear test in 1954 (which measured 15.2 Mt) and one-third that of the Soviet Union's Tsar Bomba test in 1961. A 2019 paper suggests the explosive power of the Tunguska event may have been around 20–30 megatons.

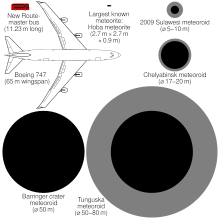
Since the second half of the 20th century, close monitoring of Earth's atmosphere through infrasound and satellite observation has shown that asteroid air bursts with energies comparable to those of nuclear weapons routinely occur, although Tunguska-sized events, on the order of 5–15 megatons, are much rarer. Eugene Shoemaker estimated that 20-kiloton events occur annually and that Tunguska-sized events occur about once every 300 years. More recent estimates place Tunguska-sized events at about once every thousand years, with 5-kiloton air bursts averaging about once per year. Most of these air bursts are thought to be caused by asteroid impactors, as opposed to mechanically weaker cometary materials, based on their typical penetration depths into the Earth's atmosphere. The largest asteroid air burst to be observed with modern instrumentation was the 500-kiloton Chelyabinsk meteor in 2013, which shattered windows and produced meteorites.

Glancing impact hypothesis

In 2020 a group of Russian scientists used a range of computer models to calculate the passage of asteroids with diameters of 200, 100, and 50 metres at oblique angles across Earth's atmosphere. They used a range of assumptions about the object's composition as if it was made of iron, rock or ice. The model which most closely matched the observed event was an iron asteroid up to 200 metres in diameter, travelling at 11.2 km per second which glanced off the Earth's atmosphere and returned into solar orbit.

Blast pattern

The explosion's effect on the trees near the hypocentre of the explosion was similar to the effects of the conventional Operation Blowdown. These effects are caused by the blast wave produced by large air-burst explosions. The trees directly below the explosion are stripped as the blast wave moves vertically downward, but remain standing upright, while trees farther away are knocked over because the blast wave is travelling closer to horizontal when it reaches them.

Soviet experiments performed in the mid-1960s, with model forests (made of matches on wire stakes) and small explosive charges slid downward on wires, produced butterfly-shaped blast patterns similar to the pattern found at the Tunguska site. The experiments suggested that the object had approached at an angle of roughly 30 degrees from the ground and 115 degrees from north and had exploded in mid-air.

Asteroid or comet?

In 1930, the British astronomer F. J. W. Whipple suggested that the Tunguska body was a small comet. A comet is composed of dust and volatiles, such as water ice and frozen gases, and could have been completely vaporised by the impact with Earth's atmosphere, leaving no obvious traces. The comet hypothesis was further supported by the glowing skies (or "skyglows" or "bright nights") observed across Eurasia for several evenings after the impact, which are possibly explained by dust and ice that had been dispersed from the comet's tail across the upper atmosphere. The cometary hypothesis gained a general acceptance among Soviet Tunguska investigators by the 1960s.

In 1978, Slovak astronomer Ľubor Kresák suggested that the body was a fragment of Comet Encke. This is a periodic comet with an extremely short period of just over three years that stays entirely within the orbit of Jupiter. It is also responsible for the Beta Taurids, an annual meteor shower with a maximum activity around 28–29 June. The Tunguska event coincided with the peak activity of that shower, and the approximate trajectory of the Tunguska object is consistent with what would be expected from a fragment of Comet Encke. It is now known that bodies of this kind explode at frequent intervals tens to hundreds of kilometres above the ground. Military satellites have been observing these explosions for decades. During 2019 astronomers searched for hypothesized asteroids ~100 metres in diameter from the Taurid swarm between 5–11 July, and 21 July – 10 August. As of February 2020, there have been no reports of discoveries of any such objects.

In 1983, astronomer Zdeněk Sekanina published a paper criticising the comet hypothesis. He pointed out that a body composed of cometary material, travelling through the atmosphere along such a shallow trajectory, ought to have disintegrated, whereas the Tunguska body apparently remained intact into the lower atmosphere. Sekanina also argued that the evidence pointed to a dense rocky object, probably of asteroidal origin. This hypothesis was further boosted in 2001, when Farinella, Foschini, et al. released a study calculating the probabilities based on orbital modelling extracted from the atmospheric trajectories of the Tunguska object. They concluded with a probability of 83% that the object moved on an asteroidal path originating from the asteroid belt, rather than on a cometary one (probability of 17%). Proponents of the comet hypothesis have suggested that the object was an extinct comet with a stony mantle that allowed it to penetrate the atmosphere.

The chief difficulty in the asteroid hypothesis is that a stony object should have produced a large crater where it struck the ground, but no such crater has been found. It has been hypothesised that the passage of the asteroid through the atmosphere caused pressures and temperatures to build up to a point where the asteroid abruptly disintegrated in a huge explosion. The destruction would have to have been so complete that no remnants of substantial size survived, and the material scattered into the upper atmosphere during the explosion would have caused the skyglows. Models published in 1993 suggested that the stony body would have been about 60 metres (200 ft) across, with physical properties somewhere between an ordinary chondrite and a carbonaceous chondrite. Typical carbonaceous chondrite substance tends to be dissolved with water rather quickly unless it is frozen.

Christopher Chyba and others have proposed a process whereby a stony meteorite could have exhibited the behaviour of the Tunguska impactor. Their models show that when the forces opposing a body's descent become greater than the cohesive force holding it together, it blows apart, releasing nearly all of its energy at once. The result is no crater, with damage distributed over a fairly wide radius, and all of the damage resulting from the thermal energy released in the blast.

Three-dimensional numerical modelling of the Tunguska impact done by Utyuzhnikov and Rudenko in 2008 supports the comet hypothesis. According to their results, the comet matter dispersed in the atmosphere, while the destruction of the forest was caused by the shock wave.

During the 1990s, Italian researchers, coordinated by the physicist Giuseppe Longo from the University of Bologna, extracted resin from the core of the trees in the area of impact to examine trapped particles that were present during the 1908 event. They found high levels of material commonly found in rocky asteroids and rarely found in comets.

Kelly et al. (2009) contend that the impact was caused by a comet because of the sightings of noctilucent clouds following the impact, a phenomenon caused by massive amounts of water vapour in the upper atmosphere. They compared the noctilucent cloud phenomenon to the exhaust plume from NASA's Endeavour space shuttle. A team of Russian researchers led by Edward Drobyshevski in 2009 have suggested that the near-Earth asteroid 2005 NB56 may be a possible candidate for the parent body of the Tunguska object as the asteroid has made a close approach of 0.06945 AU (27 LD) from Earth on 27 June 1908, three days before the Tunguska impact. The team suspected that 2005 NB₅₆'s orbit likely fits with the modelled orbit of the Tunguska object, even with the effects of weak non-gravitational forces. In 2013, analysis of fragments from the Tunguska site by a joint US-European team was consistent with an iron meteorite.

Comparison of approximate sizes of notable impactors with the Hoba meteorite, a Boeing 747 and a New Routemaster bus

The February 2013 Chelyabinsk bolide event provided ample data for scientists to create new models for the Tunguska event. Researchers used data from both Tunguska and Chelyabinsk to perform a statistical study of over 50 million combinations of bolide and entry properties that could produce Tunguska-scale damage when breaking apart or exploding at similar altitudes. Some models focused on combinations of properties which created scenarios with similar effects to the tree-fall pattern as well as the atmospheric and seismic pressure waves of Tunguska. Four different computer models produced similar results; they concluded that the likeliest candidate for the Tunguska impactor was a stony body between 50 and 80 m (164 and 262 ft) in diameter, entering the atmosphere at roughly 55,000 km/h (34,000 mph), exploding at 10 to 14 km (6 to 9 mi) altitude, and releasing explosive energy equivalent to between 10 and 30 megatons. This is similar to the blast energy equivalent of the 1980 volcanic eruption of Mount St. Helens. The researchers also concluded impactors of this size hit the Earth only at an average interval scale of millennia.

Lake Cheko

In June 2007, scientists from the University of Bologna identified a lake in the Tunguska region as a possible impact crater from the event. They do not dispute that the Tunguska body exploded in mid-air, but believe that a 10-metre (33 ft) fragment survived the explosion and struck the ground. Lake Cheko is a small bowl-shaped lake approximately 8 km (5.0 mi) north-northwest of the hypocentre.

The hypothesis has been disputed by other impact crater specialists. A 1961 investigation had dismissed a modern origin of Lake Cheko, saying that the presence of metres-thick silt deposits at the lake's bed suggests an age of at least 5,000 years, but more recent research suggests that only a metre or so of the sediment layer on the lake bed is "normal lacustrine sedimentation", a depth consistent with an age of about 100 years. Acoustic-echo soundings of the lake floor provide support for the hypothesis that the lake was formed by the Tunguska event. The soundings revealed a conical shape for the lake bed, which is consistent with an impact crater. Magnetic readings indicate a possible metre-sized chunk of rock below the lake's deepest point that may be a fragment of the colliding body. Finally, the lake's long axis points to the hypocentre of the Tunguska explosion, about 7.0 km (4.3 mi) away. Work is still being done at Lake Cheko to determine its origins.

The main points of the study are that:

Cheko, a small lake located in Siberia close to the epicentre of the 1908 Tunguska explosion, might fill a crater left by the impact of a fragment of a cosmic body. Sediment cores from the lake's bottom were studied to support or reject this hypothesis. A 175-centimetre-long (69 in) core, collected near the center of the lake, consists of an upper c. 1-metre-thick (39 in) sequence of lacustrine deposits overlaying coarser chaotic material. ²¹⁰Pb and ¹³⁷Cs indicate that the transition from lower to upper sequence occurred close to the time of the Tunguska event. Pollen analysis reveals that remains of aquatic plants are abundant in the top post-1908 sequence but are absent in the lower pre-1908 portion of the core. These results, including organic C, N and δ¹³C data, suggest that Lake Cheko formed at the time of the Tunguska event. Pollen assemblages confirm the presence of two different units, above and below the ~100‐cm level (Fig. 4). The upper 100‐cm long section, in addition to pollen of taiga forest trees such as Abies, Betula, Juniperus, Larix, Pinus, Picea, and Populus, contains abundant remains of hydrophytes, i.e., aquatic plants probably deposited under lacustrine conditions similar to those prevailing today. These include both free-floating plants and rooted plants, growing usually in water up to 3–4 meters in depth (Callitriche, Hottonia, Lemna, Hydrocharis, Myriophyllum, Nuphar, Nymphaea, Potamogeton, Sagittaria). In contrast, the lower unit (below ~100 cm) contains abundant forest tree pollen, but no hydrophytes, suggesting that no lake existed then, but a taiga forest growing on marshy ground (Fig. 5). Pollen and microcharcoal show a progressive reduction in the taiga forest, from the bottom of the core upward. This reduction may have been caused by fires (two local episodes below ~100 cm), then by the TE and the formation of the lake (between 100 and 90 cm), and again by subsequent fires (one local fire in the upper 40 cm).

In 2017, new research by Russian scientists pointed to a rejection of the theory that Lake Cheko was created by the Tunguska event. They used soil research to determine that the lake is 280 years old or even much older; in any case clearly older than the Tunguska event. In analyzing soils from the bottom of Lake Cheko, they identified a layer of radionuclide contamination from mid-20th century nuclear testing at Novaya Zemlya. The depth of this of layer gave an average annual sedimentation rate of between 3.6 and 4.6 mm a year. These sedimentation values are less than half of the 1 cm/year calculated by Gasperini et al. in their 2009 publication on their analysis of the core they took from Lake Cheko in 1999. The Russian scientists in 2017, counted at least 280 such annual varves in the 1260 mm long core sample pulled from the bottom of the lake, representing an age of the lake that would be older than the Tunguska Event.

Additionally, there are problems with impact physics: It is unlikely that a stony meteorite in the right size range would have the mechanical strength necessary to survive atmospheric passage intact, and yet still retain a velocity large enough to excavate a crater that size on reaching the ground.

Geophysical hypotheses

Though scientific consensus is that the Tunguska explosion was caused by the impact of a small asteroid, there are some dissenters. Astrophysicist Wolfgang Kundt has proposed that the Tunguska event was caused by the release and subsequent explosion of 10 million tons of natural gas from within the Earth's crust. The basic idea is that natural gas leaked out of the crust and then rose to its equal-density height in the atmosphere; from there, it drifted downwind, in a sort of wick, which eventually found an ignition source such as lightning. Once the gas was ignited, the fire streaked along the wick, and then down to the source of the leak in the ground, whereupon there was an explosion.

The similar verneshot hypothesis has also been proposed as a possible cause of the Tunguska event. Other research has supported a geophysical mechanism for the event.

Similar event

A smaller air burst occurred over a populated area on 15 February 2013, at Chelyabinsk in the Ural district of Russia. The exploding meteoroid was determined to have been an asteroid that measured about 17–20 metres (56–66 ft) across. It had an estimated initial mass of 11,000 tonnes and exploded with an energy release of approximately 500 kilotons. The air burst inflicted over 1,200 injuries, mainly from broken glass falling from windows shattered by its shock wave.

 

Orbit

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Orbit 

The International Space Station orbits Earth once about every 92 minutes, flying at about 250 miles (400 km) above sea level.

 

Two bodies of different masses orbiting a common barycenter. The relative sizes and type of orbit are similar to the Pluto–Charon system.

In physics, an orbit is the gravitationally curved trajectory of an object, such as the trajectory of a planet around a star or a natural satellite around a planet. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding of the exact mechanics of orbital motion.

History

Historically, the apparent motions of the planets were described by European and Arabic philosophers using the idea of celestial spheres. This model posited the existence of perfect moving spheres or rings to which the stars and planets were attached. It assumed the heavens were fixed apart from the motion of the spheres, and was developed without any understanding of gravity. After the planets' motions were more accurately measured, theoretical mechanisms such as deferent and epicycles were added. Although the model was capable of reasonably accurately predicting the planets' positions in the sky, more and more epicycles were required as the measurements became more accurate, hence the model became increasingly unwieldy. Originally geocentric, it was modified by Copernicus to place the Sun at the centre to help simplify the model. The model was further challenged during the 16th century, as comets were observed traversing the spheres.

The basis for the modern understanding of orbits was first formulated by Johannes Kepler whose results are summarised in his three laws of planetary motion. First, he found that the orbits of the planets in our Solar System are elliptical, not circular (or epicyclic), as had previously been believed, and that the Sun is not located at the center of the orbits, but rather at one focus. Second, he found that the orbital speed of each planet is not constant, as had previously been thought, but rather that the speed depends on the planet's distance from the Sun. Third, Kepler found a universal relationship between the orbital properties of all the planets orbiting the Sun. For the planets, the cubes of their distances from the Sun are proportional to the squares of their orbital periods. Jupiter and Venus, for example, are respectively about 5.2 and 0.723 AU distant from the Sun, their orbital periods respectively about 11.86 and 0.615 years. The proportionality is seen by the fact that the ratio for Jupiter, 5.2³/11.86², is practically equal to that for Venus, 0.723³/0.615², in accord with the relationship. Idealised orbits meeting these rules are known as Kepler orbits.

The lines traced out by orbits dominated by the gravity of a central source are conic sections: the shapes of the curves of intersection between a plane and a cone. Parabolic (1) and hyperbolic (3) orbits are escape orbits, whereas elliptical and circular orbits (2) are captive.

 

This image shows the four trajectory categories with the gravitational potential well of the central mass's field of potential energy shown in black and the height of the kinetic energy of the moving body shown in red extending above that, correlating to changes in speed as distance changes according to Kepler's laws.

Isaac Newton demonstrated that Kepler's laws were derivable from his theory of gravitation and that, in general, the orbits of bodies subject to gravity were conic sections (this assumes that the force of gravity propagates instantaneously). Newton showed that, for a pair of bodies, the orbits' sizes are in inverse proportion to their masses, and that those bodies orbit their common center of mass. Where one body is much more massive than the other (as is the case of an artificial satellite orbiting a planet), it is a convenient approximation to take the center of mass as coinciding with the center of the more massive body.

Advances in Newtonian mechanics were then used to explore variations from the simple assumptions behind Kepler orbits, such as the perturbations due to other bodies, or the impact of spheroidal rather than spherical bodies. Lagrange (1736–1813) developed a new approach to Newtonian mechanics emphasizing energy more than force, and made progress on the three body problem, discovering the Lagrangian points. In a dramatic vindication of classical mechanics, in 1846 Urbain Le Verrier was able to predict the position of Neptune based on unexplained perturbations in the orbit of Uranus.

Albert Einstein (1879-1955) in his 1916 paper The Foundation of the General Theory of Relativity explained that gravity was due to curvature of space-time and removed Newton's assumption that changes propagate instantaneously. This led astronomers to recognize that Newtonian mechanics did not provide the highest accuracy in understanding orbits. In relativity theory, orbits follow geodesic trajectories which are usually approximated very well by the Newtonian predictions (except where there are very strong gravity fields and very high speeds) but the differences are measurable. Essentially all the experimental evidence that can distinguish between the theories agrees with relativity theory to within experimental measurement accuracy. The original vindication of general relativity is that it was able to account for the remaining unexplained amount in precession of Mercury's perihelion first noted by Le Verrier. However, Newton's solution is still used for most short term purposes since it is significantly easier to use and sufficiently accurate.

Planetary orbits

Within a planetary system, planets, dwarf planets, asteroids and other minor planets, comets, and space debris orbit the system's barycenter in elliptical orbits. A comet in a parabolic or hyperbolic orbit about a barycenter is not gravitationally bound to the star and therefore is not considered part of the star's planetary system. Bodies which are gravitationally bound to one of the planets in a planetary system, either natural or artificial satellites, follow orbits about a barycenter near or within that planet.

Owing to mutual gravitational perturbations, the eccentricities of the planetary orbits vary over time. Mercury, the smallest planet in the Solar System, has the most eccentric orbit. At the present epoch, Mars has the next largest eccentricity while the smallest orbital eccentricities are seen with Venus and Neptune.

As two objects orbit each other, the periapsis is that point at which the two objects are closest to each other and the apoapsis is that point at which they are the farthest. (More specific terms are used for specific bodies. For example, perigee and apogee are the lowest and highest parts of an orbit around Earth, while perihelion and aphelion are the closest and farthest points of an orbit around the Sun.)

In the case of planets orbiting a star, the mass of the star and all its satellites are calculated to be at a single point called the barycenter. The paths of all the star's satellites are elliptical orbits about that barycenter. Each satellite in that system will have its own elliptical orbit with the barycenter at one focal point of that ellipse. At any point along its orbit, any satellite will have a certain value of kinetic and potential energy with respect to the barycenter, and that energy is a constant value at every point along its orbit. As a result, as a planet approaches periapsis, the planet will increase in speed as its potential energy decreases; as a planet approaches apoapsis, its velocity will decrease as its potential energy increases.

Understanding orbits

There are a few common ways of understanding orbits:

• A force, such as gravity, pulls an object into a curved path as it attempts to fly off in a straight line.
• As the object is pulled toward the massive body, it falls toward that body. However, if it has enough tangential velocity it will not fall into the body but will instead continue to follow the curved trajectory caused by that body indefinitely. The object is then said to be orbiting the body.

As an illustration of an orbit around a planet, the Newton's cannonball model may prove useful (see image below). This is a 'thought experiment', in which a cannon on top of a tall mountain is able to fire a cannonball horizontally at any chosen muzzle speed. The effects of air friction on the cannonball are ignored (or perhaps the mountain is high enough that the cannon is above the Earth's atmosphere, which is the same thing).

Newton's cannonball, an illustration of how objects can "fall" in a curve

 

Conic sections describe the possible orbits (yellow) of small objects around the Earth. A projection of these orbits onto the gravitational potential (blue) of the Earth makes it possible to determine the orbital energy at each point in space.

If the cannon fires its ball with a low initial speed, the trajectory of the ball curves downward and hits the ground (A). As the firing speed is increased, the cannonball hits the ground farther (B) away from the cannon, because while the ball is still falling towards the ground, the ground is increasingly curving away from it (see first point, above). All these motions are actually "orbits" in a technical sense – they are describing a portion of an elliptical path around the center of gravity – but the orbits are interrupted by striking the Earth.

If the cannonball is fired with sufficient speed, the ground curves away from the ball at least as much as the ball falls – so the ball never strikes the ground. It is now in what could be called a non-interrupted, or circumnavigating, orbit. For any specific combination of height above the center of gravity and mass of the planet, there is one specific firing speed (unaffected by the mass of the ball, which is assumed to be very small relative to the Earth's mass) that produces a circular orbit, as shown in (C).

As the firing speed is increased beyond this, non-interrupted elliptic orbits are produced; one is shown in (D). If the initial firing is above the surface of the Earth as shown, there will also be non-interrupted elliptical orbits at slower firing speed; these will come closest to the Earth at the point half an orbit beyond, and directly opposite the firing point, below the circular orbit.

At a specific horizontal firing speed called escape velocity, dependent on the mass of the planet and the distance of the object from the barycenter, an open orbit (E) is achieved that has a parabolic path. At even greater speeds the object will follow a range of hyperbolic trajectories. In a practical sense, both of these trajectory types mean the object is "breaking free" of the planet's gravity, and "going off into space" never to return.

The velocity relationship of two moving objects with mass can thus be considered in four practical classes, with subtypes:

No orbit

Suborbital trajectories

Range of interrupted elliptical paths

Orbital trajectories (or simply, orbits)

• Range of elliptical paths with closest point opposite firing point
• Circular path
• Range of elliptical paths with closest point at firing point

Open (or escape) trajectories

• Parabolic paths
• Hyperbolic paths

It is worth noting that orbital rockets are launched vertically at first to lift the rocket above the atmosphere (which causes frictional drag), and then slowly pitch over and finish firing the rocket engine parallel to the atmosphere to achieve orbit speed.

Once in orbit, their speed keeps them in orbit above the atmosphere. If e.g., an elliptical orbit dips into dense air, the object will lose speed and re-enter (i.e. fall). Occasionally a space craft will intentionally intercept the atmosphere, in an act commonly referred to as an aerobraking maneuver.

Newton's laws of motion

Newton's law of gravitation and laws of motion for two-body problems

In most situations relativistic effects can be neglected, and Newton's laws give a sufficiently accurate description of motion. The acceleration of a body is equal to the sum of the forces acting on it, divided by its mass, and the gravitational force acting on a body is proportional to the product of the masses of the two attracting bodies and decreases inversely with the square of the distance between them. To this Newtonian approximation, for a system of two-point masses or spherical bodies, only influenced by their mutual gravitation (called a two-body problem), their trajectories can be exactly calculated. If the heavier body is much more massive than the smaller, as in the case of a satellite or small moon orbiting a planet or for the Earth orbiting the Sun, it is accurate enough and convenient to describe the motion in terms of a coordinate system that is centered on the heavier body, and we say that the lighter body is in orbit around the heavier. For the case where the masses of two bodies are comparable, an exact Newtonian solution is still sufficient and can be had by placing the coordinate system at the center of mass of the system.

Defining gravitational potential energy

Energy is associated with gravitational fields. A stationary body far from another can do external work if it is pulled towards it, and therefore has gravitational potential energy. Since work is required to separate two bodies against the pull of gravity, their gravitational potential energy increases as they are separated, and decreases as they approach one another. For point masses the gravitational energy decreases to zero as they approach zero separation. It is convenient and conventional to assign the potential energy as having zero value when they are an infinite distance apart, and hence it has a negative value (since it decreases from zero) for smaller finite distances.

Orbital energies and orbit shapes

When only two gravitational bodies interact, their orbits follow a conic section. The orbit can be open (implying the object never returns) or closed (returning). Which it is depends on the total energy (kinetic + potential energy) of the system. In the case of an open orbit, the speed at any position of the orbit is at least the escape velocity for that position, in the case of a closed orbit, the speed is always less than the escape velocity. Since the kinetic energy is never negative, if the common convention is adopted of taking the potential energy as zero at infinite separation, the bound orbits will have negative total energy, the parabolic trajectories zero total energy, and hyperbolic orbits positive total energy.

An open orbit will have a parabolic shape if it has velocity of exactly the escape velocity at that point in its trajectory, and it will have the shape of a hyperbola when its velocity is greater than the escape velocity. When bodies with escape velocity or greater approach each other, they will briefly curve around each other at the time of their closest approach, and then separate, forever.

All closed orbits have the shape of an ellipse. A circular orbit is a special case, wherein the foci of the ellipse coincide. The point where the orbiting body is closest to Earth is called the perigee, and is called the periapsis (less properly, "perifocus" or "pericentron") when the orbit is about a body other than Earth. The point where the satellite is farthest from Earth is called the apogee, apoapsis, or sometimes apifocus or apocentron. A line drawn from periapsis to apoapsis is the line-of-apsides. This is the major axis of the ellipse, the line through its longest part.

Kepler's laws

Log-log plot of period T vs semi-major axis a (average of aphelion and perihelion) of some Solar System orbits (crosses denoting Kepler's values) showing that a³/T² is constant (green line)

Bodies following closed orbits repeat their paths with a certain time called the period. This motion is described by the empirical laws of Kepler, which can be mathematically derived from Newton's laws. These can be formulated as follows:

1. The orbit of a planet around the Sun is an ellipse, with the Sun in one of the focal points of that ellipse. [This focal point is actually the barycenter of the Sun-planet system; for simplicity this explanation assumes the Sun's mass is infinitely larger than that planet's.] The planet's orbit lies in a plane, called the orbital plane. The point on the orbit closest to the attracting body is the periapsis. The point farthest from the attracting body is called the apoapsis. There are also specific terms for orbits about particular bodies; things orbiting the Sun have a perihelion and aphelion, things orbiting the Earth have a perigee and apogee, and things orbiting the Moon have a perilune and apolune (or periselene and aposelene respectively). An orbit around any star, not just the Sun, has a periastron and an apastron.
2. As the planet moves in its orbit, the line from the Sun to planet sweeps a constant area of the orbital plane for a given period of time, regardless of which part of its orbit the planet traces during that period of time. This means that the planet moves faster near its perihelion than near its aphelion, because at the smaller distance it needs to trace a greater arc to cover the same area. This law is usually stated as "equal areas in equal time."
3. For a given orbit, the ratio of the cube of its semi-major axis to the square of its period is constant.

Limitations of Newton's law of gravitation

Note that while bound orbits of a point mass or a spherical body with a Newtonian gravitational field are closed ellipses, which repeat the same path exactly and indefinitely, any non-spherical or non-Newtonian effects (such as caused by the slight oblateness of the Earth, or by relativistic effects, thereby changing the gravitational field's behavior with distance) will cause the orbit's shape to depart from the closed ellipses characteristic of Newtonian two-body motion. The two-body solutions were published by Newton in Principia in 1687. In 1912, Karl Fritiof Sundman developed a converging infinite series that solves the three-body problem; however, it converges too slowly to be of much use. Except for special cases like the Lagrangian points, no method is known to solve the equations of motion for a system with four or more bodies.

Approaches to many-body problems

Rather than an exact closed form solution, orbits with many bodies can be approximated with arbitrarily high accuracy. These approximations take two forms:

One form takes the pure elliptic motion as a basis, and adds perturbation terms to account for the gravitational influence of multiple bodies. This is convenient for calculating the positions of astronomical bodies. The equations of motion of the moons, planets and other bodies are known with great accuracy, and are used to generate tables for celestial navigation. Still, there are secular phenomena that have to be dealt with by post-Newtonian methods.

The differential equation form is used for scientific or mission-planning purposes. According to Newton's laws, the sum of all the forces acting on a body will equal the mass of the body times its acceleration (F = ma). Therefore accelerations can be expressed in terms of positions. The perturbation terms are much easier to describe in this form. Predicting subsequent positions and velocities from initial values of position and velocity corresponds to solving an initial value problem. Numerical methods calculate the positions and velocities of the objects a short time in the future, then repeat the calculation ad nauseam. However, tiny arithmetic errors from the limited accuracy of a computer's math are cumulative, which limits the accuracy of this approach.

Differential simulations with large numbers of objects perform the calculations in a hierarchical pairwise fashion between centers of mass. Using this scheme, galaxies, star clusters and other large assemblages of objects have been simulated.

Newtonian analysis of orbital motion

The following derivation applies to such an elliptical orbit. We start only with the Newtonian law of gravitation stating that the gravitational acceleration towards the central body is related to the inverse of the square of the distance between them, namely

${\displaystyle F_{2}=-{\frac {Gm_{1}m_{2}}{r^{2}}}}$

where F₂ is the force acting on the mass m₂ caused by the gravitational attraction mass m₁ has for m₂, G is the universal gravitational constant, and r is the distance between the two masses centers.

From Newton's Second Law, the summation of the forces acting on m₂ related to that body's acceleration:

${\displaystyle F_{2}=m_{2}A_{2}}$

where A₂ is the acceleration of m₂ caused by the force of gravitational attraction F₂ of m₁ acting on m₂.

Combining Eq. 1 and 2:

${\displaystyle -{\frac {Gm_{1}m_{2}}{r^{2}}}=m_{2}A_{2}}$

Solving for the acceleration, A₂:

${\displaystyle A_{2}={\frac {F_{2}}{m_{2}}}=-{\frac {1}{m_{2}}}{\frac {Gm_{1}m_{2}}{r^{2}}}=-{\frac {\mu }{r^{2}}}}$

where ${\displaystyle \mu \,}$ is the standard gravitational parameter, in this case ${\displaystyle Gm_{1}}$. It is understood that the system being described is m₂, hence the subscripts can be dropped.

We assume that the central body is massive enough that it can be considered to be stationary and we ignore the more subtle effects of general relativity.

When a pendulum or an object attached to a spring swings in an ellipse, the inward acceleration/force is proportional to the distance ${\displaystyle A=F/m=-kr.}$ Due to the way vectors add, the component of the force in the ${\displaystyle {\hat {\mathbf {x} }}}$ or in the ${\displaystyle {\hat {\mathbf {y} }}}$ directions are also proportionate to the respective components of the distances, ${\displaystyle r''_{x}=A_{x}=-kr_{x}}$. Hence, the entire analysis can be done separately in these dimensions. This results in the harmonic parabolic equations ${\displaystyle x=A\cos(t)}$ and ${\displaystyle y=B\sin(t)}$ of the ellipse. In contrast, with the decreasing relationship ${\displaystyle A=\mu /r^{2}}$, the dimensions cannot be separated.

The location of the orbiting object at the current time ${\displaystyle t}$ is located in the plane using vector calculus in polar coordinates both with the standard Euclidean basis and with the polar basis with the origin coinciding with the center of force. Let ${\displaystyle r}$ be the distance between the object and the center and ${\displaystyle \theta }$ be the angle it has rotated. Let ${\displaystyle {\hat {\mathbf {x} }}}$ and ${\displaystyle {\hat {\mathbf {y} }}}$ be the standard Euclidean bases and let ${\displaystyle {\hat {\mathbf {r} }}=\cos(\theta ){\hat {\mathbf {x} }}+\sin(\theta ){\hat {\mathbf {y} }}}$ and ${\displaystyle {\hat {\boldsymbol {\theta }}}=-\sin(\theta ){\hat {\mathbf {x} }}+\cos(\theta ){\hat {\mathbf {y} }}}$ be the radial and transverse polar basis with the first being the unit vector pointing from the central body to the current location of the orbiting object and the second being the orthogonal unit vector pointing in the direction that the orbiting object would travel if orbiting in a counter clockwise circle. Then the vector to the orbiting object is

${\displaystyle {\hat {\mathbf {O} }}=r\cos(\theta ){\hat {\mathbf {x} }}+r\sin(\theta ){\hat {\mathbf {y} }}=r{\hat {\mathbf {r} }}}$

We use ${\displaystyle {\dot {r}}}$ and ${\displaystyle {\dot {\theta }}}$ to denote the standard derivatives of how this distance and angle change over time. We take the derivative of a vector to see how it changes over time by subtracting its location at time ${\displaystyle t}$ from that at time ${\displaystyle t+\delta t}$ and dividing by ${\displaystyle \delta t}$. The result is also a vector. Because our basis vector ${\displaystyle {\hat {\mathbf {r} }}}$ moves as the object orbits, we start by differentiating it. From time ${\displaystyle t}$ to ${\displaystyle t+\delta t}$, the vector ${\displaystyle {\hat {\mathbf {r} }}}$ keeps its beginning at the origin and rotates from angle ${\displaystyle \theta }$ to ${\displaystyle \theta +{\dot {\theta }}\ \delta t}$ which moves its head a distance ${\displaystyle {\dot {\theta }}\ \delta t}$ in the perpendicular direction ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ giving a derivative of ${\displaystyle {\dot {\theta }}{\hat {\boldsymbol {\theta }}}}$.

${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\cos(\theta ){\hat {\mathbf {x} }}+\sin(\theta ){\hat {\mathbf {y} }}\\{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {\mathbf {r} }}&=-\sin(\theta ){\dot {\theta }}{\hat {\mathbf {x} }}+\cos(\theta ){\dot {\theta }}{\hat {\mathbf {y} }}={\dot {\theta }}{\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\theta }}}&=-\sin(\theta ){\hat {\mathbf {x} }}+\cos(\theta ){\hat {\mathbf {y} }}\\{\frac {\delta {\hat {\boldsymbol {\theta }}}}{\delta t}}={\dot {\boldsymbol {\theta }}}&=-\cos(\theta ){\dot {\theta }}{\hat {\mathbf {x} }}-\sin(\theta ){\dot {\theta }}{\hat {\mathbf {y} }}=-{\dot {\theta }}{\hat {\mathbf {r} }}\end{aligned}}}$

We can now find the velocity and acceleration of our orbiting object.

${\displaystyle {\begin{aligned}{\hat {\mathbf {O} }}&=r{\hat {\mathbf {r} }}\\{\dot {\mathbf {O} }}&={\frac {\delta r}{\delta t}}{\hat {\mathbf {r} }}+r{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {r}}{\hat {\mathbf {r} }}+r\left[{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]\\{\ddot {\mathbf {O} }}&=\left[{\ddot {r}}{\hat {\mathbf {r} }}+{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]+\left[{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}-r{\dot {\theta }}^{2}{\hat {\mathbf {r} }}\right]\\&=\left[{\ddot {r}}-r{\dot {\theta }}^{2}\right]{\hat {\mathbf {r} }}+\left[r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}\right]{\hat {\boldsymbol {\theta }}}\end{aligned}}}$

The coefficients of ${\displaystyle {\hat {\mathbf {r} }}}$ and ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ give the accelerations in the radial and transverse directions. As said, Newton gives this first due to gravity is ${\displaystyle -\mu /r^{2}}$ and the second is zero.

${\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=-{\frac {\mu }{r^{2}}}}$

(1)

${\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}=0}$

(2)

Equation (2) can be rearranged using integration by parts.

${\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}={\frac {1}{r}}{\frac {d}{dt}}\left(r^{2}{\dot {\theta }}\right)=0}$

We can multiply through by ${\displaystyle r}$ because it is not zero unless the orbiting object crashes. Then having the derivative be zero gives that the function is a constant.

${\displaystyle r^{2}{\dot {\theta }}=h}$

(3)

which is actually the theoretical proof of Kepler's second law (A line joining a planet and the Sun sweeps out equal areas during equal intervals of time). The constant of integration, h, is the angular momentum per unit mass.

In order to get an equation for the orbit from equation (1), we need to eliminate time. In polar coordinates, this would express the distance ${\displaystyle r}$ of the orbiting object from the center as a function of its angle ${\displaystyle \theta }$. However, it is easier to introduce the auxiliary variable ${\displaystyle u=1/r}$ and to express ${\displaystyle u}$ as a function of ${\displaystyle \theta }$. Derivatives of ${\displaystyle r}$ with respect to time may be rewritten as derivatives of ${\displaystyle u}$ with respect to angle.

${\displaystyle u={1 \over r}}$

${\displaystyle {\dot {\theta }}={\frac {h}{r^{2}}}=hu^{2}}$ (reworking (3))

${\displaystyle {\begin{aligned}{\frac {\delta u}{\delta \theta }}&={\frac {\delta }{\delta t}}\left({\frac {1}{r}}\right){\frac {\delta t}{\delta \theta }}=-{\frac {\dot {r}}{r^{2}{\dot {\theta }}}}=-{\frac {\dot {r}}{h}}\\{\frac {\delta ^{2}u}{\delta \theta ^{2}}}&=-{\frac {1}{h}}{\frac {\delta {\dot {r}}}{\delta t}}{\frac {\delta t}{\delta \theta }}=-{\frac {\ddot {r}}{h{\dot {\theta }}}}=-{\frac {\ddot {r}}{h^{2}u^{2}}}\ \ \ {\text{ or }}\ \ \ {\ddot {r}}=-h^{2}u^{2}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}\end{aligned}}}$

Plugging these into (1) gives

${\displaystyle {\begin{aligned}{\ddot {r}}-r{\dot {\theta }}^{2}&=-{\frac {\mu }{r^{2}}}\\-h^{2}u^{2}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}-{\frac {1}{u}}\left(hu^{2}\right)^{2}&=-\mu u^{2}\end{aligned}}}$

${\displaystyle {\frac {\delta ^{2}u}{\delta \theta ^{2}}}+u={\frac {\mu }{h^{2}}}}$

(4)

So for the gravitational force – or, more generally, for any inverse square force law – the right hand side of the equation becomes a constant and the equation is seen to be the harmonic equation (up to a shift of origin of the dependent variable). The solution is:

${\displaystyle u(\theta )={\frac {\mu }{h^{2}}}-A\cos(\theta -\theta _{0})}$

where A and θ₀ are arbitrary constants. This resulting equation of the orbit of the object is that of an ellipse in Polar form relative to one of the focal points. This is put into a more standard form by letting ${\displaystyle e\equiv h^{2}A/\mu }$ be the eccentricity, letting ${\displaystyle a\equiv h^{2}/\mu \left(1-e^{2}\right)}$ be the semi-major axis. Finally, letting ${\displaystyle \theta _{0}\equiv 0}$ so the long axis of the ellipse is along the positive x coordinate.

${\displaystyle r(\theta )={\frac {a\left(1-e^{2}\right)}{1+e\cos \theta }}}$

When the two-body system is under the influence of torque, the angular momentum h is not a constant. After the following calculation:

${\displaystyle {\begin{aligned}{\frac {\delta r}{\delta \theta }}&=-{\frac {1}{u^{2}}}{\frac {\delta u}{\delta \theta }}=-{\frac {h}{m}}{\frac {\delta u}{\delta \theta }}\\{\frac {\delta ^{2}r}{\delta \theta ^{2}}}&=-{\frac {h^{2}u^{2}}{m^{2}}}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}-{\frac {hu^{2}}{m^{2}}}{\frac {\delta h}{\delta \theta }}{\frac {\delta u}{\delta \theta }}\\\left({\frac {\delta \theta }{\delta t}}\right)^{2}r&={\frac {h^{2}u^{3}}{m^{2}}}\end{aligned}}}$

we will get the Sturm-Liouville equation of two-body system.

${\displaystyle {\frac {\delta }{\delta \theta }}\left(h{\frac {\delta u}{\delta \theta }}\right)+hu={\frac {\mu }{h}}}$

(5)

Relativistic orbital motion

The above classical (Newtonian) analysis of orbital mechanics assumes that the more subtle effects of general relativity, such as frame dragging and gravitational time dilation are negligible. Relativistic effects cease to be negligible when near very massive bodies (as with the precession of Mercury's orbit about the Sun), or when extreme precision is needed (as with calculations of the orbital elements and time signal references for GPS satellites.).

Orbital planes

The analysis so far has been two dimensional; it turns out that an unperturbed orbit is two-dimensional in a plane fixed in space, and thus the extension to three dimensions requires simply rotating the two-dimensional plane into the required angle relative to the poles of the planetary body involved.

The rotation to do this in three dimensions requires three numbers to uniquely determine; traditionally these are expressed as three angles.

Orbital period

The orbital period is simply how long an orbiting body takes to complete one orbit.

Specifying orbits

Six parameters are required to specify a Keplerian orbit about a body. For example, the three numbers that specify the body's initial position, and the three values that specify its velocity will define a unique orbit that can be calculated forwards (or backwards) in time. However, traditionally the parameters used are slightly different.

The traditionally used set of orbital elements is called the set of Keplerian elements, after Johannes Kepler and his laws. The Keplerian elements are six:

• Inclination (i)
• Longitude of the ascending node (Ω)
• Argument of periapsis (ω)
• Eccentricity (e)
• Semimajor axis (a)
• Mean anomaly at epoch (M₀).

In principle once the orbital elements are known for a body, its position can be calculated forward and backwards indefinitely in time. However, in practice, orbits are affected or perturbed, by other forces than simple gravity from an assumed point source (see the next section), and thus the orbital elements change over time.

Orbital perturbations

An orbital perturbation is when a force or impulse which is much smaller than the overall force or average impulse of the main gravitating body and which is external to the two orbiting bodies causes an acceleration, which changes the parameters of the orbit over time.

Radial, prograde and transverse perturbations

A small radial impulse given to a body in orbit changes the eccentricity, but not the orbital period (to first order). A prograde or retrograde impulse (i.e. an impulse applied along the orbital motion) changes both the eccentricity and the orbital period. Notably, a prograde impulse at periapsis raises the altitude at apoapsis, and vice versa, and a retrograde impulse does the opposite. A transverse impulse (out of the orbital plane) causes rotation of the orbital plane without changing the period or eccentricity. In all instances, a closed orbit will still intersect the perturbation point.

Orbital decay

If an orbit is about a planetary body with significant atmosphere, its orbit can decay because of drag. Particularly at each periapsis, the object experiences atmospheric drag, losing energy. Each time, the orbit grows less eccentric (more circular) because the object loses kinetic energy precisely when that energy is at its maximum. This is similar to the effect of slowing a pendulum at its lowest point; the highest point of the pendulum's swing becomes lower. With each successive slowing more of the orbit's path is affected by the atmosphere and the effect becomes more pronounced. Eventually, the effect becomes so great that the maximum kinetic energy is not enough to return the orbit above the limits of the atmospheric drag effect. When this happens the body will rapidly spiral down and intersect the central body.

The bounds of an atmosphere vary wildly. During a solar maximum, the Earth's atmosphere causes drag up to a hundred kilometres higher than during a solar minimum.

Some satellites with long conductive tethers can also experience orbital decay because of electromagnetic drag from the Earth's magnetic field. As the wire cuts the magnetic field it acts as a generator, moving electrons from one end to the other. The orbital energy is converted to heat in the wire.

Orbits can be artificially influenced through the use of rocket engines which change the kinetic energy of the body at some point in its path. This is the conversion of chemical or electrical energy to kinetic energy. In this way changes in the orbit shape or orientation can be facilitated.

Another method of artificially influencing an orbit is through the use of solar sails or magnetic sails. These forms of propulsion require no propellant or energy input other than that of the Sun, and so can be used indefinitely.

Orbital decay can occur due to tidal forces for objects below the synchronous orbit for the body they're orbiting. The gravity of the orbiting object raises tidal bulges in the primary, and since below the synchronous orbit the orbiting object is moving faster than the body's surface the bulges lag a short angle behind it. The gravity of the bulges is slightly off of the primary-satellite axis and thus has a component along the satellite's motion. The near bulge slows the object more than the far bulge speeds it up, and as a result the orbit decays. Conversely, the gravity of the satellite on the bulges applies torque on the primary and speeds up its rotation. Artificial satellites are too small to have an appreciable tidal effect on the planets they orbit, but several moons in the Solar System are undergoing orbital decay by this mechanism. Mars' innermost moon Phobos is a prime example, and is expected to either impact Mars' surface or break up into a ring within 50 million years.

Orbits can decay via the emission of gravitational waves. This mechanism is extremely weak for most stellar objects, only becoming significant in cases where there is a combination of extreme mass and extreme acceleration, such as with black holes or neutron stars that are orbiting each other closely.

Oblateness

The standard analysis of orbiting bodies assumes that all bodies consist of uniform spheres, or more generally, concentric shells each of uniform density. It can be shown that such bodies are gravitationally equivalent to point sources.

However, in the real world, many bodies rotate, and this introduces oblateness and distorts the gravity field, and gives a quadrupole moment to the gravitational field which is significant at distances comparable to the radius of the body. In the general case, the gravitational potential of a rotating body such as, e.g., a planet is usually expanded in multipoles accounting for the departures of it from spherical symmetry. From the point of view of satellite dynamics, of particular relevance are the so-called even zonal harmonic coefficients, or even zonals, since they induce secular orbital perturbations which are cumulative over time spans longer than the orbital period. They do depend on the orientation of the body's symmetry axis in the space, affecting, in general, the whole orbit, with the exception of the semimajor axis.

Multiple gravitating bodies

The effects of other gravitating bodies can be significant. For example, the orbit of the Moon cannot be accurately described without allowing for the action of the Sun's gravity as well as the Earth's. One approximate result is that bodies will usually have reasonably stable orbits around a heavier planet or moon, in spite of these perturbations, provided they are orbiting well within the heavier body's Hill sphere.

When there are more than two gravitating bodies it is referred to as an n-body problem. Most n-body problems have no closed form solution, although some special cases have been formulated.

Light radiation and stellar wind

For smaller bodies particularly, light and stellar wind can cause significant perturbations to the attitude and direction of motion of the body, and over time can be significant. Of the planetary bodies, the motion of asteroids is particularly affected over large periods when the asteroids are rotating relative to the Sun.

Strange orbits

Mathematicians have discovered that it is possible in principle to have multiple bodies in non-elliptical orbits that repeat periodically, although most such orbits are not stable regarding small perturbations in mass, position, or velocity. However, some special stable cases have been identified, including a planar figure-eight orbit occupied by three moving bodies. Further studies have discovered that nonplanar orbits are also possible, including one involving 12 masses moving in 4 roughly circular, interlocking orbits topologically equivalent to the edges of a cuboctahedron.

Finding such orbits naturally occurring in the universe is thought to be extremely unlikely, because of the improbability of the required conditions occurring by chance.

Astrodynamics

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It is a core discipline within space mission design and control. Celestial mechanics treats more broadly the orbital dynamics of systems under the influence of gravity, including spacecraft and natural astronomical bodies such as star systems, planets, moons, and comets. Orbital mechanics focuses on spacecraft trajectories, including orbital maneuvers, orbit plane changes, and interplanetary transfers, and is used by mission planners to predict the results of propulsive maneuvers. General relativity is a more exact theory than Newton's laws for calculating orbits, and is sometimes necessary for greater accuracy or in high-gravity situations (such as orbits close to the Sun).

Earth orbits

Comparison of geostationary Earth orbit with GPS, GLONASS, Galileo and Compass (medium Earth orbit) satellite navigation system orbits with the International Space Station, Hubble Space Telescope and Iridium constellation orbits, and the nominal size of the Earth. The Moon's orbit is around 9 times larger (in radius and length) than geostationary orbit.

• Low Earth orbit (LEO): Geocentric orbits with altitudes up to 2,000 km (0–1,240 miles).
• Medium Earth orbit (MEO): Geocentric orbits ranging in altitude from 2,000 km (1,240 miles) to just below geosynchronous orbit at 35,786 kilometers (22,236 mi). Also known as an intermediate circular orbit. These are "most commonly at 20,200 kilometers (12,600 mi), or 20,650 kilometers (12,830 mi), with an orbital period of 12 hours."
• Both geosynchronous orbit (GSO) and geostationary orbit (GEO) are orbits around Earth matching Earth's sidereal rotation period. All geosynchronous and geostationary orbits have a semi-major axis of 42,164 km (26,199 mi). All geostationary orbits are also geosynchronous, but not all geosynchronous orbits are geostationary. A geostationary orbit stays exactly above the equator, whereas a geosynchronous orbit may swing north and south to cover more of the Earth's surface. Both complete one full orbit of Earth per sidereal day (relative to the stars, not the Sun).
• High Earth orbit: Geocentric orbits above the altitude of geosynchronous orbit 35,786 km (22,240 miles).

Scaling in gravity

The gravitational constant G has been calculated as:

• (6.6742 ± 0.001) × 10⁻¹¹ (kg/m³)⁻¹s⁻².

Thus the constant has dimension density⁻¹ time⁻². This corresponds to the following properties.

Scaling of distances (including sizes of bodies, while keeping the densities the same) gives similar orbits without scaling the time: if for example distances are halved, masses are divided by 8, gravitational forces by 16 and gravitational accelerations by 2. Hence velocities are halved and orbital periods and other travel times related to gravity remain the same. For example, when an object is dropped from a tower, the time it takes to fall to the ground remains the same with a scale model of the tower on a scale model of the Earth.

Scaling of distances while keeping the masses the same (in the case of point masses, or by adjusting the densities) gives similar orbits; if distances are multiplied by 4, gravitational forces and accelerations are divided by 16, velocities are halved and orbital periods are multiplied by 8.

When all densities are multiplied by 4, orbits are the same; gravitational forces are multiplied by 16 and accelerations by 4, velocities are doubled and orbital periods are halved.

When all densities are multiplied by 4, and all sizes are halved, orbits are similar; masses are divided by 2, gravitational forces are the same, gravitational accelerations are doubled. Hence velocities are the same and orbital periods are halved.

In all these cases of scaling. if densities are multiplied by 4, times are halved; if velocities are doubled, forces are multiplied by 16.

These properties are illustrated in the formula (derived from the formula for the orbital period)

${\displaystyle GT^{2}\rho =3\pi \left({\frac {a}{r}}\right)^{3},}$

for an elliptical orbit with semi-major axis a, of a small body around a spherical body with radius r and average density ρ, where T is the orbital period.