Spontaneous human combustion

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Spontaneous_human_combustion

Spontaneous human combustion (SHC) is the pseudoscientific concept of the spontaneous combustion of a living (or recently deceased) human body without an apparent external source of ignition. In addition to reported cases, descriptions of the alleged phenomenon appear in literature, and both types have been observed to share common characteristics in terms of circumstances and the remains of the victim.

Scientific investigations have attempted to analyze reported instances of SHC and have resulted in hypotheses regarding potential causes and mechanisms, including victim behavior and habits, alcohol consumption, and proximity to potential sources of ignition, as well as the behavior of fires that consume melted fats. Natural explanations, as well as unverified natural phenomena, have been proposed to explain reports of SHC. Current scientific consensus is that purported cases of SHC involve overlooked external sources of ignition.

Overview

"Spontaneous human combustion" refers to the death from a fire originating without an apparent external source of ignition; a belief that the fire starts within the body of the victim. This idea and the term "spontaneous human combustion" were both first proposed in 1746 by Paul Rolli, a Fellow of the Royal Society, in an article published in the Philosophical Transactions concerning the mysterious death of Countess Cornelia Zangheri Bandi. Writing in The British Medical Journal in 1938, coroner Gavin Thurston describes the phenomenon as having "apparently attracted the attention not only of the medical profession but of the laity one hundred years ago" (referring to a fictional account published in 1834 in the Frederick Marryat cycle). In his 1995 book Ablaze!, Larry E. Arnold, a director of ParaScience International, wrote that there had been about 200 cited reports of spontaneous human combustion worldwide over a period of around 300 years.

Characteristics

The topic received coverage in the British Medical Journal in 1938. An article by L. A. Parry cited an 1823-published book Medical Jurisprudence, which stated that commonalities among recorded cases of spontaneous human combustion included the following characteristics:

1. the victims are chronic alcoholics;
2. they are usually elderly females;
3. the body has not burned spontaneously, but some lighted substance has come into contact with it;
4. the hands and feet usually fall off;
5. the fire has caused very little damage to combustible things in contact with the body;
6. the combustion of the body has left a residue of greasy and fetid ashes, very offensive in odour

Alcoholism is a common theme in early SHC literary references, in part because some Victorian era physicians and writers believed spontaneous human combustion was the result of alcoholism.

Scientific investigation

An extensive two-year research project, involving thirty historical cases of alleged SHC, was conducted in 1984 by science investigator Joe Nickell and forensic analyst John F. Fischer. Their lengthy, two-part report was published in the journal of the International Association of Arson Investigators, as well as part of a book. Nickell has written frequently on the subject, appeared on television documentaries, conducted additional research, and lectured at the New York State Academy of Fire Science at Montour Falls, New York, as a guest instructor.

Nickell and Fischer's investigation, which looked at cases in the 18th, 19th and 20th centuries, showed that the burned bodies were close to plausible sources for the ignition: candles, lamps, fireplaces, and so on. Such sources were often omitted from published accounts of these incidents, presumably to deepen the aura of mystery surrounding an apparently "spontaneous" death. The investigations also found that there was a correlation between alleged SHC deaths and the victim's intoxication (or other forms of incapacitation) which could conceivably have caused them to be careless and unable to respond properly to an accident. Where the destruction of the body was not particularly extensive, a primary source of combustible fuel could plausibly have been the victim's clothing or a covering such as a blanket or comforter.

However, where the destruction was extensive, additional fuel sources were involved, such as chair stuffing, floor coverings, the flooring itself, and the like. The investigators described how such materials helped to retain melted fat, which caused more of the body to be burned and destroyed, yielding still more liquified fat, in a cyclic process known as the "wick effect" or the "candle effect".

According to Nickell and Fischer's investigation, nearby objects often remained undamaged because fire tends to burn upward, but burns laterally with some difficulty. The fires in question are relatively small, achieving considerable destruction by the wick effect, and relatively nearby objects may not be close enough to catch fire themselves (much as one can closely approach a modest campfire without burning). As with other mysteries, Nickell and Fischer cautioned against "single, simplistic explanation for all unusual burning deaths" but rather urged investigating "on an individual basis".

Neurologist Steven Novella has said that skepticism about spontaneous human combustion is now bleeding over into becoming popular skepticism about spontaneous combustion.

A 2002 study by Angi M. Christensen of the University of Tennessee cremated both healthy and osteoporotic samples of human bone and compared the resulting color changes and fragmentation. The study found that osteoporotic bone samples "consistently displayed more discoloration and a greater degree of fragmentation than healthy ones." The same study found that when human tissue is burned, the resulting flame produces a small amount of heat, indicating that fire is unlikely to spread from burning tissue.

Suggested explanations

The scientific consensus is that incidents which might appear as spontaneous combustion did in fact have an external source of ignition, and that spontaneous human combustion without an external ignition source is extremely implausible. Pseudoscientific hypotheses have been presented which attempt to explain how SHC might occur without an external flame source. Benjamin Radford, science writer and deputy editor of the science magazine Skeptical Inquirer, casts doubt on the plausibility of spontaneous human combustion: "If SHC is a real phenomenon (and not the result of an elderly or infirm person being too close to a flame source), why doesn't it happen more often? There are 5 billion people in the world [ ⁠today in 2011⁠], and yet we don't see reports of people bursting into flame while walking down the street, attending football games, or sipping a coffee at a local Starbucks."

Natural explanations

• Almost all postulated cases of SHC involve people with low mobility due to advanced age or obesity, along with poor health. Victims show a high likelihood of having died in their sleep, or of having been unable to move once they had caught fire.
• Smoking is often seen as the source of fire. Natural causes such as heart attacks may lead to the victim dying, subsequently dropping the cigarette, which after a period of smouldering can ignite the victim's clothes.
• The "wick effect" hypothesis suggests that a small external flame source, such as a burning cigarette, chars the clothing of the victim at a location, splitting the skin and releasing subcutaneous fat, which is in turn absorbed into the burned clothing, acting as a wick. This combustion can continue for as long as the fuel is available. This hypothesis has been successfully tested with pig tissue and is consistent with evidence recovered from cases of human combustion. The human body typically has enough stored energy in fat and other chemical stores to fully combust the body; even lean people have several pounds of fat in their tissues. This fat, once heated by the burning clothing, wicks into the clothing much as candle wax is drawn into a lit candle wick, providing the fuel needed to keep the wick burning. The protein in the body also burns, but provides less energy than fat, with the water in the body being the main impediment to combustion. However, slow combustion, lasting hours, gives the water time to evaporate slowly. In an enclosed area, such as a house, this moisture will recondense nearby, possibly on windows. Feet don't typically burn because they often have the least fat; hands also have little fat, but may burn if resting on the abdomen, which provides all of the necessary fat for combustion.
• Scalding can cause burn-like injuries, sometimes leading to death, without setting fire to clothing. Although not applicable in cases where the body is charred and burnt, this has been suggested as a cause in at least one claimed SHC-like event.
• Brian J. Ford has suggested that ketosis, possibly caused by alcoholism or low-carb dieting, produces acetone, which is highly flammable and could therefore lead to apparently spontaneous combustion.
• SHC can be confused with self-immolation as a form of suicide. In the West, self-immolation accounts for 1% of suicides, while Radford claims in developing countries the figure can be as high as 40%.
• Sometimes there are reasonable explanations for the deaths, but proponents ignore official autopsies and contradictory evidence in favor of anecdotal accounts and personal testimonies.
• Inhaling/digesting phosphorus in different forms can cause the forming of phosphine which can autoignite

Alternative theories

• Larry E. Arnold in his 1995 book Ablaze! proposed a pseudoscientific new subatomic particle, which he called "pyrotron". Arnold also wrote that the flammability of a human body could be increased by certain circumstances, like increased alcohol in the blood. He further proposed that extreme stress could be the trigger that starts many combustions. This process may use no external oxygen to spread throughout the body, since it may not be an "oxidation-reduction" reaction; however, no reaction mechanism has been proposed. Researcher Joe Nickell has criticised Arnold's hypotheses as based on selective evidence and argument from ignorance.
• In his 1976 book Fire from Heaven, UK writer Michael Harrison suggests that SHC is connected to poltergeist activity because, he argues, "the force which activates the 'poltergeist' originates in, and is supplied by, a human being". Within the concluding summary, Harrison writes: "SHC, fatal or non-fatal, belongs to the extensive range of poltergeist phenomena."
• John Abrahamson suggested that ball lightning could account for spontaneous human combustion. "This is circumstantial only, but the charring of human limbs seen in a number of ball lightning cases are [sic] very suggestive that this mechanism may also have occurred where people have had limbs combusted," says Abrahamson.

Notable examples

On 2 July 1951, Mary Reeser, a 67-year-old woman, was found burned to death in her house after her landlady realised that the house's doorknob was unusually warm. The landlady notified the police, and upon entering the home they found Reeser's remains completely burned into ash, with only one leg remaining. The chair she was sitting in was also destroyed. Reeser took sleeping pills and was also a smoker. Despite its proliferation in popular culture, the contemporary FBI investigation ruled out the possibility of SHC. A common theory was that she was smoking a cigarette after taking sleeping pills and then fell asleep while still holding the burning cigarette, which could have ignited her gown, ultimately leading to her death. Her daughter-in-law stated, "The cigarette dropped to her lap. Her fat was the fuel that kept her burning. The floor was cement, and the chair was by itself. There was nothing around her to burn".

Margaret Hogan, an 89-year-old widow who lived alone in a house on Prussia Street, Dublin, Ireland, was found burned almost to the point of complete destruction on 28 March 1970. Plastic flowers on a table in the centre of the room had been reduced to liquid and a television with a melted screen sat 12 feet from the armchair in which the ashen remains were found; otherwise, the surroundings were almost untouched. Her two feet, and both legs from below the knees, were undamaged. A small coal fire had been burning in the grate when a neighbour left the house the previous day; however, no connection between this fire and that in which Mrs. Hogan died could be found. An inquest, held on 3 April 1970, recorded death by burning, with the cause of the fire listed as "unknown".

Henry Thomas, a 73-year-old man, was found burned to death in the living room of his council house on the Rassau estate in Ebbw Vale, South Wales, in 1980. His entire body was incinerated, leaving only his skull and a portion of each leg below the knee. The feet and legs were still clothed in socks and trousers. Half of the chair in which he had been sitting was also destroyed. Police forensic officers decided that the incineration of Thomas was due to the wick effect.

In December 2010, the death of Michael Faherty, a 76-year-old man in County Galway, Ireland, was recorded as "spontaneous combustion" by the coroner. The doctor, Ciaran McLoughlin, made this statement at the inquiry into the death: "This fire was thoroughly investigated and I'm left with the conclusion that this fits into the category of spontaneous human combustion, for which there is no adequate explanation."

In this example from The Skeptic magazine, there were two children from the same family who were tragically burned to death in different places at the same time. The evidence showed that although the coincidence seemed strange, the children both loved to play with fire and had been "whipped" for this behavior in the past. Looking at all the evidence, the coroner and jury ruled that these were both accidental deaths.

In popular culture

• In the novel Redburn by Herman Melville published in 1849, a sailor, Miguel Saveda, is consumed by "animal combustion" while in a drunken stupor on the return voyage from Liverpool to New York.
• In the novel Bleak House by Charles Dickens, the character Mr. Krook dies of spontaneous combustion at the end of Part X. Dickens researched the details of a number of contemporary accounts of spontaneous human combustion before writing that part of the novel and, after receiving criticism from a scientist friend suggesting he was perpetuating a "vulgar error", cites some of these cases in Part XI and again in the preface to the one-volume edition. The death of Mr. Krook has been described as "the most famous case in literature" of spontaneous human combustion.
• In the comic story "The Glenmutchkin Railway" by William Edmondstoune Aytoun, published in 1845 in Blackwood's Magazine, one of the railway directors, Sir Polloxfen Tremens, is said to have died of spontaneous combustion.
• In the 1984 mockumentary This Is Spın̈al Tap, about the fictional heavy metal band Spinal Tap, two of the band's former drummers are said to have died in separate on-stage spontaneous human combustion incidents.
• In the episode "Confidence and Paranoia" of British science fiction series Red Dwarf, a character called the Mayor of Warsaw is said to have spontaneously exploded in the 16th century and briefly appears in a vision by an unconscious Lister (the main protagonist of the series) where he explodes in front of Rimmer (his hologram bunkmate).
• In the beginning of the 1998 video game Parasite Eve, an entire audience in Carnegie Hall spontaneously combusts (except for Aya Brea, the protagonist of the game) during an opera presentation as the main actress Melissa Pierce starts to sing.
• This phenomenon is mentioned in the TV series The X-Files.
• Bob Shaw’s 1984 sci-fi book, Fire Pattern, is about a reporter who investigates people who spontaneously combust, and discovers a startling conspiracy behind the phenomenon.
• In the episode "Heart Break" of the second season of the American action police procedural television series NCIS, a case is investigated where the victim at first glance seems to have been killed by spontaneous human combustion.
• In episode "Duty Free Rome" of the second season of the TV series Picket Fences, the town's mayor is shown to have been killed by spontaneous combustion.
• In the seventh season episode “Mars Attacks” of the American TV medical drama ER, a patient is treated for “spontaneous human combustion” and subsequently catches fire.
• The manga and anime series Fire Force (En'en no Shōbōtai) focuses on the main protagonists fighting humans who have this phenomenon.
• In the fourth episode of the first season of the English comedic drama series "Toast of London", Toast decides to finish his book by having the main character spontaneously combust. When bringing it to his literary agent, the laziness of his ending enrages her to the point of spontaneous combustion in front of Toast.
• The adult animated series South Park devoted a whole episode, titled "Spontaneous Combustion", to spontaneous human combustion.
• In Kevin Wilson's short story "Blowing Up on the Spot" (from his collection Tunneling to the Center of the Earth), the protagonist's parents died from a "double spontaneous human combustion."
• In the 2020 American black comedy horror film Spontaneous, high school students at Covington High begin to inexplicably explode.
• In episode 12 of Now and Again, Michael investigates a church that uses spontaneous human combustion.

Wi-Fi hotspot

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Wi-Fi_hotspot 

A diagram showing a Wi-Fi network

A hotspot is a physical location where people can obtain Internet access, typically using Wi-Fi technology, via a wireless local-area network (WLAN) using a router connected to an Internet service provider.

Public hotspots may be created by a business for use by customers, such as coffee shops or hotels. Public hotspots are typically created from wireless access points configured to provide Internet access, controlled to some degree by the venue. In its simplest form, venues that have broadband Internet access can create public wireless access by configuring an access point (AP), in conjunction with a router to connect the AP to the Internet. A single wireless router combining these functions may suffice.

A private hotspot, often called tethering, may be configured on a smartphone or tablet that has a network data plan, to allow Internet access to other devices via Bluetooth pairing, or through the RNDIS protocol over USB, or even when both the hotspot device and the device[s] accessing it are connected to the same Wi-Fi network but one which does not provide Internet access. Similarly, a Bluetooth or USB OTG can be used by a mobile device to provide Internet access via Wi-Fi instead of a mobile network, to a device that itself has neither Wi-Fi nor mobile network capability.

Uses

The public can use a laptop or other suitable portable device to access the wireless connection (usually Wi-Fi) provided. Of the estimated 150 million laptops, 14 million PDAs, and other emerging Wi-Fi devices sold per year for the last few years, most include the Wi-Fi feature.

The iPass 2014 interactive map, that shows data provided by the analysts Maravedis Rethink, shows that in December 2014 there are 46,000,000 hotspots worldwide and more than 22,000,000 roamable hotspots. More than 10,900 hotspots are on trains, planes and airports (Wi-Fi in motion) and more than 8,500,000 are "branded" hotspots (retail, cafés, hotels). The region with the largest number of public hotspots is Europe, followed by North America and Asia.

Libraries throughout the United States are implementing hotspot lending programs to extend access to online library services to users at home who cannot afford in-home Internet access or do not have access to Internet infrastructure. The New York Public Library was the largest program, lending out 10,000 devices to library patrons. Similar programs have existed in Kansas, Maine, and Oklahoma; and many individual libraries are implementing these programs.

Wi-Fi positioning is a method for geolocation based on the positions of nearby hotspots.

Security issues

Security is a serious concern in connection with public and private hotspots. There are three possible attack scenarios. First, there is the wireless connection between the client and the access point, which needs to be encrypted, so that the connection cannot be eavesdropped or attacked by a man-in-the-middle attack. Second, there is the hotspot itself. The WLAN encryption ends at the interface, then travels its network stack unencrypted and then, third, travels over the wired connection up to the BRAS of the ISP.

Depending upon the setup of a public hotspot, the provider of the hotspot has access to the metadata and content accessed by users of the hotspot. The safest method when accessing the Internet over a hotspot, with unknown security measures, is end-to-end encryption. Examples of strong end-to-end encryption are HTTPS and SSH.

Some hotspots authenticate users; however, this does not prevent users from viewing network traffic using packet sniffers.

Some vendors provide a download option that deploys WPA support. This conflicts with enterprise configurations that have solutions specific to their internal WLAN.

The Opportunistic Wireless Encryption (OWE) standard provides encrypted communication in open Wi-Fi networks, alongside the WPA3 standard, but is not yet widely implemented.

Unintended consequences

Main article: LinkNYC § Nuisance complaints

New York City introduced a Wi-Fi hotspot kiosk called LinkNYC with the intentions of providing modern technology for the masses as a replacement to a payphone. Businesses complained they were a homeless magnet and CBS news observed transients with wires connected to the kiosk lingering for an extended period. It was shut down following complaints about transient activity around the station and encampments forming around it. Transients/panhandlers were the most frequent users of the kiosk since its installation in early 2016 spurring complaints about public viewing of pornography and masturbation.

Locations

Public hotspots are often found at airports, bookstores, coffee shops, department stores, fuel stations, hotels, hospitals, libraries, public pay phones, restaurants, RV parks and campgrounds, supermarkets, train stations, and other public places. Additionally, many schools and universities have wireless networks on their campuses.

Types

Free hotspots

public Wi-Fi hotspot in Zurich

According to statista.com, in the year 2022, there are approximately 550 million free Wi-Fi hotspots around the world. The U.S. NSA warns against connecting to free public Wi-Fi.

Free hotspots operate in two ways:

• Using an open public network is the easiest way to create a free hotspot. All that is needed is a Wi-Fi router. Similarly, when users of private wireless routers turn off their authentication requirements, opening their connection, intentionally or not, they permit piggybacking (sharing) by anyone in range.
• Closed public networks use a HotSpot Management System to control access to hotspots. This software runs on the router itself or an external computer allowing operators to authorize only specific users to access the Internet. Providers of such hotspots often associate the free access with a menu, membership, or purchase limit. Operators may also limit each user's available bandwidth (upload and download speed) to ensure that everyone gets a good quality service. Often this is done through service-level agreements.

Commercial hotspots

A commercial hotspot may feature:

• A captive portal / login screen / splash page that users are redirected to for authentication and/or payment. The captive portal / splash page sometimes includes the social login buttons.
• A payment option using a credit card, iPass, PayPal, or another payment service (voucher-based Wi-Fi)
• A walled garden feature that allows free access to certain sites
• Service-oriented provisioning to allow for improved revenue
• Data analytics and data capture tools, to analyze and export data from Wi-Fi clients

Many services provide payment services to hotspot providers, for a monthly fee or commission from the end-user income. For example, Amazingports can be used to set up hotspots that intend to offer both fee-based and free internet access, and ZoneCD is a Linux distribution that provides payment services for hotspot providers who wish to deploy their own service.

Roaming services are expanding among major hotspot service providers. With roaming service the users of a commercial provider can have access to other providers' hotspots, either free of charge or for extra fees, which users will usually be charged on an access-per-minute basis.

Software hotspots

Main article: SoftAP

Many Wi-Fi adapters built into or easily added to consumer computers and mobile devices include the functionality to operate as private or mobile hotspots, sometimes referred to as "mi-fi". The use of a private hotspot to enable other personal devices to access the WAN (usually but not always the Internet) is a form of bridging, and known as tethering. Manufacturers and firmware creators can enable this functionality in Wi-Fi devices on many Wi-Fi devices, depending upon the capabilities of the hardware, and most modern consumer operating systems, including Android, Apple OS X 10.6 and later, Windows, and Linux include features to support this. Additionally wireless chipset manufacturers such as Atheros, Broadcom, Intel and others, may add the capability for certain Wi-Fi NICs, usually used in a client role, to also be used for hotspot purposes. However, some service providers, such as AT&T, Sprint, and T-Mobile charge users for this service or prohibit and disconnect user connections if tethering is detected.

Third-party software vendors offer applications to allow users to operate their own hotspot, whether to access the Internet when on the go, share an existing connection, or extend the range of another hotspot.

Hotspot 2.0

Hotspot 2.0, also known as HS2 and Wi-Fi Certified Passpoint, is an approach to public access Wi-Fi by the Wi-Fi Alliance. The idea is for mobile devices to automatically join a Wi-Fi subscriber service whenever the user enters a Hotspot 2.0 area, in order to provide better bandwidth and services-on-demand to end-users and relieve carrier infrastructure of some traffic.

Hotspot 2.0 is based on the IEEE 802.11u standard, which is a set of protocols published in 2011 to enable cellular-like roaming. If the device supports 802.11u and is subscribed to a Hotspot 2.0 service it will automatically connect and roam.

Supported devices

• Apple mobile devices running iOS 7 and up
• Some Samsung Galaxy smartphones
• Windows 10 devices have full support for network discovery and connection.
• Windows 8 and Windows 8.1 lack network discovery, but support connecting to a network when the credentials are known.

Billing

EDCF user-priority list

		Net traffic
		low			high
		Audio	Video	Data	Audio	Video	Data
User needs	time-critical	7	5	0	6	4	0
	not time-critical	-	-	2	-	-	2

The "user-fairness model" is a dynamic billing model, which allows volume-based billing, charged only by the amount of payload (data, video, audio). Moreover, the tariff is classified by net traffic and user needs.

If the net traffic increases, then the user has to pay the next higher tariff class. The user can be prompted to confirm that they want to continue the session in the higher traffic class. A higher class fare can also be charged for delay sensitive applications such as video and audio, versus non time-critical applications such as reading Web pages and sending e-mail.

Tariff classes of the user-fairness model

		Net traffic
		low	high
User needs	time-critical	standard	exclusive
	not time-critical	low priced	standard

The "User-fairness model" can be implemented with the help of EDCF (IEEE 802.11e). An EDCF user priority list shares the traffic in 3 access categories (data, video, audio) and user priorities (UP).

• Data [UP 0|2]
• Video [UP 5|4]
• Audio [UP 7|6]

See Service-oriented provisioning for viable implementations.

Legal issues

See also: Legality of piggybacking

Depending upon the set up of a public hotspot, the provider of the hotspot has access to the metadata and content accessed by users of the hotspot, and may have legal obligations related to privacy requirements and liability for use of the hotspot for unlawful purposes. In countries where the internet is regulated or freedom of speech more restricted, there may be requirements such as licensing, logging, or recording of user information. Concerns may also relate to child safety, and social issues such as exposure to objectionable content, protection against cyberbullying and illegal behaviours, and prevention of perpetration of such behaviors by hotspot users themselves.

European Union

The Data Retention Directive which required hotspot owners to retain key user statistics for 12 months was annulled by the Court of Justice of the European Union in 2014. The Directive on Privacy and Electronic Communications was replaced in 2018 by the General Data Protection Regulation, which imposes restrictions on data collection by hotspot operators.

United Kingdom

• Data Protection Act 1998: The hotspot owner must retain individual's information within the confines of the law.
• Digital Economy Act 2010: Deals with, among other things, copyright infringement, and imposes fines of up to £250,000 for contravention.

History

Public park in Brooklyn, New York has free Wi-Fi from a local corporation.

Public access wireless local area networks (LANs) were first proposed by Henrik Sjoden at the NetWorld+Interop conference in The Moscone Center in San Francisco in August 1993. Sjoden did not use the term "hotspot" but referred to publicly accessible wireless LANs.

The first commercial venture to attempt to create a public local area access network was a firm founded in Richardson, Texas known as PLANCOM (Public Local Area Network Communications). The founders of the venture, Mark Goode, Greg Jackson, and Brett Stewart dissolved the firm in 1998, while Goode and Jackson created MobileStar Networks. The firm was one of the first to sign such public access locations as Starbucks, American Airlines, and Hilton Hotels. The company was sold to Deutsche Telecom in 2001, who then converted the name of the firm into "T-Mobile Hotspot". It was then that the term "hotspot" entered the popular vernacular as a reference to a location where a publicly accessible wireless LAN is available.

ABI Research reported there was a total of 4.9 million global Wi-Fi hotspots in 2012. In 2016 the Wireless Broadband Alliance predicted a steady annual increase from 5.2m public hotspots in 2012 to 10.5m in 2018.

Fermi–Dirac statistics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Fermi%E2%80%93Dirac_statistics 

Fermi–Dirac statistics (F–D statistics) is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926 (although Fermi derived it before Dirac). Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.

F–D statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the F–D distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. F–D statistics is most commonly applied to electrons, a type of fermion with spin 1/2.

A counterpart to F–D statistics is Bose–Einstein statistics (B–E statistics), which applies to identical and indistinguishable particles with integer spin (0, 1, 2, etc.) called bosons. In classical physics, Maxwell–Boltzmann statistics (M–B statistics) is used to describe particles that are identical and treated as distinguishable. For both B–E and M–B statistics, more than one particle can occupy the same state, unlike F–D statistics.

Comparison of average occupancy of the ground state for three statistics

History

Before the introduction of Fermi–Dirac statistics in 1926, understanding some aspects of electron behavior was difficult due to seemingly contradictory phenomena. For example, the electronic heat capacity of a metal at room temperature seemed to come from 100 times fewer electrons than were in the electric current. It was also difficult to understand why the emission currents generated by applying high electric fields to metals at room temperature were almost independent of temperature.

The difficulty encountered by the Drude model, the electronic theory of metals at that time, was due to considering that electrons were (according to classical statistics theory) all equivalent. In other words, it was believed that each electron contributed to the specific heat an amount on the order of the Boltzmann constant k_B. This problem remained unsolved until the development of F–D statistics.

F–D statistics was first published in 1926 by Enrico Fermi and Paul Dirac. According to Max Born, Pascual Jordan developed in 1925 the same statistics, which he called Pauli statistics, but it was not published in a timely manner. According to Dirac, it was first studied by Fermi, and Dirac called it "Fermi statistics" and the corresponding particles "fermions".

F–D statistics was applied in 1926 by Ralph Fowler to describe the collapse of a star to a white dwarf. In 1927 Arnold Sommerfeld applied it to electrons in metals and developed the free electron model, and in 1928 Fowler and Lothar Nordheim applied it to field electron emission from metals. Fermi–Dirac statistics continues to be an important part of physics.

Fermi–Dirac distribution

For a system of identical fermions in thermodynamic equilibrium, the average number of fermions in a single-particle state i is given by the Fermi–Dirac (F–D) distribution,

${\displaystyle {\overline{n}}_i=\frac{1}{e^{({\epsilon }_i-\mu )/k_{\text{B}}T}+1},}$

where k_B is the Boltzmann constant, T is the absolute temperature, ε_i is the energy of the single-particle state i, and μ is the total chemical potential. The distribution is normalized by the condition

${\displaystyle \sum _i{\overline{n}}_i=N}$

that can be used to express ${\displaystyle \mu =\mu (T,N)}$ in that ${\displaystyle \mu }$ can assume either a positive or negative value.

At zero absolute temperature, μ is equal to the Fermi energy plus the potential energy per fermion, provided it is in a neighbourhood of positive spectral density. In the case of a spectral gap, such as for electrons in a semiconductor, μ, the point of symmetry, is typically called the Fermi level or—for electrons—the electrochemical potential, and will be located in the middle of the gap.

The F–D distribution is only valid if the number of fermions in the system is large enough so that adding one more fermion to the system has negligible effect on μ. Since the F–D distribution was derived using the Pauli exclusion principle, which allows at most one fermion to occupy each possible state, a result is that ${\displaystyle 0<{\overline{n}}_i<1}$ .

• Fermi–Dirac distribution
• 

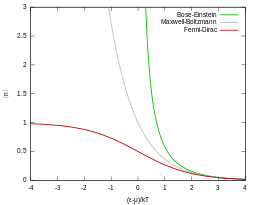
  Energy dependence. More gradual at higher T. ${\displaystyle \overline{n}=0.5}$ when ${\displaystyle \epsilon =\mu }$. Not shown is that ${\displaystyle \mu }$ decreases for higher T.

• 

  Temperature dependence for ${\displaystyle \epsilon >\mu }$.

The variance of the number of particles in state i can be calculated from the above expression for ${\displaystyle {\overline{n}}_i}$,

${\displaystyle V(n_i)=k_{\mathrm{B}}T\frac{\mathrm{\partial }}{\mathrm{\partial }\mu }{\overline{n}}_i={\overline{n}}_i(1-{\overline{n}}_i).}$

Distribution of particles over energy

Fermi function ${\displaystyle F(\epsilon )}$ with μ = 0.55 eV for various temperatures in the range 50 K ≤ T ≤ 375 K

From the Fermi–Dirac distribution of particles over states, one can find the distribution of particles over energy. The average number of fermions with energy ${\displaystyle {\epsilon }_i}$ can be found by multiplying the F–D distribution ${\displaystyle {\overline{n}}_i}$ by the degeneracy ${\displaystyle g_i}$ (i.e. the number of states with energy ${\displaystyle {\epsilon }_i}$),

${\displaystyle \begin{array}{rl}\overline{n}({\epsilon }_i)& =g_i{\overline{n}}_i\\ & =\frac{g_i}{e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}+1}.\end{array}}$

When ${\displaystyle g_i\ge 2}$, it is possible that ${\displaystyle \overline{n}({\epsilon }_i)>1}$, since there is more than one state that can be occupied by fermions with the same energy ${\displaystyle {\epsilon }_i}$.

When a quasi-continuum of energies ${\displaystyle \epsilon }$ has an associated density of states ${\displaystyle g(\epsilon )}$ (i.e. the number of states per unit energy range per unit volume), the average number of fermions per unit energy range per unit volume is

${\displaystyle \overline{\mathcal{N}}(\epsilon )=g(\epsilon )F(\epsilon ),}$

where ${\displaystyle F(\epsilon )}$ is called the Fermi function and is the same function that is used for the F–D distribution ${\displaystyle {\overline{n}}_i}$,

${\displaystyle F(\epsilon )=\frac{1}{e^{(\epsilon -\mu )/k_{\mathrm{B}}T}+1},}$

so that

${\displaystyle \overline{\mathcal{N}}(\epsilon )=\frac{g(\epsilon )}{e^{(\epsilon -\mu )/k_{\mathrm{B}}T}+1}.}$

Quantum and classical regimes

The Fermi–Dirac distribution approaches the Maxwell–Boltzmann distribution in the limit of high temperature and low particle density, without the need for any ad hoc assumptions:

• In the limit of low particle density, ${\displaystyle {\overline{n}}_i=\frac{1}{e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}+1}\ll 1}$, therefore ${\displaystyle e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}+1\gg 1}$ or equivalently ${\displaystyle e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}\gg 1}$. In that case, ${\displaystyle {\overline{n}}_i\approx \frac{1}{e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}}=\frac{N}{Z}{e}^{-{\epsilon }_i/k_{\mathrm{B}}T}}$, which is the result from Maxwell-Boltzmann statistics.
• In the limit of high temperature, the particles are distributed over a large range of energy values, therefore the occupancy on each state (especially the high energy ones with ${\displaystyle {\epsilon }_i-\mu \gg k_{\mathrm{B}}T}$) is again very small, ${\displaystyle {\overline{n}}_i=\frac{1}{e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}+1}\ll 1}$. This again reduces to Maxwell-Boltzmann statistics.

The classical regime, where Maxwell–Boltzmann statistics can be used as an approximation to Fermi–Dirac statistics, is found by considering the situation that is far from the limit imposed by the Heisenberg uncertainty principle for a particle's position and momentum. For example, in physics of semiconductor, when the density of states of conduction band is much higher than the doping concentration, the energy gap between conduction band and fermi level could be calculated using Maxwell-Boltzmann statistics. Otherwise, if the doping concentration is not negligible compared to density of states of conduction band, the F–D distribution should be used instead for accurate calculation. It can then be shown that the classical situation prevails when the concentration of particles corresponds to an average interparticle separation ${\displaystyle \overline{R}}$ that is much greater than the average de Broglie wavelength ${\displaystyle \overline{\lambda }}$ of the particles:

${\displaystyle \overline{R}\gg \overline{\lambda }\approx \frac{h}{\sqrt{3m{k}_{\mathrm{B}}T}},}$

where h is the Planck constant, and m is the mass of a particle.

For the case of conduction electrons in a typical metal at T = 300 K (i.e. approximately room temperature), the system is far from the classical regime because ${\displaystyle \overline{R}\approx \overline{\lambda }/25}$ . This is due to the small mass of the electron and the high concentration (i.e. small ${\displaystyle \overline{R}}$) of conduction electrons in the metal. Thus Fermi–Dirac statistics is needed for conduction electrons in a typical metal.

Another example of a system that is not in the classical regime is the system that consists of the electrons of a star that has collapsed to a white dwarf. Although the temperature of white dwarf is high (typically T = 10000 K on its surface), its high electron concentration and the small mass of each electron precludes using a classical approximation, and again Fermi–Dirac statistics is required.

Derivations

Grand canonical ensemble

The Fermi–Dirac distribution, which applies only to a quantum system of non-interacting fermions, is easily derived from the grand canonical ensemble. In this ensemble, the system is able to exchange energy and exchange particles with a reservoir (temperature T and chemical potential μ fixed by the reservoir).

Due to the non-interacting quality, each available single-particle level (with energy level ϵ) forms a separate thermodynamic system in contact with the reservoir. In other words, each single-particle level is a separate, tiny grand canonical ensemble. By the Pauli exclusion principle, there are only two possible microstates for the single-particle level: no particle (energy E = 0), or one particle (energy E = ε). The resulting partition function for that single-particle level therefore has just two terms:

${\displaystyle \begin{array}{rl}\mathcal{Z}& =\exp (0(\mu -\epsilon )/k_{\mathrm{B}}T)+\exp (1(\mu -\epsilon )/k_{\mathrm{B}}T)\\ & =1+\exp ((\mu -\epsilon )/k_{\mathrm{B}}T),\end{array}}$

and the average particle number for that single-particle level substate is given by

${\displaystyle ⟨N⟩=k_{\mathrm{B}}T\frac{1}{\mathcal{Z}}{\left(\frac{\mathrm{\partial }\mathcal{Z}}{\mathrm{\partial }\mu }\right)}_{V,T}=\frac{1}{\exp ((\epsilon -\mu )/k_{\mathrm{B}}T)+1}.}$

This result applies for each single-particle level, and thus gives the Fermi–Dirac distribution for the entire state of the system.

The variance in particle number (due to thermal fluctuations) may also be derived (the particle number has a simple Bernoulli distribution):

${\displaystyle ⟨(\mathrm{\Delta }N{)}^2⟩=k_{\mathrm{B}}T{\left(\frac{d⟨N⟩}{d\mu }\right)}_{V,T}=⟨N⟩(1-⟨N⟩).}$

This quantity is important in transport phenomena such as the Mott relations for electrical conductivity and thermoelectric coefficient for an electron gas, where the ability of an energy level to contribute to transport phenomena is proportional to ${\displaystyle ⟨(\mathrm{\Delta }N{)}^2⟩}$.

Canonical ensemble

It is also possible to derive Fermi–Dirac statistics in the canonical ensemble. Consider a many-particle system composed of N identical fermions that have negligible mutual interaction and are in thermal equilibrium. Since there is negligible interaction between the fermions, the energy ${\displaystyle E_R}$ of a state ${\displaystyle R}$ of the many-particle system can be expressed as a sum of single-particle energies,

${\displaystyle E_R=\sum _r{n}_r{\epsilon }_r}$

where ${\displaystyle n_r}$ is called the occupancy number and is the number of particles in the single-particle state ${\displaystyle r}$ with energy ${\displaystyle {\epsilon }_r}$. The summation is over all possible single-particle states ${\displaystyle r}$.

The probability that the many-particle system is in the state ${\displaystyle R}$, is given by the normalized canonical distribution,

${\displaystyle P_R=\frac{e^{-\beta E_R}}{{\displaystyle \sum _{R^{\prime }}{e}^{-\beta E_{R^{\prime }}}}}}$

where ${\displaystyle \beta =1/k_{\mathrm{B}}T}$, e^{${\displaystyle -\beta E_R}$} is called the Boltzmann factor, and the summation is over all possible states ${\displaystyle R^{\prime }}$ of the many-particle system.   The average value for an occupancy number ${\displaystyle n_i}$ is

${\displaystyle {\overline{n}}_i=\sum _R{n}_i{P}_R}$

Note that the state ${\displaystyle R}$ of the many-particle system can be specified by the particle occupancy of the single-particle states, i.e. by specifying ${\displaystyle n_1,n_2,\dots ,}$ so that

${\displaystyle P_R=P_{n_1,n_2,\dots }=\frac{e^{-\beta (n_1{\epsilon }_1+n_2{\epsilon }_2+\cdots )}}{{\displaystyle \sum _{{n_1}^{\prime },{n_2}^{\prime },\dots }{e}^{-\beta ({n_1}^{\prime }{\epsilon }_1+{n_2}^{\prime }{\epsilon }_2+\cdots )}}}}$

and the equation for ${\displaystyle {\overline{n}}_i}$ becomes

${\displaystyle \begin{array}{rl}{\overline{n}}_i& =\sum _{n_1,n_2,\dots }{n}_i{P}_{n_1,n_2,\dots }\\ \\ & =\frac{{\displaystyle \sum _{n_1,n_2,\dots }{n}_i{e}^{-\beta (n_1{\epsilon }_1+n_2{\epsilon }_2+\cdots +n_i{\epsilon }_i+\cdots )}}}{{\displaystyle \sum _{n_1,n_2,\dots }{e}^{-\beta (n_1{\epsilon }_1+n_2{\epsilon }_2+\cdots +n_i{\epsilon }_i+\cdots )}}}\end{array}}$

where the summation is over all combinations of values of ${\displaystyle n_1,n_2,\dots }$ which obey the Pauli exclusion principle, and ${\displaystyle n_r}$ = 0 or 1 for each ${\displaystyle r}$. Furthermore, each combination of values of ${\displaystyle n_1,n_2,\dots }$ satisfies the constraint that the total number of particles is ${\displaystyle N}$,

${\displaystyle \sum _r{n}_r=N.}$

Rearranging the summations,

${\displaystyle {\overline{n}}_i=\frac{{\displaystyle \sum _{n_i=0}^1{n}_i{e}^{-\beta (n_i{\epsilon }_i)}\underset{n_1,n_2,\dots }{\phantom{}{\sum }^{(i)}}{e}^{-\beta (n_1{\epsilon }_1+n_2{\epsilon }_2+\cdots )}}}{{\displaystyle \sum _{n_i=0}^1{e}^{-\beta (n_i{\epsilon }_i)}\underset{n_1,n_2,\dots }{\phantom{}{\sum }^{(i)}}{e}^{-\beta (n_1{\epsilon }_1+n_2{\epsilon }_2+\cdots )}}}}$

where the ${\displaystyle {}^{(i)}}$ on the summation sign indicates that the sum is not over ${\displaystyle n_i}$ and is subject to the constraint that the total number of particles associated with the summation is ${\displaystyle N_i=N-n_i}$. Note that ${\displaystyle {\mathrm{\Sigma }}^{(i)}}$ still depends on ${\displaystyle n_i}$ through the ${\displaystyle N_i}$ constraint, since in one case ${\displaystyle n_i=0}$ and ${\displaystyle {\mathrm{\Sigma }}^{(i)}}$ is evaluated with ${\displaystyle N_i=N,}$ while in the other case ${\displaystyle n_i=1}$ and ${\displaystyle {\mathrm{\Sigma }}^{(i)}}$ is evaluated with ${\displaystyle N_i=N-1.}$  To simplify the notation and to clearly indicate that ${\displaystyle {\mathrm{\Sigma }}^{(i)}}$ still depends on ${\displaystyle n_i}$ through ${\displaystyle N-n_i}$ , define

${\displaystyle Z_i(N-n_i)\equiv \underset{n_1,n_2,\dots }{\phantom{}{\sum }^{(i)}}{e}^{-\beta (n_1{\epsilon }_1+n_2{\epsilon }_2+\cdots )}}$

so that the previous expression for ${\displaystyle {\overline{n}}_i}$ can be rewritten and evaluated in terms of the ${\displaystyle Z_i}$,

${\displaystyle \begin{array}{rl}{\overline{n}}_i& =\frac{{\displaystyle \sum _{n_i=0}^1{n}_i{e}^{-\beta (n_i{\epsilon }_i)}{Z}_i(N-n_i)}}{{\displaystyle \sum _{n_i=0}^1{e}^{-\beta (n_i{\epsilon }_i)}{Z}_i(N-n_i)}}\\ & =\frac{0+e^{-\beta {\epsilon }_i}{Z}_i(N-1)}{Z_i(N)+e^{-\beta {\epsilon }_i}{Z}_i(N-1)}\\ & =\frac{1}{[Z_i(N)/Z_i(N-1)]e^{\beta {\epsilon }_i}+1}.\end{array}}$

The following approximation will be used to find an expression to substitute for ${\displaystyle Z_i(N)/Z_i(N-1)}$ .

${\displaystyle \begin{array}{rl}\ln Z_i(N-1)& \simeq \ln Z_i(N)-\frac{\mathrm{\partial }\ln Z_i(N)}{\mathrm{\partial }N}\\ & =\ln Z_i(N)-{\alpha }_i\end{array}}$

where ${\displaystyle {\alpha }_i\equiv \frac{\mathrm{\partial }\ln Z_i(N)}{\mathrm{\partial }N}.}$

If the number of particles ${\displaystyle N}$ is large enough so that the change in the chemical potential ${\displaystyle \mu }$ is very small when a particle is added to the system, then ${\displaystyle {\alpha }_i\simeq -\mu /k_{\mathrm{B}}T.}$ Taking the base e antilog of both sides, substituting for ${\displaystyle {\alpha }_i}$, and rearranging,

${\displaystyle Z_i(N)/Z_i(N-1)=e^{-\mu /k_{\mathrm{B}}T}.}$

Substituting the above into the equation for ${\displaystyle {\overline{n}}_i}$, and using a previous definition of ${\displaystyle \beta }$ to substitute ${\displaystyle 1/k_{\mathrm{B}}T}$ for ${\displaystyle \beta }$, results in the Fermi–Dirac distribution.

${\displaystyle {\overline{n}}_i=\frac{1}{e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}+1}}$

Like the Maxwell–Boltzmann distribution and the Bose–Einstein distribution the Fermi–Dirac distribution can also be derived by the Darwin–Fowler method of mean values.

Microcanonical ensemble

A result can be achieved by directly analyzing the multiplicities of the system and using Lagrange multipliers.

Suppose we have a number of energy levels, labeled by index i, each level having energy ε_i  and containing a total of n_i  particles. Suppose each level contains g_i  distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta (i.e. their momenta may be along different directions), in which case they are distinguishable from each other, yet they can still have the same energy. The value of g_i  associated with level i is called the "degeneracy" of that energy level. The Pauli exclusion principle states that only one fermion can occupy any such sublevel.

The number of ways of distributing n_i indistinguishable particles among the g_i sublevels of an energy level, with a maximum of one particle per sublevel, is given by the binomial coefficient, using its combinatorial interpretation

${\displaystyle w(n_i,g_i)=\frac{g_i!}{n_i!(g_i-n_i)!}.}$

For example, distributing two particles in three sublevels will give population numbers of 110, 101, or 011 for a total of three ways which equals 3!/(2!1!).

The number of ways that a set of occupation numbers n_i can be realized is the product of the ways that each individual energy level can be populated:

${\displaystyle W=\prod _{i}w(n_i,g_i)=\prod _i\frac{g_i!}{n_i!(g_i-n_i)!}.}$

Following the same procedure used in deriving the Maxwell–Boltzmann statistics, we wish to find the set of n_i for which W is maximized, subject to the constraint that there be a fixed number of particles, and a fixed energy. We constrain our solution using Lagrange multipliers forming the function:

${\displaystyle f(n_i)=\ln (W)+\alpha \left(N-\sum n_i\right)+\beta \left(E-\sum n_i{\epsilon }_i\right).}$

Using Stirling's approximation for the factorials, taking the derivative with respect to n_i, setting the result to zero, and solving for n_i yields the Fermi–Dirac population numbers:

${\displaystyle n_i=\frac{g_i}{e^{\alpha +\beta {\epsilon }_i}+1}.}$

By a process similar to that outlined in the Maxwell–Boltzmann statistics article, it can be shown thermodynamically that $\beta =\frac{1}{k_{\mathrm{B}}T}$ and $\alpha =-\frac{\mu }{k_{\mathrm{B}}T}$, so that finally, the probability that a state will be occupied is:

${\displaystyle {\overline{n}}_i=\frac{n_i}{g_i}=\frac{1}{e^{({\epsilon }_i-\mu )/k_{\mathrm{B}}T}+1}.}$