Cobalt-60

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Cobalt-60

Cobalt-60, ⁶⁰Co

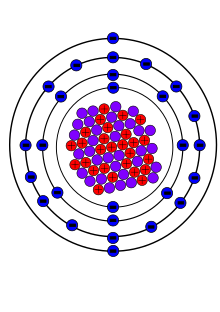
General
Symbol	60Co
Names	cobalt-60, 60Co, Co-60
Protons (Z)	27
Neutrons (N)	33
Nuclide data
Natural abundance	trace
Half-life (t1/2)	5.27 years
Isotope mass	59.9338222 Da
Spin	5+
Decay modes
Decay mode	Decay energy (MeV)
β (beta decay)	0.317
γ (gamma-rays)	1.1732,1.3325

γ-ray spectrum of cobalt-60

Cobalt-60 (⁶⁰Co) is a synthetic radioactive isotope of cobalt with a half-life of 5.2714 years. It is produced artificially in nuclear reactors. Deliberate industrial production depends on neutron activation of bulk samples of the monoisotopic and mononuclidic cobalt isotope ⁵⁹
Co
. Measurable quantities are also produced as a by-product of typical nuclear power plant operation and may be detected externally when leaks occur. In the latter case (in the absence of added cobalt) the incidentally produced ⁶⁰
Co
is largely the result of multiple stages of neutron activation of iron isotopes in the reactor's steel structures via the creation of its ⁵⁹
Co
precursor. The simplest case of the latter would result from the activation of ⁵⁸
Fe
. ⁶⁰
Co
undergoes beta decay to the stable isotope nickel-60 (⁶⁰
Ni
). The activated nickel nucleus emits two gamma rays with energies of 1.17 and 1.33 MeV, hence the overall equation of the nuclear reaction (activation and decay) is: ⁵⁹
₂₇Co
+ n → ⁶⁰
₂₇Co
→ ⁶⁰
₂₈Ni
+ e⁻ +

Activity

Corresponding to its half-life, the radioactive activity of one gram of ⁶⁰
Co
is 44 TBq (1,200 Ci). The absorbed dose constant is related to the decay energy and time. For ⁶⁰
Co
it is equal to 0.35 mSv/(GBq h) at one meter from the source. This allows calculation of the equivalent dose, which depends on distance and activity.

For example, a ⁶⁰
Co
source with an activity of 2.8 GBq, which is equivalent to 60 μg of pure ⁶⁰
Co
, generates a dose of 1 mSv at one meter distance within one hour. The swallowing of ⁶⁰
Co
reduces the distance to a few millimeters, and the same dose is achieved within seconds.

Test sources, such as those used for school experiments, have an activity of <100 kBq. Devices for nondestructive material testing use sources with activities of 1 TBq and more.

The high γ-energies result in a significant mass difference between ⁶⁰
Ni
and ⁶⁰
Co
of 0.003 u. This amounts to nearly 20 watts per gram, nearly 30 times larger than that of ²³⁸
Pu
.

Decay

The decay scheme of ⁶⁰
Co
and ^60m
Co
.

The diagram shows a (simplified) decay scheme of ⁶⁰
Co
and ^60m
Co
. The main β-decay transitions are shown. The probability for population of the middle energy level of 2.1 MeV by β-decay is 0.0022%, with a maximum energy of 665.26 keV. Energy transfers between the three levels generate six different gamma-ray frequencies. In the diagram the two important ones are marked. Internal conversion energies are well below the main energy levels.

^60m
Co
is a nuclear isomer of ⁶⁰
Co
with a half-life of 10.467 minutes.^[4] It decays by internal transition to ⁶⁰
Co
, emitting 58.6 keV gamma rays, or with a low probability (0.22%) by β-decay into ⁶⁰
Ni
.

Applications

Security screening of cars at Super Bowl XLI using ⁶⁰
Co
gamma-ray scanner (2007)

 

Prototype irradiator for food irradiation to prevent spoilage, 1984. The ⁶⁰
Co
is in the central pipes

The main advantage of ⁶⁰
Co
is that it is a high-intensity gamma-ray emitter with a relatively long half-life, 5.27 years, compared to other gamma ray sources of similar intensity. The β-decay energy is low and easily shielded; however, the gamma-ray emission lines have energies around 1.3 MeV, and are highly penetrating. The physical properties of cobalt such as resistance to bulk oxidation and low solubility in water give some advantages in safety in the case of a containment breach over some other gamma sources such as caesium-137. The main uses for ⁶⁰
Co
are:

• As a tracer for cobalt in chemical reactions
• Sterilization of medical equipment.
• Radiation source for medical radiotherapy. Cobalt therapy, using beams of gamma rays from ⁶⁰
  Co
  teletherapy machines to treat cancer.
• Radiation source for industrial radiography.
• Radiation source for leveling devices and thickness gauges.
• Radiation source for pest insect sterilization.
• As a radiation source for food irradiation and blood irradiation.

Cobalt has been discussed as a "salting" element to add to nuclear weapons, to produce a cobalt bomb, an extremely "dirty" weapon which would contaminate large areas with ⁶⁰
Co
nuclear fallout, rendering them uninhabitable. In one hypothetical design, the tamper of the weapon would be made of ⁵⁹
Co
. When the bomb exploded, the excess neutrons from the nuclear fission would irradiate the cobalt and transmute it into ⁶⁰
Co
. No country is known to have done any serious development of this type of weapon.

⁶⁰
Co
needle implanted in tumors for radiotherapy, around 1955.

 

⁶⁰
Co
teletherapy machine for cancer radiotherapy, early 1950s.

 

Brookhaven plant mutation experiment using ⁶⁰
Co
source in the pipe, center.

 

⁶⁰
Co
source for sterilizing screwflies in the 1959 Screwworm Eradication Program.

Production

There is no natural ⁶⁰
Co
in existence on earth; thus, synthetic ⁶⁰
Co
is created by bombarding a ⁵⁹
Co
target with a slow neutron source. Californium-252, moderated through water, can be used for this purpose, as can the neutron flux in a nuclear reactor. The CANDU reactors can be used to activate ⁵⁹
Co
, by substituting the control rods with cobalt rods. In the United States, it is now being produced in a BWR at Hope Creek Nuclear Generating Station. The cobalt targets are substituted here for a small number of fuel assemblies. Still, over 40% of all single-use medical devices are sterilized using ⁶⁰
Co from Bruce nuclear generating station.

⁵⁹
Co
+ n → ⁶⁰
Co

Safety

After entering a living mammal (such as a human being), some of the ⁶⁰
Co
is excreted in feces. The remainder is taken up by tissues, mainly the liver, kidneys, and bones, where the prolonged exposure to gamma radiation can cause cancer. Over time, the absorbed cobalt is eliminated in urine.

Steel contamination

Cobalt is an element used to make steel. Uncontrolled disposal of ⁶⁰
Co
in scrap metal is responsible for the radioactivity found in several iron-based products.

Circa 1983, construction was finished of 1700 apartments in Taiwan which were built with steel contaminated with cobalt-60. Approximately 10,000 people occupied these buildings during a 9–20 year period. On average, these people unknowingly received a radiation dose of 0.4 Sv. This large group did not suffer a higher incidence of cancer mortality, as the linear no-threshold model would predict, but suffered a lower cancer mortality than the general Taiwan public. These observations appear to be compatible with the radiation hormesis model.

In August 2012, Petco recalled several models of steel pet food bowls after US Customs and Border Protection determined that they were emitting low levels of radiation. The source of the radiation was determined to be ⁶⁰
Co
that had contaminated the steel.

In May 2013, a batch of metal-studded belts sold by online retailer ASOS were confiscated and held in a US radioactive storage facility after testing positive for ⁶⁰
Co
.

Incidents involving medical radiation sources

A radioactive contamination incident occurred in 1984 in Ciudad Juárez, Mexico, originating from a radiation therapy unit illegally purchased by a private medical company and subsequently dismantled for lack of personnel to operate it. The radioactive material, ⁶⁰
Co
, ended up in a junkyard, where it was sold to foundries that inadvertently smelted it with other metals and produced about 6,000 tons of contaminated rebar. These were distributed in 17 Mexican states and several cities in the United States. It is estimated that 4,000 people were exposed to radiation as a result of this incident.

In the Samut Prakan radiation accident in 2000, a disused radiotherapy head containing a ⁶⁰
Co
source was stored at an unsecured location in Bangkok, Thailand and then accidentally sold to scrap collectors. Unaware of the dangers, a junkyard employee dismantled the head and extracted the source, which remained unprotected for a period of days at the junkyard. Ten people, including the scrap collectors and workers at the junkyard, were exposed to high levels of radiation and became ill. Three of the junkyard workers subsequently died as a result of their exposure, which was estimated to be over 6 Gy. Afterward, the source was safely recovered by Thai authorities.

In December 2013, a truck carrying a disused 111 TBq ⁶⁰Co teletherapy source from a hospital in Tijuana to a radioactive waste storage center was hijacked at a gas station near Mexico City. The truck was soon recovered, but the thieves had removed the source from its shielding. It was found intact in a nearby field. Despite early reports with lurid headlines asserting that the thieves were "likely doomed", the radiation sickness was mild enough that the suspects were quickly released to police custody, and no one is known to have died from the incident.

Parity

Main article: Wu experiment

In 1957, Chien-Shiung Wu et al. discovered the β-decay process violated parity, implying nature has a handedness.

In the Wu experiment her group aligned radioactive ⁶⁰
Co
nuclei by cooling the source to low temperatures in a magnetic field. Wu's observation was that more β-rays were emitted in the opposite direction to the nuclear spin. This asymmetry violates parity conservation.

Suppliers

Argentina, Canada, India and Russia are the largest suppliers of ⁶⁰
Co
in the world. Both Argentina and Canada have (as of 2022) an all heavy water reactor fleet for power generation. Canada has the CANDU in numerous locations throughout Ontario as well as Point Lepreau Nuclear Generating Station in New Brunswick, while Argentina has two German supplied heavy water reactors at Atucha nuclear power plant and a Canadian-built CANDU at Embalse Nuclear Power Station. India has a number of CANDU reactors at the Rajasthan Atomic Power Station used for production of Cobalt-60. India had a capacity of more than 6 Million Curie of Cobalt-60 production in 2021 and this capacity is slated to increase in the coming years with more CANDU reactors being commissioned in the Rajasthan Atomic Power Station. Heavy water reactors are particularly well suited for the production of cobalt-60 because of their excellent neutron economy and because their capacity for online refueling allows targets to be inserted into the reactor core and removed after a predetermined time without the need for cold shutdown. Furthermore, the heavy water used as a moderator is commonly held at lower temperatures than the coolant in light water reactors, allowing for a lower speed of neutrons, which increases the neutron cross section and decreases unwanted (n,2n) "knockout" reactions.

Earth radius

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Earth_radius

 

Earth radius
Cross section of Earth's Interior
General information
Unit system	astronomy, geophysics
Unit of	distance
Symbol	R🜨, ${\displaystyle R_E}$, ${\displaystyle {\mathcal{R}}_{\mathrm{e}\mathrm{E}}^{\mathrm{N}}}$
Conversions
1 R🜨 in ...	... is equal to ...
SI base unit	6.3781×106 m
Metric system	6,357 to 6,378 km
English units	3,950 to 3,963 mi

Geodesy

Earth radius (denoted as R_🜨 or ${\displaystyle R_E}$) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) (equatorial radius, denoted a) to a minimum of nearly 6,357 km (3,950 mi) (polar radius, denoted b).

A nominal Earth radius is sometimes used as a unit of measurement in astronomy and geophysics, which is recommended by the International Astronomical Union to be the equatorial value.

A globally-average value is usually considered to be 6,371 kilometres (3,959 mi) with a 0.3% variability (±10 km) for the following reasons. The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the mean radius (R₁) of three radii measured at two equator points and a pole; the authalic radius, which is the radius of a sphere with the same surface area (R₂); and the volumetric radius, which is the radius of a sphere having the same volume as the ellipsoid (R₃). All three values are about 6,371 kilometres (3,959 mi).

Other ways to define and measure the Earth's radius involve the radius of curvature. A few definitions yield values outside the range between the polar radius and equatorial radius because they include local or geoidal topography or because they depend on abstract geometrical considerations.

Introduction

A scale diagram of the oblateness of the 2003 IERS reference ellipsoid, with north at the top. The light blue region is a circle. The outer edge of the dark blue line is an ellipse with the same minor axis as the circle and the same eccentricity as the Earth. The red line represents the Karman line 100 km (62 mi) above sea level, while the yellow area denotes the altitude range of the ISS in low Earth orbit.

Main articles: Figure of the Earth, Earth ellipsoid, and Reference ellipsoid

Earth's rotation, internal density variations, and external tidal forces cause its shape to deviate systematically from a perfect sphere. Local topography increases the variance, resulting in a surface of profound complexity. Our descriptions of Earth's surface must be simpler than reality in order to be tractable. Hence, we create models to approximate characteristics of Earth's surface, generally relying on the simplest model that suits the need.

Each of the models in common use involve some notion of the geometric radius. Strictly speaking, spheres are the only solids to have radii, but broader uses of the term radius are common in many fields, including those dealing with models of Earth. The following is a partial list of models of Earth's surface, ordered from exact to more approximate:

• The actual surface of Earth
• The geoid, defined by mean sea level at each point on the real surface
• A spheroid, also called an ellipsoid of revolution, geocentric to model the entire Earth, or else geodetic for regional work
• A sphere

In the case of the geoid and ellipsoids, the fixed distance from any point on the model to the specified center is called "a radius of the Earth" or "the radius of the Earth at that point". It is also common to refer to any mean radius of a spherical model as "the radius of the earth". When considering the Earth's real surface, on the other hand, it is uncommon to refer to a "radius", since there is generally no practical need. Rather, elevation above or below sea level is useful.

Regardless of the model, any radius falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (3,950 to 3,963 mi). Hence, the Earth deviates from a perfect sphere by only a third of a percent, which supports the spherical model in most contexts and justifies the term "radius of the Earth". While specific values differ, the concepts in this article generalize to any major planet.

Physics of Earth's deformation

Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by

${\displaystyle q=\frac{a^3{\omega }^2}{GM},}$

where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet. For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.

The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).

Not all deformations originate within the Earth. Gravitational attraction from the Moon or Sun can cause the Earth's surface at a given point to vary by tenths of a meter over a nearly 12-hour period (see Earth tide).

Radius and local conditions

Al-Biruni's (973 – c. 1050) method for calculation of the Earth's radius simplified measuring the circumference compared to taking measurements from two locations distant from each other.

Given local and transient influences on surface height, the values defined below are based on a "general purpose" model, refined as globally precisely as possible within 5 m (16 ft) of reference ellipsoid height, and to within 100 m (330 ft) of mean sea level (neglecting geoid height).

Additionally, the radius can be estimated from the curvature of the Earth at a point. Like a torus, the curvature at a point will be greatest (tightest) in one direction (north–south on Earth) and smallest (flattest) perpendicularly (east–west). The corresponding radius of curvature depends on the location and direction of measurement from that point. A consequence is that a distance to the true horizon at the equator is slightly shorter in the north–south direction than in the east–west direction.

In summary, local variations in terrain prevent defining a single "precise" radius. One can only adopt an idealized model. Since the estimate by Eratosthenes, many models have been created. Historically, these models were based on regional topography, giving the best reference ellipsoid for the area under survey. As satellite remote sensing and especially the Global Positioning System gained importance, true global models were developed which, while not as accurate for regional work, best approximate the Earth as a whole.

Extrema: equatorial and polar radii

The following radii are derived from the World Geodetic System 1984 (WGS-84) reference ellipsoid. It is an idealized surface, and the Earth measurements used to calculate it have an uncertainty of ±2 m in both the equatorial and polar dimensions. Additional discrepancies caused by topographical variation at specific locations can be significant. When identifying the position of an observable location, the use of more precise values for WGS-84 radii may not yield a corresponding improvement in accuracy.

The value for the equatorial radius is defined to the nearest 0.1 m in WGS-84. The value for the polar radius in this section has been rounded to the nearest 0.1 m, which is expected to be adequate for most uses. Refer to the WGS-84 ellipsoid if a more precise value for its polar radius is needed.

• The Earth's equatorial radius a, or semi-major axis, is the distance from its center to the equator and equals 6,378.1370 km (3,963.1906 mi). The equatorial radius is often used to compare Earth with other planets.

• The Earth's polar radius b, or semi-minor axis, is the distance from its center to the North and South Poles, and equals 6,356.7523 km (3,949.9028 mi).

Location-dependent radii

Three different radii as a function of Earth's latitude. R is the geocentric radius; M is the meridional radius of curvature; and N is the prime vertical radius of curvature.

Geocentric radius

Not to be confused with Geocentric distance.

The geocentric radius is the distance from the Earth's center to a point on the spheroid surface at geodetic latitude φ:

${\displaystyle R(\phi )=\sqrt{\frac{(a^2\cos \phi {)}^2+(b^2\sin \phi {)}^2}{(a\cos \phi {)}^2+(b\sin \phi {)}^2}}}$

where a and b are, respectively, the equatorial radius and the polar radius.

The extrema geocentric radii on the ellipsoid coincide with the equatorial and polar radii. They are vertices of the ellipse and also coincide with minimum and maximum radius of curvature.

Radii of curvature

See also: Spheroid § Curvature

Principal radii of curvature

There are two principal radii of curvature: along the meridional and prime-vertical normal sections.

Meridional

In particular, the Earth's meridional radius of curvature (in the north–south direction) at φ is:

${\displaystyle M(\phi )=\frac{(ab{)}^2}{((a\cos \phi {)}^2+(b\sin \phi {)}^2{)}^{\frac{3}{2}}}=\frac{a(1-e^2)}{(1-e^2{\sin }^2\phi {)}^{\frac{3}{2}}}=\frac{1-e^2}{a^2}N(\phi {)}^3.}$

where ${\displaystyle e}$ is the eccentricity of the earth. This is the radius that Eratosthenes measured in his arc measurement.

Prime vertical

The length PQ, called the prime vertical radius, is ${\displaystyle N(\varphi )}$. The length IQ is equal to ${\displaystyle e^{2}N(\varphi )}$. ${\displaystyle R=(X,Y,Z)}$.

If one point had appeared due east of the other, one finds the approximate curvature in the east–west direction.

This Earth's prime-vertical radius of curvature, also called the Earth's transverse radius of curvature, is defined perpendicular (orthogonal) to M at geodetic latitude φ and is:

${\displaystyle N(\phi )=\frac{a^2}{\sqrt{(a\cos \phi {)}^2+(b\sin \phi {)}^2}}=\frac{a}{\sqrt{1-e^2{\sin }^2\phi }}.}$

N can also be interpreted geometrically as the normal distance from the ellipsoid surface to the polar axis. The radius of a parallel of latitude is given by ${\displaystyle p=N\cos (\phi )}$.

Polar and equatorial radius of curvature

The Earth's meridional radius of curvature at the equator equals the meridian's semi-latus rectum:

b²/a = 6,335.439 km

The Earth's prime-vertical radius of curvature at the equator equals the equatorial radius, N = a.

The Earth's polar radius of curvature (either meridional or prime-vertical) is:

a²/b = 6,399.594 km

Extended content

Combined radii of curvature

Azimuthal

The Earth's azimuthal radius of curvature, along an Earth normal section at an azimuth (measured clockwise from north) α and at latitude φ, is derived from Euler's curvature formula as follows:

${\displaystyle R_{\mathrm{c}}=\frac{1}{{\displaystyle \frac{{\cos }^2\alpha }{M}}+{\displaystyle \frac{{\sin }^2\alpha }{N}}}.}$

Non-directional

It is possible to combine the principal radii of curvature above in a non-directional manner.

The Earth's Gaussian radius of curvature at latitude φ is:

${\displaystyle R_{\mathrm{a}}(\phi )=\frac{1}{\sqrt{K}}=\frac{1}{2\pi }{\int }_0^{2\pi }{R}_{\mathrm{c}}(\alpha )d\alpha =\sqrt{MN}=\frac{a^{2}b}{(a\cos \phi {)}^2+(b\sin \phi {)}^2}=\frac{a\sqrt{1-e^2}}{1-e^2{\sin }^2\phi }.}$

Where K is the Gaussian curvature, ${\displaystyle K={\kappa }_1{\kappa }_2=\frac{detB}{detA}}$.

The Earth's mean radius of curvature at latitude φ is:

${\displaystyle R_{\mathrm{m}}=\frac{2}{{\displaystyle \frac{1}{M}}+{\displaystyle \frac{1}{N}}}}$

Global radii

The Earth can be modeled as a sphere in many ways. This section describes the common ways. The various radii derived here use the notation and dimensions noted above for the Earth as derived from the WGS-84 ellipsoid; namely,

Equatorial radius: a = (6378.1370 km)

Polar radius: b = (6356.7523 km)

A sphere being a gross approximation of the spheroid, which itself is an approximation of the geoid, units are given here in kilometers rather than the millimeter resolution appropriate for geodesy.

Nominal radius

In astronomy, the International Astronomical Union denotes the nominal equatorial Earth radius as ${\displaystyle {\mathcal{R}}_{\mathrm{e}\mathrm{E}}^{\mathrm{N}}}$, which is defined to be 6,378.1 km (3,963.2 mi). The nominal polar Earth radius is defined as ${\displaystyle {\mathcal{R}}_{\mathrm{p}\mathrm{E}}^{\mathrm{N}}}$ = 6,356.8 km (3,949.9 mi). These values correspond to the zero Earth tide convention. Equatorial radius is conventionally used as the nominal value unless the polar radius is explicitly required. The nominal radius serves as a unit of length for astronomy. (The notation is defined such that it can be easily generalized for other planets; e.g., ${\displaystyle {\mathcal{R}}_{\mathrm{p}\mathrm{J}}^{\mathrm{N}}}$ for the nominal polar Jupiter radius.)

Arithmetic mean radius

Equatorial (a), polar (b) and arithmetic mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale)

In geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the Earth's arithmetic mean radius (denoted R₁) to be

${\displaystyle R_1=\frac{2a+b}{3}}$

The factor of two accounts for the biaxial symmetry in Earth's spheroid, a specialization of triaxial ellipsoid. For Earth, the arithmetic mean radius is 6,371.0088 km (3,958.7613 mi).

Authalic radius

See also: Authalic latitude

Earth's authalic radius (meaning "equal area") is the radius of a hypothetical perfect sphere that has the same surface area as the reference ellipsoid. The IUGG denotes the authalic radius as R₂. A closed-form solution exists for a spheroid:

${\displaystyle R_2=\sqrt{\frac{a^2+\frac{b^2}{e}\ln \left(\frac{1+e}{b/a}\right)}{2}}=\sqrt{\frac{a^2}{2}+\frac{b^2}{2}\frac{{\tanh }^{-1}e}{e}}=\sqrt{\frac{A}{4\pi }},}$

where e² = a² − b²/a² and A is the surface area of the spheroid.

For the Earth, the authalic radius is 6,371.0072 km (3,958.7603 mi).

The authalic radius ${\displaystyle R_2}$ also corresponds to the radius of (global) mean curvature, obtained by averaging the Gaussian curvature, ${\displaystyle K}$, over the surface of the ellipsoid. Using the Gauss–Bonnet theorem, this gives

${\displaystyle \frac{\int KdA}{A}=\frac{4\pi }{A}=\frac{1}{R_2^2}.}$

Volumetric radius

Another spherical model is defined by the Earth's volumetric radius, which is the radius of a sphere of volume equal to the ellipsoid. The IUGG denotes the volumetric radius as R₃.

${\displaystyle R_3=\sqrt[3]{a^{2}b}.}$

For Earth, the volumetric radius equals 6,371.0008 km (3,958.7564 mi).

Rectifying radius

See also: Quarter meridian and Rectifying latitude

Another global radius is the Earth's rectifying radius, giving a sphere with circumference equal to the perimeter of the ellipse described by any polar cross section of the ellipsoid. This requires an elliptic integral to find, given the polar and equatorial radii:

${\displaystyle M_{\mathrm{r}}=\frac{2}{\pi }{\int }_0^{\frac{\pi }{2}}\sqrt{a^2{\cos }^2\phi +b^2{\sin }^2\phi }d\phi .}$

The rectifying radius is equivalent to the meridional mean, which is defined as the average value of M:

${\displaystyle M_{\mathrm{r}}=\frac{2}{\pi }{\int }_0^{\frac{\pi }{2}}M(\phi )d\phi .}$

For integration limits of [0,π/2], the integrals for rectifying radius and mean radius evaluate to the same result, which, for Earth, amounts to 6,367.4491 km (3,956.5494 mi).

The meridional mean is well approximated by the semicubic mean of the two axes,

${\displaystyle M_{\mathrm{r}}\approx {\left(\frac{a^{\frac{3}{2}}+b^{\frac{3}{2}}}{2}\right)}^{\frac{2}{3}},}$

which differs from the exact result by less than 1 μm (4×10⁻⁵ in); the mean of the two axes,

${\displaystyle M_{\mathrm{r}}\approx \frac{a+b}{2},}$

about 6,367.445 km (3,956.547 mi), can also be used.

Topographical radii

See also: Earth § Size and shape

The mathematical expressions above apply over the surface of the ellipsoid. The cases below considers Earth's topography, above or below a reference ellipsoid. As such, they are topographical geocentric distances, R_t, which depends not only on latitude.

Topographical extremes

• Maximum R_t: the summit of Chimborazo is 6,384.4 km (3,967.1 mi) from the Earth's center.
• Minimum R_t: the floor of the Arctic Ocean is 6,352.8 km (3,947.4 mi) from the Earth's center.

Topographical global mean

The topographical mean geocentric distance averages elevations everywhere, resulting in a value 230 m larger than the IUGG mean radius, the authalic radius, or the volumetric radius. This topographical average is 6,371.230 km (3,958.899 mi) with uncertainty of 10 m (33 ft).

Derived quantities: diameter, circumference, arc-length, area, volume

Earth's diameter is simply twice Earth's radius; for example, equatorial diameter (2a) and polar diameter (2b). For the WGS84 ellipsoid, that's respectively:

• 2a = 12,756.2740 km (7,926.3812 mi),
• 2b = 12,713.5046 km (7,899.8055 mi).

Earth's circumference equals the perimeter length. The equatorial circumference is simply the circle perimeter: C_e=2πa, in terms of the equatorial radius, a. The polar circumference equals C_p=4m_p, four times the quarter meridian m_p=aE(e), where the polar radius b enters via the eccentricity, e=(1−b²/a²)^0.5; see Ellipse#Circumference for details.

Arc length of more general surface curves, such as meridian arcs and geodesics, can also be derived from Earth's equatorial and polar radii.

Likewise for surface area, either based on a map projection or a geodesic polygon.

Earth's volume, or that of the reference ellipsoid, is V = 4/3πa²b. Using the parameters from WGS84 ellipsoid of revolution, a = 6,378.137 km and b = 6356.7523142 km, V = 1.08321×10¹² km³ (2.5988×10¹¹ cu mi).

History

Main article: History of geodesy

The first published reference to the Earth's size appeared around 350 BC, when Aristotle reported in his book On the Heavens that mathematicians had guessed the circumference of the Earth to be 400,000 stadia. Scholars have interpreted Aristotle's figure to be anywhere from highly accurate to almost double the true value. The first known scientific measurement and calculation of the circumference of the Earth was performed by Eratosthenes in about 240 BC. Estimates of the accuracy of Eratosthenes's measurement range from 0.5% to 17%. For both Aristotle and Eratosthenes, uncertainty in the accuracy of their estimates is due to modern uncertainty over which stadion length they meant.

Around 100 BC, Posidonius of Apamea recomputed Earth's radius, and found it to be close to that by Eratosthenes, but later Strabo incorrectly attributed him a value about 3/4 of the actual size. Claudius Ptolemy around 150 AD gave empirical evidence supporting a spherical Earth, but he accepted the lesser value attributed to Posidonius. His highly influential work, the Almagest, left no doubt among medieval scholars that Earth is spherical, but they were wrong about its size.

By 1490, Christopher Columbus believed that traveling 3,000 miles west from the west coast of the Iberian peninsula would let him reach the eastern coasts of Asia. However, the 1492 enactment of that voyage brought his fleet to the Americas. The Magellan expedition (1519–1522), which was the first circumnavigation of the World, soundly demonstrated the sphericity of the Earth, and affirmed the original measurement of 40,000 km (25,000 mi) by Eratosthenes.

Around 1690, Isaac Newton and Christiaan Huygens argued that Earth was closer to an oblate spheroid than to a sphere. However, around 1730, Jacques Cassini argued for a prolate spheroid instead, due to different interpretations of the Newtonian mechanics involved. To settle the matter, the French Geodesic Mission (1735–1739) measured one degree of latitude at two locations, one near the Arctic Circle and the other near the equator. The expedition found that Newton's conjecture was correct: the Earth is flattened at the poles due to rotation's centrifugal force.