From Wikipedia, the free encyclopedia
Every bounded operator is Lipschitz continuous at 
Equivalence of boundedness and continuity
A linear operator between normed spaces is bounded if and only if it is continuous.
In topological vector spaces
A linear operator  between two topological vector spaces (TVSs) is called a bounded linear operator or just bounded if whenever
between two topological vector spaces (TVSs) is called a bounded linear operator or just bounded if whenever  is bounded in
is bounded in  then
then  is bounded in
is bounded in  A subset of a TVS is called bounded (or more precisely, von Neumann bounded) if every neighborhood of the origin absorbs it.
In a normed space (and even in a seminormed space), a subset is von Neumann bounded if and only if it is norm bounded.
Hence, for normed spaces, the notion of a von Neumann bounded set is identical to the usual notion of a norm-bounded subset.
A subset of a TVS is called bounded (or more precisely, von Neumann bounded) if every neighborhood of the origin absorbs it.
In a normed space (and even in a seminormed space), a subset is von Neumann bounded if and only if it is norm bounded.
Hence, for normed spaces, the notion of a von Neumann bounded set is identical to the usual notion of a norm-bounded subset.
Continuity and boundedness
Every sequentially continuous linear operator between TVS is a bounded operator.
This implies that every continuous linear operator between metrizable TVS is bounded.
However, in general, a bounded linear operator between two TVSs need not be continuous.
This formulation allows one to define bounded operators between
general topological vector spaces as an operator which takes bounded
sets to bounded sets.
In this context, it is still true that every continuous map is bounded,
however the converse fails; a bounded operator need not be continuous.
This also means that boundedness is no longer equivalent to Lipschitz
continuity in this context.
If the domain is a bornological space (for example, a pseudometrizable TVS, a Fréchet space, a normed space) then a linear operators into any other locally convex spaces is bounded if and only if it is continuous.
For LF spaces, a weaker converse holds; any bounded linear map from an LF space is sequentially continuous.
If  is a linear operator between two topological vector spaces and if there exists a neighborhood
is a linear operator between two topological vector spaces and if there exists a neighborhood  of the origin in
of the origin in  such that
such that  is a bounded subset of
is a bounded subset of  then
then  is continuous.
This fact is often summarized by saying that a linear operator that is
bounded on some neighborhood of the origin is necessarily continuous.
In particular, any linear functional that is bounded on some
neighborhood of the origin is continuous (even if its domain is not a normed space).
is continuous.
This fact is often summarized by saying that a linear operator that is
bounded on some neighborhood of the origin is necessarily continuous.
In particular, any linear functional that is bounded on some
neighborhood of the origin is continuous (even if its domain is not a normed space).
Bornological spaces
Bornological spaces are exactly those locally convex spaces for which
every bounded linear operator into another locally convex space is
necessarily continuous.
That is, a locally convex TVS  is a bornological space if and only if for every locally convex TVS
is a bornological space if and only if for every locally convex TVS  a linear operator
a linear operator  is continuous if and only if it is bounded.
is continuous if and only if it is bounded.
Every normed space is bornological.
Characterizations of bounded linear operators
Let  be a linear operator between topological vector spaces (not necessarily Hausdorff).
The following are equivalent:
be a linear operator between topological vector spaces (not necessarily Hausdorff).
The following are equivalent:
 is (locally) bounded;
is (locally) bounded;- (Definition):
 maps bounded subsets of its domain to bounded subsets of its codomain;
maps bounded subsets of its domain to bounded subsets of its codomain;  maps bounded subsets of its domain to bounded subsets of its image
maps bounded subsets of its domain to bounded subsets of its image  ;
; maps every null sequence to a bounded sequence;
maps every null sequence to a bounded sequence;
- A null sequence is by definition a sequence that converges to the origin.
- Thus any linear map that is sequentially continuous at the origin is necessarily a bounded linear map.
 maps every Mackey convergent null sequence to a bounded subset of
maps every Mackey convergent null sequence to a bounded subset of 
- A sequence
 is said to be Mackey convergent to the origin in
is said to be Mackey convergent to the origin in  if there exists a divergent sequence
if there exists a divergent sequence  of positive real number such that
of positive real number such that  is a bounded subset of
is a bounded subset of 
if  and
and  are locally convex then the following may be add to this list:
are locally convex then the following may be add to this list:
 maps bounded disks into bounded disks.
maps bounded disks into bounded disks. maps bornivorous disks in
maps bornivorous disks in  into bornivorous disks in
into bornivorous disks in 
if  is a bornological space and
is a bornological space and  is locally convex then the following may be added to this list:
is locally convex then the following may be added to this list:
 is sequentially continuous at some (or equivalently, at every) point of its domain.
is sequentially continuous at some (or equivalently, at every) point of its domain.
- A sequentially continuous linear map between two TVSs is always bounded,
but the converse requires additional assumptions to hold (such as the
domain being bornological and the codomain being locally convex).
- If the domain
 is also a sequential space, then
is also a sequential space, then  is sequentially continuous if and only if it is continuous.
is sequentially continuous if and only if it is continuous.
 is sequentially continuous at the origin.
is sequentially continuous at the origin.
Examples
- Any linear operator between two finite-dimensional normed spaces is
bounded, and such an operator may be viewed as multiplication by some
fixed matrix.
- Any linear operator defined on a finite-dimensional normed space is bounded.
- On the sequence space
 of eventually zero sequences of real numbers, considered with the
of eventually zero sequences of real numbers, considered with the  norm, the linear operator to the real numbers which returns the sum of a
sequence is bounded, with operator norm 1. If the same space is
considered with the
norm, the linear operator to the real numbers which returns the sum of a
sequence is bounded, with operator norm 1. If the same space is
considered with the  norm, the same operator is not bounded.
norm, the same operator is not bounded. - Many integral transforms are bounded linear operators. For instance, if
![{\displaystyle K:[a,b]\times [c,d]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/12e5a351884ee088fa093f9da368115e5a542daa) is a continuous function, then the operator
is a continuous function, then the operator  defined on the space
defined on the space ![{\displaystyle C[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1625217aad8c105c50c975599e45192b2bfbec) of continuous functions on
of continuous functions on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) endowed with the uniform norm and with values in the space
endowed with the uniform norm and with values in the space ![{\displaystyle C[c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e34aa528c6ca24eb41e62b64bd5bf5c41347d87) with
with  given by the formula
given by the formula
 is bounded. This operator is in fact a compact operator. The compact operators form an important class of bounded operators.
is bounded. This operator is in fact a compact operator. The compact operators form an important class of bounded operators. - The Laplace operator
 (its domain is a Sobolev space and it takes values in a space of square-integrable functions) is bounded.
(its domain is a Sobolev space and it takes values in a space of square-integrable functions) is bounded. - The shift operator on the Lp space
 of all sequences
of all sequences  of real numbers with
of real numbers with 
 is bounded. Its operator norm is easily seen to be
is bounded. Its operator norm is easily seen to be 
Unbounded linear operators
Let  be the space of all trigonometric polynomials on
be the space of all trigonometric polynomials on ![{\displaystyle [-\pi ,\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d9f0d54c7944ecc029624a4317a7aee63b3ee14) with the norm
with the norm

The operator  that maps a polynomial to its derivative is not bounded. Indeed, for
that maps a polynomial to its derivative is not bounded. Indeed, for  with
with  we have
we have  while
while  as
as  so
so  is not bounded.
is not bounded.
Properties of the space of bounded linear operators
The space of all bounded linear operators from  to
to  is denoted by
is denoted by  .
.
 is a normed vector space.
is a normed vector space.- If
 is Banach, then so is
is Banach, then so is  ; in particular, dual spaces are Banach.
; in particular, dual spaces are Banach. - For any
 the kernel of
the kernel of  is a closed linear subspace of
is a closed linear subspace of  .
. - If
 is Banach and
is Banach and  is nontrivial, then
is nontrivial, then  is Banach.
is Banach.




![{\displaystyle \alpha \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daf3c62599ea71319c85f715c9e590d2bab2d036)









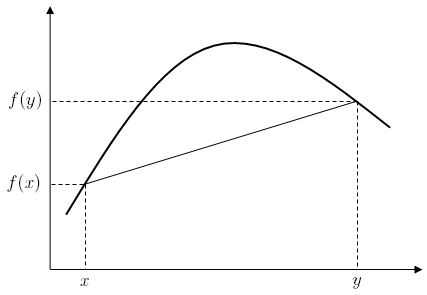

![{\displaystyle f(y)\leq f(x)+f'(x)[y-x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad4b94b94e56ebbdad4a9badaa4412142b032c08)













![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)



































![{\displaystyle K:[a,b]\times [c,d]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/12e5a351884ee088fa093f9da368115e5a542daa)
![{\displaystyle C[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1625217aad8c105c50c975599e45192b2bfbec)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle C[c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e34aa528c6ca24eb41e62b64bd5bf5c41347d87)







![{\displaystyle [-\pi ,\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d9f0d54c7944ecc029624a4317a7aee63b3ee14)









