Inequality (mathematics)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Inequality_(mathematics)

The feasible regions of linear programming are defined by a set of inequalities.

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. The main types of inequality are less than (<) and greater than (>).

Notation

There are several different notations used to represent different kinds of inequalities:

• The notation a < b means that a is less than b.
• The notation a > b means that a is greater than b.

In either case, a is not equal to b. These relations are known as strict inequalities, meaning that a is strictly less than or strictly greater than b. Equality is excluded.

In contrast to strict inequalities, there are two types of inequality relations that are not strict:

• The notation a ≤ b or a ⩽ b or a ≦ b means that a is less than or equal to b (or, equivalently, at most b, or not greater than b).
• The notation a ≥ b or a ⩾ b or a ≧ b means that a is greater than or equal to b (or, equivalently, at least b, or not less than b).

In the 17th and 18th centuries, personal notations or typewriting signs were used to signal inequalities. For example, In 1670, John Wallis used a single horizontal bar above rather than below the < and >. Later in 1734, ≦ and ≧, known as "less than (greater-than) over equal to" or "less than (greater than) or equal to with double horizontal bars", first appeared in Pierre Bouguer's work . After that, mathematicians simplified Bouguer's symbol to "less than (greater than) or equal to with one horizontal bar" (≤), or "less than (greater than) or slanted equal to" (⩽).

The relation not greater than can also be represented by ${\displaystyle a\ngtr b,}$ the symbol for "greater than" bisected by a slash, "not". The same is true for not less than, ${\displaystyle a\nless b.}$

The notation a ≠ b means that a is not equal to b; this inequation sometimes is considered a form of strict inequality. It does not say that one is greater than the other; it does not even require a and b to be member of an ordered set.

In engineering sciences, less formal use of the notation is to state that one quantity is "much greater" than another, normally by several orders of magnitude.

• The notation a ≪ b means that a is much less than b.
• The notation a ≫ b means that a is much greater than b.

This implies that the lesser value can be neglected with little effect on the accuracy of an approximation (such as the case of ultrarelativistic limit in physics).

In all of the cases above, any two symbols mirroring each other are symmetrical; a < b and b > a are equivalent, etc.

Properties on the number line

Inequalities are governed by the following properties. All of these properties also hold if all of the non-strict inequalities (≤ and ≥) are replaced by their corresponding strict inequalities (< and >) and — in the case of applying a function — monotonic functions are limited to strictly monotonic functions.

Converse

The relations ≤ and ≥ are each other's converse, meaning that for any real numbers a and b:

a ≤ b and b ≥ a are equivalent.

Transitivity

The transitive property of inequality states that for any real numbers a, b, c:

If a ≤ b and b ≤ c, then a ≤ c.

If either of the premises is a strict inequality, then the conclusion is a strict inequality:

If a ≤ b and b < c, then a < c.

If a < b and b ≤ c, then a < c.

Addition and subtraction

If x < y, then x + a < y + a.

A common constant c may be added to or subtracted from both sides of an inequality. So, for any real numbers a, b, c:

If a ≤ b, then a + c ≤ b + c and a − c ≤ b − c.

In other words, the inequality relation is preserved under addition (or subtraction) and the real numbers are an ordered group under addition.

Multiplication and division

If x < y and a > 0, then ax < ay.

If x < y and a < 0, then ax > ay.

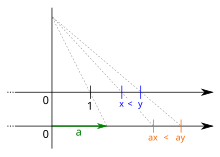
The properties that deal with multiplication and division state that for any real numbers, a, b and non-zero c:

If a ≤ b and c > 0, then ac ≤ bc and a/c ≤ b/c.

If a ≤ b and c < 0, then ac ≥ bc and a/c ≥ b/c.

In other words, the inequality relation is preserved under multiplication and division with positive constant, but is reversed when a negative constant is involved. More generally, this applies for an ordered field. For more information, see § Ordered fields.

Additive inverse

The property for the additive inverse states that for any real numbers a and b:

If a ≤ b, then −a ≥ −b.

Multiplicative inverse

If both numbers are positive, then the inequality relation between the multiplicative inverses is opposite of that between the original numbers. More specifically, for any non-zero real numbers a and b that are both positive (or both negative):

If a ≤ b, then ⁠1/a⁠ ≥ ⁠1/b⁠.

All of the cases for the signs of a and b can also be written in chained notation, as follows:

If 0 < a ≤ b, then ⁠1/a⁠ ≥ ⁠1/b⁠ > 0.

If a ≤ b < 0, then 0 > ⁠1/a⁠ ≥ ⁠1/b⁠.

If a < 0 < b, then ⁠1/a⁠ < 0 < ⁠1/b⁠.

Applying a function to both sides

The graph of y = ln x

Any monotonically increasing function, by its definition, may be applied to both sides of an inequality without breaking the inequality relation (provided that both expressions are in the domain of that function). However, applying a monotonically decreasing function to both sides of an inequality means the inequality relation would be reversed. The rules for the additive inverse, and the multiplicative inverse for positive numbers, are both examples of applying a monotonically decreasing function.

If the inequality is strict (a < b, a > b) and the function is strictly monotonic, then the inequality remains strict. If only one of these conditions is strict, then the resultant inequality is non-strict. In fact, the rules for additive and multiplicative inverses are both examples of applying a strictly monotonically decreasing function.

A few examples of this rule are:

• Raising both sides of an inequality to a power n > 0 (equiv., −n < 0), when a and b are positive real numbers:
  0 ≤ a ≤ b ⇔ 0 ≤ aⁿ ≤ bⁿ.
  0 ≤ a ≤ b ⇔ a⁻ⁿ ≥ b⁻ⁿ ≥ 0.
• Taking the natural logarithm on both sides of an inequality, when a and b are positive real numbers:
  0 < a ≤ b ⇔ ln(a) ≤ ln(b).
  0 < a < b ⇔ ln(a) < ln(b).
  (this is true because the natural logarithm is a strictly increasing function.)

Formal definitions and generalizations

A (non-strict) partial order is a binary relation ≤ over a set P which is reflexive, antisymmetric, and transitive. That is, for all a, b, and c in P, it must satisfy the three following clauses:

• a ≤ a (reflexivity)
• if a ≤ b and b ≤ a, then a = b (antisymmetry)
• if a ≤ b and b ≤ c, then a ≤ c (transitivity)

A set with a partial order is called a partially ordered set. Those are the very basic axioms that every kind of order has to satisfy.

A strict partial order is a relation < that satisfies:

• a <⃥͏ a (irreflexivity)
• if a < b, then b <⃥͏ a (asymmetry)
• if a < b and b < c, then a < c (transitivity)

Some types of partial orders are specified by adding further axioms, such as:

• Total order: For every a and b in P, a ≤ b or b ≤ a .
• Dense order: For all a and b in P for which a < b, there is a c in P such that a < c < b.
• Least-upper-bound property: Every non-empty subset of P with an upper bound has a least upper bound (supremum) in P.

Ordered fields

Main article: Ordered field

If (F, +, ×) is a field and ≤ is a total order on F, then (F, +, ×, ≤) is called an ordered field if and only if:

• a ≤ b implies a + c ≤ b + c;
• 0 ≤ a and 0 ≤ b implies 0 ≤ a × b.

Both ⁠${\displaystyle (\mathbb{Q},+,\times ,\le )}$⁠ and ⁠${\displaystyle (\mathbb{R},+,\times ,\le )}$⁠ are ordered fields, but ≤ cannot be defined in order to make ⁠${\displaystyle (\mathbb{C},+,\times ,\le )}$⁠ an ordered field, because −1 is the square of i and would therefore be positive.

Besides being an ordered field, R also has the Least-upper-bound property. In fact, R can be defined as the only ordered field with that quality.

Chained notation

The notation a < b < c stands for "a < b and b < c", from which, by the transitivity property above, it also follows that a < c. By the above laws, one can add or subtract the same number to all three terms, or multiply or divide all three terms by same nonzero number and reverse all inequalities if that number is negative. Hence, for example, a < b + e < c is equivalent to a − e < b < c − e.

This notation can be generalized to any number of terms: for instance, a₁ ≤ a₂ ≤ ... ≤ a_n means that a_i ≤ a_i+1 for i = 1, 2, ..., n − 1. By transitivity, this condition is equivalent to a_i ≤ a_j for any 1 ≤ i ≤ j ≤ n.

When solving inequalities using chained notation, it is possible and sometimes necessary to evaluate the terms independently. For instance, to solve the inequality 4x < 2x + 1 ≤ 3x + 2, it is not possible to isolate x in any one part of the inequality through addition or subtraction. Instead, the inequalities must be solved independently, yielding x < ⁠1/2⁠ and x ≥ −1 respectively, which can be combined into the final solution −1 ≤ x < ⁠1/2⁠.

Occasionally, chained notation is used with inequalities in different directions, in which case the meaning is the logical conjunction of the inequalities between adjacent terms. For example, the defining condition of a zigzag poset is written as a₁ < a₂ > a₃ < a₄ > a₅ < a₆ > ... . Mixed chained notation is used more often with compatible relations, like <, =, ≤. For instance, a < b = c ≤ d means that a < b, b = c, and c ≤ d. This notation exists in a few programming languages such as Python. In contrast, in programming languages that provide an ordering on the type of comparison results, such as C, even homogeneous chains may have a completely different meaning.

Sharp inequalities

An inequality is said to be sharp if it cannot be relaxed and still be valid in general. Formally, a universally quantified inequality φ is called sharp if, for every valid universally quantified inequality ψ, if ψ ⇒ φ holds, then ψ ⇔ φ also holds. For instance, the inequality ∀a ∈ R. a² ≥ 0 is sharp, whereas the inequality ∀a ∈ R. a² ≥ −1 is not sharp.

Inequalities between means

See also: Inequality of arithmetic and geometric means

There are many inequalities between means. For example, for any positive numbers a₁, a₂, ..., a_n we have

${\displaystyle H\le G\le A\le Q,}$

where they represent the following means of the sequence:

• Harmonic mean : ${\displaystyle H=\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdots +\frac{1}{a_n}}}$
• Geometric mean : ${\displaystyle G=\sqrt[n]{a_1\cdot a_2\cdots a_n}}$
• Arithmetic mean : ${\displaystyle A=\frac{a_1+a_2+\cdots +a_n}{n}}$
• Quadratic mean : ${\displaystyle Q=\sqrt{\frac{a_1^2+a_2^2+\cdots +a_n^2}{n}}}$

Cauchy–Schwarz inequality

See also: Cauchy–Schwarz inequality

The Cauchy–Schwarz inequality states that for all vectors u and v of an inner product space it is true that $${\displaystyle |⟨\mathbf{u},\mathbf{v}⟩{|}^2\le ⟨\mathbf{u},\mathbf{u}⟩\cdot ⟨\mathbf{v},\mathbf{v}⟩,}$$ where ${\displaystyle ⟨\cdot ,\cdot ⟩}$ is the inner product. Examples of inner products include the real and complex dot product; In Euclidean space Rⁿ with the standard inner product, the Cauchy–Schwarz inequality is $${\displaystyle (\sum _{i=1}^n{u}_i{v}_i{)}^2\le (\sum _{i=1}^n{u}_i^2)(\sum _{i=1}^n{v}_i^2).}$$

Power inequalities

A power inequality is an inequality containing terms of the form a^b, where a and b are real positive numbers or variable expressions. They often appear in mathematical olympiads exercises.

Examples:

• For any real x, $${\displaystyle e^x\ge 1+x.}$$
• If x > 0 and p > 0, then $${\displaystyle \frac{x^p-1}{p}\ge \ln (x)\ge \frac{1-\frac{1}{x^p}}{p}.}$$ In the limit of p → 0, the upper and lower bounds converge to ln(x).
• If x > 0, then $${\displaystyle x^x\ge {\left(\frac{1}{e}\right)}^{\frac{1}{e}}.}$$
• If x > 0, then $${\displaystyle x^{x^x}\ge x.}$$
• If x, y, z > 0, then $${\displaystyle {\left(x+y\right)}^z+{\left(x+z\right)}^y+{\left(y+z\right)}^x>2.}$$
• For any real distinct numbers a and b, $${\displaystyle \frac{e^b-e^a}{b-a}>e^{(a+b)/2}.}$$
• If x, y > 0 and 0 < p < 1, then $${\displaystyle x^p+y^p>{\left(x+y\right)}^p.}$$
• If x, y, z > 0, then $${\displaystyle x^x{y}^y{z}^z\ge {\left(xyz\right)}^{(x+y+z)/3}.}$$
• If a, b > 0, then $${\displaystyle a^a+b^b\ge a^b+b^a.}$$
• If a, b > 0, then $${\displaystyle a^{ea}+b^{eb}\ge a^{eb}+b^{ea}.}$$
• If a, b, c > 0, then $${\displaystyle a^{2a}+b^{2b}+c^{2c}\ge a^{2b}+b^{2c}+c^{2a}.}$$
• If a, b > 0, then $${\displaystyle a^b+b^a>1.}$$

Well-known inequalities

See also: List of inequalities

Mathematicians often use inequalities to bound quantities for which exact formulas cannot be computed easily. Some inequalities are used so often that they have names:

• Azuma's inequality
• Bernoulli's inequality
• Bell's inequality
• Boole's inequality
• Cauchy–Schwarz inequality
• Chebyshev's inequality
• Chernoff's inequality
• Cramér–Rao inequality
• Hoeffding's inequality
• Hölder's inequality
• Inequality of arithmetic and geometric means
• Jensen's inequality
• Kolmogorov's inequality
• Markov's inequality
• Minkowski inequality
• Nesbitt's inequality
• Pedoe's inequality
• Poincaré inequality
• Samuelson's inequality
• Sobolev inequality
• Triangle inequality

Complex numbers and inequalities

The set of complex numbers ${\displaystyle \mathbb{C}}$ with its operations of addition and multiplication is a field, but it is impossible to define any relation ≤ so that ${\displaystyle (\mathbb{C},+,\times ,\le )}$ becomes an ordered field. To make ${\displaystyle (\mathbb{C},+,\times ,\le )}$ an ordered field, it would have to satisfy the following two properties:

• if a ≤ b, then a + c ≤ b + c;
• if 0 ≤ a and 0 ≤ b, then 0 ≤ ab.

Because ≤ is a total order, for any number a, either 0 ≤ a or a ≤ 0 (in which case the first property above implies that 0 ≤ −a). In either case 0 ≤ a²; this means that i² > 0 and 1² > 0; so −1 > 0 and 1 > 0, which means (−1 + 1) > 0; contradiction.

However, an operation ≤ can be defined so as to satisfy only the first property (namely, "if a ≤ b, then a + c ≤ b + c"). Sometimes the lexicographical order definition is used:

• a ≤ b, if
  • Re(a) < Re(b), or
  • Re(a) = Re(b) and Im(a) ≤ Im(b)

It can easily be proven that for this definition a ≤ b implies a + c ≤ b + c.

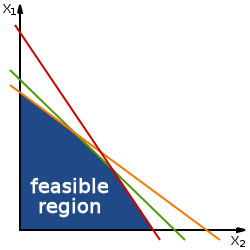
Systems of inequalities

Systems of linear inequalities can be simplified by Fourier–Motzkin elimination.

The cylindrical algebraic decomposition is an algorithm that allows testing whether a system of polynomial equations and inequalities has solutions, and, if solutions exist, describing them. The complexity of this algorithm is doubly exponential in the number of variables. It is an active research domain to design algorithms that are more efficient in specific cases.

Lie point symmetry

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Lie_point_symmetry 

 

Lie groups and Lie algebras

Lie point symmetry is a concept in advanced mathematics. Towards the end of the nineteenth century, Sophus Lie introduced the notion of Lie group in order to study the solutions of ordinary differential equations (ODEs). He showed the following main property: the order of an ordinary differential equation can be reduced by one if it is invariant under one-parameter Lie group of point transformations. This observation unified and extended the available integration techniques. Lie devoted the remainder of his mathematical career to developing these continuous groups that have now an impact on many areas of mathematically based sciences. The applications of Lie groups to differential systems were mainly established by Lie and Emmy Noether, and then advocated by Élie Cartan.

Roughly speaking, a Lie point symmetry of a system is a local group of transformations that maps every solution of the system to another solution of the same system. In other words, it maps the solution set of the system to itself. Elementary examples of Lie groups are translations, rotations and scalings.

The Lie symmetry theory is a well-known subject. In it are discussed continuous symmetries opposed to, for example, discrete symmetries. The literature for this theory can be found, among other places, in these notes.

Overview

Types of symmetries

Lie groups and hence their infinitesimal generators can be naturally "extended" to act on the space of independent variables, state variables (dependent variables) and derivatives of the state variables up to any finite order. There are many other kinds of symmetries. For example, contact transformations let coefficients of the transformations infinitesimal generator depend also on first derivatives of the coordinates. Lie-Bäcklund transformations let them involve derivatives up to an arbitrary order. The possibility of the existence of such symmetries was recognized by Noether. For Lie point symmetries, the coefficients of the infinitesimal generators depend only on coordinates, denoted by ${\displaystyle Z}$.

Applications

Lie symmetries were introduced by Lie in order to solve ordinary differential equations. Another application of symmetry methods is to reduce systems of differential equations, finding equivalent systems of differential equations of simpler form. This is called reduction. In the literature, one can find the classical reduction process, and the moving frame-based reduction process. Also symmetry groups can be used for classifying different symmetry classes of solutions.

Geometrical framework

Infinitesimal approach

Lie's fundamental theorems underline that Lie groups can be characterized by elements known as infinitesimal generators. These mathematical objects form a Lie algebra of infinitesimal generators. Deduced "infinitesimal symmetry conditions" (defining equations of the symmetry group) can be explicitly solved in order to find the closed form of symmetry groups, and thus the associated infinitesimal generators.

Let ${\displaystyle Z=(z_1,\dots ,z_n)}$ be the set of coordinates on which a system is defined where ${\displaystyle n}$ is the cardinality of ${\displaystyle Z}$. An infinitesimal generator ${\displaystyle \delta }$ in the field ${\displaystyle \mathbb{R}(Z)}$ is a linear operator ${\displaystyle \delta :\mathbb{R}(Z)\to \mathbb{R}(Z)}$ that has ${\displaystyle \mathbb{R}}$ in its kernel and that satisfies the Leibniz rule:

${\displaystyle \mathrm{\forall }(f_1,f_2)\in \mathbb{R}(Z{)}^2,\delta f_1{f}_2=f_1\delta f_2+f_2\delta f_1}$.

In the canonical basis of elementary derivations ${\displaystyle \left\{\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_1},\dots ,\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_n}\right\}}$, it is written as:

${\displaystyle \delta =\sum _{i=1}^n{\xi }_{z_i}(Z)\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_i}}$

where ${\displaystyle {\xi }_{z_i}}$ is in ${\displaystyle \mathbb{R}(Z)}$ for all ${\displaystyle i}$ in ${\displaystyle \left\{1,\dots ,n\right\}}$.

Lie groups and Lie algebras of infinitesimal generators

Lie algebras can be generated by a generating set of infinitesimal generators as defined above. To every Lie group, one can associate a Lie algebra. Roughly, a Lie algebra ${\displaystyle \mathfrak{g}}$ is an algebra constituted by a vector space equipped with Lie bracket as additional operation. The base field of a Lie algebra depends on the concept of invariant. Here only finite-dimensional Lie algebras are considered.

Continuous dynamical systems

A dynamical system (or flow) is a one-parameter group action. Let us denote by ${\displaystyle \mathcal{D}}$ such a dynamical system, more precisely, a (left-)action of a group ${\displaystyle (G,+)}$ on a manifold ${\displaystyle M}$:

${\displaystyle \begin{array}{rccc}\mathcal{D}:& G\times M& \to & M\\ & \nu \times Z& \to & \mathcal{D}(\nu ,Z)\end{array}}$

such that for all point ${\displaystyle Z}$ in ${\displaystyle M}$:

• ${\displaystyle \mathcal{D}(e,Z)=Z}$ where ${\displaystyle e}$ is the neutral element of ${\displaystyle G}$;
• for all ${\displaystyle (\nu ,\hat{\nu })}$ in ${\displaystyle G^2}$, ${\displaystyle \mathcal{D}(\nu ,\mathcal{D}(\hat{\nu },Z))=\mathcal{D}(\nu +\hat{\nu },Z)}$.

A continuous dynamical system is defined on a group ${\displaystyle G}$ that can be identified to ${\displaystyle \mathbb{R}}$ i.e. the group elements are continuous.

Invariants

An invariant, roughly speaking, is an element that does not change under a transformation.

Definition of Lie point symmetries

In this paragraph, we consider precisely expanded Lie point symmetries i.e. we work in an expanded space meaning that the distinction between independent variable, state variables and parameters are avoided as much as possible.

A symmetry group of a system is a continuous dynamical system defined on a local Lie group ${\displaystyle G}$ acting on a manifold ${\displaystyle M}$. For the sake of clarity, we restrict ourselves to n-dimensional real manifolds ${\displaystyle M={\mathbb{R}}^n}$ where ${\displaystyle n}$ is the number of system coordinates.

Lie point symmetries of algebraic systems

Let us define algebraic systems used in the forthcoming symmetry definition.

Algebraic systems

Let ${\displaystyle F=(f_1,\dots ,f_k)=(p_1/q_1,\dots ,p_k/q_k)}$ be a finite set of rational functions over the field ${\displaystyle \mathbb{R}}$ where ${\displaystyle p_i}$ and ${\displaystyle q_i}$ are polynomials in ${\displaystyle \mathbb{R}[Z]}$ i.e. in variables ${\displaystyle Z=(z_1,\dots ,z_n)}$ with coefficients in ${\displaystyle \mathbb{R}}$. An algebraic system associated to ${\displaystyle F}$ is defined by the following equalities and inequalities:

${\displaystyle \begin{array}{ccc}\{\begin{array}{l}{p}_1(Z)=0,\\ ⋮\\ p_k(Z)=0\end{array}& \text{and}& \{\begin{array}{l}{q}_1(Z)\ne 0,\\ ⋮\\ q_k(Z)\ne 0.\end{array}\end{array}}$

An algebraic system defined by ${\displaystyle F=(f_1,\dots ,f_k)}$ is regular (a.k.a. smooth) if the system ${\displaystyle F}$ is of maximal rank ${\displaystyle k}$, meaning that the Jacobian matrix ${\displaystyle (\mathrm{\partial }{f}_i/\mathrm{\partial }{z}_j)}$ is of rank ${\displaystyle k}$ at every solution ${\displaystyle Z}$ of the associated semi-algebraic variety.

Definition of Lie point symmetries

The following theorem gives necessary and sufficient conditions so that a local Lie group ${\displaystyle G}$ is a symmetry group of an algebraic system.

Theorem. Let ${\displaystyle G}$ be a connected local Lie group of a continuous dynamical system acting in the n-dimensional space ${\displaystyle {\mathbb{R}}^n}$. Let ${\displaystyle F:{\mathbb{R}}^n\to {\mathbb{R}}^k}$ with ${\displaystyle k\le n}$ define a regular system of algebraic equations:

${\displaystyle f_i(Z)=0\mathrm{\forall }i\in \{1,\dots ,k\}.}$

Then ${\displaystyle G}$ is a symmetry group of this algebraic system if, and only if,

${\displaystyle \delta f_i(Z)=0\mathrm{\forall }i\in \{1,\dots ,k\}\text{ whenever }{f}_1(Z)=\cdots =f_k(Z)=0}$

for every infinitesimal generator ${\displaystyle \delta }$ in the Lie algebra ${\displaystyle \mathfrak{g}}$ of ${\displaystyle G}$.

Example

Consider the algebraic system defined on a space of 6 variables, namely ${\displaystyle Z=(P,Q,a,b,c,l)}$ with:

${\displaystyle \{\begin{array}{l}{f}_1(Z)=(1-cP)+bQ+1,\\ f_2(Z)=aP-lQ+1.\end{array}}$

The infinitesimal generator

${\displaystyle \delta =a(a-1){\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }a}}+(l+b){\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }b}}+(2ac-c){\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }c}}+(-aP+P){\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }P}}}$

is associated to one of the one-parameter symmetry groups. It acts on 4 variables, namely ${\displaystyle a,b,c}$ and ${\displaystyle P}$. One can easily verify that ${\displaystyle \delta f_1=f_1-f_2}$ and ${\displaystyle \delta f_2=0}$. Thus the relations ${\displaystyle \delta f_1=\delta f_2=0}$ are satisfied for any ${\displaystyle Z}$ in ${\displaystyle {\mathbb{R}}^6}$ that vanishes the algebraic system.

Lie point symmetries of dynamical systems

Let us define systems of first-order ODEs used in the forthcoming symmetry definition.

Systems of ODEs and associated infinitesimal generators

Let ${\displaystyle d\cdot /dt}$ be a derivation w.r.t. the continuous independent variable ${\displaystyle t}$. We consider two sets ${\displaystyle X=(x_1,\dots ,x_k)}$ and ${\displaystyle \mathrm{\Theta }=({\theta }_1,\dots ,{\theta }_l)}$. The associated coordinate set is defined by ${\displaystyle Z=(z_1,\dots ,z_n)=(t,x_1,\dots ,x_k,{\theta }_1,\dots ,{\theta }_l)}$ and its cardinal is ${\displaystyle n=1+k+l}$. With these notations, a system of first-order ODEs is a system where:

${\displaystyle \{\begin{array}{l}{\displaystyle \frac{d{x}_i}{dt}}=f_i(Z)\text{ with }{f}_i\in \mathbb{R}(Z)\mathrm{\forall }i\in \{1,\dots ,k\},\\ {\displaystyle \frac{d{\theta }_j}{dt}}=0\mathrm{\forall }j\in \{1,\dots ,l\}\end{array}}$

and the set ${\displaystyle F=(f_1,\dots ,f_k)}$ specifies the evolution of state variables of ODEs w.r.t. the independent variable. The elements of the set ${\displaystyle X}$ are called state variables, these of ${\displaystyle \mathrm{\Theta }}$ parameters.

One can associate also a continuous dynamical system to a system of ODEs by resolving its equations.

An infinitesimal generator is a derivation that is closely related to systems of ODEs (more precisely to continuous dynamical systems). For the link between a system of ODEs, the associated vector field and the infinitesimal generator, see section 1.3 of. The infinitesimal generator ${\displaystyle \delta }$ associated to a system of ODEs, described as above, is defined with the same notations as follows:

${\displaystyle \delta ={\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}}+\sum _{i=1}^k{f}_i(Z){\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }{x}_i}}\cdot }$

Definition of Lie point symmetries

Here is a geometrical definition of such symmetries. Let ${\displaystyle \mathcal{D}}$ be a continuous dynamical system and ${\displaystyle {\delta }_{\mathcal{D}}}$ its infinitesimal generator. A continuous dynamical system ${\displaystyle \mathcal{S}}$ is a Lie point symmetry of ${\displaystyle \mathcal{D}}$ if, and only if, ${\displaystyle \mathcal{S}}$ sends every orbit of ${\displaystyle \mathcal{D}}$ to an orbit. Hence, the infinitesimal generator ${\displaystyle {\delta }_{\mathcal{S}}}$ satisfies the following relation based on Lie bracket:

${\displaystyle [{\delta }_{\mathcal{D}},{\delta }_{\mathcal{S}}]=\lambda {\delta }_{\mathcal{D}}}$

where ${\displaystyle \lambda }$ is any constant of ${\displaystyle {\delta }_{\mathcal{D}}}$ and ${\displaystyle {\delta }_{\mathcal{S}}}$ i.e. ${\displaystyle {\delta }_{\mathcal{D}}\lambda ={\delta }_{\mathcal{S}}\lambda =0}$. These generators are linearly independent.

One does not need the explicit formulas of ${\displaystyle \mathcal{D}}$ in order to compute the infinitesimal generators of its symmetries.

Example

Consider Pierre François Verhulst's logistic growth model with linear predation, where the state variable ${\displaystyle x}$ represents a population. The parameter ${\displaystyle a}$ is the difference between the growth and predation rate and the parameter ${\displaystyle b}$ corresponds to the receptive capacity of the environment:

${\displaystyle {\displaystyle \frac{dx}{dt}}=(a-bx)x,{\displaystyle \frac{da}{dt}}={\displaystyle \frac{db}{dt}}=0.}$

The continuous dynamical system associated to this system of ODEs is:

${\displaystyle \begin{array}{rccc}\mathcal{D}:& (\mathbb{R},+)\times {\mathbb{R}}^4& \to & {\mathbb{R}}^4\\ & (\hat{t},(t,x,a,b))& \to & \left(t+\hat{t},\frac{ax{e}^{a\hat{t}}}{a-(1-e^{a\hat{t}})bx},a,b\right).\end{array}}$

The independent variable ${\displaystyle \hat{t}}$ varies continuously; thus the associated group can be identified with ${\displaystyle \mathbb{R}}$.

The infinitesimal generator associated to this system of ODEs is:

${\displaystyle {\delta }_{\mathcal{D}}={\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}}+((a-bx)x){\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }x}}\cdot }$

The following infinitesimal generators belong to the 2-dimensional symmetry group of ${\displaystyle \mathcal{D}}$:

${\displaystyle {\delta }_{{\mathcal{S}}_1}=-x{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }x}}+b{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }b}},{\delta }_{{\mathcal{S}}_2}=t{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}}-x{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }x}}-a{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }a}}\cdot }$

Software

There exist many software packages in this area. For example, the package liesymm of Maple provides some Lie symmetry methods for PDEs. It manipulates integration of determining systems and also differential forms. Despite its success on small systems, its integration capabilities for solving determining systems automatically are limited by complexity issues. The DETools package uses the prolongation of vector fields for searching Lie symmetries of ODEs. Finding Lie symmetries for ODEs, in the general case, may be as complicated as solving the original system.