Chaos theory

From Wikipedia, the free encyclopedia

A plot of the Lorenz attractor for values r = 28, σ = 10, b = 8/3

A double rod pendulum animation showing chaotic behavior. Starting the pendulum from a slightly different initial condition would result in a completely different trajectory. The double rod pendulum is one of the simplest dynamical systems that has chaotic solutions.

Chaos theory is a field of study in mathematics, with applications in several disciplines including meteorology, sociology, physics, engineering, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions—a response popularly referred to as the butterfly effect. Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general.^[1] This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved.^[2] In other words, the deterministic nature of these systems does not make them predictable.^[3][4] This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as follows:^[5]

Chaos: When the present determines the future, but the approximate present does not approximately determine the future.

Chaotic behavior can be observed in many natural systems, such as weather and climate.^[6][7] This behavior can be studied through analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps.

Introduction

Chaos theory concerns deterministic systems whose behavior can in principle be predicted. Chaotic systems are predictable for a while and then appear to become random. The amount of time for which the behavior of a chaotic system can be effectively predicted depends on three things: How much uncertainty we are willing to tolerate in the forecast; how accurately we are able to measure its current state; and a time scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, ~1 millisecond; weather systems, a couple of days (unproven); the solar system, 50 million years. In chaotic systems the uncertainty in a forecast increases exponentially with elapsed time. Hence doubling the forecast time more than squares the proportional uncertainty in the forecast. This means that in practice a meaningful prediction cannot be made over an interval of more than two or three times the Lyapunov time. When meaningful predictions cannot be made, the system appears to be random.^[8]

Chaotic dynamics

The map defined by x → 4 x (1 – x) and y → x + y mod 1 displays sensitivity to initial conditions. Here two series of x and y values diverge markedly over time from a tiny initial difference. Note, however, that the y coordinate is effectively only defined modulo one, so the square region is actually depicting a cylinder, and the two points are closer than they look

In common usage, "chaos" means "a state of disorder".^[9] However, in chaos theory, the term is defined more precisely. Although there is no universally accepted mathematical definition of chaos, a commonly used definition says that, for a dynamical system to be classified as chaotic, it must have the following properties:^[10]

1. it must be sensitive to initial conditions;
2. it must be topologically mixing; and
3. it must have dense periodic orbits.

Sensitivity to initial conditions

Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points with significantly different future paths, or trajectories. Thus, an arbitrarily small change, or perturbation, of the current trajectory may lead to significantly different future behavior.
It has been shown that in some cases the last two properties in the above actually imply sensitivity to initial conditions,^[11][12] and if attention is restricted to intervals, the second property implies the other two^[13] (an alternative, and in general weaker, definition of chaos uses only the first two properties in the above list).^[14] It is interesting that the most practically significant property, that of sensitivity to initial conditions, is redundant in the definition, being implied by two (or for intervals, one) purely topological properties, which are therefore of greater interest to mathematicians.

Sensitivity to initial conditions is popularly known as the "butterfly effect", so called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C., entitled Predictability: Does the Flap of a Butterfly’s Wings in Brazil set off a Tornado in Texas?.^[15] The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different.

A consequence of sensitivity to initial conditions is that if we start with only a finite amount of information about the system (as is usually the case in practice), then beyond a certain time the system will no longer be predictable. This is most familiar in the case of weather, which is generally predictable only about a week ahead.^[16] Of course this does not mean that we cannot say anything about events far in the future; there are some restrictions on the system. With weather, we know that the temperature will never reach 100 degrees Celsius or fall to -130 degrees Celsius on earth, but we are not able to say exactly what day we will have the hottest temperature of the year.

In more mathematical terms, the Lyapunov exponent measures the sensitivity to initial conditions. Given two starting trajectories in the phase space that are infinitesimally close, with initial separation $\delta {\mathbf {Z}}_{0}$ end up diverging at a rate given by

$|\delta {\mathbf {Z}}(t)|\approx e^{{\lambda t}}|\delta {\mathbf {Z}}_{0}|\ $

where t is the time and λ is the Lyapunov exponent. The rate of separation depends on the orientation of the initial separation vector, so there is a whole spectrum of Lyapunov exponents. The number of Lyapunov exponents is equal to the number of dimensions of the phase space, though it is common to just refer to the largest one. For example, the maximal Lyapunov exponent (MLE) is most often used because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.

There are also other properties that relate to sensitivity of initial conditions, such as measure-theoretical mixing (as discussed in ergodic theory) and properties of a K-system.^[4]

Topological mixing

The map defined by x → 4 x (1 – x) and y → x + y mod 1 also displays topological mixing. Here the blue region is transformed by the dynamics first to the purple region, then to the pink and red regions, and eventually to a cloud of points scattered across the space.

Topological mixing (or topological transitivity) means that the system will evolve over time so that any given region or open set of its phase space will eventually overlap with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.

Topological mixing is often omitted from popular accounts of chaos, which equate chaos with only sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points will eventually become widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behavior: all points except 0 will tend to positive or negative infinity.

Density of periodic orbits

For a chaotic system to have a dense periodic orbit means that every point in the space is approached arbitrarily closely by periodic orbits.^[17] The one-dimensional logistic map defined by x → 4 x (1 – x) is one of the simplest systems with density of periodic orbits. For example, ${\tfrac {5-{\sqrt {5}}}{8}}$ → ${\tfrac {5+{\sqrt {5}}}{8}}$ → ${\tfrac {5-{\sqrt {5}}}{8}}$ (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).^[18]

Sharkovskii's theorem is the basis of the Li and Yorke^[19] (1975) proof that any one-dimensional system that exhibits a regular cycle of period three will also display regular cycles of every other length as well as completely chaotic orbits.

Strange attractors

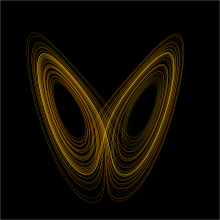
The Lorenz attractor displays chaotic behavior. These two plots demonstrate sensitive dependence on initial conditions within the region of phase space occupied by the attractor.

Some dynamical systems, like the one-dimensional logistic map defined by x → 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor, since then a large set of initial conditions will lead to orbits that converge to this chaotic region.

An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it was not only one of the first, but it is also one of the most complex and as such gives rise to a very interesting pattern, that with a little imagination, looks like the wings of a butterfly.

Unlike fixed-point attractors and limit cycles, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set which forms at the boundary between basins of attraction of fixed points – Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and the fractal dimension can be calculated for them.

Minimum complexity of a chaotic system

Bifurcation diagram of the logistic map x → r x (1 – x). Each vertical slice shows the attractor for a specific value of r. The diagram displays period-doubling as r increases, eventually producing chaos.

Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. In contrast, for continuous dynamical systems, the Poincaré–Bendixson theorem shows that a strange attractor can only arise in three or more dimensions. Finite-dimensional linear systems are never chaotic; for a dynamical system to display chaotic behavior, it has to be either nonlinear or infinite-dimensional.

The Poincaré–Bendixson theorem states that a two-dimensional differential equation has very regular behavior. The Lorenz attractor discussed above is generated by a system of three differential equations such as:

${\begin{aligned}{\frac {{\mathrm {d}}x}{{\mathrm {d}}t}}&=\sigma y-\sigma x,\\{\frac {{\mathrm {d}}y}{{\mathrm {d}}t}}&=\rho x-xz-y,\\{\frac {{\mathrm {d}}z}{{\mathrm {d}}t}}&=xy-\beta z.\end{aligned}}$

where $x$, $y$, and $z$ make up the system state, $t$ is time, and $\sigma$, $\rho$, $\beta$ are the system parameters. Five of the terms on the right hand side are linear, while two are quadratic; a total of seven terms. Another well-known chaotic attractor is generated by the Rossler equations which have only one nonlinear term out of seven. Sprott ^[20] found a three-dimensional system with just five terms, that had only one nonlinear term, which exhibits chaos for certain parameter values. Zhang and Heidel ^[21][22] showed that, at least for dissipative and conservative quadratic systems, three-dimensional quadratic systems with only three or four terms on the right-hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic to a two-dimensional surface and therefore solutions are well behaved.

While the Poincaré–Bendixson theorem shows that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can exhibit chaotic behavior.^[23] Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite dimensional.^[24] A theory of linear chaos is being developed in a branch of mathematical analysis known as functional analysis.

Jerk systems

In physics, jerk is the third derivative of position, and as such, in mathematics differential equations of the form

$J\left({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\right)=0$

are sometimes called Jerk equations. It has been shown, that a jerk equation, which is equivalent to a system of three first order, ordinary, non-linear differential equation is in a certain sense the minimal setting for solutions showing chaotic behaviour. This motivates mathematical interest in jerk systems.

Systems involving a fourth or higher derivative are called accordingly hyperjerk systems.^[25]
A jerk system is a system whose behavior is described by a jerk equation, and for certain jerk equations simple electronic circuits may be designed which model the solutions to this equation. These circuits are known as jerk circuits.

One of the most interesting properties of jerk circuits is the possibility of chaotic behavior. In fact, certain well-known chaotic systems, such as the Lorenz attractor and the Rössler map, are conventionally described as a system of three first-order differential equations, but which may be combined into a single (although rather complicated) jerk equation. It has been shown, that non-linear jerk systems are in a sense minimally complex systems to show chaotic behaviour, there is no chaotic system involving only two first order, ordinary differential equations (the system resulting in an equation of second order only).
An example of a jerk equation with non-linearity in the magnitude of $x$, is:

${\frac {{\mathrm {d}}^{3}x}{{\mathrm {d}}t^{3}}}+A{\frac {{\mathrm {d}}^{2}x}{{\mathrm {d}}t^{2}}}+{\frac {{\mathrm {d}}x}{{\mathrm {d}}t}}-|x|+1=0.$

Here A is an adjustable parameter. This equation has a chaotic solution for A=3/5 and can be implemented with the following jerk circuit; the required non-linearity is brought about by the two diodes:

In the above circuit, all resistors are of equal value, except $R_{A}=R/A=5R/3$, and all capacitors are of equal size. The dominant frequency will be $1/2\pi RC$. The output of op amp 0 will correspond to the x variable, the output of 1 will correspond to the first derivative of x and the output of 2 will correspond to the second derivative.

Spontaneous order

Under the right conditions chaos will spontaneously evolve into a lockstep pattern. In the Kuramoto model, four conditions suffice to produce synchronization in a chaotic system. Examples include the coupled oscillation of Christiaan Huygens' pendulums, fireflies, neurons, the London Millenium Bridge resonance, and large arrays of Josephson junctions.^[26]

History[edit]

Barnsley fern created using the chaos game. Natural forms (ferns, clouds, mountains, etc.) may be recreated through an Iterated function system (IFS).

An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits that are nonperiodic, and yet not forever increasing nor approaching a fixed point.^[27][28] In 1898 Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature, called "Hadamard's billiards".^[29] Hadamard was able to show that all trajectories are unstable, in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.

Chaos Theory got its start in the field of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by George David Birkhoff,^[30] Andrey Nikolaevich Kolmogorov,^[31][32][33] Mary Lucy Cartwright and John Edensor Littlewood,^[34] and Stephen Smale.^[35] Except for Smale, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood.^{[citation needed]} Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.

Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident to some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behavior of certain experiments like that of the logistic map. What had been attributed to measure imprecision and simple "noise" was considered by chaos theorists as a full component of the studied systems.

The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems. As a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers and noticed, on Nov. 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.^[36][37]

Turbulence in the tip vortex from an airplane wing. Studies of the critical point beyond which a system creates turbulence were important for chaos theory, analyzed for example by the Soviet physicist Lev Landau, who developed the Landau-Hopf theory of turbulence. David Ruelle and Floris Takens later predicted, against Landau, that fluid turbulence could develop through a strange attractor, a main concept of chaos theory.

An early pioneer of the theory was Edward Lorenz whose interest in chaos came about accidentally through his work on weather prediction in 1961.^[6] Lorenz was using a simple digital computer, a Royal McBee LGP-30, to run his weather simulation. He wanted to see a sequence of data again and to save time he started the simulation in the middle of its course. He was able to do this by entering a printout of the data corresponding to conditions in the middle of his simulation which he had calculated last time. To his surprise the weather that the machine began to predict was completely different from the weather calculated before. Lorenz tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 was printed as 0.506. This difference is tiny and the consensus at the time would have been that it should have had practically no effect. However, Lorenz had discovered that small changes in initial conditions produced large changes in the long-term outcome.^[38] Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modelling cannot, in general, make precise long-term weather predictions.

In 1963, Benoit Mandelbrot found recurring patterns at every scale in data on cotton prices.^[39] Beforehand he had studied information theory and concluded noise was patterned like a Cantor set: on any scale the proportion of noise-containing periods to error-free periods was a constant – thus errors were inevitable and must be planned for by incorporating redundancy.^[40] Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards).^[41][42] This challenged the idea that changes in price were normally distributed. In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device.^[43] Arguing that a ball of twine appears to be a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (examples include the Menger sponge, the Sierpiński gasket, and the Koch curve or "snowflake", which is infinitely long yet encloses a finite space and has a fractal dimension of circa 1.2619). In 1982 Mandelbrot published The Fractal Geometry of Nature, which became a classic of chaos theory. Biological systems such as the branching of the circulatory and bronchial systems proved to fit a fractal model.^[44]

In December 1977, the New York Academy of Sciences organized the first symposium on Chaos, attended by David Ruelle, Robert May, James A. Yorke (coiner of the term "chaos" as used in mathematics), Robert Shaw, and the meteorologist Edward Lorenz. The following year, independently Pierre Coullet and Charles Tresser with the article "Iterations d'endomorphismes et groupe de renormalisation" and Mitchell Feigenbaum with the article "Quantitative Universality for a Class of Nonlinear Transformations" described logistic maps.^[45][46] They notably discovered the universality in chaos, permitting the application of chaos theory to many different phenomena.

In 1979, Albert J. Libchaber, during a symposium organized in Aspen by Pierre Hohenberg, presented his experimental observation of the bifurcation cascade that leads to chaos and turbulence in Rayleigh–Bénard convection systems. He was awarded the Wolf Prize in Physics in 1986 along with Mitchell J. Feigenbaum for their inspiring achievements.^[47]

In 1986, the New York Academy of Sciences co-organized with the National Institute of Mental Health and the Office of Naval Research the first important conference on chaos in biology and medicine. There, Bernardo Huberman presented a mathematical model of the eye tracking disorder among schizophrenics.^[48] This led to a renewal of physiology in the 1980s through the application of chaos theory, for example, in the study of pathological cardiac cycles.

In 1987, Per Bak, Chao Tang and Kurt Wiesenfeld published a paper in Physical Review Letters^[49] describing for the first time self-organized criticality (SOC), considered to be one of the mechanisms by which complexity arises in nature.

Alongside largely lab-based approaches such as the Bak–Tang–Wiesenfeld sandpile, many other investigations have focused on large-scale natural or social systems that are known (or suspected) to display scale-invariant behavior. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including earthquakes (which, long before SOC was discovered, were known as a source of scale-invariant behavior such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes, and the Omori law^[50] describing the frequency of aftershocks), solar flares, fluctuations in economic systems such as financial markets (references to SOC are common in econophysics), landscape formation, forest fires, landslides, epidemics, and biological evolution (where SOC has been invoked, for example, as the dynamical mechanism behind the theory of "punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). Given the implications of a scale-free distribution of event sizes, some researchers have suggested that another phenomenon that should be considered an example of SOC is the occurrence of wars. These investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.

In the same year, James Gleick published Chaos: Making a New Science, which became a best-seller and introduced the general principles of chaos theory as well as its history to the broad public, though his history under-emphasized important Soviet contributions.^[51] Initially the domain of a few, isolated individuals, chaos theory progressively emerged as a transdisciplinary and institutional discipline, mainly under the name of nonlinear systems analysis. Alluding to Thomas Kuhn's concept of a paradigm shift exposed in The Structure of Scientific Revolutions (1962), many "chaologists" (as some described themselves) claimed that this new theory was an example of such a shift, a thesis upheld by Gleick.

The availability of cheaper, more powerful computers broadens the applicability of chaos theory. Currently, chaos theory continues to be a very active area of research,^[52] involving many different disciplines (mathematics, topology, physics, social systems, population modeling, biology, meteorology, astrophysics, information theory, computational neuroscience, etc.).

Distinguishing random from chaotic data

It can be difficult to tell from data whether a physical or other observed process is random or chaotic, because in practice no time series consists of a pure "signal". There will always be some form of corrupting noise, even if it is present as round-off or truncation error. Thus any real time series, even if mostly deterministic, will contain some randomness.^[53][54]

All methods for distinguishing deterministic and stochastic processes rely on the fact that a deterministic system always evolves in the same way from a given starting point.^[53][55] Thus, given a time series to test for determinism, one can

1. pick a test state;
2. search the time series for a similar or nearby state; and
3. compare their respective time evolutions.

Define the error as the difference between the time evolution of the test state and the time evolution of the nearby state. A deterministic system will have an error that either remains small (stable, regular solution) or increases exponentially with time (chaos). A stochastic system will have a randomly distributed error.^[56]

Essentially, all measures of determinism taken from time series rely upon finding the closest states to a given test state (e.g., correlation dimension, Lyapunov exponents, etc.). To define the state of a system, one typically relies on phase space embedding methods.^[57] Typically one chooses an embedding dimension and investigates the propagation of the error between two nearby states. If the error looks random, one increases the dimension. If the dimension can be increased to obtain a deterministically looking error, then analysis is done. Though it may sound simple, one complication is that as the dimension increases, the search for a nearby state requires a lot more computation time and a lot of data (the amount of data required increases exponentially with embedding dimension) to find a suitably close candidate. If the embedding dimension (number of measures per state) is chosen too small (less than the "true" value), deterministic data can appear to be random, but in theory there is no problem choosing the dimension too large – the method will work.

When a nonlinear deterministic system is attended by external fluctuations, its trajectories present serious and permanent distortions. Furthermore, the noise is amplified due to the inherent nonlinearity and reveals totally new dynamical properties. Statistical tests attempting to separate noise from the deterministic skeleton or inversely isolate the deterministic part risk failure. Things become worse when the deterministic component is a nonlinear feedback system.^[58] In presence of interactions between nonlinear deterministic components and noise, the resulting nonlinear series can display dynamics that traditional tests for nonlinearity are sometimes not able to capture.^[59]

The question of how to distinguish deterministic chaotic systems from stochastic systems has also been discussed in philosophy. It has been shown that they might be observationally equivalent.^[60]

Applications

A conus textile shell, similar in appearance to Rule 30, a cellular automaton with chaotic behaviour.^[61]

Chaos theory was born from observing weather patterns, but it has become applicable to a variety of other situations. Some areas benefiting from chaos theory today are geology, mathematics, microbiology, biology, computer science, economics,^[62][63][64] engineering,^[65] finance,^[66][67] algorithmic trading,^[68][69][70] meteorology, philosophy, physics, politics, population dynamics,^[71] psychology, and robotics. A few categories are listed below with examples, but this is by no means a comprehensive list as new applications are appearing every day.

Computer science

Chaos theory is not new to computer science and has been used for many years in cryptography. One type of encryption, secret key or symmetric key, relies on diffusion and confusion, which is modeled well by chaos theory.^[72] Another type of computing, DNA computing, when paired with chaos theory, offers a more efficient way to encrypt images and other information.^[73] Robotics is another area that has recently benefited from chaos theory. Instead of robots acting in a trial-and-error type of refinement to interact with their environment, chaos theory has been used to build a predictive model.^[74]

Biology

For over a hundred years, biologists have been keeping track of populations of different species with population models. Most models are deterministic systems, but recently scientists have been able to implement chaotic models in certain populations.^[75] For example, a study on models of Canadian lynx showed there was chaotic behavior in the population growth.^[76] Chaos can also be found in ecological systems, such as hydrology. While a chaotic model for hydrology has its shortcomings, there is still much to be learned from looking at the data through the lens of chaos theory.^[77] Another biological application is found in cardiotocography. Fetal surveillance is a delicate balance of obtaining accurate information while being as noninvasive as possible. Better models of warning signs of fetal hypoxia can be obtained through chaotic modeling.^[78]

Other areas

In chemistry, predicting gas solubility is essential to manufacturing polymers, but models using particle swarm optimization (PSO) tend to converge to the wrong points. An improved version of PSO has been created by introducing chaos, which keeps the simulations from getting stuck.^[79] In celestial mechanics, especially when observing asteroids, applying chaos theory leads to better predictions about when these objects will come in range of Earth and other planets.^[80] In quantum physics and electrical engineering, the study of large arrays of Josephson junctions benefitted greatly from chaos theory.^[81] Closer to home, coal mines have always been dangerous places where frequent natural gas leaks cause many deaths. Until recently, there was no reliable way to predict when they would occur. But these gas leaks have chaotic tendencies that, when properly modeled, can be predicted fairly accurately.^[82]

Chaos theory can be applied outside of the natural sciences. By adapting a model of career counseling to include a chaotic interpretation of the relationship between employees and the job market, better suggestions can be made to people struggling with career decisions.^[83] Modern organizations are increasingly seen as open complex adaptive systems, with fundamental natural nonlinear structures, subject to internal and external forces which may be sources of chaos. The chaos metaphor—used in verbal theories—grounded on mathematical models and psychological aspects of human behavior provides helpful insights to describing the complexity of small work groups, that go beyond the metaphor itself.^[84]

It is possible that economic models can also be improved through an application of chaos theory, but predicting the health of an economic system and what factors influence it most is an extremely complex task.^[85] Economic and financial systems are fundamentally different from those in the physical and natural sciences since the former are inherently stochastic in nature, as they result from the interactions of people, and thus pure deterministic models are unlikely to provide accurate representations of the data. The empirical literature that tests for chaos in economics and finance presents very mixed results, in part due to confusion between specific tests for chaos and more general tests for non-linear relationships.^[86]

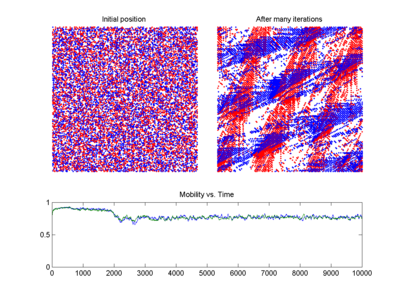
Traffic forecasting is another area that greatly benefits from applications of chaos theory. Better predictions of when traffic will occur would allow measures to be taken for it to be dispersed before the traffic starts, rather than after. Combining chaos theory principles with a few other methods has led to a more accurate short-term prediction model (see the plot of the BML traffic model at right).^[87]

Chaos theory also finds applications in psychology. For example, in modeling group behavior in which heterogeneous members may behave as if sharing to different degrees what in Wilfred Bion's theory is a basic assumption, the group dynamics is the result of the individual dynamics of the members: each individual reproduces the group dynamics in a different scale, and the chaotic behavior of the group is reflected in each member.^[88]

Emergence

From Wikipedia, the free encyclopedia

Snowflakes forming complex symmetrical and fractal patterns is an example of emergence in a physical system.

A termite "cathedral" mound produced by a termite colony is a classic example of emergence in nature.

In philosophy, systems theory, science, and art, emergence is conceived as a process whereby larger entities, patterns, and regularities arise through interactions among smaller or simpler entities that themselves do not exhibit such properties. In philosophy, almost all accounts of emergence include a form of irreducibility (either epistemic or ontological) to the lower levels.^[1] Also, emergence is central in theories of integrative levels and of complex systems. For instance, the phenomenon life as studied in biology is commonly perceived as an emergent property of interacting molecules as studied in chemistry, whose phenomena reflect interactions among elementary particles, modeled in particle physics, that at such higher mass—via substantial conglomeration—exhibit motion as modeled in gravitational physics. Neurobiological phenomena are often presumed to suffice as the underlying basis of psychological phenomena, whereby economic phenomena are in turn presumed to principally emerge.

Definitions

The idea of emergence has been around since at least the time of Aristotle.^[2]  John Stuart Mill^[3] and Julian Huxley^[4] are two of many scientists and philosophers who have written on the concept.
The term "emergent" was coined by philosopher G. H. Lewes, who wrote:

"Every resultant is either a sum or a difference of the co-operant forces; their sum, when their directions are the same -- their difference, when their directions are contrary. Further, every resultant is clearly traceable in its components, because these are homogeneous and commensurable. It is otherwise with emergents, when, instead of adding measurable motion to measurable motion, or things of one kind to other individuals of their kind, there is a co-operation of things of unlike kinds. The emergent is unlike its components insofar as these are incommensurable, and it cannot be reduced to their sum or their difference."^[5][6]

Economist Jeffrey Goldstein provided a current definition of emergence in the journal Emergence.^[7] Goldstein initially defined emergence as: "the arising of novel and coherent structures, patterns and properties during the process of self-organization in complex systems".

Goldstein's definition can be further elaborated to describe the qualities of this definition in more detail:

"The common characteristics are: (1) radical novelty (features not previously observed in systems); (2) coherence or correlation (meaning integrated wholes that maintain themselves over some period of time); (3) A global or macro "level" (i.e. there is some property of "wholeness"); (4) it is the product of a dynamical process (it evolves); and (5) it is "ostensive" (it can be perceived). For good measure, Goldstein throws in supervenience."^[8]

Systems scientist Peter Corning also points out that living systems cannot be reduced to underlying laws of physics:

Rules, or laws, have no causal efficacy; they do not in fact “generate” anything. They serve merely to describe regularities and consistent relationships in nature. These patterns may be very illuminating and important, but the underlying causal agencies must be separately specified (though often they are not). But that aside, the game of chess illustrates ... why any laws or rules of emergence and evolution are insufficient. Even in a chess game, you cannot use the rules to predict “history” — i.e., the course of any given game. Indeed, you cannot even reliably predict the next move in a chess game. Why? Because the “system” involves more than the rules of the game. It also includes the players and their unfolding, moment-by-moment decisions among a very large number of available options at each choice point. The game of chess is inescapably historical, even though it is also constrained and shaped by a set of rules, not to mention the laws of physics. Moreover, and this is a key point, the game of chess is also shaped by teleonomic, cybernetic, feedback-driven influences. It is not simply a self-ordered process; it involves an organized, “purposeful” activity.^[8]

Strong and weak emergence

Usage of the notion "emergence" may generally be subdivided into two perspectives, that of "weak emergence" and "strong emergence". In terms of physical systems, weak emergence is a type of emergence in which the emergent property is amenable to computer simulation. This is opposed to the older notion of strong emergence, in which the emergent property cannot be simulated by a computer.

Some common points between the two notions are that emergence concerns new properties produced as the system grows, which is to say ones which are not shared with its components or prior states. Also, it is assumed that the properties are supervenient rather than metaphysically primitive (Bedau 1997).

Weak emergence describes new properties arising in systems as a result of the interactions at an elemental level. However, it is stipulated that the properties can be determined by observing or simulating the system, and not by any process of a priori analysis.

Bedau notes that weak emergence is not a universal metaphysical solvent, as weak emergence leads to the conclusion that matter itself contains elements of awareness to it. However, Bedau concludes that adopting this view would provide a precise notion that emergence is involved in consciousness, and second, the notion of weak emergence is metaphysically benign (Bedau 1997).

Strong emergence describes the direct causal action of a high-level system upon its components; qualities produced this way are irreducible to the system's constituent parts (Laughlin 2005). The whole is greater than the sum of its parts. It follows that no simulation of the system can exist, for such a simulation would itself constitute a reduction of the system to its constituent parts (Bedau 1997).

However, "the debate about whether or not the whole can be predicted from the properties of the parts misses the point. Wholes produce unique combined effects, but many of these effects may be co-determined by the context and the interactions between the whole and its environment(s)" (Corning 2002). In accordance with his Synergism Hypothesis (Corning 1983 2005), Corning also stated, "It is the synergistic effects produced by wholes that are the very cause of the evolution of complexity in nature." Novelist Arthur Koestler used the metaphor of Janus (a symbol of the unity underlying complements like open/shut, peace/war) to illustrate how the two perspectives (strong vs. weak or holistic vs. reductionistic) should be treated as non-exclusive, and should work together to address the issues of emergence (Koestler 1969). Further,

The ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe. The constructionist hypothesis breaks down when confronted with the twin difficulties of scale and complexity. At each level of complexity entirely new properties appear. Psychology is not applied biology, nor is biology applied chemistry. We can now see that the whole becomes not merely more, but very different from the sum of its parts. (Anderson 1972)

The plausibility of strong emergence is questioned by some as contravening our usual understanding of physics. Mark A. Bedau observes:

Although strong emergence is logically possible, it is uncomfortably like magic. How does an irreducible but supervenient downward causal power arise, since by definition it cannot be due to the aggregation of the micro-level potentialities? Such causal powers would be quite unlike anything within our scientific ken. This not only indicates how they will discomfort reasonable forms of materialism. Their mysteriousness will only heighten the traditional worry that emergence entails illegitimately getting something from nothing.^[9]

Meanwhile, others have worked towards developing analytical evidence of strong emergence. In 2009, Gu et al. presented a class of physical systems that exhibits non-computable macroscopic properties.^[10][11] More precisely, if one could compute certain macroscopic properties of these systems from the microscopic description of these systems, they one would be able to solve computational problems known to be undecidable in computer science. They concluded that

Although macroscopic concepts are essential for understanding our world, much of fundamental physics has been devoted to the search for a `theory of everything', a set of equations that perfectly describe the behavior of all fundamental particles. The view that this is the goal of science rests in part on the rationale that such a theory would allow us to derive the behavior of all macroscopic concepts, at least in principle. The evidence we have presented suggests that this view may be overly optimistic. A `theory of everything' is one of many components necessary for complete understanding of the universe, but is not necessarily the only one. The development of macroscopic laws from first principles may involve more than just systematic logic, and could require conjectures suggested by experiments, simulations or insight.^[10]

Objective or subjective quality

The properties of complexity and organization of any system are considered by Crutchfield to be subjective qualities determined by the observer.

"Defining structure and detecting the emergence of complexity in nature are inherently subjective, though essential, scientific activities. Despite the difficulties, these problems can be analysed in terms of how model-building observers infer from measurements the computational capabilities embedded in non-linear processes. An observer’s notion of what is ordered, what is random, and what is complex in its environment depends directly on its computational resources: the amount of raw measurement data, of memory, and of time available for estimation and inference. The discovery of structure in an environment depends more critically and subtly, though, on how those resources are organized. The descriptive power of the observer’s chosen (or implicit) computational model class, for example, can be an overwhelming determinant in finding regularity in data."(Crutchfield 1994)

On the other hand, Peter Corning argues "Must the synergies be perceived/observed in order to qualify as emergent effects, as some theorists claim? Most emphatically not. The synergies associated with emergence are real and measurable, even if nobody is there to observe them." (Corning 2002)

In philosophy, religion, art and human sciences

In philosophy, emergence is often understood to be a much weaker claim about the etiology of a system's properties. An emergent property of a system, in this context, is one that is not a property of any component of that system, but is still a feature of the system as a whole. Nicolai Hartmann, one of the first modern philosophers to write on emergence, termed this categorial novum (new category).

In religion, emergence grounds expressions of religious naturalism in which a sense of the sacred is perceived in the workings of entirely naturalistic processes by which more complex forms arise or evolve from simpler forms. Examples are detailed in a 2006 essay titled 'The Sacred Emergence of Nature' by Ursula Goodenough and Terrence Deacon and a 2006 essay titled 'Beyond Reductionism: Reinventing the Sacred' by Stuart Kauffman.

An early argument (1904-5) for the emergence of social formations, in part stemming from religion, can be found in Max Weber's most famous work, The Protestant Ethic and the Spirit of Capitalism ^[12]

In art, emergence is used to explore the origins of novelty, creativity, and authorship. Some art/literary theorists (Wheeler, 2006;^[13] Alexander, 2011^[14]) have proposed alternatives to postmodern understandings of "authorship" using the complexity sciences and emergence theory. They contend that artistic selfhood and meaning are emergent, relatively objective phenomena. The concept of emergence has also been applied to the theory of literature and art, history, linguistics, cognitive sciences, etc. by the teachings of Jean-Marie Grassin at the University of Limoges (v. esp.: J. Fontanille, B. Westphal, J. Vion-Dury, éds. L'Émergence—Poétique de l'Émergence, en réponse aux travaux de Jean-Marie Grassin, Bern, Berlin, etc., 2011; and: the article "Emergence" in the International Dictionary of Literary Terms (DITL).

In international development, concepts of emergence have been used within a theory of social change termed SEED-SCALE to show how standard principles interact to bring forward socio-economic development fitted to cultural values, community economics, and natural environment (local solutions emerging from the larger socio-econo-biosphere). These principles can be implemented utilizing a sequence of standardized tasks that self-assemble in individually specific ways utilizing recursive evaluative criteria.^[15]

In postcolonial studies, the term "Emerging Literature" refers to a contemporary body of texts that is gaining momentum in the global literary landscape (v. esp.: J.M. Grassin, ed. Emerging Literatures, Bern, Berlin, etc. : Peter Lang, 1996). By opposition, "emergent literature" is rather a concept used in the theory of literature.

Emergent properties and processes

An emergent behavior or emergent property can appear when a number of simple entities (agents) operate in an environment, forming more complex behaviors as a collective. If emergence happens over disparate size scales, then the reason is usually a causal relation across different scales. In other words there is often a form of top-down feedback in systems with emergent properties.^[16] The processes from which emergent properties result may occur in either the observed or observing system, and can commonly be identified by their patterns of accumulating change, most generally called 'growth'. Emergent behaviours can occur because of intricate causal relations across different scales and feedback, known as interconnectivity. The emergent property itself may be either very predictable or unpredictable and unprecedented, and represent a new level of the system's evolution.
The complex behaviour or properties are not a property of any single such entity, nor can they easily be predicted or deduced from behaviour in the lower-level entities, and might in fact be irreducible to such behavior. The shape and behaviour of a flock of birds [3] or school of fish are good examples of emergent properties.

One reason why emergent behaviour is hard to predict is that the number of interactions between components of a system increases exponentially with the number of components, thus potentially allowing for many new and subtle types of behaviour to emerge.

On the other hand, merely having a large number of interactions is not enough by itself to guarantee emergent behaviour; many of the interactions may be negligible or irrelevant, or may cancel each other out. In some cases, a large number of interactions can in fact work against the emergence of interesting behaviour, by creating a lot of "noise" to drown out any emerging "signal"; the emergent behaviour may need to be temporarily isolated from other interactions before it reaches enough critical mass to be self-supporting. Thus it is not just the sheer number of connections between components which encourages emergence; it is also how these connections are organised. A hierarchical organisation is one example that can generate emergent behaviour (a bureaucracy may behave in a way quite different from that of the individual humans in that bureaucracy); but perhaps more interestingly, emergent behaviour can also arise from more decentralized organisational structures, such as a marketplace. In some cases, the system has to reach a combined threshold of diversity, organisation, and connectivity before emergent behaviour appears.

Unintended consequences and side effects are closely related to emergent properties. Luc Steels writes: "A component has a particular functionality but this is not recognizable as a subfunction of the global functionality. Instead a component implements a behaviour whose side effect contributes to the global functionality [...] Each behaviour has a side effect and the sum of the side effects gives the desired functionality" (Steels 1990). In other words, the global or macroscopic functionality of a system with "emergent functionality" is the sum of all "side effects", of all emergent properties and functionalities.

Systems with emergent properties or emergent structures may appear to defy entropic principles and the second law of thermodynamics, because they form and increase order despite the lack of command and central control. This is possible because open systems can extract information and order out of the environment.

Emergence helps to explain why the fallacy of division is a fallacy.

Emergent structures in nature

Ripple patterns in a sand dune created by wind or water is an example of an emergent structure in nature.

Giant's Causeway in Northern Ireland is an example of a complex emergent structure created by natural processes.

Emergent structures are patterns that emerge via collective actions of many individual entities. To explain such patterns, one might conclude, per Aristotle,^[2] that emergent structures are more than the sum of their parts on the assumption that the emergent order will not arise if the various parts simply interact independently of one another. However, there are those who disagree.^[17] According to this argument, the interaction of each part with its immediate surroundings causes a complex chain of processes that can lead to order in some form. In fact, some systems in nature are observed to exhibit emergence based upon the interactions of autonomous parts, and some others exhibit emergence that at least at present cannot be reduced in this way. See the discussion in this article of strong and weak emergence.

Emergent structures can be found in many natural phenomena, from the physical to the biological domain. For example, the shape of weather phenomena such as hurricanes are emergent structures. The development and growth of complex, orderly crystals, as driven by the random motion of water molecules within a conducive natural environment, is another example of an emergent process, where randomness can give rise to complex and deeply attractive, orderly structures.

Water crystals forming on glass demonstrate an emergent, fractal natural process occurring under appropriate conditions of temperature and humidity.

However, crystalline structure and hurricanes are said to have a self-organizing phase.

Symphony of the Stones carved by Goght River at Garni Gorge in Armenia is an example of an emergent natural structure.

It is useful to distinguish three forms of emergent structures. A first-order emergent structure occurs as a result of shape interactions (for example, hydrogen bonds in water molecules lead to surface tension). A second-order emergent structure involves shape interactions played out sequentially over time (for example, changing atmospheric conditions as a snowflake falls to the ground build upon and alter its form). Finally, a third-order emergent structure is a consequence of shape, time, and heritable instructions. For example, an organism's genetic code sets boundary conditions on the interaction of biological systems in space and time.

Non-living, physical systems

In physics, emergence is used to describe a property, law, or phenomenon which occurs at macroscopic scales (in space or time) but not at microscopic scales, despite the fact that a macroscopic system can be viewed as a very large ensemble of microscopic systems.

An emergent property need not be more complicated than the underlying non-emergent properties which generate it. For instance, the laws of thermodynamics are remarkably simple, even if the laws which govern the interactions between component particles are complex. The term emergence in physics is thus used not to signify complexity, but rather to distinguish which laws and concepts apply to macroscopic scales, and which ones apply to microscopic scales.

Some examples include:

• Classical mechanics: The laws of classical mechanics can be said to emerge as a limiting case from the rules of quantum mechanics applied to large enough masses. This is particularly strange since quantum mechanics is generally thought of as more complicated than classical mechanics.
• Friction: Forces between elementary particles are conservative. However, friction emerges when considering more complex structures of matter, whose surfaces can convert mechanical energy into heat energy when rubbed against each other. Similar considerations apply to other emergent concepts in continuum mechanics such as viscosity, elasticity, tensile strength, etc.
• Patterned ground: the distinct, and often symmetrical geometric shapes formed by ground material in periglacial regions.
• Statistical mechanics was initially derived using the concept of a large enough ensemble that fluctuations about the most likely distribution can be all but ignored. However, small clusters do not exhibit sharp first order phase transitions such as melting, and at the boundary it is not possible to completely categorize the cluster as a liquid or solid, since these concepts are (without extra definitions) only applicable to macroscopic systems. Describing a system using statistical mechanics methods is much simpler than using a low-level atomistic approach.
• Electrical networks: The bulk conductive response of binary (RC) electrical networks with random arrangements can be seen as emergent properties of such physical systems. Such arrangements can be used as simple physical prototypes for deriving mathematical formulae for the emergent responses of complex systems.^[18]
• Weather.

Temperature is sometimes used as an example of an emergent macroscopic behaviour. In classical dynamics, a snapshot of the instantaneous momenta of a large number of particles at equilibrium is sufficient to find the average kinetic energy per degree of freedom which is proportional to the temperature. For a small number of particles the instantaneous momenta at a given time are not statistically sufficient to determine the temperature of the system. However, using the ergodic hypothesis, the temperature can still be obtained to arbitrary precision by further averaging the momenta over a long enough time.

Convection in a liquid or gas is another example of emergent macroscopic behaviour that makes sense only when considering differentials of temperature. Convection cells, particularly Bénard cells, are an example of a self-organizing system (more specifically, a dissipative system) whose structure is determined both by the constraints of the system and by random perturbations: the possible realizations of the shape and size of the cells depends on the temperature gradient as well as the nature of the fluid and shape of the container, but which configurations are actually realized is due to random perturbations (thus these systems exhibit a form of symmetry breaking).

In some theories of particle physics, even such basic structures as mass, space, and time are viewed as emergent phenomena, arising from more fundamental concepts such as the Higgs boson or strings. In some interpretations of quantum mechanics, the perception of a deterministic reality, in which all objects have a definite position, momentum, and so forth, is actually an emergent phenomenon, with the true state of matter being described instead by a wavefunction which need not have a single position or momentum. Most of the laws of physics themselves as we experience them today appear to have emerged during the course of time making emergence the most fundamental principle in the universe and raising the question of what might be the most fundamental law of physics from which all others emerged. Chemistry can in turn be viewed as an emergent property of the laws of physics. Biology (including biological evolution) can be viewed as an emergent property of the laws of chemistry. Similarly, psychology could be understood as an emergent property of neurobiological laws. Finally, free-market theories understand economy as an emergent feature of psychology.

In Laughlin's book, he explains that for many particle systems, nothing can be calculated exactly from the microscopic equations, and that macroscopic systems are characterised by broken symmetry: the symmetry present in the microscopic equations is not present in the macroscopic system, due to phase transitions. As a result, these macroscopic systems are described in their own terminology, and have properties that do not depend on many microscopic details. This does not mean that the microscopic interactions are irrelevant, but simply that you do not see them anymore — you only see a renormalized effect of them. Laughlin is a pragmatic theoretical physicist: if you cannot, possibly ever, calculate the broken symmetry macroscopic properties from the microscopic equations, then what is the point of talking about reducibility?

Living, biological systems

Emergence and evolution

Life is a major source of complexity, and evolution is the major process behind the varying forms of life. In this view, evolution is the process describing the growth of complexity in the natural world and in speaking of the emergence of complex living beings and life-forms, this view refers therefore to processes of sudden changes in evolution.
Regarding causality in evolution Peter Corning observes:

"Synergistic effects of various kinds have played a major causal role in the evolutionary process generally and in the evolution of cooperation and complexity in particular... Natural selection is often portrayed as a “mechanism”, or is personified as a causal agency... In reality, the differential “selection” of a trait, or an adaptation, is a consequence of the functional effects it produces in relation to the survival and reproductive success of a given organism in a given environment. It is these functional effects that are ultimately responsible for the trans-generational continuities and changes in nature." (Corning 2002)

Per his definition of emergence, Corning also addresses emergence and evolution:

"[In] evolutionary processes, causation is iterative; effects are also causes. And this is equally true of the synergistic effects produced by emergent systems. In other words, emergence itself... has been the underlying cause of the evolution of emergent phenomena in biological evolution; it is the synergies produced by organized systems that are the key." (Corning 2002)

Swarming is a well-known behaviour in many animal species from marching locusts to schooling fish to flocking birds. Emergent structures are a common strategy found in many animal groups: colonies of ants, mounds built by termites, swarms of bees, shoals/schools of fish, flocks of birds, and herds/packs of mammals.

An example to consider in detail is an ant colony. The queen does not give direct orders and does not tell the ants what to do. Instead, each ant reacts to stimuli in the form of chemical scent from larvae, other ants, intruders, food and buildup of waste, and leaves behind a chemical trail, which, in turn, provides a stimulus to other ants. Here each ant is an autonomous unit that reacts depending only on its local environment and the genetically encoded rules for its variety of ant. Despite the lack of centralized decision making, ant colonies exhibit complex behavior and have even been able to demonstrate the ability to solve geometric problems. For example, colonies routinely find the maximum distance from all colony entrances to dispose of dead bodies.^[19]

Organization of life

A broader example of emergent properties in biology is viewed in the biological organisation of life, ranging from the subatomic level to the entire biosphere. For example, individual atoms can be combined to form molecules such as polypeptide chains, which in turn fold and refold to form proteins, which in turn create even more complex structures. These proteins, assuming their functional status from their spatial conformation, interact together and with other molecules to achieve higher biological functions and eventually create an organism. Another example is how cascade phenotype reactions, as detailed in chaos theory, arise from individual genes mutating respective positioning.^[20] At the highest level, all the biological communities in the world form the biosphere, where its human participants form societies, and the complex interactions of meta-social systems such as the stock market.

In humanity

Spontaneous order

Groups of human beings, left free to each regulate themselves, tend to produce spontaneous order, rather than the meaningless chaos often feared. This has been observed in society at least since Chuang Tzu in ancient China. A classic traffic roundabout is a good example, with cars moving in and out with such effective organization that some modern cities have begun replacing stoplights at problem intersections with traffic circles [4], and getting better results. Open-source software and Wiki projects form an even more compelling illustration.
Emergent processes or behaviours can be seen in many other places, such as cities, cabal and market-dominant minority phenomena in economics, organizational phenomena in computer simulations and cellular automata. Whenever you have a multitude of individuals interacting with one another, there often comes a moment when disorder gives way to order and something new emerges: a pattern, a decision, a structure, or a change in direction (Miller 2010, 29).^[21]

Economics

The stock market (or any market for that matter) is an example of emergence on a grand scale. As a whole it precisely regulates the relative security prices of companies across the world, yet it has no leader; when no central planning is in place, there is no one entity which controls the workings of the entire market. Agents, or investors, have knowledge of only a limited number of companies within their portfolio, and must follow the regulatory rules of the market and analyse the transactions individually or in large groupings. Trends and patterns emerge which are studied intensively by technical analysts.^{[citation needed]}

Money

Money, insofar as being a medium of exchange and of deferred payment, is also an example of an emergent phenomenon between market participators. In their strive to possess a commodity with greater marketability than their own commodity, such that the possession of these more marketable commodities (money) facilitate the search for commodities that participators want (e.g. consumables).

Austrian School economist Carl Menger wrote in his work Principles of Economics, "As each economizing individual becomes increasingly more aware of his economic interest, he is led by this interest, without any agreement, without legislative compulsion, and even without regard to the public interest, to give his commodities in exchange for other, more saleable, commodities, even if he does not need them for any immediate consumption purpose. With economic progress, therefore, we can everywhere observe the phenomenon of a certain number of goods, especially those that are most easily saleable at a given time and place, becoming, under the powerful influence of custom, acceptable to everyone in trade, and thus capable of being given in exchange for any other commodity."^[22]

World Wide Web and the Internet

The World Wide Web is a popular example of a decentralized system exhibiting emergent properties. There is no central organization rationing the number of links, yet the number of links pointing to each page follows a power law in which a few pages are linked to many times and most pages are seldom linked to. A related property of the network of links in the World Wide Web is that almost any pair of pages can be connected to each other through a relatively short chain of links. Although relatively well known now, this property was initially unexpected in an unregulated network. It is shared with many other types of networks called small-world networks (Barabasi, Jeong, & Albert 1999, pp. 130–131).

Internet traffic can also exhibit some seemingly emergent properties. In the congestion control mechanism, TCP flows can become globally synchronized at bottlenecks, simultaneously increasing and then decreasing throughput in coordination. Congestion, widely regarded as a nuisance, is possibly an emergent property of the spreading of bottlenecks across a network in high traffic flows which can be considered as a phase transition [see review of related research in (Smith 2008, pp. 1–31)].

Another important example of emergence in web-based systems is social bookmarking (also called collaborative tagging). In social bookmarking systems, users assign tags to resources shared with other users, which gives rise to a type of information organisation that emerges from this crowdsourcing process. Recent research which analyzes empirically the complex dynamics of such systems^[23] has shown that consensus on stable distributions and a simple form of shared vocabularies does indeed emerge, even in the absence of a central controlled vocabulary. Some believe that this could be because users who contribute tags all use the same language, and they share similar semantic structures underlying the choice of words. The convergence in social tags may therefore be interpreted as the emergence of structures as people who have similar semantic interpretation collaboratively index online information, a process called semantic imitation.^{[24] [25]}

Open-source software, or Wiki projects such as Wikipedia and Wikivoyage are other impressive examples of emergence. The "zeroeth law of Wikipedia" is often cited by its editors to highlight its apparently surprising and unpredictable quality: The problem with Wikipedia is that it only works in practice. In theory, it can never work.

Architecture and cities

Traffic patterns in cities can be seen as an example of spontaneous order^{[citation needed]}

Emergent structures appear at many different levels of organization or as spontaneous order. Emergent self-organization appears frequently in cities where no planning or zoning entity predetermines the layout of the city. (Krugman 1996, pp. 9–29) The interdisciplinary study of emergent behaviors is not generally considered a homogeneous field, but divided across its application or problem domains.

Architects and Landscape Architects may not design all the pathways of a complex of buildings. Instead they might let usage patterns emerge and then place pavement where pathways have become worn in.^{[citation needed]}

The on-course action and vehicle progression of the 2007 Urban Challenge could possibly be regarded as an example of cybernetic emergence. Patterns of road use, indeterministic obstacle clearance times, etc. will work together to form a complex emergent pattern that can not be deterministically planned in advance.

The architectural school of Christopher Alexander takes a deeper approach to emergence attempting to rewrite the process of urban growth itself in order to affect form, establishing a new methodology of planning and design tied to traditional practices, an Emergent Urbanism. Urban emergence has also been linked to theories of urban complexity (Batty 2005) and urban evolution (Marshall 2009).

Building ecology is a conceptual framework for understanding architecture and the built environment as the interface between the dynamically interdependent elements of buildings, their occupants, and the larger environment. Rather than viewing buildings as inanimate or static objects, building ecologist Hal Levin views them as interfaces or intersecting domains of living and non-living systems.^[26] The microbial ecology of the indoor environment is strongly dependent on the building materials, occupants, contents, environmental context and the indoor and outdoor climate. The strong relationship between atmospheric chemistry and indoor air quality and the chemical reactions occurring indoors. The chemicals may be nutrients, neutral or biocides for the microbial organisms. The microbes produce chemicals that affect the building materials and occupant health and well being. Humans manipulate the ventilation, temperature and humidity to achieve comfort with the concomitant effects on the microbes that populate and evolve.^[26][27][28]

Eric Bonabeau's attempt to define emergent phenomena is through traffic: "traffic jams are actually very complicated and mysterious. On an individual level, each driver is trying to get somewhere and is following (or breaking) certain rules, some legal (the speed limit) and others societal or personal (slow down to let another driver change into your lane). But a traffic jam is a separate and distinct entity that emerges from those individual behaviors. Gridlock on a highway, for example, can travel backward for no apparent reason, even as the cars are moving forward." He has also likened emergent phenomena to the analysis of market trends and employee behavior.^[29]

Computational emergent phenomena have also been utilized in architectural design processes, for example for formal explorations and experiments in digital materiality.^[30]

Computer AI

Some artificially intelligent computer applications utilize emergent behavior for animation. One example is Boids, which mimics the swarming behavior of birds.

Language

It has been argued that the structure and regularity of language--grammar, or at least language change, is an emergence phenomenon (Hopper 1998).While each speaker merely tries to reach his or her own communicative goals, he or she uses language in a particular way. If enough speakers behave in that way, language is changed (Keller 1994). In a wider sense, the norms of a language, i.e. the linguistic conventions of its speech society, can be seen as a system emerging from long-time participation in communicative problem-solving in various social circumstances. (Määttä 2000)

Emergent change processes

Within the field of group facilitation and organization development, there have been a number of new group processes that are designed to maximize emergence and self-organization, by offering a minimal set of effective initial conditions. Examples of these processes include SEED-SCALE, Appreciative Inquiry, Future Search, the World Cafe or Knowledge Cafe, Open Space Technology, and others. (Holman, 2010)

Zero-energy universe

From Wikipedia, the free encyclopedia

The zero-energy universe theory states that the total amount of energy in the universe is exactly zero: its amount of positive energy in the form of matter is exactly canceled out by its negative energy in the form of gravity.^[1][2]

The theory originated in 1973, when Edward Tryon proposed in the Nature journal that the Universe emerged from a large-scale quantum fluctuation of vacuum energy, resulting in its positive mass-energy being exactly balanced by its negative gravitational potential energy.^[3]

Free-lunch interpretation

A generic property of inflation is the balancing of the negative gravitational energy, within the inflating region, with the positive energy of the inflaton field to yield a post-inflationary universe with negligible or zero energy density.^[4][5] It is this balancing of the total universal energy budget that enables the open-ended growth possible with inflation; during inflation energy flows from the gravitational field (or geometry) to the inflaton field—the total gravitational energy decreases (i.e. becomes more negative) and the total inflaton energy increases (becomes more positive). But the respective energy densities remain constant and opposite since the region is inflating. Consequently, inflation explains the otherwise curious cancellation of matter and gravitational energy on cosmological scales, which is consistent with astronomical observations.^[6]

Quantum fluctuation

Due to quantum uncertainty, energy fluctuations such as an electron and its anti-particle, a positron, can arise spontaneously out of vacuum space, but must disappear rapidly. The lower the energy of the bubble, the longer it can exist. A gravitational field has negative energy. Matter has positive energy. The two values cancel out provided the Universe is completely flat. In that case, the Universe has zero energy and can theoretically last forever.^[3][7]

Hawking gravitational energy

Stephen Hawking notes in his 2010 book The Grand Design: "If the total energy of the universe must always remain zero, and it costs energy to create a body, how can a whole universe be created from nothing? That is why there must be a law like gravity. Because gravity is attractive, gravitational energy is negative: One has to do work to separate a gravitationally bound system, such as the Earth and moon. This negative energy can balance the positive energy needed to create matter, but it’s not quite that simple. The negative gravitational energy of the Earth, for example, is less than a billionth of the positive energy of the matter particles the Earth is made of. A body such as a star will have more negative gravitational energy, and the smaller it is (the closer the different parts of it are to each other), the greater the negative gravitational energy will be. But before it can become greater (in magnitude) than the positive energy of the matter, the star will collapse to a black hole, and black holes have positive energy. That’s why empty space is stable. Bodies such as stars or black holes cannot just appear out of nothing. But a whole universe can." (p. 180)