From Wikipedia, the free encyclopedia
The second law of thermodynamics states that in a natural thermodynamic process, there is an increase in the sum of the entropies of the participating systems.
The second law is an empirical finding that has been accepted as an axiom of thermodynamic theory.
The law defines the concept of thermodynamic entropy for a thermodynamic system in its own state of internal thermodynamic equilibrium. It considers a process in which that state changes, with increases in entropy due to dissipation of energy and to dispersal of matter and energy.
The law envisages a compound thermodynamic system that initially has interior walls that constrain transfers within it. The law then envisages a process that is initiated by a thermodynamic operation that changes those constraints, and isolates the compound system from its surroundings, except that an externally imposed unchanging force field is allowed to stay subject to the condition that the compound system moves as a whole within that field so that in net, there is no transfer of energy as work between the compound system and the surroundings, and finally, eventually, the system is stationary within that field.
During the process, there may occur chemical reactions, and transfers of matter and of energy. In each adiabatically separated compartment, the temperature becomes spatially homogeneous, even in the presence of the externally imposed unchanging external force field. If, between two adiabatically separated compartments, transfer of energy as work is possible, then it proceeds until the sum of the entropies of the equilibrated compartments is maximum subject to the other constraints. If the externally imposed force field is zero, then the chemical concentrations also become as spatially homogeneous as is allowed by the permeabilities of the interior walls, and by the possibilities of phase separations, which occur so as to maximize the sum of the entropies of the equilibrated phases subject to the other constraints. Such homogeneity and phase separation is characteristic of the state of internal thermodynamic equilibrium of a thermodynamic system.[1][2] If the externally imposed force field is non-zero, then the chemical concentrations spatially redistribute themselves so as to maximize the sum of the equilibrated entropies subject to the other constraints and phase separations.
Statistical thermodynamics, classical or quantum, explains the law.
The second law has been expressed in many ways. Its first formulation is credited to the French scientist Sadi Carnot in 1824 (see Timeline of thermodynamics).
The concept of energy in the first law does not, however, account for the observation that natural processes have a preferred direction of progress. The first law is symmetrical with respect to the initial and final states of an evolving system. But the second law asserts that a natural process runs only in one sense, and is not reversible. For example, heat always flows spontaneously from hotter to colder bodies, and never the reverse, unless external work is performed on the system. The key concept for the explanation of this phenomenon through the second law of thermodynamics is the definition of a new physical quantity, the entropy.[5][6]
For mathematical analysis of processes, entropy is introduced as follows. In a fictive reversible process, an infinitesimal increment in the entropy (dS) of a system results from an infinitesimal transfer of heat (δQ) to a closed system divided by the common temperature (T) of the system and the surroundings which supply the heat.[7]
The second law allows a distinguished temperature scale, which defines an absolute, thermodynamic temperature, independent of the properties of any particular reference thermometric body.[9][10]
Heat cannot spontaneously flow from cold regions to hot regions without external work being performed on the system, which is evident from ordinary experience of refrigeration, for example. In a refrigerator, heat flows from cold to hot, but only when forced by an external agent, the refrigeration system.
Suppose there is an engine violating the Kelvin statement: i.e., one that drains heat and converts it completely into work in a cyclic fashion without any other result. Now pair it with a reversed Carnot engine as shown by the figure. The net and sole effect of this newly created engine consisting of the two engines mentioned is transferring heat

from the cooler reservoir to the hotter one, which violates the Clausius statement. Thus a violation of the Kelvin statement implies a violation of the Clausius statement, i.e. the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, and hence the two are equivalent.
 .[34] [clarification needed]
.[34] [clarification needed]
Though it is almost customary in textbooks to say that Carathéodory's principle expresses the second law and to treat it as equivalent to the Clausius or to the Kelvin-Planck statements, such is not the case. To get all the content of the second law, Carathéodory's principle needs to be supplemented by Planck's principle, that isochoric work always increases the internal energy of a closed system that was initially in its own internal thermodynamic equilibrium.[35][36][37][38] [clarification needed]
Not mentioning entropy, this principle of Planck is stated in physical terms. It is very closely related to the Kelvin statement given just above.[43] Nevertheless, this principle of Planck is not actually Planck's preferred statement of the second law, which is quoted above, in a previous sub-section of the present section of this present article, and relies on the concept of entropy.
The link to Kelvin's statement is illustrated by an equivalent statement by Allahverdyan & Nieuwenhuizen, which they attribute to Kelvin: "No work can be extracted from a closed equilibrium system during a cyclic variation of a parameter by an external source."[44][45]
However, this is not always the case for systems in which the gravitational force is important. The most striking examples are black holes, which – according to theory – have negative heat capacity. The larger the black hole, the more energy it contains, but the lower its temperature. Thus, the supermassive black hole in the center of the Milky Way is supposed to have a temperature of 10−14 K, much lower than the cosmic microwave background temperature of 2.7 K[citation needed], but as it absorbs photons of the cosmic microwave background its mass is increasing so that its low temperature further decreases with time[dubious ].
For this reason, gravitational systems tend towards non-even distribution of mass and energy. The universe in large scale is importantly a gravitational system, and the second law may therefore not apply to it.[dubious ]
Though formulated in terms of caloric (see the obsolete caloric theory), rather than entropy, this was an early insight into the second law.
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, any reversible heat engine operating between temperatures T1 and T2 must have the same efficiency, that is to
say, the efficiency is the function of temperatures only: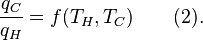
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 andT3. This can only be the case if
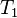 is a fixed reference temperature: the temperature of the triple point of water. Then for any T2 and T3,
is a fixed reference temperature: the temperature of the triple point of water. Then for any T2 and T3,
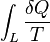 is path independent.
is path independent.
So we can define a state function S called entropy, which satisfies
For any irreversible process, since entropy is a state function, we can always connect the initial and terminal states with an imaginary reversible process and integrating on that path to calculate the difference in entropy.
Now reverse the reversible process and combine it with the said irreversible process. Applying Clausius inequality on this loop,
Notice that if the process is an adiabatic process, then , so
, so  .
.
Whatever changes to dS and dSR occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy Stot of the isolated total system must not decrease:
Now the heat leaving the reservoir and entering the sub-system is
Second Law inequality from above.
It therefore follows that any net work δw done by the sub-system must obey
In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in E for an irreversible process and no change for a reversible process.
This approach to the Second Law is widely utilized in engineering practice, environmental accounting, systems ecology, and other disciplines.

The first theory of the conversion of heat into mechanical work is due to Nicolas Léonard Sadi Carnot in 1824. He was the first to realize correctly that the efficiency of this conversion depends on the difference of temperature between an engine and its environment.
Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).
Established during the 19th century, the Kelvin-Planck statement of the Second Law says, "It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work." This was shown to be equivalent to the statement of Clausius.
The ergodic hypothesis is also important for the Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over a long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.
It has been shown that not only classical systems but also quantum mechanical ones tend to maximize their entropy over time. Thus the second law follows, given initial conditions with low entropy. More precisely, it has been shown that the local von Neumann entropy is at its maximum value with a very high probability.[49] The result is valid for a large class of isolated quantum systems (e.g. a gas in a container). While the full system is pure and therefore does not have any entropy, the entanglement between gas and container gives rise to an increase of the local entropy of the gas. This result is one of the most important achievements of quantum thermodynamics.[dubious ]
Today, much effort in the field is attempting to understand why the initial conditions early in the universe were those of low entropy,[50][51] as this is seen as the origin of the second law (see below).
In 1856, the German physicist Rudolf Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:[53]
In terms of time variation, the mathematical statement of the second law for an isolated system undergoing an arbitrary transformation is:
 the sum of the rate of entropy production by all processes inside the system. The advantage of this formulation is that it shows the effect of the entropy production. The rate of entropy production is a very important concept since it determines (limits) the efficiency of thermal machines. Multiplied with ambient temperature
the sum of the rate of entropy production by all processes inside the system. The advantage of this formulation is that it shows the effect of the entropy production. The rate of entropy production is a very important concept since it determines (limits) the efficiency of thermal machines. Multiplied with ambient temperature  it gives the so-called dissipated energy
it gives the so-called dissipated energy 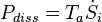 .
.
The expression of the second law for closed systems (so, allowing heat exchange and moving boundaries, but not exchange of matter) is:
For open systems (also allowing exchange of matter):
 is the flow of entropy into the system associated with the flow of matter entering the system. It should not be confused with the time derivative of the entropy. If matter is supplied at several places we have to take the algebraic sum of these contributions.
is the flow of entropy into the system associated with the flow of matter entering the system. It should not be confused with the time derivative of the entropy. If matter is supplied at several places we have to take the algebraic sum of these contributions.
Statistical mechanics gives an explanation for the second law by postulating that a material is composed of atoms and molecules which are in constant motion. A particular set of positions and velocities for each particle in the system is called a microstate of the system and because of the constant motion, the system is constantly changing its microstate. Statistical mechanics postulates that, in equilibrium, each microstate that the system might be in is equally likely to occur, and when this assumption is made, it leads directly to the conclusion that the second law must hold in a statistical sense. That is, the second law will hold on average, with a statistical variation on the order of 1/√N where N is the number of particles in the system. For everyday (macroscopic) situations, the probability that the second law will be violated is practically zero. However, for systems with a small number of particles, thermodynamic parameters, including the entropy, may show significant statistical deviations from that predicted by the second law. Classical thermodynamic theory does not deal with these statistical variations.
Given these assumptions, in statistical mechanics, the Second Law is not a postulate, rather it is a consequence of the fundamental postulate, also known as the equal prior probability postulate, so long as one is clear that simple probability arguments are applied only to the future, while for the past there are auxiliary sources of information which tell us that it was low entropy.[citation needed] The first part of the second law, which states that the entropy of a thermally isolated system can only increase, is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of is:
is:
 is the number of quantum states in a small interval between
is the number of quantum states in a small interval between  and
and 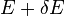 . Here
. Here  is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of
is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of  . However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on
. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on  .
.
Suppose we have an isolated system whose macroscopic state is specified by a number of variables. These macroscopic variables can, e.g., refer to the total volume, the positions of pistons in the system, etc. Then will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that
will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that  is maximized as that is the most probable situation in equilibrium.
is maximized as that is the most probable situation in equilibrium.
If the variable was initially fixed to some value then upon release and when the new equilibrium has been reached, the fact the variable will adjust itself so that is maximized, implies that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value). Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number
is maximized, implies that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value). Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number  of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of
of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of  . We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity H increases monotonically as a function of time during the intermediate out of equilibrium state.
. We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity H increases monotonically as a function of time during the intermediate out of equilibrium state.
The generalized force, X, corresponding to the external variable x is defined such that is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate
is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate  is given by:
is given by:
 , we define the generalized force for the system as the expectation value of the above expression:
, we define the generalized force for the system as the expectation value of the above expression:
 energy eigenstates by counting how many of them have a value for
energy eigenstates by counting how many of them have a value for 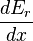 within a range between
within a range between  and
and  . Calling this number
. Calling this number  , we have:
, we have:
 will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between
will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between  and
and 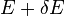 . Let's focus again on the energy eigenstates for which
. Let's focus again on the energy eigenstates for which 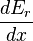 lies within the range between
lies within the range between 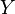 and
and  . Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E – Y dx to E move from below E to above E. There are
. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E – Y dx to E move from below E to above E. There are
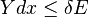 , all these energy eigenstates will move into the range between
, all these energy eigenstates will move into the range between  and
and 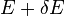 and contribute to an increase in
and contribute to an increase in  . The number of energy eigenstates that move from below
. The number of energy eigenstates that move from below 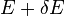 to above
to above 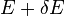 is, of course, given by
is, of course, given by 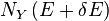 . The difference
. The difference
 . Note that if Y dx is larger than
. Note that if Y dx is larger than  there will be the energy eigenstates that move from below E to above
there will be the energy eigenstates that move from below E to above 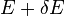 . They are counted in both
. They are counted in both  and
and 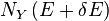 , therefore the above expression is also valid in that case.
, therefore the above expression is also valid in that case.
Expressing the above expression as a derivative w.r.t. E and summing over Y yields the expression:
 w.r.t. x is thus given by:
w.r.t. x is thus given by:
 for the canonical ensemble in here gives:
for the canonical ensemble in here gives:
This derivation is quite general, based on the Shannon entropy, and does not require any assumptions beyond unitarity, which is universally accepted. It is a consequence of the irreversibility or singular nature of the general transition matrix.
For purposes of physical analysis, it is often enough convenient to make an assumption of thermodynamic equilibrium. Such an assumption may rely on trial and error for its justification. If the assumption is justified, it can often be very valuable and useful because it makes available the theory of thermodynamics. Elements of the equilibrium assumption are that a system is observed to be unchanging over an indefinitely long time, and that there are so many particles in a system, that its particulate nature can be entirely ignored. Under such an equilibrium assumption, in general, there are no macroscopically detectable fluctuations. There is an exception, the case of critical states, which exhibit to the naked eye the phenomenon of critical opalescence. For laboratory studies of critical states, exceptionally long observation times are needed.
In all cases, the assumption of thermodynamic equilibrium, once made, implies as a consequence that no putative candidate "fluctuation" alters the entropy of the system.
It can easily happen that a physical system exhibits internal macroscopic changes that are fast enough to invalidate the assumption of the constancy of the entropy. Or that a physical system has so few particles that the particulate nature is manifest in observable fluctuations. Then the assumption of thermodynamic equilibrium is to be abandoned. There is no unqualified general definition of entropy for non-equilibrium states.[61]
Non-equilibrium thermodynamics is then appropriate. There are intermediate cases, in which the assumption of local thermodynamic equilibrium is a very good approximation,[62][63][64][65] but strictly speaking it is still an approximation, not theoretically ideal. For non-equilibrium situations in general, it may be useful to consider statistical mechanical definitions of quantities that may be conveniently called 'entropy'. These indeed belong to statistical mechanics, not to macroscopic thermodynamics.
The physics of macroscopically observable fluctuations is beyond the scope of this article.

James Clerk Maxwell imagined one container divided into two parts, A and B. Both parts are filled with the same gas at equal temperatures and placed next to each other. Observing the molecules on both sides, an imaginary demon guards a trapdoor between the two parts. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics.
One of the most famous responses to this question was suggested in 1929 by Leó Szilárd and later by Léon Brillouin. Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy.
Maxwell's demon repeatedly alters the permeability of the wall between A and B. It is therefore performing thermodynamic operations, not just presiding over natural processes.
One proposed resolution of this paradox is as follows. The Loschmidt scenario refers to a strictly isolated system or to a strictly adiabatically isolated system. Heat and matter transfers are not allowed. The Loschmidt reversal times are fantastically long, far longer than any laboratory isolation of the required degree of perfection could be maintained in practice. In this sense, the Loschmidt scenario will never be subjected to empirical testing. Also in this sense, the second law, stated for an isolated system, will never be subjected to empirical testing. A system, supposedly perfectly isolated, in strictly perfect thermodynamic equilibrium, can be observed only once in its entire life, because the observation must break the isolation. Two observations would be needed to check empirically for a change of state, one initial and one final. When transfer of heat or matter are permitted, the requirements of perfection are not so tight. In practical laboratory reality, therefore, the second law can be tested only for systems with transfer of heat or matter, and not for isolated systems.
Due to this paradox, derivations of the second law have to make an assumption regarding the past, namely that the system is uncorrelated at some time in the past or, equivalently, that the entropy in the past was lower than in the future. This assumption is usually thought as a boundary condition, and thus the second Law is ultimately derived from the initial conditions of the Big Bang.[54][67]
 .[68] The result applies to physical systems in which energy is conserved. The Recurrence theorem apparently contradicts the Second law of thermodynamics, which says that large dynamical systems evolve irreversibly towards the state with higher entropy, so that if one starts with a low-entropy state, the system will never return to it. There are many possible ways to resolve this paradox, but none of them is universally accepted.[citation needed] The most reasonable argument is that for typical thermodynamical systems the recurrence time is so large (many many times longer than the lifetime of the universe) that, for all practical purposes, one cannot observe the recurrence.
.[68] The result applies to physical systems in which energy is conserved. The Recurrence theorem apparently contradicts the Second law of thermodynamics, which says that large dynamical systems evolve irreversibly towards the state with higher entropy, so that if one starts with a low-entropy state, the system will never return to it. There are many possible ways to resolve this paradox, but none of them is universally accepted.[citation needed] The most reasonable argument is that for typical thermodynamical systems the recurrence time is so large (many many times longer than the lifetime of the universe) that, for all practical purposes, one cannot observe the recurrence.
The second law is an empirical finding that has been accepted as an axiom of thermodynamic theory.
The law defines the concept of thermodynamic entropy for a thermodynamic system in its own state of internal thermodynamic equilibrium. It considers a process in which that state changes, with increases in entropy due to dissipation of energy and to dispersal of matter and energy.
The law envisages a compound thermodynamic system that initially has interior walls that constrain transfers within it. The law then envisages a process that is initiated by a thermodynamic operation that changes those constraints, and isolates the compound system from its surroundings, except that an externally imposed unchanging force field is allowed to stay subject to the condition that the compound system moves as a whole within that field so that in net, there is no transfer of energy as work between the compound system and the surroundings, and finally, eventually, the system is stationary within that field.
During the process, there may occur chemical reactions, and transfers of matter and of energy. In each adiabatically separated compartment, the temperature becomes spatially homogeneous, even in the presence of the externally imposed unchanging external force field. If, between two adiabatically separated compartments, transfer of energy as work is possible, then it proceeds until the sum of the entropies of the equilibrated compartments is maximum subject to the other constraints. If the externally imposed force field is zero, then the chemical concentrations also become as spatially homogeneous as is allowed by the permeabilities of the interior walls, and by the possibilities of phase separations, which occur so as to maximize the sum of the entropies of the equilibrated phases subject to the other constraints. Such homogeneity and phase separation is characteristic of the state of internal thermodynamic equilibrium of a thermodynamic system.[1][2] If the externally imposed force field is non-zero, then the chemical concentrations spatially redistribute themselves so as to maximize the sum of the equilibrated entropies subject to the other constraints and phase separations.
Statistical thermodynamics, classical or quantum, explains the law.
The second law has been expressed in many ways. Its first formulation is credited to the French scientist Sadi Carnot in 1824 (see Timeline of thermodynamics).
Introduction
The first law of thermodynamics provides the basic definition of thermodynamic energy, also called internal energy, associated with all thermodynamic systems, but unknown in classical mechanics, and states the rule of conservation of energy in nature.[3][4]The concept of energy in the first law does not, however, account for the observation that natural processes have a preferred direction of progress. The first law is symmetrical with respect to the initial and final states of an evolving system. But the second law asserts that a natural process runs only in one sense, and is not reversible. For example, heat always flows spontaneously from hotter to colder bodies, and never the reverse, unless external work is performed on the system. The key concept for the explanation of this phenomenon through the second law of thermodynamics is the definition of a new physical quantity, the entropy.[5][6]
For mathematical analysis of processes, entropy is introduced as follows. In a fictive reversible process, an infinitesimal increment in the entropy (dS) of a system results from an infinitesimal transfer of heat (δQ) to a closed system divided by the common temperature (T) of the system and the surroundings which supply the heat.[7]
The second law allows a distinguished temperature scale, which defines an absolute, thermodynamic temperature, independent of the properties of any particular reference thermometric body.[9][10]
Various statements of the law
The second law of thermodynamics may be expressed in many specific ways,[11] the most prominent classical statements[12] being the statement by Rudolf Clausius (1854), the statement by Lord Kelvin (1851), and the statement in axiomatic thermodynamics by Constantin Carathéodory (1909). These statements cast the law in general physical terms citing the impossibility of certain processes. The Clausius and the Kelvin statements have been shown to be equivalent.[13]Carnot's principle
The historical origin of the second law of thermodynamics was in Carnot's principle. It refers to a cycle of a Carnot engine, fictively operated in the limiting mode of extreme slowness known as quasi-static, so that the heat and work transfers are between subsystems that are always in their own internal states of thermodynamic equilibrium. The Carnot engine is an idealized device of special interest to engineers who are concerned with the efficiency of heat engines. Carnot's principle was recognized by Carnot at a time when the caloric theory of heat was seriously considered, before the recognition of the first law of thermodynamics, and before the mathematical expression of the concept of entropy. Interpreted in the light of the first law, it is physically equivalent to the second law of thermodynamics, and remains valid today. It statesThe efficiency of a quasi-static or reversible Carnot cycle depends only on the temperatures of the two heat reservoirs, and is the same, whatever the working substance. A Carnot engine operated in this way is the most efficient possible heat engine using those two temperatures.[14][15][16][17][18][19][20][clarification needed]
Clausius statement
The German scientist Rudolf Clausius laid the foundation for the second law of thermodynamics in 1850 by examining the relation between heat transfer and work.[21] His formulation of the second law, which was published in German in 1854, is known as the Clausius statement:Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.[22]The statement by Clausius uses the concept of 'passage of heat'. As is usual in thermodynamic discussions, this means 'net transfer of energy as heat', and does not refer to contributory transfers one way and the other.
Heat cannot spontaneously flow from cold regions to hot regions without external work being performed on the system, which is evident from ordinary experience of refrigeration, for example. In a refrigerator, heat flows from cold to hot, but only when forced by an external agent, the refrigeration system.
Kelvin statement
Lord Kelvin expressed the second law asIt is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects.[23]
Equivalence of the Clausius and the Kelvin statements
Suppose there is an engine violating the Kelvin statement: i.e., one that drains heat and converts it completely into work in a cyclic fashion without any other result. Now pair it with a reversed Carnot engine as shown by the figure. The net and sole effect of this newly created engine consisting of the two engines mentioned is transferring heat

from the cooler reservoir to the hotter one, which violates the Clausius statement. Thus a violation of the Kelvin statement implies a violation of the Clausius statement, i.e. the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, and hence the two are equivalent.
Planck's proposition
Planck offered the following proposition as derived directly from experience. This is sometimes regarded as his statement of the second law, but he regarded it as a starting point for the derivation of the second law.Relation between Kelvin's statement and Planck's proposition
It is almost customary in textbooks to speak of the "Kelvin-Planck statement" of the law, as for example in the text by ter Haar and Wergeland.[26] One text gives a statement that for all the world looks like Planck's proposition, but attributes it to Kelvin without mention of Planck.[27] One monograph quotes Planck's proposition as the "Kelvin-Planck" formulation, the text naming Kelvin as its author, though it correctly cites Planck in its references.[28] The reader may compare the two statements quoted just above here.Planck's statement
Planck stated the second law as follows.Principle of Carathéodory
Constantin Carathéodory formulated thermodynamics on a purely mathematical axiomatic foundation. His statement of the second law is known as the Principle of Carathéodory, which may be formulated as follows:[32]In every neighborhood of any state S of an adiabatically enclosed system there are states inaccessible from S.[33]With this formulation, he described the concept of adiabatic accessibility for the first time and provided the foundation for a new subfield of classical thermodynamics, often called geometrical thermodynamics. It follows from Carathéodory's principle that quantity of energy quasi-statically transferred as heat is a holonomic process function, in other words,
 .[34] [clarification needed]
.[34] [clarification needed]Though it is almost customary in textbooks to say that Carathéodory's principle expresses the second law and to treat it as equivalent to the Clausius or to the Kelvin-Planck statements, such is not the case. To get all the content of the second law, Carathéodory's principle needs to be supplemented by Planck's principle, that isochoric work always increases the internal energy of a closed system that was initially in its own internal thermodynamic equilibrium.[35][36][37][38] [clarification needed]
Planck's Principle
In 1926, Max Planck wrote an important paper on the basics of thermodynamics.[37][39] He indicated the principleNot mentioning entropy, this principle of Planck is stated in physical terms. It is very closely related to the Kelvin statement given just above.[43] Nevertheless, this principle of Planck is not actually Planck's preferred statement of the second law, which is quoted above, in a previous sub-section of the present section of this present article, and relies on the concept of entropy.
The link to Kelvin's statement is illustrated by an equivalent statement by Allahverdyan & Nieuwenhuizen, which they attribute to Kelvin: "No work can be extracted from a closed equilibrium system during a cyclic variation of a parameter by an external source."[44][45]
Statement for a system that has a known expression of its internal energy as a function of its extensive state variables
The second law has been shown to be equivalent to the internal energy U being a weakly convex function, when written as a function of extensive properties (mass, volume, entropy, ...).[46][47] [clarification needed]Gravitational systems
In non-gravitational systems, objects always have positive heat capacity, meaning that the temperature rises with energy. Therefore, when energy flows from a high-temperature object to a low-temperature object, the source temperature is decreased while the sink temperature is increased; hence temperature differences tend to diminish over time.However, this is not always the case for systems in which the gravitational force is important. The most striking examples are black holes, which – according to theory – have negative heat capacity. The larger the black hole, the more energy it contains, but the lower its temperature. Thus, the supermassive black hole in the center of the Milky Way is supposed to have a temperature of 10−14 K, much lower than the cosmic microwave background temperature of 2.7 K[citation needed], but as it absorbs photons of the cosmic microwave background its mass is increasing so that its low temperature further decreases with time[dubious ].
For this reason, gravitational systems tend towards non-even distribution of mass and energy. The universe in large scale is importantly a gravitational system, and the second law may therefore not apply to it.[dubious ]
Corollaries
Perpetual motion of the second kind
Before the establishment of the Second Law, many people who were interested in inventing a perpetual motion machine had tried to circumvent the restrictions of First Law of Thermodynamics by extracting the massive internal energy of the environment as the power of the machine. Such a machine is called a "perpetual motion machine of the second kind". The second law declared the impossibility of such machines.Carnot theorem
Carnot's theorem (1824) is a principle that limits the maximum efficiency for any possible engine. The efficiency solely depends on the temperature difference between the hot and cold thermal reservoirs. Carnot's theorem states:- All irreversible heat engines between two heat reservoirs are less efficient than a Carnot engine operating between the same reservoirs.
- All reversible heat engines between two heat reservoirs are equally efficient with a Carnot engine operating between the same reservoirs.
Though formulated in terms of caloric (see the obsolete caloric theory), rather than entropy, this was an early insight into the second law.
Clausius Inequality
The Clausius Theorem (1854) states that in a cyclic processThermodynamic temperature
For an arbitrary heat engine, the efficiency is:Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, any reversible heat engine operating between temperatures T1 and T2 must have the same efficiency, that is to
say, the efficiency is the function of temperatures only:
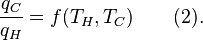
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 andT3. This can only be the case if
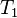 is a fixed reference temperature: the temperature of the triple point of water. Then for any T2 and T3,
is a fixed reference temperature: the temperature of the triple point of water. Then for any T2 and T3,Entropy
According to the Clausius equality, for a reversible process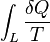 is path independent.
is path independent.So we can define a state function S called entropy, which satisfies
For any irreversible process, since entropy is a state function, we can always connect the initial and terminal states with an imaginary reversible process and integrating on that path to calculate the difference in entropy.
Now reverse the reversible process and combine it with the said irreversible process. Applying Clausius inequality on this loop,
Notice that if the process is an adiabatic process, then
 , so
, so  .
.Energy, available useful work
An important and revealing idealized special case is to consider applying the Second Law to the scenario of an isolated system (called the total system or universe), made up of two parts: a sub-system of interest, and the sub-system's surroundings. These surroundings are imagined to be so large that they can be considered as an unlimited heat reservoir at temperature TR and pressure PR — so that no matter how much heat is transferred to (or from) the sub-system, the temperature of the surroundings will remain TR; and no matter how much the volume of the sub-system expands (or contracts), the pressure of the surroundings will remain PR.Whatever changes to dS and dSR occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy Stot of the isolated total system must not decrease:
Now the heat leaving the reservoir and entering the sub-system is
Second Law inequality from above.
It therefore follows that any net work δw done by the sub-system must obey
In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in E for an irreversible process and no change for a reversible process.
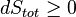 Is equivalent to
Is equivalent to 
This approach to the Second Law is widely utilized in engineering practice, environmental accounting, systems ecology, and other disciplines.
History

Nicolas Léonard Sadi Carnot in the traditional uniform of a student of the École Polytechnique.
The first theory of the conversion of heat into mechanical work is due to Nicolas Léonard Sadi Carnot in 1824. He was the first to realize correctly that the efficiency of this conversion depends on the difference of temperature between an engine and its environment.
Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).
Established during the 19th century, the Kelvin-Planck statement of the Second Law says, "It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work." This was shown to be equivalent to the statement of Clausius.
The ergodic hypothesis is also important for the Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over a long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.
It has been shown that not only classical systems but also quantum mechanical ones tend to maximize their entropy over time. Thus the second law follows, given initial conditions with low entropy. More precisely, it has been shown that the local von Neumann entropy is at its maximum value with a very high probability.[49] The result is valid for a large class of isolated quantum systems (e.g. a gas in a container). While the full system is pure and therefore does not have any entropy, the entanglement between gas and container gives rise to an increase of the local entropy of the gas. This result is one of the most important achievements of quantum thermodynamics.[dubious ]
Today, much effort in the field is attempting to understand why the initial conditions early in the universe were those of low entropy,[50][51] as this is seen as the origin of the second law (see below).
Informal descriptions
The second law can be stated in various succinct ways, including:- It is impossible to produce work in the surroundings using a cyclic process connected to a single heat reservoir (Kelvin, 1851).
- It is impossible to carry out a cyclic process using an engine connected to two heat reservoirs that will have as its only effect the transfer of a quantity of heat from the low-temperature reservoir to the high-temperature reservoir (Clausius, 1854).
- If thermodynamic work is to be done at a finite rate, free energy must be expended. (Stoner, 2000)[52]
Mathematical descriptions
In 1856, the German physicist Rudolf Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:[53]
The entropy of the universe tends to a maximum.This statement is the best-known phrasing of the second law. Because of the looseness of its language, e.g. universe, as well as lack of specific conditions, e.g. open, closed, or isolated, many people take this simple statement to mean that the second law of thermodynamics applies virtually to every subject imaginable. This, of course, is not true; this statement is only a simplified version of a more extended and precise description.
In terms of time variation, the mathematical statement of the second law for an isolated system undergoing an arbitrary transformation is:
- S is the entropy of the system and
- t is time.
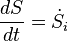 with
with 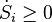
 the sum of the rate of entropy production by all processes inside the system. The advantage of this formulation is that it shows the effect of the entropy production. The rate of entropy production is a very important concept since it determines (limits) the efficiency of thermal machines. Multiplied with ambient temperature
the sum of the rate of entropy production by all processes inside the system. The advantage of this formulation is that it shows the effect of the entropy production. The rate of entropy production is a very important concept since it determines (limits) the efficiency of thermal machines. Multiplied with ambient temperature  it gives the so-called dissipated energy
it gives the so-called dissipated energy 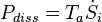 .
.The expression of the second law for closed systems (so, allowing heat exchange and moving boundaries, but not exchange of matter) is:
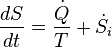 with
with 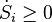
 is the heat flow into the system
is the heat flow into the system is the temperature at the point where the heat enters the system.
is the temperature at the point where the heat enters the system.
For open systems (also allowing exchange of matter):
 with
with 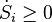
 is the flow of entropy into the system associated with the flow of matter entering the system. It should not be confused with the time derivative of the entropy. If matter is supplied at several places we have to take the algebraic sum of these contributions.
is the flow of entropy into the system associated with the flow of matter entering the system. It should not be confused with the time derivative of the entropy. If matter is supplied at several places we have to take the algebraic sum of these contributions.Statistical mechanics gives an explanation for the second law by postulating that a material is composed of atoms and molecules which are in constant motion. A particular set of positions and velocities for each particle in the system is called a microstate of the system and because of the constant motion, the system is constantly changing its microstate. Statistical mechanics postulates that, in equilibrium, each microstate that the system might be in is equally likely to occur, and when this assumption is made, it leads directly to the conclusion that the second law must hold in a statistical sense. That is, the second law will hold on average, with a statistical variation on the order of 1/√N where N is the number of particles in the system. For everyday (macroscopic) situations, the probability that the second law will be violated is practically zero. However, for systems with a small number of particles, thermodynamic parameters, including the entropy, may show significant statistical deviations from that predicted by the second law. Classical thermodynamic theory does not deal with these statistical variations.
Derivation from statistical mechanics
Due to Loschmidt's paradox, derivations of the Second Law have to make an assumption regarding the past, namely that the system is uncorrelated at some time in the past; this allows for simple probabilistic treatment. This assumption is usually thought as a boundary condition, and thus the second Law is ultimately a consequence of the initial conditions somewhere in the past, probably at the beginning of the universe (the Big Bang), though other scenarios have also been suggested.[54][55][56]Given these assumptions, in statistical mechanics, the Second Law is not a postulate, rather it is a consequence of the fundamental postulate, also known as the equal prior probability postulate, so long as one is clear that simple probability arguments are applied only to the future, while for the past there are auxiliary sources of information which tell us that it was low entropy.[citation needed] The first part of the second law, which states that the entropy of a thermally isolated system can only increase, is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of
 is:
is: is the number of quantum states in a small interval between
is the number of quantum states in a small interval between  and
and 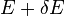 . Here
. Here  is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of
is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of  . However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on
. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on  .
.Suppose we have an isolated system whose macroscopic state is specified by a number of variables. These macroscopic variables can, e.g., refer to the total volume, the positions of pistons in the system, etc. Then
 will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that
will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that  is maximized as that is the most probable situation in equilibrium.
is maximized as that is the most probable situation in equilibrium.If the variable was initially fixed to some value then upon release and when the new equilibrium has been reached, the fact the variable will adjust itself so that
 is maximized, implies that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value). Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number
is maximized, implies that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value). Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number  of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of
of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of  . We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity H increases monotonically as a function of time during the intermediate out of equilibrium state.
. We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity H increases monotonically as a function of time during the intermediate out of equilibrium state.Derivation of the entropy change for reversible processes
The second part of the Second Law states that the entropy change of a system undergoing a reversible process is given by:The generalized force, X, corresponding to the external variable x is defined such that
 is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate
is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate  is given by:
is given by: , we define the generalized force for the system as the expectation value of the above expression:
, we define the generalized force for the system as the expectation value of the above expression: energy eigenstates by counting how many of them have a value for
energy eigenstates by counting how many of them have a value for 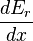 within a range between
within a range between 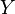 and
and  . Calling this number
. Calling this number  , we have:
, we have: will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between
will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between  and
and 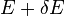 . Let's focus again on the energy eigenstates for which
. Let's focus again on the energy eigenstates for which 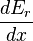 lies within the range between
lies within the range between 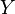 and
and  . Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E – Y dx to E move from below E to above E. There are
. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E – Y dx to E move from below E to above E. There are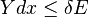 , all these energy eigenstates will move into the range between
, all these energy eigenstates will move into the range between  and
and 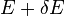 and contribute to an increase in
and contribute to an increase in  . The number of energy eigenstates that move from below
. The number of energy eigenstates that move from below 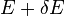 to above
to above 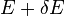 is, of course, given by
is, of course, given by 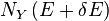 . The difference
. The difference . Note that if Y dx is larger than
. Note that if Y dx is larger than  there will be the energy eigenstates that move from below E to above
there will be the energy eigenstates that move from below E to above 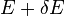 . They are counted in both
. They are counted in both  and
and 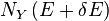 , therefore the above expression is also valid in that case.
, therefore the above expression is also valid in that case.Expressing the above expression as a derivative w.r.t. E and summing over Y yields the expression:
 w.r.t. x is thus given by:
w.r.t. x is thus given by:Derivation for systems described by the canonical ensemble
If a system is in thermal contact with a heat bath at some temperature T then, in equilibrium, the probability distribution over the energy eigenvalues are given by the canonical ensemble: for the canonical ensemble in here gives:
for the canonical ensemble in here gives:General derivation from unitarity of quantum mechanics
The time development operator in quantum theory is unitary, because the Hamiltonian is hermitian. Consequently, the transition probability matrix is doubly stochastic, which implies the Second Law of Thermodynamics.[57][58]This derivation is quite general, based on the Shannon entropy, and does not require any assumptions beyond unitarity, which is universally accepted. It is a consequence of the irreversibility or singular nature of the general transition matrix.
Non-equilibrium states
The theory of classical or equilibrium thermodynamics is idealized. A main postulate or assumption, often not even explicitly stated, is the existence of systems in their own internal states of thermodynamic equilibrium. In general, a region of space containing a physical system at a given time, that may be found in nature, is not in thermodynamic equilibrium, read in the most stringent terms. In looser terms, nothing in the entire universe is or has ever been truly in exact thermodynamic equilibrium.[59][60]For purposes of physical analysis, it is often enough convenient to make an assumption of thermodynamic equilibrium. Such an assumption may rely on trial and error for its justification. If the assumption is justified, it can often be very valuable and useful because it makes available the theory of thermodynamics. Elements of the equilibrium assumption are that a system is observed to be unchanging over an indefinitely long time, and that there are so many particles in a system, that its particulate nature can be entirely ignored. Under such an equilibrium assumption, in general, there are no macroscopically detectable fluctuations. There is an exception, the case of critical states, which exhibit to the naked eye the phenomenon of critical opalescence. For laboratory studies of critical states, exceptionally long observation times are needed.
In all cases, the assumption of thermodynamic equilibrium, once made, implies as a consequence that no putative candidate "fluctuation" alters the entropy of the system.
It can easily happen that a physical system exhibits internal macroscopic changes that are fast enough to invalidate the assumption of the constancy of the entropy. Or that a physical system has so few particles that the particulate nature is manifest in observable fluctuations. Then the assumption of thermodynamic equilibrium is to be abandoned. There is no unqualified general definition of entropy for non-equilibrium states.[61]
Non-equilibrium thermodynamics is then appropriate. There are intermediate cases, in which the assumption of local thermodynamic equilibrium is a very good approximation,[62][63][64][65] but strictly speaking it is still an approximation, not theoretically ideal. For non-equilibrium situations in general, it may be useful to consider statistical mechanical definitions of quantities that may be conveniently called 'entropy'. These indeed belong to statistical mechanics, not to macroscopic thermodynamics.
The physics of macroscopically observable fluctuations is beyond the scope of this article.
Arrow of time
The second law of thermodynamics is a physical law that is not symmetric to reversal of the time direction.The second law has been proposed to supply an explanation of the difference between moving forward and backwards in time, such as why the cause precedes the effect (the causal arrow of time).[66]Controversies
Maxwell's demon

James Clerk Maxwell imagined one container divided into two parts, A and B. Both parts are filled with the same gas at equal temperatures and placed next to each other. Observing the molecules on both sides, an imaginary demon guards a trapdoor between the two parts. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics.
One of the most famous responses to this question was suggested in 1929 by Leó Szilárd and later by Léon Brillouin. Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy.
Maxwell's demon repeatedly alters the permeability of the wall between A and B. It is therefore performing thermodynamic operations, not just presiding over natural processes.
Loschmidt's paradox
Loschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics. This puts the time reversal symmetry of nearly all known low-level fundamental physical processes at odds with any attempt to infer from them the second law of thermodynamics which describes the behavior of macroscopic systems. Both of these are well-accepted principles in physics, with sound observational and theoretical support, yet they seem to be in conflict; hence the paradox.One proposed resolution of this paradox is as follows. The Loschmidt scenario refers to a strictly isolated system or to a strictly adiabatically isolated system. Heat and matter transfers are not allowed. The Loschmidt reversal times are fantastically long, far longer than any laboratory isolation of the required degree of perfection could be maintained in practice. In this sense, the Loschmidt scenario will never be subjected to empirical testing. Also in this sense, the second law, stated for an isolated system, will never be subjected to empirical testing. A system, supposedly perfectly isolated, in strictly perfect thermodynamic equilibrium, can be observed only once in its entire life, because the observation must break the isolation. Two observations would be needed to check empirically for a change of state, one initial and one final. When transfer of heat or matter are permitted, the requirements of perfection are not so tight. In practical laboratory reality, therefore, the second law can be tested only for systems with transfer of heat or matter, and not for isolated systems.
Due to this paradox, derivations of the second law have to make an assumption regarding the past, namely that the system is uncorrelated at some time in the past or, equivalently, that the entropy in the past was lower than in the future. This assumption is usually thought as a boundary condition, and thus the second Law is ultimately derived from the initial conditions of the Big Bang.[54][67]
Poincaré recurrence theorem
The Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence, which is of the order of .[68] The result applies to physical systems in which energy is conserved. The Recurrence theorem apparently contradicts the Second law of thermodynamics, which says that large dynamical systems evolve irreversibly towards the state with higher entropy, so that if one starts with a low-entropy state, the system will never return to it. There are many possible ways to resolve this paradox, but none of them is universally accepted.[citation needed] The most reasonable argument is that for typical thermodynamical systems the recurrence time is so large (many many times longer than the lifetime of the universe) that, for all practical purposes, one cannot observe the recurrence.
.[68] The result applies to physical systems in which energy is conserved. The Recurrence theorem apparently contradicts the Second law of thermodynamics, which says that large dynamical systems evolve irreversibly towards the state with higher entropy, so that if one starts with a low-entropy state, the system will never return to it. There are many possible ways to resolve this paradox, but none of them is universally accepted.[citation needed] The most reasonable argument is that for typical thermodynamical systems the recurrence time is so large (many many times longer than the lifetime of the universe) that, for all practical purposes, one cannot observe the recurrence.Quotations
The law that entropy always increases holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equations — then so much the worse for Maxwell's equations. If it is found to be contradicted by observation — well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.
—Sir Arthur Stanley Eddington, The Nature of the Physical World (1927)
There have been nearly as many formulations of the second law as there have been discussions of it.
—Philosopher / Physicist P.W. Bridgman, (1941)
Clausius is the author of the sibyllic utterance, "The energy of the universe is constant; the entropy of the universe tends to a maximum." The objectives of continuum thermomechanics stop far short of explaining the "universe", but within that theory we may easily derive an explicit statement in some ways reminiscent of Clausius, but referring only to a modest object: an isolated body of finite size.
—Truesdell, C., Muncaster, R.G. (1980). Fundamentals of Maxwell's Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics, Academic Press, New York, ISBN0-12-701350-4, p.17.




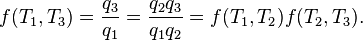
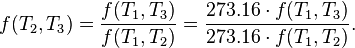



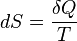









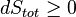 Is equivalent to
Is equivalent to 

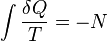
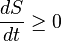
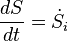 with
with 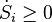
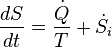 with
with  is the heat flow into the system
is the heat flow into the system is the temperature at the point where the heat enters the system.
is the temperature at the point where the heat enters the system. with
with ![S = k_{\mathrm B} \ln\left[\Omega\left(E\right)\right]\,](http://upload.wikimedia.org/math/c/9/a/c9a4155c99dc196648017bba2b85e0c1.png)

![\frac{1}{k_{\mathrm B} T}\equiv\beta\equiv\frac{d\ln\left[\Omega\left(E\right)\right]}{dE}](http://upload.wikimedia.org/math/9/a/a/9aa130c8295d811f02f994634ee80ca4.png)















