Ideal gas law

From Wikipedia, the free encyclopedia

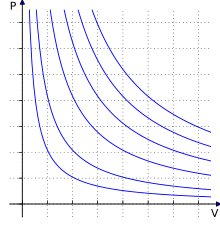
Isotherms of an ideal gas. The curved lines represent the relationship between pressure (on the vertical axis) and volume (on the horizontal axis) for an ideal gas at different temperatures: lines that are farther away from the origin (that is, lines that are nearer to the top right-hand corner of the diagram) represent higher temperatures.

The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written as

${\displaystyle PV=nRT,}$

where ${\displaystyle P}$, ${\displaystyle V}$ and ${\displaystyle T}$ are the pressure, volume and absolute temperature; ${\displaystyle n}$ is the number of moles of gas; and ${\displaystyle R}$ is the ideal gas constant. It is the same for all gases. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856 and Rudolf Clausius in 1857.

Equation

Molecular collisions within a closed container (the propane tank) are shown (right). The arrows represent the random motions and collisions of these molecules. The pressure and temperature of the gas are directly proportional: as the temperature is increased, the pressure of the propane increases by the same factor. A simple consequence of this proportionality is that on a hot summer day, the propane tank pressure will be elevated, and thus propane tanks must be rated to withstand such increases in pressure.

The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropriate SI unit is the kelvin.

Common forms

The most frequently introduced form is

${\displaystyle PV=nRT=Nk_{\text{B}}T,}$

where:

• ${\displaystyle P}$ is the pressure of the gas,
• ${\displaystyle V}$ is the volume of the gas,
• ${\displaystyle n}$ is the amount of substance of gas (also known as number of moles),
• ${\displaystyle N}$ is the number of gas molecules (or the Avogadro constant times the amount of substance ${\displaystyle N_{\text{A}}n}$),
• ${\displaystyle R}$ is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
• ${\displaystyle k_{\text{B}}}$ is the Boltzmann constant,
• ${\displaystyle T}$ is the absolute temperature of the gas.

In SI units, P is measured in pascals, V is measured in cubic metres, n is measured in moles, and T in kelvins (the Kelvin scale is a shifted Celsius scale, where 0.00 K = −273.15 °C, the lowest possible temperature). R has the value 8.314 J/(K·mol) ≈ 2 cal/(K·mol), or 0.08206 L·atm/(mol·K).

Molar form

How much gas is present could be specified by giving the mass instead of the chemical amount of gas. Therefore, an alternative form of the ideal gas law may be useful. The chemical amount (n) (in moles) is equal to total mass of the gas (m) (in grams) divided by the molar mass (M) (in grams per mole):

${\displaystyle n={\frac {m}{M}}.}$

By replacing n with m/M and subsequently introducing density ρ = m/V, we get:

${\displaystyle PV={\frac {m}{M}}RT}$,

 

${\displaystyle P={\frac {m}{V}}{\frac {RT}{M}}}$,

 

${\displaystyle P=\rho {\frac {R}{M}}T}$.

Defining the specific gas constant R_specific(r) as the ratio R/M,

${\displaystyle P=\rho R_{\text{specific}}T}$.

This form of the ideal gas law is very useful because it links pressure, density, and temperature in a unique formula independent of the quantity of the considered gas. Alternatively, the law may be written in terms of the specific volume v, the reciprocal of density, as

${\displaystyle Pv=R_{\text{specific}}T.}$

It is common, especially in engineering applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as ${\displaystyle {\bar {R}}}$ to distinguish it. In any case, the context and/or units of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to.

Statistical mechanics

In statistical mechanics the following molecular equation is derived from first principles

${\displaystyle P=nk_{\text{B}}T,}$

where P is the absolute pressure of the gas, n is the number of molecules in the given volume V (the number density is given by the ratio n = N/V, in contrasts to the previous formulation in which n is the number of moles), T is the absolute temperature, and k_B is the Boltzmann constant relating temperature and energy, given by:

${\displaystyle k_{\text{B}}={\frac {R}{N_{\text{A}}}}}$

where N_A is the Avogadro constant.

From this we notice that for a gas of mass m, with an average particle mass of μ times the atomic mass constant, m_u, (i.e., the mass is μ u) the number of molecules will be given by

${\displaystyle N={\frac {m}{\mu m_{\text{u}}}},}$

and since ρ = m/V = nμm_u, we find that the ideal gas law can be rewritten as

${\displaystyle P={\frac {1}{V}}{\frac {m}{\mu m_{\text{u}}}}k_{\text{B}}T={\frac {k_{\text{B}}}{\mu m_{\text{u}}}}\rho T.}$

In SI units, P is measured in pascals, V in cubic metres, and T in measured kelvins. k_B has the value 1.38·10⁻²³ J/K in SI units.

Energy associated with a gas

According to the assumptions of the kinetic theory of gases, we assumed that there are no intermolecular attractions between the molecules of an ideal gas. In other words, its potential energy is zero. Hence, all the energy possessed by the gas is kinetic energy.

${\displaystyle E={\frac {3}{2}}RT}$.

This is the kinetic energy of one mole of a gas.

Energy of gas	Mathematical formula
Energy associated with one mole of a gas	${\displaystyle E={\frac {3}{2}}RT}$
Energy associated with one gram of a gas	${\displaystyle E={\frac {3}{2}}rT}$
Energy associated with one molecule of a gas	${\displaystyle E={\frac {3}{2}}k_{B}T}$

Applications to thermodynamic processes

The table below essentially simplifies the ideal gas equation for a particular processes, thus making this equation easier to solve using numerical methods.

A thermodynamic process is defined as a system that moves from state 1 to state 2, where the state number is denoted by subscript. As shown in the first column of the table, basic thermodynamic processes are defined such that one of the gas properties (P, V, T, S, or H) is constant throughout the process.

For a given thermodynamics process, in order to specify the extent of a particular process, one of the properties ratios (which are listed under the column labeled "known ratio") must be specified (either directly or indirectly). Also, the property for which the ratio is known must be distinct from the property held constant in the previous column (otherwise the ratio would be unity, and not enough information would be available to simplify the gas law equation).

In the final three columns, the properties (P, V, or T) at state 2 can be calculated from the properties at state 1 using the equations listed.

Process	Constant	Known ratio or delta	P2	V2	T2
Isobaric process	Pressure	V2/V1	P2 = P1	V2 = V1(V2/V1)	T2 = T1(V2/V1)
		T2/T1	P2 = P1	V2 = V1(T2/T1)	T2 = T1(T2/T1)
Isochoric process (Isovolumetric process) (Isometric process)	Volume	P2/P1	P2 = P1(P2/P1)	V2 = V1	T2 = T1(P2/P1)
		T2/T1	P2 = P1(T2/T1)	V2 = V1	T2 = T1(T2/T1)
Isothermal process	Temperature	P2/P1	P2 = P1(P2/P1)	V2 = V1/(P2/P1)	T2 = T1
		V2/V1	P2 = P1/(V2/V1)	V2 = V1(V2/V1)	T2 = T1
Isentropic process (Reversible adiabatic process)	Entropy	P2/P1	P2 = P1(P2/P1)	V2 = V1(P2/P1)(−1/γ)	T2 = T1(P2/P1)(γ − 1)/γ
		V2/V1	P2 = P1(V2/V1)−γ	V2 = V1(V2/V1)	T2 = T1(V2/V1)(1 − γ)
		T2/T1	P2 = P1(T2/T1)γ/(γ − 1)	V2 = V1(T2/T1)1/(1 − γ)	T2 = T1(T2/T1)
Polytropic process	P Vn	P2/P1	P2 = P1(P2/P1)	V2 = V1(P2/P1)(-1/n)	T2 = T1(P2/P1)(n − 1)/n
		V2/V1	P2 = P1(V2/V1)−n	V2 = V1(V2/V1)	T2 = T1(V2/V1)(1 − n)
		T2/T1	P2 = P1(T2/T1)n/(n − 1)	V2 = V1(T2/T1)1/(1 − n)	T2 = T1(T2/T1)
Isenthalpic process (Irreversible adiabatic process)	Enthalpy	P2 − P1	P2 = P1 + (P2 − P1)		T2 = T1 + μJT(P2 − P1)
		T2 − T1	P2 = P1 + (T2 − T1)/μJT		T2 = T1 + (T2 − T1)

In an isentropic process, system entropy (S) is constant. Under these conditions, P₁ V₁^γ = P₂ V₂^γ, where γ is defined as the heat capacity ratio, which is constant for a calorifically perfect gas. The value used for γ is typically 1.4 for diatomic gases like nitrogen (N₂) and oxygen (O₂), (and air, which is 99% diatomic). Also γ is typically 1.6 for mono atomic gases like the noble gases helium (He), and argon (Ar). In internal combustion engines γ varies between 1.35 and 1.15, depending on constitution gases and temperature.

In an isenthalpic process, system enthalpy (H) is constant. In the case of free expansion for an ideal gas, there are no molecular interactions, and the temperature remains constant. For real gasses, the molecules do interact via attraction or repulsion depending on temperature and pressure, and heating or cooling does occur. This is known as the Joule–Thomson effect. For reference, the Joule–Thomson coefficient μ_JT for air at room temperature and sea level is 0.22 °C/bar.

Deviations from ideal behavior of real gases

The equation of state given here (PV=nRT) applies only to an ideal gas, or as an approximation to a real gas that behaves sufficiently like an ideal gas. There are in fact many different forms of the equation of state. Since the ideal gas law neglects both molecular size and inter molecular attractions, it is most accurate for monatomic gases at high temperatures and low pressures. The neglect of molecular size becomes less important for lower densities, i.e. for larger volumes at lower pressures, because the average distance between adjacent molecules becomes much larger than the molecular size. The relative importance of intermolecular attractions diminishes with increasing thermal kinetic energy, i.e., with increasing temperatures. More detailed equations of state, such as the van der Waals equation, account for deviations from ideality caused by molecular size and intermolecular forces.

A residual property is defined as the difference between a real gas property and an ideal gas property, both considered at the same pressure, temperature, and composition.

Derivations

Empirical

The empirical laws that led to the derivation of the ideal gas law were discovered with experiments that changed only 2 state variables of the gas and kept every other one constant.

All the possible gas laws that could have been discovered with this kind of setup are:

${\displaystyle {PV}=C_{1}}$ or ${\displaystyle P_{1}V_{1}=P_{2}V_{2}}$ (1), known as Boyle´s law,
 
${\displaystyle {\frac {V}{T}}=C_{2}}$ or ${\displaystyle {\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}}$ (2), known as Charles´s law,
 
${\displaystyle {\frac {V}{N}}=C_{3}}$ or ${\displaystyle {\frac {V_{1}}{N_{1}}}={\frac {V_{2}}{N_{2}}}}$ (3), known as Avogadro´s law,
 
${\displaystyle {\frac {P}{T}}=C_{4}}$or ${\displaystyle {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}}$ (4), known as Gay-Lussac´s law,
 
${\displaystyle NT=C_{5}}$or ${\displaystyle N_{1}T_{1}=N_{2}T_{2}}$ (5),

${\displaystyle {\frac {P}{N}}=C_{6}}$ or ${\displaystyle {\frac {P_{1}}{N_{1}}}={\frac {P_{2}}{N_{2}}}}$ (6).

Where "P" stands for pressure, "V" for volume, "N" for number of particles in the gas and "T" for temperature; Where ${\displaystyle C_{1},C_{2},C_{3},C_{4},C_{5},C_{6}}$ are not actual constants but are in this context because of each equation requiring only the parameters explicitly noted in it changing.

To derive the ideal gas law one does not need to know all 6 formulas, one can just know 3 and with those derive the rest or just one more to be able to get the ideal gas law, which needs 4.

Since each formula only holds when only the state variables involved in said formula change while the others remain constant, we cannot simply use algebra and directly combine them all. I.e. Boyle did his experiments while keeping N and T constant and this must be taken into account.

Keeping this in mind, to carry the derivation on correctly, one must imagine the gas being altered by one process at a time. The derivation using 4 formulas can look as follows:

At first the gas has parameters ${\displaystyle P_{1},V_{1},N_{1},T_{1}}$.

Starting to change only pressure and volume according to Boyle's law (1), then (7). After this process, the gas has parameters ${\displaystyle P_{2},V_{2},N_{1},T_{1}}$.

Using (5) to change the number of particles in the gas and the temperature yields  (8). After this process, the gas has parameters ${\displaystyle P_{2},V_{2},N_{2},T_{2}}$.

Using then Eq. (6) to change the pressure and the number of particles yields (9). After this process, the gas has parameters ${\displaystyle P_{3},V_{2},N_{3},T_{2}}$.

Using then Charles´s law to change the volume and temperature of the gas, (10). After this process, the gas has parameters ${\displaystyle P_{3},V_{3},N_{3},T_{3}}$.

Using simple algebra on equations (7), (8), (9) and (10) yields the result:

${\displaystyle {\frac {P_{1}V_{1}}{N_{1}T_{1}}}={\frac {P_{3}V_{3}}{N_{3}T_{3}}}}$ or ${\displaystyle {\frac {PV}{NT}}=K_{B}}$, Where ${\displaystyle K_{B}}$ stands for Boltzman´s constant.

Another equivalent result, using the fact that ${\displaystyle nR=NK_{B}}$ ,where "n" is the number of moles in the gas and "R" is the universal gas constant, is:

${\displaystyle PV=nRT}$, which is known as the ideal gas law.

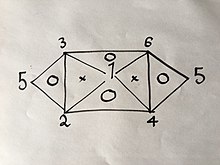
If you know or have found with an experiment 3 of the 6 formulas, you can easily derive the rest using the same method explained above; but due to the properties of said equations, namely that they only have 2 variables in them, they cant be any 3 formulas. For example if you were to have Eqs. (1), (2) and (4) you would not be able to get any more because combining any two of them will give you the third; But if you had Eqs. (1), (2) and (3) you would be able to get all 6 Equations without having to do the rest of the experiments because combining (1) and (2) will yield (4), then (1) and (3) will yield (6), then (4) and (6) will yield (5), as well as would the combination of (2) and (3) as is visually explained in the following visual relation:

Relationship between the 6 gas laws

(The numbers represent the gas laws numbered above.)

If you were to use the same method used above on 2 of the 3 laws on the vertices of one triangle that has a "O" inside it, you would get the third.

For example:

Change only pressure and volume first, ${\displaystyle P_{1}V_{1}=P_{2}V_{2}}$ (1´), then only volume and temperature, ${\displaystyle {\frac {V_{2}}{T_{1}}}={\frac {V_{3}}{T_{2}}}}$ (2´), then as we can choose any value for ${\displaystyle V_{3}}$, if we set ${\displaystyle V_{1}=V_{3}}$, Eq. (2´) becomes(3´).

Combining equations (1´) and (3´) yields ${\displaystyle {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}}$ , which is Eq. (4), of which we had no prior knowledge until this derivation.

Theoretical

Kinetic theory

The ideal gas law can also be derived from first principles using the kinetic theory of gases, in which several simplifying assumptions are made, chief among which are that the molecules, or atoms, of the gas are point masses, possessing mass but no significant volume, and undergo only elastic collisions with each other and the sides of the container in which both linear momentum and kinetic energy are conserved.

Statistical mechanics

Let q = (q_x, q_y, q_z) and p = (p_x, p_y, p_z) denote the position vector and momentum vector of a particle of an ideal gas, respectively. Let F denote the net force on that particle. Then the time-averaged kinetic energy of the particle is:

${\displaystyle {\begin{aligned}\langle \mathbf {q} \cdot \mathbf {F} \rangle &={\Bigl \langle }q_{x}{\frac {dp_{x}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{y}{\frac {dp_{y}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{z}{\frac {dp_{z}}{dt}}{\Bigr \rangle }\\&=-{\Bigl \langle }q_{x}{\frac {\partial H}{\partial q_{x}}}{\Bigr \rangle }-{\Bigl \langle }q_{y}{\frac {\partial H}{\partial q_{y}}}{\Bigr \rangle }-{\Bigl \langle }q_{z}{\frac {\partial H}{\partial q_{z}}}{\Bigr \rangle }=-3k_{B}T,\end{aligned}}}$

where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition theorem. Summing over a system of N particles yields

${\displaystyle 3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }.}$

By Newton's third law and the ideal gas assumption, the net force of the system is the force applied by the walls of the container, and this force is given by the pressure P of the gas. Hence

${\displaystyle -{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=P\oint _{\mathrm {surface} }\mathbf {q} \cdot d\mathbf {S} ,}$

where dS is the infinitesimal area element along the walls of the container. Since the divergence of the position vector q is

${\displaystyle \nabla \cdot \mathbf {q} ={\frac {\partial q_{x}}{\partial q_{x}}}+{\frac {\partial q_{y}}{\partial q_{y}}}+{\frac {\partial q_{z}}{\partial q_{z}}}=3,}$

the divergence theorem implies that

${\displaystyle P\oint _{\mathrm {surface} }\mathbf {q} \cdot d\mathbf {S} =P\int _{\mathrm {volume} }\left(\nabla \cdot \mathbf {q} \right)dV=3PV,}$

where dV is an infinitesimal volume within the container and V is the total volume of the container.

Putting these equalities together yields

${\displaystyle 3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=3PV,}$

which immediately implies the ideal gas law for N particles:

${\displaystyle PV=Nk_{B}T=nRT,\,}$

where n = N/N_A is the number of moles of gas and R = N_Ak_B is the gas constant.

Arrhenius equation

From Wikipedia, the free encyclopedia

The Arrhenius equation is a formula for the temperature dependence of reaction rates. The equation was proposed by Svante Arrhenius in 1889, based on the work of Dutch chemist Jacobus Henricus van 't Hoff who had noted in 1884 that Van 't Hoff's equation for the temperature dependence of equilibrium constants suggests such a formula for the rates of both forward and reverse reactions. This equation has a vast and important application in determining rate of chemical reactions and for calculation of energy of activation. Arrhenius provided a physical justification and interpretation for the formula. Currently, it is best seen as an empirical relationship. It can be used to model the temperature variation of diffusion coefficients, population of crystal vacancies, creep rates, and many other thermally-induced processes/reactions. The Eyring equation, developed in 1935, also expresses the relationship between rate and energy.

Equation

In almost all practical cases, ${\displaystyle E_{a}>>RT}$ and k increases rapidly with T.

Mathematically, at very high temperatures so that ${\displaystyle E_{a}<$, k levels off and approaches A as a limit, but this case does not occur under practical conditions.

Arrhenius' equation gives the dependence of the rate constant of a chemical reaction on the absolute temperature, a pre-exponential factor and other constants of the reaction:

${\displaystyle k=Ae^{\frac {-E_{a}}{RT}}}$,

where

• k is the rate constant,
• T is the absolute temperature (in kelvin),
• A is the pre-exponential factor, a constant for each chemical reaction. According to collision theory, A is the frequency of collisions in the correct orientation,
• E_a is the activation energy for the reaction (in the same units as R*T),
• R is the universal gas constant.

Alternatively, the equation may be expressed as

${\displaystyle k=Ae^{\frac {-E_{a}}{k_{B}T}}}$

where

• E_a is the activation energy for the reaction (in the same units as k_B*T),
• k_B is the Boltzmann constant.

The only difference is the energy units of E_a: the former form uses energy per mole, which is common in chemistry, while the latter form uses energy per molecule directly, which is common in physics. The different units are accounted for in using either the gas constant, R, or the Boltzmann constant, k_B, as the multiplier of temperature T.

The units of the pre-exponential factor A are identical to those of the rate constant and will vary depending on the order of the reaction. If the reaction is first order it has the units: s⁻¹, and for that reason it is often called the frequency factor or attempt frequency of the reaction. Most simply, k is the number of collisions that result in a reaction per second, A is the number of collisions (leading to a reaction or not) per second occurring with the proper orientation to react and ${\displaystyle e^{{-E_{a}}/{(RT)}}\ \ \ }$is the probability that any given collision will result in a reaction. It can be seen that either increasing the temperature or decreasing the activation energy (for example through the use of catalysts) will result in an increase in rate of reaction.

Given the small temperature range of kinetic studies, it is reasonable to approximate the activation energy as being independent of the temperature. Similarly, under a wide range of practical conditions, the weak temperature dependence of the pre-exponential factor is negligible compared to the temperature dependence of the ${\displaystyle \exp(-E_{a}/(RT))\ \ }$ factor; except in the case of "barrierless" diffusion-limited reactions, in which case the pre-exponential factor is dominant and is directly observable.

Arrhenius plot

Arrhenius linear plot: ln(k) against 1/T.

Taking the natural logarithm of Arrhenius' equation yields

${\displaystyle \ln(k)=\ln(A)-{\frac {E_{a}}{R}}{\frac {1}{T}}}$.

Rearranging yields

${\displaystyle \ln(k)={\frac {-E_{a}}{R}}\left({\frac {1}{T}}\right)+\ln(A)}$.

This has the same form as an equation for a straight line:

${\displaystyle y=mx+c}$,

where x is the reciprocal of T.

So, when a reaction has a rate constant that obeys Arrhenius' equation, a plot of ln(k) versus T ⁻¹ gives a straight line, whose gradient and intercept can be used to determine E_a and A . This procedure has become so common in experimental chemical kinetics that practitioners have taken to using it to define the activation energy for a reaction. That is the activation energy is defined to be (−R) times the slope of a plot of ln(k) vs. (1/T ):

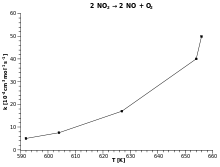
${\displaystyle \ E_{a}\equiv -R\left[{\frac {\partial \ln k}{\partial ~(1/T)}}\right]_{P}}$.

Modified Arrhenius' equation

The modified Arrhenius' equation makes explicit the temperature dependence of the pre-exponential factor. The modified equation is usually of the form

${\displaystyle k=AT^{n}e^{{-E_{a}}/{(RT)}}}$.

The original Arrhenius expression above corresponds to n = 0. Fitted rate constants typically lie in the range −1 < n < 1. Theoretical analyses yield various predictions for n. It has been pointed out that "it is not feasible to establish, on the basis of temperature studies of the rate constant, whether the predicted T^½ dependence of the pre-exponential factor is observed experimentally." However, if additional evidence is available, from theory and/or from experiment (such as density dependence), there is no obstacle to incisive tests of the Arrhenius law.

Another common modification is the stretched exponential form:

${\displaystyle k=A\exp \left[-\left({\frac {E_{a}}{RT}}\right)^{\beta }\right]}$,

where β is a purely dimensionless number of order 1. This is typically regarded as a purely empirical correction or fudge factor to make the model fit the data, but can have theoretical meaning, for example showing the presence of a range of activation energies or in special cases like the Mott variable range hopping.

Theoretical interpretation of the equation

Arrhenius' concept of activation energy

Arrhenius argued that for reactants to transform into products, they must first acquire a minimum amount of energy, called the activation energy E_a. At an absolute temperature T, the fraction of molecules that have a kinetic energy greater than E_a can be calculated from statistical mechanics. The concept of activation energy explains the exponential nature of the relationship, and in one way or another, it is present in all kinetic theories.

The calculations for reaction rate constants involve an energy averaging over a Maxwell–Boltzmann distribution with ${\displaystyle E_{a}}$as lower bound and so are often of the type of incomplete gamma functions, which turn out to be proportional to ${\displaystyle \ e^{\frac {-E_{a}}{RT}}}$.

Collision theory

One example comes from the collision theory of chemical reactions, developed by Max Trautz and William Lewis in the years 1916-18. In this theory, molecules are supposed to react if they collide with a relative kinetic energy along their lines-of-center that exceeds E_a. This leads to an expression very similar to the Arrhenius equation.

Transition state theory

The Eyring equation, another Arrhenius-like expression, appears in the "transition state theory" of chemical reactions, formulated by Wigner, Eyring, Polanyi and Evans in the 1930s. This takes various forms, but one of the most common is

${\displaystyle \ k={\frac {k_{B}T}{h}}e^{-{\frac {\Delta G^{\ddagger }}{RT}}}}$,

where ${\displaystyle \Delta G^{\ddagger }}$ is the Gibbs energy of activation, ${\displaystyle k_{B}}$ is Boltzmann's constant, and ${\displaystyle h}$ is Planck's constant.

At first sight this looks like an exponential multiplied by a factor that is linear in temperature. However, free energy is itself a temperature dependent quantity. The free energy of activation is the difference of an enthalpy term and an entropy term multiplied by the absolute temperature. When all of the details are worked out one ends up with an expression that again takes the form of an Arrhenius exponential multiplied by a slowly varying function of T. The precise form of the temperature dependence depends upon the reaction, and can be calculated using formulas from statistical mechanics involving the partition functions of the reactants and of the activated complex.

Limitations of the idea of Arrhenius activation energy

Both the Arrhenius activation energy and the rate constant k are experimentally determined, and represent macroscopic reaction-specific parameters that are not simply related to threshold energies and the success of individual collisions at the molecular level. Consider a particular collision (an elementary reaction) between molecules A and B. The collision angle, the relative translational energy, the internal (particularly vibrational) energy will all determine the chance that the collision will produce a product molecule AB. Macroscopic measurements of E and k are the result of many individual collisions with differing collision parameters. To probe reaction rates at molecular level, experiments are conducted under near-collisional conditions and this subject is often called molecular reaction dynamics.

There are deviations from the Arrhenius law during the glass transition in all classes of glass-forming matter. The Arrhenius law predicts that the motion of the structural units (atoms, molecules, ions, etc.) should slow down at a slower rate through the glass transition than is experimentally observed. In other words, the structural units slow down at a faster rate than is predicted by the Arrhenius law. This observation is made reasonable assuming that the units must overcome an energy barrier by means of a thermal activation energy. The thermal energy must be high enough to allow for translational motion of the units which leads to viscous flow of the material.