Straightedge and compass construction

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Straightedge_and_compass_construction

 

Creating a regular hexagon with a straightedge and compass

Straightedge-and-compass construction, also known as ruler-and-compass construction or classical construction, is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.

The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, the only permissible constructions are those granted by the first three postulates of Euclid's Elements.

It turns out to be the case that every point constructible using straightedge and compass may also be constructed using compass alone, or by straightedge alone if given a single circle and its center.

The ancient Greek mathematicians first conceived straightedge-and-compass constructions, and a number of ancient problems in plane geometry impose this restriction. The ancient Greeks developed many constructions, but in some cases were unable to do so. Gauss showed that some polygons are constructible but that most are not. Some of the most famous straightedge-and-compass problems were proved impossible by Pierre Wantzel in 1837, using the mathematical theory of fields.

In spite of existing proofs of impossibility, some persist in trying to solve these problems.^[1] Many of these problems are easily solvable provided that other geometric transformations are allowed: for example, doubling the cube is possible using geometric constructions, but not possible using straightedge and compass alone.

In terms of algebra, a length is constructible if and only if it represents a constructible number, and an angle is constructible if and only if its cosine is a constructible number. A number is constructible if and only if it can be written using the four basic arithmetic operations and the extraction of square roots but of no higher-order roots.

Straightedge and compass tools

Straightedge and compass

 

A compass

The "straightedge" and "compass" of straightedge-and-compass constructions are idealizations of rulers and compasses in the real world:

• The straightedge is infinitely long, but it has no markings on it and has only one straight edge, unlike ordinary rulers. The line drawn is infinitesimally thin point-width. It can only be used to draw a line segment between two points, with infinite precision to those points, or to extend an existing segment.
• The compass can be opened arbitrarily wide, but (unlike some real compasses) it has no markings on it. Circles can only be drawn starting from two given points: the centre and a point on the circle, and aligned to those points with infinite precision. The arc that is drawn is infinitesimally thin point-width. The compass may or may not collapse when it is not drawing a circle.

Actual compasses do not collapse and modern geometric constructions often use this feature. A 'collapsing compass' would appear to be a less powerful instrument. However, by the compass equivalence theorem in Proposition 2 of Book 1 of Euclid's Elements, no power is lost by using a collapsing compass. Although the proposition is correct, its proofs have a long and checkered history. In any case, the equivalence is why this feature is not stipulated in the definition of the ideal compass.

Each construction must be exact. "Eyeballing" it (essentially looking at the construction and guessing at its accuracy, or using some form of measurement, such as the units of measure on a ruler) and getting close does not count as a solution.

Each construction must terminate. That is, it must have a finite number of steps, and not be the limit of ever closer approximations.

Stated this way, straightedge-and-compass constructions appear to be a parlour game, rather than a serious practical problem; but the purpose of the restriction is to ensure that constructions can be proved to be exactly correct.

History

The ancient Greek mathematicians first attempted straightedge-and-compass constructions, and they discovered how to construct sums, differences, products, ratios, and square roots of given lengths. They could also construct half of a given angle, a square whose area is twice that of another square, a square having the same area as a given polygon, and a regular polygon with 3, 4, or 5 sides (or one with twice the number of sides of a given polygon). But they could not construct one third of a given angle except in particular cases, or a square with the same area as a given circle, or a regular polygon with other numbers of sides. Nor could they construct the side of a cube whose volume would be twice the volume of a cube with a given side.

Hippocrates and Menaechmus showed that the volume of the cube could be doubled by finding the intersections of hyperbolas and parabolas, but these cannot be constructed by straightedge and compass. In the fifth century BCE, Hippias used a curve that he called a quadratrix to both trisect the general angle and square the circle, and Nicomedes in the second century BCE showed how to use a conchoid to trisect an arbitrary angle; but these methods also cannot be followed with just straightedge and compass.

No progress on the unsolved problems was made for two millennia, until in 1796 Gauss showed that a regular polygon with 17 sides could be constructed; five years later he showed the sufficient criterion for a regular polygon of n sides to be constructible.

In 1837 Pierre Wantzel published a proof of the impossibility of trisecting an arbitrary angle or of doubling the volume of a cube, based on the impossibility of constructing cube roots of lengths. He also showed that Gauss's sufficient constructibility condition for regular polygons is also necessary.

Then in 1882 Lindemann showed that ${\displaystyle \pi }$ is a transcendental number, and thus that it is impossible by straightedge and compass to construct a square with the same area as a given circle.

The basic constructions

The basic constructions

All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:

• Creating the line through two existing points
• Creating the circle through one point with centre another point
• Creating the point which is the intersection of two existing, non-parallel lines
• Creating the one or two points in the intersection of a line and a circle (if they intersect)
• Creating the one or two points in the intersection of two circles (if they intersect).

For example, starting with just two distinct points, we can create a line or either of two circles (in turn, using each point as centre and passing through the other point). If we draw both circles, two new points are created at their intersections. Drawing lines between the two original points and one of these new points completes the construction of an equilateral triangle.

Therefore, in any geometric problem we have an initial set of symbols (points and lines), an algorithm, and some results. From this perspective, geometry is equivalent to an axiomatic algebra, replacing its elements by symbols. Probably Gauss first realized this, and used it to prove the impossibility of some constructions; only much later did Hilbert find a complete set of axioms for geometry.

Much used straightedge-and-compass constructions

The most-used straightedge-and-compass constructions include:

• Constructing the perpendicular bisector from a segment
• Finding the midpoint of a segment.
• Drawing a perpendicular line from a point to a line.
• Bisecting an angle
• Mirroring a point in a line
• Constructing a line through a point tangent to a circle
• Constructing a circle through 3 noncollinear points
• Drawing a line through a given point parallel to a given line.

Constructible points

Main article: Constructible number

 

Straightedge-and-compass constructions corresponding to algebraic operations

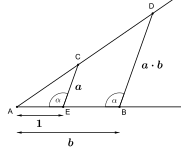
x = a·b   (intercept theorem)

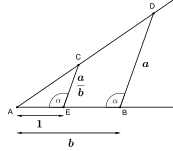
x = a/b   (intercept theorem)

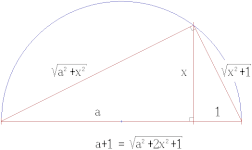
x=√a   (Pythagorean theorem)

One can associate an algebra to our geometry using a Cartesian coordinate system made of two lines, and represent points of our plane by vectors. Finally we can write these vectors as complex numbers.

Using the equations for lines and circles, one can show that the points at which they intersect lie in a quadratic extension of the smallest field F containing two points on the line, the center of the circle, and the radius of the circle. That is, they are of the form x +y√k, where x, y, and k are in F.

Since the field of constructible points is closed under square roots, it contains all points that can be obtained by a finite sequence of quadratic extensions of the field of complex numbers with rational coefficients. By the above paragraph, one can show that any constructible point can be obtained by such a sequence of extensions. As a corollary of this, one finds that the degree of the minimal polynomial for a constructible point (and therefore of any constructible length) is a power of 2. In particular, any constructible point (or length) is an algebraic number, though not every algebraic number is constructible; for example, ³√2 is algebraic but not constructible.

Constructible angles

There is a bijection between the angles that are constructible and the points that are constructible on any constructible circle. The angles that are constructible form an abelian group under addition modulo 2π (which corresponds to multiplication of the points on the unit circle viewed as complex numbers). The angles that are constructible are exactly those whose tangent (or equivalently, sine or cosine) is constructible as a number. For example, the regular heptadecagon (the seventeen-sided regular polygon) is constructible because

${\displaystyle {\begin{aligned}\cos {\left({\frac {2\pi }{17}}\right)}&=\,-{\frac {1}{16}}\,+\,{\frac {1}{16}}{\sqrt {17}}\,+\,{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\\[5mu]&\qquad +\,{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}\end{aligned}}}$

as discovered by Gauss.

The group of constructible angles is closed under the operation that halves angles (which corresponds to taking square roots in the complex numbers). The only angles of finite order that may be constructed starting with two points are those whose order is either a power of two, or a product of a power of two and a set of distinct Fermat primes. In addition there is a dense set of constructible angles of infinite order.

Relation to complex arithmetic

Given a set of points in the Euclidean plane, selecting any one of them to be called 0 and another to be called 1, together with an arbitrary choice of orientation allows us to consider the points as a set of complex numbers.

Given any such interpretation of a set of points as complex numbers, the points constructible using valid straightedge-and-compass constructions alone are precisely the elements of the smallest field containing the original set of points and closed under the complex conjugate and square root operations (to avoid ambiguity, we can specify the square root with complex argument less than π). The elements of this field are precisely those that may be expressed as a formula in the original points using only the operations of addition, subtraction, multiplication, division, complex conjugate, and square root, which is easily seen to be a countable dense subset of the plane. Each of these six operations corresponding to a simple straightedge-and-compass construction. From such a formula it is straightforward to produce a construction of the corresponding point by combining the constructions for each of the arithmetic operations. More efficient constructions of a particular set of points correspond to shortcuts in such calculations.

Equivalently (and with no need to arbitrarily choose two points) we can say that, given an arbitrary choice of orientation, a set of points determines a set of complex ratios given by the ratios of the differences between any two pairs of points. The set of ratios constructible using straightedge and compass from such a set of ratios is precisely the smallest field containing the original ratios and closed under taking complex conjugates and square roots.

For example, the real part, imaginary part and modulus of a point or ratio z (taking one of the two viewpoints above) are constructible as these may be expressed as

${\displaystyle \mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;}$

${\displaystyle \mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;}$

${\displaystyle \left|z\right|={\sqrt {z{\bar {z}}}}.\;}$

Doubling the cube and trisection of an angle (except for special angles such as any φ such that φ/(2π) is a rational number with denominator not divisible by 3) require ratios which are the solution to cubic equations, while squaring the circle requires a transcendental ratio. None of these are in the fields described, hence no straightedge-and-compass construction for these exists.

Impossible constructions

The ancient Greeks thought that the construction problems they could not solve were simply obstinate, not unsolvable. With modern methods, however, these straightedge-and-compass constructions have been shown to be logically impossible to perform. (The problems themselves, however, are solvable, and the Greeks knew how to solve them without the constraint of working only with straightedge and compass.)

Squaring the circle

Main article: Squaring the circle

The most famous of these problems, squaring the circle, otherwise known as the quadrature of the circle, involves constructing a square with the same area as a given circle using only straightedge and compass.

Squaring the circle has been proved impossible, as it involves generating a transcendental number, that is, √π. Only certain algebraic numbers can be constructed with ruler and compass alone, namely those constructed from the integers with a finite sequence of operations of addition, subtraction, multiplication, division, and taking square roots. The phrase "squaring the circle" is often used to mean "doing the impossible" for this reason.

Without the constraint of requiring solution by ruler and compass alone, the problem is easily solvable by a wide variety of geometric and algebraic means, and was solved many times in antiquity.

A method which comes very close to approximating the "quadrature of the circle" can be achieved using a Kepler triangle.

Doubling the cube

Main article: Doubling the cube

Doubling the cube is the construction, using only a straightedge and compass, of the edge of a cube that has twice the volume of a cube with a given edge. This is impossible because the cube root of 2, though algebraic, cannot be computed from integers by addition, subtraction, multiplication, division, and taking square roots. This follows because its minimal polynomial over the rationals has degree 3. This construction is possible using a straightedge with two marks on it and a compass.

Angle trisection

Main article: Angle trisection

Angle trisection is the construction, using only a straightedge and a compass, of an angle that is one-third of a given arbitrary angle. This is impossible in the general case. For example, the angle 2π/5 radians (72° = 360°/5) can be trisected, but the angle of π/3 radians (60°) cannot be trisected. The general trisection problem is also easily solved when a straightedge with two marks on it is allowed (a neusis construction).

Distance to an ellipse

The line segment from any point in the plane to the nearest point on a circle can be constructed, but the segment from any point in the plane to the nearest point on an ellipse of positive eccentricity cannot in general be constructed.

Alhazen's problem

In 1997, the Oxford mathematician Peter M. Neumann proved the theorem that there is no ruler-and-compass construction for the general solution of the ancient Alhazen's problem (billiard problem or reflection from a spherical mirror).

Constructing regular polygons

Main article: Constructible polygon

 

Construction of a regular pentagon

Some regular polygons (e.g. a pentagon) are easy to construct with straightedge and compass; others are not. This led to the question: Is it possible to construct all regular polygons with straightedge and compass?

Carl Friedrich Gauss in 1796 showed that a regular 17-sided polygon can be constructed, and five years later showed that a regular n-sided polygon can be constructed with straightedge and compass if the odd prime factors of n are distinct Fermat primes. Gauss conjectured that this condition was also necessary, but he offered no proof of this fact, which was provided by Pierre Wantzel in 1837.

The first few constructible regular polygons have the following numbers of sides:

3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272... (sequence A003401 in the OEIS)

There are known to be an infinitude of constructible regular polygons with an even number of sides (because if a regular n-gon is constructible, then so is a regular 2n-gon and hence a regular 4n-gon, 8n-gon, etc.). However, there are only 31 known constructible regular n-gons with an odd number of sides.

Constructing a triangle from three given characteristic points or lengths

Sixteen key points of a triangle are its vertices, the midpoints of its sides, the feet of its altitudes, the feet of its internal angle bisectors, and its circumcenter, centroid, orthocenter, and incenter. These can be taken three at a time to yield 139 distinct nontrivial problems of constructing a triangle from three points. Of these problems, three involve a point that can be uniquely constructed from the other two points; 23 can be non-uniquely constructed (in fact for infinitely many solutions) but only if the locations of the points obey certain constraints; in 74 the problem is constructible in the general case; and in 39 the required triangle exists but is not constructible.

Twelve key lengths of a triangle are the three side lengths, the three altitudes, the three medians, and the three angle bisectors. Together with the three angles, these give 95 distinct combinations, 63 of which give rise to a constructible triangle, 30 of which do not, and two of which are underdefined.

Restricted Constructions

Various attempts have been made to restrict the allowable tools for constructions under various rules, in order to determine what is still constructable and how it may be constructed, as well as determining the minimum criteria necessary to still be able to construct everything that compass and straightedge can.

Constructing with only ruler or only compass

It is possible (according to the Mohr–Mascheroni theorem) to construct anything with just a compass if it can be constructed with a ruler and compass, provided that the given data and the data to be found consist of discrete points (not lines or circles). The truth of this theorem depends on the truth of Archimedes' axiom, which is not first-order in nature. Examples of compass-only constructions include Napoleon's problem.

It is impossible to take a square root with just a ruler, so some things that cannot be constructed with a ruler can be constructed with a compass; but (by the Poncelet–Steiner theorem) given a single circle and its center, they can be constructed.

Extended constructions

The ancient Greeks classified constructions into three major categories, depending on the complexity of the tools required for their solution. If a construction used only a straightedge and compass, it was called planar; if it also required one or more conic sections (other than the circle), then it was called solid; the third category included all constructions that did not fall into either of the other two categories. This categorization meshes nicely with the modern algebraic point of view. A complex number that can be expressed using only the field operations and square roots (as described above) has a planar construction. A complex number that includes also the extraction of cube roots has a solid construction.

In the language of fields, a complex number that is planar has degree a power of two, and lies in a field extension that can be broken down into a tower of fields where each extension has degree two. A complex number that has a solid construction has degree with prime factors of only two and three, and lies in a field extension that is at the top of a tower of fields where each extension has degree 2 or 3.

Solid constructions

A point has a solid construction if it can be constructed using a straightedge, compass, and a (possibly hypothetical) conic drawing tool that can draw any conic with already constructed focus, directrix, and eccentricity. The same set of points can often be constructed using a smaller set of tools. For example, using a compass, straightedge, and a piece of paper on which we have the parabola y=x² together with the points (0,0) and (1,0), one can construct any complex number that has a solid construction. Likewise, a tool that can draw any ellipse with already constructed foci and major axis (think two pins and a piece of string) is just as powerful.

The ancient Greeks knew that doubling the cube and trisecting an arbitrary angle both had solid constructions. Archimedes gave a solid construction of the regular 7-gon. The quadrature of the circle does not have a solid construction.

A regular n-gon has a solid construction if and only if n=2^j3^km where m is a product of distinct Pierpont primes (primes of the form 2^r3^s+1). The set of such n is the sequence

7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97... (sequence A051913 in the OEIS)

The set of n for which a regular n-gon has no solid construction is the sequence

11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100... (sequence A048136 in the OEIS)

Like the question with Fermat primes, it is an open question as to whether there are an infinite number of Pierpont primes.

Angle trisection

What if, together with the straightedge and compass, we had a tool that could (only) trisect an arbitrary angle? Such constructions are solid constructions, but there exist numbers with solid constructions that cannot be constructed using such a tool. For example, we cannot double the cube with such a tool. On the other hand, every regular n-gon that has a solid construction can be constructed using such a tool.

Origami

Main article: Huzita–Hatori axioms

The mathematical theory of origami is more powerful than straightedge-and-compass construction. Folds satisfying the Huzita–Hatori axioms can construct exactly the same set of points as the extended constructions using a compass and conic drawing tool. Therefore, origami can also be used to solve cubic equations (and hence quartic equations), and thus solve two of the classical problems.

Markable rulers

Main article: Neusis construction

Archimedes, Nicomedes and Apollonius gave constructions involving the use of a markable ruler. This would permit them, for example, to take a line segment, two lines (or circles), and a point; and then draw a line which passes through the given point and intersects the two given lines, such that the distance between the points of intersection equals the given segment. This the Greeks called neusis ("inclination", "tendency" or "verging"), because the new line tends to the point. In this expanded scheme, we can trisect an arbitrary angle (see Archimedes' trisection) or extract an arbitrary cube root (due to Nicomedes). Hence, any distance whose ratio to an existing distance is the solution of a cubic or a quartic equation is constructible. Using a markable ruler, regular polygons with solid constructions, like the heptagon, are constructible; and John H. Conway and Richard K. Guy give constructions for several of them.

The neusis construction is more powerful than a conic drawing tool, as one can construct complex numbers that do not have solid constructions. In fact, using this tool one can solve some quintics that are not solvable using radicals. It is known that one cannot solve an irreducible polynomial of prime degree greater or equal to 7 using the neusis construction, so it is not possible to construct a regular 23-gon or 29-gon using this tool. Benjamin and Snyder proved that it is possible to construct the regular 11-gon, but did not give a construction. It is still open as to whether a regular 25-gon or 31-gon is constructible using this tool.

Trisect a straight segment

Trisection of a straight edge procedure.

Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of intercept theorem

Computation of binary digits

In 1998 Simon Plouffe gave a ruler-and-compass algorithm that can be used to compute binary digits of certain numbers. The algorithm involves the repeated doubling of an angle and becomes physically impractical after about 20 binary digits.

Space warfare

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Space_warfare 

Space warfare is hypothetical combat in which one or more belligerents are situated in outer space. The scope of space warfare therefore includes ground-to-space warfare, such as attacking satellites from the Earth; space-to-space warfare, such as satellites attacking satellites; and space-to-ground warfare, such as satellites attacking Earth-based targets. Space warfare in fiction is thus sub-genre and theme of science fiction, where it is portrayed with a range of realism and plausibility.

As of 2022, no actual warfare is known to have taken place in space, though a number of tests and demonstrations have been performed. International treaties are in place that attempt to regulate conflicts in space and limit the installation of space weapon systems, especially nuclear weapons.

From 1985 to 2002 there was a United States Space Command, which in 2002 merged with the United States Strategic Command, leaving the United States Space Force (formerly Air Force Space Command until 2019) as the primary American military space force. The Russian Space Force, established on August 10, 1992, which became an independent section of the Russian military on June 1, 2001, was replaced by the Russian Aerospace Defence Forces starting December 1, 2011, but was reestablished as a component of the Russian Aerospace Forces on August 1, 2015. In 2019 India conducted a test of the ASAT missile making it the fourth country with that capability. In April 2019, the Indian government established the Defence Space Agency, or DSA.

History

1960s

Early efforts to conduct space warfare were directed at space-to-space warfare, as ground-to-space systems were considered to be too slow and too isolated by Earth's atmosphere and gravity to be effective at the time. The history of active space warfare development goes back to the 1960s when the Soviet Union began the Almaz project, a project designed to give them the ability to do on-orbit inspections of satellites and destroy them if needed. Similar planning in the United States took the form of the Blue Gemini project, which consisted of modified Gemini capsules that would be able to deploy weapons and perform surveillance.

One early test of electronic space warfare, the so-called Starfish Prime test, took place in 1962, when the United States exploded a ground-launched nuclear weapon in space to test the effects of an electromagnetic pulse. The result was a deactivation of many then-orbiting satellites, both American and Soviet. The deleterious and unfocused effects of the EMP test led to the banning of nuclear weapons in space in the Outer Space Treaty of 1967. (See high-altitude nuclear explosion.)

In the early 1960s the U.S. military produced a film called Space and National Security which depicted space warfare.

1970s–1990s

A USAF F-15 Eagle launching an ASM-135 ASAT (anti-satellite) missile in 1985

Through the 1970s, the Soviet Union continued their project and test-fired a cannon to test space station defense. This was considered too dangerous to do with a crew on board, however, so the test was conducted after the crew had returned to Earth.

A 1976 Soviet report suggested that the design of the Space Shuttle had been guided by a requirement to deliver a payload- such as a bomb- over Russia and return to land after a single orbit. This may have been a confusion based on requirements 3A and 3B for the shuttle's design, which required the craft to be able to deploy or retrieve an object from a polar orbit in a single pass.

Both the Soviets and the United States developed anti-satellite weaponry designed to shoot down satellites. While early efforts paralleled other space-to-space warfare concepts, the United States was able in the 1980s to develop ground-to-space laser anti-satellite weapons. None of these systems are known to be active today; however, a less powerful civilian version of the ground-to-space laser system is commonly used in the astronomical technique of adaptive optics.

In 1984 the Strategic Defence Initiative (SDI) was proposed. It was nicknamed Star Wars after the popular science fiction franchise Star Wars.

In 1985 a USAF pilot in an F-15 successfully shot down the P78-1, an American research satellite, in a 345-mile (555 km) orbit with a missile.

Since 2000

A SM-3 missile is launched from a U.S. ship to intercept a failing spy satellite

 

Launch of an interceptor derived from Indian Ballistic Missile Defence Programme for ASAT test on 27 March 2019

The People's Republic of China successfully tested (see 2007 Chinese anti-satellite missile test) a ballistic missile-launched anti-satellite weapon on January 11, 2007. This resulted in harsh criticism from the United States of America, Britain, and Japan.

The U.S. developed an interceptor missile, the SM-3, testing it by hitting ballistic test targets while they were in space. On February 21, 2008, the U.S. used a SM-3 missile to destroy a spy satellite, USA-193, while it was 247 kilometers (133 nautical miles) above the Pacific Ocean.

Japan fields the U.S.-made SM-3 missile, and there have been plans to base the land-based version in Romania and Vietnam.

In March 2019, India shot down a satellite orbiting in a low Earth orbit using an ASAT missile during an operation code named Mission Shakti, thus making its way to the list of space warfare nations, establishing the Defense Space Agency the following month, followed by its first-ever simulated space warfare exercise on 25 July which would inform a joint military space doctrine.

In July 2019 Emmanuel Macron "called for a space high command to protect" France's satellites. This was followed by a plan released by military officials. French Defense Minister, Florence Parly, announced a space weapons program that would move the country's space surveillance strategy towards active protection of its assets in space, e.g. satellites. The projects outlined include: patrolling nano-satellites swarms, ground-based laser systems to blind spying satellites, and machine guns mounted on satellites.

Theoretical space weaponry

Ballistic warfare

A Trident missile launched from a Royal Navy Vanguard-class ballistic missile submarine

In the late 1970s and through the 1980s the Soviet Union and the United States theorized, designed and in some cases tested a variety of weaponry designed for warfare in outer space. Space warfare was seen primarily as an extension of nuclear warfare, and so many theoretical systems were based around the destruction or defense of ground and sea-based missiles. Space-based missiles were not attempted due to the Outer Space Treaty, which banned the use, testing or storage of nuclear weapons outside the Earth's atmosphere. When the U.S. gained "interest in utilizing space-based lasers for ballistic missile defense", two facts emerged. One being that the ballistic missiles are fragile and two, chemical lasers project missile killing energy (3,000 kilometers). This meant that lasers could be put into space to intercept a ballistic missile.

Ronald Reagan revealing the idea for the Strategic Defense Initiative on March 23, 1983

Systems proposed ranged from measures as simple as ground and space-based anti-missiles to railguns, space based lasers, orbital mines and similar weaponry. Deployment of these systems was seriously considered in the mid-1980s under the banner of the Strategic Defense Initiative announced by Ronald Reagan in 1983, using the term "evil empire" to describe the Soviets (hence the popular nickname "Star Wars"). If the Cold War had continued, many of these systems could potentially have seen deployment: the United States developed working railguns, and a laser that could destroy missiles at range, though the power requirements, range, and firing cycles of both were impractical. Weapons like the space-based laser was rejected, not just by the government, but by universities, moral thinkers, and religious people because it would have increased the waging of the arms race and questioned the United States' role in the Cold War.

Electronic warfare

With the end of the Cold War and continued development of satellite and electronics technology, attention was focused on space as a supporting theatre for conventional warfare. Currently, military operations in space primarily concern either the vast tactical advantages of satellite-based surveillance, communications, and positioning systems or mechanisms used to deprive an opponent of said tactical advantages.

Accordingly, most space-borne proposals which would traditionally be considered "weapons" (a communications or reconnaissance satellite may be useful in warfare but isn't generally classified as a weapon) are designed to jam, sabotage, and outright destroy enemy satellites, and conversely to protect friendly satellites against such attacks. To this end, the US (and presumably other countries) is researching groups of small, highly mobile satellites called "microsats" (about the size of a refrigerator) and "picosats" (approximately 1 cubic foot (≈27 litres) in volume) nimble enough to maneuver around and interact with other orbiting objects to repair, sabotage, hijack, or simply collide with them.

Kinetic bombardment

US Army THAAD launcher

Another theorized use involves the extension of conventional weaponry into orbit for deployment against ground targets. Though international treaties ban the deployment of nuclear missiles outside the atmosphere, other categories of weapons are largely unregulated. Traditional ground-based weapons are generally not useful in orbital environments, and few if any would survive re-entry even if they were, but as early as the 1950s, the United States has toyed with kinetic bombardment, i.e. orbiting magazines of non-explosive projectiles to be dropped onto hardened targets from low Earth orbit.

Kinetic weapons have always been widespread in conventional warfare—bullets, arrows, swords, clubs, etc.—but the energy a projectile would gain while falling from orbit would make such a weapon rival all but the most powerful explosives. A direct hit would presumably destroy all but the most hardened targets without the need for nuclear weapons.

Such a system would involve a 'spotter' satellite, which would identify targets from orbit with high-power sensors, and a nearby 'magazine' satellite to de-orbit a long, needle-like tungsten dart onto it with a small rocket motor or just dropping a very big rock from orbit (such as an asteroid). This would be more useful against a larger but less hardened target (such as a city). Though a common device in science fiction, there is no publicly available evidence that any such systems have actually been deployed by any nation.

Directed-energy weapons

A USAF Boeing YAL-1 airborne laser

 

A vision for the future of the US Space Command for 2020: a space-based high-energy laser destroys a terrestrial target

Weapon systems that fall under this category include lasers, linear particle accelerators or particle-beam based weaponry, microwaves and plasma-based weaponry. Particle beams involve the acceleration of charged or neutral particles in a stream towards a target at extremely high velocities, the impact of which creates a reaction causing immense damage. Most of these weapons are theoretical or impractical to implement currently, aside from lasers which are starting to be used in terrestrial warfare. That said, directed-energy weapons are more practical and more effective in a vacuum (i.e. space) than in the Earth's atmosphere, as in the atmosphere the particles of air interfere with and disperse the directed energy. Nazi Germany had a project for such a weapon, considered a wunderwaffe, the sun gun, which would have been an orbital concave mirror able to concentrate the sun's energy on a ground target.

Practical considerations

Space warfare is likely to be done at far bigger distances and speeds than combat on Earth. The vast distances pose big challenges for targeting and tracking, as even light requires a few seconds to cover hundreds of thousands of kilometers. For example, if trying to fire on a target at the distance of the Moon from the Earth, one sees the position of the target slightly more than a second earlier. Thus even a laser would need ~1.28 seconds, meaning a laser-based weapon system would need to lead a target's apparent position by 1.28×2 = 2.56 seconds. A projectile from a railgun recently tested by the US Navy would take over 18 hours to cross that distance, if it travels in a straight line at a constant velocity of 5.8 km/s along its entire trajectory.

Three factors make engaging targets in space very difficult. First, the vast distances mean that an error of even a fraction of a degree in the firing solution can mean a miss by thousands of kilometers. Second, spaceflight involves tremendous speeds by terrestrial standards—a geostationary satellite moves at 3.07 km/s, and objects in low Earth orbit move at ~8 km/s. Third, though distances are huge, targets remain relatively small. The International Space Station, currently the largest artificial object in Earth orbit, measures slightly over 100m at its largest span. Other satellites can be vastly smaller, e.g. Quickbird measures only 3.04m. External ballistics for stationary terrestrial targets is enormously complicated—some of the earliest analog computers were used to calculate firing solutions for naval artillery, as the problems were already beyond manual solutions in any reasonable time—and targeting objects in space is far harder. And, though not a problem for orbital kinetic weapons, any directed energy weapon would need huge amounts of electricity. So far the most practical batteries are lithium, and the most practical means of generating electricity in space is photovoltaic modules, which are currently only up to 30% efficient, and fuel cells, which have limited fuel. Current technology might not be practical for powering effective lasers, particle beams, and railguns in space. In the context of the Strategic Defense Initiative, the Lawrence Livermore National Laboratory in the United States worked on a project for expandable space-based x-ray lasers powered by a nuclear explosion, Project Excalibur, a project canceled in 1992 for lack of results.

General William L. Shelton has said that in order to protect against attacks, Space Situational Awareness is much more important than additional hardening or armoring of satellites. The Air Force Space Command has indicated that their defensive focus will be on "Disaggregated Space Architectures".

Space debris

Anti-satellite attacks, especially ones with kinetic kill vehicles, can form space debris which can stay in orbit for many years and could interfere with future space activity or in a worst case trigger Kessler syndrome. In January 2007 China did a satellite knock out whose detonation alone caused more than 40,000 new chunks of debris with a diameter > 1cm and a sudden increase in the total amount of debris in orbit. The PRC is reported to be developing "soft-kill" techniques such as jamming and vision kills that do not generate much debris.

Possible warfare over space

Most of the world's communications systems rely heavily on the presence of satellites in orbit around Earth. Protecting these assets might seriously motivate nations dependent upon them to consider deploying more space-based weaponry, especially in conflicts involving advanced countries with access to space.

Since 2017, the United States Air Force has run an annual military exercise called "Space Flag" at Peterson Space Force Base, which involves a red team simulating attacks on U.S. satellites.

Robert Zubrin, aerospace engineer and advocate for human exploration of Mars, stated that anti-satellite weapons capabilities of nations increases, space infrastructures must be able to defend itself using other satellites that can destroy such weapons. Or else, he states, satellite-based navigation, communications and reconnaissance capabilities would be severely limited and easily influenced by adversaries.

Science fictional space warfare

Main article: Science fictional space warfare

Further information: Space opera, Military science fiction, and Space Western

See also: Interstellar war and Galactic empire

Space warfare is a staple of science fiction, where it is shown with a wide range of realism and plausibility. Fictional space warfare includes anticipated future technology and tactics, and fantasy- or history-based scenarios in a scifi setting. Some portray a space military as like an air force; others depict a more naval framework. Still others suggest forces more like space marine: highly mobile forces doing interplanetary and interstellar war but most of the conflict happens in terrestrial environments. The main sub-genres of the science fictional space warfare thematic genre are space opera, Military and Space Western. Though sword and planet stories like Finisterre universe by C. J. Cherryh might be considered, they rarely feature such technologies. These three genres often intertwine and have themes that are common to all. Written Space Westerns are often based directly on existing established scifi space opera franchises with expanded universes like Star Wars and Star Trek, including Warhammer 40,000: the most popular space opera military miniature wargame which spawned successful spin-off media: novels, video-games and on-going live adaption based on books by Dan Abnett.

Both kinetic and directed energy weapons are often seen, along with various military space vessels. E. E. Smith's Lensman is an early example, which also inspired the term space opera due to the grandiose scale of the stories. Orson Scott Card's Ender's Game series is a notable example in that it makes a conjecture as to what sort of tactics and training would be needed for war in outer space. Other scifi authors have also delved into the tactics of space combat, such as David Weber in his Honorverse series, and Larry Niven and Jerry Pournelle in their Mote in God's Eye series. A more recent example is Alastair Reynolds' Revelation Space universe, which explores combat at relativistic speed. Robert A. Heinlein's Starship Troopers is perhaps one of the best-known and earliest explorations of the "space marine" idea.

Space-based vehicular combat is portrayed in many movies and video games, most notably Star Wars, "Stargate", Halo, Descent, Gundam, Macross, Babylon 5, and Star Trek. Games such as the Homeworld series have interesting concepts for space warfare, such as 3D battle formations, plasma-based projectors that get their energy from a ship's propulsion system, and automated uncrewed space combat vehicles. Other series, such as Gundam, prominently show vehicular combat in and among many near future concepts, such as O'Neill cylinders.

Fictional galaxies with space warfare are far too many to list, but popular examples include Star Trek (in all of its forms), Star Wars, Halo, Stargate, Warhammer 40,000, Babylon 5, Buck Rogers, Flash Gordon, Battlestar Galactica, Mass Effect, Freespace and many comic book franchises. Video games often touch the subject; the Wing Commander franchise is a prototypical example. Few games try to simulate realistic distance and speed, though Independence War and Frontier: Elite II both do, as does the board game Attack Vector: Tactical.

Many authors have either used a galaxy-spanning fictional empire as background or written about the growth and/or decline of such an empire. Said empire's capital is often a core world, such as a planet relatively close to a galaxy's supermassive black hole. Characterization can vary wildly from malevolent forces attacking sympathetic victims to apathetic bureaucracies to more reasonable entities focused on social progress, and anywhere in between. Scifi writers generally posit some form of faster-than-light drive in order to facilitate interstellar war. Writers such as Larry Niven have developed plausible interplanetary conflict based on human colonization of the asteroid belt and outer planets via technologies using currently known physics.