Comparison of
classical and
quantum harmonic oscillator
conceptions for a single spinless particle. The two processes differ
greatly. The classical process (A–B) is represented as the motion of a
particle along a trajectory. The quantum process (C–H) has no such
trajectory. Rather, it is represented as a wave; here, the vertical axis
shows the real part (blue) and imaginary part (red) of the wave
function. Panels (C–F) show four different standing-wave solutions of
the
Schrödinger equation. Panels (G–H) further show two different wave functions that are solutions of the Schrödinger equation but not standing waves.
In quantum physics, a wave function is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude,
and the probabilities for the possible results of measurements made on
the system can be derived from it. The most common symbols for a wave
function are the Greek letters ψ and Ψ (lower-case and capital psi, respectively).
The wave function is a function of the degrees of freedom corresponding to some maximal set of commuting observables. Once such a representation is chosen, the wave function can be derived from the quantum state.
For a given system, the choice of which commuting degrees of freedom to use is not unique, and correspondingly the domain
of the wave function is also not unique. For instance, it may be taken
to be a function of all the position coordinates of the particles over
position space, or the momenta of all the particles over momentum space; the two are related by a Fourier transform. Some particles, like electrons and photons, have nonzero spin,
and the wave function for such particles includes spin as an intrinsic,
discrete degree of freedom; other discrete variables can also be
included, such as isospin.
When a system has internal degrees of freedom, the wave function at
each point in the continuous degrees of freedom (e.g., a point in space)
assigns a complex number for each possible value of the discrete degrees of freedom (e.g., z-component of spin) – these values are often displayed in a column matrix (e.g., a 2 × 1 column vector for a non-relativistic electron with spin 1⁄2).
According to the superposition principle
of quantum mechanics, wave functions can be added together and
multiplied by complex numbers to form new wave functions and form a Hilbert space.
The inner product between two wave functions is a measure of the
overlap between the corresponding physical states and is used in the
foundational probabilistic interpretation of quantum mechanics, the Born rule, relating transition probabilities to inner products. The Schrödinger equation determines how wave functions evolve over time, and a wave function behaves qualitatively like other waves, such as water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation. This explains the name "wave function", and gives rise to wave–particle duality. However, the wave function in quantum mechanics describes a kind of physical phenomenon, still open to different interpretations, which fundamentally differs from that of classic mechanical waves.
In Born's statistical interpretation in non-relativistic quantum mechanics,
the squared modulus of the wave function, |ψ|2, is a real number interpreted as the probability density of measuring
a particle as being at a given place – or having a given momentum – at a
given time, and possibly having definite values for discrete degrees of
freedom. The integral of this quantity, over all the system's degrees
of freedom, must be 1 in accordance with the probability interpretation.
This general requirement that a wave function must satisfy is called
the normalization condition. Since the wave function is
complex-valued, only its relative phase and relative magnitude can be
measured—its value does not, in isolation, tell anything about the
magnitudes or directions of measurable observables; one has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.
Historical background
In 1900, Max Planck postulated the proportionality between the frequency  of a photon and its energy
of a photon and its energy  ,
,  ,
and in 1916 the corresponding relation between a photon's momentum
,
and in 1916 the corresponding relation between a photon's momentum  and wavelength
and wavelength  ,
,  ,
where
,
where  is the Planck constant. In 1923, De Broglie was the first to suggest that the relation
is the Planck constant. In 1923, De Broglie was the first to suggest that the relation  , now called the De Broglie relation, holds for massive particles, the chief clue being Lorentz invariance, and this can be viewed as the starting point for the modern development of quantum mechanics. The equations represent wave–particle duality for both massless and massive particles.
, now called the De Broglie relation, holds for massive particles, the chief clue being Lorentz invariance, and this can be viewed as the starting point for the modern development of quantum mechanics. The equations represent wave–particle duality for both massless and massive particles.
In the 1920s and 1930s, quantum mechanics was developed using calculus and linear algebra. Those who used the techniques of calculus included Louis de Broglie, Erwin Schrödinger, and others, developing "wave mechanics". Those who applied the methods of linear algebra included Werner Heisenberg, Max Born, and others, developing "matrix mechanics". Schrödinger subsequently showed that the two approaches were equivalent.
In 1926, Schrödinger published the famous wave equation now named after him, the Schrödinger equation. This equation was based on classical conservation of energy using quantum operators and the de Broglie relations and the solutions of the equation are the wave functions for the quantum system. However, no one was clear on how to interpret it.
At first, Schrödinger and others thought that wave functions represent
particles that are spread out with most of the particle being where the
wave function is large.
This was shown to be incompatible with the elastic scattering of a wave
packet (representing a particle) off a target; it spreads out in all
directions.
While a scattered particle may scatter in any direction, it does not
break up and take off in all directions. In 1926, Born provided the
perspective of probability amplitude.
This relates calculations of quantum mechanics directly to
probabilistic experimental observations. It is accepted as part of the Copenhagen interpretation of quantum mechanics. There are many other interpretations of quantum mechanics. In 1927, Hartree and Fock made the first step in an attempt to solve the N-body wave function, and developed the self-consistency cycle: an iterative algorithm to approximate the solution. Now it is also known as the Hartree–Fock method. The Slater determinant and permanent (of a matrix) was part of the method, provided by John C. Slater.
Schrödinger did encounter an equation for the wave function that satisfied relativistic energy conservation before he published the non-relativistic one, but discarded it as it predicted negative probabilities and negative energies. In 1927, Klein, Gordon and Fock also found it, but incorporated the electromagnetic interaction and proved that it was Lorentz invariant. De Broglie also arrived at the same equation in 1928. This relativistic wave equation is now most commonly known as the Klein–Gordon equation.
In 1927, Pauli phenomenologically found a non-relativistic equation to describe spin-1/2 particles in electromagnetic fields, now called the Pauli equation.
Pauli found the wave function was not described by a single complex
function of space and time, but needed two complex numbers, which
respectively correspond to the spin +1/2 and −1/2 states of the fermion.
Soon after in 1928, Dirac found an equation from the first successful unification of special relativity and quantum mechanics applied to the electron, now called the Dirac equation. In this, the wave function is a spinor represented by four complex-valued components: two for the electron and two for the electron's antiparticle, the positron. In the non-relativistic limit, the Dirac wave function resembles the Pauli wave function for the electron. Later, other relativistic wave equations were found.
Wave functions and wave equations in modern theories
All
these wave equations are of enduring importance. The Schrödinger
equation and the Pauli equation are under many circumstances excellent
approximations of the relativistic variants. They are considerably
easier to solve in practical problems than the relativistic
counterparts.
The Klein–Gordon equation and the Dirac equation,
while being relativistic, do not represent full reconciliation of
quantum mechanics and special relativity. The branch of quantum
mechanics where these equations are studied the same way as the
Schrödinger equation, often called relativistic quantum mechanics, while very successful, has its limitations (see e.g. Lamb shift) and conceptual problems (see e.g. Dirac sea).
Relativity makes it inevitable that the number of particles in a system is not constant. For full reconciliation, quantum field theory is needed.
In this theory, the wave equations and the wave functions have their
place, but in a somewhat different guise. The main objects of interest
are not the wave functions, but rather operators, so called field operators
(or just fields where "operator" is understood) on the Hilbert space of
states (to be described next section). It turns out that the original
relativistic wave equations and their solutions are still needed to
build the Hilbert space. Moreover, the free fields operators,
i.e. when interactions are assumed not to exist, turn out to (formally)
satisfy the same equation as do the fields (wave functions) in many
cases.
Thus the Klein–Gordon equation (spin 0) and the Dirac equation (spin 1⁄2) in this guise remain in the theory. Higher spin analogues include the Proca equation (spin 1), Rarita–Schwinger equation (spin 3⁄2), and, more generally, the Bargmann–Wigner equations. For massless free fields two examples are the free field Maxwell equation (spin 1) and the free field Einstein equation (spin 2) for the field operators.
All of them are essentially a direct consequence of the requirement of Lorentz invariance. Their solutions must transform under Lorentz transformation in a prescribed way, i.e. under a particular representation of the Lorentz group and that together with few other reasonable demands, e.g. the cluster decomposition property,
with implications for causality is enough to fix the equations.
This applies to free field equations; interactions are not
included. If a Lagrangian density (including interactions) is available,
then the Lagrangian formalism will yield an equation of motion at the
classical level. This equation may be very complex and not amenable to
solution. Any solution would refer to a fixed number of particles
and would not account for the term "interaction" as referred to in
these theories, which involves the creation and annihilation of
particles and not external potentials as in ordinary "first quantized"
quantum theory.
In string theory,
the situation remains analogous. For instance, a wave function in
momentum space has the role of Fourier expansion coefficient in a
general state of a particle (string) with momentum that is not sharply
defined.
Definition (one spinless particle in one dimension)
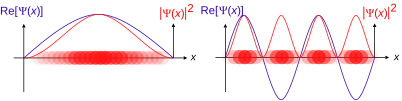
Travelling waves of a free particle.
The
real parts of position wave function
Ψ(x) and momentum wave function
Φ(p), and corresponding probability densities
|Ψ(x)|2 and
|Φ(p)|2, for one spin-0 particle in one
x or
p dimension. The colour opacity of the particles corresponds to the probability density (
not the wave function) of finding the particle at position
x or momentum
p.
For now, consider the simple case of a non-relativistic single particle, without spin, in one spatial dimension. More general cases are discussed below.
Position-space wave functions
The state of such a particle is completely described by its wave function,

where
x is position and
t is time. This is a
complex-valued function of two real variables
x and
t.
For one spinless particle in one dimension, if the wave function is interpreted as a probability amplitude, the square modulus of the wave function, the positive real number

is interpreted as the
probability density that the particle is at
x. The asterisk indicates the
complex conjugate. If the particle's position is
measured, its location cannot be determined from the wave function, but is described by a
probability distribution.
Normalization condition
The probability that its position x will be in the interval a ≤ x ≤ b is the integral of the density over this interval:

where
t is the time at which the particle was measured. This leads to the
normalization condition:

because if the particle is measured, there is 100% probability that it will be
somewhere.
For a given system, the set of all possible normalizable wave functions (at any given time) forms an abstract mathematical vector space, meaning that it is possible to add together different wave functions, and multiply wave functions by complex numbers (see vector space for details). Technically, because of the normalization condition, wave functions form a projective space rather than an ordinary vector space. This vector space is infinite-dimensional,
because there is no finite set of functions which can be added together
in various combinations to create every possible function. Also, it is a
Hilbert space, because the inner product of two wave functions Ψ1 and Ψ2 can be defined as the complex number (at time t)

More details are given below. Although the inner product of two wave functions is a complex number, the inner product of a wave function Ψ with itself,

is
always a positive real number. The number
‖Ψ‖ (not
‖Ψ‖2) is called the
norm of the wave function
Ψ.
If (Ψ, Ψ) = 1, then Ψ is normalized. If Ψ is not normalized, then dividing by its norm gives the normalized function Ψ/‖Ψ‖. Two wave functions Ψ1 and Ψ2 are orthogonal if (Ψ1, Ψ2) = 0. If they are normalized and orthogonal, they are orthonormal.
Orthogonality (hence also orthonormality) of wave functions is not a
necessary condition wave functions must satisfy, but is instructive to
consider since this guarantees linear independence of the functions. In a linear combination of orthogonal wave functions Ψn we have,

If the wave functions Ψn were nonorthogonal, the coefficients would be less simple to obtain.
Quantum states as vectors
In the Copenhagen interpretation, the modulus squared of the inner product (a complex number) gives a real number

which, assuming both wave functions are normalized, is interpreted as the probability of the wave function
Ψ2 "collapsing" to the new wave function
Ψ1 upon measurement of an observable, whose eigenvalues are the possible results of the measurement, with
Ψ1 being an eigenvector of the resulting eigenvalue. This is the
Born rule, and is one of the fundamental postulates of quantum mechanics.
At a particular instant of time, all values of the wave function Ψ(x, t) are components of a vector. There are uncountably infinitely many of them and integration is used in place of summation. In Bra–ket notation, this vector is written

and is referred to as a "quantum state vector", or simply "quantum
state". There are several advantages to understanding wave functions as
representing elements of an abstract vector space:
- All the powerful tools of linear algebra can be used to manipulate and understand wave functions. For example:
- Linear algebra explains how a vector space can be given a basis,
and then any vector in the vector space can be expressed in this basis.
This explains the relationship between a wave function in position
space and a wave function in momentum space and suggests that there are
other possibilities too.
- Bra–ket notation can be used to manipulate wave functions.
- The idea that quantum states are vectors in an abstract vector space is completely general in all aspects of quantum mechanics and quantum field theory, whereas the idea that quantum states are complex-valued "wave" functions of space is only true in certain situations.
The time parameter is often suppressed, and will be in the following. The x coordinate is a continuous index. The |x⟩ are the basis vectors, which are orthonormal so their inner product is a delta function;

thus

and

which illuminates the
identity operator

Finding the identity operator in a basis allows the abstract
state to be expressed explicitly in a basis, and more (the inner product
between two state vectors, and other operators for observables, can be
expressed in the basis).
Momentum-space wave functions
The particle also has a wave function in momentum space:

where
p is the
momentum in one dimension, which can be any value from
−∞ to
+∞, and
t is time.
Analogous to the position case, the inner product of two wave functions Φ1(p, t) and Φ2(p, t) can be defined as:

One particular solution to the time-independent Schrödinger equation is

a
plane wave, which can be used in the description of a particle with momentum exactly
p,
since it is an eigenfunction of the momentum operator. These functions
are not normalizable to unity (they aren't square-integrable), so they
are not really elements of physical Hilbert space. The set

forms what is called the
momentum basis. This "basis" is not a
basis in the usual mathematical sense. For one thing, since the
functions aren't normalizable, they are instead
normalized to a delta function,
[nb 2]

For another thing, though they are linearly independent, there
are too many of them (they form an uncountable set) for a basis for
physical Hilbert space. They can still be used to express all functions
in it using Fourier transforms as described next.
Relations between position and momentum representations
The x and p representations are

Now take the projection of the state Ψ onto eigenfunctions of momentum using the last expression in the two equations,

Then utilizing the known expression for suitably normalized
eigenstates of momentum in the position representation solutions of the
free Schrödinger equation

one obtains

Likewise, using eigenfunctions of position,

The position-space and momentum-space wave functions are thus found to be Fourier transforms of each other.
The two wave functions contain the same information, and either one
alone is sufficient to calculate any property of the particle. As
representatives of elements of abstract physical Hilbert space, whose
elements are the possible states of the system under consideration, they
represent the same state vector, hence identical physical states, but they are not generally equal when viewed as square-integrable functions.
In practice, the position-space wave function is used much more
often than the momentum-space wave function. The potential entering the
relevant equation (Schrödinger, Dirac, etc.) determines in which basis
the description is easiest. For the harmonic oscillator, x and p
enter symmetrically, so there it does not matter which description one
uses. The same equation (modulo constants) results. From this, with a
little bit of afterthought, it follows that solutions to the wave
equation of the harmonic oscillator are eigenfunctions of the Fourier
transform in L2.
Definitions (other cases)
Following
are the general forms of the wave function for systems in higher
dimensions and more particles, as well as including other degrees of
freedom than position coordinates or momentum components.
One-particle states in 3d position space
The
position-space wave function of a single particle without spin in three
spatial dimensions is similar to the case of one spatial dimension
above:

where
r is the
position vector in three-dimensional space, and
t is time. As always
Ψ(r, t) is a complex-valued function of real variables. As a single vector in
Dirac notation

All the previous remarks on inner products, momentum space
wave functions, Fourier transforms, and so on extend to higher
dimensions.
For a particle with spin, ignoring the position degrees of freedom, the wave function is a function of spin only (time is a parameter);

where
sz is the
spin projection quantum number along the
z axis. (The
z axis is an arbitrary choice; other axes can be used instead if the wave function is transformed appropriately, see below.) The
sz parameter, unlike
r and
t, is a
discrete variable. For example, for a
spin-1/2 particle,
sz can only be
+1/2 or
−1/2, and not any other value. (In general, for spin
s,
sz can be
s, s − 1, ..., −s + 1, −s). Inserting each quantum number gives a complex valued function of space and time, there are
2s + 1 of them. These can be arranged into a
column vector

In bra–ket notation, these easily arrange into the components of a vector

The entire vector ξ is a solution of the Schrödinger equation (with a suitable Hamiltonian), which unfolds to a coupled system of 2s + 1 ordinary differential equations with solutions ξ(s, t), ξ(s − 1, t), ..., ξ(−s, t).
The term "spin function" instead of "wave function" is used by some
authors. This contrasts the solutions to position space wave functions,
the position coordinates being continuous degrees of freedom, because
then the Schrödinger equation does take the form of a wave equation.
More generally, for a particle in 3d with any spin, the wave function can be written in "position–spin space" as:

and these can also be arranged into a column vector

in which the spin dependence is placed in indexing the entries, and the
wave function is a complex vector-valued function of space and time
only.
All values of the wave function, not only for discrete but continuous variables also, collect into a single vector

For a single particle, the tensor product ⊗ of its position state vector |ψ⟩ and spin state vector |ξ⟩ gives the composite position-spin state vector

with the identifications



The tensor product factorization is only possible if the orbital and spin angular momenta of the particle are separable in the Hamiltonian operator underlying the system's dynamics (in other words, the Hamiltonian can be split into the sum of orbital and spin terms).
The time dependence can be placed in either factor, and time evolution
of each can be studied separately. The factorization is not possible for
those interactions where an external field or any space-dependent
quantity couples to the spin; examples include a particle in a magnetic field, and spin–orbit coupling.
The preceding discussion is not limited to spin as a discrete variable, the total angular momentum J may also be used. Other discrete degrees of freedom, like isospin, can expressed similarly to the case of spin above.
Many-particle states in 3d position space
Traveling
waves of two free particles, with two of three dimensions suppressed.
Top is position-space wave function, bottom is momentum-space wave
function, with corresponding probability densities.
If there are many particles, in general there is only one wave
function, not a separate wave function for each particle. The fact that one wave function describes many particles is what makes quantum entanglement and the EPR paradox possible. The position-space wave function for N particles is written:

where
ri is the position of the
i-th particle in three-dimensional space, and
t is time. Altogether, this is a complex-valued function of
3N + 1 real variables.
In quantum mechanics there is a fundamental distinction between identical particles and distinguishable
particles. For example, any two electrons are identical and
fundamentally indistinguishable from each other; the laws of physics
make it impossible to "stamp an identification number" on a certain
electron to keep track of it. This translates to a requirement on the wave function for a system of identical particles:

where the
+ sign occurs if the particles are
all bosons and
− sign if they are
all fermions.
In other words, the wave function is either totally symmetric in the
positions of bosons, or totally antisymmetric in the positions of
fermions.
The physical interchange of particles corresponds to mathematically
switching arguments in the wave function. The antisymmetry feature of
fermionic wave functions leads to the
Pauli principle. Generally, bosonic and fermionic symmetry requirements are the manifestation of
particle statistics and are present in other quantum state formalisms.
For N distinguishable particles (no two being identical,
i.e. no two having the same set of quantum numbers), there is no
requirement for the wave function to be either symmetric or
antisymmetric.
For a collection of particles, some identical with coordinates r1, r2, ... and others distinguishable x1, x2, ...
(not identical with each other, and not identical to the aforementioned
identical particles), the wave function is symmetric or antisymmetric
in the identical particle coordinates ri only:

Again, there is no symmetry requirement for the distinguishable particle coordinates xi.
The wave function for N particles each with spin is the complex-valued function

Accumulating all these components into a single vector,

For identical particles, symmetry requirements apply to both
position and spin arguments of the wave function so it has the overall
correct symmetry.
The formulae for the inner products are integrals over all
coordinates or momenta and sums over all spin quantum numbers. For the
general case of N particles with spin in 3-d,

this is altogether
N three-dimensional
volume integrals and
N sums over the spins. The differential volume elements
d3ri are also written "
dVi" or "
dxi dyi dzi".
The multidimensional Fourier transforms of the position or
position–spin space wave functions yields momentum or momentum–spin
space wave functions.
Probability interpretation
For the general case of N particles with spin in 3d, if Ψ is interpreted as a probability amplitude, the probability density is

and the probability that particle 1 is in region R1 with spin sz1 = m1 and particle 2 is in region R2 with spin sz2 = m2 etc. at time t is the integral of the probability density over these regions and evaluated at these spin numbers:

Time dependence
For systems in time-independent potentials, the wave function can
always be written as a function of the degrees of freedom multiplied by a
time-dependent phase factor, the form of which is given by the
Schrödinger equation. For N particles, considering their positions only and suppressing other degrees of freedom,

where
E is the energy eigenvalue of the system corresponding to the eigenstate
Ψ. Wave functions of this form are called
stationary states.
The time dependence of the quantum state and the operators can
be placed according to unitary transformations on the operators and
states. For any quantum state |Ψ⟩ and operator O, in the Schrödinger picture |Ψ(t)⟩ changes with time according to the Schrödinger equation while O is constant. In the Heisenberg picture it is the other way round, |Ψ⟩ is constant while O(t)
evolves with time according to the Heisenberg equation of motion. The
Dirac (or interaction) picture is intermediate, time dependence is
places in both operators and states which evolve according to equations
of motion. It is useful primarily in computing S-matrix elements.
Non-relativistic examples
The following are solutions to the Schrödinger equation for one non-relativistic spinless particle.
Finite potential barrier
Scattering at a finite potential barrier of height V0.
The amplitudes and direction of left and right moving waves are
indicated. In red, those waves used for the derivation of the reflection
and transmission amplitude. E > V0 for this illustration.
One of the most prominent features of wave mechanics is the
possibility for a particle to reach a location with a prohibitive (in
classical mechanics) force potential. A common model is the "potential barrier", the one-dimensional case has the potential

and the steady-state solutions to the wave equation have the form (for some constants
k, κ)

Note that these wave functions are not normalized; see scattering theory for discussion.
The standard interpretation of this is as a stream of particles
being fired at the step from the left (the direction of negative x): setting Ar = 1 corresponds to firing particles singly; the terms containing Ar and Cr signify motion to the right, while Al and Cl – to the left. Under this beam interpretation, put Cl = 0
since no particles are coming from the right. By applying the
continuity of wave functions and their derivatives at the boundaries, it
is hence possible to determine the constants above.
3D
confined electron wave functions in a quantum dot. Here, rectangular
and triangular-shaped quantum dots are shown. Energy states in
rectangular dots are more s-type and p-type. However, in a triangular dot the wave functions are mixed due to confinement symmetry. (Click for animation)
In a semiconductor crystallite whose radius is smaller than the size of its exciton Bohr radius, the excitons are squeezed, leading to quantum confinement. The energy levels can then be modeled using the particle in a box model in which the energy of different states is dependent on the length of the box.
Quantum harmonic oscillator
The wave functions for the quantum harmonic oscillator can be expressed in terms of Hermite polynomials Hn, they are

where
n = 0, 1, 2, ....
The electron probability density for the first few
hydrogen atom electron
orbitals shown as cross-sections. These orbitals form an
orthonormal basis for the wave function of the electron. Different orbitals are depicted with different scale.
Hydrogen atom
The wave functions of an electron in a Hydrogen atom are expressed in terms of spherical harmonics and generalized Laguerre polynomials (these are defined differently by different authors—see main article on them and the hydrogen atom).
It is convenient to use spherical coordinates, and the wave function can be separated into functions of each coordinate,

where
R are radial functions and
Ym
ℓ(θ, φ) are
spherical harmonics of degree
ℓ and order
m.
This is the only atom for which the Schrödinger equation has been
solved exactly. Multi-electron atoms require approximative methods. The
family of solutions is:
![{\displaystyle \Psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79cdce8d7174c4b860efa65d1422b5550537284f)
where
a0 = 4πε0ħ2/mee2 is the
Bohr radius,
L2ℓ + 1
n − ℓ − 1 are the
generalized Laguerre polynomials of degree
n − ℓ − 1,
n = 1, 2, ... is the
principal quantum number,
ℓ = 0, 1, ..., n − 1 the
azimuthal quantum number,
m = −ℓ, −ℓ + 1, ..., ℓ − 1, ℓ the
magnetic quantum number.
Hydrogen-like atoms have very similar solutions.
This solution does not take into account the spin of the electron.
In the figure of the hydrogen orbitals, the 19 sub-images are
images of wave functions in position space (their norm squared). The
wave functions represent the abstract state characterized by the triple
of quantum numbers (n, ℓ, m),
in the lower right of each image. These are the principal quantum
number, the orbital angular momentum quantum number, and the magnetic
quantum number. Together with one spin-projection quantum number of the
electron, this is a complete set of observables.
The figure can serve to illustrate some further properties of the function spaces of wave functions.
- In this case, the wave functions are square integrable. One can
initially take the function space as the space of square integrable
functions, usually denoted L2.
- The displayed functions are solutions to the Schrödinger equation. Obviously, not every function in L2 satisfies the Schrödinger equation for the hydrogen atom. The function space is thus a subspace of L2.
- The displayed functions form part of a basis for the function space. To each triple (n, ℓ, m),
there corresponds a basis wave function. If spin is taken into account,
there are two basis functions for each triple. The function space thus
has a countable basis.
- The basis functions are mutually orthonormal.
Wave functions and function spaces
The concept of function spaces
enters naturally in the discussion about wave functions. A function
space is a set of functions, usually with some defining requirements on
the functions (in the present case that they are square integrable), sometimes with an algebraic structure on the set (in the present case a vector space structure with an inner product), together with a topology
on the set. The latter will sparsely be used here, it is only needed to
obtain a precise definition of what it means for a subset of a function
space to be closed. It will be concluded below that the function space of wave functions is a Hilbert space. This observation is the foundation of the predominant mathematical formulation of quantum mechanics.
Vector space structure
A wave function is an element of a function space partly characterized by the following concrete and abstract descriptions.
- The Schrödinger equation is linear. This means that the
solutions to it, wave functions, can be added and multiplied by scalars
to form a new solution. The set of solutions to the Schrödinger equation
is a vector space.
- The superposition principle of quantum mechanics. If Ψ and Φ are two states in the abstract space of states of a quantum mechanical system, and a and b are any two complex numbers, then aΨ + bΦ is a valid state as well. (Whether the null vector counts as a valid state ("no system present") is a matter of definition. The null vector does not at any rate describe the vacuum state in quantum field theory.) The set of allowable states is a vector space.
This similarity is of course not accidental. There are also a distinctions between the spaces to keep in mind.
Representations
Basic states are characterized by a set of quantum numbers. This is a set of eigenvalues of a maximal set of commuting observables.
Physical observables are represented by linear operators, also called
observables, on the vectors space. Maximality means that there can be
added to the set no further algebraically independent observables that
commute with the ones already present. A choice of such a set may be
called a choice of representation.
- It is a postulate of quantum mechanics that a physically
observable quantity of a system, such as position, momentum, or spin, is
represented by a linear Hermitian operator on the state space. The possible outcomes of measurement of the quantity are the eigenvalues of the operator. At a deeper level, most observables, perhaps all, arise as generators of symmetries.
- The physical interpretation is that such a set represents what can –
in theory – simultaneously be measured with arbitrary precision. The Heisenberg uncertainty relation prohibits simultaneous exact measurements of two non-commuting observables.
- The set is non-unique. It may for a one-particle system, for example, be position and spin z-projection, (x, Sz), or it may be momentum and spin y-projection, (p, Sy). In this case, the operator corresponding to position (a multiplication operator in the position representation) and the operator corresponding to momentum (a differential operator in the position representation) do not commute.
- Once a representation is chosen, there is still arbitrariness. It
remains to choose a coordinate system. This may, for example, correspond
to a choice of x, y- and z-axis, or a choice of curvilinear coordinates as exemplified by the spherical coordinates
used for the Hydrogen atomic wave functions. This final choice also
fixes a basis in abstract Hilbert space. The basic states are labeled by
the quantum numbers corresponding to the maximal set of commuting
observables and an appropriate coordinate system.
The abstract states are "abstract" only in that an arbitrary choice necessary for a particular explicit
description of it is not given. This is the same as saying that no
choice of maximal set of commuting observables has been given. This is
analogous to a vector space without a specified basis. Wave functions
corresponding to a state are accordingly not unique. This non-uniqueness
reflects the non-uniqueness in the choice of a maximal set of commuting
observables. For one spin particle in one dimension, to a particular
state there corresponds two wave functions, Ψ(x, Sz) and Ψ(p, Sy), both describing the same state.
- For each choice of maximal commuting sets of observables for the
abstract state space, there is a corresponding representation that is
associated to a function space of wave functions.
- Between all these different function spaces and the abstract state
space, there are one-to-one correspondences (here disregarding
normalization and unobservable phase factors), the common denominator
here being a particular abstract state. The relationship between the
momentum and position space wave functions, for instance, describing the
same state is the Fourier transform.
Each choice of representation should be thought of as specifying a
unique function space in which wave functions corresponding to that
choice of representation lives. This distinction is best kept, even if
one could argue that two such function spaces are mathematically equal,
e.g. being the set of square integrable functions. One can then think of
the function spaces as two distinct copies of that set.
Inner product
There is an additional algebraic structure on the vector spaces of wave functions and the abstract state space.
- Physically, different wave functions are interpreted to overlap to some degree. A system in a state Ψ that does not overlap with a state Φ cannot be found to be in the state Φ upon measurement. But if Φ1, Φ2, … overlap Ψ to some degree, there is a chance that measurement of a system described by Ψ will be found in states Φ1, Φ2, …. Also selection rules
are observed apply. These are usually formulated in the preservation of
some quantum numbers. This means that certain processes allowable from
some perspectives (e.g. energy and momentum conservation) do not occur
because the initial and final total wave functions do not overlap.
- Mathematically, it turns out that solutions to the Schrödinger equation for particular potentials are orthogonal in some manner, this is usually described by an integral

This motivates the introduction of an inner product
on the vector space of abstract quantum states, compatible with the
mathematical observations above when passing to a representation. It is
denoted (Ψ, Φ), or in the Bra–ket notation ⟨Ψ|Φ⟩. It yields a complex number. With the inner product, the function space is an inner product space.
The explicit appearance of the inner product (usually an integral or a
sum of integrals) depends on the choice of representation, but the
complex number (Ψ, Φ) does not. Much of the physical interpretation of quantum mechanics stems from the Born rule. It states that the probability p of finding upon measurement the state Φ given the system is in the state Ψ is

where
Φ and
Ψ are assumed normalized. Consider a
scattering experiment. In quantum field theory, if
Φout describes a state in the "distant future" (an "out state") after interactions between scattering particles have ceased, and
Ψin an "in state" in the "distant past", then the quantities
(Φout, Ψin), with
Φout and
Ψin varying over a complete set of in states and out states respectively, is called the
S-matrix or
scattering matrix. Knowledge of it is, effectively, having
solved the theory at hand, at least as far as predictions go. Measurable quantities such as
decay rates and
scattering cross sections are calculable from the S-matrix.
Hilbert space
The
above observations encapsulate the essence of the function spaces of
which wave functions are elements. However, the description is not yet
complete. There is a further technical requirement on the function
space, that of completeness,
that allows one to take limits of sequences in the function space, and
be ensured that, if the limit exists, it is an element of the function
space. A complete inner product space is called a Hilbert space.
The property of completeness is crucial in advanced treatments and
applications of quantum mechanics. For instance, the existence of projection operators or orthogonal projections relies on the completeness of the space. These projection operators, in turn, are essential for the statement and proof of many useful theorems, e.g. the spectral theorem.
It is not very important in introductory quantum mechanics, and
technical details and links may be found in footnotes like the one that
follows.
The space L2 is a Hilbert space, with inner product presented later. The function space of the example of the figure is a subspace of L2. A subspace of a Hilbert space is a Hilbert space if it is closed.
In summary, the set of all possible normalizable wave functions
for a system with a particular choice of basis, together with the null
vector, constitute a Hilbert space.
Not all functions of interest are elements of some Hilbert space, say L2. The most glaring example is the set of functions e2πip · x⁄h. These are plane wave solutions of the Schrödinger equation for a free particle, but are not normalizable, hence not in L2. But they are nonetheless fundamental for the description. One can, using them, express functions that are normalizable using wave packets. They are, in a sense, a basis (but not a Hilbert space basis, nor a Hamel basis)
in which wave functions of interest can be expressed. There is also the
artifact "normalization to a delta function" that is frequently
employed for notational convenience, see further down. The delta
functions themselves aren't square integrable either.
The above description of the function space containing the wave
functions is mostly mathematically motivated. The function spaces are,
due to completeness, very large in a certain sense. Not all functions are realistic descriptions of any physical system. For instance, in the function space L2 one can find the function that takes on the value 0 for all rational numbers and -i for the irrationals in the interval [0, 1]. This is square integrable,
but can hardly represent a physical state.
Common Hilbert spaces
While
the space of solutions as a whole is a Hilbert space there are many
other Hilbert spaces that commonly occur as ingredients.
- Square integrable complex valued functions on the interval [0, 2π]. The set {eint/2π, n ∈ ℤ} is a Hilbert space basis, i.e. a maximal orthonormal set.
- The Fourier transform takes functions in the above space to elements of l2(ℤ), the space of square summable functions ℤ → ℂ. The latter space is a Hilbert space and the Fourier transform is an isomorphism of Hilbert spaces. Its basis is {ei, i ∈ ℤ} with ei(j) = δij, i, j ∈ ℤ.
- The most basic example of spanning polynomials is in the space of square integrable functions on the interval [–1, 1] for which the Legendre polynomials is a Hilbert space basis (complete orthonormal set).
- The square integrable functions on the unit sphere S2 is a Hilbert space. The basis functions in this case are the spherical harmonics.
The Legendre polynomials are ingredients in the spherical harmonics.
Most problems with rotational symmetry will have "the same" (known)
solution with respect to that symmetry, so the original problem is
reduced to a problem of lower dimensionality.
- The associated Laguerre polynomials
appear in the hydrogenic wave function problem after factoring out the
spherical harmonics. These span the Hilbert space of square integrable
functions on the semi-infinite interval [0, ∞).
More generally, one may consider a unified treatment of all second order polynomial solutions to the Sturm–Liouville equations in the setting of Hilbert space. These include the Legendre and Laguerre polynomials as well as Chebyshev polynomials, Jacobi polynomials and Hermite polynomials. All of these actually appear in physical problems, the latter ones in the harmonic oscillator, and what is otherwise a bewildering maze of properties of special functions becomes an organized body of facts. For this, see Byron & Fuller (1992, Chapter 5).
There occurs also finite-dimensional Hilbert spaces. The space ℂn is a Hilbert space of dimension n.
The inner product is the standard inner product on these spaces. In it,
the "spin part" of a single particle wave function resides.
- In the non-relativistic description of an electron one has n = 2 and the total wave function is a solution of the Pauli equation.
- In the corresponding relativistic treatment, n = 4 and the wave function solves the Dirac equation.
With more particles, the situations is more complicated. One has to employ tensor products and use representation theory of the symmetry groups involved (the rotation group and the Lorentz group
respectively) to extract from the tensor product the spaces in which
the (total) spin wave functions reside. (Further problems arise in the
relativistic case unless the particles are free. See the Bethe–Salpeter equation.) Corresponding remarks apply to the concept of isospin, for which the symmetry group is SU(2). The models of the nuclear forces of the sixties (still useful today, see nuclear force) used the symmetry group SU(3). In this case, as well, the part of the wave functions corresponding to the inner symmetries reside in some ℂn or subspaces of tensor products of such spaces.
- In quantum field theory the underlying Hilbert space is Fock space.
It is built from free single-particle states, i.e. wave functions when a
representation is chosen, and can accommodate any finite, not
necessarily constant in time, number of particles. The interesting (or
rather the tractable) dynamics lies not in the wave functions but in the field operators that are operators acting on Fock space. Thus the Heisenberg picture is the most common choice (constant states, time varying operators).
Due to the infinite-dimensional nature of the system, the appropriate mathematical tools are objects of study in functional analysis.
Simplified description
Continuity of the wave function and its first spatial derivative (in the x direction, y and z coordinates not shown), at some time t.
Not all introductory textbooks take the long route and introduce the
full Hilbert space machinery, but the focus is on the non-relativistic
Schrödinger equation in position representation for certain standard
potentials. The following constraints on the wave function are sometimes
explicitly formulated for the calculations and physical interpretation
to make sense:
- The wave function must be square integrable. This is motivated by the Copenhagen interpretation of the wave function as a probability amplitude.
- It must be everywhere continuous and everywhere continuously differentiable. This is motivated by the appearance of the Schrödinger equation for most physically reasonable potentials.
It is possible to relax these conditions somewhat for special purposes.
If these requirements are not met, it is not possible to interpret the wave function as a probability amplitude.
This does not alter the structure of the Hilbert space that these
particular wave functions inhabit, but the subspace of the
square-integrable functions L2, which is a Hilbert space, satisfying the second requirement is not closed in L2, hence not a Hilbert space in itself.
The functions that does not meet the requirements are still needed for both technical and practical reasons.
More on wave functions and abstract state space
As has been demonstrated, the set of all possible wave functions in some representation for a system constitute an in general infinite-dimensional
Hilbert space. Due to the multiple possible choices of representation
basis, these Hilbert spaces are not unique. One therefore talks about an
abstract Hilbert space, state space, where the choice of
representation and basis is left undetermined. Specifically, each state
is represented as an abstract vector in state space. A quantum state |Ψ⟩ in any representation is generally expressed as a vector

where
- |α, ω⟩ the basis vectors of the chosen representation
- dmω = dω1dω2...dωm a "differential volume element" in the continuous degrees of freedom
- Ψ(α, ω, t) a component of the vector |Ψ⟩, called the wave function of the system
- α = (α1, α2, ..., αn) dimensionless discrete quantum numbers
- ω = (ω1, ω2, ..., ωm) continuous variables (not necessarily dimensionless)
These quantum numbers index the components of the state vector. More, all α are in an n-dimensional set A = A1 × A2 × ... × An where each Ai is the set of allowed values for αi; all ω are in an m-dimensional "volume" Ω ⊆ ℝm where Ω = Ω1 × Ω2 × ... × Ωm and each Ωi ⊆ R is the set of allowed values for ωi, a subset of the real numbers R. For generality n and m are not necessarily equal.
Example:
- For a single particle in 3d with spin s, neglecting other degrees of freedom, using Cartesian coordinates, we could take α = (sz) for the spin quantum number of the particle along the z direction, and ω = (x, y, z) for the particle's position coordinates. Here A = {−s, −s + 1, ..., s − 1, s} is the set of allowed spin quantum numbers and Ω = R3 is the set of all possible particle positions throughout 3d position space.
- An alternative choice is α = (sy) for the spin quantum number along the y direction and ω = (px, py, pz) for the particle's momentum components. In this case A and Ω are the same as before.
The probability density of finding the system at time  at state |α, ω⟩ is
at state |α, ω⟩ is

The probability of finding system with α in some or all possible discrete-variable configurations, D ⊆ A, and ω in some or all possible continuous-variable configurations, C ⊆ Ω, is the sum and integral over the density,

Since the sum of all probabilities must be 1, the normalization condition

must hold at all times during the evolution of the system.
The normalization condition requires ρ dmω to be dimensionless, by dimensional analysis Ψ must have the same units as (ω1ω2...ωm)−1/2.
Ontology
Whether the wave function really exists, and what it represents, are major questions in the interpretation of quantum mechanics. Many famous physicists of a previous generation puzzled over this problem, such as Schrödinger, Einstein and Bohr. Some advocate formulations or variants of the Copenhagen interpretation (e.g. Bohr, Wigner and von Neumann) while others, such as Wheeler or Jaynes, take the more classical approach
and regard the wave function as representing information in the mind of
the observer, i.e. a measure of our knowledge of reality. Some,
including Schrödinger, Bohm and Everett
and others, argued that the wave function must have an objective,
physical existence. Einstein thought that a complete description of
physical reality should refer directly to physical space and time, as
distinct from the wave function, which refers to an abstract
mathematical space.







































































![{\displaystyle \Psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79cdce8d7174c4b860efa65d1422b5550537284f)








