
Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for Ordnung, meaning the order of approximation.
In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; a famous example of such a difference is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates.
Big O notation characterizes functions according to their growth rates: different functions with the same asymptotic growth rate may be represented using the same O notation. The letter O is used because the growth rate of a function is also referred to as the order of the function. A description of a function in terms of big O notation usually only provides an upper bound on the growth rate of the function.
Associated with big O notation are several related notations, using the symbols o, Ω, ω, and Θ, to describe other kinds of bounds on asymptotic growth rates.
Formal definition
Let , the function to be estimated, be a real or complex valued function and let , the comparison function, be a real valued function. Let both functions be defined on some unbounded subset of the positive real numbers, and be strictly positive for all large enough values of . One writes
In many contexts, the assumption that we are interested in the growth rate as the variable goes to infinity is left unstated, and one writes more simply that
The notation can also be used to describe the behavior of near some real number (often, ): we say
As is chosen to be strictly positive for such values of , both of these definitions can be unified using the limit superior:
And in both of these definitions the limit point (whether or not) is a cluster point of the domains of and , i. e., in every neighbourhood of there have to be infinitely many points in common. Moreover, as pointed out in the article about the limit inferior and limit superior, the (at least on the extended real number line) always exists.
In computer science, a slightly more restrictive definition is common: and are both required to be functions from some unbounded subset of the positive integers to the nonnegative real numbers; then if there exist positive integer numbers and such that for all .
Example
In typical usage the O notation is asymptotical, that is, it refers to very large x. In this setting, the contribution of the terms that grow "most quickly" will eventually make the other ones irrelevant. As a result, the following simplification rules can be applied:
- If f(x) is a sum of several terms, if there is one with largest growth rate, it can be kept, and all others omitted.
- If f(x) is a product of several factors, any constants (factors in the product that do not depend on x) can be omitted.
For example, let f(x) = 6x4 − 2x3 + 5, and suppose we wish to simplify this function, using O notation, to describe its growth rate as x approaches infinity. This function is the sum of three terms: 6x4, −2x3, and 5. Of these three terms, the one with the highest growth rate is the one with the largest exponent as a function of x, namely 6x4. Now one may apply the second rule: 6x4 is a product of 6 and x4 in which the first factor does not depend on x. Omitting this factor results in the simplified form x4. Thus, we say that f(x) is a "big O" of x4. Mathematically, we can write f(x) = O(x4). One may confirm this calculation using the formal definition: let f(x) = 6x4 − 2x3 + 5 and g(x) = x4. Applying the formal definition from above, the statement that f(x) = O(x4) is equivalent to its expansion,
Usage
Big O notation has two main areas of application:
- In mathematics, it is commonly used to describe how closely a finite series approximates a given function, especially in the case of a truncated Taylor series or asymptotic expansion
- In computer science, it is useful in the analysis of algorithms
In both applications, the function g(x) appearing within the O(·) is typically chosen to be as simple as possible, omitting constant factors and lower order terms.
There are two formally close, but noticeably different, usages of this notation:
- infinite asymptotics
- infinitesimal asymptotics.
This distinction is only in application and not in principle, however—the formal definition for the "big O" is the same for both cases, only with different limits for the function argument.
Infinite asymptotics
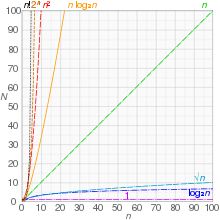
Big O notation is useful when analyzing algorithms for efficiency. For example, the time (or the number of steps) it takes to complete a problem of size n might be found to be T(n) = 4n2 − 2n + 2. As n grows large, the n2 term will come to dominate, so that all other terms can be neglected—for instance when n = 500, the term 4n2 is 1000 times as large as the 2n term. Ignoring the latter would have negligible effect on the expression's value for most purposes. Further, the coefficients become irrelevant if we compare to any other order of expression, such as an expression containing a term n3 or n4. Even if T(n) = 1,000,000n2, if U(n) = n3, the latter will always exceed the former once n grows larger than 1,000,000 (T(1,000,000) = 1,000,0003 = U(1,000,000)). Additionally, the number of steps depends on the details of the machine model on which the algorithm runs, but different types of machines typically vary by only a constant factor in the number of steps needed to execute an algorithm. So the big O notation captures what remains: we write either
or
and say that the algorithm has order of n2 time complexity. The sign "=" is not meant to express "is equal to" in its normal mathematical sense, but rather a more colloquial "is", so the second expression is sometimes considered more accurate (see the "Equals sign" discussion below) while the first is considered by some as an abuse of notation.
Infinitesimal asymptotics
Big O can also be used to describe the error term in an approximation to a mathematical function. The most significant terms are written explicitly, and then the least-significant terms are summarized in a single big O term. Consider, for example, the exponential series and two expressions of it that are valid when x is small:
The second expression (the one with O(x3)) means the absolute-value of the error ex − (1 + x + x2/2) is at most some constant times |x3| when x is close enough to 0.
Properties
If the function f can be written as a finite sum of other functions, then the fastest growing one determines the order of f(n). For example,
In particular, if a function may be bounded by a polynomial in n, then as n tends to infinity, one may disregard lower-order terms of the polynomial. The sets O(nc) and O(cn) are very different. If c is greater than one, then the latter grows much faster. A function that grows faster than nc for any c is called superpolynomial. One that grows more slowly than any exponential function of the form cn is called subexponential. An algorithm can require time that is both superpolynomial and subexponential; examples of this include the fastest known algorithms for integer factorization and the function nlog n.
We may ignore any powers of n inside of the logarithms. The set O(log n) is exactly the same as O(log(nc)). The logarithms differ only by a constant factor (since log(nc) = c log n) and thus the big O notation ignores that. Similarly, logs with different constant bases are equivalent. On the other hand, exponentials with different bases are not of the same order. For example, 2n and 3n are not of the same order.
Changing units may or may not affect the order of the resulting algorithm. Changing units is equivalent to multiplying the appropriate variable by a constant wherever it appears. For example, if an algorithm runs in the order of n2, replacing n by cn means the algorithm runs in the order of c2n2, and the big O notation ignores the constant c2. This can be written as c2n2 = O(n2). If, however, an algorithm runs in the order of 2n, replacing n with cn gives 2cn = (2c)n. This is not equivalent to 2n in general. Changing variables may also affect the order of the resulting algorithm. For example, if an algorithm's run time is O(n) when measured in terms of the number n of digits of an input number x, then its run time is O(log x) when measured as a function of the input number x itself, because n = O(log x).
Product
Sum
If and then . It follows that if and then . In other words, this second statement says that is a convex cone.
Multiplication by a constant
Let k be a nonzero constant. Then . In other words, if , then
Multiple variables
Big O (and little o, Ω, etc.) can also be used with multiple variables. To define big O formally for multiple variables, suppose and are two functions defined on some subset of . We say
if and only if there exist constants and such that for all with for some Equivalently, the condition that for some can be written , where denotes the Chebyshev norm. For example, the statement
asserts that there exist constants C and M such that
whenever either or holds. This definition allows all of the coordinates of to increase to infinity. In particular, the statement
(i.e., ) is quite different from
(i.e., ).
Under this definition, the subset on which a function is defined is significant when generalizing statements from the univariate setting to the multivariate setting. For example, if and , then if we restrict and to , but not if they are defined on .
This is not the only generalization of big O to multivariate functions, and in practice, there is some inconsistency in the choice of definition.
Matters of notation
Equals sign
The statement "f(x) is O(g(x))" as defined above is usually written as f(x) = O(g(x)). Some consider this to be an abuse of notation, since the use of the equals sign could be misleading as it suggests a symmetry that this statement does not have. As de Bruijn says, O(x) = O(x2) is true but O(x2) = O(x) is not. Knuth describes such statements as "one-way equalities", since if the sides could be reversed, "we could deduce ridiculous things like n = n2 from the identities n = O(n2) and n2 = O(n2)." In another letter, Knuth also pointed out that "the equality sign is not symmetric with respect to such notations", as, in this notation, "mathematicians customarily use the = sign as they use the word "is" in English: Aristotle is a man, but a man isn't necessarily Aristotle".
For these reasons, it would be more precise to use set notation and write f(x) ∈ O(g(x)) (read as: "f(x) is an element of O(g(x))", or "f(x) is in the set O(g(x))"), thinking of O(g(x)) as the class of all functions h(x) such that |h(x)| ≤ Cg(x) for some positive real number C. However, the use of the equals sign is customary.
Other arithmetic operators
Big O notation can also be used in conjunction with other arithmetic operators in more complicated equations. For example, h(x) + O(f(x)) denotes the collection of functions having the growth of h(x) plus a part whose growth is limited to that of f(x). Thus,
expresses the same as
Example
Suppose an algorithm is being developed to operate on a set of n elements. Its developers are interested in finding a function T(n) that will express how long the algorithm will take to run (in some arbitrary measurement of time) in terms of the number of elements in the input set. The algorithm works by first calling a subroutine to sort the elements in the set and then perform its own operations. The sort has a known time complexity of O(n2), and after the subroutine runs the algorithm must take an additional 55n3 + 2n + 10 steps before it terminates. Thus the overall time complexity of the algorithm can be expressed as T(n) = 55n3 + O(n2). Here the terms 2n + 10 are subsumed within the faster-growing O(n2). Again, this usage disregards some of the formal meaning of the "=" symbol, but it does allow one to use the big O notation as a kind of convenient placeholder.
Multiple uses
In more complicated usage, O(·) can appear in different places in an equation, even several times on each side. For example, the following are true for :
Typesetting
Big O is typeset as an italicized uppercase "O", as in the following example: . In TeX, it is produced by simply typing O inside math mode. Unlike Greek-named Bachmann–Landau notations, it needs no special symbol. Yet, some authors use the calligraphic variant instead.
Orders of common functions
Here is a list of classes of functions that are commonly encountered when analyzing the running time of an algorithm. In each case, c is a positive constant and n increases without bound. The slower-growing functions are generally listed first.
| Notation | Name | Example |
|---|---|---|
| constant | Determining if a binary number is even or odd; Calculating ; Using a constant-size lookup table | |
| double logarithmic | Average number of comparisons spent finding an item using interpolation search in a sorted array of uniformly distributed values | |
| logarithmic | Finding an item in a sorted array with a binary search or a balanced search tree as well as all operations in a binomial heap | |
| polylogarithmic | Matrix chain ordering can be solved in polylogarithmic time on a parallel random-access machine. | |
| fractional power | Searching in a k-d tree | |
| linear | Finding an item in an unsorted list or in an unsorted array; adding two n-bit integers by ripple carry | |
| n log-star n | Performing triangulation of a simple polygon using Seidel's algorithm, where | |
| linearithmic, loglinear, quasilinear, or "n log n" | Performing a fast Fourier transform; fastest possible comparison sort; heapsort and merge sort | |
| quadratic | Multiplying two n-digit numbers by schoolbook multiplication; simple sorting algorithms, such as bubble sort, selection sort and insertion sort; (worst-case) bound on some usually faster sorting algorithms such as quicksort, Shellsort, and tree sort | |
| polynomial or algebraic | Tree-adjoining grammar parsing; maximum matching for bipartite graphs; finding the determinant with LU decomposition | |
| L-notation or sub-exponential | Factoring a number using the quadratic sieve or number field sieve | |
| exponential | Finding the (exact) solution to the travelling salesman problem using dynamic programming; determining if two logical statements are equivalent using brute-force search | |
| factorial | Solving the travelling salesman problem via brute-force search; generating all unrestricted permutations of a poset; finding the determinant with Laplace expansion; enumerating all partitions of a set |
The statement is sometimes weakened to to derive simpler formulas for asymptotic complexity. For any and , is a subset of for any , so may be considered as a polynomial with some bigger order.
Related asymptotic notations
Big O is widely used in computer science. Together with some other related notations, it forms the family of Bachmann–Landau notations.
Little-o notation
Intuitively, the assertion "f(x) is o(g(x))" (read "f(x) is little-o of g(x)") means that g(x) grows much faster than f(x). As before, let f be a real or complex valued function and g a real valued function, both defined on some unbounded subset of the positive real numbers, such that g(x) is strictly positive for all large enough values of x. One writes
if for every positive constant ε there exists a constant such that
For example, one has
- and both as
The difference between the definition of the big-O notation and the definition of little-o is that while the former has to be true for at least one constant M, the latter must hold for every positive constant ε, however small. In this way, little-o notation makes a stronger statement than the corresponding big-O notation: every function that is little-o of g is also big-O of g, but not every function that is big-O of g is also little-o of g. For example, but .
As g(x) is nonzero, or at least becomes nonzero beyond a certain point, the relation is equivalent to
- (and this is in fact how Landau originally defined the little-o notation).
Little-o respects a number of arithmetic operations. For example,
- if c is a nonzero constant and then , and
- if and then
It also satisfies a transitivity relation:
- if and then
Big Omega notation
Another asymptotic notation is , read "big omega". There are two widespread and incompatible definitions of the statement
- as ,
where a is some real number, ∞, or −∞, where f and g are real functions defined in a neighbourhood of a, and where g is positive in this neighbourhood.
The Hardy–Littlewood definition is used mainly in analytic number theory, and the Knuth definition mainly in computational complexity theory; the definitions are not equivalent.
The Hardy–Littlewood definition
In 1914 Godfrey Harold Hardy and John Edensor Littlewood introduced the new symbol , which is defined as follows:
- as if
Thus is the negation of .
In 1916 the same authors introduced the two new symbols and , defined as:
- as if ;
- as if
These symbols were used by Edmund Landau, with the same meanings, in 1924. After Landau, the notations were never used again exactly thus; became and became .
These three symbols , as well as (meaning that and are both satisfied), are now currently used in analytic number theory.
Simple examples
We have
- as
and more precisely
- as
We have
- as
and more precisely
- as
however
- as
The Knuth definition
In 1976 Donald Knuth published a paper to justify his use of the -symbol to describe a stronger property. Knuth wrote: "For all the applications I have seen so far in computer science, a stronger requirement ... is much more appropriate". He defined
with the comment: "Although I have changed Hardy and Littlewood's definition of , I feel justified in doing so because their definition is by no means in wide use, and because there are other ways to say what they want to say in the comparatively rare cases when their definition applies."
Family of Bachmann–Landau notations
| Notation | Name | Description | Formal definition | Limit definition |
|---|---|---|---|---|
| Small O; Small Oh | f is dominated by g asymptotically | |||
| Big O; Big Oh; Big Omicron | is bounded above by g (up to constant factor) asymptotically | |||
| Big Theta | f is bounded both above and below by g asymptotically | and (Knuth version) | ||
| On the order of | f is equal to g asymptotically | |||
| Big Omega in complexity theory (Knuth) | f is bounded below by g asymptotically | |||
| Small Omega | f dominates g asymptotically | |||
| Big Omega in number theory (Hardy–Littlewood) | is not dominated by g asymptotically |
The limit definitions assume for sufficiently large . The table is (partly) sorted from smallest to largest, in the sense that (Knuth's version of) on functions correspond to on the real line (the Hardy–Littlewood version of , however, doesn't correspond to any such description).
Computer science uses the big , big Theta , little , little omega and Knuth's big Omega notations. Analytic number theory often uses the big , small , Hardy–Littlewood's big Omega (with or without the +, − or ± subscripts) and notations. The small omega notation is not used as often in analysis.
Use in computer science
Informally, especially in computer science, the big O notation often can be used somewhat differently to describe an asymptotic tight bound where using big Theta Θ notation might be more factually appropriate in a given context For example, when considering a function T(n) = 73n3 + 22n2 + 58, all of the following are generally acceptable, but tighter bounds (such as numbers 2 and 3 below) are usually strongly preferred over looser bounds (such as number 1 below).
- T(n) = O(n100)
- T(n) = O(n3)
- T(n) = Θ(n3)
The equivalent English statements are respectively:
- T(n) grows asymptotically no faster than n100
- T(n) grows asymptotically no faster than n3
- T(n) grows asymptotically as fast as n3.
So while all three statements are true, progressively more information is contained in each. In some fields, however, the big O notation (number 2 in the lists above) would be used more commonly than the big Theta notation (items numbered 3 in the lists above). For example, if T(n) represents the running time of a newly developed algorithm for input size n, the inventors and users of the algorithm might be more inclined to put an upper asymptotic bound on how long it will take to run without making an explicit statement about the lower asymptotic bound.
Other notation
In their book Introduction to Algorithms, Cormen, Leiserson, Rivest and Stein consider the set of functions f which satisfy
In a correct notation this set can, for instance, be called O(g), where
The authors state that the use of equality operator (=) to denote set membership rather than the set membership operator (∈) is an abuse of notation, but that doing so has advantages. Inside an equation or inequality, the use of asymptotic notation stands for an anonymous function in the set O(g), which eliminates lower-order terms, and helps to reduce inessential clutter in equations, for example:
Extensions to the Bachmann–Landau notations
Another notation sometimes used in computer science is Õ (read soft-O), which hides polylogarithmic factors. There are two definitions in use: some authors use f(n) = Õ(g(n)) as shorthand for f(n) = O(g(n) logk n) for some k, while others use it as shorthand for f(n) = O(g(n) logk g(n)). When g(n) is polynomial in n, there is no difference; however, the latter definition allows one to say, e.g. that while the former definition allows for for any constant k. Some authors write O* for the same purpose as the latter definition. Essentially, it is big O notation, ignoring logarithmic factors because the growth-rate effects of some other super-logarithmic function indicate a growth-rate explosion for large-sized input parameters that is more important to predicting bad run-time performance than the finer-point effects contributed by the logarithmic-growth factor(s). This notation is often used to obviate the "nitpicking" within growth-rates that are stated as too tightly bounded for the matters at hand (since logk n is always o(nε) for any constant k and any ε > 0).
Also the L notation, defined as
is convenient for functions that are between polynomial and exponential in terms of .
The generalization to functions taking values in any normed vector space is straightforward (replacing absolute values by norms), where f and g need not take their values in the same space. A generalization to functions g taking values in any topological group is also possible. The "limiting process" x → xo can also be generalized by introducing an arbitrary filter base, i.e. to directed nets f and g. The o notation can be used to define derivatives and differentiability in quite general spaces, and also (asymptotical) equivalence of functions,
which is an equivalence relation and a more restrictive notion than the relationship "f is Θ(g)" from above. (It reduces to lim f / g = 1 if f and g are positive real valued functions.) For example, 2x is Θ(x), but 2x − x is not o(x).
History (Bachmann–Landau, Hardy, and Vinogradov notations)
The symbol O was first introduced by number theorist Paul Bachmann in 1894, in the second volume of his book Analytische Zahlentheorie ("analytic number theory"). The number theorist Edmund Landau adopted it, and was thus inspired to introduce in 1909 the notation o; hence both are now called Landau symbols. These notations were used in applied mathematics during the 1950s for asymptotic analysis. The symbol (in the sense "is not an o of") was introduced in 1914 by Hardy and Littlewood. Hardy and Littlewood also introduced in 1916 the symbols ("right") and ("left"), precursors of the modern symbols ("is not smaller than a small o of") and ("is not larger than a small o of"). Thus the Omega symbols (with their original meanings) are sometimes also referred to as "Landau symbols". This notation became commonly used in number theory at least since the 1950s. In the 1970s the big O was popularized in computer science by Donald Knuth, who introduced the related Theta notation, and proposed a different definition for the Omega notation.
Landau never used the big Theta and small omega symbols.
Hardy's symbols were (in terms of the modern O notation)
- and
(Hardy however never defined or used the notation , nor , as it has been sometimes reported). Hardy introduced the symbols and (as well as some other symbols) in his 1910 tract "Orders of Infinity", and made use of them only in three papers (1910–1913). In his nearly 400 remaining papers and books he consistently used the Landau symbols O and o.
Hardy's notation is not used anymore. On the other hand, in the 1930s, the Russian number theorist Ivan Matveyevich Vinogradov introduced his notation , which has been increasingly used in number theory instead of the notation. We have
and frequently both notations are used in the same paper.
The big-O originally stands for "order of" ("Ordnung", Bachmann 1894), and is thus a Latin letter. Neither Bachmann nor Landau ever call it "Omicron". The symbol was much later on (1976) viewed by Knuth as a capital omicron, probably in reference to his definition of the symbol Omega. The digit zero should not be used.


































![{\displaystyle {\begin{aligned}e^{x}&=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\dotsb &{\text{for all }}x\\[4pt]&=1+x+{\frac {x^{2}}{2}}+O(x^{3})&{\text{as }}x\to 0\\[4pt]&=1+x+O(x^{2})&{\text{as }}x\to 0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f78f0e8f34f3b3cbe295591de6e949c2477ef4)






















































![{\displaystyle L_{n}[\alpha ,c]=e^{(c+o(1))(\ln n)^{\alpha }(\ln \ln n)^{1-\alpha }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40715162d91a34daf9bcfed5f41d8e336417f803)



































































































