Subjective logic

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Subjective_logic 

Subjective logic is a type of probabilistic logic that explicitly takes epistemic uncertainty and source trust into account. In general, subjective logic is suitable for modeling and analysing situations involving uncertainty and relatively unreliable sources. For example, it can be used for modeling and analysing trust networks and Bayesian networks.

Arguments in subjective logic are subjective opinions about state variables which can take values from a domain (aka state space), where a state value can be thought of as a proposition which can be true or false. A binomial opinion applies to a binary state variable, and can be represented as a Beta PDF (Probability Density Function). A multinomial opinion applies to a state variable of multiple possible values, and can be represented as a Dirichlet PDF (Probability Density Function). Through the correspondence between opinions and Beta/Dirichlet distributions, subjective logic provides an algebra for these functions. Opinions are also related to the belief representation in Dempster–Shafer belief theory.

A fundamental aspect of the human condition is that nobody can ever determine with absolute certainty whether a proposition about the world is true or false. In addition, whenever the truth of a proposition is expressed, it is always done by an individual, and it can never be considered to represent a general and objective belief. These philosophical ideas are directly reflected in the mathematical formalism of subjective logic.

Subjective opinions

Subjective opinions express subjective beliefs about the truth of state values/propositions with degrees of epistemic uncertainty, and can explicitly indicate the source of belief whenever required. An opinion is usually denoted as ${\displaystyle {\omega }_X^A}$ where ${\displaystyle A}$ is the source of the opinion, and ${\displaystyle X}$ is the state variable to which the opinion applies. The variable ${\displaystyle X}$ can take values from a domain (also called state space) e.g. denoted as ${\displaystyle \mathbb{X}}$. The values of a domain are assumed to be exhaustive and mutually disjoint, and sources are assumed to have a common semantic interpretation of a domain. The source and variable are attributes of an opinion. Indication of the source can be omitted whenever irrelevant.

Binomial opinions

Let ${\displaystyle x}$ be a state value in a binary domain. A binomial opinion about the truth of state value ${\displaystyle x}$ is the ordered quadruple ${\displaystyle {\omega }_x=(b_x,d_x,u_x,a_x)}$ where:

${\displaystyle b_x}$: belief mass	is the belief that ${\displaystyle x}$ is true.
${\displaystyle d_x}$: disbelief mass	is the belief that ${\displaystyle x}$ is false.
${\displaystyle u_x}$: uncertainty mass	is the amount of uncommitted belief, also interpreted as epistemic uncertainty.
${\displaystyle a_x}$: base rate	is the prior probability in the absence of belief or disbelief.

These components satisfy ${\displaystyle b_x+d_x+u_x=1}$ and ${\displaystyle b_x,d_x,u_x,a_x\in [0,1]}$. The characteristics of various opinion classes are listed below.

An opinion	where ${\displaystyle b_x=1}$	is an absolute opinion which is equivalent to Boolean TRUE,
	where ${\displaystyle d_x=1}$	is an absolute opinion which is equivalent to Boolean FALSE,
	where ${\displaystyle b_x+d_x=1}$	is a dogmatic opinion which is equivalent to a traditional probability,
	where ${\displaystyle b_x+d_x<1}$	is an uncertain opinion which expresses degrees of epistemic uncertainty, and
	where ${\displaystyle b_x+d_x=0}$	is a vacuous opinion which expresses total epistemic uncertainty or total vacuity of belief.

The projected probability of a binomial opinion is defined as ${\displaystyle {\mathrm{P}}_x=b_x+a_x{u}_x}$.

Binomial opinions can be represented on an equilateral triangle as shown below. A point inside the triangle represents a ${\displaystyle (b_x,d_x,u_x)}$ triple. The b,d,u-axes run from one edge to the opposite vertex indicated by the Belief, Disbelief or Uncertainty label. For example, a strong positive opinion is represented by a point towards the bottom right Belief vertex. The base rate, also called the prior probability, is shown as a red pointer along the base line, and the projected probability, ${\displaystyle {\mathrm{P}}_x}$, is formed by projecting the opinion onto the base, parallel to the base rate projector line. Opinions about three values/propositions X, Y and Z are visualized on the triangle to the left, and their equivalent Beta PDFs (Probability Density Functions) are visualized on the plots to the right. The numerical values and verbal qualitative descriptions of each opinion are also shown. 

The Beta PDF is normally denoted as ${\displaystyle \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(p(x);\alpha ,\beta )}$ where ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are its two strength parameters. The Beta PDF of a binomial opinion ${\displaystyle {\omega }_x=(b_x,d_x,u_x,a_x)}$ is the function ${\displaystyle \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(p(x);\alpha ,\beta )\text{ where }\{\begin{array}{ll}\alpha & =\frac{W{b}_x}{u_x}+W{a}_x\\ \beta & =\frac{W{d}_x}{u_x}+W(1-a_x)\end{array}}$ where ${\displaystyle W}$ is the non-informative prior weight, also called a unit of evidence, normally set to ${\displaystyle W=2}$.

Multinomial opinions

Let ${\displaystyle X}$ be a state variable which can take state values ${\displaystyle x\in \mathbb{X}}$. A multinomial opinion over ${\displaystyle X}$ is the composite tuple ${\displaystyle {\omega }_X=(b_X,u_X,a_X)}$, where ${\displaystyle b_X}$ is a belief mass distribution over the possible state values of ${\displaystyle X}$, ${\displaystyle u_X}$ is the uncertainty mass, and ${\displaystyle a_X}$ is the prior (base rate) probability distribution over the possible state values of ${\displaystyle X}$. These parameters satisfy ${\displaystyle u_X+\sum b_X(x)=1}$ and ${\displaystyle \sum a_X(x)=1}$ as well as ${\displaystyle b_X(x),u_X,a_X(x)\in [0,1]}$.

Trinomial opinions can be simply visualised as points inside a tetrahedron, but opinions with dimensions larger than trinomial do not lend themselves to simple visualisation.

Dirichlet PDFs are normally denoted as ${\displaystyle \mathrm{D}\mathrm{i}\mathrm{r}(p_X;{\alpha }_X)}$ where ${\displaystyle p_X}$ is a probability distribution over the state values of ${\displaystyle X}$, and ${\displaystyle {\alpha }_X}$ are the strength parameters. The Dirichlet PDF of a multinomial opinion ${\displaystyle {\omega }_X=(b_X,u_X,a_X)}$ is the function ${\displaystyle \mathrm{D}\mathrm{i}\mathrm{r}(p_X;{\alpha }_X)}$ where the strength parameters are given by ${\displaystyle {\alpha }_X(x)=\frac{W{b}_X(x)}{u_X}+W{a}_X(x)}$, where ${\displaystyle W}$ is the non-informative prior weight, also called a unit of evidence, normally set to the number of classes.

Operators

Most operators in the table below are generalisations of binary logic and probability operators. For example addition is simply a generalisation of addition of probabilities. Some operators are only meaningful for combining binomial opinions, and some also apply to multinomial opinion. Most operators are binary, but complement is unary, and abduction is ternary. See the referenced publications for mathematical details of each operator.

Subjective logic operators, notations, and corresponding propositional/binary logic operators

Subjective logic operator	Operator notation	Propositional/binary logic operator
Addition	${\displaystyle {\omega }_{x\cup y}^A={\omega }_x^A+{\omega }_y^A}$	Union
Subtraction	${\displaystyle {\omega }_{x\mathrm{\setminus }y}^A={\omega }_x^A-{\omega }_y^A}$	Difference
Multiplication	${\displaystyle {\omega }_{x\wedge y}^A={\omega }_x^A\cdot {\omega }_y^A}$	Conjunction / AND
Division	${\displaystyle {\omega }_{x\overline{\wedge }y}^A={\omega }_x^A/{\omega }_y^A}$	Unconjunction / UN-AND
Comultiplication	${\displaystyle {\omega }_{x\vee y}^A={\omega }_x^A\bigsqcup {\omega }_y^A}$	Disjunction / OR
Codivision	${\displaystyle {\omega }_{x\overline{\vee }y}^A={\omega }_x^A\overline{\bigsqcup }{\omega }_y^A}$	Undisjunction / UN-OR
Complement	${\displaystyle {\omega }_{\overline{x}}^A=\mathrm{\neg }{\omega }_x^A}$	NOT
Deduction	${\displaystyle {\omega }_{Y\Vert X}^A={\omega }_{Y|X}^A⊚{\omega }_X^A}$	Modus ponens
Subjective Bayes' theorem	${\displaystyle {\omega }_{X\widetilde{|}Y}^A={\omega }_{Y|X}^A\tilde{\varphi }{a}_X}$	Contraposition
Abduction	${\displaystyle {\omega }_{X\tilde{\Vert }Y}^A={\omega }_{Y|X}^A\widetilde{⊚}(a_X,{\omega }_Y^A)}$	Modus tollens
Transitivity / discounting	${\displaystyle {\omega }_X^{A;B}={\omega }_B^A\otimes {\omega }_X^B}$	n.a.
Cumulative fusion	${\displaystyle {\omega }_X^{A\diamond B}={\omega }_X^A\oplus {\omega }_X^B}$	n.a.
Constraint fusion	${\displaystyle {\omega }_X^{A\mathrm{\&}B}={\omega }_X^A\odot {\omega }_X^B}$	n.a.

Transitive source combination can be denoted in a compact or expanded form. For example, the transitive trust path from analyst/source ${\displaystyle A}$ via source ${\displaystyle B}$ to the variable ${\displaystyle X}$ can be denoted as ${\displaystyle [A;B,X]}$ in compact form, or as ${\displaystyle [A;B]:[B,X]}$ in expanded form. Here, ${\displaystyle [A;B]}$ expresses that ${\displaystyle A}$ has some trust/distrust in source ${\displaystyle B}$, whereas ${\displaystyle [B,X]}$ expresses that ${\displaystyle B}$ has an opinion about the state of variable ${\displaystyle X}$ which is given as an advice to ${\displaystyle A}$. The expanded form is the most general, and corresponds directly to the way subjective logic expressions are formed with operators.

Properties

In case the argument opinions are equivalent to Boolean TRUE or FALSE, the result of any subjective logic operator is always equal to that of the corresponding propositional/binary logic operator. Similarly, when the argument opinions are equivalent to traditional probabilities, the result of any subjective logic operator is always equal to that of the corresponding probability operator (when it exists).

In case the argument opinions contain degrees of uncertainty, the operators involving multiplication and division (including deduction, abduction and Bayes' theorem) will produce derived opinions that always have correct projected probability but possibly with approximate variance when seen as Beta/Dirichlet PDFs. All other operators produce opinions where the projected probabilities and the variance are always analytically correct.

Different logic formulas that traditionally are equivalent in propositional logic do not necessarily have equal opinions. For example ${\displaystyle {\omega }_{x\wedge (y\vee z)}\ne {\omega }_{(x\wedge y)\vee (x\wedge z)}}$ in general although the distributivity of conjunction over disjunction, expressed as ${\displaystyle x\wedge (y\vee z)\iff (x\wedge y)\vee (x\wedge z)}$, holds in binary propositional logic. This is no surprise as the corresponding probability operators are also non-distributive. However, multiplication is distributive over addition, as expressed by ${\displaystyle {\omega }_{x\wedge (y\cup z)}={\omega }_{(x\wedge y)\cup (x\wedge z)}}$. De Morgan's laws are also satisfied as e.g. expressed by ${\displaystyle {\omega }_{\overline{x\wedge y}}={\omega }_{\overline{x}\vee \overline{y}}}$.

Subjective logic allows very efficient computation of mathematically complex models. This is possible by approximation of the analytically correct functions. While it is relatively simple to analytically multiply two Beta PDFs in the form of a joint Beta PDF, anything more complex than that quickly becomes intractable. When combining two Beta PDFs with some operator/connective, the analytical result is not always a Beta PDF and can involve hypergeometric series. In such cases, subjective logic always approximates the result as an opinion that is equivalent to a Beta PDF.

Applications

Subjective logic is applicable when the situation to be analysed is characterised by considerable epistemic uncertainty due to incomplete knowledge. In this way, subjective logic becomes a probabilistic logic for epistemic-uncertain probabilities. The advantage is that uncertainty is preserved throughout the analysis and is made explicit in the results so that it is possible to distinguish between certain and uncertain conclusions.

The modelling of trust networks and Bayesian networks are typical applications of subjective logic.

Subjective trust networks

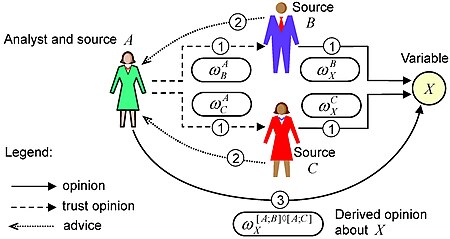
Subjective trust networks can be modelled with a combination of the transitivity and fusion operators. Let ${\displaystyle [A;B]}$ express the referral trust edge from ${\displaystyle A}$ to ${\displaystyle B}$, and let ${\displaystyle [B,X]}$ express the belief edge from ${\displaystyle B}$ to ${\displaystyle X}$. A subjective trust network can for example be expressed as ${\displaystyle ([A;B]:[B,X])\diamond ([A;C]:[C,X])}$ as illustrated in the figure below.

The indices 1, 2 and 3 indicate the chronological order in which the trust edges and advice are formed. Thus, given the set of trust edges with index 1, the origin trustor ${\displaystyle A}$ receives advice from ${\displaystyle B}$ and ${\displaystyle C}$, and is thereby able to derive belief in variable ${\displaystyle X}$. By expressing each trust edge and belief edge as an opinion, it is possible for ${\displaystyle A}$ to derive belief in ${\displaystyle X}$ expressed as ${\displaystyle {\omega }_X^A={\omega }_X^{[A;B]\diamond [A;C]}=({\omega }_B^A\otimes {\omega }_X^B)\oplus ({\omega }_C^A\otimes {\omega }_X^C)}$.

Trust networks can express the reliability of information sources, and can be used to determine subjective opinions about variables that the sources provide information about.

Evidence-based subjective logic (EBSL) describes an alternative trust-network computation, where the transitivity of opinions (discounting) is handled by applying weights to the evidence underlying the opinions.

Subjective Bayesian networks

In the Bayesian network below, ${\displaystyle X}$ and ${\displaystyle Y}$ are parent variables and ${\displaystyle Z}$ is the child variable. The analyst must learn the set of joint conditional opinions ${\displaystyle {\omega }_{Z|XY}}$ in order to apply the deduction operator and derive the marginal opinion ${\displaystyle {\omega }_{Z\Vert XY}}$ on the variable ${\displaystyle Z}$. The conditional opinions express a conditional relationship between the parent variables and the child variable.

The deduced opinion is computed as ${\displaystyle {\omega }_{Z\Vert XY}={\omega }_{Z|XY}⊚{\omega }_{XY}}$. The joint evidence opinion ${\displaystyle {\omega }_{XY}}$ can be computed as the product of independent evidence opinions on ${\displaystyle X}$ and ${\displaystyle Y}$, or as the joint product of partially dependent evidence opinions.

Subjective networks

The combination of a subjective trust network and a subjective Bayesian network is a subjective network. The subjective trust network can be used to obtain from various sources the opinions to be used as input opinions to the subjective Bayesian network, as illustrated in the figure below.

Traditional Bayesian network typically do not take into account the reliability of the sources. In subjective networks, the trust in sources is explicitly taken into account.

If and only if

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/If_and_only_if

↔⇔≡⟺
Logical symbols representing iff  

In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, P if and only if Q means that P is true whenever Q is true, and the only case in which P is true is if Q is also true, whereas in the case of P if Q, there could be other scenarios where P is true and Q is false.

In writing, phrases commonly used as alternatives to P "if and only if" Q include: Q is necessary and sufficient for P, for P it is necessary and sufficient that Q, P is equivalent (or materially equivalent) to Q (compare with material implication), P precisely if Q, P precisely (or exactly) when Q, P exactly in case Q, and P just in case Q. Some authors regard "iff" as unsuitable in formal writing; others consider it a "borderline case" and tolerate its use. In logical formulae, logical symbols, such as ${\displaystyle \leftrightarrow }$ and ${\displaystyle \iff }$, are used instead of these phrases; see § Notation below.

Definition

The truth table of P ${\displaystyle \iff }$ Q is as follows:

Truth table

P	Q	P ${\displaystyle \Rightarrow }$ Q	P ${\displaystyle \Leftarrow }$ Q	P ${\displaystyle \iff }$ Q
T	T	T	T	T
T	F	F	T	F
F	T	T	F	F
F	F	T	T	T

It is equivalent to that produced by the XNOR gate, and opposite to that produced by the XOR gate.

Usage

Notation

The corresponding logical symbols are "${\displaystyle \leftrightarrow }$", "${\displaystyle \iff }$", and ${\displaystyle \equiv }$, and sometimes "iff". These are usually treated as equivalent. However, some texts of mathematical logic (particularly those on first-order logic, rather than propositional logic) make a distinction between these, in which the first, ↔, is used as a symbol in logic formulas, while ⇔ is used in reasoning about those logic formulas (e.g., in metalogic). In Łukasiewicz's Polish notation, it is the prefix symbol ${\displaystyle E}$.

Another term for the logical connective, i.e., the symbol in logic formulas, is exclusive nor.

In TeX, "if and only if" is shown as a long double arrow: ${\displaystyle ⟺}$ via command \iff or \Longleftrightarrow.

Proofs

In most logical systems, one proves a statement of the form "P iff Q" by proving either "if P, then Q" and "if Q, then P", or "if P, then Q" and "if not-P, then not-Q". Proving these pairs of statements sometimes leads to a more natural proof, since there are not obvious conditions in which one would infer a biconditional directly. An alternative is to prove the disjunction "(P and Q) or (not-P and not-Q)", which itself can be inferred directly from either of its disjuncts—that is, because "iff" is truth-functional, "P iff Q" follows if P and Q have been shown to be both true, or both false.

Origin of iff and pronunciation

Usage of the abbreviation "iff" first appeared in print in John L. Kelley's 1955 book General Topology. Its invention is often credited to Paul Halmos, who wrote "I invented 'iff,' for 'if and only if'—but I could never believe I was really its first inventor."

It is somewhat unclear how "iff" was meant to be pronounced. In current practice, the single 'word' "iff" is almost always read as the four words "if and only if". However, in the preface of General Topology, Kelley suggests that it should be read differently: "In some cases where mathematical content requires 'if and only if' and euphony demands something less I use Halmos' 'iff'". The authors of one discrete mathematics textbook suggest: "Should you need to pronounce iff, really hang on to the 'ff' so that people hear the difference from 'if'", implying that "iff" could be pronounced as [ɪfː].

Usage in definitions

Technically, definitions are "if and only if" statements; some texts — such as Kelley's General Topology — follow the strict demands of logic, and use "if and only if" or iff in definitions of new terms. However, this logically correct usage of "if and only if" is relatively uncommon and overlooks the linguistic fact that the "if" of a definition is interpreted as meaning "if and only if". The majority of textbooks, research papers and articles (including English Wikipedia articles) follow the linguistic convention to interpret "if" as "if and only if" whenever a mathematical definition is involved (as in "a topological space is compact if every open cover has a finite subcover").

Distinction from "if" and "only if"

• "Madison will eat the fruit if it is an apple." (equivalent to "Only if Madison will eat the fruit, can it be an apple" or "Madison will eat the fruit ← the fruit is an apple")

  This states that Madison will eat fruits that are apples. It does not, however, exclude the possibility that Madison might also eat bananas or other types of fruit. All that is known for certain is that she will eat any and all apples that she happens upon. That the fruit is an apple is a sufficient condition for Madison to eat the fruit.

• "Madison will eat the fruit only if it is an apple." (equivalent to "If Madison will eat the fruit, then it is an apple" or "Madison will eat the fruit → the fruit is an apple")

  This states that the only fruit Madison will eat is an apple. It does not, however, exclude the possibility that Madison will refuse an apple if it is made available, in contrast with (1), which requires Madison to eat any available apple. In this case, that a given fruit is an apple is a necessary condition for Madison to be eating it. It is not a sufficient condition since Madison might not eat all the apples she is given.

• "Madison will eat the fruit if and only if it is an apple." (equivalent to "Madison will eat the fruit ↔ the fruit is an apple")

  This statement makes it clear that Madison will eat all and only those fruits that are apples. She will not leave any apple uneaten, and she will not eat any other type of fruit. That a given fruit is an apple is both a necessary and a sufficient condition for Madison to eat the fruit.

Sufficiency is the converse of necessity. That is to say, given P→Q (i.e. if P then Q), P would be a sufficient condition for Q, and Q would be a necessary condition for P. Also, given P→Q, it is true that ¬Q→¬P (where ¬ is the negation operator, i.e. "not"). This means that the relationship between P and Q, established by P→Q, can be expressed in the following, all equivalent, ways:

P is sufficient for Q

Q is necessary for P

¬Q is sufficient for ¬P

¬P is necessary for ¬Q

As an example, take the first example above, which states P→Q, where P is "the fruit in question is an apple" and Q is "Madison will eat the fruit in question". The following are four equivalent ways of expressing this very relationship:

If the fruit in question is an apple, then Madison will eat it.

Only if Madison will eat the fruit in question, is it an apple.

If Madison will not eat the fruit in question, then it is not an apple.

Only if the fruit in question is not an apple, will Madison not eat it.

Here, the second example can be restated in the form of if...then as "If Madison will eat the fruit in question, then it is an apple"; taking this in conjunction with the first example, we find that the third example can be stated as "If the fruit in question is an apple, then Madison will eat it; and if Madison will eat the fruit, then it is an apple".

In terms of Euler diagrams

• 

  A is a proper subset of B. A number is in A only if it is in B; a number is in B if it is in A.

• 

  C is a subset but not a proper subset of B. A number is in B if and only if it is in C, and a number is in C if and only if it is in B.

Euler diagrams show logical relationships among events, properties, and so forth. "P only if Q", "if P then Q", and "P→Q" all mean that P is a subset, either proper or improper, of Q. "P if Q", "if Q then P", and Q→P all mean that Q is a proper or improper subset of P. "P if and only if Q" and "Q if and only if P" both mean that the sets P and Q are identical to each other.

More general usage

Iff is used outside the field of logic as well. Wherever logic is applied, especially in mathematical discussions, it has the same meaning as above: it is an abbreviation for if and only if, indicating that one statement is both necessary and sufficient for the other. This is an example of mathematical jargon (although, as noted above, if is more often used than iff in statements of definition).

The elements of X are all and only the elements of Y means: "For any z in the domain of discourse, z is in X if and only if z is in Y."

Music and mathematics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Music_and_mathematics 

A spectrogram of a violin waveform, with linear frequency on the vertical axis and time on the horizontal axis. The bright lines show how the spectral components change over time. The intensity colouring is logarithmic (black is −120 dBFS).

Music theory analyzes the pitch, timing, and structure of music. It uses mathematics to study elements of music such as tempo, chord progression, form, and meter. The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory.

While music theory has no axiomatic foundation in modern mathematics, the basis of musical sound can be described mathematically (using acoustics) and exhibits "a remarkable array of number properties".

History

Though ancient Chinese, Indians, Egyptians and Mesopotamians are known to have studied the mathematical principles of sound, the Pythagoreans (in particular Philolaus and Archytas) of ancient Greece were the first researchers known to have investigated the expression of musical scales in terms of numerical ratios, particularly the ratios of small integers. Their central doctrine was that "all nature consists of harmony arising out of numbers".

From the time of Plato, harmony was considered a fundamental branch of physics, now known as musical acoustics. Early Indian and Chinese theorists show similar approaches: all sought to show that the mathematical laws of harmonics and rhythms were fundamental not only to our understanding of the world but to human well-being. Confucius, like Pythagoras, regarded the small numbers 1,2,3,4 as the source of all perfection.

Time, rhythm, and meter

Without the boundaries of rhythmic structure – a fundamental equal and regular arrangement of pulse repetition, accent, phrase and duration – music would not be possible. Modern musical use of terms like meter and measure also reflects the historical importance of music, along with astronomy, in the development of counting, arithmetic and the exact measurement of time and periodicity that is fundamental to physics.

The elements of musical form often build strict proportions or hypermetric structures (powers of the numbers 2 and 3).

Musical form

Main article: Musical form

Musical form is the plan by which a short piece of music is extended. The term "plan" is also used in architecture, to which musical form is often compared. Like the architect, the composer must take into account the function for which the work is intended and the means available, practicing economy and making use of repetition and order. The common types of form known as binary and ternary ("twofold" and "threefold") once again demonstrate the importance of small integral values to the intelligibility and appeal of music.

Frequency and harmony

Chladni figures produced by sound vibrations in fine powder on a square plate. (Ernst Chladni, Acoustics, 1802)

A musical scale is a discrete set of pitches used in making or describing music. The most important scale in the Western tradition is the diatonic scale but many others have been used and proposed in various historical eras and parts of the world. Each pitch corresponds to a particular frequency, expressed in hertz (Hz), sometimes referred to as cycles per second (c.p.s.). A scale has an interval of repetition, normally the octave. The octave of any pitch refers to a frequency exactly twice that of the given pitch.

Succeeding superoctaves are pitches found at frequencies four, eight, sixteen times, and so on, of the fundamental frequency. Pitches at frequencies of half, a quarter, an eighth and so on of the fundamental are called suboctaves. There is no case in musical harmony where, if a given pitch be considered accordant, that its octaves are considered otherwise. Therefore, any note and its octaves will generally be found similarly named in musical systems (e.g. all will be called doh or A or Sa, as the case may be).

When expressed as a frequency bandwidth an octave A₂–A₃ spans from 110 Hz to 220 Hz (span=110 Hz). The next octave will span from 220 Hz to 440 Hz (span=220 Hz). The third octave spans from 440 Hz to 880 Hz (span=440 Hz) and so on. Each successive octave spans twice the frequency range of the previous octave.

The exponential nature of octaves when measured on a linear frequency scale.

This diagram presents octaves as they appear in the sense of musical intervals, equally spaced.

Because we are often interested in the relations or ratios between the pitches (known as intervals) rather than the precise pitches themselves in describing a scale, it is usual to refer to all the scale pitches in terms of their ratio from a particular pitch, which is given the value of one (often written 1/1), generally a note which functions as the tonic of the scale. For interval size comparison, cents are often used.

Oscillogram of middle C (262 Hz). (Scale: 1 square is equal to 1 millisecond)

C5, an octave above middle C. The frequency is twice that of middle C (523 Hz).

C3, an octave below middle C. The frequency is half that of middle C (131 Hz).

Common term	Example name	Hz	Multiple of fundamental	Ratio of within octave	Cents within octave
Fundamental	A2	110	${\displaystyle 1x}$	${\displaystyle 1/1=1x}$	0
Octave	A3	220	${\displaystyle 2x}$	${\displaystyle 2/1=2x}$	1200
				${\displaystyle 2/2=1x}$	0
Perfect Fifth	E4	330	${\displaystyle 3x}$	${\displaystyle 3/2=1.5x}$	702
Octave	A4	440	${\displaystyle 4x}$	${\displaystyle 4/2=2x}$	1200
				${\displaystyle 4/4=1x}$	0
Major Third	C♯5	550	${\displaystyle 5x}$	${\displaystyle 5/4=1.25x}$	386
Perfect Fifth	E5	660	${\displaystyle 6x}$	${\displaystyle 6/4=1.5x}$	702
Harmonic seventh	G5	770	${\displaystyle 7x}$	${\displaystyle 7/4=1.75x}$	969
Octave	A5	880	${\displaystyle 8x}$	${\displaystyle 8/4=2x}$	1200
				${\displaystyle 8/8=1x}$	0

Tuning systems

Main articles: Musical tuning and Musical temperament

There are two main families of tuning systems: equal temperament and just tuning. Equal temperament scales are built by dividing an octave into intervals which are equal on a logarithmic scale, which results in perfectly evenly divided scales, but with ratios of frequencies which are irrational numbers. Just scales are built by multiplying frequencies by rational numbers, which results in simple ratios between frequencies, but with scale divisions that are uneven.

One major difference between equal temperament tunings and just tunings is differences in acoustical beat when two notes are sounded together, which affects the subjective experience of consonance and dissonance. Both of these systems, and the vast majority of music in general, have scales that repeat on the interval of every octave, which is defined as frequency ratio of 2:1. In other words, every time the frequency is doubled, the given scale repeats.

Below are Ogg Vorbis files demonstrating the difference between just intonation and equal temperament. You might need to play the samples several times before you can detect the difference.

• Two sine waves played consecutively – this sample has half-step at 550 Hz (C♯ in the just intonation scale), followed by a half-step at 554.37 Hz (C♯ in the equal temperament scale).
• Same two notes, set against an A440 pedal – this sample consists of a "dyad". The lower note is a constant A (440 Hz in either scale), the upper note is a C♯ in the equal-tempered scale for the first 1", and a C♯ in the just intonation scale for the last 1". Phase differences make it easier to detect the transition than in the previous sample.

Just tunings

The first 16 harmonics, their names and frequencies, showing the exponential nature of the octave and the simple fractional nature of non-octave harmonics.

The first 16 harmonics, with frequencies and log frequencies.

5-limit tuning, the most common form of just intonation, is a system of tuning using tones that are regular number harmonics of a single fundamental frequency. This was one of the scales Johannes Kepler presented in his Harmonices Mundi (1619) in connection with planetary motion. The same scale was given in transposed form by Scottish mathematician and musical theorist, Alexander Malcolm, in 1721 in his 'Treatise of Musick: Speculative, Practical and Historical', and by theorist Jose Wuerschmidt in the 20th century. A form of it is used in the music of northern India.

American composer Terry Riley also made use of the inverted form of it in his "Harp of New Albion". Just intonation gives superior results when there is little or no chord progression: voices and other instruments gravitate to just intonation whenever possible. However, it gives two different whole tone intervals (9:8 and 10:9) because a fixed tuned instrument, such as a piano, cannot change key. To calculate the frequency of a note in a scale given in terms of ratios, the frequency ratio is multiplied by the tonic frequency. For instance, with a tonic of A4 (A natural above middle C), the frequency is 440 Hz, and a justly tuned fifth above it (E5) is simply 440×(3:2) = 660 Hz.

Semitone	Ratio	Interval	Natural	Half Step
0	1:1	unison	480	0
1	16:15	semitone	512	16:15
2	9:8	major second	540	135:128
3	6:5	minor third	576	16:15
4	5:4	major third	600	25:24
5	4:3	perfect fourth	640	16:15
6	45:32	diatonic tritone	675	135:128
7	3:2	perfect fifth	720	16:15
8	8:5	minor sixth	768	16:15
9	5:3	major sixth	800	25:24
10	9:5	minor seventh	864	27:25
11	15:8	major seventh	900	25:24
12	2:1	octave	960	16:15

Pythagorean tuning is tuning based only on the perfect consonances, the (perfect) octave, perfect fifth, and perfect fourth. Thus the major third is considered not a third but a ditone, literally "two tones", and is (9:8)² = 81:64, rather than the independent and harmonic just 5:4 = 80:64 directly below. A whole tone is a secondary interval, being derived from two perfect fifths minus an octave, (3:2)²/2 = 9:8.

The just major third, 5:4 and minor third, 6:5, are a syntonic comma, 81:80, apart from their Pythagorean equivalents 81:64 and 32:27 respectively. According to Carl Dahlhaus (1990, p. 187), "the dependent third conforms to the Pythagorean, the independent third to the harmonic tuning of intervals."

Western common practice music usually cannot be played in just intonation but requires a systematically tempered scale. The tempering can involve either the irregularities of well temperament or be constructed as a regular temperament, either some form of equal temperament or some other regular meantone, but in all cases will involve the fundamental features of meantone temperament. For example, the root of chord ii, if tuned to a fifth above the dominant, would be a major whole tone (9:8) above the tonic. If tuned a just minor third (6:5) below a just subdominant degree of 4:3, however, the interval from the tonic would equal a minor whole tone (10:9). Meantone temperament reduces the difference between 9:8 and 10:9. Their ratio, (9:8)/(10:9) = 81:80, is treated as a unison. The interval 81:80, called the syntonic comma or comma of Didymus, is the key comma of meantone temperament.

Equal temperament tunings

In equal temperament, the octave is divided into equal parts on the logarithmic scale. While it is possible to construct equal temperament scale with any number of notes (for example, the 24-tone Arab tone system), the most common number is 12, which makes up the equal-temperament chromatic scale. In western music, a division into twelve intervals is commonly assumed unless it is specified otherwise.

For the chromatic scale, the octave is divided into twelve equal parts, each semitone (half-step) is an interval of the twelfth root of two so that twelve of these equal half steps add up to exactly an octave. With fretted instruments it is very useful to use equal temperament so that the frets align evenly across the strings. In the European music tradition, equal temperament was used for lute and guitar music far earlier than for other instruments, such as musical keyboards. Because of this historical force, twelve-tone equal temperament is now the dominant intonation system in the Western, and much of the non-Western, world.

Equally tempered scales have been used and instruments built using various other numbers of equal intervals. The 19 equal temperament, first proposed and used by Guillaume Costeley in the 16th century, uses 19 equally spaced tones, offering better major thirds and far better minor thirds than normal 12-semitone equal temperament at the cost of a flatter fifth. The overall effect is one of greater consonance. Twenty-four equal temperament, with twenty-four equally spaced tones, is widespread in the pedagogy and notation of Arabic music. However, in theory and practice, the intonation of Arabic music conforms to rational ratios, as opposed to the irrational ratios of equally tempered systems.

While any analog to the equally tempered quarter tone is entirely absent from Arabic intonation systems, analogs to a three-quarter tone, or neutral second, frequently occur. These neutral seconds, however, vary slightly in their ratios dependent on maqam, as well as geography. Indeed, Arabic music historian Habib Hassan Touma has written that "the breadth of deviation of this musical step is a crucial ingredient in the peculiar flavor of Arabian music. To temper the scale by dividing the octave into twenty-four quarter-tones of equal size would be to surrender one of the most characteristic elements of this musical culture."

53 equal temperament arises from the near equality of 53 perfect fifths with 31 octaves, and was noted by Jing Fang and Nicholas Mercator.

Connections to mathematics

Set theory

Main article: Set theory (music)

Musical set theory uses the language of mathematical set theory in an elementary way to organize musical objects and describe their relationships. To analyze the structure of a piece of (typically atonal) music using musical set theory, one usually starts with a set of tones, which could form motives or chords. By applying simple operations such as transposition and inversion, one can discover deep structures in the music. Operations such as transposition and inversion are called isometries because they preserve the intervals between tones in a set.

Abstract algebra

Main article: Abstract algebra

Expanding on the methods of musical set theory, some theorists have used abstract algebra to analyze music. For example, the pitch classes in an equally tempered octave form an abelian group with 12 elements. It is possible to describe just intonation in terms of a free abelian group.

Transformational theory is a branch of music theory developed by David Lewin. The theory allows for great generality because it emphasizes transformations between musical objects, rather than the musical objects themselves.

Theorists have also proposed musical applications of more sophisticated algebraic concepts. The theory of regular temperaments has been extensively developed with a wide range of sophisticated mathematics, for example by associating each regular temperament with a rational point on a Grassmannian.

The chromatic scale has a free and transitive action of the cyclic group ${\displaystyle \mathbb{Z}/12\mathbb{Z}}$, with the action being defined via transposition of notes. So the chromatic scale can be thought of as a torsor for the group.

Numbers and series

Some composers have incorporated the golden ratio and Fibonacci numbers into their work.

Category theory

Main article: Category theory

The mathematician and musicologist Guerino Mazzola has used category theory (topos theory) for a basis of music theory, which includes using topology as a basis for a theory of rhythm and motives, and differential geometry as a basis for a theory of musical phrasing, tempo, and intonation.

Musicians who were or are also mathematicians

• Albert Einstein - Accomplished pianist and violinist.
• Art Garfunkel (Simon & Garfunkel) – Masters in Mathematics Education, Columbia University
• Brian May (Queen) - BSc (Hons) in Mathematics and Physics, PhD in Astrophysics, both from Imperial College London.
• Dan Snaith – PhD Mathematics, Imperial College London
• Delia Derbyshire - BA in mathematics and music from Cambridge.
• Jonny Buckland (Coldplay) - Studied astronomy and mathematics at University College London.
• Kit Armstrong - Degree in music and MSc in mathematics.
• Manjul Bhargava - Plays the tabla, won the Fields Medal in 2014.
• Phil Alvin (The Blasters) – Mathematics, University of California, Los Angeles
• Philip Glass - Studied mathematics and philosophy at the University of Chicago.
• Tom Lehrer - BA mathematics from Harvard University.
• William Herschel - Astronomer and played the oboe, violin, harpsichord and organ. He composed 24 symphonies and many concertos, as well as some church music.
• Jerome Hines - Five articles published in Mathematics Magazine 1951–6.
• Donald Knuth - Knuth is an organist and a composer. In 2016 he completed a musical piece for organ titled Fantasia Apocalyptica. It was premièred in Sweden on January 10, 2018