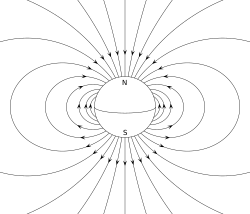
The
Earth's magnetic field, approximated as a magnetic dipole. However, the "N" and "S" (north and south) poles are labeled here
geographically, which is the opposite of the convention for labeling the poles of a magnetic dipole moment.
In
physics, there are several kinds of
dipole:
- An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some (usually small) distance. A permanent electric dipole is called an electret.
- A magnetic dipole is a closed circulation of electric current. A simple example of this is a single loop of wire with some constant current through it.[1][2]
- A current dipole is a current from a sink of current to a source of current within a (usually conducting) medium. Current dipoles are often used to model neuronal sources of electromagnetic fields that can be measured using Magnetoencephalography or Electroencephalography.
Dipoles can be characterized by their dipole moment, a vector quantity. For the simple electric dipole given above, the
electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition of the dipole moment, one should always consider the "dipole limit", where e.g. the distance of the generating charges should
converge to 0, while simultaneously the charge strength should
diverge to infinity in such a way that the product remains a positive constant.)
For the current loop, the
magnetic dipole moment points through the loop (according to the
right hand grip rule), with a magnitude equal to the current in the loop times the area of the loop.
In addition to current loops, the
electron, among other
fundamental particles, has a magnetic dipole moment. This is because it generates a
magnetic field that is identical to that generated by a very small current loop. However, the electron's magnetic moment is not due to a current loop, but is instead an
intrinsic property of the electron.
[3] It is also possible that the electron has an
electric dipole moment, although this has not yet been observed (see
electron electric dipole moment for more information).
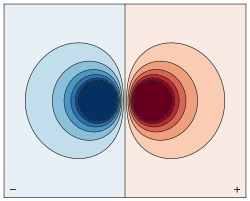
Contour plot of the
electrostatic potential of a horizontally oriented electrical dipole of finite size. Strong colors indicate highest and lowest potential (where the opposing charges of the dipole are located).
A permanent magnet, such as a bar magnet, owes its magnetism to the intrinsic magnetic dipole moment of the electron. The two ends of a bar magnet are referred to as poles (not to be confused with
monopoles), and may be labeled "north" and "south". In terms of the Earth's magnetic field, these are respectively "north-seeking" and "south-seeking" poles, that is if the magnet were freely suspended in the Earth's magnetic field, the north-seeking pole would point towards the north and the south-seeking pole would point twards the south. The dipole moment of the bar magnet points from its magnetic
south to its magnetic
north pole. The north pole of a bar magnet in a
compass points north. However, this means that Earth's geomagnetic north pole is the
south pole (south-seeking pole) of its dipole moment, and vice versa.
The only known mechanisms for the creation of magnetic dipoles are by current loops or quantum-mechanical
spin since the existence of
magnetic monopoles has never been experimentally demonstrated.
The term comes from the
Greek δίς (
dis), "twice"
[4] and πόλος (
pòlos), "axis".
[5][6]
Classification
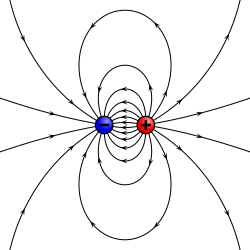
Electric field lines of two opposing charges separated by a finite distance.
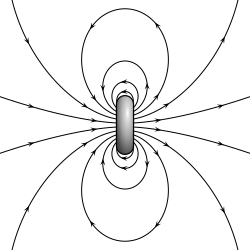
Magnetic field lines of a ring current of finite diameter.

Field lines of a point dipole of any type, electric, magnetic, acoustic, …
A
physical dipole consists of two equal and opposite point charges: in the literal sense, two poles. Its field at large distances (i.e., distances large in comparison to the separation of the poles) depends almost entirely on the dipole moment as defined above. A
point (electric) dipole is the limit obtained by letting the separation tend to 0 while keeping the dipole moment fixed. The field of a point dipole has a particularly simple form, and the order-1 term in the
multipole expansion is precisely the point dipole field.
Although there are no known
magnetic monopoles in nature, there are magnetic dipoles in the form of the quantum-mechanical
spin associated with particles such as
electrons (although the accurate description of such effects falls outside of classical electromagnetism). A theoretical magnetic
point dipole has a magnetic field of exactly the same form as the electric field of an electric point dipole. A very small current-carrying loop is approximately a magnetic point dipole; the magnetic dipole moment of such a loop is the product of the current flowing in the loop and the (vector) area of the loop.
Any configuration of charges or currents has a 'dipole moment', which describes the dipole whose field is the best approximation, at large distances, to that of the given configuration. This is simply one term in the multipole expansion when the total charge ("monopole moment") is 0 — as it
always is for the magnetic case, since there are no magnetic monopoles. The dipole term is the dominant one at large distances: Its field falls off in proportion to 1/
r3, as compared to 1/
r4 for the next (
quadrupole) term and higher powers of 1/
r for higher terms, or 1/
r2 for the monopole term.
Molecular dipoles
Many
molecules have such dipole moments due to non-uniform distributions of positive and negative charges on the various atoms. Such is the case with
polar compounds like
hydrogen fluoride (HF), where
electron density is shared unequally between atoms. Therefore, a molecule's dipole is an
electric dipole with an inherent electric field which should not be confused with a
magnetic dipole which generates a magnetic field.
The physical chemist
Peter J. W. Debye was the first scientist to study molecular dipoles extensively, and, as a consequence, dipole moments are measured in units named
debye in his honor.
For molecules there are three types of dipoles:
- Permanent dipoles: These occur when two atoms in a molecule have substantially different electronegativity: One atom attracts electrons more than another, becoming more negative, while the other atom becomes more positive. A molecule with a permanent dipole moment is called a polar molecule. See dipole-dipole attractions.
- Instantaneous dipoles: These occur due to chance when electrons happen to be more concentrated in one place than another in a molecule, creating a temporary dipole. See instantaneous dipole.
- Induced dipoles: These can occur when one molecule with a permanent dipole repels another molecule's electrons, inducing a dipole moment in that molecule. A molecule is polarized when it carries an induced dipole. See induced-dipole attraction.
More generally, an induced dipole of
any polarizable charge distribution
ρ (remember that a molecule has a charge distribution) is caused by an electric field external to
ρ. This field may, for instance, originate from an ion or polar molecule in the vicinity of
ρ or may be macroscopic (e.g., a molecule between the plates of a charged
capacitor). The size of the induced dipole is equal to the product of the strength of the external field and the dipole
polarizability of
ρ.
Dipole moment values can be obtained from measurement of the
dielectric constant. Some typical gas phase values in
debye units are:
[7]

The linear molecule CO
2 has a zero dipole as the two bond dipoles cancel.
KBr has one of the highest dipole moments because it is a very
ionic molecule (which only exists as a molecule in the gas phase).

The bent molecule H
2O has a net dipole. The two bond dipoles do not cancel.
The overall dipole moment of a molecule may be approximated as a
vector sum of
bond dipole moments. As a vector sum it depends on the relative orientation of the bonds, so that from the dipole moment information can be deduced about the
molecular geometry. For example the zero dipole of CO
2 implies that the two C=O bond dipole moments cancel so that the molecule must be linear. For H
2O the O-H bond moments do not cancel because the molecule is bent. For ozone (O
3) which is also a bent molecule, the bond dipole moments are not zero even though the O-O bonds are between similar atoms. This agrees with the Lewis structures for the resonance forms of ozone which show a positive charge on the central oxygen atom.

An example in organic chemistry of the role of geometry in determining dipole moment is the
cis and trans isomers of
1,2-dichloroethene. In the cis isomer the two polar C-Cl bonds are on the same side of the C=C double bond and the molecular dipole moment is 1.90 D. In the trans isomer, the dipole moment is zero because the two C-Cl bond are on opposite sides of the C=C and cancel (and the two bond moments for the much less polar C-H bonds also cancel).
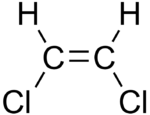
Cis isomer, dipole moment 1.90 D

Trans isomer, dipole moment zero
Another example of the role of molecular geometry is
boron trifluoride, which has three polar bonds with a difference in
electronegativity greater than the traditionally cited threshold of 1.7 for
ionic bonding. However, due to the equilateral triangular distribution of the fluoride ions about the boron cation center, the molecule
as a whole does not exhibit any identifiable pole: one cannot construct a plane that divides the molecule into a net negative part and a net positive part.
Quantum mechanical dipole operator
Consider a collection of
N particles with charges
qi and position vectors
ri. For instance, this collection may be a molecule consisting of electrons, all with
charge −
e, and nuclei with charge
eZi, where
Zi is the
atomic number of the
i th nucleus. The dipole observable (physical quantity) has the quantum mechanical
dipole operator:
[citation needed]

Notice that this definition is valid only for non-charged dipoles, i.e. total charge equal to zero. To a charged dipole we have the next equation:

where

is the center of mass of the molecule/group of particles.
[8]
Atomic dipoles
A non-degenerate (S-state) atom can have only a zero permanent dipole. This fact follows quantum mechanically from the inversion symmetry of atoms. All 3 components of the dipole operator are antisymmetric under
inversion with respect to the nucleus,

where

is the dipole operator and

is the inversion operator. The permanent dipole moment of an atom in a non-degenerate state (see
degenerate energy level) is given as the expectation (average) value of the dipole operator,

where

is an S-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion:
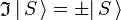
. Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse,

it follows that the expectation value changes sign under inversion. We used here the fact that

, being a symmetry operator, is
unitary:

and
by definition the Hermitian adjoint
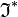
may be moved from bra to ket and then becomes

. Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,

In the case of open-shell atoms with degenerate energy levels, one could define a dipole moment by the aid of the first-order
Stark effect. This gives a non-vanishing dipole (by definition proportional to a non-vanishing first-order Stark shift) only if some of the wavefunctions belonging to the degenerate energies have opposite
parity; i.e., have different behavior under inversion. This is a rare occurrence, but happens for the excited H-atom, where 2s and 2
p states are "accidentally" degenerate (see article
Laplace–Runge–Lenz vector for the origin of this degeneracy) and have opposite parity (2s is even and 2p is odd).
Field of a static magnetic dipole
Magnitude
The far-field strength,
B, of a dipole magnetic field is given by

where
- B is the strength of the field, measured in teslas
- r is the distance from the center, measured in metres
- λ is the magnetic latitude (equal to 90° − θ) where θ is the magnetic colatitude, measured in radians or degrees from the dipole axis[note 1]
- m is the dipole moment (VADM=virtual axial dipole moment), measured in ampere square-metres (A·m2), which equals joules per tesla
- μ0 is the permeability of free space, measured in henries per metre.
Conversion to cylindrical coordinates is achieved using
r2 = z2 + ρ2 and
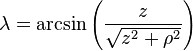
where
ρ is the perpendicular distance from the
z-axis. Then,

Vector form
The field itself is a vector quantity:
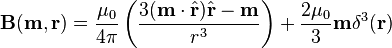
where
- B is the field
- r is the vector from the position of the dipole to the position where the field is being measured
- r is the absolute value of r: the distance from the dipole
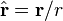 is the unit vector parallel to r;
is the unit vector parallel to r;- m is the (vector) dipole moment
- μ0 is the permeability of free space
- δ3 is the three-dimensional delta function.[note 2]
This is
exactly the field of a point dipole,
exactly the dipole term in the multipole expansion of an arbitrary field, and
approximately the field of any dipole-like configuration at large distances.
Magnetic vector potential
The
vector potential A of a magnetic dipole is

with the same definitions as above.
Field from an electric dipole
The
electrostatic potential at position
r due to an electric dipole at the origin is given by:

where
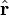 is a unit vector in the direction of r, p is the (vector) dipole moment, and ε0 is the permittivity of free space.
is a unit vector in the direction of r, p is the (vector) dipole moment, and ε0 is the permittivity of free space.
This term appears as the second term in the
multipole expansion of an arbitrary electrostatic potential Φ(
r). If the source of Φ(
r) is a dipole, as it is assumed here, this term is the only non-vanishing term in the multipole expansion of Φ(
r). The
electric field from a dipole can be found from the
gradient of this potential:
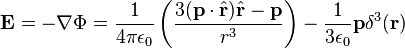
where
E is the electric field and
δ3 is the 3-dimensional
delta function.
[note 2] This is formally identical to the magnetic
H field of a point magnetic dipole with only a few names changed.
Torque on a dipole
Since the direction of an
electric field is defined as the direction of the force on a positive charge, electric field lines point away from a positive charge and toward a negative charge.
When placed in an
electric or
magnetic field, equal but opposite
forces arise on each side of the dipole creating a
torque τ:

for an
electric dipole moment p (in coulomb-meters), or
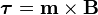
for a
magnetic dipole moment m (in ampere-square meters).
The resulting torque will tend to align the dipole with the applied field, which in the case of an electric dipole, yields a potential energy of
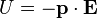 .
.
The energy of a magnetic dipole is similarly
 .
.
Dipole radiation

Evolution of the magnetic field of an oscillating electric dipole. The field lines, which are horizontal rings around the axis of the vertically oriented dipole, are perpendicularly crossing the x-y-plane of the image. Shown as a colored
contour plot is the z-component of the field. Cyan is zero magnitude, green–yellow–red and blue–pink–red are increasing strengths in opposing directions.
In addition to dipoles in electrostatics, it is also common to consider an electric or magnetic dipole that is oscillating in time. It is an extension, or a more physical next-step, to
spherical wave radiation.
In particular, consider a harmonically oscillating electric dipole, with
angular frequency ω and a dipole moment
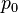
along the
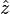
direction of the form

In vacuum, the exact field produced by this oscillating dipole can be derived using the
retarded potential formulation as:
![\mathbf{E} = \frac{1}{4\pi\varepsilon_0} \left\{ \frac{\omega^2}{c^2 r}
( \hat{\mathbf{r}} \times \mathbf{p} ) \times \hat{\mathbf{r}}
+ \left( \frac{1}{r^3} - \frac{i\omega}{cr^2} \right) \left[ 3 \hat{\mathbf{r}} (\hat{\mathbf{r}} \cdot \mathbf{p}) - \mathbf{p} \right] \right\} e^{i\omega r/c} e^{-i\omega t}](//upload.wikimedia.org/math/7/b/4/7b487096b3b9661fd46a5768a8a36407.png)

For

, the far-field takes the simpler form of a radiating "spherical" wave, but with angular dependence embedded in the cross-product:
[9]
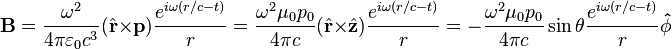
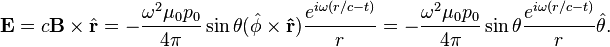
The time-averaged
Poynting vector
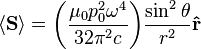
is not distributed isotropically, but concentrated around the directions lying perpendicular to the dipole moment, as a result of the non-spherical electric and magnetic waves. In fact, the
spherical harmonic function (
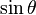
) responsible for such "donut-shaped" angular distribution is precisely the
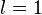
"p" wave.
The total time-average power radiated by the field can then be derived from the Poynting vector as

Notice that the dependence of the power on the fourth power of the frequency of the radiation is in accordance with the
Rayleigh scattering, and the underlying effects why the sky consists of mainly blue colour.
A circular polarized dipole is described as a superposition of two linear dipoles.

 .
. which is a microscopic property.
which is a microscopic property.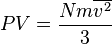 , we may combine it with the ideal gas law
, we may combine it with the ideal gas law (1)
(1) is the Boltzmann constant and
is the Boltzmann constant and  the absolute temperature defined by the ideal gas law, to obtain
the absolute temperature defined by the ideal gas law, to obtain ,
, .
. . Then the temperature
. Then the temperature  takes the form
takes the form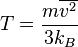 (2)
(2) (3)
(3) (4)
(4) degrees of freedom in a monatomic-gas system with
degrees of freedom in a monatomic-gas system with 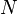 particles, the kinetic energy per degree of freedom per molecule is
particles, the kinetic energy per degree of freedom per molecule is (5)
(5)



 .
.



 ,
, .
.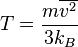



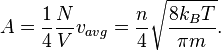





 .
. , so that equation (1) for the potential energy function simplifies to:
, so that equation (1) for the potential energy function simplifies to:
 . This yields:
. This yields:













 is the center of mass of the molecule/group of particles.
is the center of mass of the molecule/group of particles.
 is the dipole operator and
is the dipole operator and  is the inversion operator. The permanent dipole moment of an atom in a non-degenerate state (see
is the inversion operator. The permanent dipole moment of an atom in a non-degenerate state (see 
 is an S-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion:
is an S-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion: 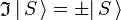 . Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse,
. Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse,
 , being a symmetry operator, is
, being a symmetry operator, is  and
and 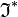 may be moved from bra to ket and then becomes
may be moved from bra to ket and then becomes  . Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,
. Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,

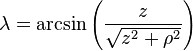

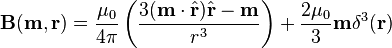
 is the unit vector parallel to r;
is the unit vector parallel to r;

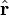 is a unit vector in the direction of r, p is the (vector)
is a unit vector in the direction of r, p is the (vector) 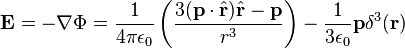

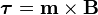
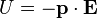 .
. .
.
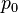 along the
along the 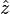 direction of the form
direction of the form

 , the far-field takes the simpler form of a radiating "spherical" wave, but with angular dependence embedded in the cross-product:
, the far-field takes the simpler form of a radiating "spherical" wave, but with angular dependence embedded in the cross-product: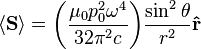
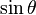 ) responsible for such "donut-shaped" angular distribution is precisely the
) responsible for such "donut-shaped" angular distribution is precisely the  "p" wave.
"p" wave.
