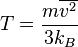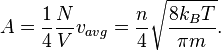From Wikipedia, the free encyclopedia


The temperature of an ideal monatomic gas is proportional to the average kinetic energy of its atoms. The size of helium atoms relative to their spacing is shown to scale under 1950 atmospheres of pressure. The atoms have a certain, average speed, slowed down here two trillion fold from room temperature.
Kinetic theory defines temperature in its own way, not identical with the thermodynamic definition.[1]

Under a microscope, the molecules making up a liquid are too small to be visible, but the jittering motion of pollen grains or dust particles can be seen. Known as Brownian motion, it results directly from collisions between the grains or particles and liquid molecules. As analyzed by Albert Einstein in 1905, this experimental evidence for kinetic theory is generally seen as having confirmed the concrete material existence of atoms and molecules.

Assumptions

The theory for ideal gases makes the following assumptions:
  • The gas consists of very small particles known as molecules. This smallness of their size is such that the total volume of the individual gas molecules added up is negligible compared to the volume of the smallest open ball containing all the molecules. This is equivalent to stating that the average distance separating the gas particles is large compared to their size.
  • These particles have the same mass.
  • The number of molecules is so large that statistical treatment can be applied.
  • These molecules are in constant, random, and rapid motion.
  • The rapidly moving particles constantly collide among themselves and with the walls of the container. All these collisions are perfectly elastic. This means, the molecules are considered to be perfectly spherical in shape, and elastic in nature.
  • Except during collisions, the interactions among molecules are negligible. (That is, they exert no forces on one another.)
This implies:
1. Relativistic effects are negligible.
2. Quantum-mechanical effects are negligible. This means that the inter-particle distance is much larger than the thermal de Broglie wavelength and the molecules are treated as classical objects.
3. Because of the above two, their dynamics can be treated classically. This means, the equations of motion of the molecules are time-reversible.
  • The average kinetic energy of the gas particles depends only on the absolute temperature of the system. The kinetic theory has its own definition of temperature, not identical with the thermodynamic definition.
  • The time during collision of molecule with the container's wall is negligible as compared to the time between successive collisions.
  • Because they have mass, the gas molecules will be affected by gravity.
More modern developments relax these assumptions and are based on the Boltzmann equation. These can accurately describe the properties of dense gases, because they include the volume of the molecules. The necessary assumptions are the absence of quantum effects, molecular chaos and small gradients in bulk properties. Expansions to higher orders in the density are known as virial expansions.

An important book on kinetic theory is that by Chapman and Cowling.[1] An important approach to the subject is called Chapman–Enskog theory.[2] There have been many modern developments and there is an alternative approach developed by Grad based on moment expansions.[3] In the other limit, for extremely rarefied gases, the gradients in bulk properties are not small compared to the mean free paths. This is known as the Knudsen regime and expansions can be performed in the Knudsen number.

Properties

Pressure and kinetic energy

Pressure is explained by kinetic theory as arising from the force exerted by molecules or atoms impacting on the walls of a container. Consider a gas of N molecules, each of mass m, enclosed in a cuboidal container of volume V=L3. When a gas molecule collides with the wall of the container perpendicular to the x coordinate axis and bounces off in the opposite direction with the same speed (an elastic collision), then the momentum lost by the particle and gained by the wall is:
\Delta p = p_{i,x} - p_{f,x} = p_{i,x} - (-p_{i,x}) = 2 p_{i,x} = 2 m v_x\,
where vx is the x-component of the initial velocity of the particle.

The particle impacts one specific side wall once every
\Delta t = \frac{2L}{v_x}
(where L is the distance between opposite walls).

The force due to this particle is:
F = \frac{\Delta p}{\Delta t} = \frac{m v_x^2}{L}.
The total force on the wall is
F = \frac{Nm\overline{v_x^2}}{L}
where the bar denotes an average over the N particles. Since the assumption is that the particles move in random directions, we will have to conclude that if we divide the velocity vectors of all particles in three mutually perpendicular directions, the average value along each direction must be equal (though their proportions are arbitrary for individual particles). That is,
\overline{v_x^2} = \overline{v^2}/3 .
We can rewrite the force as
F = \frac{Nm\overline{v^2}}{3L}.
This force is exerted on an area L2. Therefore the pressure of the gas is
P = \frac{F}{L^2} = \frac{Nm\overline{v^2}}{3V}
where V=L3 is the volume of the box. The ratio n=N/V is the number density of the gas (the mass density ρ=nm is less convenient for theoretical derivations on atomic level). Using n, we can rewrite the pressure as
P = \frac{n m \overline{v^2}}{3}.
This is a first non-trivial result of the kinetic theory because it relates pressure, a macroscopic property, to the average (translational) kinetic energy per molecule {1 \over 2} m\overline{v^2} which is a microscopic property.

Temperature and kinetic energy

Rewriting the above result for the pressure as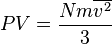 PV = {Nm\overline{v^2}\over 3} , we may combine it with the ideal gas law
\displaystyle PV = N k_B T ,




(1)
where \displaystyle k_B is the Boltzmann constant and \displaystyle T the absolute temperature defined by the ideal gas law, to obtain
k_B T = {m\overline{v^2}\over 3} ,
which leads to the expression of the average kinetic energy of a molecule,
\displaystyle \frac {1} {2} m\overline{v^2} = \frac {3} {2} k_B T.
The kinetic energy of the system is N times that of a molecule, namely K= \frac {1} {2} N m \overline{v^2} . Then the temperature \displaystyle T takes the form
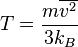\displaystyle T = {m\overline{v^2}\over 3 k_B}




(2)
which becomes
\displaystyle T = \frac {2} {3} \frac {K} {N k_B}.




(3)
Eq.(3) is one important result of the kinetic theory: The average molecular kinetic energy is proportional to the ideal gas law's absolute temperature. From Eq.(1) and Eq.(3), we have
\displaystyle PV = \frac {2} {3} K.




(4)
Thus, the product of pressure and volume per mole is proportional to the average (translational) molecular kinetic energy.

Eq.(1) and Eq.(4) are called the "classical results", which could also be derived from statistical mechanics; for more details, see .[4]

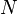Since there are \displaystyle 3N degrees of freedom in a monatomic-gas system with \displaystyle N particles, the kinetic energy per degree of freedom per molecule is
\displaystyle \frac {K} {3 N} = \frac {k_B T} {2}




(5)
In the kinetic energy per degree of freedom, the constant of proportionality of temperature is 1/2 times Boltzmann constant. In addition to this, the temperature will decrease when the pressure drops to a certain point.[why?] This result is related to the equipartition theorem.

As noted in the article on heat capacity, diatomic gases should have 7 degrees of freedom, but the lighter gases act as if they have only 5.

Thus the kinetic energy per kelvin (monatomic ideal gas) is:
  • per mole: 12.47 J
  • per molecule: 20.7 yJ = 129 μeV.
At standard temperature (273.15 K), we get:
  • per mole: 3406 J
  • per molecule: 5.65 zJ = 35.2 meV.....

Collisions with container

One can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time.

Assuming an ideal gas, a derivation[5] results in an equation for total number of collisions per unit time per area:
A = \frac{1}{4}\frac{N}{V} v_{avg} = \frac{n}{4} \sqrt{\frac{8 k_{B} T}{\pi m}} . \,
This quantity is also known as the "impingement rate" in vacuum physics.

Speed of molecules

From the kinetic energy formula it can be shown that
v_\mathrm{rms} = \sqrt {{3 k_{B} T}\over{m}}
with v in m/s, T in kelvins, and m is the molecular mass (kg). The most probable speed is 81.6% of the rms speed, and the mean speeds 92.1% (isotropic distribution of speeds).

Transport properties

The kinetic theory of gases deals not only with gases in thermodynamic equilibrium, but also very importantly with gases not in thermodynamic equilibrium. This means considering what are known as 'transport properties', such a viscosity and thermal conductivity.

History

In approximately 50 BCE, the Roman philosopher Lucretius proposed that apparently static macroscopic bodies were composed on a small scale of rapidly moving atoms all bouncing off each other.[6] This Epicurean atomistic point of view was rarely considered in the subsequent centuries, when Aristotlean ideas were dominant.


Hydrodynamica front cover

In 1738 Daniel Bernoulli published Hydrodynamica, which laid the basis for the kinetic theory of gases. In this work, Bernoulli posited the argument, still used to this day, that gases consist of great numbers of molecules moving in all directions, that their impact on a surface causes the gas pressure that we feel, and that what we experience as heat is simply the kinetic energy of their motion. The theory was not immediately accepted, in part because conservation of energy had not yet been established, and it was not obvious to physicists how the collisions between molecules could be perfectly elastic.[7]:36–37

Other pioneers of the kinetic theory (which were neglected by their contemporaries) were Mikhail Lomonosov (1747),[8] Georges-Louis Le Sage (ca. 1780, published 1818),[9] John Herapath (1816)[10] and John James Waterston (1843),[11] which connected their research with the development of mechanical explanations of gravitation. In 1856 August Krönig (probably after reading a paper of Waterston) created a simple gas-kinetic model, which only considered the translational motion of the particles.[12]

In 1857 Rudolf Clausius, according to his own words independently of Krönig, developed a similar, but much more sophisticated version of the theory which included translational and contrary to Krönig also rotational and vibrational molecular motions. In this same work he introduced the concept of mean free path of a particle. [13] In 1859, after reading a paper by Clausius, James Clerk Maxwell formulated the Maxwell distribution of molecular velocities, which gave the proportion of molecules having a certain velocity in a specific range. This was the first-ever statistical law in physics.[14] In his 1873 thirteen page article 'Molecules', Maxwell states: "we are told that an 'atom' is a material point, invested and surrounded by 'potential forces' and that when 'flying molecules' strike against a solid body in constant succession it causes what is called pressure of air and other gases."[15] In 1871, Ludwig Boltzmann generalized Maxwell's achievement and formulated the Maxwell–Boltzmann distribution. Also the logarithmic connection between entropy and probability was first stated by him.

In the beginning of the twentieth century, however, atoms were considered by many physicists to be purely hypothetical constructs, rather than real objects. An important turning point was Albert Einstein's (1905)[16] and Marian Smoluchowski's (1906)[17] papers on Brownian motion, which succeeded in making certain accurate quantitative predictions based on the kinetic theory.