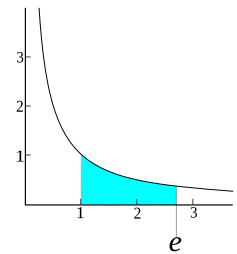
Graph of the equation  Here, e is the unique number larger than 1 that makes the shaded area equal to 1.
Here, e is the unique number larger than 1 that makes the shaded area equal to 1.
 Here, e is the unique number larger than 1 that makes the shaded area equal to 1.
Here, e is the unique number larger than 1 that makes the shaded area equal to 1.The number e is a mathematical constant, approximately equal to 2.71828, which appears in many different settings throughout mathematics. It was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest,[1] where e arises as the limit of (1 + 1/n)n as n approaches infinity. The number e can also be calculated as the sum of the infinite series[2]
The number e is of eminent importance in mathematics,[4] alongside 0, 1, π and i. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant π, e is irrational: it is not a ratio of integers. Also like π, e is transcendental: it is not a root of any non-zero polynomial with rational coefficients. The numerical value of e truncated to 50 decimal places is
The function f(x) = ex is called the (natural) exponential function, and is the unique exponential function of type ax equal to its own derivative (f(x) = f′(x) = ex), so e can be spotted as the unique positive number a such that the graph of the function y = ax has unit slope at x = 0.[5] The natural logarithm, or logarithm to base e, is the inverse function to the natural exponential function. The natural logarithm of a number k > 1 can also be defined directly as the area under the curve y = 1/x between x = 1 and x = k, in which case e is the value of k for which this area equals one (see image). In this view e is the unique number whose natural logarithm is equal to one.[6]
History
The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier.[1] However, this did not contain the constant itself, but simply a list of logarithms calculated from the constant. It is assumed that the table was written by William Oughtred. The discovery of the constant itself is credited to Jacob Bernoulli in 1683,[7][8] who attempted to find the value of the following expression (which is in fact e):The constant has been historically typeset as "e", in italics, although the ISO 80000-2:2009 standard recommends typesetting constants in an upright style.
Applications
Compound interest
The effect of earning 20% annual interest on an initial $1,000 investment at various compounding frequencies
Jacob Bernoulli discovered this constant in 1683 by studying a question about compound interest:[1]
- An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?
Bernoulli noticed that this sequence approaches a limit (the force of interest) with larger n and, thus, smaller compounding intervals. Compounding weekly (n = 52) yields $2.692597..., while compounding daily (n = 365) yields $2.714567..., just two cents more. The limit as n grows large is the number that came to be known as e; with continuous compounding, the account value will reach $2.7182818... More generally, an account that starts at $1 and offers an annual interest rate of R will, after t years, yield eRt dollars with continuous compounding. (Here R is the decimal equivalent of the rate of interest expressed as a percentage, so for 5% interest, R = 5/100 = 0.05)
Bernoulli trials
Graphs of probability P of not observing independent events each of probability 1/n after n Bernoulli trials, and 1 - P vs n ; it can be observed that as n increases, the probability of a 1/n-chance event never appearing after n tries rapidly converges to 1/e.
The number e itself also has applications to probability theory, where it arises in a way not obviously related to exponential growth. Suppose that a gambler plays a slot machine that pays out with a probability of one in n and plays it n times. Then, for large n (such as a million) the probability that the gambler will lose every bet is approximately 1/e. For n = 20 it is already approximately 1/2.79.
This is an example of a Bernoulli trial process. Each time the gambler plays the slots, there is a one in one million chance of winning. Playing one million times is modelled by the binomial distribution, which is closely related to the binomial theorem. The probability of winning k times out of a million trials is:
Derangements
Another application of e, also discovered in part by Jacob Bernoulli along with Pierre Raymond de Montmort, is in the problem of derangements, also known as the hat check problem:[13] n guests are invited to a party, and at the door each guest checks his hat with the butler who then places them into n boxes, each labelled with the name of one guest. But the butler does not know the identities of the guests, and so he puts the hats into boxes selected at random. The problem of de Montmort is to find the probability that none of the hats gets put into the right box. The answer is:Optimal planning problems
A stick of length L is broken into n equal parts. The value of n that maximizes the product of the lengths is then either[15] occurs at
occurs at  (Steiner's problem, discussed below). The quantity
(Steiner's problem, discussed below). The quantity  is a measure of information gleaned from an event occurring with probability
is a measure of information gleaned from an event occurring with probability  , so that essentially the same optimal division appears in optimal planning problems like the secretary problem.
, so that essentially the same optimal division appears in optimal planning problems like the secretary problem.Asymptotics
The number e occurs naturally in connection with many problems involving asymptotics. A prominent example is Stirling's formula for the asymptotics of the factorial function, in which both the numbers e and π enter:.
Standard normal distribution
The simplest case of a normal distribution is known as the standard normal distribution, described by this probability density function: in this expression ensures that the total area under the curve ϕ(x) is equal to one. The 1/2
in the exponent ensures that the distribution has unit variance (and
therefore also unit standard deviation). This function is symmetric
around x = 0, where it attains its maximum value
in this expression ensures that the total area under the curve ϕ(x) is equal to one. The 1/2
in the exponent ensures that the distribution has unit variance (and
therefore also unit standard deviation). This function is symmetric
around x = 0, where it attains its maximum value  ; and has inflection points at +1 and −1.
; and has inflection points at +1 and −1.In calculus
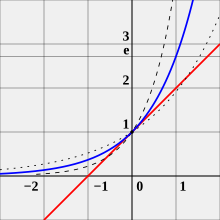
Function f(x) = ax for several values of a. e is the value of a such that the gradient of f(x) = ax at x = 0 equals 1. This is the blue curve, ex. Functions 2x (dotted curve) and 4x (dashed curve) are also shown; they also pass through the point (0, 1), but they are not tangent to the (red) line of slope 1.
The value of the natural log with argument e, ln(e), is 1.
Another motivation comes from considering the derivative of the base-a logarithm,[17] i.e., of loga x for x > 0:
There are thus two ways in which to select a special number a = e. One way is to set the derivative of the exponential function ax to ax, and solve for a. The other way is to set the derivative of the base a logarithm to 1/x and solve for a. In each case, one arrives at a convenient choice of base for doing calculus. In fact, these two solutions for a are actually the same, the number e.
Alternative characterizations
The five shaded regions are of equal area, and define units of hyperbolic angle along the hyperbola  .
.
 .
.Other characterizations of e are also possible: one is as the limit of a sequence, another is as the sum of an infinite series, and still others rely on integral calculus. So far, the following two (equivalent) properties have been introduced:
- The number e is the unique positive real number such that
.
- The number e is the unique positive real number such that
.
- The number e is the limit
- The number e is the sum of the infinite series
- The number e is the unique positive real number such that
- If f(t) is an exponential function, then the quantity
is a constant, sometimes called the time constant (it is the reciprocal of the exponential growth constant or decay constant). The time constant is the time it takes for the exponential function to increase by a factor of e:
.
Properties
Calculus
As in the motivation, the exponential function ex is important in part because it is the unique nontrivial function (up to multiplication by a constant) which is its own derivativeInequalities
The number e is the unique real number such thatAlso, we have the inequality
Exponential-like functions
Steiner's problem asks to find the global maximum for the function
 , from above, evaluated at
, from above, evaluated at  and simplifying gives
and simplifying gives  . So
. So  for all positive x.[19]
for all positive x.[19]Similarly, x = 1/e is where the global minimum occurs for the function
The infinite tetration
or
Number theory
The real number e is irrational. Euler proved this by showing that its simple continued fraction expansion is infinite.[21] (See also Fourier's proof that e is irrational.)Furthermore, by the Lindemann–Weierstrass theorem, e is transcendental, meaning that it is not a solution of any non-constant polynomial equation with rational coefficients. It was the first number to be proved transcendental without having been specifically constructed for this purpose (compare with Liouville number); the proof was given by Charles Hermite in 1873.
It is conjectured that e is normal, meaning that when e is expressed in any base the possible digits in that base are uniformly distributed (occur with equal probability in any sequence of given length).
Complex numbers
The exponential function ex may be written as a Taylor seriesThe expression
Differential equations
The general functionRepresentations
The number e can be represented as a real number in a variety of ways: as an infinite series, an infinite product, a continued fraction, or a limit of a sequence. The chief among these representations, particularly in introductory calculus courses is the limitLess common is the continued fraction (sequence A003417 in the OEIS).
which written out looks like
Stochastic representations
In addition to exact analytical expressions for representation of e, there are stochastic techniques for estimating e. One such approach begins with an infinite sequence of independent random variables X1, X2..., drawn from the uniform distribution on [0, 1]. Let V be the least number n such that the sum of the first n observations exceeds 1:Known digits
The number of known digits of e has increased substantially during the last decades. This is due both to the increased performance of computers and to algorithmic improvements.[25][26]| Date | Decimal digits | Computation performed by | |
|---|---|---|---|
| 1690 | 1 | Jacob Bernoulli[7] | |
| 1714 | 13 | Roger Cotes[27] | |
| 1748 | 23 | Leonhard Euler[28] | |
| 1853 | 137 | William Shanks[29] | |
| 1871 | 205 | William Shanks[30] | |
| 1884 | 346 | J. Marcus Boorman[31] | |
| 1949 | 2,010 | John von Neumann (on the ENIAC) | |
| 1961 | 100,265 | Daniel Shanks and John Wrench[32] | |
| 1978 | 116,000 | Steve Wozniak on the Apple II[33] |
Since that time, the proliferation of modern high-speed desktop computers has made it possible for amateurs, with the right hardware, to compute trillions of digits of e.[34]
In computer culture
In contemporary internet culture, individuals and organizations frequently pay homage to the number e.For instance, in the IPO filing for Google in 2004, rather than a typical round-number amount of money, the company announced its intention to raise $2,718,281,828, which is e billion dollars rounded to the nearest dollar. Google was also responsible for a billboard[35] that appeared in the heart of Silicon Valley, and later in Cambridge, Massachusetts; Seattle, Washington; and Austin, Texas. It read "{first 10-digit prime found in consecutive digits of e}.com". Solving this problem and visiting the advertised (now defunct) web site led to an even more difficult problem to solve, which in turn led to Google Labs where the visitor was invited to submit a résumé.[36] The first 10-digit prime in e is 7427466391, which starts at the 99th digit.[37]
In another instance, the computer scientist Donald Knuth let the version numbers of his program Metafont approach e. The versions are 2, 2.7, 2.71, 2.718, and so forth.[38]
























![{\sqrt[{x}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b4a0a76158849854a302fc639dfc882ec16008)















![e=[1;0.5,12,5,28,9,44,13,\ldots ,4(4n-1),(4n+1),\ldots ],](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4cb71149be6d3d2beb14c6785740cc1c6c46580)


