Electromagnetism is one of the fundamental forces of nature. Early on, electricity and magnetism were studied separately and regarded as separate phenomena. Hans Christian Ørsted discovered that the two were related – electric currents give rise to magnetism. Michael Faraday discovered the converse, that magnetism could induce electric currents, and James Clerk Maxwell put the whole thing together in a unified theory of electromagnetism. Maxwell's equations further indicated that electromagnetic waves existed, and the experiments of Heinrich Hertz confirmed this, making radio possible. Maxwell also postulated, correctly, that light was a form of electromagnetic wave, thus making all of optics a branch of electromagnetism. Radio waves differ from light only in that the wavelength of the former is much longer than the latter. Albert Einstein showed that the magnetic field arises through the relativistic motion of the electric field and thus magnetism is merely a side effect of electricity. The modern theoretical treatment of electromagnetism is as a quantum field in quantum electrodynamics.
In many situations of interest to electrical engineering, it is not necessary to apply quantum theory to get correct results. Classical physics is still an accurate approximation in most situations involving macroscopic objects. With few exceptions, quantum theory is only necessary at the atomic scale and a simpler classical treatment can be applied. Further simplifications of treatment are possible in limited situations. Electrostatics deals only with stationary electric charges so magnetic fields do not arise and are not considered. Permanent magnets can be described without reference to electricity or electromagnetism. Circuit theory deals with electrical networks where the fields are largely confined around current carrying conductors. In such circuits, even Maxwell's equations can be dispensed with and simpler formulations used. On the other hand, a quantum treatment of electromagnetism is important in chemistry. Chemical reactions and chemical bonding are the result of quantum mechanical interactions of electrons around atoms. Quantum considerations are also necessary to explain the behaviour of many electronic devices, for instance the tunnel diode.
Electric charge
Electromagnetism is one of the fundamental forces of nature alongside gravity, the strong force and the weak force. Whereas gravity acts on all things that have mass, electromagnetism acts on all things that have electric charge. Furthermore, as there is the conservation of mass according to which mass cannot be created or destroyed, there is also the conservation of charge which means that the charge in a closed system (where no charges are leaving or entering) must remain constant. The fundamental law that describes the gravitational force on a massive object in classical physics is Newton's law of gravity. Analogously, Coulomb's law is the fundamental law that describes the force that charged objects exert on one another. It is given by the formula
where F is the force, ke is the Coulomb constant, q1 and q2 are the magnitudes of the two charges, and r2 is the square of the distance between them. It describes the fact that like charges repel one another whereas opposite charges attract one another and that the stronger the charges of the particles, the stronger the force they exert on one another. The law is also an inverse square law which means that as the distance between two particles is doubled, the force on them is reduced by a factor of four.
Electric and magnetic fields
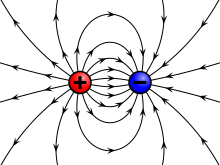
In physics, fields are entities that interact with matter and can be described mathematically by assigning a value to each point in space and time. Vector fields are fields which are assigned both a numerical value and a direction at each point in space and time. Electric charges produce a vector field called the electric field. The numerical value of the electric field, also called the electric field strength, determines the strength of the electric force that a charged particle will feel in the field and the direction of the field determines which direction the force will be in. By convention, the direction of the electric field is the same as the direction of the force on positive charges and opposite to the direction of the force on negative charges. Because positive charges are repelled by other positive charges and are attracted to negative charges, this means the electric fields point away from positive charges and towards negative charges. These properties of the electric field are encapsulated in the equation for the electric force on a charge written in terms of the electric field:
where F is the force on a charge q in an electric field E.
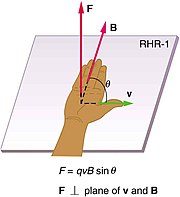
As well as producing an electric field, charged particles will produce a magnetic field when they are in a state of motion that will be felt by other charges that are in motion (as well as permanent magnets). The direction of the force on a moving charge from a magnetic field is perpendicular to both the direction of motion and the direction of the magnetic field lines and can be found using the right-hand rule. The strength of the force is given by the equation
where F is the force on a charge q with speed v in a magnetic field B which is pointing in a direction of angle θ from the direction of motion of the charge.
The combination of the electric and magnetic forces on a charged particle is called the Lorentz force. Classical electromagnetism is fully described by the Lorentz force alongside a set of equations called Maxwell's equations. The first of these equations is known as Gauss's law. It describes the electric field produced by charged particles and by charge distributions. According to Gauss's law, the flux (or flow) of electric field through any closed surface is proportional to the amount of charge that is enclosed by that surface. This means that the greater the charge, the greater the electric field that is produced. It also has other important implications. For example, this law means that if there is no charge enclosed by the surface, then either there is no electric field at all or, if there is a charge near to but outside of the closed surface, the flow of electric field into the surface must exactly cancel with the flow out of the surface. The second of Maxwell's equations is known as Gauss's law for magnetism and, similarly to the first Gauss's law, it describes flux, but instead of electric flux, it describes magnetic flux. According to Gauss's law for magnetism, the flow of magnetic field through a closed surface is always zero. This means that if there is a magnetic field, the flow into the closed surface will always cancel out with the flow out of the closed surface. This law has also been called "no magnetic monopoles" because it means that any magnetic flux flowing out of a closed surface must flow back into it, meaning that positive and negative magnetic poles must come together as a magnetic dipole and can never be separated into magnetic monopoles. This is in contrast to electric charges which can exist as separate positive and negative charges.
The third of Maxwell's equations is called the Ampère–Maxwell law. It states that a magnetic field can be generated by an electric current. The direction of the magnetic field is given by Ampère's right-hand grip rule. If the wire is straight, then the magnetic field is curled around it like the gripped fingers in the right-hand rule. If the wire is wrapped into coils, then the magnetic field inside the coils points in a straight line like the outstretched thumb in the right-hand grip rule. When electric currents are used to produce a magnet in this way, it is called an electromagnet. Electromagnets often use a wire curled up into solenoid around an iron core which strengthens the magnetic field produced because the iron core becomes magnetised. Maxwell's extension to the law states that a time-varying electric field can also generate a magnetic field. Similarly, Faraday's law of induction states that a magnetic field can produce an electric current. For example, a magnet pushed in and out of a coil of wires can produce an electric current in the coils which is proportional to the strength of the magnet as well as the number of coils and the speed at which the magnet is inserted and extracted from the coils. This principle is essential for transformers which are used to transform currents from high voltage to low voltage, and vice versa. They are needed to convert high voltage mains electricity into low voltage electricity which can be safely used in homes. Maxwell's formulation of the law is given in the Maxwell–Faraday equation—the fourth and final of Maxwell's equations—which states that a time-varying magnetic field produces an electric field.
Together, Maxwell's equations provide a single uniform theory of the electric and magnetic fields and Maxwell's work in creating this theory has been called "the second great unification in physics" after the first great unification of Newton's law of universal gravitation. The solution to Maxwell's equations in free space (where there are no charges or currents) produces wave equations corresponding to electromagnetic waves (with both electric and magnetic components) travelling at the speed of light. The observation that these wave solutions had a wave speed exactly equal to the speed of light led Maxwell to hypothesise that light is a form of electromagnetic radiation and to posit that other electromagnetic radiation could exist with different wavelengths. The existence of electromagnetic radiation was proved by Heinrich Hertz in a series of experiments ranging from 1886 to 1889 in which he discovered the existence of radio waves. The full electromagnetic spectrum (in order of increasing frequency) consists of radio waves, microwaves, infrared radiation, visible light, ultraviolet light, X-rays and gamma rays.
A further unification of electromagnetism came with Einstein's special theory of relativity. According to special relativity, observers moving at different speeds relative to one another occupy different observational frames of reference. If one observer is in motion relative to another observer then they experience length contraction where unmoving objects appear closer together to the observer in motion than to the observer at rest. Therefore, if an electron is moving at the same speed as the current in a neutral wire, then they experience the flowing electrons in the wire as standing still relative to it and the positive charges as contracted together. In the lab frame, the electron is moving and so feels a magnetic force from the current in the wire but because the wire is neutral it feels no electric force. But in the electron's rest frame, the positive charges seem closer together compared to the flowing electrons and so the wire seems positively charged. Therefore, in the electron's rest frame it feels no magnetic force (because it is not moving in its own frame) but it does feel an electric force due to the positively charged wire. This result from relativity proves that magnetic fields are just electric fields in a different reference frame (and vice versa) and so the two are different manifestations of the same underlying electromagnetic field.
Conductors, insulators and circuits
Conductors
A conductor is a material that allows electrons to flow easily. The most effective conductors are usually metals because they can be described fairly accurately by the free electron model in which electrons delocalize from the atomic nuclei, leaving positive ions surrounded by a cloud of free electrons. Examples of good conductors include copper, aluminum, and silver. Wires in electronics are often made of copper.
The main properties of conductors are:
- The electric field is zero inside a perfect conductor. Because charges are free to move in a conductor, when they are disturbed by an external electric field they rearrange themselves such that the field that their configuration produces exactly cancels the external electric field inside the conductor.
- The electric potential is the same everywhere inside the conductor and is constant across the surface of the conductor. This follows from the first statement because the field is zero everywhere inside the conductor and therefore the potential is constant within the conductor too.
- The electric field is perpendicular to the surface of a conductor. If this were not the case, the field would have a nonzero component on the surface of the conductor, which would cause the charges in the conductor to move around until that component of the field is zero.
- The net electric flux through a surface is proportional to the charge enclosed by the surface. This is a restatement of Gauss' law.
In some materials, the electrons are bound to the atomic nuclei and so are not free to move around but the energy required to set them free is low. In these materials, called semiconductors, the conductivity is low at low temperatures but as the temperature is increased the electrons gain more thermal energy and the conductivity increases. Silicon is an example of a semiconductors that can be used to create solar panels which become more conductive the more energy they receive from photons from the sun.
Superconductors are materials that exhibit little to no resistance to the flow of electrons when cooled below a certain critical temperature. Superconductivity can only be explained by the quantum mechanical Pauli exclusion principle which states that no two fermions (an electron is a type of fermion) can occupy exactly the same quantum state. In superconductors, below a certain temperature the electrons form boson bound pairs which do not follow this principle and this means that all the electrons can fall to the same energy level and move together uniformly in a current.
Insulators
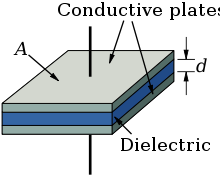
Insulators are material which are highly resistive to the flow of electrons and so are often used to cover conducting wires for safety. In insulators, electrons are tightly bound to atomic nuclei and the energy to free them is very high so they are not free to move and are resistive to induced movement by an external electric field. However, some insulators, called dielectrics, can be polarised under the influence of an external electric field so that the charges are minutely displaced forming dipoles that create a positive and negative side. Dielectrics are used in capacitors to allow them to store more electric potential energy in the electric field between the capacitor plates.
Capacitors
A capacitor is an electronic component that stores electrical potential energy in an electric field between two oppositely charged conducting plates. If one of the conducting plates has a charge density of +Q/A and the other has a charge of -Q/A where A is the area of the plates, then there will be an electric field between them. The potential difference between two parallel plates V can be derived mathematically as
where d is the plate separation and is the permittivity of free space. The ability of the capacitor to store electrical potential energy is measured by the capacitance which is defined as and for a parallel plate capacitor this is
If a dielectric is placed between the plates then the permittivity of free space is multiplied by the relative permittivity of the dielectric and the capacitance increases. The maximum energy that can be stored by a capacitor is proportional to the capacitance and the square of the potential difference between the plates
Inductors
An inductor is an electronic component that stores energy in a magnetic field inside a coil of wire. A current-carrying coil of wire induces a magnetic field according to Ampère's circuital law. The greater the current I, the greater the energy stored in the magnetic field and the lower the inductance which is defined where is the magnetic flux produced by the coil of wire. The inductance is a measure of the circuit's resistance to a change in current and so inductors with high inductances can also be used to oppose alternating current.
Other circuit components
| Component | Main function | Schematic symbol |
|---|---|---|
| Resistor | Impedes the flow of current | |
| Battery | Acts as a power source | |
| DC voltage source | Acts as a source of direct current (DC), a constant current which points in one direction | |
| AC voltage source | Acts as a source of alternating current (AC), a varying current which periodically reverses direction | |
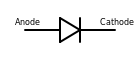
| Diode | Allows current to flow easily in one direction but not another | |
| Capacitor | Stores energy in electric fields, stores charge, passes low frequency alternating current | |
| Inductor | Stores energy in magnetic fields, resists change in current |
Circuit laws
Circuit theory deals with electrical networks where the fields are largely confined around current carrying conductors. In such circuits, simple circuit laws can be used instead of deriving all the behaviour of the circuits directly from electromagnetic laws. Ohm's law states the relationship between the current I and the voltage V of a circuit by introducing the quantity known as resistance R
Ohm's law:
Power is defined as so Ohm's law can be used to tell us the power of the circuit in terms of other quantities
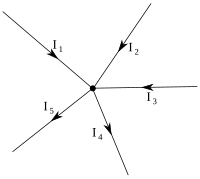
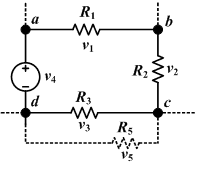
Kirchhoff's junction rule states that the current going into a junction (or node) must equal the current that leaves the node. This comes from charge conservation, as current is defined as the flow of charge over time. If a current splits as it exits a junction, the sum of the resultant split currents is equal to the incoming circuit.
Kirchhoff's loop rule states that the sum of the voltage in a closed loop around a circuit equals zero. This comes from the fact that the electric field is conservative which means that no matter the path taken, the potential at a point does not change when you get back there.
Rules can also tell us how to add up quantities such as the current and voltage in series and parallel circuits.
For series circuits, the current remains the same for each component and the voltages and resistances add up:
For parallel circuits, the voltage remains the same for each component and the currents and resistances are related as shown: