Trigonometry

From Wikipedia, the free encyclopedia

The Canadarm2 robotic manipulator on the International Space Station is operated by controlling the angles of its joints. Calculating the final position of the astronaut at the end of the arm requires repeated use of trigonometric functions of those angles.

Trigonometry (from Greek trigōnon, "triangle" and metron, "measure"^[1]) is a branch of mathematics that studies relationships involving lengths and angles of triangles. The field emerged during the 3rd century BC from applications of geometry to astronomical studies.^[2]
The 3rd-century astronomers first noted that the lengths of the sides of a right-angle triangle and the angles between those sides have fixed relationships: that is, if at least the length of one side and the value of one angle is known, then all other angles and lengths can be determined algorithmically.
These calculations soon came to be defined as the trigonometric functions and today are pervasive in both pure and applied mathematics: fundamental methods of analysis such as the Fourier transform, for example, or the wave equation, use trigonometric functions to understand cyclical phenomena across many applications in fields as diverse as physics, mechanical and electrical engineering, music and acoustics, astronomy, ecology, and biology. Trigonometry is also the foundation of surveying.

Trigonometry is most simply associated with planar right-angle triangles (each of which is a two-dimensional triangle with one angle equal to 90 degrees). The applicability to non-right-angle triangles exists, but, since any non-right-angle triangle (on a flat plane) can be bisected to create two right-angle triangles, most problems can be reduced to calculations on right-angle triangles. Thus the majority of applications relate to right-angle triangles. One exception to this is spherical trigonometry, the study of triangles on spheres, surfaces of constant positive curvature, in elliptic geometry (a fundamental part of astronomy and navigation). Trigonometry on surfaces of negative curvature is part of hyperbolic geometry.

Trigonometry basics are often taught in schools, either as a separate course or as a part of a precalculus course.

History

Hipparchus, credited with compiling the first trigonometric table, is known as "the father of trigonometry".^[3]

Sumerian astronomers studied angle measure, using a division of circles into 360 degrees.^[4] They, and later the Babylonians, studied the ratios of the sides of similar triangles and discovered some properties of these ratios but did not turn that into a systematic method for finding sides and angles of triangles. The ancient Nubians used a similar method.^[5]

In the 3rd century BCE, classical Greek mathematicians (such as Euclid and Archimedes) studied the properties of chords and inscribed angles in circles, and they proved theorems that are equivalent to modern trigonometric formulae, although they presented them geometrically rather than algebraically.

The modern sine function was first defined in the Surya Siddhanta, and its properties were further documented by the 5th century (CE) Indian mathematician and astronomer Aryabhata.^[6] These Greek and Indian works were translated and expanded by medieval Islamic mathematicians. By the 10th century, Islamic mathematicians were using all six trigonometric functions, had tabulated their values, and were applying them to problems in spherical geometry.^{[citation needed]} At about the same time, Chinese mathematicians developed trigonometry independently, although it was not a major field of study for them. Knowledge of trigonometric functions and methods reached Europe via Latin translations of the works of Persian and Arabic astronomers such as Al Battani and Nasir al-Din al-Tusi.^[7] One of the earliest works on trigonometry by a European mathematician is De Triangulis by the 15th century German mathematician Regiomontanus. Trigonometry was still so little known in 16th-century Europe that Nicolaus Copernicus devoted two chapters of De revolutionibus orbium coelestium to explain its basic concepts.

Driven by the demands of navigation and the growing need for accurate maps of large geographic areas, trigonometry grew into a major branch of mathematics.^[8] Bartholomaeus Pitiscus was the first to use the word, publishing his Trigonometria in 1595.^[9] Gemma Frisius described for the first time the method of triangulation still used today in surveying. It was Leonhard Euler who fully incorporated complex numbers into trigonometry. The works of James Gregory in the 17th century and Colin Maclaurin in the 18th century were influential in the development of trigonometric series.^[10] Also in the 18th century, Brook Taylor defined the general Taylor series.^[11]

Overview

In this right triangle: sin A = a/c; cos A = b/c; tan A = a/b.

If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a triangle is completely determined, except for similarity, by the angles. Once the angles are known, the ratios of the sides are determined, regardless of the overall size of the triangle. If the length of one of the sides is known, the other two are determined. These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:

• Sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.

$\sin A={\frac {{\textrm {opposite}}}{{\textrm {hypotenuse}}}}={\frac {a}{\,c\,}}\,.$

• Cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.

$\cos A={\frac {{\textrm {adjacent}}}{{\textrm {hypotenuse}}}}={\frac {b}{\,c\,}}\,.$

• Tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.

$\tan A={\frac {{\textrm {opposite}}}{{\textrm {adjacent}}}}={\frac {a}{\,b\,}}={\frac {a}{\,c\,}}*{\frac {c}{\,b\,}}={\frac {a}{\,c\,}}/{\frac {b}{\,c\,}}={\frac {\sin A}{\cos A}}\,.$

The hypotenuse is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle and one of the two sides adjacent to angle A. The adjacent leg is the other side that is adjacent to angle A. The opposite side is the side that is opposite to angle A. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below under Mnemonics).

The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec), and cotangent (cot), respectively:

$cosecA={\frac {1}{\sin A}}={\frac {{\textrm {hypotenuse}}}{{\textrm {opposite}}}}={\frac {c}{a}},$

$\sec A={\frac {1}{\cos A}}={\frac {{\textrm {hypotenuse}}}{{\textrm {adjacent}}}}={\frac {c}{b}},$

$\cot A={\frac {1}{\tan A}}={\frac {{\textrm {adjacent}}}{{\textrm {opposite}}}}={\frac {\cos A}{\sin A}}={\frac {b}{a}}.$

The inverse functions are called the arcsine, arccosine, and arctangent, respectively. There are arithmetic relations between these functions, which are known as trigonometric identities. The cosine, cotangent, and cosecant are so named because they are respectively the sine, tangent, and secant of the complementary angle abbreviated to "co-".

With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and their included angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since every polygon may be described as a finite combination of triangles.

Extending the definitions

Fig. 1a – Sine and cosine of an angle θ defined using the unit circle.

The above definitions only apply to angles between 0 and 90 degrees (0 and π/2 radians). Using the unit circle, one can extend them to all positive and negative arguments (see trigonometric function). The trigonometric functions are periodic, with a period of 360 degrees or 2π radians. That means their values repeat at those intervals. The tangent and cotangent functions also have a shorter period, of 180 degrees or π radians.

The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from calculus and infinite series. With these definitions the trigonometric functions can be defined for complex numbers. The complex exponential function is particularly useful.

$e^{{x+iy}}=e^{x}(\cos y+i\sin y).$

• Graphing process of y = sin(x) using a unit circle.
• 

  Graphing process of y = csc(x), the reciprocal of sine, using a unit circle.
• 

  Graphing process of y = tan(x) using a unit circle.

Mnemonics

A common use of mnemonics is to remember facts and relationships in trigonometry. For example, the sine, cosine, and tangent ratios in a right triangle can be remembered by representing them and their corresponding sides as strings of letters. For instance, a mnemonic is SOH-CAH-TOA:^[12]

Sine = Opposite ÷ Hypotenuse

Cosine = Adjacent ÷ Hypotenuse

Tangent = Opposite ÷ Adjacent

One way to remember the letters is to sound them out phonetically (i.e., SOH-CAH-TOA, which is pronounced 'so-kə-toe-uh' /soʊkəˈtoʊə/). Another method is to expand the letters into a sentence, such as "Some Old Hippy Caught Another Hippy Trippin' On Acid".^[13]

Calculating trigonometric functions

Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions.
Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan, and sometimes cis and their inverses). Most allow a choice of angle measurement methods: degrees, radians, and sometimes gradians. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers has built-in instructions for calculating trigonometric functions.^[14]

Applications of trigonometry

Sextants are used to measure the angle of the sun or stars with respect to the horizon. Using trigonometry and a marine chronometer, the position of the ship can be determined from such measurements.

There is an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.

Fields that use trigonometry or trigonometric functions include astronomy (especially for locating apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, audio synthesis, acoustics, optics, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, image compression, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.

Pythagorean identities

Identities are those equations that hold true for any value.

$\sin ^{2}A+\cos ^{2}A=1\ $

(The following two can be derived from the first.)

$\sec ^{2}A-\tan ^{2}A=1\ $

$\csc ^{2}A-\cot ^{2}A=1\ $

Angle transformation formulae

$\sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B$

$\cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B$

$\tan(A\pm B)={\frac {\tan A\pm \tan B}{1\mp \tan A\ \tan B}}$

$\cot(A\pm B)={\frac {\cot A\ \cot B\mp 1}{\cot B\pm \cot A}}$

Common formulae

Triangle with sides a,b,c and respectively opposite angles A,B,C

Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. Some identities equate an expression to a different expression involving the same angles. These are listed in List of trigonometric identities. Triangle identities that relate the sides and angles of a given triangle are listed below.

In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles (as shown in the diagram).

Law of sines

The law of sines (also known as the "sine rule") for an arbitrary triangle states:

${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R={\frac {abc}{2\Delta }},$

where $\Delta$ is the area of the triangle and R is the radius of the circumscribed circle of the triangle:

$R={\frac {abc}{{\sqrt {(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}}}.$

Another law involving sines can be used to calculate the area of a triangle. Given two sides a and b and the angle between the sides C, the area of the triangle is given by half the product of the lengths of two sides and the sine of the angle between the two sides:

${\mbox{Area}}=\Delta ={\frac {1}{2}}ab\sin C.$

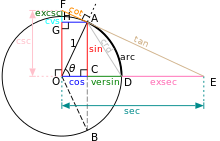
All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O.

Law of cosines

The law of cosines (known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:

$c^{2}=a^{2}+b^{2}-2ab\cos C,\,$

or equivalently:

$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.\,$

The law of cosines may be used to prove Heron's formula, which is another method that may be used to calculate the area of a triangle. This formula states that if a triangle has sides of lengths a, b, and c, and if the semiperimeter is

$s={\frac {1}{2}}(a+b+c),$

then the area of the triangle is:

${\mbox{Area}}=\Delta ={\sqrt {s(s-a)(s-b)(s-c)}}={\frac {abc}{4R}}$,

where R is the radius of the circumcircle of the triangle.

Law of tangents

The law of tangents:

${\frac {a-b}{a+b}}={\frac {\tan \left[{\tfrac {1}{2}}(A-B)\right]}{\tan \left[{\tfrac {1}{2}}(A+B)\right]}}$

Euler's formula

Euler's formula, which states that $e^{{ix}}=\cos x+i\sin x$, produces the following analytical identities for sine, cosine, and tangent in terms of e and the imaginary unit i:

$\sin x={\frac {e^{{ix}}-e^{{-ix}}}{2i}},\qquad \cos x={\frac {e^{{ix}}+e^{{-ix}}}{2}},\qquad \tan x={\frac {i(e^{{-ix}}-e^{{ix}})}{e^{{ix}}+e^{{-ix}}}}.$

Parsec

From Wikipedia, the free encyclopedia

Parsec
A parsec is the distance from the Sun to an astronomical object that has a parallax angle of one arcsecond. (the diagram is not to scale).
Unit information
Unit system	astronomical units
Unit of	length
Symbol	pc
Unit conversions
1 pc in ...	... is equal to ...
metric (SI) units	3.0857×1016 m
imperial & US units	1.9174×1013 mi
astronomical units	2.0626×105 au    3.26156 ly

A parsec (symbol: pc) is a unit of length used to measure the astronomically large distances to objects outside the Solar System. One parsec is the distance at which one astronomical unit subtends an angle of one arcsecond.^[1] About 3.26 light-years (31 trillion kilometres or 19 trillion miles) in length, the parsec is shorter than the distance from our solar system to the nearest star, Proxima Centauri, which is 1.3 parsecs from the Sun.^[2] Nevertheless, most of the stars visible to the unaided eye in the nighttime sky are within 500 parsecs of the Sun.

The parsec unit was likely first suggested in 1913 by British astronomer Herbert Hall Turner.^[3] Named from an abbreviation of the parallax of one arcsecond, it was defined so as to make calculations of astronomical distances quick and easy for astronomers from only their raw observational data. Partly for this reason, it is still the unit preferred in astronomy and astrophysics, though the light year remains prominent in popular science texts and more everyday usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs for the more distant objects within and around the Milky Way, megaparsecs for the nearer of other galaxies, and gigaparsecs for many quasars and the most distant galaxies.

History and derivation

The parsec is defined as being equal to the length of the longer leg of an extremely elongated imaginary right triangle in space. The two dimensions on which this triangle is based are its shorter leg, of length one astronomical unit (the average Earth-Sun distance), and the subtended angle of the vertex opposite that leg, measuring one arcsecond. Applying the rules of trigonometry to these two values, the unit length of the other leg of the triangle (the parsec) can be derived.

One of the oldest methods for astronomers to calculate the distance to a star was to record the difference in angle between two measurements of the position of the star in the sky. The first measurement was taken from the Earth on one side of the Sun, and the second was taken half a year later when the Earth was on the opposite side of the Sun. The distance between the two positions of the Earth when the two measurements were taken was known to be twice the distance between the Earth and the Sun. The difference in angle between the two measurements was known to be twice the parallax angle, which is formed by lines from the Sun and Earth to the star at the distant vertex. Then the distance to the star could be calculated using trigonometry.^[4] The first successful published direct measurements of an object at interstellar distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used this approach to calculate the three and a half parsec distance of 61 Cygni.^[5]

stellar parallax motion from annual parallax

The parallax of a star is taken to be half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. Equivalently, it is the subtended angle, from that star's perspective, of the semi-major axis of Earth's orbit. The star, the Sun and the Earth form the corners of an imaginary right triangle in space: the right angle is the corner at the Sun, and the corner at the star is the parallax angle. The length of the opposite side to the parallax angle is the distance from the Earth to the Sun (defined as one astronomical unit (au), and the length of the adjacent side gives the distance from the sun to the star. Therefore, given a measurement of the parallax angle, along with the rules of trigonometry, the distance from the Sun to the star can be found. A parsec is defined as the length of the side adjacent to the vertex occupied by a star whose parallax angle is one arcsecond.

The use of the parsec as a unit of distance follows naturally from Bessel's method, because the distance in parsecs can be computed simply as the reciprocal of the parallax angle in arcseconds (i. e., if the parallax angle is 1 arcsecond, the object is 1 pc from the Sun; If the parallax angle is 0.5 arcsecond, the object is 2 pc away; etc.). No trigonometric functions are required in this relationship because the very small angles involved mean that the approximate solution of the skinny triangle can be applied.

Though it may have been used before, the term parsec was first mentioned in an astronomical publication in 1913. Astronomer Royal Frank Watson Dyson expressed his concern for the need of a name for that unit of distance. He proposed the name astron, but mentioned that Carl Charlier had suggested siriometer and Herbert Hall Turner had proposed parsec.^[6] It was Turner's proposal that stuck.

Calculating the value of a parsec

In the diagram above (not to scale), S represents the Sun, and E the Earth at one point in its orbit. Thus the distance ES is one astronomical unit (AU). The angle SDE is one arcsecond (¹⁄₃₆₀₀ of a degree) so by definition D is a point in space at a distance of one parsec from the Sun. By trigonometry, the distance SD is

$SD={\frac {{\mathrm {ES}}}{\tan 1^{{\prime \prime }}}}$

Using the small-angle approximation,^{[Note 1]} by which the tangent of an extremely small angle is almost equal to the angle itself (in radians),

$SD\approx {\frac {{\mathrm {ES}}}{1^{{\prime \prime }}}}={\frac {1\,{\mbox{AU}}}{({\tfrac {1}{60\times 60}}\times {\tfrac {\pi }{180}})}}={\frac {648\,000}{\pi }}\,{\mbox{AU}}\approx 206\,264.81{\mbox{ AU}}.$

Because the astronomical unit is defined to be 149597870700 metres,^[7] the following can be calculated.

1 parsec	≈ 206264.81 astronomical units
	≈ 3.0856776×1016 metres
	≈ 19.173512 trillion miles
	≈ 3.2615638 light years

A corollary is that 1 parsec is also the distance from which a disc with a diameter of 1 AU must be viewed for it to have an angular diameter of 1 arcsecond (by placing the observer at D and a diameter of the disc on ES).

Usage and measurement

The parallax method is the fundamental calibration step for distance determination in astrophysics; however, the accuracy of ground-based telescope measurements of parallax angle is limited to about 0.01 arcsecond, and thus to stars no more than 100 pc distant.^[8] This is because the Earth’s atmosphere limits the sharpness of a star's image.^[9] Space-based telescopes are not limited by this effect and can accurately measure distances to objects beyond the limit of ground-based observations. Between 1989 and 1993, the Hipparcos satellite, launched by the European Space Agency (ESA), measured parallaxes for about 100000 stars with an astrometric precision of about 0.97 milliarcsecond, and obtained accurate measurements for stellar distances of stars up to 1000 pc away.^[10][11]

ESA's Gaia satellite, which launched on 19 December 2013, is intended to measure one billion stellar distances to within 20 microarcseconds, producing errors of 10% in measurements as far as the Galactic Centre, about 8000 pc away in the constellation of Sagittarius.^[12]

Distances in parsecs

Distances less than a parsec

Distances expressed in fractions of a parsec usually involve objects within a single star system. So, for example:

• One astronomical unit (au), the distance from the Sun to the Earth, is just under 5×10⁻⁶ parsecs.
• The most distant space probe, Voyager 1, was 0.0006 parsecs from Earth as of May 2013^[update]. It took Voyager 35 years to cover that distance.
• The Oort cloud is estimated to be approximately 0.6 parsecs in diameter

The jet erupting from the active galactic nucleus of M87 is thought to be 1.5 kiloparsecs (4890 ly) long. (image from Hubble Space Telescope)

Parsecs and kiloparsecs

Distances expressed in parsecs (pc) include distances between nearby stars, such as those in the same spiral arm or globular cluster. A distance of 1000 parsecs (3262 light-years) is commonly denoted by the kiloparsec (kpc). Astronomers typically use kiloparsecs to express distances between parts of a galaxy, or within groups of galaxies. So, for example:

• One parsec is approximately 3.26 light-years.
• The nearest known star to the Earth, other than the Sun, Proxima Centauri, is about 1.30 parsecs (4.24 light-years) away, by direct parallax measurement.
• The distance to the open cluster Pleiades is 130 ± 10 pc (420 ± 32.6 light-years) from us, per Hipparcos parallax measurement.
• The centre of the Milky Way is more than 8 kiloparsecs (26000 ly) from the Earth, and the Milky Way is roughly 34 kpc (110000 ly) across.
• The Andromeda Galaxy (M31) is ~780 kpc (~2.5 million light-years) away from the Earth.

Megaparsecs and gigaparsecs

A distance of one million parsecs is commonly denoted by the megaparsec (Mpc). Astronomers typically express the distances between neighbouring galaxies and galaxy clusters in megaparsecs.
Galactic distances are sometimes given in units of Mpc/h (as in "50/h Mpc"). h is a parameter in the range [0.5,0.75] reflecting the uncertainty in the value of the Hubble constant H for the rate of expansion of the universe: h = H / (100 km/s/Mpc). The Hubble constant becomes relevant when converting an observed redshift z into a distance d using the formula d ≈ (c / H) × z.^[13]

One gigaparsec (Gpc) is one billion parsecs — one of the largest units of length commonly used. One gigaparsec is about 3.26 billion light-years (3.26 "Gly"), or roughly one fourteenth of the distance to the horizon of the observable universe (dictated by the cosmic background radiation). Astronomers typically use gigaparsecs to express the sizes of large-scale structures such as the size of, and distance to, the CfA2 Great Wall; the distances between galaxy clusters; and the distance to quasars.

For example:

• The Andromeda Galaxy is about 0.78 Mpc (2.5 million light-years) from the Earth.
• The nearest large galaxy cluster, the Virgo Cluster, is about 16.5 Mpc (54 million light-years) from the Earth.^[14]
• The galaxy RXJ1242-11, observed to have a supermassive black hole core similar to the Milky Way's, is about 200 Mpc (650 million light-years) from the Earth.
• The galaxy filament Hercules–Corona Borealis Great Wall, currently the largest known structure in the universe, is about 3 Gpc (10 billion light-years) across.
• The particle horizon (the boundary of the observable universe) has a radius of about 14.0 Gpc (46 billion light-years).^[15]

Volume units

To determine the number of stars in the Milky Way, volumes in cubic kiloparsecs^[a] (kpc³) are selected in various directions. All the stars in these volumes are counted and the total number of stars statistically determined. The number of globular clusters, dust clouds, and interstellar gas is determined in a similar fashion. To determine the number of galaxies in superclusters, volumes in cubic megaparsecs^[a] (Mpc³) are selected. All the galaxies in these volumes are classified and tallied.
The total number of galaxies can then be determined statistically. The huge void in Boötes^[16] is measured in cubic megaparsecs.

In cosmology, volumes of cubic gigaparsecs^[a] (Gpc³) are selected to determine the distribution of matter in the visible universe and to determine the number of galaxies and quasars. The Sun is alone in its cubic parsec,^[a] (pc³) but in globular clusters the stellar density per cubic parsec could be from 100 to 1000.

Light-year

From Wikipedia, the free encyclopedia

Light-year
Unit system	astronomical units
Unit of	length
Symbol	ly
Unit conversions
1 ly in ...	... is equal to ...
metric (SI) units	9.4607×1015 m
imperial & US units	5.8786×1012 mi
astronomical units	6.3241×104 au    0.3066 pc

A light-year (symbol: ly), sometimes written light year or lightyear, is a unit of length used informally to express astronomical distances. It is approximately 10 trillion kilometres (or about 6 trillion miles).^{[note 1]} As defined by the International Astronomical Union (IAU), a light-year is the distance that light travels in vacuum in one Julian year.^[1] Because it includes the word year, the term light-year is sometimes misinterpreted as a unit of time.

The light-year is most often used when expressing distances to stars and other distances on a galactic scale, especially in non-specialist and popular science publications. The unit usually used in professional astrometry is the parsec (symbol: pc, approximately 3.26 light-years; the distance at which one astronomical unit subtends an angle of one second of arc).^[1]

Definitions

As defined by the IAU, the light-year is the product of the Julian year^{[note 2]} (365.25 days as opposed to the 365.2425-day Gregorian year) and the speed of light (299792458 m/s).^{[note 3]} Both these values are included in the IAU (1976) System of Astronomical Constants, used since 1984.^[3] From this the following conversions can be derived.

1 light-year	= 9460730472580800 metres (exactly)
	≈ 9.461 petametres
	≈ 5.878625 trillion miles
	≈ 63241.077 astronomical units
	≈ 0.306601 parsecs

Before 1984, the tropical year (not the Julian year) and a measured (not defined) speed of light were included in the IAU (1964) System of Astronomical Constants, used from 1968 to 1983.^[4] The product of Simon Newcomb's J1900.0 mean tropical year of 31556925.9747 ephemeris seconds and a speed of light of 299792.5 km/s produced a light-year of 9.460530×10¹⁵ m (rounded to the seven significant digits in the speed of light) found in several modern sources^[5][6][7] was probably derived from an old source such as C. W. Allen's 1973 Astrophysical Quantities reference work,^[8] which was updated in 2000.^{[9][clarification needed]}

Other high-precision values are not derived from a coherent IAU system. A value of 9.460536207×10¹⁵ m found in some modern sources^[10][11] is the product of a mean Gregorian year (365.2425 days or 31556952 s) and the defined speed of light (299792458 m/s). Another value, 9.460528405×10¹⁵ m,^[12][13] is the product of the J1900.0 mean tropical year and the defined speed of light.

History

The light-year unit appeared a few years after the first successful measurement of the distance to a star other than our Sun, by Friedrich Bessel in 1838. The star was 61 Cygni, and he used a 6.2-inch (160 mm) heliometer designed by Joseph von Fraunhofer. The largest unit for expressing distances across space at that time was the astronomical unit, equal to the radius of the Earth's orbit (1.50×10⁸ km or 9.30×10⁷ mi). In those terms, trigonometric calculations based on 61 Cygni's parallax of 0.314 arcseconds, showed the distance to the star to be 660000 astronomical units (9.9×10¹³ km or 6.1×10¹³ mi). Bessel added that light employs 10.3 years to traverse this distance.^[14] He recognized that his readers would enjoy the mental picture of the approximate transit time for light, but he refrained from using the light-year as a unit. He may have resented expressing distances in light-years because it would deteriorate the accuracy of his parallax data due to multiplying with the uncertain parameter of the speed of light. The speed of light was not yet precisely known in 1838; its value changed in 1849 (Fizeau) and 1862 (Foucault). It was not yet considered to be a fundamental constant of nature, and the propagation of light through the aether or space was still enigmatic. The light-year unit appeared, however, in 1851 in a German popular astronomical article by Otto Ule.^[15] The paradox of a distance unit name ending on year was explained by Ule by comparing it to a hiking road hour (Wegstunde). A contemporary German popular astronomical book also noticed that light-year is an odd name.^[16] In 1868 an English journal labelled the light-year as a unit used by the Germans.^[17] Eddington called the light-year an inconvenvient and irrelevant unit, which had sometimes crept from popular use into technical investigations.^[18]

Although modern astronomers often prefer to use the parsec, light years are also popularly used to gauge the expanses of interstellar and intergalactic space.

Usage of term

Distances expressed in light-years include those between stars in the same general area, such as those belonging to the same spiral arm or globular cluster. Galaxies themselves span from a few thousand to a few hundred thousand light-years in diameter, and are separated from neighbouring galaxies and galaxy clusters by millions of light-years. Distances to objects such as quasars and the Sloan Great Wall run up into the billions of light-years.

List of orders of magnitude for length

Scale (ly)	Value	Item
10−9	40.4×10−9 ly	Reflected sunlight from the Moon's surface takes 1.2–1.3 seconds to travel the distance to the Earth's surface (travelling roughly 350000 to 400000 kilometres).
10−6	15.8×10−6 ly	One astronomical unit (the distance from the Sun to the Earth). It takes approximately 499 seconds (8.32 minutes) for light to travel this distance.[19]
	127×10−6 ly	The Huygens probe lands on Titan off Saturn and transmits images from its surface 1.2 billion kilometres to the Earth.
10−3	2.04×10−3 ly	The most distant space probe, Voyager 1, was about 18 light-hours away from the Earth as of October 2014[update].[20] It will take about 17500 years to reach one light-year (1.0×100 ly) at its current speed of about 17 km/s (38000 mph) relative to the Sun. On September 12, 2013, NASA scientists announced that Voyager 1 had entered the interstellar medium of space on August 25, 2012, becoming the first manmade object to leave the Solar System.[21]
100	1.6×100 ly	The Oort cloud is approximately two light-years in diameter. Its inner boundary is speculated to be at 50000 AU, with its outer edge at 100000 au.
	2.0×100 ly	Maximum extent of the Sun's gravitational dominance (Hill sphere/Roche sphere, 125000 AU). Beyond this is the deep ex-solar gravitational interstellar medium.
	4.22×100 ly	The nearest known star (other than our Sun), Proxima Centauri, is about 4.22 light-years away.[22][23]
	8.60×100 ly	Sirius, the brightest star of the night sky. Twice as massive and 25 times more luminous than the Sun, it outshines more luminous stars due to its relative proximity.
	11.90×100 ly	HD 10700 e, an extrasolar candidate for a habitable planet. 6.6 times as massive as the earth, it is in the middle of the habitable zone of star Tau Ceti.[24][25]
	20.5×100 ly	Gliese 581, a red-dwarf star with several detectable exoplanets.
	310×100 ly	Canopus, second in brightness in the terrestrial sky only to Sirius, a type F supergiant 15000 times more luminous than the Sun.
103	26×103 ly	The centre of our galaxy, the Milky Way, is about 26 kilolight-years away.[26][27]
	100×103 ly	The Milky Way is about 100000 light-years across.
	165×103 ly	R136a1, in the Large Magellanic Cloud, the most luminous star known at 8.7 million times the luminosity of the Sun, has an apparent magnitude 12.77, just brighter than 3C 273.
106	2.5×106 ly	The Andromeda Galaxy is approximately 2.5 megalight-years away.
	3×106 ly	The Triangulum Galaxy (M33), at about 3 megalight-years away, is the most distant object visible to the naked eye.
	59×106 ly	The nearest large galaxy cluster, the Virgo Cluster, is about 59 megalight-years away.
	150×106 – 250×106 ly	The Great Attractor lies at a distance of somewhere between 150 and 250 megalight-years (the latter being the most recent estimate).
109	1.2×109 ly	The Sloan Great Wall (not to be confused with Great Wall and Her–CrB GW) has been measured to be approximately one gigalight-year distant.
	2.4×109 ly	3C 273, optically the brightest quasar, of apparent magnitude 12.9, just dimmer than R136a1.
	45.7×109 ly	The comoving distance from the Earth to the edge of the visible universe is about 45.7 gigalight-years in any direction; this is the comoving radius of the observable universe. This is larger than the age of the universe dictated by the cosmic background radiation; see size of the universe: misconceptions for why this is possible.

Related units

Distances between objects within a star system tend to be small fractions of a light year, and are usually expressed in astronomical units. However, smaller units of length can similarly be formed usefully by multiplying units of time by the speed of light. For example, the light-second, useful in astronomy, telecommunications and relativistic physics, is exactly 299792458 metres or ¹⁄_31557600 of a light-year. Units such as the light-minute, light-hour and light-day are sometimes used in popular science publications. The light-month, roughly one-twelfth of a light-year, is also used occasionally for approximate measures.^[28][29] The Hayden Planetarium specifies the light month more precisely as 30 days of light travel time.^[30]

Metric prefixes are occasionally applied to the light-year. Thus one thousand, one million and one billion light-years are sometimes called a "kilolight-year", a "megalight-year" and a "gigalight-year" (abbreviated "kly", "Mly" and "Gly") respectively.

Light travels approximately one foot in a nanosecond; the term "light-foot" is sometimes used as an informal measure of time.