Scanning electron microscope

From Wikipedia, the free encyclopedia

Photo of pollen grains taken on an SEM shows the characteristic depth of field of SEM micrographs

 

M. von Ardenne's first SEM

 

Play media

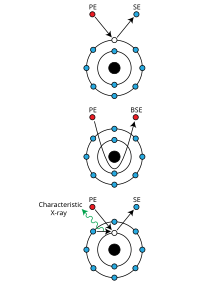
Operating principle of a Scanning Electron Microscope (SEM)

 

SEM opened sample chamber

 

Analog type SEM

 

A scanning electron microscope (SEM) is a type of electron microscope that produces images of a sample by scanning the surface with a focused beam of electrons. The electrons interact with atoms in the sample, producing various signals that contain information about the sample's surface topography and composition. The electron beam is scanned in a raster scan pattern, and the beam's position is combined with the detected signal to produce an image. SEM can achieve resolution better than 1 nanometer. Specimens can be observed in high vacuum in conventional SEM, or in low vacuum or wet conditions in variable pressure or environmental SEM, and at a wide range of cryogenic or elevated temperatures with specialized instruments.^[1]

The most common SEM mode is detection of secondary electrons emitted by atoms excited by the electron beam. The number of secondary electrons that can be detected depends, among other things, on specimen topography. By scanning the sample and collecting the secondary electrons that are emitted using a special detector, an image displaying the topography of the surface is created.

History

An account of the early history of SEM has been presented by McMullan.^[2][3] Although Max Knoll produced a photo with a 50 mm object-field-width showing channeling contrast by the use of an electron beam scanner,^[4] it was Manfred von Ardenne who in 1937 invented^[5] a true microscope with high magnification by scanning a very small raster with a demagnified and finely focused electron beam. Ardenne applied the scanning principle not only to achieve magnification but also to purposefully eliminate the chromatic aberration otherwise inherent in the electron microscope. He further discussed the various detection modes, possibilities and theory of SEM,^[6] together with the construction of the first high magnification SEM.^[7] Further work was reported by Zworykin's group,^[8] followed by the Cambridge groups in the 1950s and early 1960s^{[9][10][11][12]} headed by Charles Oatley, all of which finally led to the marketing of the first commercial instrument by Cambridge Scientific Instrument Company as the "Stereoscan" in 1965, which was delivered to DuPont.

Principles and capacities

The signals used by a scanning electron microscope to produce an image result from interactions of the electron beam with atoms at various depths within the sample. Various types of signals are produced including secondary electrons (SE), reflected or back-scattered electrons (BSE), characteristic X-rays and light (cathodoluminescence) (CL), absorbed current (specimen current) and transmitted electrons. Secondary electron detectors are standard equipment in all SEMs, but it is rare that a single machine would have detectors for all other possible signals.

In secondary electron imaging, or SEI, the secondary electrons are emitted from very close to the specimen surface. Consequently, SEM can produce very high-resolution images of a sample surface, revealing details less than 1 nm in size. Back-scattered electrons (BSE) are beam electrons that are reflected from the sample by elastic scattering. They emerge from deeper locations within the specimen and consequently the resolution of BSE images is less than SE images. However, BSE are often used in analytical SEM along with the spectra made from the characteristic X-rays, because the intensity of the BSE signal is strongly related to the atomic number (Z) of the specimen. BSE images can provide information about the distribution of different elements in the sample. For the same reason, BSE imaging can image colloidal gold immuno-labels of 5 or 10 nm diameter, which would otherwise be difficult or impossible to detect in secondary electron images in biological specimens.^[13] Characteristic X-rays are emitted when the electron beam removes an inner shell electron from the sample, causing a higher-energy electron to fill the shell and release energy. These characteristic X-rays are used to identify the composition and measure the abundance of elements in the sample.

Due to the very narrow electron beam, SEM micrographs have a large depth of field yielding a characteristic three-dimensional appearance useful for understanding the surface structure of a sample.^[14] This is exemplified by the micrograph of pollen shown above. A wide range of magnifications is possible, from about 10 times (about equivalent to that of a powerful hand-lens) to more than 500,000 times, about 250 times the magnification limit of the best light microscopes.

Sample preparation

A spider sputter-coated in gold, having been prepared for viewing with an SEM

 

Low-voltage micrograph (300 V) of distribution of adhesive droplets on a Post-it note. No conductive coating was applied: such a coating would alter this fragile specimen.

Samples for SEM have to be prepared to withstand the vacuum conditions and high energy beam of electrons, and have to be of a size that will fit on the specimen stage. Samples are generally mounted rigidly to a specimen holder or stub using a conductive adhesive. SEM is used extensively for defect analysis of semiconductor wafers, and manufacturers make instruments that can examine any part of a 300 mm semiconductor wafer. Many instruments have chambers that can tilt an object of that size to 45° and provide continuous 360° rotation.^{[citation needed]}

Nonconductive specimens collect charge when scanned by the electron beam, and especially in secondary electron imaging mode, this causes scanning faults and other image artifacts. For conventional imaging in the SEM, specimens must be electrically conductive, at least at the surface, and electrically grounded to prevent the accumulation of electrostatic charge. Metal objects require little special preparation for SEM except for cleaning and conductively mounting to a specimen stub. Non-conducting materials are usually coated with an ultrathin coating of electrically conducting material, deposited on the sample either by low-vacuum sputter coating or by high-vacuum evaporation. Conductive materials in current use for specimen coating include gold, gold/palladium alloy, platinum, iridium, tungsten, chromium, osmium,^[13] and graphite. Coating with heavy metals may increase signal/noise ratio for samples of low atomic number (Z). The improvement arises because secondary electron emission for high-Z materials is enhanced.

An alternative to coating for some biological samples is to increase the bulk conductivity of the material by impregnation with osmium using variants of the OTO staining method (O-osmium tetroxide, T-thiocarbohydrazide, O-osmium).^[15][16]

Nonconducting specimens may be imaged without coating using an environmental SEM (ESEM) or low-voltage mode of SEM operation.^[17] In ESEM instruments the specimen is placed in a relatively high-pressure chamber and the electron optical column is differentially pumped to keep vacuum adequately low at the electron gun. The high-pressure region around the sample in the ESEM neutralizes charge and provides an amplification of the secondary electron signal.^{[citation needed]} Low-voltage SEM is typically conducted in an FEG-SEM because field emission guns (FEG) are capable of producing high primary electron brightness and small spot size even at low accelerating potentials. To prevent charging of non-conductive specimens, operating conditions must be adjusted such that the incoming beam current is equal to sum of outcoming secondary and backscattered electrons currents a condition that is more often met at accelerating voltages of 0.3–4 kV.^{[citation needed]}

Synthetic replicas can be made to avoid the use of original samples when they are not suitable or available for SEM examination due to methodological obstacles or legal issues. This technique is achieved in two steps: (1) a mold of the original surface is made using a silicone-based dental elastomer, and (2) a replica of the original surface is obtained by pouring a synthetic resin into the mold.^[18]

Embedding in a resin with further polishing to a mirror-like finish can be used for both biological and materials specimens when imaging in backscattered electrons or when doing quantitative X-ray microanalysis.

The main preparation techniques are not required in the environmental SEM outlined below, but some biological specimens can benefit from fixation.

Biological samples

For SEM, a specimen is normally required to be completely dry, since the specimen chamber is at high vacuum. Hard, dry materials such as wood, bone, feathers, dried insects, or shells (including egg shells^{[19][not in citation given]}) can be examined with little further treatment,^{[citation needed]} but living cells and tissues and whole, soft-bodied organisms require chemical fixation to preserve and stabilize their structure.

Fixation is usually performed by incubation in a solution of a buffered chemical fixative, such as glutaraldehyde, sometimes in combination with formaldehyde^[20][21][22] and other fixatives,^[23] and optionally followed by postfixation with osmium tetroxide.^[20] The fixed tissue is then dehydrated. Because air-drying causes collapse and shrinkage, this is commonly achieved by replacement of water in the cells with organic solvents such as ethanol or acetone, and replacement of these solvents in turn with a transitional fluid such as liquid carbon dioxide by critical point drying.^[24] The carbon dioxide is finally removed while in a supercritical state, so that no gas–liquid interface is present within the sample during drying.

The dry specimen is usually mounted on a specimen stub using an adhesive such as epoxy resin or electrically conductive double-sided adhesive tape, and sputter-coated with gold or gold/palladium alloy before examination in the microscope. Samples may be sectioned (with a microtome) if information about the organism's internal ultrastructure is to be exposed for imaging.

If the SEM is equipped with a cold stage for cryo microscopy, cryofixation may be used and low-temperature scanning electron microscopy performed on the cryogenically fixed specimens.^[20] Cryo-fixed specimens may be cryo-fractured under vacuum in a special apparatus to reveal internal structure, sputter-coated and transferred onto the SEM cryo-stage while still frozen.^[25] Low-temperature scanning electron microscopy (LT-SEM) is also applicable to the imaging of temperature-sensitive materials such as ice^[26][27] and fats.^[28]

Freeze-fracturing, freeze-etch or freeze-and-break is a preparation method particularly useful for examining lipid membranes and their incorporated proteins in "face on" view. The preparation method reveals the proteins embedded in the lipid bilayer.

Materials

Back-scattered electron imaging, quantitative X-ray analysis, and X-ray mapping of specimens often requires grinding and polishing the surfaces to an ultra smooth surface. Specimens that undergo WDS or EDS analysis are often carbon-coated. In general, metals are not coated prior to imaging in the SEM because they are conductive and provide their own pathway to ground.

Fractography is the study of fractured surfaces that can be done on a light microscope or, commonly, on an SEM. The fractured surface is cut to a suitable size, cleaned of any organic residues, and mounted on a specimen holder for viewing in the SEM.

Integrated circuits may be cut with a focused ion beam (FIB) or other ion beam milling instrument for viewing in the SEM. The SEM in the first case may be incorporated into the FIB.^{[clarification needed]}

Metals, geological specimens, and integrated circuits all may also be chemically polished for viewing in the SEM.

Special high-resolution coating techniques are required for high-magnification imaging of inorganic thin films.

Scanning process and image formation

Schematic of an SEM

In a typical SEM, an electron beam is thermionically emitted from an electron gun fitted with a tungsten filament cathode. Tungsten is normally used in thermionic electron guns because it has the highest melting point and lowest vapor pressure of all metals, thereby allowing it to be electrically heated for electron emission, and because of its low cost. Other types of electron emitters include lanthanum hexaboride (LaB
₆) cathodes, which can be used in a standard tungsten filament SEM if the vacuum system is upgraded or field emission guns (FEG), which may be of the cold-cathode type using tungsten single crystal emitters or the thermally assisted Schottky type, that use emitters of zirconium oxide.

The electron beam, which typically has an energy ranging from 0.2 keV to 40 keV, is focused by one or two condenser lenses to a spot about 0.4 nm to 5 nm in diameter. The beam passes through pairs of scanning coils or pairs of deflector plates in the electron column, typically in the final lens, which deflect the beam in the x and y axes so that it scans in a raster fashion over a rectangular area of the sample surface.

Signals emitted from different parts of the interaction volume

 

Mechanisms of emission of secondary electrons, backscattered electrons, and characteristic X-rays from atoms of the sample

When the primary electron beam interacts with the sample, the electrons lose energy by repeated random scattering and absorption within a teardrop-shaped volume of the specimen known as the interaction volume, which extends from less than 100 nm to approximately 5 µm into the surface. The size of the interaction volume depends on the electron's landing energy, the atomic number of the specimen and the specimen's density. The energy exchange between the electron beam and the sample results in the reflection of high-energy electrons by elastic scattering, emission of secondary electrons by inelastic scattering and the emission of electromagnetic radiation, each of which can be detected by specialized detectors. The beam current absorbed by the specimen can also be detected and used to create images of the distribution of specimen current. Electronic amplifiers of various types are used to amplify the signals, which are displayed as variations in brightness on a computer monitor (or, for vintage models, on a cathode ray tube). Each pixel of computer video memory is synchronized with the position of the beam on the specimen in the microscope, and the resulting image is therefore a distribution map of the intensity of the signal being emitted from the scanned area of the specimen. In older microscopes images may be captured by photography from a high-resolution cathode ray tube, but in modern machines they are digitised and saved as digital images.

Low-temperature SEM magnification series for a snow crystal. The crystals are captured, stored, and sputter-coated with platinum at cryogenic temperatures for imaging.

Magnification

Magnification in a SEM can be controlled over a range of about 6 orders of magnitude from about 10 to 500,000 times. Unlike optical and transmission electron microscopes, image magnification in an SEM is not a function of the power of the objective lens. SEMs may have condenser and objective lenses, but their function is to focus the beam to a spot, and not to image the specimen. Provided the electron gun can generate a beam with sufficiently small diameter, an SEM could in principle work entirely without condenser or objective lenses, although it might not be very versatile or achieve very high resolution. In an SEM, as in scanning probe microscopy, magnification results from the ratio of the dimensions of the raster on the specimen and the raster on the display device. Assuming that the display screen has a fixed size, higher magnification results from reducing the size of the raster on the specimen, and vice versa. Magnification is therefore controlled by the current supplied to the x, y scanning coils, or the voltage supplied to the x, y deflector plates, and not by objective lens power.

Detection of secondary electrons

The most common imaging mode collects low-energy (<50 a="" are="" atoms="" beam="" by="" class="mw-redirect" due="" ejected="" electrons.="" electrons="" energy="" ev="" few="" from="" href="https://en.wikipedia.org/wiki/Nanometer" inelastic="" interactions="" k-shell="" low="" of="" originate="" scattering="" secondary="" specimen="" that="" the="" their="" these="" title="Nanometer" to="" with="" within="">nanometers
from the sample surface.^[14] The electrons are detected by an Everhart-Thornley detector,^[29] which is a type of scintillator-photomultiplier system. The secondary electrons are first collected by attracting them towards an electrically biased grid at about +400 V, and then further accelerated towards a phosphor or scintillator positively biased to about +2,000 V. The accelerated secondary electrons are now sufficiently energetic to cause the scintillator to emit flashes of light (cathodoluminescence), which are conducted to a photomultiplier outside the SEM column via a light pipe and a window in the wall of the specimen chamber. The amplified electrical signal output by the photomultiplier is displayed as a two-dimensional intensity distribution that can be viewed and photographed on an analogue video display, or subjected to analog-to-digital conversion and displayed and saved as a digital image. This process relies on a raster-scanned primary beam. The brightness of the signal depends on the number of secondary electrons reaching the detector. If the beam enters the sample perpendicular to the surface, then the activated region is uniform about the axis of the beam and a certain number of electrons "escape" from within the sample. As the angle of incidence increases, the interaction volume increases and the "escape" distance of one side of the beam decreases, resulting in more secondary electrons being emitted from the sample. Thus steep surfaces and edges tend to be brighter than flat surfaces, which results in images with a well-defined, three-dimensional appearance. Using the signal of secondary electrons image resolution less than 0.5 nm is possible.

Detection of backscattered electrons

Comparison of SEM techniques:
Top: backscattered electron analysis – composition
Bottom: secondary electron analysis – topography

Backscattered electrons (BSE) consist of high-energy electrons originating in the electron beam, that are reflected or back-scattered out of the specimen interaction volume by elastic scattering interactions with specimen atoms. Since heavy elements (high atomic number) backscatter electrons more strongly than light elements (low atomic number), and thus appear brighter in the image, BSE are used to detect contrast between areas with different chemical compositions.^[14] The Everhart-Thornley detector, which is normally positioned to one side of the specimen, is inefficient for the detection of backscattered electrons because few such electrons are emitted in the solid angle subtended by the detector, and because the positively biased detection grid has little ability to attract the higher energy BSE. Dedicated backscattered electron detectors are positioned above the sample in a "doughnut" type arrangement, concentric with the electron beam, maximizing the solid angle of collection. BSE detectors are usually either of scintillator or of semiconductor types. When all parts of the detector are used to collect electrons symmetrically about the beam, atomic number contrast is produced. However, strong topographic contrast is produced by collecting back-scattered electrons from one side above the specimen using an asymmetrical, directional BSE detector; the resulting contrast appears as illumination of the topography from that side. Semiconductor detectors can be made in radial segments that can be switched in or out to control the type of contrast produced and its directionality.

Backscattered electrons can also be used to form an electron backscatter diffraction (EBSD) image that can be used to determine the crystallographic structure of the specimen.

Beam-injection analysis of semiconductors

The nature of the SEM's probe, energetic electrons, makes it uniquely suited to examining the optical and electronic properties of semiconductor materials. The high-energy electrons from the SEM beam will inject charge carriers into the semiconductor. Thus, beam electrons lose energy by promoting electrons from the valence band into the conduction band, leaving behind holes.

In a direct bandgap material, recombination of these electron-hole pairs will result in cathodoluminescence; if the sample contains an internal electric field, such as is present at a p-n junction, the SEM beam injection of carriers will cause electron beam induced current (EBIC) to flow. Cathodoluminescence and EBIC are referred to as "beam-injection" techniques, and are very powerful probes of the optoelectronic behavior of semiconductors, in particular for studying nanoscale features and defects.

Cathodoluminescence

Color cathodoluminescence overlay on SEM image of an InGaN polycrystal. The blue and green channels represent real colors, the red channel corresponds to UV emission.

Cathodoluminescence, the emission of light when atoms excited by high-energy electrons return to their ground state, is analogous to UV-induced fluorescence, and some materials such as zinc sulfide and some fluorescent dyes, exhibit both phenomena. Over the last decades, cathodoluminescence was most commonly experienced as the light emission from the inner surface of the cathode ray tube in television sets and computer CRT monitors. In the SEM, CL detectors either collect all light emitted by the specimen or can analyse the wavelengths emitted by the specimen and display an emission spectrum or an image of the distribution of cathodoluminescence emitted by the specimen in real color.

X-ray microanalysis

Characteristic X-rays that are produced by the interaction of electrons with the sample may also be detected in an SEM equipped for energy-dispersive X-ray spectroscopy or wavelength dispersive X-ray spectroscopy. Analysis of the x-ray signals may be used to map the distribution and estimate the abundance of elements in the sample.

Resolution of the SEM

Play media

A video illustrating a typical practical magnification range of a scanning electron microscope designed for biological specimens. The video starts at 25x, about 6 mm across the whole field of view, and zooms in to 12000×, about 12 μm across the whole field of view. The spherical objects are glass beads with a diameter of 10 μm, similar in diameter to a red blood cell.

SEM is not a camera and the detector is not continuously image-forming like a CCD array or film. Unlike in an optical system, the resolution is not limited by the diffraction limit, fineness of lenses or mirrors or detector array resolution. The focusing optics can be large and coarse, and the SE detector is fist-sized and simply detects current. Instead, the spatial resolution of the SEM depends on the size of the electron spot, which in turn depends on both the wavelength of the electrons and the electron-optical system that produces the scanning beam. The resolution is also limited by the size of the interaction volume, the volume of specimen material that interacts with the electron beam. The spot size and the interaction volume are both large compared to the distances between atoms, so the resolution of the SEM is not high enough to image individual atoms, as is possible with transmission electron microscope (TEM). The SEM has compensating advantages, though, including the ability to image a comparatively large area of the specimen; the ability to image bulk materials (not just thin films or foils); and the variety of analytical modes available for measuring the composition and properties of the specimen. Depending on the instrument, the resolution can fall somewhere between less than 1 nm and 20 nm. As of 2009, The world's highest resolution conventional (≤30 kV) SEM can reach a point resolution of 0.4 nm using a secondary electron detector.^[30]

Environmental SEM

Conventional SEM requires samples to be imaged under vacuum, because a gas atmosphere rapidly spreads and attenuates electron beams. As a consequence, samples that produce a significant amount of vapour, e.g. wet biological samples or oil-bearing rock, must be either dried or cryogenically frozen. Processes involving phase transitions, such as the drying of adhesives or melting of alloys, liquid transport, chemical reactions, and solid-air-gas systems, in general cannot be observed. Some observations of living insects have been possible however.^[31]
The first commercial development of the ESEM in the late 1980s^[32][33] allowed samples to be observed in low-pressure gaseous environments (e.g. 1–50 Torr or 0.1–6.7 kPa) and high relative humidity (up to 100%). This was made possible by the development of a secondary-electron detector^[34][35] capable of operating in the presence of water vapour and by the use of pressure-limiting apertures with differential pumping in the path of the electron beam to separate the vacuum region (around the gun and lenses) from the sample chamber.

The first commercial ESEMs were produced by the ElectroScan Corporation in USA in 1988. ElectroScan was taken over by Philips (who later sold their electron-optics division to FEI Company) in 1996.^[36]

ESEM is especially useful for non-metallic and biological materials because coating with carbon or gold is unnecessary. Uncoated Plastics and Elastomers can be routinely examined, as can uncoated biological samples. Coating can be difficult to reverse, may conceal small features on the surface of the sample and may reduce the value of the results obtained. X-ray analysis is difficult with a coating of a heavy metal, so carbon coatings are routinely used in conventional SEMs, but ESEM makes it possible to perform X-ray microanalysis on uncoated non-conductive specimens; however some specific for ESEM artifacts are introduced in X-ray analysis. ESEM may be the preferred for electron microscopy of unique samples from criminal or civil actions, where forensic analysis may need to be repeated by several different experts.

It is possible to study specimens in liquid with ESEM or with other liquid-phase electron microscopy methods.^[37]

Transmission SEM

The SEM can also be used in transmission mode by simply incorporating an appropriate detector below a thin specimen section.^[38] Both bright and dark field imaging has been reported in the generally low accelerating beam voltage range used in SEM, which increases the contrast of unstained biological specimens at high magnifications with a field emission electron gun. This mode of operation has been abbreviated by the acronym tSEM.

Color in SEM

Electron microscopes do not naturally produce color images, as an SEM produces a single value per pixel; this value corresponds to the number of electrons received by the detector during a small period of time of the scanning when the beam is targeted to the (x, y) pixel position.

This single number is usually represented, for each pixel, by a grey level, forming a "black-and-white" image.^[39] However, several ways have been used to get color electron microscopy images.^[40]

False color using a single detector

• On compositional images of flat surfaces (typically BSE):

The easiest way to get color is to associate to this single number an arbitrary color, using a color look-up table (i.e. each grey level is replaced by a chosen color). This method is known as false color. On a BSE image, false color may be performed to better distinguish the various phases of the sample.

• On textured-surface images:

As an alternative to simply replacing each grey level by a color, a sample observed by an oblique beam allows researchers to create an approximative topography image. Such topography can then be processed by 3D-rendering algorithms for a more natural rendering of the surface texture

• 

  Surface of a kidney stone
  
• 

  The same after re-processing of the color from the estimated topography
  
• 

  SEM image of a diagenetically altered discoaster
  
• 

  The same image after similar colorization
  

SEM image coloring

Very often, published SEM images are artificially colored. This may be done for aesthetic effect, to clarify structure or to add a realistic appearance to the sample^[41] and generally does not add information about the specimen.^[42]

Coloring may be performed manually with photo-editing software, or semi-automatically with dedicated software using feature-detection or object-oriented segmentation.^[43]

• 

  SEM image of Cobaea scandens pollen
  
• 

  The same after semi-automatic coloring. Arbitrary colors help identifying the various elements of the structure
  
• 

  Colored SEM image of Tradescantia pollen and stamens
  

Color built using multiple electron detectors

In some configurations more information is gathered per pixel, often by the use of multiple detectors.^[44]

As a common example, secondary electron and backscattered electron detectors are superimposed and a color is assigned to each of the images captured by each detector,^[45][46] with an end result of a combined color image where colors are related to the density of the components. This method is known as density-dependent color SEM (DDC-SEM). Micrographs produced by DDC-SEM retain topographical information, which is better captured by the secondary electrons detector and combine it to the information about density, obtained by the backscattered electron detector.^[47][48]

• 

  DDC-SEM of calcified particle in cardiac tissue - Signal 1 : SE
  
• 

  Signal 2 : BSE
  
• 

  Colorized image obtained from the two previous. Density-dependent color scanning electron micrograph SEM (DDC-SEM) of cardiovascular calcification, showing in orange a calcium phosphate spherical particle (denser material) and, in green, the extracellular matrix (less dense material)
  
• 

  Same work with a larger view, part of a study on human cardiovascular tissue calcification
  

Analytical signals based on generated photons

Measurement of the energy of photons emitted from the specimen is a common method to get analytical capabilities. Examples are the energy-dispersive X-ray spectroscopy (EDS) detectors used in elemental analysis and cathodoluminescence microscope (CL) systems that analyse the intensity and spectrum of electron-induced luminescence in (for example) geological specimens. In SEM systems using these detectors it is common to color code these extra signals and superimpose them in a single color image, so that differences in the distribution of the various components of the specimen can be seen clearly and compared. Optionally, the standard secondary electron image can be merged with the one or more compositional channels, so that the specimen's structure and composition can be compared. Such images can be made while maintaining the full integrity of the original signal data, which is not modified in any way.

3D in SEM

SEMs do not naturally provide 3D images contrary to SPMs. However 3D data can be obtained using an SEM with different methods as follows.

3D SEM reconstruction from a stereo pair

• photogrammetry (two and three dimensional images from tilted specimen)

• 

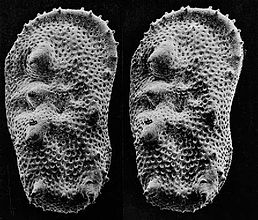
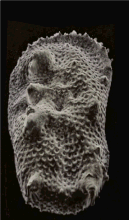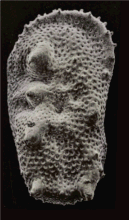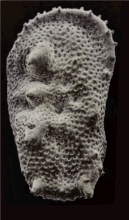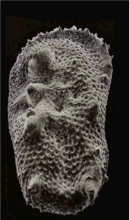
  An SEM stereo pair of microfossils of less than 1 mm in size (Ostracoda) produced by tilting along the longitudinal axis.
  
• 

  From this pair of SEM images, the third dimension has been reconstructed by photogrammetry (using MountainsMap software) ; then a series of 3D representations with different angles have been made and assembled into a GIF file to produce this animation.
  

Photometric 3D SEM reconstruction from a four-quadrant detector "shape from shading"

This method typically uses a four-quadrant BSE detector. The microscope produces four images of the same specimen at the same time, so no tilt is required. The method gives metrological 3D dimensions as far as the slope of the specimen remains reasonable.

Some scanning electron microscopes are provided with software which uses a vendor-specific and usually closed-source algorithm to determine the 3D profile of the sample from the four-quadrant BSE detector. The supplied algorithms can be very simple line-by-line approaches, that only compare pixels next to each other. Due to the sample and conditions changing, this produces reasonable results only along the scan direction and is only practical for 1D line cuts along the scanning axis. Other approaches use more sophisticated (and sometimes GPU-intensive) methods like the optimal estimation algorithm and offer much better results at the cost of high demands on computing power.

As this approach works by integration of the slope, vertical slopes and overhangs are ignored; for instance, if an entire sphere lies on a flat, little more than the upper hemisphere is seen emerging above the flat, resulting in wrong altitude of the sphere apex. The prominence of this effect depends on the angle of the BSE detectors with respect to the sample, but these detectors are usually situated around (and close to) the electron beam, so this effect is very common.

Photometric 3D rendering from a single SEM image

This method requires an SEM image obtained in oblique low angle lighting. The grey-level is then interpreted as the slope, and the slope integrated to restore the specimen topography. This method is interesting for visual enhancement and the detection of the shape and position of objects ; however the vertical heights cannot usually be calibrated, contrary to other methods such as photogrammetry.

• 

  SEM image of a house fly compound eye surface at 450× magnification.
  
• 

  Detail of the previous image.
  
• 

  SEM 3D reconstruction from the previous using shape from shading algorithms.
  
• 

  Same as the previous, but with lighting homogenized before applying the shape from shading algorithms
  

Other types of 3D SEM reconstruction

• inverse reconstruction using electron-material interactive models
• vertical stacks of SEM micrographs plus image-processing software

• Multi-Resolution reconstruction using single 2D File: High-quality 3D imaging may be an ultimate solution for revealing the complexities of any porous media, but acquiring them is costly and time consuming. High-quality 2D SEM images, on the other hand, are widely available. Recently, a novel three-step, multiscale, multiresolution reconstruction method is presented that directly uses 2D images in order to develop 3D models. This method, based on a Shannon Entropy and conditional simulation, can be used for most of the available stationary materials and can build various stochastic 3D models just using a few thin sections.

Applications of 3D SEM

One possible application is measuring the roughness of ice crystals. This method can combine variable-pressure environmental SEM and the 3D capabilities of the SEM to measure roughness on individual ice crystal facets, convert it into a computer model and run further statistical analysis on the model. Other measurements include fractal dimension, examining fracture surface of metals, characterization of materials, corrosion measurement, and dimensional measurements at the nano scale (step height, volume, angle, flatness, bearing ratio, coplanarity, etc.).

Scanning tunneling microscope

From Wikipedia, the free encyclopedia

Image of reconstruction on a clean gold (100) surface

The silicon atoms on the surface of a crystal of silicon carbide (SiC). Image obtained using an STM.

An STM image of a single-walled carbon nanotube

A scanning tunneling microscope (STM) is an instrument for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer (at IBM Zürich), the Nobel Prize in Physics in 1986.^[1][2] For a STM, good resolution is considered to be 0.1 nm lateral resolution and 0.01 nm (10 pm) depth resolution.^[3] With this resolution, individual atoms within materials are routinely imaged and manipulated. The STM can be used not only in ultra-high vacuum but also in air, water, and various other liquid or gas ambients, and at temperatures ranging from near zero kelvin to over 1000 °C.^[4][5]

STM is based on the concept of quantum tunneling. When a conducting tip is brought very near to the surface to be examined, a bias (voltage difference) applied between the two can allow electrons to tunnel through the vacuum between them. The resulting tunneling current is a function of tip position, applied voltage, and the local density of states (LDOS) of the sample.^[4] Information is acquired by monitoring the current as the tip's position scans across the surface, and is usually displayed in image form. STM can be a challenging technique, as it requires extremely clean and stable surfaces, sharp tips, excellent vibration control, and sophisticated electronics, but nonetheless many hobbyists have built their own.^[6]

Play media

Scanning tunneling microscope operating principle

Procedure

A close-up of a simple scanning tunneling microscope head using a platinum–iridium tip.

First, a voltage bias is applied and the tip is brought close to the sample by coarse sample-to-tip control, which is turned off when the tip and sample are sufficiently close. At close range, fine control of the tip in all three dimensions when near the sample is typically piezoelectric, maintaining tip-sample separation W typically in the 4-7 Å (0.4-0.7 nm) range, which is the equilibrium position between attractive (3[4]

In this situation, the voltage bias will cause electrons to tunnel between the tip and sample, creating a current that can be measured. Once tunneling is established, the tip's bias and position with respect to the sample can be varied (with the details of this variation depending on the experiment) and data are obtained from the resulting changes in current.

If the tip is moved across the sample in the x-y plane, the changes in surface height and density of states causes changes in current. These changes are mapped in images. This change in current with respect to position can be measured itself, or the height, z, of the tip corresponding to a constant current can be measured.^[4] These two modes are called constant height mode and constant current mode, respectively. In constant current mode, feedback electronics adjust the height by a voltage to the piezoelectric height control mechanism.^[7] This leads to a height variation and thus the image comes from the tip topography across the sample and gives a constant charge density surface; this means contrast on the image is due to variations in charge density.^[8] In constant height mode, the voltage and height are both held constant while the current changes to keep the voltage from changing; this leads to an image made of current changes over the surface, which can be related to charge density.^[8] The benefit to using a constant height mode is that it is faster, as the piezoelectric movements require more time to register the height change in constant current mode than the current change in constant height mode.^[8] All images produced by STM are grayscale, with color optionally added in post-processing in order to visually emphasize important features.

In addition to scanning across the sample, information on the electronic structure at a given location in the sample can be obtained by sweeping voltage and measuring current at a specific location.^[3] This type of measurement is called scanning tunneling spectroscopy (STS) and typically results in a plot of the local density of states as a function of energy within the sample. The advantage of STM over other measurements of the density of states lies in its ability to make extremely local measurements: for example, the density of states at an impurity site can be compared to the density of states far from impurities.^[9]

Frame rates of at least 25 Hz enable so called video-rate STM.^[10][11] Framerates up to 80 Hz are possible with fully working feedback that adjusts the height of the tip.^[12] Due to the line-by-line scanning motion, a proper comparison on the speed requires not only the framerate, but also the number of pixels in an image: with a framerate of 10 Hz and 100x100 pixels the tip moves with a line frequency of 1 kHz, whereas it moves with only with 500 Hz, when measuring with a faster framerate of 50 Hz but only 10x10 pixels. Video-rate STM can be used to scan surface diffusion.^[13]

Instrumentation

Schematic view of an STM

The components of an STM include scanning tip, piezoelectric controlled height and x,y scanner, coarse sample-to-tip control, vibration isolation system, and computer.^[7]

The resolution of an image is limited by the radius of curvature of the scanning tip of the STM. Additionally, image artifacts can occur if the tip has two tips at the end rather than a single atom; this leads to “double-tip imaging,” a situation in which both tips contribute to the tunneling.^[3] Therefore, it has been essential to develop processes for consistently obtaining sharp, usable tips. Recently, carbon nanotubes have been used in this instance.^[14]

The tip is often made of tungsten or platinum-iridium, though gold is also used.^[3] Tungsten tips are usually made by electrochemical etching, and platinum-iridium tips by mechanical shearing.^[3]

Due to the extreme sensitivity of tunnel current to height, proper vibration insulation or an extremely rigid STM body is imperative for obtaining usable results. In the first STM by Binnig and Rohrer, magnetic levitation was used to keep the STM free from vibrations; now mechanical spring or gas spring systems are often used.^[4] Additionally, mechanisms for reducing eddy currents are sometimes implemented.

Maintaining the tip position with respect to the sample, scanning the sample and acquiring the data is computer controlled.^[7] The computer may also be used for enhancing the image with the help of image processing^[15][16] as well as performing quantitative measurements.^[17][18]

Other STM related studies

Nanomanipulation via STM of a self-assembled organic semiconductor monolayer (here: PTCDA molecules) on graphite, in which the logo of the Center for NanoScience (CeNS), LMU has been written.

Image of a graphite surface at an atomic level obtained by an STM.

Many other microscopy techniques have been developed based upon STM. These include photon scanning microscopy (PSTM), which uses an optical tip to tunnel photons;^[3] scanning tunneling potentiometry (STP), which measures electric potential across a surface;^[3] spin polarized scanning tunneling microscopy (SPSTM), which uses a ferromagnetic tip to tunnel spin-polarized electrons into a magnetic sample,^[19] and atomic force microscopy (AFM), in which the force caused by interaction between the tip and sample is measured.

Other STM methods involve manipulating the tip in order to change the topography of the sample. This is attractive for several reasons. Firstly the STM has an atomically precise positioning system which allows very accurate atomic scale manipulation. Furthermore, after the surface is modified by the tip, it is a simple matter to then image with the same tip, without changing the instrument. IBM researchers developed a way to manipulate xenon atoms adsorbed on a nickel surface.^[3] This technique has been used to create electron "corrals" with a small number of adsorbed atoms, which allows the STM to be used to observe electron Friedel oscillations on the surface of the material. Aside from modifying the actual sample surface, one can also use the STM to tunnel electrons into a layer of electron beam photoresist on a sample, in order to do lithography. This has the advantage of offering more control of the exposure than traditional electron beam lithography. Another practical application of STM is atomic deposition of metals (gold, silver, tungsten, etc.) with any desired (pre-programmed) pattern, which can be used as contacts to nanodevices or as nanodevices themselves.

Variable temperature STM was used to investigate temperature dependency of molecular rotations on single crystalline surfaces.^[20] Rotating molecules appear blurred compared to non-rotating ones.

Recently groups have found they can use the STM tip to rotate individual bonds within single molecules.^{[citation needed]} The electrical resistance of the molecule depends on the orientation of the bond, so the molecule effectively becomes a molecular switch.

Principle of operation

The first STM produced commercially, 1986.

Tunneling is a functioning concept that arises from quantum mechanics. Classically, an object hitting an impenetrable barrier will not pass through. In contrast, objects with a very small mass, such as the electron, have wavelike characteristics which permit such an event, referred to as tunneling.

Electrons behave as beams of energy, and in the presence of a potential U(z), assuming 1-dimensional case, the energy levels ψ_n(z) of the electrons are given by solutions to Schrödinger’s equation,

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\psi _{n}(z)}{\partial z^{2}}}+U(z)\psi _{n}(z)=E\psi _{n}(z)}$

where ħ is the reduced Planck’s constant, z is the position, and m is the mass of an electron.^[4] If an electron of energy E is incident upon an energy barrier of height U(z), the electron wave function is a traveling wave solution,

${\displaystyle \psi _{n}(z)=\psi _{n}(0)e^{\pm ikz}}$

where

${\displaystyle k={\frac {\sqrt {2m(E-U(z))}}{\hbar }}}$

if E > U(z), which is true for a wave function inside the tip or inside the sample.^[4] Inside a barrier, E < U(z) so the wave functions which satisfy this are decaying waves,

${\displaystyle \psi _{n}(z)=\psi _{n}(0)e^{\pm \kappa z}}$

where

${\displaystyle \kappa ={\frac {\sqrt {2m(U-E)}}{\hbar }}}$

quantifies the decay of the wave inside the barrier, with the barrier in the +z direction for ${\displaystyle -\kappa }$.^[4]

Knowing the wave function allows one to calculate the probability density for that electron to be found at some location. In the case of tunneling, the tip and sample wave functions overlap such that when under a bias, there is some finite probability to find the electron in the barrier region and even on the other side of the barrier.^[4] Let us assume the bias is V and the barrier width is W. This probability, P, that an electron at z=0 (left edge of barrier) can be found at z=W (right edge of barrier) is proportional to the wave function squared,

${\displaystyle P\propto |\psi _{n}(0)|^{2}e^{-2\kappa W}}$.^[4]

If the bias is small, we can let U − E ≈ φM in the expression for κ, where φM, the work function, gives the minimum energy needed to bring an electron from an occupied level, the highest of which is at the Fermi level (for metals at T=0 kelvins), to vacuum level. When a small bias V is applied to the system, only electronic states very near the Fermi level, within eV (a product of electron charge and voltage, not to be confused here with electronvolt unit), are excited.^[4] These excited electrons can tunnel across the barrier. In other words, tunneling occurs mainly with electrons of energies near the Fermi level.

A large scanning tunneling microscope, in the labs of the London Centre for Nanotechnology

However, tunneling does require that there be an empty level of the same energy as the electron for the electron to tunnel into on the other side of the barrier. It is because of this restriction that the tunneling current can be related to the density of available or filled states in the sample. The current due to an applied voltage V (assume tunneling occurs sample to tip) depends on two factors: 1) the number of electrons between E_f and eV in the sample, and 2) the number among them which have corresponding free states to tunnel into on the other side of the barrier at the tip.^[4] The higher the density of available states the greater the tunneling current. When V is positive, electrons in the tip tunnel into empty states in the sample; for a negative bias, electrons tunnel out of occupied states in the sample into the tip.^[4]

Mathematically, this tunneling current is given by

${\displaystyle I\propto \sum _{E_{f}-eV}^{E_{f}}|\psi _{n}(0)|^{2}e^{-2\kappa W}}$.

One can sum the probability over energies between E_f − eV and E_f to get the number of states available in this energy range per unit volume, thereby finding the local density of states (LDOS) near the Fermi level.^[4] The LDOS near some energy E in an interval ε is given by

${\displaystyle \rho _{s}(z,E)={\frac {1}{\epsilon }}\sum _{E-\epsilon }^{E}|\psi _{n}(z)|^{2}}$,

and the tunnel current at a small bias V is proportional to the LDOS near the Fermi level, which gives important information about the sample.^[4] It is desirable to use LDOS to express the current because this value does not change as the volume changes, while probability density does.^[4] Thus the tunneling current is given by

${\displaystyle I\propto V\rho _{s}(0,E_{f})e^{-2\kappa W}}$

where ρ_s(0,E_f) is the LDOS near the Fermi level of the sample at the sample surface.^[4] This current can also be expressed in terms of the LDOS near the Fermi level of the sample at the tip surface,

${\displaystyle I\propto V\rho _{s}(W,E_{f})}$

The exponential term in the above equations means that small variations in W greatly influence the tunnel current. If the separation is decreased by 1 Å, the current increases by an order of magnitude, and vice versa.^[8]

This approach fails to account for the rate at which electrons can pass the barrier. This rate should affect the tunnel current, so it can be treated using the Fermi's golden rule with the appropriate tunneling matrix element. John Bardeen solved this problem in his study of the metal-insulator-metal junction.^[21] He found that if he solved Schrödinger’s equation for each side of the junction separately to obtain the wave functions ψ and χ for each electrode, he could obtain the tunnel matrix, M, from the overlap of these two wave functions.^[4] This can be applied to STM by making the electrodes the tip and sample, assigning ψ and χ as sample and tip wave functions, respectively, and evaluating M at some surface S between the metal electrodes, where z=0 at the sample surface and z=W at the tip surface.^[4]

Now, Fermi’s Golden Rule gives the rate for electron transfer across the barrier, and is written

${\displaystyle w={\frac {2\pi }{\hbar }}|M|^{2}\delta (E_{\psi }-E_{\chi })}$,

where δ(E_ψ–E_χ) restricts tunneling to occur only between electron levels with the same energy.^[4] The tunnel matrix element, given by

${\displaystyle M={\frac {\hbar ^{2}}{2m}}\int _{z=z_{0}}(\chi *{\frac {\partial \psi }{\partial z}}-\psi {\frac {\partial \chi *}{\partial z}})dS}$,

is a description of the lower energy associated with the interaction of wave functions at the overlap, also called the resonance energy.^[4]

Summing over all the states gives the tunneling current as

${\displaystyle I={\frac {4\pi e}{\hbar }}\int _{-\infty }^{+\infty }[f(E_{f}-eV+\epsilon )-f(E_{f}+\epsilon )]\rho _{s}(E_{f}-eV+\epsilon )\rho _{T}(E_{f}+\epsilon )|M|^{2}d\epsilon }$,

where f is the Fermi function, ρ_s and ρ_T are the density of states in the sample and tip, respectively.^[4] The Fermi distribution function describes the filling of electron levels at a given temperature T.

Early invention

An earlier, similar invention, the Topografiner of R. Young, J. Ward, and F. Scire from the NIST,^[22] relied on field emission. However, Young is credited by the Nobel Committee as the person who realized that it should be possible to achieve better resolution by using the tunnel effect.^[23]