From Wikipedia, the free encyclopedia
Content
Exponential growth
Kurzweil characterizes
evolution
throughout all time as progressing through six epochs, each one
building on the one before. He says the four epochs which have occurred
so far are
Physics and Chemistry,
Biology and DNA,
Brains, and
Technology. Kurzweil predicts the Singularity will coincide with the next epoch,
The Merger of Human Technology with Human Intelligence. After the Singularity he says the final epoch will occur,
The Universe Wakes Up.
Kurzweil explains that evolutionary progress is
exponential because of
positive feedback;
the results of one stage are used to create the next stage. Exponential
growth is deceptive, nearly flat at first until it hits what Kurzweil
calls "the knee in the curve" then rises almost vertically.
In fact Kurzweil believes evolutionary progress is super-exponential
because more resources are deployed to the winning process. As an
example of super-exponential growth Kurzweil cites the computer chip
business. The overall budget for the whole industry increases over time,
since the fruits of exponential growth make it an attractive
investment; meanwhile the additional budget fuels more innovation which
makes the industry grow even faster, effectively an example of "double"
exponential growth.
Kurzweil says evolutionary progress looks smooth, but that really it
is divided into paradigms, specific methods of solving problems. Each
paradigm starts with slow growth, builds to rapid growth, and then
levels off. As one paradigm levels off, pressure builds to find or
develop a new paradigm. So what looks like a single smooth curve is
really series of smaller
S curves. For example, Kurzweil notes that when
vacuum tubes stopped getting faster, cheaper
transistors became popular and continued the overall exponential growth.
Kurzweil calls this exponential growth the law of accelerating
returns, and he believes it applies to many human-created technologies
such as
computer memory,
transistors,
microprocessors,
DNA sequencing,
magnetic storage,
the number of Internet hosts,
Internet traffic, decrease in device size, and nanotech citations and patents. Kurzweil cites two historical examples of exponential growth: the
Human Genome Project and the
growth of the Internet.
Kurzweil claims the whole world economy is in fact growing
exponentially, although short term booms and busts tend to hide this
trend.
Computational capacity
A fundamental pillar of Kurzweil's argument is that to get to the
Singularity, computational capacity is as much of a bottleneck as other
things like quality of algorithms and understanding of the human brain.
Moore's Law
predicts the capacity of integrated circuits grows exponentially, but
not indefinitely. Kurzweil feels the increase in the capacity of
integrated circuits will probably slow by the year 2020.
He feels confident that a new paradigm will debut at that point to
carry on the exponential growth predicted by his law of accelerating
returns. Kurzweil describes four paradigms of computing that came before
integrated circuits: electromechanical, relay, vacuum tube, and
transistors.
What technology will follow integrated circuits, to serve as the sixth
paradigm, is unknown, but Kurzweil believes nanotubes are the most
likely alternative among a number of possibilities:
nanotubes and nanotube circuitry, molecular computing, self-assembly
in nanotube circuits, biological systems emulating circuit assembly, computing with DNA, spintronics (computing with the spin of electrons), computing with light, and quantum computing.
Since Kurzweil believes
computational capacity
will continue to grow exponentially long after Moore's Law ends it will
eventually rival the raw computing power of the human brain. Kurzweil
looks at several different estimates of how much computational capacity
is in the brain and settles on 10
16 calculations per second and 10
13 bits of memory. He writes that $1,000 will buy computer power equal to a single brain "by around 2020"
while by 2045, the onset of the Singularity, he says same amount of
money will buy one billion times more power than all human brains
combined today.
Kurzweil admits the exponential trend in increased computing power will
hit a limit eventually, but he calculates that limit to be trillions of
times beyond what is necessary for the Singularity.
The brain
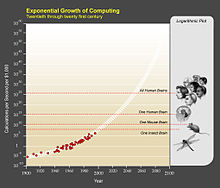
Exponential Growth of Computing
Kurzweil notes that computational capacity alone will not create
artificial intelligence. He asserts that the best way to build machine
intelligence is to first understand human intelligence. The first step
is to image the brain, to peer inside it. Kurzweil claims imaging
technologies such as
PET and
fMRI are increasing exponentially in resolution
while he predicts even greater detail will be obtained during the 2020s
when it becomes possible to scan the brain from the inside using
nanobots.
Once the physical structure and connectivity information are known,
Kurzweil says researchers will have to produce functional models of
sub-cellular components and synapses all the way up to whole brain
regions.
The human brain is "a complex hierarchy of complex systems, but it does
not represent a level of complexity beyond what we are already capable
of handling".
Beyond reverse engineering the brain in order to understand and
emulate it, Kurzweil introduces the idea of "uploading" a specific brain
with every mental process intact, to be instantiated on a "suitably
powerful computational substrate". He writes that general modeling
requires 10
16 calculations per second and 10
13 bits of memory, but then explains uploading requires additional detail, perhaps as many as 10
19 cps and 10
18 bits. Kurzweil says the technology to do this will be available by 2040. Rather than an instantaneous scan and conversion to digital form,
Kurzweil feels humans will most likely experience gradual conversion as
portions of their brain are augmented with neural implants, increasing
their proportion of non-biological intelligence slowly over time.
Kurzweil believes there is "no objective test that can conclusively determine" the presence of consciousness.
Therefore, he says nonbiological intelligences will claim to have
consciousness and "the full range of emotional and spiritual experiences
that humans claim to have"; he feels such claims will generally be accepted.
Genetics, nanotechnology and robotics (AI)
Kurzweil says revolutions in
genetics,
nanotechnology and
robotics will usher in the beginning of the Singularity.
Kurzweil feels with sufficient genetic technology it should be possible
to maintain the body indefinitely, reversing aging while curing
cancer,
heart disease and other illnesses.
Much of this will be possible thanks to nanotechnology, the second
revolution, which entails the molecule by molecule construction of tools
which themselves can "rebuild the physical world".
Finally, the revolution in robotics will really be the development of
strong AI, defined as machines which have human-level intelligence or
greater. This development will be the most important of the century, "comparable in importance to the development of biology itself".
Kurzweil concedes that every technology carries with it the risk of
misuse or abuse, from viruses and nanobots to out-of-control AI
machines. He believes the only countermeasure is to invest in defensive
technologies, for example by allowing new genetics and medical
treatments, monitoring for dangerous pathogens, and creating limited
moratoriums on certain technologies. As for artificial intelligence
Kurzweil feels the best defense is to increase the "values of liberty,
tolerance, and respect for knowledge and diversity" in society, because
"the nonbiological intelligence will be embedded in our society and will
reflect our values".
The Singularity

Countdown to the Singularity
Kurzweil touches on the history of the Singularity concept, tracing it back to
John von Neumann in the 1950s and
I. J. Good
in the 1960s. He compares his Singularity to that of a mathematical or
astrophysical singularity. While his ideas of a Singularity is not
actually infinite, he says it looks that way from any limited
perspective.
During the Singularity, Kurzweil predicts that "human life will be irreversibly transformed" and that humans will transcend the "limitations of our biological bodies and brain".
He looks beyond the Singularity to say that "the intelligence that will
emerge will continue to represent the human civilization." Further, he
feels that "future machines will be human, even if they are not
biological".
Kurzweil claims once nonbiological intelligence predominates the nature of human life will be radically altered: there will be radical changes in how humans learn, work, play, and wage war. Kurzweil envisions nanobots which allow people to eat whatever they
want while remaining thin and fit, provide copious energy, fight off
infections or cancer, replace organs and augment their brains.
Eventually people's bodies will contain so much augmentation they'll be
able to alter their "physical manifestation at will".
Kurzweil says the law of accelerating returns suggests that once a
civilization develops primitive mechanical technologies, it is only a
few centuries before they achieve everything outlined in the book, at
which point it will start expanding outward, saturating the universe
with intelligence. Since people have found no evidence of other
civilizations, Kurzweil believes humans are likely alone in the
universe. Thus Kurzweil concludes it is humanity's destiny to do the
saturating, enlisting all matter and energy in the process.
As for individual identities during these radical changes, Kurzweil
suggests people think of themselves as an evolving pattern rather than a
specific collection of molecules. Kurzweil says evolution moves towards
"greater complexity, greater elegance, greater knowledge, greater
intelligence, greater beauty, greater creativity, and greater levels of
subtle attributes such as love". He says that these attributes, in the limit, are generally used to
describe God. That means, he continues, that evolution is moving towards
a conception of God and that the transition away from biological roots
is in fact a spiritual undertaking.
Predictions
Kurzweil does not include an actual written timeline of the past and future, as he did in
The Age of Intelligent Machines and
The Age of Spiritual Machines,
however he still makes many specific predictions. Kurzweil writes that
by 2010 a supercomputer will have the computational capacity to emulate
human intelligence and "by around 2020" this same capacity will be available "for one thousand dollars".
After that milestone he expects human brain scanning to contribute to
an effective model of human intelligence "by the mid-2020s". These two elements will culminate in computers that can pass the
Turing test by 2029.
By the early 2030s the amount of non-biological computation will exceed
the "capacity of all living biological human intelligence".
Finally the exponential growth in computing capacity will lead to the
Singularity. Kurzweil spells out the date very clearly: "I set the date
for the Singularity—representing a profound and disruptive
transformation in human capability—as 2045".
Reception
Analysis
A
common criticism of the book relates to the "exponential growth
fallacy". As an example, in 1969, man landed on the moon. Extrapolating
exponential growth from there one would expect huge lunar bases and
manned missions to distant planets. Instead, exploration stalled or even
regressed after that.
Paul Davies writes "the key point about exponential growth is that it never lasts"
[43] often due to resource constraints.
Theodore Modis says "nothing in nature follows a pure exponential" and suggests the
logistic function
is a better fit for "a real growth process". The logistic function
looks like an exponential at first but then tapers off and flattens
completely. For example, world population and the United States's oil
production both appeared to be rising exponentially, but both have
leveled off because they were logistic. Kurzweil says "the knee in the
curve" is the time when the exponential trend is going to explode, while
Modis claims if the process is logistic when you hit the "knee" the
quantity you are measuring is only going to increase by a factor of 100
more.
[44]
While some critics complain that the law of accelerating returns is not a law of nature
[43]
others question the religious motivations or implications of Kurzweil's
Singularity. The buildup towards the Singularity is compared with
Judeo-Christian end-of-time scenarios. Beam calls it "a
Buck Rogers vision of the hypothetical Christian Rapture".
[45] John Gray says "the Singularity echoes apocalyptic myths in which history is about to be interrupted by a world-transforming event".
[46]
The radical nature of Kurzweil's predictions is often discussed.
Anthony Doerr
says that before you "dismiss it as techno-zeal" consider that "every
day the line between what is human and what is not quite human blurs a
bit more". He lists technology of the day, in 2006, like computers that
land
supersonic airplanes or
in vitro fertility treatments and asks whether
brain implants that access the internet or robots in our blood really are that unbelievable.
[47]
In regard to reverse engineering the brain, neuroscientist
David J. Linden
writes that "Kurzweil is conflating biological data collection with
biological insight". He feels that data collection might be growing
exponentially, but insight is increasing only linearly. For example, the
speed and cost of sequencing genomes is also improving exponentially,
but our understanding of genetics is growing very slowly. As for
nanobots Linden believes the spaces available in the brain for
navigation are simply too small. He acknowledges that someday we will
fully understand the brain, just not on Kurzweil's timetable.
[48]
Reviews
Paul Davies wrote in
Nature that
The Singularity is Near
is a "breathless romp across the outer reaches of technological
possibility" while warning that the "exhilarating speculation is great
fun to read, but needs to be taken with a huge dose of salt."
[43]
Anthony Doerr in
The Boston Globe
wrote "Kurzweil's book is surprisingly elaborate, smart, and
persuasive. He writes clean methodical sentences, includes humorous
dialogues with characters in the future and past, and uses graphs that
are almost always accessible."
[47] while his colleague
Alex Beam points out that "Singularitarians have been greeted with hooting skepticism"
[45] Janet Maslin in
The New York Times wrote "
The Singularity is Near
is startling in scope and bravado", but says "much of his thinking
tends to be pie in the sky". She observes that he's more focused on
optimistic outcomes rather than the risks.
[49]
Film adaptations
In 2006,
Barry Ptolemy and his production company Ptolemaic Productions licensed the rights to
The Singularity Is Near from Kurzweil. Inspired by the book, Ptolemy directed and produced the film
Transcendent Man, which went on to bring more attention to the book.
Kurzweil has also directed his own adaptation, called
The Singularity is Near, which mixes documentary with a science-fiction story involving his robotic avatar Ramona's transformation into an
artificial general intelligence. It was screened at the
World Film Festival, the
Woodstock Film Festival, the
Warsaw International FilmFest, the
San Antonio Film Festival in 2010 and the
San Francisco Indie Film Festival in 2011. The movie was released generally on July 20, 2012.
[50] It is available on DVD or digital download
[51] and a trailer is available.
[52]
The 2014 film
Lucy
is roughly based upon the predictions made by Kurzweil about what the
year 2045 will look like, including the immortality of man.
[53]
,













![{\displaystyle K_{\mathrm {a} }={\frac {[\mathrm {H^{+}} ][\mathrm {A^{-}} ]}{[\mathrm {HA} ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d45faa1d34eda090e28481c7a733292d0afface)