Buffer solution

From Wikipedia, the free encyclopedia

 

A buffer solution (more precisely, pH buffer or hydrogen ion buffer) is an aqueous solution consisting of a mixture of a weak acid and its conjugate base, or vice versa. Its pH changes very little when a small amount of strong acid or base is added to it. Buffer solutions are used as a means of keeping pH at a nearly constant value in a wide variety of chemical applications. In nature, there are many systems that use buffering for pH regulation. For example, the bicarbonate buffering system is used to regulate the pH of blood.

Principles of buffering

Simulated titration of an acidified solution of a weak acid (pK_a = 4.7) with alkali.

Addition of hydroxide to an equilibrium mixture of a weak acid. HA, and its conjugate base, A⁻

Buffer solutions achieve their resistance to pH change because of the presence of an equilibrium between the acid HA and its conjugate base A⁻.

HA ⇌ H⁺ + A⁻

When some strong acid is added to an equilibrium mixture of the weak acid and its conjugate base, the equilibrium is shifted to the left, in accordance with Le Châtelier's principle. Because of this, the hydrogen ion concentration increases by less than the amount expected for the quantity of strong acid added. Similarly, if strong alkali is added to the mixture the hydrogen ion concentration decreases by less than the amount expected for the quantity of alkali added. The effect is illustrated by the simulated titration of a weak acid with pK_a = 4.7. The relative concentration of undissociated acid is shown in blue and of its conjugate base in red. The pH changes relatively slowly in the buffer region, pH = pK_a ± 1, centered at pH = 4.7 where [HA] = [A⁻]. The hydrogen ion concentration decreases by less than the amount expected because most of the added hydroxide ion is consumed in the reaction

OH⁻ + HA → H₂O + A⁻

and only a little is consumed in the neutralization reaction which results in an increase in pH.

OH⁻ + H⁺ → H₂O

Once the acid is more than 95% deprotonated the pH rises rapidly because most of the added alkali is consumed in the neutralization reaction.

Buffer capacity

Buffer capacity, β, is a quantitative measure of the resistance of a buffer solution to pH change on addition of hydroxide ions. It can be defined as follows.

${\displaystyle \beta ={\frac {dn}{d(\mathrm {pH} )}}}$,

where dn is an infinitesimal amount of added base and d(p[H⁺]) is the resulting infinitesimal change in the cologarithm of the hydrogen ion concentration. With this definition the buffer capacity of a weak acid, with a dissociation constant K_a, can be expressed as:

${\displaystyle {\frac {dn}{d(\mathrm {pH} )}}=\ln {10}{\frac {C_{\mathrm {A} }K_{\mathrm {a} }[\mathrm {H^{+}} ]}{\left(K_{\mathrm {a} }+[\mathrm {H^{+}} ]\right)^{2}}}\approx 2.303{\frac {C_{\mathrm {A} }K_{\mathrm {a} }[\mathrm {H^{+}} ]}{\left(K_{\mathrm {a} }+[\mathrm {H^{+}} ]\right)^{2}}}}$

Buffer capacity for a 0.1 M solution of an acid with pK_a 

of 7

for pH close to the pK_a. C_A is the analytical concentration of the acid.^[1][2] pH is defined as −log₁₀[H⁺]. For simple buffers there are three regions of raised buffer capacity.

1. At very low pH the buffer capacity rises exponentially with decreasing pH.
2. The buffer capacity of a buffering agent is at a local maximum when pH = pK_a. It falls to about 33% of the maximum value at pH = pK_a ± 1 and to about 12% at pH = pK_a ± 1.5. For this reason the useful range is approximately pK_a ± 1. Buffer capacity is proportional to the concentration of the buffering agent, C_A, so dilute solutions have little buffer capacity.
3. At very high pH the buffer capacity rises exponentially with increasing pH.

Properties 1 and 3 are independent of the presence or absence of added buffering agents. They are concentration effects and reflect the fact that pH is related to the logarithm of the hydrogen ion concentration.

Applications

Buffer solutions are necessary to keep the correct pH for enzymes in many organisms to work. Many enzymes work only under very precise conditions; if the pH moves outside of a narrow range, the enzymes slow or stop working and can denature. In many cases denaturation can permanently disable their catalytic activity.^[3] A buffer of carbonic acid (H
₂ CO
₃) and bicarbonate (HCO⁻
₃) is present in blood plasma, maintaining a pH between 7.35 and 7.45.

Industrially, buffer solutions are used in fermentation processes and in setting the correct conditions for dyes used in colouring fabrics. They are also used in chemical analysis^[2] and calibration of pH meters.

The majority of biological samples that are used in research are made in buffers, especially phosphate buffered saline (PBS) at pH 7.4.

Simple buffering agents

Buffering agent	pKa	Useful pH range
Citric acid	3.13, 4.76, 6.40	2.1–7.4
Acetic acid	4.8	3.8–5.8
KH2PO4	7.2	6.2–8.2
CHES	9.3	8.3–10.3
Borate	9.24	8.25–10.25

For buffers in acid regions, the pH may be adjusted to a desired value by adding a strong acid such as hydrochloric acid to the buffering agent. For alkaline buffers, a strong base such as sodium hydroxide may be added. Alternatively, a buffer mixture can be made from a mixture of an acid and its conjugate base. For example, an acetate buffer can be made from a mixture of acetic acid and sodium acetate. Similarly an alkaline buffer can be made from a mixture of the base and its conjugate acid.

"Universal" buffer mixtures

By combining substances with pK_a values differing by only two or less and adjusting the pH, a wide range of buffers can be obtained. Citric acid is a useful component of a buffer mixture because it has three pK_a values, separated by less than two. The buffer range can be extended by adding other buffering agents. The following mixtures (McIlvaine's buffer solutions) have a buffer range of pH 3 to 8.^[4]

0.2 M Na2HPO4 (mL)	0.1 M citric acid (mL)	pH
20.55	79.45	3.0
38.55	61.45	4.0
51.50	48.50	5.0
63.15	36.85	6.0
82.35	17.65	7.0
97.25	2.75	8.0

A mixture containing citric acid, monopotassium phosphate, boric acid, and diethyl barbituric acid can be made to cover the pH range 2.6 to 12.^[5]

Other universal buffers are the Carmody buffer^[6] and the Britton–Robinson buffer, developed in 1931.

Common buffer compounds used in biology

Common name	Structure	pKa at 25 °C	Temp. effect dpH/dT (K−1)[7]	Mol. weight
TAPS		8.43	−0.018	243.3
Bicine		8.35	−0.018	163.2
Tris		8.07*	−0.028	121.14
Tricine		8.05	−0.021	179.2
TAPSO		7.635		259.3
HEPES		7.48	−0.014	238.3
TES		7.40	−0.020	229.20
MOPS		7.20	−0.015	209.3
PIPES		6.76	−0.008	302.4
Cacodylate		6.27		138.0
MES		6.15	−0.011	195.2

(*) Tris is a base, the pK_a of 8.07 refers to its conjugate acid.

Calculating buffer pH

Monoprotic acids

First write down the equilibrium expression.

HA ⇌ A⁻ + H⁺

This shows that when the acid dissociates equal amounts of hydrogen ion and anion are produced. The equilibrium concentrations of these three components can be calculated in an ICE table.

ICE table for a monoprotic acid

	[HA]	[A−]	[H+]
I	C0	0	y
C	−x	x	x
E	C0 − x	x	x + y

The first row, labelled I, lists the initial conditions: the concentration of acid is C₀, initially undissociated, so the concentrations of A⁻ and H⁺ would be zero; y is the initial concentration of added strong acid, such as hydrochloric acid. If strong alkali, such as sodium hydroxide, is added y will have a negative sign because alkali removes hydrogen ions from the solution. The second row, labelled C for change, specifies the changes that occur when the acid dissociates. The acid concentration decreases by an amount −x and the concentrations of A⁻ and H⁺ both increase by an amount +x. This follows from the equilibrium expression. The third row, labelled E for equilibrium concentrations, adds together the first two rows and shows the concentrations at equilibrium.

To find x, use the formula for the equilibrium constant in terms of concentrations:

${\displaystyle K_{\mathrm {a} }={\frac {[\mathrm {H^{+}} ][\mathrm {A^{-}} ]}{[\mathrm {HA} ]}}}$

Substitute the concentrations with the values found in the last row of the ICE table:

${\displaystyle K_{\mathrm {a} }={\frac {x(x+y)}{C_{0}-x}}}$

Simplify to:

${\displaystyle x^{2}+(K_{\mathrm {a} }+y)x-K_{\mathrm {a} }C_{0}=0}$

With specific values for C₀, K_a and y this equation can be solved for x. Assuming that pH = −log₁₀[H⁺] the pH can be calculated as pH = −log₁₀(x + y).

Polyprotic acids

% species formation calculated for a 10 millimolar solution of citric acid.

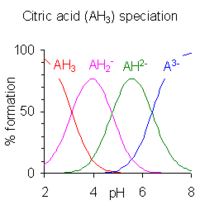
Polyprotic acids are acids that can lose more than one proton. The constant for dissociation of the first proton may be denoted as K_a1 and the constants for dissociation of successive protons as K_a2, etc. Citric acid, H₃A, is an example of a polyprotic acid as it can lose three protons.

Equilibrium	pKa value
H3A ⇌ H2A− + H+	pKa1 = 3.13
H2A− ⇌ HA2− + H+	pKa2 = 4.76
HA2− ⇌ A3− + H+	pKa3 = 6.40

When the difference between successive pK_a values is less than about three there is overlap between the pH range of existence of the species in equilibrium. The smaller the difference, the more the overlap. In the case of citric acid, the overlap is extensive and solutions of citric acid are buffered over the whole range of pH 2.5 to 7.5.

Calculation of the pH with a polyprotic acid requires a speciation calculation to be performed. In the case of citric acid, this entails the solution of the two equations of mass balance

${\displaystyle {\begin{aligned}C_{{\ce {A}}}&=[{\ce {A^3-}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3}\\C_{{\ce {H}}}&=[{\ce {H+}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+2\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+3\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3}-K_{{\ce {w}}}[{\ce {H+}}]^{-1}\end{aligned}}}$

C_A is the analytical concentration of the acid, C_H is the analytical concentration of added hydrogen ions, β_q are the cumulative association constants

${\displaystyle \log \beta _{1}={\ce {p}}K_{{\ce {a3}}},\quad \log \beta _{2}={\ce {p}}K_{{\ce {a2}}}+{\ce {p}}K_{{\ce {a3}}},\quad \log \beta _{3}={\ce {p}}K_{{\ce {a1}}}+{\ce {p}}K_{{\ce {a2}}}+{\ce {p}}K_{{\ce {a3}}}}$

K_w is the constant for self-ionization of water. There are two non-linear simultaneous equations in two unknown quantities [A³⁻] and [H⁺]. Many computer programs are available to do this calculation. The speciation diagram for citric acid was produced with the program HySS.^[8]